Prediction and measurement of an autoregulatory genetic module

Abstract

The deduction of phenotypic cellular responses from the structure and behavior of complex gene regulatory networks is one of the defining challenges of systems biology. This goal will require a quantitative understanding of the modular components that constitute such networks. We pursued an integrated approach, combining theory and experiment, to analyze and describe the dynamics of an isolated genetic module, an in vivo autoregulatory gene network. As predicted by the model, temperature-induced protein destabilization led to the existence of two expression states, thus elucidating the trademark bistability of the positive feedback-network architecture. After sweeping the temperature, observed population distributions and coefficients of variation were in quantitative agreement with those predicted by a stochastic version of the model. Because model fluctuations originated from small molecule-number effects, the experimental validation underscores the importance of internal noise in gene expression. This work demonstrates that isolated gene networks, coupled with proper quantitative descriptions, can elucidate key properties of functional genetic modules. Such an approach could lead to the modular dissection of naturally occurring gene regulatory networks, the deduction of cellular processes such as differentiation, and the development of engineered cellular control.

Most cellular functions result from various interactions among genes, RNAs, proteins, and metabolites. These interactions are controlled by complex regulatory networks, and it has been proposed that these systems can be dissected into smaller functional modules (1, 2). Importantly, such modules can be carefully extracted from natural networks and studied from both theoretical and experimental perspectives as isolated subsystems. The ultimate goal of such an approach would be to couple well characterized modules together, thereby increasing network complexity, to better understand cellular behavior. Specific network building blocks, or motifs (3, 4), have been identified in many biological systems, and detailed studies of these networks may establish a framework for logical cellular control.

Feedback loops, present in many cellular networks, use their output as a regulatory input to perform a number of functions. These functions can include the regulation of output to a required precision (5), the rapid switching between two or more outputs (6), and even the suppression or amplification of noise (7, 8). With regard to biological networks, feedback plays a central role in diverse processes from pattern formation to development, and it is commonly found in the network diagrams that describe the coordination of the precise behavior of cells (9). Theoretical models of protein–DNA feedback loops and gene regulatory networks have long been proposed (7, 10, 11), and certain qualitative features of such models have been experimentally corroborated recently (8, 12–15). However, to make further progress toward understanding how sets of modules interact in large-scale networks (16, 17), one needs to quantitatively characterize the functionality of individual modules.

Here we studied an in vivo autoregulatory genetic module that was motivated by our theoretical studies (18, 19) predicting the trademark bistability of the positive feedback-network architecture (18, 20–23). To quantitatively understand the key properties of the positive feedback module, we chose to isolate an autoregulatory network (Fig. 1A) from the genetic switch of bacteriophage λ (5, 24, 25). This network was chosen for two important reasons. First, because activation is a common mode of gene regulation (26), positive feedback plays a significant role in the pathways that govern the behavior of many organisms (3, 4). Second, because we seek to quantitatively describe the module, it is of utmost importance that the biochemical parameters describing relative protein production, protein dimer formation, dimer–operator site binding affinity, and protein cooperativity are known (5, 25, 27–29). Thus, our approach, which incorporates these biochemical parameters, provides a system-specific quantitative model tailored for detailed comparison with experimental observation.

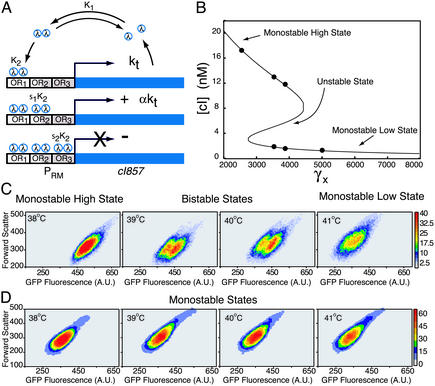
Fig. 1.

Autoregulatory network, theoretical predictions, and GFP-expression results. (A) The promoter region contains three operator sites, known as OR1–OR3. The cI857 gene expresses λ repressor (λ), which in turn dimerizes and binds to one of the three binding sites, OR1, OR2 [10-fold activation (29)], or OR3 (repression). (B) The nonlinearity of the governing model equation (see Modeling the Autoregulatory Module) leads to a bistable regime of the steady-state repressor concentration [cI] at specific model destabilization rates (γ_x). (C and D) Contour plots obtained from flow cytometry depict fluorescence in log-binned arbitrary units (A.U.) at varying temperatures. (C) Bistability is detected at 39 and 40°C in cultures of the autoregulatory network (pT2002b) containing the temperature-sensitive repressor (cI857). Bistability can be distinguished in the illustrated contour plots, whereas in GFP fluorescence distributions of the whole population we observed blurring between the high and low states. (D) Cultures containing the autoregulatory system (pT202b) with the wild-type cI gene maintain an activated monostable state.

Methods

Plasmid Construction, Cell Strains, and Reagents. Standard molecular biology techniques were implemented to construct network plasmids (30). All plasmids contained the ColE1 origin of replication and the bla gene as the selective marker rendering ampicillin resistance. The autoregulatory system was constructed on a high copy number [50–70 copies per cell (31)] Escherichia coli plasmid (pT2002b) (Fig. 5, which is published as supporting information on the PNAS web site, www.pnas.org). Oligonucleotide primers were purchased from Operon Technologies (Alameda, CA) and Integrated DNA Technologies (Coralville, IA). All genes and promoters were PCR-amplified by using the PTC-100 PCR machine (MJ Research, Cambridge, MA) with PfuTurbo DNA polymerase (Stratagene). DNA sequences were obtained as follows: the cI857 gene and the right operator (OR) of the λ phage were obtained from pGW7 (ATCC no. 40166), the cI gene was obtained from pCS19 (ATCC no. 77409), the gfpmut3 gene (32) was obtained from pTAK117 (13), and gfp(asv) was obtained from pJBA113 (33).

All plasmids were constructed by using restriction endonucleases and T4 DNA ligase from New England Biolabs. Plasmids were introduced into E. coli by using standard heat shock, transformation and storage solution, transformation protocols (30). The E. coli 2.300 strain (E. coli Genetic Stock Center no. 5002, λ-, lacI22, rpsL135, and thi-1) was used for all experiments. All cells were grown in the selective medium: LB (Difco) and 100 μg/ml ampicillin (Sigma). Plasmid isolation was performed by using Eppendorf's miniprep kit. Subcloning was confirmed by restriction analysis. Plasmid modifications were verified by sequencing with the PE Biosystems ABI Prism 377 sequencer.

Gene-Expression Experiments. Experiments involved growth of E. coli in the temperature range of 36–43°C ± 0.5°C. Growth curves of the E. coli strain were performed over the range of temperatures used to normalize growth rate across samples at different temperatures. The expression state of the cells was determined during logarithmic growth at an OD₆₀₀ of 0.1–0.3. A negative control, pTOR2G (plasmid lacking the activating cI857 gene), was constructed such that the P_RM promoter drives the expression of gfpmut3. Low expression levels from cells containing pTOR2G were used to determine the basal rate of expression from P_RM. An additional control plasmid, pT202b, was constructed where transcription from the P_RM promoter drives the expression of the wild-type cI gene and gfpmut3. pT202b consists of the same positive feedback network as pT2002b with the exception of the wild-type cI gene subcloned in place of the mutant cI857 gene. GFP expression from cells containing pT202b were in an activated monostable state throughout the entire temperature range (36–43°C) and not subject to temperature-induced protein destabilization (Fig. 1D). At low temperature, expression levels from pT202b were 3-fold lower than expression from cells containing pT2002b (6- to 7-fold above that of cells containing pTOR2G), and pT202b maintained the activated level of expression throughout the temperature sweep. Differences in the level of expression between the wild-type cI and mutant cI857 genes warrant further exploration. A positive control (pMTRCG) consisting of the P_trc constitutive promoter driving the expression of the gfpmut3 gene was used to monitor the expression state of a strong constitutive promoter.

GFP Quantification by Using the Flow Cytometer. All expression data were collected by using a Becton Dickinson FACSCalibur flow cytometer with a 488-nm argon laser and a 515- to 545-nm emission filter (FL1) at a low flow rate. Before analysis, cells were pelleted and resuspended in filtered PBS (pH 7.2; Life Technologies, Grand Island, NY) immediately after each time point. Calibrite beads (Becton Dickinson) were used to calibrate the flow cytometer. InSpeck green fluorescent beads (Molecular Probes) were used to determine fluorescence sensitivity and size measurements. Each fluorescent measurement of gene expression was obtained from three independent cultures exposed to identical conditions. Two measurements were made for each culture: 500,000 unfiltered cells and 50,000 cells filtered in a narrow band of forward- and side-scattering space. The introduction of a scattering filter normalizes the cellular size and morphology variability, thereby providing a better basis of comparison with simulations (34). Flow-cytometry standard data files were converted to ASCII format by using MFI software (E. Martz, University of Massachusetts, Amherst) and analyzed with software written in FORTRAN and MATLAB (Mathworks, Natick, MA).

Results and Discussion

Experimental Characterization of the Autoregulatory Module. The autoregulatory network was extracted from the OR of phage λ, which controls its own viral life cycle by coordinately regulating the expression of the cI and cro genes transcribed by the promoters P_RM and P_R, respectively. Isolation of OR and the cI gene provides the autoregulatory network (Fig. 1 A). The OR was positioned upstream of the cI857 gene, which codes for the temperature-sensitive λ repressor protein such that the P_RM promoter regulates its expression. The gfpmut3 (32) gene was positioned as the second cistron downstream of the P_RM promoter, ensuring that transcription from P_RM results in the expression of λ repressor (cI857 gene) and GFP (gfpmut3 gene). By varying temperature (35), one can tune the stability of the λ repressor protein and thus vary the degree of activation to examine the expression dynamics of the positive feedback loop. Cultures of E. coli cells containing the autoregulatory pT2002b plasmids (Fig. 5) were initially grown at low temperatures (30–36°C) to confirm a high monostable steady state (data not shown). To probe for conditions of bistability, three identical cell cultures were grown independently at 36°C, and the temperature was gradually increased in 1°C increments to 43°C. Cultures were maintained in logarithmic growth for five to six cell divisions to reach steady state at each temperature condition.

Flow-cytometric measurements of GFP expression from single cells containing pT2002b are shown in Figs. 1C and 2A. From 36 to 38°C, there was a single population of cells in a high monostable state. Then, as the temperature was increased to 39°C (temperature-sensitive λ repressor undergoes increased destabilization, see Fig. 3B), the high monostable state split into two coexisting stable populations and remained in two states through 40°C. Finally, as the temperature was increased >40°C, the high state vanished, leaving only a single low state. Figs. 1C and 2 A depict typical unimodal and bimodal populations throughout the temperature sweep in contour plots and fluorescence histograms, respectively. Cells possessing an additional plasmid, pT2002bsv [containing gfp(asv), which reduces the half-life of gfpmut3 (33)] and grown under the same conditions displayed similar qualitative features (Fig. 6, which is published as supporting information on the PNAS web site). Cultures containing a control plasmid (pT202b), which consists of the same positive feedback network as pT2002b with the wild-type cI gene subcloned in place of the cI857 gene, demonstrate an activated high monostable state throughout the entire temperature range (Fig. 1D), indicating that protein destabilization in the pT2002b network is responsible for the observed bimodality.

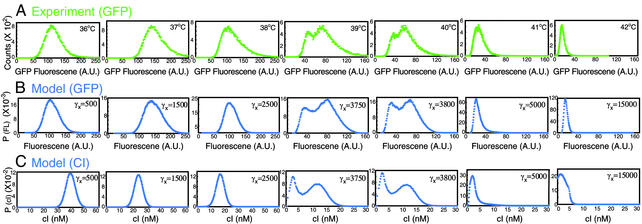
Fig. 2.

Comparison of model and experiment over entire temperature and γ_x ranges. (A) GFP-expression histograms (green) expressed as linear values [in arbititrary units (A.U.)] from autoregulatory network cultures were filtered across narrow forward and side scatter to normalize for cell size and morphology and thus permit direct comparison to model. The simulations for GFP (B) and repressor (CI) (C) at increasing γ_x values are shown in blue.

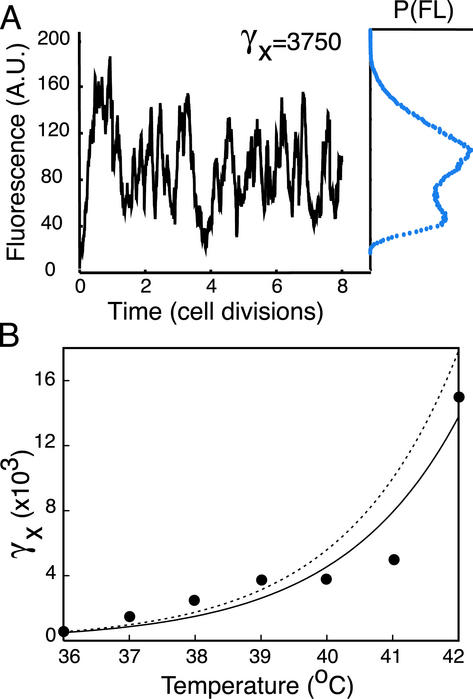
Fig. 3.

(A) Model results for the time evolution of the fluorescence at an intermediate protein-destabilization value (γ_x = 3,750). The corresponding probability distribution is depicted at the end of the time series. A.U., arbititrary units. (B) Relationship between γ_x (model) and temperature (experiment). The best-fit exponential curve (solid line) for the data [γ_xαe^{0.55(T - 32)}]is in close agreement with an exponential fit (broken line) obtained in a previous study (35) [γ_xαe^{0.58(T - 32)}] (see Table 1 for parameter list).

Modeling the Autoregulatory Module. Experiments were designed to quantitatively describe simulation results from a previously reported deterministic model of an autoregulatory single-gene network (19). The model is derived from a straightforward application of the chemical kinetics describing the processes depicted in Fig. 1 A. In Supporting Text, which is published as supporting information on the PNAS web site, we provide a detailed description of the derivation of the governing equations. The result is the following set of equations governing the temporal evolution of the number of cI (x) and GFP (g) monomers,

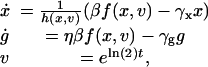where the cell volume v and the time t are scaled by the volume of an E. coli cell and the cell-division time, respectively; i.e., just after cell division the volume is 1 and the time is 0, and we let the volume increase exponentially to 2 at t = 1. At division, the volume halves, and we let x → x/2 and g → g/2. Likewise, the destabilization rates γ_x and γ_g of cI and GFP are scaled by the cell-division time, and β and η represent the basal production rate of cI and relative efficiency of GFP production, respectively. The “synthesis function” f(x, v) represents the net effect of transcription and translation, whereas h(x, v) arises from the vast separation of time scales set by the transcription and protein-dimerization rates (36). A detailed analysis leads to their functional form (see Supporting Text),

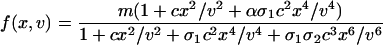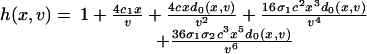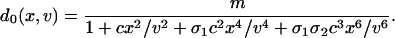The form of the synthesis term f(x,v) dictates the equilibrium number of repressor monomers, and its functional dependence on x along with the coefficients can be understood as follows. The even polynomials in x occur due to dimerization and subsequent binding to the promoter region. As depicted in Fig. 1 A, the σ_i prefactors denote the relative affinities for dimer binding to OR1 versus that of binding to OR2 (σ₁) and OR3 (σ₂). The prefactor α > 1onthe x⁴ term is present because transcription is enhanced when the two operator sites OR1 and OR2 are occupied (x²x²). The x⁶ term represents the occupation of all three operator sites and arises in the denominator, because dimer occupation of OR3 inhibits polymerase binding and shuts off transcription.

Importantly, because our focus is on an autoregulatory system derived from λ phage, most of the parameters are known, enabling the derivation of a quantitative model. For the operator region of λ phage (5, 24, 27–29), we have σ₁ ≈ 2, σ₂ ≈ 0.08, α ≈ 11, c₁ ≈ 0.05, and c₂ ≈ 0.33 so that the destabilization rate γ_x and plasmid copy number m determine the steady-state number of repressor molecules. Finally, to compare model results with experiment directly, we needed to convert the GFP molecule number g to a corresponding fluorescence value F. It is known that GFP fluorescence is temperature-dependent (37); therefore we assumed a destabilization-dependent proportionality between the number of GFP molecules and the corresponding fluorescence, letting F = c(γ_x)(g + b₀), where b₀ is a fixed constant and c(γ_x) is chosen for each destabilization (i.e., γ_x) value (Fig. 7, which is published as supporting information on the PNAS web site). We refer the reader to the Supporting Text for a complete tabulation of the parameters used in the simulations (Table 1, which is published as supporting information on the PNAS web site).

Because the experimental results revealed significant fluctuations (see Figs. 1C and 2 A), we generalized the formulation to include stochastic terms. Provided the dynamics of the deterministic system reduces to equations as shown above, the fluctuations arising from small molecule-number effects can be incorporated into the deterministic picture (36, 38). The result is the following Langevin equations,

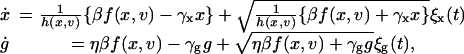where the ξ_i(t) are rapidly fluctuating random terms with zero mean (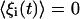), and the statistics of the ξ_i(t) are such that 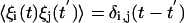. It is important to note that the noise arises from the small number of reactant molecules, and in this regard there is no external “noise parameter” tuned to a particular value. This type of noise is always present in chemical reactions but is typically ignored in other contexts when the number of molecules is large.

In this model (19), transcriptional activation and protein multimerization yield nonlinearities in the governing equations, and for sufficient activation and λ repressor protein destabilization these nonlinearities lead to a multistable regime in the steady-state protein concentration. In Fig. 1B we plot the theoretical steady state of λ repressor protein concentration as a function of the destabilization parameter γ_x (correlated to temperature). At low temperature (low destabilization rate), the system is predicted to be in a monostable state characterized by a high λ repressor protein concentration. As the temperature is increased, the system undergoes a transition, and three possible steady-state concentrations emerge. Then, at high temperature (high destabilization rate), the concentration returns to a monostable state, which is now characterized by a low protein concentration. Within the region of multistability (intermediate destabilization rates), the top and bottom branches are stable, so that concentrations near these values will remain nearby despite fluctuations. The middle branch, on the other hand, is unstable so that tiny fluctuations will drive the protein concentration toward one of the stable states. Hence, within the multistable region, the system is predicted to have two experimentally accessible states and thus is bistable.

Comparison of Experiment and Model. The experimental data (Figs. 1C and 2 A) agree quite favorably with the simulation results (Fig. 2 B and C). Following the histograms from left to right (Fig. 2) corresponds to an increase in the destabilization rate for the model and temperature-induced destabilization of λ repressor in the experiment (Fig. 1B shows the corresponding values of the mean concentration on the theoretical bifurcation curve). In the monostable regimes, both the experimental and theoretical populations demonstrate a positive skewness manifest in distributions with a steep rise and a long tail. The bistable regime appears as overlapping distributions, indicating that relatively rapid transitions are occurring between the two states. This is predicted by the model: The temporal evolution of a single cell elicits transitions between states on time scales less than the cell-division time (Fig. 3A). In generating the model results of Fig. 2, the destabilization rate, γ_x, was adjusted to give good agreement between the theoretical and experimental distributions over the entire temperature regime. Using the obtained model parameters for λ repressor destabilization, we plotted γ_x as a function of temperature (Fig. 3B). The resulting best-fit exponential rise is in excellent agreement with previously reported results (35) characterizing the graded enzymatic activity of the temperature-sensitive λ repressor protein.

Theoretical and experimental results for mean GFP values from the distributions in Fig. 2 are plotted in Fig. 4 (see Fig. 6 for pT2002bsv results). Both experiment and theory show an initial increase in the mean GFP concentration, which can be understood with the aid of the model as follows. In the steady state, the proportionality between the concentrations of GFP and repressor is given by [GFP] = (γ_x/γ_g)[cI] (see Supporting Text), and because the destabilization rate γ_x is an increasing function of temperature, there is an initial rise in GFP relative to repressor. In addition, the initial rise in GFP between 36 and 37°C might be due to a loss of λ repressor protein repression at OR3. The initial rise is followed by the bistable regime. This regime is characterized by a steep upper branch and a relatively flat lower branch. Finally, for large destabilization rates, both model and experiment are again monostable, characteristic of a low basal rate (unactivated) of protein production. In an attempt to demonstrate hysteresis in the mean GFP expression, the experiment was repeated in the reverse direction from 43 to 36°C. We observed the same bimodal populations regardless of the direction of the temperature sweep, and thus no hysteresis in gene expression was apparent. The absence of hysteresis suggests that noise-induced transitions between states may occur on time scales less than the incubation time for each temperature (five to six cell divisions). Importantly, hysteresis was a prediction generated from the deterministic model (18), and our failure to observe hysteresis can be viewed as a rejection of this model, which led to its refinement. The observed expression dynamics and large fluctuations were captured only when noise terms were incorporated into the deterministic model.

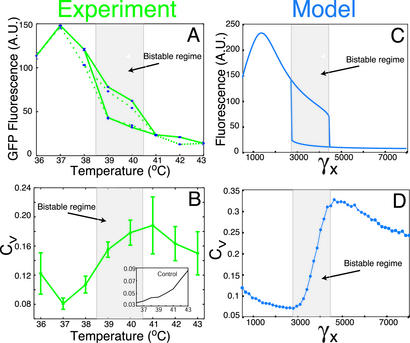
Fig. 4.

Quantitative comparisons of experiment (A and B) and model (C and D). (A) Mean GFP expression versus temperature of three independent cultures of population distributions from Fig. 2 A. Cultures were initially grown at either a high (36°C, solid green line) or low (43°C, dotted green line) state and swept through a bistable regime to the alternate stable state. (B) The coefficient of variation (C_V) as a function of temperature for three typical independent cultures is in agreement with the C_V calculations obtained from the model (D). (Inset) C_V for a strong constitutive promoter [positive control (see Methods)] is consistently low and distinct from the bistable autoregulatory network.

Along these lines, our results underscore the importance of noise (34, 36, 38–41) in gene regulation and support the premise (39) that differing cellular states can be accessed by way of noise-induced transitions. In this regard, state transitions were only observed once the system was destabilized by tuning to a temperature corresponding to the bistable regime of the autoregulatory module. This bistable regime is distinct from the bistable regime that exists in phage λ, where in addition to the autoregulatory module there is a second gene (cro) that represses cI. In natural lysogenic studies, if wild-type cI was replaced with cI857, then transitions are likely to occur more frequently at high temperatures (38, 42). Furthermore, studies of genetic modules at differing plasmid copy numbers, including single-copy systems, will be critical in assessing the stability and switching dynamics of low copy-number genomic networks.

To compare the distributions of Fig. 2 quantitatively, we explored the coefficient of variation (C_V) to assess the relative dispersion defined as the variance normalized by the square of the mean. The experimental results presented in Fig. 4B depict an S-shaped curve: We observed an initially low and slowly decreasing C_V followed by a transition zone marking the bistable regime and increasing C_V and finally a relatively high and slowly decreasing C_V denoting the low state of the system. The simulation results presented in Fig. 4D compare quite well with the experiment. Initially, with the system in a high stable state the C_V is low and slowly decreasing. Because in the simulations the source of the fluctuations is small molecule numbers, the relatively low C_V results from the relatively large number of molecules in the high state. After entering the region of bistability, the C_V begins to transition to a higher value. The transition zone is a signature of the bistable regime, because the relatively low C_V marks the high state, and a high C_V is characteristic of the low state, so that the C_V in the transition zone correlates with a weighted average over the two states. Once the system enters the low stable state, the C_V reaches a high value and begins to slowly decrease. Taken together, the experiments and simulations suggest that a significant source of noise in gene expression is due to fluctuations in the absolute number of molecules caused by random variation in the timing of individual biochemical reaction events (34, 36, 39, 40).

These results demonstrate that the incorporation of fluctuations in the model is required to capture the essence of the autoregulatory module. More specifically, our theoretical and experimental results show that with lower strengths of activation, the positive feedback module can switch between states spontaneously. Such variability in gene expression has phenotypic consequences that may affect cellular processes such as differentiation and may lead to disease (9, 43). For instance, the transformed phenotype identified in some cases of tumor formation can be attributed to the instability of autocrine positive feedback loops (44). In contrast, our model shows that with higher activation a positive feedback loop is resistant to noise-induced transitions and maintains discrete stable states with inherited patterns of gene expression. Such differences in phenotype are not subtle and thus require quantitative descriptions, particularly in light of the important role that positive feedback loops play in complex signaling outcomes (9).

This study highlights the importance of assessing the stability of states and its potential implications on the resulting phenotype. We have integrated model predictions and experiments to provide insight into biomolecular processes that affect the stability of gene-expression states. Although model simulations predict (Fig. 3A) relatively rapid switching between high and low states, direct experimental verification is necessary. A complementary microscopic study might permit temporal measurement of transitions occurring on time scales less than the cell-division time and enable direct model–experiment comparison at the single-cell level, whereas flow cytometry (used in this study) provides single-cell statistics across a population of cells. Additionally, it is important to note that maturation time and turnover rate of the GFP protein may pose additional temporal constraints of experimentally determining rapid switching times. Advances in new fluorescent proteins and imaging systems (45) might enable direct experimental measurement of switching rates and nicely complement existing computational and experimental techniques that investigate complex cellular processes.

In this study we demonstrated how an integrated approach, which combines an isolated autoregulatory gene network and a quantitative model, can be used to elucidate key properties of a common functional module. A combined theoretical and experimental approach of this sort can be a valuable tool in resolving the complexity of large-scale gene regulatory networks. The top-down approaches, which are used by many investigators to analyze the expression states of thousands of genes, have contributed toward understanding the global patterns of gene expression and assessing gene lethality. Our bottom-up approach, which reduces the complexity of these gene networks to their essential components, will lead to the modular dissection of network architectures (1, 2) and refined descriptions of gene-expression dynamics. The combination of these two complementary approaches will eventually lead to the elucidation of the organization and functioning of gene regulatory networks.