Abstract
Regulation of gene expression involves formation of specific protein–DNA complexes in which the DNA is often bent or sharply kinked. Kinetics measurements of DNA bending when in complex with the protein are essential for understanding the molecular mechanism that leads to precise recognition of specific DNA-binding sites. Previous kinetics measurements on several DNA-bending proteins used stopped-flow techniques that have limited time resolution of few milliseconds. Here we use a nanosecond laser temperature-jump apparatus to probe, with submillisecond time resolution, the kinetics of bending/unbending of a DNA substrate bound to integration host factor (IHF), an architectural protein from Escherichia coli. The kinetics are monitored with time-resolved FRET, with the DNA substrates end-labeled with a FRET pair. The temperature-jump measurements, in combination with stopped-flow measurements, demonstrate that the binding of IHF to its cognate DNA site involves an intermediate state with straight or, possibly, partially bent DNA. The DNA bending rates range from ≈2 ms−1 at ≈37°C to ≈40 ms−1 at ≈10°C and correspond to an activation energy of ≈14 ± 3 kcal/mol. These rates and activation energy are similar to those of a single A:T base pair opening inside duplex DNA. Thus, our results suggest that spontaneous thermal disruption in base-paring, nucleated at an A:T site, may be sufficient to overcome the free energy barrier needed to partially bend/kink DNA before forming a tight complex with IHF.
Keywords: DNA bending kinetics, laser temperature jump, protein–DNA interactions, time-resolved FRET measurements
Regulation of gene transcription in both prokaryotes and eukaryotes involves formation of specific protein–DNA complexes of higher order, by bringing distant regions of DNA together. Such structures frequently require specific proteins that can kink, bend, or curve DNA. Sharply bent DNA is also critical for the packaging of DNA inside the cell. In many protein–DNA complexes, the protein also undergoes extensive conformational rearrangements that facilitate favorable interactions with DNA. These concerted changes in proteins and DNA are believed to be a key feature underlying the induced-fit mechanism proposed for the recognition of specific binding sites on DNA by proteins. An understanding of the forces that are responsible for the sharp bending of DNA and protein rearrangements to form specific complexes are thus of considerable biological significance. The details of the recognition mechanism remain elusive. In particular, very little is known about the dynamics of the conformational rearrangements that lead to the precise recognition.
A wealth of crystallographic studies that provide three-dimensional structures of the protein with and without the DNA substrate have offered much insight into the conformational differences among specific and nonspecific protein–DNA complexes and free protein (1, 2). A dramatic distortion of the canonical double-helix structure is observed in several DNA–protein complexes that bend DNA, sometimes by nearly 160° over a few helical turns (3–8). The energetic costs of DNA bending on such short lengths is compensated by very specific interactions between protein and DNA that lower the free energy of the complex.
One fundamental question underlying the binding mechanism is whether the protein binds to DNA and then distorts it or whether the DNA is capable of undergoing spontaneous fluctuations in which the distorted conformations are energetically accessible, and the protein binds with high affinity to these distorted conformations (9). Sharply bent or kinked DNA conformations that are thermally accessible could be playing an important role in the binding of proteins to DNA (10, 11). Another fundamental question is whether the rates of DNA bending play a role in the exquisite specificity shown by DNA-bending proteins. For example, slower rates of DNA bending or unbending at noncognate sites may be a contributing factor to the specificity of binding (12). Answers to these questions will come from careful kinetics measurements of DNA bending dynamics with and without the bound protein.
The kinetics of protein–DNA interactions for several systems, in which the DNA is bent in the complex, has been investigated with stopped-flow techniques to address the question of whether DNA binding and bending is sequential or concerted (12–15). The salient result from these published measurements is that the relaxation kinetics measured by spectroscopic probes that monitor DNA bending (e.g., fluorescent donor and acceptor pair attached at either end of a short DNA oligomer, to monitor the end-to-end distance) are indistinguishable from the relaxation kinetics measured by spectroscopic probes that monitor the bimolecular association step (e.g., fluorescent anisotropy decay of single-labeled DNA oligomers). These measurements are not inconsistent with the possibility that DNA bending is in fact simultaneous with the binding step, with only one transition state. However, an alternative explanation is that DNA bending occurs at a much faster rate than DNA binding and is not resolved in stopped-flow measurements. The time resolution of previous stopped-flow measurements would suggest a bending rate in excess of 100 s−1, thus requiring the development of fast techniques.
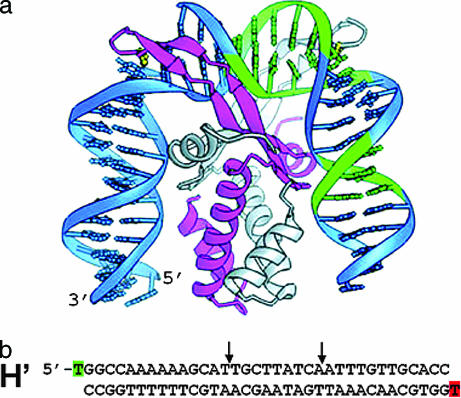
In this study, we focus on the DNA bending dynamics of a short (≈35 bp) DNA substrate that contains one of the cognate sites (H′ site from base pairs 15–49 of phage λDNA) and that binds specifically to Escherichia coli integration host factor (IHF). IHF is a multipurpose architectural protein, which plays an essential role in several cellular processes including site-specific recombination, transcription, DNA replication, and λ phage packaging (16–19). The crystal structure of IHF bound to the H′ site indicates that the DNA is kinked at two sites separated by ≈9 bp and that the overall bend in the DNA is ≈160° (Fig. 1) (7). Thus, the end-to-end distance of the 35-bp DNA duplex is shortened from ≈100 Å to ≈50 Å upon IHF binding. Equilibrium FRET measurements in solution demonstrate that the end-to-end distance of H′ in complex with IHF is in agreement with the crystal structure (20, 21). Thus, the H′ substrate labeled with fluorescent dyes is sensitive to the distance change and is suitable for direct measurement of DNA bending in solution by time-resolved FRET measurements.
Fig. 1.
Structure of IHF bound to the H′ site from bacteriophage λDNA. (a) Figure reproduced with permission from Swinger et al. (49) (Copyright 2003, Nature Publishing Group). (b) The H′ binding site used in this study, with fluorescein and TAMRA attached to the thymine at the 5′ end of the top strand and bottom strand, respectively. The positions of the kinks in the crystal structure are indicated by the two arrows. The crystal structure was obtained with a nicked H′ substrate, with a nick in the sugar phosphate backbone located one position to the right of the left arrow (7).
A motivation for investigating the bending dynamics of H′ bound to IHF comes from the results of Sugimura and Crothers (22), who show in the accompanying article that the observed relaxation rate for IHF binding to H′, obtained by using stopped-flow with time-resolved FRET, saturates at high concentrations of IHF. These results suggest that the binding of IHF to H′ and the bending of the H′ substrate occur sequentially, and that at high IHF concentrations the bending of DNA becomes the rate-limiting step.
Here, we report direct measurements of the bending/unbending kinetics of H′ bound to IHF, on submillisecond time scales, using a nanosecond laser temperature-jump (T-jump) to perturb the complex, and time-resolved FRET to monitor the kinetics. In the last decade, laser T-jump has emerged as a powerful tool whereby conformational changes in biomolecules can be monitored on time scales of submicroseconds-to-milliseconds (23–29). The T-jump measurements, in combination with stopped-flow measurements, demonstrate that the binding of IHF to its cognate DNA site involves an intermediate state with straight or, possibly, partially bent DNA (Fig. 2). Our results and analysis show that the time scales for DNA bending, when in complex with the protein, are consistent with spontaneous thermal fluctuations in base-pairing that can sharply bend/kink DNA.
Fig. 2.
Kinetic scheme for binding of proteins to DNA oligomers, with a bimolecular association step and a unimolecular DNA bending step.
Results
We have combined two experimental techniques to probe the kinetics of DNA bending when the H′ substrate binds to IHF: (i) conventional stopped-flow (time window ≈3 ms to a few seconds) and (ii) laser T-jump techniques (time window ≈200 ns to 20 ms). The termini of the 35-bp duplex DNA comprised of the H′ site were labeled with fluorescein and TAMRA at the 5′ ends of both strands in the duplex (Fig. 1b), to monitor changes in the end-to-end distance. The buffer conditions in all measurements were 20 mM Tris·HCl (pH 8.0), 100 mM KCl, and 1 mM EDTA.
Equilibrium FRET Measurements on H′ Binding to IHF.
To examine the thermal dissociation of the complex, and to determine the temperatures at which to carry out laser T-jump studies, equilibrium FRET measurements were carried out as a function of temperature. Previous equilibrium measurements have shown that the dissociation constant KD for the IHF–H′ complex is <10 nM under ionic and buffer conditions similar to our conditions (20, 21, 30, 31). Thus, at concentrations at which the T-jump measurements are carried out, at [IHF] ≈ 5 μM and [H′] ≈ 5 μM, we have 100% complex at 20°C.
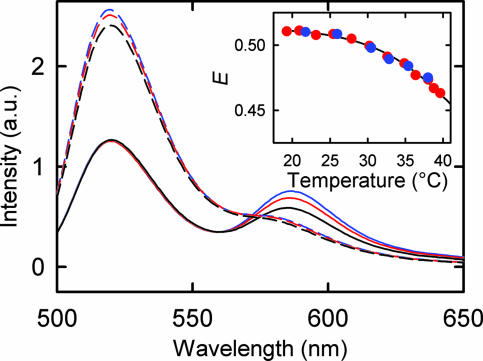
A representative set of fluorescence emission spectra of double-labeled (donor and acceptor) D-H′-A substrates, with and without IHF bound, are shown in Fig. 3. Measurements of single-labeled (donor only) D-H′ and D-H′-A substrates, in the absence of IHF, show essentially identical fluorescence emission spectra, when excited at the donor wavelength of 492 nm (21). This result is consistent with the fact that, in the unbound, straight DNA duplex, the distances between the donor and acceptor are too far for any appreciable energy transfer. (Using a Förster distance, for which the FRET efficiency is 50%, of Ro ≈ 50 Å for this pair, and separation between labels of ≈100 Å for a 35-bp DNA oligomer, the FRET efficiency is estimated to be <2% for straight DNA). Furthermore, the fluorescence emission of D-H′, with and without IHF, also show identical donor intensities, indicating that the quantum yield of the donor is not affected by interaction with IHF (21). Therefore the ratio of the donor intensity of D-H′-A, with and without IHF, may be used directly to calculate the FRET efficiency, as described in Materials and Methods. Note that the small shoulder corresponding to acceptor fluorescence in the emission spectra of D-H′-A, in the absence of IHF, is most likely from direct excitation of TAMRA at 492 nm, consistent with the low absorption of TAMRA at that wavelength. Furthermore, the apparent lack of temperature dependence of the donor fluorescence in D-H′-A bound to IHF is as a result of a corresponding change in the donor fluorescence from a temperature-dependent change in FRET efficiency, as discussed below.
Fig. 3.
Steady-state fluorescence emission spectra of 5 μM double-labeled H′ substrate (D-H′-A) in the presence (continuous lines) and absence (dashed lines) of 5 μM IHF, after excitation at 492 nm, at 25°C (blue), 30°C (red), and 40°C (black). (Inset) FRET efficiency (E) as a function of temperature, calculated by using the ratio of fluorescence intensity at the maximum of the donor emission (≈520 nm) in D-H′-A in the presence and absence of IHF, with concentrations of IHF and H′ in the complex of 5 μM:5 μM (red circles) and 200 nM:200 nM (blue circles).
The FRET efficiency of D-H′-A bound to IHF decreases, from ≈0.51 to ≈0.45, as the sample is heated from ≈17°C to ≈40°C, indicating that the DNA unbends slightly, on average, as the complex is heated up (Fig. 3 Inset). The equilibrium measurements were also done at lower concentrations of IHF and H′ (≈200 nM:200 nM). Although the absolute FRET value, obtained at 20°C, exhibits significant variations, of ±0.1, from one set of measurements to another, the relative change in the FRET for the two sets of measurements are independent of IHF or H′ concentrations. Thus, at these concentrations, the decrease in FRET efficiency with increasing temperature is from a unimolecular process, and not from thermal dissociation of the protein from the complex. We interpret this change in FRET as arising from thermal unbending of the DNA while still bound to IHF.
Thermal Stability of H′ and IHF.
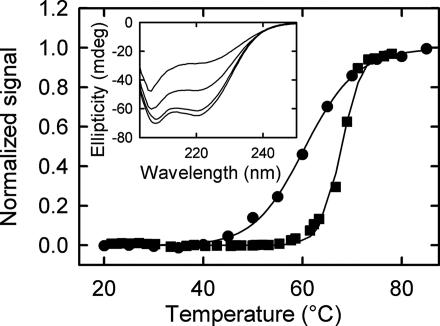
To ensure that H′ and IHF remain stable under conditions of the T-jump measurements, we carried out thermal melting/unfolding measurements on H′ and IHF. The thermal melting of H′ was monitored by absorbance changes at 266 nm, at H′ concentration of ≈4.5 μM. The melting temperature under our buffer conditions is ≈68°C (Fig. 4). The thermal unfolding of IHF was monitored by temperature-dependent changes in the far-UV CD spectra, in the temperature range of ≈15–80°C. No changes in the CD spectra are observed at temperatures below 40°C (Fig. 4 Inset), with a thermal unfolding transition observed at ≈62°C (Fig. 4). Similar set of CD measurements, carried out on a structurally analogous protein, Anabaena HU (8), at buffer conditions 10 mM Hepes (pH 7), 100 mM NaCl, and 1 mM EDTA, show that the thermal stability of HU increases with bound duplex, with the midpoint of the unfolding transition shifting from ≈57°C to ≈66°C (data not shown). Thus, we expect the H′–IHF complex to be additionally stable. It should be kept in mind that changes in the far-UV CD spectra monitor only the secondary structure disruption and are not proof that the tertiary structure is not disrupted. Nevertheless, the CD experiments, together with the consistent set of relaxation rates for the unimolecular process obtained from the stopped-flow measurements (22), and T-jump measurements, as described in the next section, suggest that IHF is in its native conformation up to at least 40°C.
Fig. 4.
Fractional change in ellipticity of IHF (12.5 μM concentration) at 222 nm (●) and absorbance of H′ substrate (≈4.5 μM concentration) at 266 nm (■), after subtraction of upper and lower baselines, is plotted as a function of temperature. The continuous lines are a fit to the data by using a van't Hoff relation for fraction unfolded (or melted). The midpoints of the transitions are at ≈62°C for IHF and at ≈68°C for H′. (Inset) CD spectra of IHF at, from bottom to top curves, 20°C, 40°C, 60°C, and 80°C.
Stopped-Flow Measurements on H′ Binding to IHF.
Stopped-flow measurements were carried out to monitor the overall association rate for the binding of IHF to H′, under pseudofirst order conditions, with IHF concentration in large excess over the DNA oligomer concentration (22). The relaxation kinetics, obtained with a time resolution of ≈3 ms, were monitored by time-resolved changes in the fluorescence emission of fluorescein, and are well described by a single exponential. The observed relaxation rates (kobs) at low IHF concentrations scale linearly with the concentration, as expected for a pseudo first order bimolecular reaction, but saturate at high IHF concentrations (see figure 3 of ref. 22). In the context of a two-step mechanism, illustrated in Fig. 2, this nonlinear dependence on the concentration implies that, at low IHF concentrations, the bending rate is fast compared with the bimolecular association step, and the kinetics monitor the bimolecular association, whereas, at high IHF concentrations, the unimolecular bending step becomes rate-limiting.
T-Jump Measurements on H′–IHF Complex.
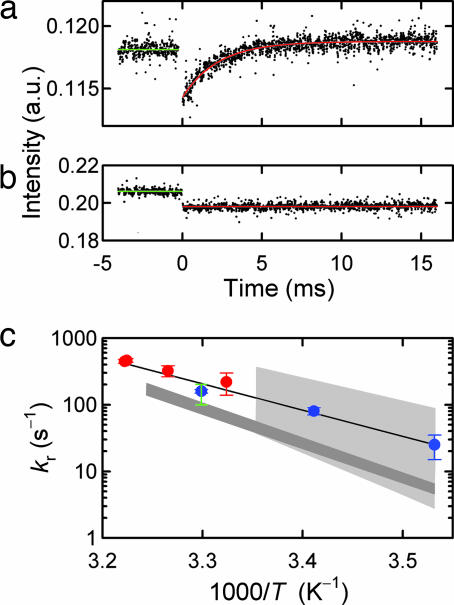
To test the hypothesis that the binding of H′ to IHF proceeds through an intermediate state with DNA possibly partially bent, relaxation kinetics in response to a laser T-jump perturbation were carried out on H′–IHF complex, at concentrations of (5 μM:5 μM). The relaxation kinetics are well described by a single-exponential in the temperature range of 28–37°C (Fig. 5a). No kinetics are observed on labeled H′ substrate, in the absence of IHF (Fig. 5b). The observed relaxation rates, obtained from the T-jump measurements, are in excellent agreement with the limiting values obtained at high IHF concentrations in the stopped-flow measurements (Fig. 5c). These results lend support to the interpretation that the stopped-flow measurements do indeed monitor the unimolecular bending/unbending relaxation at high IHF concentrations, and which is the same relaxation, albeit at higher temperatures, that is monitored in our T-jump experiments.
Fig. 5.
Laser T-jump measurements on H′–IHF complex. (a) Relaxation kinetics in response to an ≈8°C T-jump (from 29°C to 37°C) for H′–IHF complex probed by fluorescence changes at 520 nm. The kinetics are well described by a single-exponential decay (red line), with relaxation time ≈ 2 ms. (b) Control experiment in response to a T-jump on labeled H′ in the absence of IHF. (c) Relaxation rates (kr) obtained from T-jump measurements (red circles) and maximum value of kobs (blue circles) at high IHF concentrations, obtained from the stopped-flow measurements (figure 3 of ref. 22), plotted versus inverse temperature. The continuous line is an Arrhenius fit to the relaxation rates, with a slope that yields an apparent activation energy of ≈18 kcal/mol. The gray shaded regions represent the range of base pair opening rates from imino proton exchange measurements of Coman and Russu (37), with the light gray region indicating the A:T base pair rates and the dark gray region indicating the C:G base pair rates. The green vertical line is the range of A:T base pair opening rates at 30°C from Dhavan et al. (36).
As a control, we also carried out equilibrium and T-jump measurements on a 14-bp DNA duplex, d(GGCGGATATCGCGG), end-labeled with identical FRET pair. For this length of DNA, there is energy transfer between the donor and acceptor in the absence of bound protein (12). Thermal melting profiles, obtained from (i) fluorescence of donor and (ii) absorbance at 266 nm, showed identical melting profiles, with a melting temperature of ≈51°C (data not shown). T-jump experiments on this control oligomer exhibited no relaxation kinetics up to ≈50°C, indicating that the kinetics observed in the H′–IHF complex are not from any fortuitous change in FRET as a result of the T-jump, e.g., from thermal fraying of the ends of the duplex. We attribute the relaxation kinetics observed in our T-jump measurements to the overall unbending kinetics of H′ bound to IHF.
The temperature-dependence of the relaxation rates for the bending/unbending step obtained from the T-jump measurements are well described by an Arrhenius equation, with an apparent activation energy of ≈14.5 kcal/mol, which is consistent with the activation energy of ≈16 ± 3 kcal/mol obtained from the stopped-flow data (22). A global fit to the relaxation rates from the T-jump and stopped-flow data combined yields an apparent activation energy of ≈18 ± 3 kcal/mol. The relaxation rate for the unimolecular step is kuni ≈ kbend + kunbend A separation of the measured relaxation rate into kbend and kunbend is not straightforward, without prior knowledge of the preequilibrium constant for the bent/unbent conformations in the bound complex, and this separation is further complicated by the possibility that, in fact, there must be a distribution of conformations. However, under the conditions of our measurements, where the complex is still mostly bent, we can safely assume that kbend ≫ kunbend and that the activation energy corresponds primarily to the enthalpy of bending the DNA, minus a small contribution to the measured activation energy (≈4 kcal/mol) from a temperature-dependent change in the viscosity of water (32). Thus, the activation energy for the bending step is estimated to be ≈14 ± 3 kcal/mol.
Discussion
We have used laser T-jump measurements to perturb a complex of IHF bound to one of its specific sites, H′, and to monitor the DNA bending/unbending dynamics while still in complex with the protein. The relaxation rates for this unimolecular process are found to be consistent with the limiting values for the overall association rate constant obtained from stopped-flow measurements at high IHF concentrations (Fig. 5c). These results support the sequential model of DNA binding and bending to IHF, as illustrated in the kinetic scheme of Fig. 2, with the bending/unbending step becoming rate-limiting for the complex formation at high IHF concentrations. This minimal scheme is not meant to capture the complexity of the dynamics of complex formation, which most likely includes multiple conformations of the DNA and the protein in each of the distinct states. For example, the unbound DNA (or protein) may exist as a distribution of structures, with the overall association rate depending on the equilibrium fraction of DNA (or protein) molecules that are in the right conformation to facilitate DNA binding (14, 33).
Thus, one may pose the questions: Are prebent DNA conformations thermally accessible, and do they play a role in determining the specificity of binding? There is no doubt that the conformational flexibility of both the protein and the DNA plays an important role in finding the right fit. The correlation between sequence specific DNA “bendability” and binding affinity has been demonstrated very nicely for the binding of a repressor protein to sequences with differing elastic properties (34). Micromanipulation experiments on RecA binding to DNA demonstrate that the binding affinity of RecA increases for mechanically prestretched DNA, suggesting that spontaneous thermal stretching fluctuations may be playing a role in the binding of RecA to DNA, and that RecA binds preferentially to thermally stretched DNA (9).
Recently there has been a renewed interest in developing theoretical descriptions of the bendability of DNA beyond the wormlike chain description that have raised the question of spontaneous, sharp bending of DNA, either from local melting that leads to highly flexible single-stranded regions (11), or from a sharp kink at sites of low stacking energy (35). Yan and Marko (11) have proposed that, for short DNA fragments, a “teardrop” configuration with a sharp bend in the middle as a result of local bubble formation, has a lower free energy than the smoothly bent circle.
We now address the question as to whether the time scales of DNA bending observed in our experiments are consistent with spontaneous bending of DNA as a result of thermal disruption of one or more contiguous base pairs. Recent determination of base pair lifetimes, monitored by NMR measurement of imino proton exchange kinetics (36, 37), have shown that single A:T base pair opening rates in B-DNA bracket the measured DNA bending rate from 10°C to 30°C (Fig. 5c). In addition, the slope of the Arhennius plot in Fig. 5c for DNA bending is within the range of activation energies determined for single base pair opening (37). Hence, it is plausible that opening a single A:T base pair is sufficient to nucleate DNA bending. However, we cannot rule out a slightly larger bubble size as the key nucleus for bending. The opening rate for G:C pairs appears to be too small to serve as the primary locus of bending.
The opening/closing dynamics of bubbles in a cognate DNA substrate bound to IHF, monitored with imino proton exchange measurements, yield concerted opening and closing times of ≈750 ms and ≈5 μs, respectively, at 30°C, for bubbles of size up to ≈6 bp in the consensus region of the DNA sequence (36). Thus, the opening of bubbles in the DNA duplex, when it is tightly wrapped around IHF, is much slower than the DNA bending times observed in our kinetics measurements, and also much slower than the opening/closing times observed at a single base pair level for uncomplexed B-DNA (36–38).
The opening/closing dynamics of internal bubbles in AT-rich stretches of dsDNA, flanked by GC-rich “clamps,” have also been monitored by fluctuation correlation spectroscopy (39). These measurements yield characteristic relaxation time scales of 30–100 μs for bubble dynamics in the temperature range of 20–50°C. Because these measurements were done below the melting temperature of the AT-rich regions, the observed relaxation times reflect primarily the closing kinetics, with the opening kinetics occurring much slower. These closing times are significantly slower than previously reported closing times for single base pairs, which are found to be in the range of ≈10–300 ns (38, 40–42), and suggest that large bubbles are additionally stabilized, perhaps by stacking interactions in the single-stranded regions (39).
Our experimental results suggest that the rate-limiting step in the bending of DNA is the disruption of one (or two) base pairs, nucleated at an A:T site. Thus, we can estimate the free energy barrier ΔGbubble† for opening a minimal internal bubble that is sufficient to locally bend/kink DNA, by using the equation τbend ≈ τbubble = τ0 exp(ΔGbubble†/RT), where τ0 is the preexponential factor (or the reconfiguration time) and R is the gas constant. An approximate estimate of this reconfiguration time is obtained from comparison of statistical mechanical calculations of the zipping and unzipping of double-stranded DNA (dsDNA) with experiments, which yields values for τ0 of ≈125 ns (43), ≈300 ns (42), and ≈4–190 ns (44). Therefore, for τbend ≈ 2.4 ms at 37°C and assuming that τ0 ranges from 10 to 300 ns, we get ΔGbubble† in the range of 5.6–7.7 kcal/mol. Similarly, for τbend ≈ 12.8 ms at 20°C, we get ΔGbubble† in the range of 6.2–8.3 kcal/mol. These estimates for the free energy cost of opening a bubble inside DNA correlate very well with the range of equilibrium free energy changes, of ≈5.6–9.2 kcal/mol, for single base pair opening at 22°C, obtained from imino-proton exchange measurements (37), and lend further support to the suggestion that that the bending times observed in our measurements correspond to the time scale for disruption of a single internal base pair in B-DNA.
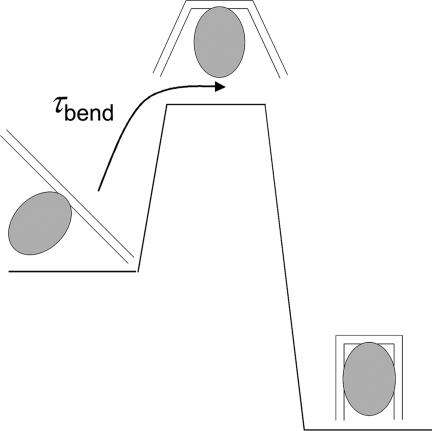
Thus, a possible model for complex formation is one in which IHF binds nonspecifically to an ≈8-bp region of straight DNA, between the kink sites, with the A:T pairs located at the site of the kinks serving as nucleation sites for bubble formation and subsequent bending. Once the protein–DNA system overcomes this free energy barrier that characterizes the transition state (Fig. 6), favorable interactions of the bent DNA with the protein, and conformational adjustments of the protein, such as the intercalation of the proline at the kinked sites, stabilize the complex.
Fig. 6.
Schematic of a free energy barrier separating the nonspecifically bound protein–DNA complex from the complex in which the DNA is fully bent. The transition state is indicated as a high-free-energy (low-probability) state in which the DNA is partially bent as a result of a thermal fluctuation. The rate-limiting step for the bending of DNA in the complex in this schematic is the rate of thermal fluctuations that spontaneously bend/kink DNA.
Summary and Conclusions
Stopped-flow measurements on IHF binding to its native H′ substrate indicate that the DNA binding and bending events are sequential and that, at protein concentrations in excess of ≈150 nM, the DNA bending/unbending becomes the rate-limiting step in the association reaction. Laser T-jump measurements, in which the protein–DNA complex is disrupted by a rapid T-jump perturbation, provide an enhanced time window that extends the time resolution to shorter time scales, and allow for the complete observation of the time course of this unimolecular step. The stopped-flow and T-jump kinetics support the sequential model of DNA binding and bending to IHF. The time scales and activation energy for DNA bending are found to be within the range of the time scales and activation energies for the opening of a single, internal A:T base pair, thus suggesting that spontaneous opening of a small internal bubble nucleated at an A:T site may be sufficient to sharply bend/kink DNA.
The laser T-jump measurements presented here represent just the beginning of the wealth of detailed information that one can obtain by probing the dynamics of molecular rearrangements in proteins and DNA during complex formation and open up the possibility of extending these studies to other protein–DNA systems.
Materials and Methods
Materials.
Unlabeled and single-labeled DNA oligomers with either 5-(and 6-)carboxyfluorescein succinimidyl ester (Fl) or 5-(and 6-)carboxytetramethylrhodamine succinimidyl ester (Rh) at the 5′ end were synthesized by the W. M. Keck Foundation and additionally purified as described by Sugimura and Crothers (22). Concentrations of the single-stranded oligomers were determined by measuring the absorbance at 260 nm using the extinction coefficients from Borer (45). To verify the extent of labeling, Fl and Rh concentrations were also determined in the labeled samples by measuring the absorbance of Fl-labeled strands at 494 nm and Rh-labeled strands at 555 nm and compared with the concentrations of the oligomers. For the dyes, the molar extinction coefficients at 260, 494, and 555 nm were taken from Haugland (46). Equal molar concentrations of the complementary strands were mixed in the appropriate buffer conditions, and the sample was heated to 90°C followed by slow cooling to room temperature to allow for complete annealing. The protein concentrations were measured by absorbance measurements at 276 nm for IHF, with an extinction coefficient of 5,800 M−1cm−1 (31).
Equilibrium FRET Measurements.
The static fluorescence emission spectra were measured on a FluoroMax2 spectrofluorimeter (Jobin Yvon, Edison, NJ). The equilibrium FRET measurements were made by measuring the fluorescence emission spectra of double-labeled, Fl–H′–Rh substrates, with and without bound IHF, respectively, in the wavelength range of 500–650 nm, with excitation at 492 nm. The emission spectra were obtained as a function of temperature, with the cuvette temperature controlled by a circulating water bath. The sample temperature was measured by using a thermistor (YSI 44008; YSI, Yellow Springs, OH) in direct contact with the sample cell.
The efficiency of energy transfer (E) between donor and acceptor can be calculated as the ratio of the donor fluorescence intensity of the single-labeled (Fl–H′) substrate (ID) with the donor fluorescence intensity of the double-labeled (Fl–H′–Rh) substrate (IDA), under identical conditions (e.g., with bound protein) to yield E = 1 − IDA/ID. Measurement of the FRET efficiency gives information about the distance between the two ends of the DNA oligomer. The FRET efficiency is related to the donor-acceptor distance R, according to E = [1 + (R/R0)6]−1 where R0 is the Förster distance at which the energy transfer efficiency is 50% (47).
Previous measurements by Sugimura (21), on Fl–H′ and Fl–H′–Rh substrates, with and without bound IHF, showed that the fluorescence emission spectra of Fl–H′ is unperturbed in the presence of IHF, and that the donor intensities of Fl–H′ and Fl–H′–Rh are identical, in the absence of IHF. Thus, under these conditions, ID may be obtained from the donor intensity of double-labeled substrates without IHF, and the FRET efficiency in the complex with IHF can be obtained by the ratio of the donor intensity in Fl–H′–Rh samples, with and without IHF (Fig. 3).
The temperature-dependent change in FRET was obtained by measuring the emission spectra of the Fl–H′–Rh substrate, with and without IHF, as a function of temperature. The error in our FRET measurements, from one sample to another, is about ± 0.1. The primary source of error is from variations in the IHF and H′ concentrations from one sample to another. To compare the temperature-dependent change in the FRET efficiency for two sets of samples at different concentrations of the IHF–H′ complex (5 μM:5 μM and 200 nM:200 nM), the ratio IDA/ID for one set of measurements was multiplied by a scale factor to maximize the overlap in the FRET values between the two sets of measurements in the range of 17°C to 40°C, shown in Fig. 3.
Laser T-Jump Spectrometer.
Our T-jump spectrometer consists of a multimode Q-switched Nd:YAG laser (Continuum Surelite II, Santa Clara, CA; fwhm = 6 ns, 300 mJ per pulse at 1.06 μm) that is used to pump a 1-m-long Raman cell consisting of high pressure methane gas (27, 48). The first Stokes line is separated from the fundamental by using a Pellin–Broca prism. The conversion efficiency at 1.54 μm (measured after the prism) is ≈25%. The energy of the 1.54-μm beam, measured at the sample position, is ≈40 mJ per pulse. The 1.54-μm beam is focused to ≈1 mm (fwhm) on the sample cell. A typical T-jump achieved with this set-up is ≈10°C in a cell with path length of ≈500 μm. The probe source is a 200-W Hg/Xe lamp, with an interference filter at the wavelength of choice. The light throughput from the lamp is optimized by focusing the UV beam on to an ≈300-μm aperture, which is reimaged inside the heated volume of the sample. The fluorescence emission (perpendicular to the incident heater and probe beams) is detected by using a Hamamatsu (Bridgewater, NJ) R928 photomultiplier tube. The photomultiplier signals are amplified with a 5-MHz current-to-voltage converter (C1053-51; Hamamatsu) and digitized with a 500-MHz transient digitizer (54825A; Hewlett–Packard, Colorado Springs, CO). The extent of the T-jump is obtained from the measured change in fluorescence of a control sample and calibrated against equilibrium measurements of the changes in the static fluorescence. The fluorescence was excited by using an interference filter centered at 470 ± 5 nm, and the emission was monitored perpendicular to the excitation direction, with a combination of a long pass filter (>490 nm) and a short pass filter (<550 nm).
Acknowledgments
We benefited from helpful discussions with Phoebe Rice (University of Chicago, Chicago, IL) and John Marko. We thank Phoebe Rice for generously providing the IHF protein and Timothy Keiderling (University of Illinois, Chicago, IL) for access to his CD spectrometer. This work was supported in part by National Science Foundation Grant MCB-0211254 (to A.A.), American Chemical Society Petroleum Research Fund Grant 43640-AC4 (to A.A.), and National Institutes of Health Grant GM 21966 (to D.M.C.).
Abbreviations
- T-jump
temperature-jump
- IHF
integration host factor
- Fl
5-(and 6-)carboxyfluorescein succinimidyl ester
- Rh
5-(and 6-)carboxytetramethylrhodamine succinimidyl ester.
Footnotes
The authors declare no conflict of interest.
References
- 1.Winkler FK, Banner DW, Oefner C, Tsernoglou D, Brown RS, Heathman SP, Bryan RK, Martin PD, Petratos K, Wilson KS. EMBO J. 1993;12:1781–1795. doi: 10.2210/pdb4rve/pdb. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Luscombe NM, Austin SE, Berman HM, Thornton JM. Genome Biol. 2000;1:1–37. doi: 10.1186/gb-2000-1-1-reviews001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Kim Y, Geiger JH, Hahn S, Sigler PB. Nature. 1993;365:512–520. doi: 10.1038/365512a0. [DOI] [PubMed] [Google Scholar]
- 4.Love JJ, Li X, Case DA, Giese K, Grosschedl R, Wright PE. Nature. 1995;376:791–795. doi: 10.1038/376791a0. [DOI] [PubMed] [Google Scholar]
- 5.Juo ZS, Chiu TK, Leiberman PM, Baikalov I, Berk AJ, Dickerson RE. J Mol Biol. 1996;261:239–254. doi: 10.1006/jmbi.1996.0456. [DOI] [PubMed] [Google Scholar]
- 6.Werner MH, Gronenborn AM, Clore GM. Science. 1996;271:778–784. doi: 10.1126/science.271.5250.778. [DOI] [PubMed] [Google Scholar]
- 7.Rice PA, Yang S, Mizuuchi K, Nash HA. Cell. 1996;87:1295–1306. doi: 10.1016/s0092-8674(00)81824-3. [DOI] [PubMed] [Google Scholar]
- 8.Swinger KK, Rice PA. Curr Opin Struct Biol. 2004;14:28–35. doi: 10.1016/j.sbi.2003.12.003. [DOI] [PubMed] [Google Scholar]
- 9.Leger JF, Robert J, Bourdieu L, Chatenay D, Marko JF. Proc Natl Acad Sci USA. 1998;95:12295–12299. doi: 10.1073/pnas.95.21.12295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Cloutier TE, Widom J. Proc Natl Acad Sci USA. 2005;102:3645–3650. doi: 10.1073/pnas.0409059102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Yan J, Marko JF. Phys Rev Lett. 2004;93:108108. doi: 10.1103/PhysRevLett.93.108108. [DOI] [PubMed] [Google Scholar]
- 12.Hiller DA, Fogg JM, Martin AM, Beechem JM, Reich NO, Perona JJ. Biochemistry. 2003;42:14375–14385. doi: 10.1021/bi035520w. [DOI] [PubMed] [Google Scholar]
- 13.Perez-Howard GM, Weil PA, Beechem JM. Biochemistry. 1995;34:8005–8017. doi: 10.1021/bi00025a006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Parkhurst KM, Brenowitz M, Parkhurst LJ. Biochemistry. 1996;35:7459–7465. doi: 10.1021/bi9530301. [DOI] [PubMed] [Google Scholar]
- 15.Dhavan GM, Crothers DM, Chance MR, Brenowitz M. J Mol Biol. 2002;315:1027–1037. doi: 10.1006/jmbi.2001.5303. [DOI] [PubMed] [Google Scholar]
- 16.Nash HA, Robertson CA. J Biol Chem. 1981;256:9246–9253. [PubMed] [Google Scholar]
- 17.Winkelman JW, Hatfield GW. J Biol Chem. 1990;265:10055–10060. [PubMed] [Google Scholar]
- 18.Polaczek P, Kwan K, Liberies DA, Campbell JL. Mol Microbiol. 1997;26:261–275. doi: 10.1046/j.1365-2958.1997.5701931.x. [DOI] [PubMed] [Google Scholar]
- 19.Xin W, Feiss M. J Mol Biol. 1993;230:492–504. doi: 10.1006/jmbi.1993.1166. [DOI] [PubMed] [Google Scholar]
- 20.Lorenz M, Hillisch A, Goodman SD, Diekmann S. Nucleic Acids Res. 1999;27:4619–4625. doi: 10.1093/nar/27.23.4619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Sugimura S. PhD thesis. New Haven, CT: Yale Univ; 2005. [Google Scholar]
- 22.Sugimura S, Crothers DM. Proc Natl Acad Sci USA. 2006;103:18510–18514. doi: 10.1073/pnas.0608337103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Dyer RB, Gai F, Woodruff WH, Gilmanshin R, Callender RH. Acc Chem Res. 1998;31:709–716. [Google Scholar]
- 24.Gruebele M, Sabelko J, Ballew R, Ervin J. Acc Chem Res. 1998;31:699–707. [Google Scholar]
- 25.Eaton WA, Munoz V, Hagen SJ, Jas GS, Lapidus LJ, Henry ER, Hofrichter J. Annu Rev Biophys Biomol Struct. 2000;29:327–359. doi: 10.1146/annurev.biophys.29.1.327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hofrichter J. Methods Mol Biol. 2001;168:159–191. doi: 10.1385/1-59259-193-0:159. [DOI] [PubMed] [Google Scholar]
- 27.Ansari A, Kuznetsov SV, Shen Y. Proc Natl Acad Sci USA. 2001;98:7771–7776. doi: 10.1073/pnas.131477798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Brauns EB, Dyer RB. Biophys J. 2005;89:3523–3530. doi: 10.1529/biophysj.105.061531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kuznetsov SV, Kozlov AG, Lohman TM, Ansari A. J Mol Biol. 2006;359:55–65. doi: 10.1016/j.jmb.2006.02.070. [DOI] [PubMed] [Google Scholar]
- 30.Yang CC, Nash HA. Cell. 1989;57:869–880. doi: 10.1016/0092-8674(89)90801-5. [DOI] [PubMed] [Google Scholar]
- 31.Lynch TW, Read EK, Mattis AN, Gardner JF, Rice PA. J Mol Biol. 2003;330:493–502. doi: 10.1016/s0022-2836(03)00529-1. [DOI] [PubMed] [Google Scholar]
- 32.Horowitz SB, Fenichel IR. Ann NY Acad Sci. 1965;125:572–594. doi: 10.1111/j.1749-6632.1965.tb45415.x. [DOI] [PubMed] [Google Scholar]
- 33.Erskine SG, Baldwin GS, Halford SE. Biochemistry. 1997;36:7567–7576. doi: 10.1021/bi970155s. [DOI] [PubMed] [Google Scholar]
- 34.Hogan ME, Austin RH. Nature. 1987;329:263–266. doi: 10.1038/329263a0. [DOI] [PubMed] [Google Scholar]
- 35.Wiggins PA, Phillips R, Nelson PC. Phys Rev E. 2005;71:021909. doi: 10.1103/PhysRevE.71.021909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Dhavan GM, Lapham J, Yang S, Crothers DM. J Mol Biol. 1999;288:659–671. doi: 10.1006/jmbi.1999.2690. [DOI] [PubMed] [Google Scholar]
- 37.Coman D, Russu IM. Biophys J. 2005;89:3285–3292. doi: 10.1529/biophysj.105.065763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Gueron M, Leroy JL. Methods Enzymol. 1995;261:383–413. doi: 10.1016/s0076-6879(95)61018-9. [DOI] [PubMed] [Google Scholar]
- 39.Altan-Bonnet G, Libchaber A, Krichevsky O. Phys Rev Lett. 2003;90:138101. doi: 10.1103/PhysRevLett.90.138101. [DOI] [PubMed] [Google Scholar]
- 40.Porschke D, Eigen M. J Mol Biol. 1971;62:361–381. doi: 10.1016/0022-2836(71)90433-5. [DOI] [PubMed] [Google Scholar]
- 41.Craig ME, Crothers DM, Doty P. J Mol Biol. 1971;62:383–401. doi: 10.1016/0022-2836(71)90434-7. [DOI] [PubMed] [Google Scholar]
- 42.Cocco S, Marko JF, Monasson R. Eur Phys J E. 2003;10:153–161. doi: 10.1140/epje/e2003-00019-8. [DOI] [PubMed] [Google Scholar]
- 43.Porschke D. Biophys Chem. 1974;2:97–101. doi: 10.1016/0301-4622(74)80029-3. [DOI] [PubMed] [Google Scholar]
- 44.Ansari A, Kuznetsov SV. In: Biological Nanostructures and Applications of Nanostructures in Biology: Electrical, Mechanical, and Optical Properties. Stroscio MA, Dutta M, editors. New York: Kluwer; 2004. pp. 99–147. [Google Scholar]
- 45.Borer PN. In: Handbook of Biochemistry and Molecular Biology. Fasman GD, editor. Cleveland: CRC; 1975. p. 589. [Google Scholar]
- 46.Haugland RP. Handbook of Fluorescent Probes and Research Products. 8th Ed. Eugene, OR: Molecular Probes; 2001. [Google Scholar]
- 47.Lakowicz JR. Principles of Fluorescence Spectroscopy. New York: Plenum; 1983. [Google Scholar]
- 48.Shen Y, Kuznetsov SV, Ansari A. J Phys Chem B. 2001;105:12202–12211. [Google Scholar]
- 49.Swinger KK, Lemberg KM, Zhang Y, Rice PA. EMBO J. 2003;22:3749–3760. doi: 10.1093/emboj/cdg351. [DOI] [PMC free article] [PubMed] [Google Scholar]