Quantitative modeling of sensitivity in bacterial chemotaxis: The role of coupling among different chemoreceptor species

Abstract

We propose a general theoretical framework for modeling receptor sensitivity in bacterial chemotaxis, taking into account receptor interactions, including those among different receptor species. We show that our model can quantitatively explain the recent in vivo measurements of receptor sensitivity at different ligand concentrations for both mutant and wild-type strains. For mutant strains, our model can fit the experimental data exactly. For the wild-type cell, our model is capable of achieving high gain while having modest values of Hill coefficient for the response curves. Furthermore, the high sensitivity of the wild-type cell in our model is maintained for a wide range of ambient ligand concentrations, facilitated by near-perfect adaptation and dependence of ligand binding on receptor activity. Our study reveals the importance of coupling among different chemoreceptor species, in particular strong interactions between the aspartate (Tar) and serine (Tsr) receptors, which is crucial in explaining both the mutant and wild-type data. Predictions for the sensitivity of other mutant strains and possible improvements of our model for the wild-type cell are also discussed.

The bacterial chemotaxis pathway is one of the best characterized signal transduction pathways in biology (see refs. 1–3 for recent reviews of the subject). The molecular hardware of the chemotaxis response has been worked out, and we have a rather complete qualitative description of how the signal is received, transduced (to the motor), and regulated. However, at the quantitative level, there are still many unanswered questions. One long-lasting puzzle in bacterial chemotaxis is the problem of gain (4), i.e., a small change in external concentration of attractant or repellent can cause substantial change in the cell's swimming behavior. One possible source of gain could be the interaction of the signaling molecule CheY-P with the motor complex, in particular the FliM protein. However, despite the large Hill coefficient for the rotation bias vs. CheY-P concentration relation discovered recently in tethered single-cell experiments (5), a simple calculation quickly shows that the amplification at the motor level can only be part of the story, because quantitatively it simply cannot account for all the gain of the system (6). Therefore, there has to be significant amplification from the ligand concentration change to the change in CheY-P concentration. Recently, this high signal amplification was demonstrated directly in a set of beautiful experiments by Sourjik and Berg (SB) (7), where CheY-P concentration was measured in vivo for the first time by using fluorescence resonance energy transfer. In their study, SB measured the sensitivity of the wild-type and different mutant strains of Escherichia coli in their response to different concentrations of methyl-aspartate (MeAsp). The wild type is found to have extremely high sensitivity, which translates into a high gain of ≈36 once the receptor occupancy is inferred by a simple approximation.

Because of their direct, quantitative, and systematic nature, the SB data provide us with a unique opportunity to understand the internal workings of the bacterial chemotaxis signaling pathway. In this paper, we construct a model framework capable of explaining the SB data quantitatively.

Motivation, Models, and Methods

The Motivation. Six mutant strains were studied in ref. 7. The cheR^- and cheB^- mutants correspond to strains with either CheR or CheB unexpressed. Four cheRcheB mutants correspond to strains missing both CheR and CheB and with the Tar receptor genetically engineered to be in different methylation states (EEEE, QEEE, QEQE, and QQQE). A careful look at the response data for all the mutant strains from the SB paper (reproduced here in Fig. 1a) reveals several suggestive features, which we describe in the following to motivate the construction of our model.

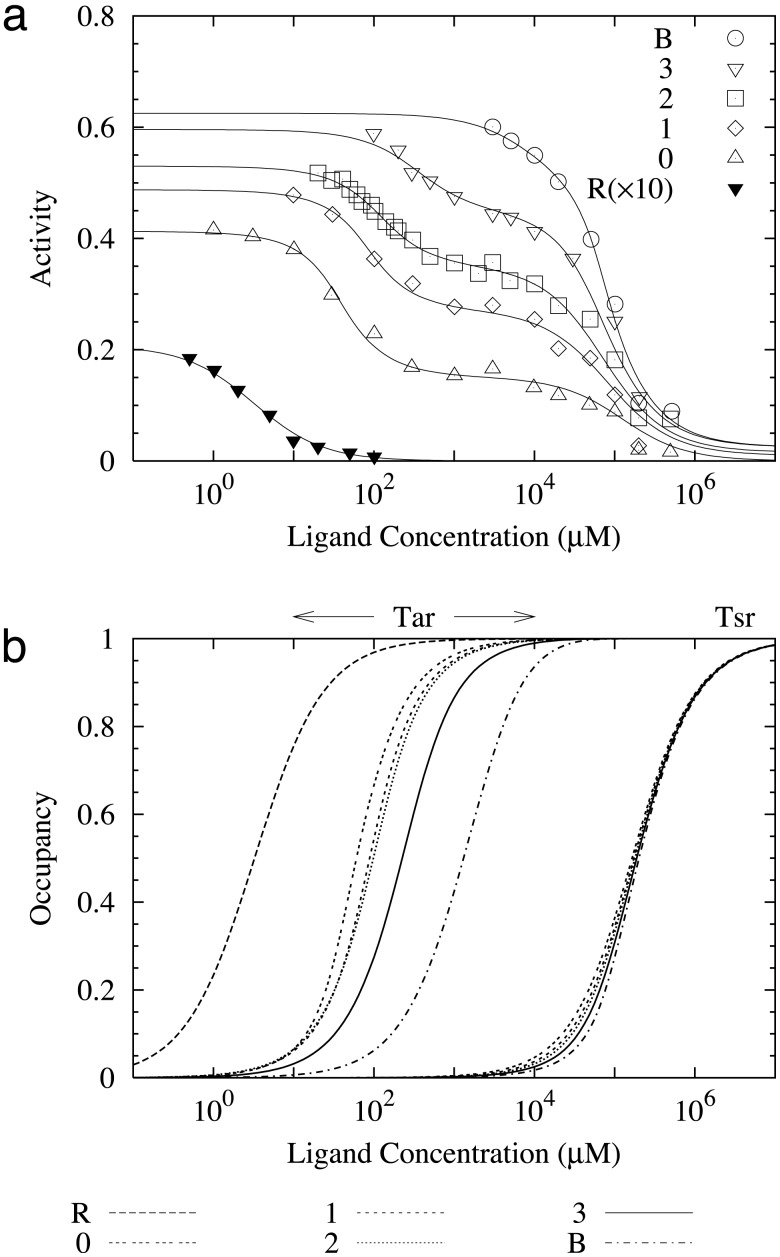
Fig. 1.

(a) Fitting of our model to the response data for all mutant strains reported in ref. 7. The horizontal axis is the MeAsp concentration. The lines are the results of our model with the parameters given in Table 1. The symbols are the experimental data rescaled to their absolute values according to the activity at [L] = 0 provided in ref. 7. For the cheRcheB mutants, the Tsr receptors are in the m = 2 methylation state, and Tar receptors are in m = 0(▵), m = 1(⋄), m = 2 (□), or m = 3 (▿) methylation state, respectively. The cheR(×10) and cheB mutants are represented by ▾ and ○. (b) The receptor occupancy for Tar and Tsr for all mutant strains calculated from our model for the same parameters as in a. The half-occupancy ligand concentrations are: K_1/2 = 3.53, 42.2, 86.6, 97, 267, and 996 μM for Tar in cheR, cheRcheB(EEEE), cheRcheB(QEEE), cheRcheB(QEQE), cheRcheB(QEQQ), and cheB cells, respectively.

For the four cheRcheB mutants, the response curves have two steep drops as the MeAsp concentration increases: the first one corresponds to the transition of the aspartate receptor (Tar) between its ligand free state and its ligand occupied state; the second corresponds to the same transition for the serine receptor (Tsr) at a higher ligand concentration. The sizes of these two activity drops are different for different cheRcheB mutants. Although the difference for the first drops among different cheRcheB mutants could be explained by the different modification states of Tar in different mutant strains, the difference for the second activity drops is very intriguing, because the Tsr receptors should be in the same methylation state (QEQE) for all cheRcheB mutants. This observation suggests that Tsr activity is affected by Tar receptors, and the interaction depends on the methylation state of the Tar receptors.

For the cheR^- mutant, the receptors (including both Tar and Tsr) are all expected to be in their most demethylated states (EEEE) because of the unbalanced demethylation of receptors by CheB. Therefore, the Tar receptors should be in the same methylation state (EEEE) in both cheR^- and cheRcheB(EEEE) mutants. However, the responses of these two strains to MeAsp are extremely different, as shown in ref. 7. The cheR^- strain is found to respond to much lower ligand concentration but with much-reduced activity as compared with the cheRcheB (EEEE) strain. To understand this difference, it is important to note that even though the Tar receptors are in the same methylation states in both cheR^- and cheRcheB(EEEE) strains, the Tsr receptors are in different methylation states for these two strains: one in its most demethylated state (EEEE) and the other in its unmodified state (QEQE). Therefore, the different behaviors between cheR^- and cheRcheB(EEEE) could be understood if we assume again there is strong coupling between Tar and Tsr, and the interaction depends on the methylation state of the Tsr receptor.

These two observations of SB's response data lead us to construct a theoretical model, in which one of the main ingredients is the coupling among receptors, in particular among different types of receptors. Cooperativity between receptors as a mechanism for the system's large gain was first suggested by Bray, Levin, and Morton-Firth (8). Later, Shi and Duke (9) proposed an Ising-type model, where identical receptors on a regular extended lattice interact with their nearest neighbors, as a materialization of the idea. Duke and Bray (10) eventually implemented a Monte Carlo version of the simple Ising-type model and demonstrated that it is capable of enhancing the gain of the system. Although conceptually appealing, these models lack the necessary ingredients, such as a proper description of different methylation states of the receptors and the inclusion of heterogeneous receptor interactions among different types of receptors, which are essential in explaining the quantitative data in the SB experiment. In this paper, we will construct and study a simple model that implements the general idea of receptor coupling among different types of receptors and a detailed description of the properties of receptors in different methylation levels, with the aim of understanding the SB data quantitatively.

The General Structure of the Model. We first assume that each receptor (complex) has two distinct states: active and inactive. Each receptor, T_qmλ, is characterized by three parameters: q is the type of receptor, only the two high-abundance types of receptors with q = 1 for Tar and q = 2 for Tsr being considered in this paper, and the total number of Tsr being twice that of Tar; m ∈ [0, 4] is the number of methyl groups; and λ = 0, 1 represents vacant and ligand-occupied receptors, respectively. We assume the probability of finding the receptor in the active or inactive state is controlled by their energy difference and obeys the Boltzmann distribution (9). The average activity for receptor T_qmλ is then given by:

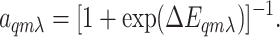[1]

ΔE_qmλ is the dimensionless total energy difference between the active and inactive states for receptor T_qmλ. All energies in this paper are in units of the thermal energy k_BT.

The total energy difference ΔE_qmλ contains two different kind of contributions: a self energy E_qmλ depending on the properties of the receptor T_qmλ itself, and an interaction energy coming from coupling to other receptors (characterized by q′m′λ′):

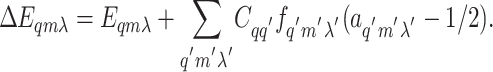[2]

Without detailed knowledge of the geometrical nature of the interaction, we adopt the mean-field approach, where each receptor's local environment is approximated by the overall (fractional) receptor population f_{q′m′λ′}. Preferential coupling between different types of receptor can be captured by the coupling strength C_qq′ between receptor types q and q′. For generality, symmetric coupling (C_qq′ = C_q′q) is not enforced. In principle, coupling strength may depend on the methylation levels or ligand-binding status of the receptors; however, such extra degrees of freedom are not needed for fitting the SB data.

In Eq. 2, we have used the simplest form of interaction, wherein the interaction energy depends linearly on the other receptor's activity. The interpretation of Eq. 2 is quite transparent. The activity of a given receptor T_qmλ is determined by both its own properties characterized by E_qmλ and those of its interacting neighbors. If its neighbors' activity is higher, then through positive coupling implemented by having C_qq′ < 0, the total energy difference ΔE_qmλ will be lowered, leading to higher activity for receptor T_qmλ from Eq. 1. The activity value at which the interaction is zero is set to 1/2 for convenience, and it can be shown easily that setting it to another value simply amounts to a renormalization of the local energy E_qmλ.

To complete the description of the system, we need to know how each type of receptor is distributed among its different methylation and ligand-binding states, i.e., the values of f_qmλ. From the experimental data, particularly the comparison between cheR^- and cheRcheB(EEEE), it is evident that the ligand-binding kinetics may depend on the activity itself. Assuming the time scale for active/inactive transition is faster than that of the ligand-binding/unbinding reaction, the ligand-binding dynamics can be written as:

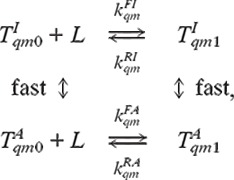[3]

where and are the receptors in the inactive and active states, and L represents the ligand. The steady-state ratio between ligand-bounded and unbounded receptor populations is given by:

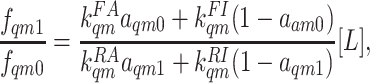[4]

where [L] is the ligand concentration, and 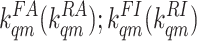are the ligand-binding (unbinding) rates for the active and inactive receptors, respectively. To include the possibility that the ligand-binding kinetics described in Eq. 3 is not an isolated process, no thermodynamics constraints are used to relate the rate constants with the receptor energy differences. However, such constraints are not expected to change the main results of this paper due to the underdetermined nature of the problem.

The Model for the Mutants. For all the mutants studied by SB, the normal methylation process is disabled, because either one or both of the methylation and demethylation enzymes is missing. Therefore, for any given mutant strain, each receptor type q(=1, 2) is in a unique methylation state m_q, e.g., m₁ = 0 and m₂ = 0 for the cheR^- mutant; and m₁ = 2 and m₂ = 2 for the cheRcheB(QEQE) mutant. For a given mutant characterized by m₁ and m₂, the coupled nonlinear Eqs. 1, 2, and 4 can be solved together at any given ligand concentration to obtain the activities and receptor distribution functions a_qmqλ and f_qmqλ, from which the (average) activity of the whole system A = Σ_qλ a_qmqλf_qmqλ can be determined. In this paper, we assume that CheY-P concentration is linearly proportional to the total (kinase) activity A, therefore the behavior of A from our model is directly compared with that of the (experimentally measured) CheY-P concentrations. The parameters of this model are the self-energies for each receptor type E_qmλ, the coupling strengths C_qq′, and the kinetic rates for describing the ligand-binding kinetics. To validate our model quantitatively, our goal is to find a set of parameters such that the behaviors of the model would agree with the experimental data for all six mutant strains in ref. 7.

The Model for the Wild Type. To model the response behavior of the wild type properly, we need to introduce the methylation/demethylation kinetics. At a given ambient ligand concentration, the receptors in a wild-type cell are distributed in different methylation states due to adaptation mediated by the methylation/demethylation kinetics. To make this a tractable problem, we use a coarse-grained description for the Tar receptors with only five methylation states characterized by their total number of methyl groups m ∈ [0, 4] instead of considering all 16 possible methylation states. Hence m has a slightly different meaning here from that in the mutant model. For example, although parameters with m = 1 in the wild-type model represent the average properties of all receptors with one methylated site, i.e., (QEEE), (EQEE), (EEQE), and (EEEQ), they describe the properties of the specific methylation state studied in the current mutant experiments, i.e., (QEEE). Therefore, the parameters from these two models may not be the same, and we choose to fit the mutant and wild-type data separately.

It is known that E. coli adapts almost perfectly to MeAsp, i.e., the steady-state total activity is independent of the ambient ligand concentration. As shown in previous studies on adaptation (11–14) one of the key conditions for achieving perfect adaptation is that the methylation/demethylation rates depend on the activity of the receptor. Assuming that only inactive receptors can be methylated, and only active receptors can be demethylated (12, 14), we use the following simplified methylation flux balance equation between any two consecutive methylation levels to determine the steady-state distribution of the receptors in different methylation states:

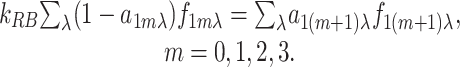[5]

k_RB is the ratio of the methylation/demethylation rates, which depends on the enzyme concentrations and methylation kinetic constants. It is easy to show by summing Eq. 5 over m that the total activity of the Tar receptors, A₁ = Σ_λ,0≤m≤4 f_1mλa_1mλ, is a constant if the fully methylated receptors are always active, a_14λ = 1, and the least methylated receptors are always inactive, a_10λ = 0. This is also one of the conditions for perfect adaptation found in our earlier work by studying a full adaptation model (14).

The Tsr receptor distribution in different methylation states, f_2m, can be determined similarly as in Eq. 5. Because of perfect adaptation and the fact that Tsr does not bind to MeAsp in the concentration range (<10 mM) where the wild-type experiments were performed, the steady-state Tsr distribution f_2m is independent of the ambient MeAsp concentration. To avoid introducing too many parameters describing the details of the different Tsr methylation states, we simplify our model by approximating f_2m = δ_mm0 (m₀ is set to 2 for bookkeeping purposes), i.e., all Tsr receptors are in the same methylation state. This is a reasonable approximation for studying the MeAsp response, because f_2m is independent of the ambient MeAsp concentration, and f_2m is usually dominated by a single methylation level (see supporting information on the PNAS web site, www.pnas.org, for Tar distribution f_1m).

Eq. 5, together with Eqs. 1, 2, and 4, defines the steady-state receptor distributions (in different methylation states) of the wild-type cell for any given ambient MeAsp concentration. Because methylation/demethylation is much slower than the ligand-binding process, the short time response of the wild-type cell to different added/removed MeAsp concentrations can be calculated by solving just Eqs. 1, 2, and 4 for the fast processes, while keeping the receptor distribution in different methylation states the same as that of the (prestimulus) steady state. These responses can be directly compared with the wild-type data provided in SB's study.

The types of parameters in the wild-type model are similar to that of the mutant, except that there is only one Tsr state in the wild-type model. In addition, we have introduced an extra parameter k_RB for describing the methylation/demethylation processes.

The Fitting Method. We construct an error function by summing the square of the difference between the model's predicted response and the experimental value at each data point. A global scaling factor is also introduced as a fitting parameter in converting the model's predicted activity into the experimentally observed CheY-P concentration. The Newton–Raphson method (15) is used for solving the self-consistent equations for a given set of parameters, and Powell's quadratically convergent method (15) is used subsequently in minimizing the error function in the parameter space with different initial parameter values.

Results

The Mutant Strains. Because there is not enough range of activity change for the Tar receptor in m = 1, 2, 3, and 4 states in the experimental data, the ligand-binding/unbinding rates of Tar for m ∈ (1, 4) are underdetermined; i.e., there are many sets of ligand-binding/unbinding rates that can produce the same good fit to the data. However, for Tar (q = 1) with m = 0, the best fit to the data always results in 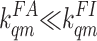and 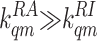. To eliminate the unnecessary degeneracy in our fitting, we have reduced the number of parameters by fixing 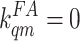and 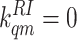for all receptor and methylation levels for both the mutant and wild-type models. However, it is important to keep in mind for future studies that this requirement may be necessary only for Tar with m = 0. Now the ligand-binding/unbinding balance equation can be simplified: f_qm1/f_qm0 = (1-a_qm0)[L]/(a_qm1K_qm), which depends on only one parameter, 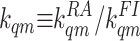, instead of the three ratios between the four kinetic rates in Eq. 4.

From all the initial parameters we tried, the fitting converges to the same point in the parameter space. However, the attraction basin is very flat, i.e., there are many sets of parameters that can fit the mutant data within the experimental error. Fig. 1a shows one such good fit of our model to the experimental data, the corresponding parameters being given in Table 1 (see supporting information for examples of other good fits). Overall, the model fits the data remarkably well, considering that the number of parameters is rather small. Although more experiments are needed to remove the ambiguity in the parameters, some parameters of the model, do seem to be constrained by the existing data, e.g., the interaction strength from Tsr to Tar, C₁₂, is found to be always big as compared with other coupling constants.

Table 1. A set of parameters for which our model fits all the mutant strain data well.

m	0	1	2	3	4
E1m0(A1m0B)	-2.07 (0.89)	-2.51 (0.93)	-2.93 (0.95)	-15.4 (1.0)	-16.0 (1.0)
E1m1(A1m1B)	6.22 (0.0)	-1.31 (0.79)	-1.77 (0.85)	-2.27 (0.91)	-2.27 (0.91)
E2m0(A2m0B)	∞ (0.0)	—	0.53 (0.37)	—	0.419 (0.40)
E2m1(A2m1B)	—	—	13.2 (0.0)	—	12.9 (0.0)
K1m	185681	77.5	32.4	0.00018	0.00111
K2m	∞	—	1.86 × 1011	—	1.35 × 1011

Cqq′	q′ = 1	q′ = 2
q = 1	-1.0	-13.9
q = 2	-1.60	-2.38

Next to the self-energy differences E_qmλ, we have included the “bare” activity values A_qmλ^B ≡ (1 + exp(E_qmλ))^-1 for reference only; the actual receptor activities are always different from their bare values because of receptor coupling

By using our model, we can also directly measure the fractional ligand occupancy of both the Tar and Tsr receptors, the results being shown in Fig. 1b. Comparing Fig. 1 a and b, it is clear that even though the trends of ligand occupancy and the activity curve for a given receptor are correlated, they can be quite different quantitatively. Due to the effect of receptor coupling, high ligand occupancy does not necessarily mean proportionally large suppression of activity. Depending on the details of the model, K_1/2 (the half-maximum ligand concentration) of the ligand occupancy curve can be either bigger or smaller than that of the corresponding activity curve, as shown in Fig. 1.

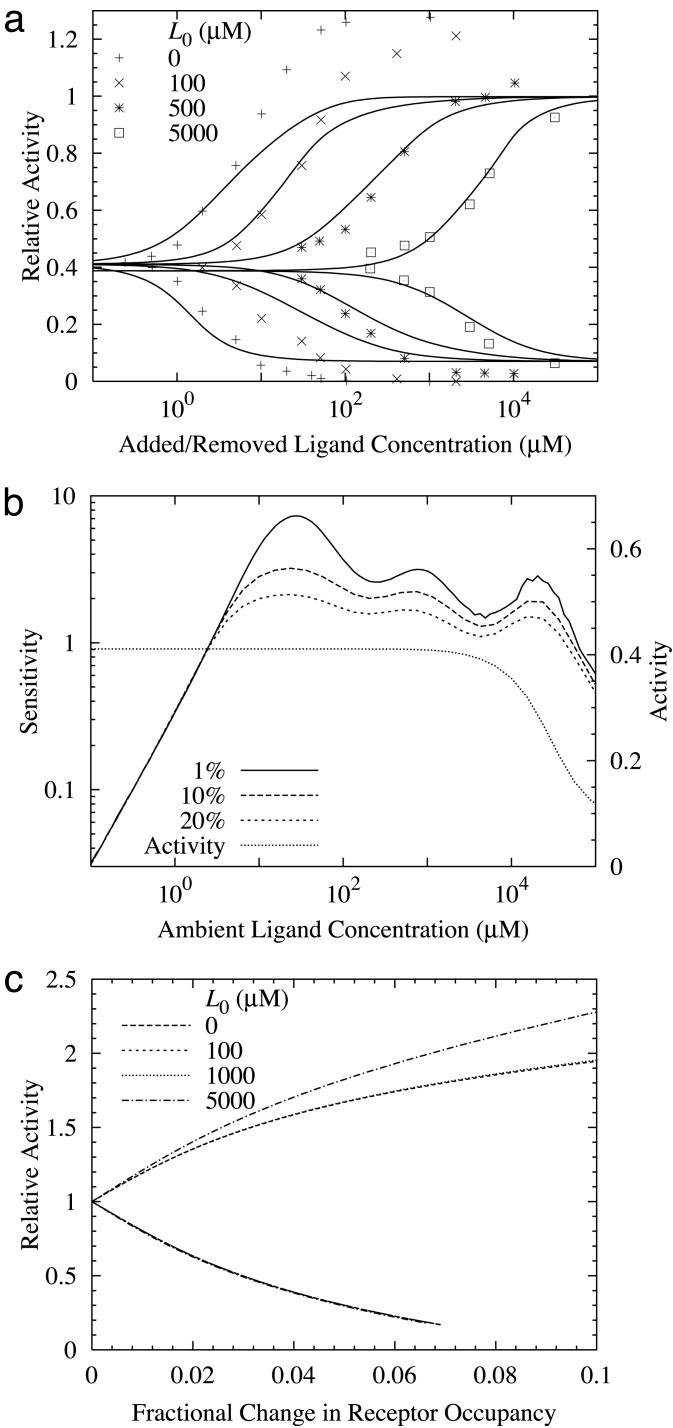
The Wild Type. The fitting for the wild-type data is significantly more difficult than for the mutant data, because of the complexity introduced by multiple Tar methylation states. The best fit to the wild-type data we have found so far within our model is shown in Fig. 2a, with the parameters given in Table 2. There is no guarantee that this is the unique, or globally minimum, solution. The general behavior of the response of the wild-type cell to increasing and reducing ligand concentration predicted by our model is highly consistent with the experimental results. Due to the simplifications made in our wild-type model, the quantitative agreement is not as perfect as for the mutant studies, especially for the large MeAsp concentration changes. However, for a relatively small MeAsp concentration change, our model has captured the essential features for producing high sensitivity and high gain in the wild-type response. At a given ambient ligand concentration [L], the system is characterized by its receptor occupancy L and total activity A. On a sudden change of ligand concentration Δ[L], the resulting (fast) changes (before methylation/demethylation takes place) in receptor occupancy and total activity are represented by ΔL and ΔA. Following SB (7), sensitivity (S) and gain (G) are defined as: S ≡ ([L]/A)(ΔA/Δ[L]); G ≡ (1/A)(ΔA/ΔL). While S measures the sensitivity of the cell's kinase activity with respect to the (external) ligand concentration change, G measures the signal amplification within the cell.

Fig. 2.

(a) The instantaneous response to a sudden change in ligand concentration. Different curves refer to different initial (ambient) MeAsp concentrations (in μM). The horizontal axis is the amount added and then removed. The lower curves are the responses to the ligand increase and the upper curves are the responses to the ligand decrease. (b) The sensitivity and total (steady-state) activity of the wild-type cells at a given MeAsp concentration. The sensitivity is defined as the fractional change in activity divided by the fractional change in MeAsp concentration. The percentages refer to the fractional changes in concentration used in calculating the sensitivity. (c) The fractional change in activity vs. change in (total) ligand occupancy for different initial (ambient) ligand concentrations. The upper and lower curves are for decreasing and increasing ligand concentrations, respectively. The gain is defined as the ratio between the fractional activity change and the change in receptor occupancy. For small changes in receptor occupancy, the gain is ≈20.

Table 2. A set of parameters for which our model fits the wild-type data well.

m	0	1	2	3	4
E1m0(A1m0B)	∞ (0.0)	-12.4 (1.0)	-11.5 (1.0)	-16.0 (1.0)	-30.5 (1.0)
E1m1(A1m1B)	∞ (0.0)	15.8 (0.0)	14.3 (0.0)	11.0 (0.0)	11.0 (0.0)
E2m0(A1m0B)	—	—	-1.76 (0.85)	—	—
K1m	—	486	1679	12.4	2.32 × 10-4
K2m	—	—	∞	—	—

Cqq′	q′ = 1	q′ = 2
q = 1	-6.85	-0.680
q = 2	-17.9	-3.54

The methylation/demethylation ratio: k_RB = 0.26

In Fig. 2b, we show the sensitivity for the full range of ambient ligand concentrations, in the same way as in ref. 7 (see figure 3b in their paper) for small relative MeAsp concentration changes Δ[L]/[L] = 1%, 10%, 20%. For >4 decades of ambient ligand concentrations, high sensitivity is maintained between 1 and 8, consistent with ref. 7. In Fig. 2b, the steady-state activity of our model is also plotted. The system adapts nearly perfectly, i.e., the steady-state activity is a constant independent of ambient ligand concentration, from zero concentration to ≈1 mM. The adaptation becomes imperfect for higher ligand concentrations (75% activity at 10 mM), because one of the perfect adaptation conditions a_14λ = 1 is not satisfied, and the m = 4 state becomes highly populated at high ligand concentrations (14). To determine the gain, we have plotted the relative activity change ΔA/A vs. the change in receptor occupancy ΔL for several ambient ligand concentrations. As shown in Fig. 2c, most curves for different ambient MeAsp concentrations collapse onto a single one (as in ref. 7). The deviation from common behavior at the extremely high ambient MeAsp concentration (5 mM) is probably caused by violation of perfect adaptation at such high MeAsp concentration in our model. For small ΔL, the relative activity change is linearly proportional to the receptor occupancy change with a high slope (≈20). In SB's paper (7), receptor occupancy of the wild-type cell was estimated from the data of a single mutant strain; this inaccuracy in determining the receptor occupancy may be responsible for the discrepancy between the gain calculated in our model (≈20) and that reported from their work (≈36).

So, where does the high gain come from? In our model, we can easily calculate the contributions to the gain by Tar and Tsr separately. For the parameters in Table 2, the gain from Tsr constitutes a large fraction (>80%) of the total gain for MeAsp response (see supporting information for a detailed derivation). Quantitatively, the gain from Tsr at a given ambient concentration is determined mainly by two factors: the coupling strength from Tar to Tsr, i.e., C₂₁; and Tsr's activity at the ambient ligand concentration A₂, which determines the susceptibility of the Tsr activity with respect to change of its neighbor's activity. From Table 2, we can see that a large value of the coupling constant C₂₁ is required to fit the experimental data.§ Another reason for the high gain from Tsr is that in our model, the Tsr activity A₂ is kept around 1/2, where Tsr activity is most susceptible to the change of its neighbor's activities, and the perfect adaptation of the system is responsible for keeping the Tsr receptors at their most susceptible states for all ambient ligand concentrations.¶ This observation provides another mechanism in which perfect (or near-perfect) adaptation may be required for the system to have high gain over a large range of ambient ligand concentrations.

What causes the high sensitivity? From its definition, we can easily relate the sensitivity to the gain:

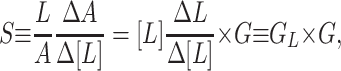[6]

where G_L ≡ [L] (ΔL/Δ[L]) represents how receptor occupancy changes in response to (relative) ligand concentration change. From Eq. 6, it is clear that high gain alone does not guarantee high sensitivity unless G_L is also kept consistently high for the same range of [L]. To have a sense of how G_L behaves, we consider the case where ligand binding obeys simple kinetics with a single dissociation constant 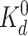for all Tar receptors. In this case, G_L reaches its maximum value: max(G_L) = 1/12 at 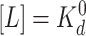and decays rapidly as [L] moves away from 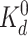. Fortunately, in bacterial chemotaxis, the receptors exist in different methylation states with different dissociation constants. Due to adaptation, as the ambient MeAsp concentration increases, the Tar receptor population shifts toward higher methylation states with higher dissociation constants; consequently the effective K_d for all Tar receptors increases with [L]. In addition, the dependence of ligand binding on receptor activity, as assumed in our model, increases max(G_L), the maximum value of G_L, for each individual methylation state. Therefore, the dependence of ligand binding on receptor activity increases G_L, and the tracking of the effective K_d with the ambient ligand concentration keeps the high G_L value through a wide range of ambient ligand concentrations (see supporting information for details). Finally, large G_L, together with high gain G, leads to persistently high sensitivity.

Summary and Discussion

In trying to understand and model recent in vivo experiments on bacterial chemotaxis response by SB, we discover that receptor coupling, in particular among different types of receptors, and dependence of ligand binding on receptor activity are the two most important ingredients in explaining their data. For the mutant data, these two ingredients are essential in explaining some of the intriguing findings in ref. 7, in particular the different activities of the same Tsr methylation state in different cheR-cheB mutants and the significant difference in both activity and sensitivity of the two mutant strains, cheRcheB(EEEE) and cheR^-. From fitting the wild-type data, the results from our model confirm that the large gain can indeed be explained by receptor coupling quantitatively. More specifically, our model suggests that most of the gain in response to MeAsp could come from Tsr. Even though Tsr does not bind to MeAsp directly except for extremely high MeAsp concentration (>10 mM), its activity is indirectly affected by the change of MeAsp concentration because of its coupling to Tar. The strong coupling between Tar and Tsr may be related to the preferred mixture of Tar and Tsr within the trimer of dimer complex, as recently discovered by Ames et al. (16). The same sort of large indirect contribution of gain from Tsr (or Tar) may also exist in the response of the system to ligands that bind directly with low-abundance chemoreceptors. Finally, we find that, besides the high gain, the tracking of effective K_d with ambient ligand concentration through adaptation and the dependence of ligand binding on receptor activity are crucial in maintaining the system's high sensitivity.

The wild-type and mutant data are fitted separately in this study, mainly due to the different resolutions used in describing the methylation states for these two data sets. With more experimental data becoming available, the ultimate goal is to find a single set of parameters that can explain both the mutant and the wild-type data within our model. For example, the heterogeneous coupling constants are found to be large (C₁₂ from the mutant study, C₂₁ from the wild-type study); the challenge is whether a unified theory with large values for both C₁₂ and C₂₁ can explain both data sets. Despite the large difference between the mutant and wild-type parameters in the specific solutions shown in this paper (Tables 1 and 2), a unique set of parameters is still possible because of the existence of many equally good solutions when each data set is fitted separately. However, it may also turn out that extra mechanistic ingredients, such as the dependence of the coupling constants on the methylation level, have to be included in the model to explain all the data. Before such a unified theory can be attempted, we need to improve our wild-type model to achieve the same level of quantitative agreement between model and experiment as for the mutants; in particular, a more accurate description of the methylation states and dynamics are needed for both the Tar and Tsr receptors. Furthermore, the mean-field-type model used in this paper (Eq. 2) needs to be improved to incorporate the appropriate spatial (maybe even temporal) information on receptor interaction once we understand whether the receptor interaction is mediated by a spatially extended lattice of receptors (17), just by the trimer of dimer complex (18), or through a dynamically changing network of interacting receptors.

In this paper, we have used the in vivo data of ref. 7 for constructing and validating our model. There are several other related recent experimental studies (both in vitro and in vivo), which are interesting to examine in light of our model. Bornhorst and Falke (19) measured the activities of all 16 methylation states of Tar receptors in vitro. Qualitatively, the concentration that induces half-maximal inhibition (K_1/2) is found to be highly correlated with the activity of the receptor, which is consistent with our model. It is also interesting to note that the K_1/2s for the same methylation states have different values in refs. 7 and 19, further evidence that the sensitivities of the receptors may depend on receptor interactions and therefore may be different in different systems. The Hill coefficients for the response curves are all found to be between 1 and 3 for Tar receptors (19) but as high as 8–10 for the Tsr receptors (20). In our model, the Hill coefficient depends on interaction strengths among receptors. Therefore, these experiments can be understood within our model, because the interaction strengths can be different for Tar–Tar and Tsr–Tsr interaction, which can also be different from their value in wild-type cells. In a related study, Levit and Stock (21) measured directly the receptor occupancy together with the activity and found that they can be quite different, far from the linear relations that are often assumed. This is again consistent with our model, as seen from the comparison of Fig. 1 a and b. Recently, by using a synthesized multivalent chemoattractant for Trg, Gestwicki and Kiessling (22) discovered a large increase in sensitivity of the cell's response not only to the synthesized chemoattractant itself but also to serine. This is in support of the notion that the sensitivity of ligand binding is affected by receptor interactions, which might be enhanced by the multivalent chemoattractant.

Specific experiments may also be suggested for validating our model. For example, in our model, the large difference between the behaviors of cheR^- and cheRcheB(EEEE) mutants is explained by the difference of the Tsr methylation states for these two mutant strains. Another possible scenario is that CheB could inhibit receptor activity, as proposed by Barkai et al. (23). A possible test could be to make a cheRcheB mutant with both Tar and Tsr in their lowest methylation state (EEEE) and measure its response to MeAsp. According to our model, the response to MeAsp for this new mutant should behave more like the cheR^- strain because of the similarity in the methylation state for the two major receptors, whereas the other theory would predict it to be more like cheRcheB(EEEE), because both of them have no cheB.