Chirality sensing by Escherichia coli topoisomerase IV and the mechanism of type II topoisomerases

Abstract

Escherichia coli topoisomerase (Topo) IV is an essential type II Topo that removes DNA entanglements created during DNA replication. Topo IV relaxes (+) supercoils much faster than (–) supercoils, promoting replication while sparing the essential (–) supercoils. Here, we investigate the mechanism underlying this chiral preference. Using DNA binding assays and a single-molecule DNA braiding system, we show that Topo IV recognizes the chiral crossings imposed by the left-handed superhelix of a (+) supercoiled DNA, rather than global topology, twist deformation, or local writhe. Monte Carlo simulations of braid, supercoil, and catenane configurations demonstrate how a preference for a single-crossing geometry during strand passage can allow Topo IV to perform its physiological functions. Single-enzyme braid relaxation experiments also provide a direct measure of the processivity of the enzyme and offer insight into its mechanochemical cycle.

The interwound structure of duplex DNA demands that the two DNA strands be unlinked from each other during semiconservative DNA replication in vivo. Unlinking is carried out primarily by the cooperation of helicases and topoisomerases (Topos). DNA helicases unwind the parental double helix, which generates (+) supercoils or precatenanes (Fig. 1A) (1). Most of these topological entanglements are removed by Topos during replication, but those that remain form catenanes of circular genomes and braids of linear chromosomes. Both of these structures also are unlinked by Topos.

Fig. 1.

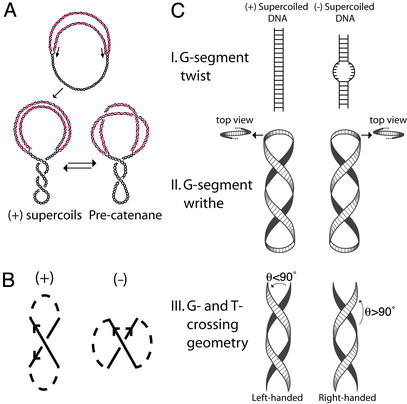
Structure of replication intermediates and models for Topo IV chirality sensing. (A) Replication intermediates. (Upper) A partially replicated circular chromosome, with parental DNA in black and progeny in red. During replication, unwinding of the parental DNA generates (+) supercoils, which may diffuse across the fork to form precatenanes. (B) Topological sign convention for DNA crossings. The orientation of crossing DNA segments is indicated by arrows and the connecting path is dashed. The sign of the crossing is determined by rotating the overlying strand by an angle ≤180° so that the arrows point in the same direction. If rotation is counterclockwise, the node is given a (+) sign. If clockwise, the node is given a (–) sign. (C) Three models for chirality sensing by Topo IV. Duplex DNA is represented by a ribbon. (Top) In the G-segment twist model, the enzyme detects differences in twist and/or the ease of denaturation of a bound G-segment. (Middle) In the G-segment writhe model, Topo IV recognizes the chirality of G-segment writhe at either an apex of the superhelix or elsewhere. For (+) supercoiled DNA, the superhelix is left-handed, and, for (–) supercoiled DNA, it is right-handed. (Bottom) In the G- and T-segment crossing geometry model, Topo IV senses the local geometry of DNA crossings imposed by the handedness of the superhelix. We define the angle of G- and T-segment juxtaposition (θ) by a counterclockwise rotation of the underlying segment (black) to the overlying segment (white). For a left-handed superhelix, θ < 90°, and, for a right-handed superhelix, θ > 90°.

Topos are divided into two classes depending on whether one (type I) or both (type II) strands of DNA are broken during topoisomerization (2). With type II enzymes, one DNA segment, called the transfer or T-segment, is passed through the gap of another DNA segment, designated the gate or G-segment (3). Type II Topos initially bind to the G-segment and subsequently capture the T-segment in an ATP-dependent manner. Next, the G-segment is transiently cleaved, to allow the passage of the T-segment. The free energy of ATP hydrolysis allows type II Topos to work energetically uphill to suppress DNA entanglements favored by the high concentrations of DNA found in vivo (4).

Bacteria possess two type II Topos, DNA gyrase and Topo IV. Gyrase has the unique ability among all Topos to introduce (–) supercoils into DNA. A steady state of (–) supercoiling in the chromosome is required for DNA compaction and for metabolic processes that melt DNA (5, 6). The (–) supercoiling also cancels the (+) supercoiling introduced by DNA replication. Topo IV ensures proper segregation of daughter chromosomes at the end of replication by removing any remaining (+) intertwinings (1, 7). Topo IV also can relax supercoils generated during transcription and is capable of replacing gyrase during replication elongation in vitro and partially in vivo (8, 9).

Topo IV relaxes (+) supercoiled DNA far more efficiently than (–) supercoiled DNA (10), contributing to elongation of the replication fork without simultaneously removing the (–) supercoils essential for the cell. It is unlikely that a Topo can discriminate between (+) and (–) supercoiling by direct detection of topological sign. An enzyme can detect the overlay and local orientation of crossing DNA segments, but topological sign also depends on the path of the DNA connecting the segments (Fig. 1B), which occurs over length scales much larger than the enzyme itself. Therefore, Topo IV must recognize some secondary local indicator of global topology. We can imagine three classes of models for the mechanism of chirality sensing (Fig. 1C).

In model I, G-segment twist recognition, Topo IV recognizes the difference in G-segment twist in (+) and (–) supercoiled DNA. (+) Supercoiling both increases twist and inhibits strand separation, whereas (–) supercoiling has the opposite effects. If this model were correct, Topo IV would then be the opposite of type IA Topos that preferentially relax (–) supercoils because DNA unwinding is essential to their activity (11).

In model II, G-segment writhe recognition, Topo IV senses the handedness of the DNA superhelix, which is left- or right-handed in (+) or (–) supercoiled DNA, respectively. Topo IV could interact with the G-segment along the helical path of the DNA or at the nonplanar apex of a plectoneme. The latter is promoted by the sharp bending of DNA that accompanies Topo IV binding (12).

In model III, Topo IV recognizes the geometric arrangement of G- and T-segments imposed by the superhelix. We define an angle (θ) between juxtaposed G- and T-segments. A (+) supercoiled molecule has left-handed superhelical crossings with θ < 90°, whereas a (–) supercoiled molecule has right-handed superhelical crossings with θ > 90° (13). The substrate specificity of Topo IV can be explained if the enzyme preferentially relaxes crossings with θ < 90°.

Experiments with supercoiled DNA molecules alone cannot be used to distinguish among these models because the potential specificity determinants in the aforementioned models are coupled in such molecules. A (+) supercoiled DNA is thermodynamically difficult to denature and has an increased twist, a left-handed superhelical path, and superhelical crossings with θ < 90°. A (–) supercoiled DNA has all of the opposite properties.

To distinguish among the three models, we combined single-molecule studies of enzymatic activity on right- and left-handed braids, with ensemble DNA binding experiments. DNA braids do not possess apical bends as does supercoiled DNA. Moreover, because the braided DNA molecules are nicked, braids of opposite handedness cannot have differences in helical twist. Thus, braids can be used to dissect the effects of the specificity determinants of Topo IV activity. We conclude that Topo IV's substrate specificity occurs through recognition of the appropriate geometric arrangement of the G- and T-segments, as depicted in model III. Moreover, distributions of crossing angles obtained from Monte Carlo simulations of braided, supercoiled, and catenated DNA conformations explain the diverse physiological roles of Topo IV by showing how an enzyme with a sharp preference for a left-handed crossing geometry can nonetheless efficiently unlink catenanes of the opposite superhelical handedness.

Materials and Methods

Measurement of DNA Binding by Topo IV. Linear 2.7-kb DNA was generated by digesting pUC18 with XbaI and then was end-labeled with ³²P by using T4 polynucleotide kinase. DNA binding reactions (15 μl) containing 50 mM Tris·HCl (pH 7.6), 20 mM potassium glutamate, 10 mM MgCl₂,2mMDTT,50 μg/ml BSA, and the indicated amounts of DNA and Topo IV were incubated at 30°C for 20 min. The mixture was passed through a Millipore slot blot apparatus that contained a nitrocellulose filter to capture DNA bound by Topo IV and a DEAE filter to capture the free DNA. The protocols have been described (14).

DNA Constructs for Optical Tweezers Assays. λ-Phage DNA (New England Biolabs) was cyclized, ligated, and digested with XbaI and KpnI. The 41-kb product was purified by agarose gel electrophoresis and ligated to DNA linkers (≈500 bp) generated by digestion of PCR products modified by either biotin-16-dUMP or digoxigenin-16-dUMP residues (Roche Molecular Biochemicals). To introduce a site-specific nick in the ligated construct, the biotin-labeled linker was dephosphorylated by treatment with calf intestinal phosphatase (Roche Molecular Biochemicals). To make 44-kb torsionally constrained molecules, p-PIA6 plasmid (15) was cut with BamHI and SalI. Trimers of the 14.8-kb digestion product were ligated to DNA linkers described above.

DNA Micromanipulation and Geometric Modeling of Braids. A dual-beam optical tweezers apparatus (16) was modified by the introduction of a rotating glass micropipette coupled to a computer-controlled dc motor. Video data were captured at 25 frames per second, and the displacements of the beads were analyzed by using a bead-tracking algorithm written for nih image. Braid compaction was calibrated as a function of the number of turns (n) and fit by using a geometric model: 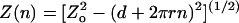, where Z(n) is the extension of a braid with n turns, Z_o is the maximal extension of the DNA, d is the distance between points of attachment of the two DNA ends on each bead, and r is the radius of the braid (G. Charvin, personal communication). For the calibration fits, the values of d and r(F) were allowed to vary. Z_o(F) is well fit by the worm-like chain model, and r(F) = r_o + AF^–(3/4) (G. Charvin, personal communication). (See ref. 17 and Fig. 7, which is published as supporting information on the PNAS web site, www.pnas.org.)

Enzyme and Braid Relaxation Reaction Conditions. Braid relaxation reactions contained 25 mM Tris·HCl (pH 7.6), 100 mM potassium glutamate, 10 mM MgCl₂,50 μg/ml BSA, 1.5 mM ATP, 5% glycerol, and purified Topo IV (18) (100–300 pM tetramer). DNA molecules were oriented in the optical tweezers by attaching the ends to a streptavidin-coated bead held by the micropipette and an anti-digoxigenin (polyclonal, Roche Molecular Biochemicals)-coated bead held in the optical trap (Fig. 3A). We determined that there were exactly two DNA molecules oriented between the beads by measuring the force needed to overstretch the tethers (≈65 pN for one nicked DNA and ≈130 pN for two DNAs) (see Fig. 8, which is published as supporting information on the PNAS web site; refs. 19 and 20). Turns were introduced into the DNA braids by rotation of the micropipette. Tension applied to the DNA braid was held constant by using stage-based force-feedback (16). Enzymatic activity was monitored by changes in the braid extension. We calibrated changes in braid extension by performing a two-point fit to the aforementioned geometric model, using the relaxed braid extension and the extension of the braided DNAs before the onset of Topo IV activity. Previously calibrated values for r(F) were used in the fits (Fig. 7), and the value of d was allowed to vary.

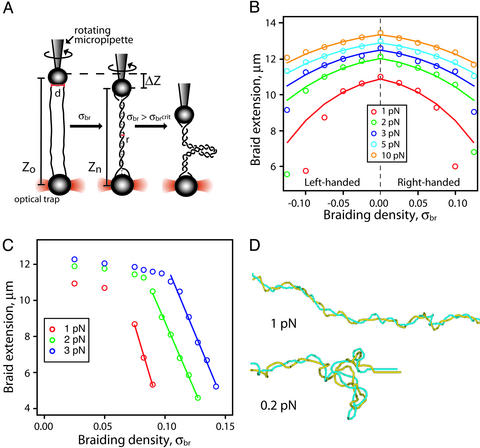
Fig. 3.

Characterization of a single-molecule DNA braiding system. (A) Two nicked DNA molecules (solid black lines) are oriented between one bead on a rotating micropipette and another bead held in an optical trap. As braiding density, |σ_br|, increases, the length of the braid, Z, diminishes gradually until a critical braiding density is reached, |σ_br^crit|, at which point the braid buckles, forms a second-order plectonemic superhelix, and shortens much more dramatically with each introduced turn. (B) Shortening of braids as a function of braid density. Braid length for σ_br < σ_br^crit can be approximated by a geometric model, 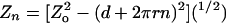, where Z_n is the extension of a braid with n turns, Z_o is the maximal extension of the braid, d is the distance between points of attachment of the two DNA ends on each bead, and r is the effective radius of the braid. Braid extensions are shown over a range of σ_br and tensions. ○, Experimental data; solid lines represent the fit to the model. (C) For |σ_br| > |σ_br^crit|, the braid compaction no longer obeys the simple model because of the buckling of the DNA braid into a plectonemic superhelix (second-order). The compaction of the braid in this regime is ≈35 nm for each additional turn. (D) Monte Carlo simulations of DNA braids. Braids of two individual 3.5-kb DNA molecules (blue and yellow) with a σ_br = 0.05, held under 1 pN or 0.2 pN of force, are shown.

Monte Carlo Simulations. A discrete worm-like chain model that also accounts for excluded volume and electrostatic interaction between the segments was used to simulate equilibrium sets of the braid conformations. The Metropolis simulation procedure used is described in the legend for Fig. 9, which is published as supporting information on the PNAS web site, and is analogous to that described for simulations of supercoiled and catenated DNA (21, 22).

Results

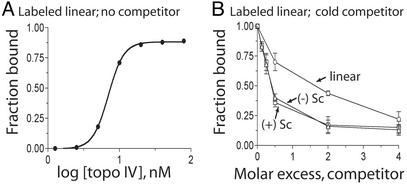
Topo IV Binding to Supercoiled DNA. To determine whether chirality sensing by Topo IV is due to preferential binding to (+) supercoiled DNA, we conducted competitive DNA binding assays with (+) supercoiled, (–) supercoiled, and linear DNA (Fig. 2). Binding of Topo IV to the G-segment alone should be sufficient to retain the DNA on the filter. Topo IV bound the linear form with a K_d of 7.5 nM, in close agreement with previous measurements (Fig. 2 A) (14). More than 80% of the linear DNA was complexed with Topo IV at saturating levels of enzyme (Fig. 2A). In competition experiments, we found that Topo IV has an ≈4-fold preference for binding supercoiled over linear DNA, but (+) and (–) supercoiled DNA competed equally well (Fig. 2B).

Fig. 2.

Binding of Topo IV to linear, (+) supercoiled, and (–) supercoiled DNA. (A) Reactions containing linear ³²P-labeled pUC18 (1.3 nM) were incubated in binding buffer and the indicated concentration of Topo IV for 20 min at 30°C. The fraction of DNA bound to Topo IV was determined by filter binding. (B) Topo IV binding to linear ³²P-labeled pUC18 was competed against unlabeled linear (○), (+) supercoiled (Sc) (▵), or (–) supercoiled (Sc) (□) DNAs. Error bars are the standard deviations of duplicate experiments.

This result implies that Topo IV binds the G-segment of (+) and (–) supercoiled DNA with equal affinity, providing evidence against models I and II, which fix substrate recognition at G-segment binding. The preference for supercoiled over linear DNA is likely due to the bending of DNA on Topo IV binding (12), which is energetically favored in both (+) and (–) forms of supercoiled DNA. Chirality sensing is likely at a step in the reaction cycle subsequent to G-segment binding but before G-segment cleavage, because (+) supercoiled DNA is cleaved preferentially (10). Recognition of G- and T-segment crossing geometry is the most likely step. We next tested this proposal directly.

Characterization of Single DNA Braids. To test the role of G- and T-segment geometry in Topo IV chirality sensing, we required DNA substrates with controlled superhelical geometry that are not supercoiled. [We restrict the term “supercoiled” to DNA molecules whose linking number is different from that of relaxed DNA (23) and use “superhelix” to refer to a helical conformation of any DNA. Thus, braided, catenated, and supercoiled DNA all can have a superhelical conformation.] Although it is possible to make right-handed catenanes, we know of no method for generating left-handed DNA catenanes. We therefore developed an optical tweezers-based system to generate right- and left-handed DNA braids by adapting existing single-molecule braiding techniques (24).

We braided two 41-kb nicked DNAs in a dual-beam optical tweezers apparatus with a rotating micropipette (Fig. 3A). This apparatus allows us to generate specific braiding densities and apply a wide range of tensions (16). We define braiding density (σ_br) as the number of turns introduced into the braid (n) divided by the total number of helical repeats in each DNA duplex (no. of base pairs/10.5). By convention, σ_br is (+) for right-handed braids and is (–) for left-handed braids. The compaction of the braid as a function of σ_br is symmetric about σ_br = 0 for all forces (Fig. 3B). Beyond a critical braiding density (σ_br^crit), which varied with force, the braid contracted rapidly with additional winding (Fig. 3C), attributable to buckling of the braid, to form a second-order plectonemic superhelix (Fig. 3A) (17, 21). At these high braiding densities, the data are no longer described by the geometric braid model. In accordance with the general properties of writhe, the handedness of the second-order superhelical crossings must be opposite that of the first-order superhelix (25).

To visualize the conformations of the braided DNA substrates, we performed Monte Carlo simulations of braids held under force. To conserve computational time, we simulated molecules that were only 3.5 kb in length but matched the σ_br to those used in our experiments. At a σ_br = 0.05 and a force of 1 pN, the braid has a fairly regular superhelical conformation (Fig. 3D, Upper). At 1 pN of force, it is computationally impractical to obtain an equilibrium set of conformations at the higher braid densities required to form a second-order plectonemic superhelix. However, we could easily see the expected second-order superhelical structures at σ_br = 0.05 in braids held at 0.2 pN (Fig. 3D, Lower).

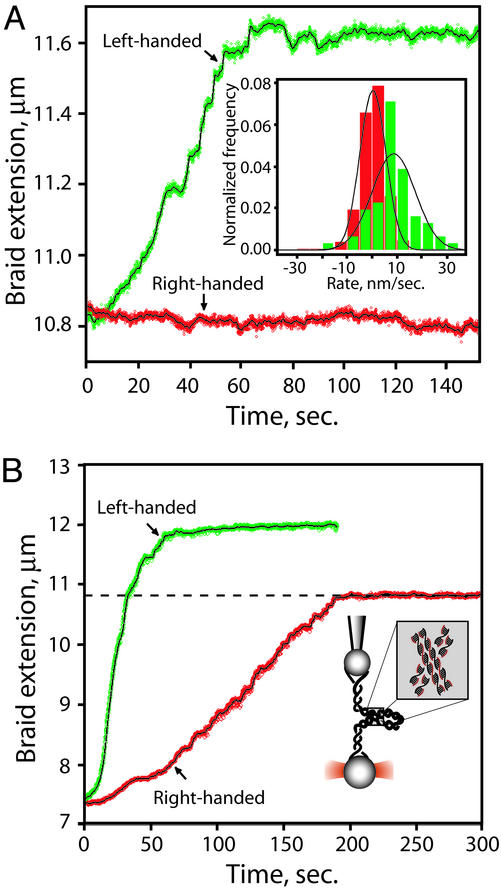
Topo IV Preferentially Relaxes Left-Handed DNA Crossings. We tested the ability of Topo IV to relax left- and right-handed braids. First, a left-handed first-order superhelix with σ_br = –0.05 was generated in the presence of 300 pM Topo IV. To prevent loss of turns during rotation of the micropipette, the braid was held at a tension of ≈30 pN, which completely inhibits Topo IV unbraiding. Once the desired σ_br was reached, we followed the activity of the enzyme by monitoring changes in extension of the braid held at constant tension (1 pN). We observed rapid and complete relaxation of the left-handed braid, as indicated by the restoration of the DNA molecules to their original unbraided extension (Fig. 4A, green). Immediately thereafter, a right-handed braid with an equal |σ_br| was generated. This braid was incubated at the same tension, but no relaxation was detected (Fig. 4A, red). A histogram of the unbraiding rates over successive 5-sec windows compiled from 10 independent experiments is shown (Fig. 4A Inset). The mean unbraiding rate, expressed as the change in extension per unit time, was 9 ± 1.4 nm/sec for left-handed braids and 0.3 ± 0.3 nm/sec for right-handed braids.

Fig. 4.

Topo IV unbraiding of single DNA braids. (A) Preferential relaxation of left-handed braids. Topo IV activity was assayed by monitoring the extension of the braids held under constant tension (1 pN). Raw data are plotted in green (left-handed braid) and red (right-handed braid), and a 1-sec moving average is shown as a solid black line. (Inset) Histogrammed rates of unbraiding were calculated as ΔZ/Δt for successive 5-sec windows in 10 independent runs each on right- and left-handed braids (|σ_br| = 0.05). To avoid effects of limiting substrate, only those portions of the traces where |σ_br| > 0.02 were included. The mean unbraiding rate was 9 ± 1.4 nm/sec for left-handed braids (green) and 0.3 ± 0.3 nm/sec for right-handed braids (red). (B) Topo IV relaxation of high-density DNA braids for |σ_br| > 0.15 and 2 pN of tension. The first-order DNA braid folds into a plectonemic second-order superhelix, with DNA crossings possessing the opposite handedness of the first-order superhelix. Symbols are as in A. The dashed black line is the extension for |σ_br^crit| at 2 pN.

Left-handed crossings also occur in the second-order helices formed in high-density right-handed braids. To test the ability of Topo IV to relax a left-handed second-order superhelix, we incubated high-density right-handed braids (σ_br > σ_br^crit =+0.13, 2 pN) with Topo IV (300 pM). Prompt relaxation was observed, which ceased when all of the left-handed second-order crossings were removed (i.e., σ_br = σ_br^crit) (Fig. 4B, red). In contrast, high-density left-handed braids were relaxed to completion by the removal of left-handed first-order crossings (Fig. 4B, green). These results with first- and second-order superhelices clearly show that Topo IV preferentially relaxes DNA crossings with a left-handed geometry, strongly supporting model III.

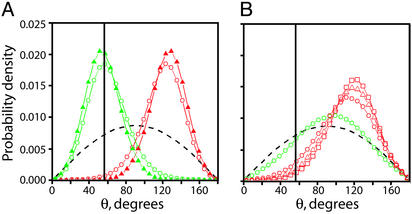
Distribution of DNA Crossing Angles in Supercoiled, Braided, and Catenated DNA. To investigate further the geometric basis of chiral discrimination, we used the conformations generated in Monte Carlo simulations to calculate distributions of DNA crossing angles (θ) for supercoiled, braided, and catenated DNA. The most probable crossing angle in both (+) supercoiled DNA and left-handed braids (σ_br = –0.05) is ≈60°; this angle is ≈25-fold less probable in (–) supercoiled DNA and right-handed braids (σ_br = +0.05), where the most probable angle is ≈120° (Fig. 5A). This difference suffices to rationalize the preferential activity of Topo IV on the left-handed superhelices in (+) supercoiled DNA and left-handed first-order braids.

Fig. 5.

Comparison of crossing segment juxtaposition angles in supercoiled, braided, and catenated DNA. (A) We define the angle of juxtaposed crossing segments (θ) for braids in Fig. 1C and analogously for supercoiled and catenated DNA. The angular distribution between juxtaposed segments of DNA in simulated 3.5-kb (+) supercoiled (σ =+0.05, green circles) and (–) supercoiled (σ = –0.05, red circles) DNA under no force is plotted along with the angular distribution between juxtaposed segments of DNA in simulated left-handed (σ_br = –0.05, green triangles) and right-handed (σ_br = +0.05, red triangles) braids of 3.5-kb nicked DNAs held under 1 pN of tension. For comparison, the distribution of crossing angles between randomly juxtaposed segments is shown (dashed black line). The vertical solid black line is at θ = 57°. (B) The angular distribution between juxtaposed segments of DNA in simulated DNA catenanes with σ_cat = 0.045 (red squares), 0.036 (red triangles), 0.024 (red circles), and 0.012 (green circles). The distribution of crossing angles between randomly juxtaposed segments is shown (dashed black line). The vertical solid black line corresponds to θ = 57°.

In vivo, Topo IV also relaxes right-handed precatenanes and catenanes. To address how an enzyme with a strong preference for left-handed crossing angles can relax right-handed substrates, we calculated the distribution of crossing angles in simulated DNA catenane conformations (Fig. 5B). At catenation densities comparable with those observed in vivo in the absence of Topo IV activity (σ_cat = 0.01) (26), the angular distribution approaches that of randomly juxtaposed segments (Fig. 5B, dashed black line). These results suggest that the loosely catenated substrates encountered in vivo often adopt a left-handed crossing geometry and thus can be efficiently relaxed by Topo IV.

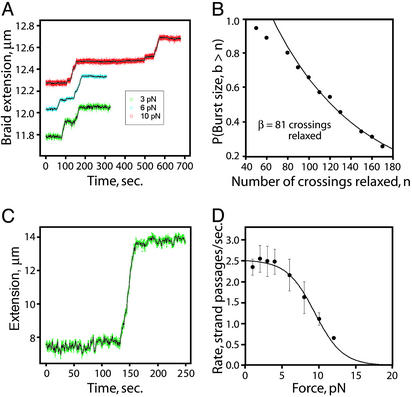
Processivity and Force-Dependent Rate of Unbraiding by Single Topo IV Molecules. The above unbraiding results were obtained at enzyme concentrations at which several enzymes likely acted simultaneously. To study the activity of single Topo IV molecules, we reduced the enzyme concentration to 100 pM. At these concentrations, extended waiting times were observed between periods of unbraiding action, corresponding to single enzyme molecules acting at a time (Fig. 6A) (27).

Fig. 6.

Relaxation of braids by single Topo IV molecules. (A) Representative single-enzyme traces are shown for the indicated tensions and σ_br = –0.05. (B) Processivity of unbraiding by single Topo IV molecules. The burst sizes (b) from 31 experiments are plotted as a cumulative histogram. Fitting of this histogram with a single exponential (neglecting undersampled short burst sizes) yields a decay constant (β) of 81 crossings. (C) Processive relaxation of a 44-kb (+) supercoiled DNA. A representative single Topo IV molecule supercoil relaxation experiment is shown for a DNA molecule (σ = +0.03) held at 0.7 pN. Seventy-five crossings were relaxed in a single burst. (D) The effect of force on the rate of Topo IV unbraiding. The rates of relaxation were determined over each burst of activity and were fit to v(F) = v_o/[1 + (v_o/v₁)e^{(0.5FΔx)/(kT)}] (black line), where v(F) is the reaction velocity at force F, k is Boltzmann's constant, T is temperature, and v_o is the rate of the force-independent kinetic step. For the force-dependent step, v₁ and Δx are, respectively, the unperturbed rate and the distance along the pulling axis to the transition state. (v_o = 2.5 catalytic cycles per sec, v₁ = 360 catalytic cycles per sec, and Δx = 4.3 nm.)

Topos can relax many DNA crossings before dissociation from the substrate, presumably as a result of multiple captures of T-segments for every G-segment binding event. Burst sizes (b, defined as the number of crossings relaxed during a period of activity) from 31 experiments (F = 1–4 pN) are plotted in a cumulative histogram along with a fit to a single exponential, yielding a characteristic burst size (β) of ≈80 crossings, corresponding to a processivity k_forward/(k_forward + k_off) = 99%. (Fig. 6B). The departure from the fit for small burst sizes may be because of undersampling of short periods of activity. To ensure that this high processivity is not specific to relaxation of DNA braids, we measured the relaxation of 44-kb supercoiled DNA molecules by a single Topo IV enzyme. In this experiment, all 75 DNA crossings were often relaxed in a single burst of activity, consistent with the processivity of DNA braid relaxation (Fig. 6C).

Previous single-molecule studies of Drosophila Topo II activity demonstrated an exponential decrease in the rate of supercoil relaxation with increasing tension (27). Tension-dependent effects on Topo activity on DNA braids are easier to interpret than on supercoiled molecules because tension is applied directly along the braid axis. In contrast, the applied tension in not uniformly distributed for supercoiled molecules and falls to near zero in the plectonemic region, where the enzyme acts. The rate of Topo IV unbraiding of left-handed braids (σ_br = –0.05) was unaffected by tensions up to 4 pN, indicating that under these conditions the rate-limiting step is not force-dependent. In this force range, Topo IV relaxes left-handed braids at a rate of 2.5 ± 0.14 crossings per sec (n = 31), in agreement with the single-molecule (+) supercoil relaxation rate (10). A further increase in tension resulted in an exponential decay in the rate of braid relaxation. Fitting these data to a simple Arrhenius model (28) suggests that the enzyme undergoes a force-sensitive conformational change over a distance of 4.3 nm to reach a transition state of the force-sensitive step (Fig. 6D). This may reflect the range of motion necessary to religate the cleaved DNA ends of the G-segment after passage of the T-segment (27, 29).

Discussion

Mechanism of Topo IV Chirality Sensing. We systematically tested three models for chirality sensing by Topo IV: recognition of G-segment twist (model I), G-segment writhe (model II), and the geometric arrangement of G- and T-segment crossings (model III) (Fig. 1C). Precedence for model I is provided by type IA Topos, which relax only (–) supercoiled DNA because of their requirement for single-stranded DNA (30). However, model I is conclusively eliminated by the results obtained here on braids of nicked DNA. Thus, chirality sensing by Topo IV cannot be mediated through changes in twist.

Recently, model II was analyzed quantitatively by using Monte Carlo simulations, which showed that a left-handed, nonplanar bend in the G-segment could explain the chiral discrimination of Topo IV (31). However, the results of our binding experiments imply that Topo IV does not discriminate between (+) and (–) supercoiled DNA at the level of G-segment binding (Fig. 2B).

Our finding that Topo IV relaxes left-handed DNA braids far more efficiently than right-handed braids (Fig. 4A) strongly supports model III. The model is further supported by the selective relaxation of high-density right-handed braids that possess second-order superhelices with left-handed crossings (Fig. 4B).

Model III is consistent with previous observations of chirality sensing. First, Topo IV preferentially cleaves (+) supercoiled DNA (10). This might seem paradoxical, as strand passage is not needed for G-segment cleavage. However, there is clear evidence that T-segment binding promotes cleavage for two other type II Topos (32, 33). Second, the preferential relaxation of (+) supercoiled DNA is due to both an increase in the rate of the initial strand passage and the processivity of relaxation. With (+) supercoiled DNA, crossing strands are already in a favorable configuration for binding to the enzyme. However, with (–) supercoiled DNA, each strand passage would require a reorganization of the substrate to bind the T-segment properly, thereby increasing the probability of dissociation of the enzyme.

These results provide constraints on the existing view of the reaction sequence of type II Topos. First, the Topo binds to a G-segment. Subsequent to G-segment binding but before G-segment cleavage, a T-segment with the preferred geometry is bound. Once bound to both G- and T-segments, the enzyme is activated for cleavage and strand passage. The requirement for proper G- and T-segment orientation in the substrate prevents unproductive DNA cleavage, which might otherwise expose the cell to the hazards of a double-strand break.

Processivity of Topo IV. Processivity in Topos must operate by a different mechanism than for DNA tracking enzymes such as polymerases, helicases, and nucleases, in which the key is efficient translocation between successive catalytic events. A processive type II Topo must capture and pass many consecutive T-segments for a single G-segment binding event. After each strand passage through a G-segment and the enzyme, the T-segment must be released and the conformation of the substrate DNA must reequilibrate to provide another T-segment in the proper orientation. Previous estimates of the processivity of Topos were limited by the amount of substrate presented to the enzyme (10). Our experiments on 41-kb DNA braids enabled us to introduce 200 turns, showing that Topo IV is highly processive, relaxing ≈80 DNA crossings in a single burst of activity (Fig. 6 B and C).

Further Implications. Because of its chirality sensing, Topo IV can aid gyrase in promoting replication fork progression by relaxing (+) supercoils ahead of the fork without continuously relaxing the essential (–) supercoils in the bacterial chromosome. The Monte Carlo simulations of supercoiled, braided, and catenated DNA demonstrate how Topo IV, possessing a strong preference for left-handed DNA crossings, can relax all of its in vivo substrates. All of the activities of Topo IV are consistent with an optimal crossing angle of ≈60°, which is the most probable angle in (+) supercoiled DNA, highly probable in left-handed braids, improbable in (–) supercoiled DNA and right-handed braids, and easily accessible in loose right-handed precatenane and catenane structures (Fig. 5 A and B). Future single-molecule unbraiding experiments should be able to determine precisely the optimal crossing angle for Topo IV. This angle might, in principle, be observed in a crystal structure of Topo IV bound to both G- and T-segment DNA.

The mechanism of chirality sensing by Topo IV presented here is directly analogous to the resolution of another previously puzzling phenomenon, site orientation specificity for site-specific recombination. In a supercoiled DNA molecule, enzymes belonging to the resolvase family will recombine only sites that are directly repeated (head-to-tail orientation), whereas invertases recombine only sites with an inverse orientation (head-to-head) (6, 34). The basis of this selectivity is the specific DNA crossing geometry imposed by supercoiled DNA. The initial experiments showing this selectivity involved the replacement of the supercoiled substrate by nicked, knotted, or catenated DNA (34, 35). These results parallel the Topo IV results presented here and suggest that the importance of the geometry of DNA crossings may be a more general phenomenon in proteins that bind supercoiled DNA.