¹⁸O Spatial Patterns of Vein Xylem Water, Leaf Water, and Dry Matter in Cotton Leaves

Abstract

Three leaf water models (two-pool model, Péclet effect, and string-of-lakes) were assessed for their robustness in predicting leaf water enrichment and its spatial heterogeneity. This was achieved by studying the ¹⁸O spatial patterns of vein xylem water, leaf water, and dry matter in cotton (Gossypium hirsutum) leaves grown at different humidities using new experimental approaches. Vein xylem water was collected from intact transpiring cotton leaves by pressurizing the roots in a pressure chamber, whereas the isotopic content of leaf water was determined without extracting it from fresh leaves with the aid of a purpose-designed leaf punch. Our results indicate that veins have a significant degree of lateral exchange with highly enriched leaf water. Vein xylem water is thus slightly, but progressively enriched in the direction of water flow. Leaf water enrichment is dependent on the relative distances from major veins, with water from the marginal and intercostal regions more enriched and that next to veins and near the leaf base more depleted than the Craig-Gordon modeled enrichment of water at the sites of evaporation. The spatial pattern of leaf water enrichment varies with humidity, as expected from the string-of-lakes model. This pattern is also reflected in leaf dry matter. All three models are realistic, but none could fully account for all of the facets of leaf water enrichment. Our findings acknowledge the presence of capacitance in the ground tissues of vein ribs and highlight the essential need to incorporate Péclet effects into the string-of-lakes model when applying it to leaves.

The isotopic composition of leaf water reflects local humidity, and its imprints on plant cellulose and other fossil materials have been widely explored for palaeoclimatic reconstruction. To date, isotopic values of wood cellulose (Epstein et al., 1977; Yapp and Epstein, 1982; Edwards et al., 1985; Edwards and Fritz, 1986; Roden et al., 2000), grassland phytoliths (Webb and Longstaffe, 2000), and deer bone (Cormie et al., 1994) have been shown to be related to leaf water isotopic composition. Leaf water isotopic signature is not only imprinted on plant organic matter but is also recorded in atmospheric CO₂ and O₂. The CO₂ interacts and undergoes isotopic exchange with leaf water, and O₂ is released by the plant during photosynthesis. Changes in the oxygen isotope ratios of CO₂ and O₂ can thus be used to study variations in the net exchange of CO₂ in terrestrial ecosystems (Farquhar et al., 1993) and in the balance of terrestrial and marine productivity (Bender et al., 1985; Bender et al., 1994). Because all of these applications critically depend on estimation of the leaf water oxygen isotopic ratio, a good understanding of the nature of leaf water enrichment is needed.

The isotopic composition of leaf water is most commonly estimated from the model of a freely evaporating water surface (Craig and Gordon, 1965) where isotopic fractionation is driven by the lower vapor pressure and diffusivity of the heavier molecules. Although the Craig-Gordon model basically describes water enrichment at the sites of evaporation compared with locally transpired water, it cannot adequately account for other aspects of leaf water enrichment, particularly the spatial variation of leaf water ¹⁸O and/or D contents (Luo and Sternberg, 1992; Bariac et al., 1994; Wang and Yakir, 1995; Helliker and Ehleringer, 2000). Also, the Craig-Gordon model has often been found to overestimate the isotopic enrichment of bulk leaf water (Allison et al., 1985; Bariac et al., 1989; Walker et al., 1989; Walker and Brunel, 1990; Yakir et al., 1990; Flanagan et al., 1991a, 1991b, 1994; Wang et al., 1998). To explain such observations, several other models have been suggested in conjunction with the Craig-Gordon model, namely the two-pool model (Leaney et al., 1985), the Péclet model (Farquhar and Lloyd, 1993), and the string-of-lakes model (Gat and Bowser, 1991). The objective of this paper is to examine and assess the applicability of these various leaf water models by studying the ¹⁸O spatial patterns of vein xylem water, leaf mesophyll water, and dry matter in cotton (Gossypium hirsutum) leaves at different humidity treatments. To accomplish this, new experimental approaches are employed in the direct collection of vein xylem water from an intact transpiring leaf using a root pressure chamber and in the isotopic measurement of leaf water without extracting it from the leaves with the aid of a purpose-designed leaf punch. Bleeding xylem water directly from the petiole and veins of intact plants should give a good representation of the transpiration stream entering the leaf mesophyll cells. This technique allows us to map the isotopic gradient along the main water flow in leaf veins.

Applying the Craig-Gordon model to leaves (Dongmann et al., 1974; Farquhar et al., 1989), the isotopic enrichment of leaf water above source water (Δ_lw) at the evaporative sites of intercellular air spaces would be equal to the Craig-Gordon prediction (Δ_C) where

1

where Δ_v is the isotopic composition of atmospheric water vapor relative to source water. The water vapor pressures in the atmosphere and intercellular spaces are e_a and e_i, respectively, ε* is the equilibrium fractionation factor arising from the lower vapor pressure of H₂¹⁸O molecules at liquid-vapor phase equilibrium, and ε_k is the kinetic fractionation factor caused by the lower diffusivity of heavy H₂¹⁸O molecules. Equation 1 assumes that isotopic steady state has been achieved, where the isotopic composition of transpired water (δ_E) equals the value of source water (δ_S). In calculating the kinetic fractionation factor, the different layers of boundary resistance developing from the leaf evaporative sites to the fully turbulent atmospheric air need to be considered. The boundary layer is fully stagnant in the leaf substomatal air spaces (¹⁸O kinetic fractionation, 28.5‰), whereas a laminar flow is expected near the leaf surface (¹⁸O kinetic fractionation, 18.9‰). Taking into account the weighted effects of these different boundary layers, Farquhar et al. (1989) expressed the overall kinetic fractionation as

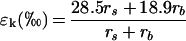2

where r_s and r_b are the leaf stomatal and boundary layer resistances to water vapor diffusion, respectively. An alternative method to calculate ε_k is described by Buhay et al. (1996), taking leaf size and morphology into consideration.

To explain the observation that bulk leaf water is less enriched than that predicted by the Craig-Gordon model, Leaney et al. (1985) described leaf water as consisting of two pools: evaporatively enriched leaf tissue water and isotopically unaltered vascular water (Fig. 1A). On the basis of this definition, the isotopic composition of bulk leaf water (δ_{lw, bulk}) could simply be expressed as

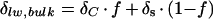3

where f is the fraction of leaf water subject to fractionation and δ_C is the isotopic composition predicted from the Craig-Gordon model (Eq. 1) with Δ_C = δ_C − δ_s. To reconcile the differences between the observed and Craig-Gordon predicted isotopic ratios, the fraction of vein water would have to be in the range of 25% to 50% total leaf water (Leaney et al., 1985; Walker et al., 1989). After the removal of the mid-vein from leaves of Betula occidentalis and Populus angustifolia, the estimated unenriched water fraction in the remaining leaves was reduced to 10% (Roden and Ehleringer, 1999).

Figure 1.

Box-diagram representation of the leaf water models. A, Two-pool model; B, Péclet model; C, string-of-lakes model; and D, Péclet-continuous evaporative enrichment model incorporating ground tissue capacitance. In the last model, the left compartment represents vein ribs and is further divided into two components: the capacitance arising from rib ground tissue and vein xylem water. The right compartment represents leaf lamina tissue water. The intensity of shading indicates the extent of leaf water enrichment. Double-headed arrows represent a Péclet effect, where the advection of unenriched water from the transpiration stream opposes the back-diffusion of enriched water; a bigger arrowhead implies a larger contribution in that direction.

Farquhar and Lloyd (1993) modified the physical model of a single-leaf water pool to one having a continuum of isotopic composition (Fig. 1B). They proposed that advection of unenriched water via the transpiration stream opposes the back-diffusion of enriched water from evaporation sites (Péclet effect). A continuous isotopic gradient is thereby created within the leaf. The enrichment at the leaf evaporative sites (δ_e) can be described by Equation 1 and is proposed to decay exponentially to the isotopic signature of source water (δ_s) at the veins. An integration of this isotopic variation would give a lower isotopic enrichment of bulk leaf water above source water (Δ_{lw, bulk}),

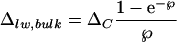4

where leaf Péclet number, ℘ = EL/CD. In the latter term, E is transpiration rate, L is the scaled effective path length of water between the xylem and sites of evaporation in leaves, C is the molar concentration of water (55.5 × 10³ mol m⁻³), and D is the diffusivity of H₂¹⁸O in water (2.66 × 10⁻⁹ m² s⁻¹). Equation 4 also predicts an increasing disparity between measured Δ_{lw, bulk} and the Craig-Gordon predicted Δ_C with increasing transpiration rate. The Péclet model not only accounts for the lower than expected enrichment of bulk leaf water but also predicts, in principle, the nonuniform isotopic distribution of leaf water at the small scale between stomata and xylem. However, the Péclet model based on Equation 4 is unable to describe variation of isotopic enrichment on a larger scale.

An explanation for the larger scale spatial variation of leaf water was provided by Yakir (1992), who suggested that the isotopic gradient within a leaf could be a consequence of enrichment along the path of evaporation (Fig. 1C). This is analogous to a string of evaporating lakes along a river. In this string-of-lakes model, the outflow from one evaporating element enters into the next element in the series, leading to a progressive enrichment of heavy isotopes along the path of water flow. A formulation of this model is given by Gat and Bowser (1991):

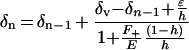5

where δ_v is the isotopic composition of atmospheric water vapor, δ_n is that of liquid water entering the nth evaporating element, F₊ and E represent the influx and evaporative efflux of the nth element, h is the relative humidity (RH) and, ε = ε* + (1 − h)ε_k.

Direct and indirect leaf water measurements supporting the different leaf water models have been reported: Craig-Gordon model (Roden and Ehleringer, 1999), Péclet model (Walker et al., 1989; Flanagan et al., 1991b; Barbour et al., 2000), and string-of-lakes model (Yakir, 1992; Wang and Yakir, 1995; Helliker and Ehleringer, 2000, 2002). Given the importance of leaf water modeling to studies of plant-environment interactions, there is a pressing need to reconcile these apparently disparate results. To assess best the applicability of the various leaf water models, we examined the ¹⁸O content of water along its pathway in the leaf, from the petiole to the vein network and then to the lamina tissue. The first step in our study was to clarify the extent of enrichment in vein xylem water, which is presumed to be unfractionated and to have the same isotopic composition as soil water (Leaney et al., 1985). Next, for a better representation of the lamina tissue water, we removed uncertainties such as the inclusion of vein water in leaf water measurements. This was achieved using a purpose-designed leaf punch that cuts and seals a small leaf disc sample for direct pyrolysis during isotopic measurements. The ¹⁸O content of the leaf dry matter, which provides an integrated record of leaf water isotopic composition, was analyzed as a check on the results from leaf water measurements. Last, distribution of stomatal and venation densities across the leaf were studied to assess the possible anatomical basis for spatial heterogeneity of leaf water.

RESULTS

Δ¹⁸O Patterns of Vein Xylem Water

Water expressed from the petiole (δ_petiole = −6.6‰ ± 0.1‰ [± se], n = 28) was not significantly more enriched than the tap water (δ_s = −6.8‰ ± 0.1‰, n = 28) used to water the plants. At low humidity (vapor-pressure deficit [VPD] of air, 2.4 kPa), the oxygen isotopic composition of petiole water (δ_petiole = −6.5‰ ± 0.1‰, n = 13) was similar to its high-humidity (VPD of air, 1.0 kPa) counterpart (δ_petiole = −6.7‰ ± 0.1‰, n = 15). In contrast to the common assumption that the water pool in leaf veins was unaltered with respect to the source water, we noted an increasing ¹⁸O enrichment as xylem water moves along a vein (Fig. 2). At low humidity, enrichment of xylem water above petiole water (Δ_vw) around the mid-point of the primary veins was usually lower (0.07‰–0.4‰) than that at high humidity (0.5‰–0.9‰; Fig. 2A). However, enrichment near the distal tip of the primary veins was similar (1.6‰–1.7‰) at both levels of humidity. Compared with primary veins, secondary veins (Fig. 2B) showed a higher degree of enrichment ranging from 0.7‰ to 3.6‰. As before, upstream xylem water showed less enrichment (0.7‰–1.6‰) than downstream water near the vein endings (1.5‰–3.6‰). It appears that xylem water near the vein endings tends to be more enriched at low humidity than at high humidity, whereas no consistent humidity-driven difference is observed for the upstream xylem water of secondary veins.

Figure 2.

Spatial distribution of vein xylem water isotopic composition (Δ_vw, ‰) in cotton leaves at low (top line) and high (bottom line) humidities. Given alongside in brackets is Δ_vw/Δ_C expressed as a percentage, indicating the proportion contributed by back-diffusion of enriched water from leaf evaporative sites. Δ_C refers to the enrichment of leaf water above source water (expressed from the petiole) and is calculated according to the Craig-Gordon model (Eq. 1). Mean δ_petiole were −6.5‰ and −6.7‰ at low and high humidities, respectively. Values of δ_v and e_i are taken from the experiments on leaf water sampling. The calculated Δ_C are 19.0‰ (low humidity) and 14.0‰ (high humidity). Data of Δ_vw represent the average of three samples on different days. The mean vapor pressure deficits of air at low (RH 44%) and high (RH 75%) humidities were 2.4 and 1.0 kPa, respectively. The letters A through F indicate vein incision locations for data in Table I.

To compare the two humidity treatments, we were careful in our choice of incision locations, ensuring that the relative positions of various sap collection points were retained. However, there is natural variation of venation from leaf to leaf. We also noted that the isotopic signature of xylem water near the vein endings where veins begin to taper was highly variable (deduced from the larger se; data not shown). Rather than comparing results from two leaves of different treatments, as presented in Figure 2, comparison is made from the same leaf with the same sap collection points by changing the ambient humidity during the experiment. On the basis of leaf water volume and transpiration rate, we estimated the leaf water turnover time to be approximately 9 min at low humidity and 16 min at high humidity. Hence, 1 h after a humidity step change was assumed to be sufficient in achieving a new isotopic steady state. In either a step change from low to high humidity or vice versa (Table I), xylem water was mostly more enriched at low humidity, with several incision points showing a humidity-driven change in enrichment as high as 2.7‰. When Δ_vw is normalized against Δ_C (the enrichment expected for leaf water according to Eq. 1), the difference between humidity treatments is not as distinct, even though the low-humidity leaves generally show higher Δ_vw/Δ_C values. The results also demonstrate that on approaching the vein endings, the xylem water was enriched by 0.13 to 0.17 Δ_C. The effect of humidity change on gas exchange parameters is summarized in Table I. In general, increasing humidity led to an increase in stomatal conductance and was accompanied by a decrease in transpiration rate and modest changes in assimilation rates.

Table I.

Δ_vw (‰) and Δ_vw/Δ_C of vein xylem water collected from various incision points (refer to Fig. 2 for location) before and after a step change of humidity (H) for two different cotton leaves (first line for leaf 3, second line for leaf 4) of the same plant

	Δvw (‰)						Δvw/ΔC
	Low → High humidity			High → Low humidity			Low → High humidity			High → Low humidity
	Low H	High H	Difference	High H	Low H	Difference	Low H	High H	Difference	High H	Low H	Difference
Incision
A	1.4	1.3	−0.1	1.7	2.2	0.5	0.08	0.09	0.02	0.12	0.11	−0.01
	2.2	1.2	−1.0	1.7	1.9	0.2	0.12	0.09	−0.03	0.12	0.10	−0.02
B	2.4	1.0	−1.4	1.9	2.6	0.7	0.13	0.07	−0.05	0.13	0.13	0.00
	1.3	1.3	0.0	1.9	1.9	0.0	0.07	0.10	0.03	0.14	0.10	−0.04
C	4.2	1.6	−2.7	1.6	2.6	1.0	0.23	0.11	−0.11	0.11	0.13	0.02
	3.5	2.3	−1.2	2.5	3.4	0.9	0.19	0.17	−0.02	0.18	0.18	0.00
D	3.4	1.1	−2.3	1.8	1.9	0.1	0.18	0.08	−0.10	0.13	0.10	−0.03
	3.1	2.0	−1.1	1.9	2.6	0.7	0.16	0.14	−0.02	0.13	0.13	0.00
E	4.2	2.0	−2.2	1.7	3.7	2.0	0.23	0.14	−0.08	0.12	0.19	0.07
	2.7	2.0	−0.7	2.2	4.4	2.2	0.14	0.15	0.00	0.15	0.23	0.07
F	4.6	2.8	−1.8	1.4	3.4	2.0	0.24	0.20	−0.04	0.10	0.18	0.08
	4.4	3.2	−1.2	2.0	3.0	1.0	0.23	0.23	−0.01	0.14	0.16	0.01
Mean	3.1	1.8	−1.3	1.9	2.8	0.9	0.17	0.13	−0.04	0.13	0.14	0.01
se	0.3	0.2	0.2	0.1	0.2	0.2	0.02	0.01	0.01	0.01	0.01	0.01
Gas-exchange parameters
gs (mol m−2 s−1)	0.47	0.75	0.3	0.86	0.37	−0.5
E (mmol m−2 s−1)	11.2	7.5	−3.7	8.0	9.6	1.6
A (μmol m−2 s−1)	24.0	24.8	0.8	25.1	21.8	−3.3

Collection of xylem water was made from the same incision points 1 h after the step change in humidity. The vapor pressure deficits of air at low (RH 46%) and high (RH 80%) humidity were 2.3 and 0.8 kPa, respectively. Δ_C refers to the enrichment of leaf water above source water (expressed from the petiole, δ_s = −6.8‰) that is calculated according to the Craig-Gordon model (Eq. 1). Values of δ_v and e_i were taken from the experiments on leaf water sampling. For low → high humidity experiment, Δ_C = 18.7‰ (low humidity) and 13.8‰ (high humidity); high → low humidity experiment, Δ_C = 19.3‰ (low humidity) and 14.1‰ (high humidity). Different plants were used for each humidity step change experiment. Gas exchange data were recorded for leaf 5 of both plants throughout the experiment. Parameters g_s, E, and A refer to stomatal conductance to water vapor diffusion, transpiration rate, and assimilation rate, respectively.

Δ¹⁸O Patterns of Leaf Water and Organic Matter

A typical Δ¹⁸O pattern of leaf mesophyll water for a cotton leaf is shown in Figure 3. Leaf water clearly is not isotopically uniform spatially and varies by as much as 10‰ at low humidity. Closer examination shows a trend to more enriched waters at the leaf edge and intercostal regions, whereas discs at the leaf base and adjacent to major veins are often less enriched. This enrichment pattern is seen to be more distinct when Δ_lw (the observed enrichment of leaf water over petiole water) is plotted against Δ_C for the 6 d of sampling (Fig. 4). The isotopic compositions of leaf water from marginal and intercostal regions mostly fall above the 1:1 line, indicating enrichment above that predicted by the Craig-Gordon model. Those adjacent to veins and at the leaf base are generally more depleted than expected from the model.

Figure 3.

A typical Δ¹⁸O (‰) spatial variation of cotton leaf mesophyll water for the four lamina regions (margin, intercostal, venous, and basal) at low humidity (RH 40%; VPD of air, 2.4 kPa). The Craig-Gordon values of Δ_C (‰) = 22.1 (margin), 23.6 (intercostal), 23.9 (venous), and 24.4 (basal). Variation of Δ_C is attributable to the gradual increase of leaf temperature with progressive sampling from the margin to the base. Leaf discs containing a visible fine vein are excluded from this representation.

Figure 4.

Comparison of the measured Δ_lw and Craig-Gordon predicted Δ_C of leaf water for the four lamina zones (margin [x], intercostal [+], venous [○], and basal [□]) of cotton leaves at low (black symbols) and high (gray symbols) humidities. Three leaves sampled on different days are shown for each humidity treatment. The mean vapor pressure deficits of air at low (RH 35%) and high (RH 75%) humidities were 2.8 and 1.0 kPa, respectively. The line represents a 1:1 relationship.

At high humidity, there is less spatial heterogeneity of leaf water, where for certain days, enrichment at the leaf edge could be small or the venous region could be equally or more enriched than that predicted (Fig. 5A). The relatively more homogeneous isotopic pattern at high humidity is also apparent in the leaf dry matter (Fig. 5, B and C) where there is no significant difference in Δ_om (isotopic enrichment of leaf dry matter over source water) from one leaf zone to another. Leaves grown in low humidity generally have significantly higher Δ_om in the margin and intercostal regions and lower values for the venous and basal regions. This reflects the measured isotopic pattern of leaf water. Figure 6 shows that the adaxial stomatal densities of the four leaf zones were not significantly different from one another. However, the abaxial stomatal density of the intercostal region was slightly higher than that of the other three zones.

Figure 5.

Spatial differences in the four lamina regions (margin, intercostal, venous, and basal) of cotton leaves. A, Δ_lw − Δ_C (same data set as Fig. 4); B, oxygen isotope composition of leaf dry matter, Δ_om, obtained from leaf punches; C, Δ_om, obtained from trimming, at low and high humidities. The mean vapor pressure deficits of air at low (RH 35%) and high (RH 75%) humidities were 2.8 and 1.0 kPa, respectively. For A and B, each set of bars represents a leaf sample. For C, each set of bars represents six leaf samples. Error bars represent se (n = 2–17). High-humidity treatments are gray.

Figure 6.

Stomatal densities on the four leaf lamina regions of a cotton leaf. Adaxial (white) and abaxial (gray) stomatal densities are expressed as number of stomata per square millimeter of leaf surface. Error bars represent ses (n = 3–4).

DISCUSSION

¹⁸O Spatial Variation of Vein Xylem and Leaf Water

Water expressed from the petiole of an intact cotton plant was not significantly more enriched than the tap water used to water the plants. This is in agreement with previous observations (White et al., 1985; Bariac et al., 1989, 1994) that there is little fractionation associated with uptake of soil water by roots, or its subsequent movement up the stem. An exception would be the fractionation of hydrogen isotopes in mangroves (Lin and Sternberg, 1993). The absence of isotopic fractionation during water uptake by most plants has previously been used to support the assumption that water in leaf veins would similarly be unenriched relative to the soil water (Leaney et al., 1985). Previous sampling of vein water by pressurizing a detached leaf in a pressure chamber indicated good agreement between the isotopic composition of irrigation water and that assigned to vein water (Yakir et al., 1989). In contrast, based on vacuum distillation of excised vein segments, δ²H of vein water had been shown to increase along the main vein from the leaf base to the tip (Luo and Sternberg, 1992). The data of Figure 2 give direct evidence of xylem water enrichment in the leaf veins of an intact transpiring leaf. One possible contribution to the enrichment of vein water is the back-diffusion of enriched water from evaporative sites on the leaf lamina. The report of the lateral escape of tritiated water from the xylem vessels of tomato (Lycopersicon esculentum) internodes being driven by diffusion (van Bel, 1976) lends support to this hypothesis. The tritiated water moved down a concentration gradient and was mostly absorbed in the cells and cell walls around the xylem vessels. The idea of progressive enrichment of vein water by tissue water was first mooted by Yakir (1992) and elaborated by Wang and Yakir (1995) and Helliker and Ehleringer (2000) to explain the spatial heterogeneity of leaf water. This phenomenon is strongly supported by our observations that the isotopic composition of xylem water in veins (δ_vw) is responsive to changes in environmental conditions such as humidity (Table I). Water at the evaporative sites is more enriched at lower humidity and the back-diffusion of this highly enriched water will consequently increase the extent of vein water enrichment at low humidity. δ_vw could be expressed mathematically as

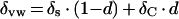6

where d is the proportional contribution by back-diffusion of enriched water from leaf lamina. In terms of enrichment over source water, Equation 6 can be re-expressed as

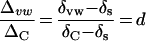7

The term Δ_vw/Δ_C thus reflects the proportion of vein water contributed by back-diffusion of enriched water. Figure 2 shows that Δ_vw/Δ_C increases downstream along the vein and in secondary veins compared with primary veins. This implies that back-diffusion is actively occurring throughout the vein length regardless of the vein type. Thus, enriched water continues to accumulate within the veins in the direction of water flow.

Isotopic enrichment of leaf water (Δ_lw) from the leaf base to the tip has been observed in several crop plants by Wang and Yakir (1995). Our results indicate that leaf water enrichment should be more dependent on the relative distances from major veins because discs sampled adjacent to the veins are noted to have smaller Δ_lw (Fig. 3). In general, leaf water from the marginal and intercostal regions is more enriched than the Craig-Gordon prediction, whereas that from sites adjacent to veins and at the leaf base is more depleted than expected (Figs. 4 and 5). This pattern is more apparent in the low-humidity leaves, an observation reinforced by the leaf dry matter isotopic pattern, Δ_om (Fig. 5C). Leaf dry matter has a significant store of nonstructural carbohydrates (21% total dry weight; Wong, 1990) from current assimilation, and its isotopic composition has been shown to vary with the diurnal changes of Δ_lw (Cernusak et al., 2002). In addition, Δ¹⁸O of cellulose, the major component in leaf dry matter, has been shown to be strongly correlated to that of the dry matter of cotton leaves (Barbour and Farquhar, 2000) and the leaf water of grasses (Helliker and Ehleringer, 2002). Assuming a constant lignin to cellulose ratio across the leaf, Δ_om could be expected to reflect the spatial heterogeneity of leaf water isotopic content arising from non-transient influences.

Anatomical Basis of Spatial Variation

Measurements of stomatal density did not reveal a spatial variation consistent with the leaf water measurements. Microscopic examination of the leaf vasculature also showed no apparent difference in the venation density across the whole-leaf area. These leaf anatomical studies show that the differential enrichment of leaf water across the leaf blade could not simply be a direct result of particular leaf zones having more or fewer evaporative sites or of entrapping more xylem water in the disc samples.

Accounting for the ¹⁸O Spatial Variation of Leaf Water: String-of-Lakes Model

On the basis of our observations of specific leaf regions having δ_lw values above and below those predicted by the Craig-Gordon equation, we deduce that water flow in cotton leaves could probably behave somewhat like a string of interconnected evaporating lakes. The resemblance to this hydrological model was first suggested by Yakir (1992) for maize (Zea mays) and has been noted in a variety of dicotyledon plants and grasses (Wang and Yakir, 1995; Helliker and Ehleringer, 2000, 2002). From Figure 3, areas next to the veins and near the base, showing an enrichment less than the Craig-Gordon prediction, could represent the first elements in the string of lakes and be feeding partially enriched water to surrounding cells and the neighboring veins (accounting for enrichment in vein xylem water). The enriched water would not only move along a series of cells but could also be propagated through the veins to more distal areas. This could account for the higher degree of enrichment at the intercostal lamina regions and at the leaf margin (representing terminal water elements).

The first quantitative application to leaves of the Gat-Bowser formulation was by Helliker and Ehleringer (2000). This approach requires the leaf blade to be divided into a discrete, finite number of evaporating elements. The authors chose seven elements to represent the whole evaporative process occurring in grasses. The rationale behind this choice was not discussed, and the number was presumably chosen to give the best fit to the observed δ_lw or was chosen out of convenience to match the number of segments into which the whole blade was divided. We found that based on Equation 5, isotopic enrichment at any given point along the water pathway is sensitive to the total number of evaporating elements, even though the average enrichment over the whole leaf is independent of this number (Fig. 7). A smaller number of evaporating elements tends to overestimate the isotopic enrichment near the leaf base and underestimate it toward the leaf tip. The Gat-Bowser formulation would need to be modified for use in leaves where evaporative sites are continuous and non-discrete.

Figure 7.

Gat-Bowser formulation of the string-of-lakes model. Top, Effect of the number of evaporating elements on the ¹⁸O enrichment, Δ, along the whole length of a leaf blade at low humidity. Bottom, Different ¹⁸O enrichment patterns, Δ, along the length of a blade for different RH (h) values. All lines are plotted by assuming 50 evaporating elements, of which the steps have been smoothed for clarity. Inset, An expansion of the bottom portion of the main graph. Note that Δ at very high humidity can be larger than that at low humidity near the basal region. l/l_m refers to the relative distance from the leaf base with l_m the maximum distance from base to tip. Values of ε* = 8.3‰, ε_k = 22.9‰, and Δ_v = −5.1‰ are used in Equation 5, assuming all elements have equal evaporation rates.

Different Isotopic Enrichment Patterns at Different Humidities

The string-of-lakes model not only predicts an increasing isotopic enrichment but also dictates a different pattern of isotopic enrichment along the water pathway for different humidity treatments, as depicted in Figure 7. At high humidity, the increase in isotopic enrichment along the path of water flow is much smaller than that at low humidity. Thus, we would expect the isotopic composition of leaf water at high humidity to be similar along most of the water pathway. This expectation is largely confirmed in the spatial variation of Δ_lw and Δ_om (Fig. 5). At high humidity, isotopic enrichment of the leaf dry matter is rather homogenous over the whole-leaf area, unlike the definite isotopic pattern obtained at low humidity.

Our results on the ¹⁸O spatial variation of vein xylem water also support the prediction of different isotopic enrichment patterns (as well as magnitudes) at different humidities. Smaller Δ_vw/Δ_C of upstream xylem water was observed in the leaf veins at low humidity, compared with the high-humidity leaves (Fig. 2). At the vein endings, Δ_vw/Δ_C at low humidity is mostly greater than that at high humidity, though this difference is not always statistically significant (Table I). Although the string-of-lakes model served well in predicting different spatial patterns of leaf water enrichment at different humidity, it could not adequately account for our observations of bulk leaf water enrichment.

Lower Enrichment of Bulk Leaf Water Arising from Capacitance in Vein Ribs

When cotton leaf water is extracted in bulk by azeotropic distillation, Δ_{lw, bulk} is noted to be lower than Δ_C despite the removal of big primary veins from the leaves (Fig. 8). By solving Equation 3, the fraction of leaf water subject to fractionation (f) is given by 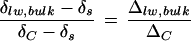with the assumption that the fractionated water is enriched at Δ_C. Thus, if the vein water is assumed to be unfractionated according to the two-pool model, its proportion in the bulk leaf water would be indicated by the term 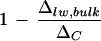. However, if vein water is partially enriched such that Δ_vw > 0, δ_s in Equation 3 will be replaced by δ_vw and the proportion of vein water in bulk leaf water will be given by 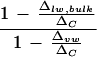. Averaging the low- and high-humidity treatments (Fig. 8), there is approximately 30% unenriched water present in the bulk leaf water of whole leaves with veins intact. Upon the removal of primary veins, the proportion of unenriched water in the bulk leaf water is reduced to approximately 15%. This implies that the water fraction associated with primary veins constitutes about 15%. In view of our earlier finding that vein water can be enriched by as much as 0.19Δ_C at the vein endings (Fig. 2) and that the average vein water enrichment is likely to be less than this value, the water fraction contributed by the primary veins should be higher, with the maximum possible estimated to be about 18.5%. In relatively close agreement with these observations, our independent assessment of this water fraction by gravimetric analysis gave a value of 14.2% ± 1.9% total leaf water. Such a high proportion of non-fractionating water has previously been noted (Leaney et al., 1985; Walker et al., 1989) but criticized as unlikely (Luo and Sternberg, 1992) given independent estimates of vein water fraction to be ≤5%. Anatomical analysis of mesophyll and vessel areas in young barley (Hordeum vulgare) leaves suggested 0.8% total tissue water was found in the lumen of vessels (Rayan and Matsuda, 1988). Using a pressure bomb to express water from a single leaf at increasing balancing pressure, Yakir et al. (1989) estimated the vein water fraction to be 1% to 3% total leaf water in sunflower (Helianthus annuus) and ivy leaves, and water in the cell walls to be another 22% to 38%.

Figure 8.

Discrepancy between the measured Δ_{lw, bulk} of bulk leaf water and the Craig-Gordon predicted Δ_C for leaves of cotton plants. The term 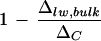signifies the unenriched fraction present in the bulk leaf water (see “Discussion”). Comparison is made between low- and high-humidity treatments. The vapor pressure deficits of air at low (RH 25%) and high (RH 75%) humidity were 3.2 and 1.0 kPa, respectively. Unshaded bars refer to the removal of primary veins. Error bars represent ses (n = 4).

In our experiment, the removal of primary veins not only excluded water in the big xylem vessels but also removed the total water present in the massive ground tissues of vein ribs. The layers of collenchyma forming the vein ridge are closely packed with negligible air spaces for evaporative enrichment and would be expected to have a large store of relatively unenriched water. Thus, the ground tissues of vein ribs could be perceived as a capacitance having little interaction with enriched water at the leaf evaporative sites, and its isotopic content is expected to be similar to that of the vein xylem.

Lower Enrichment of Bulk Leaf Water Arising from Péclet Effect

The two-pool model suggested by Leaney et al. (1985) seemed to be appropriate in accounting for the observed lower enrichment of bulk leaf water. However, the unenriched water fraction need not arise from the vascular pool alone but could be attributed to other factors. Our results show that the vein xylem water is partly enriched, with the extent of enrichment depending on the ambient humidity. Isotope mixing by diffusion can clearly be rather efficient in leaves. Yet, the degree of enrichment in vein water could not match that observed for the lamina tissue water in the same vicinity (Figs. 2 and 3). Despite the short distance between these two tissues, their enrichment difference can be as large as 20‰ or more. It is likely that the mesophyll tissues are not directly fed by the big veins but by some higher order fine veins that are relatively more enriched. Also, a Péclet effect might be involved, with the transpiration flux opposing the back-diffusion of enriched water in the lamina and along the veins. As a result, the isotopic content of bulk leaf water should be lower than that predicted by the Craig-Gordon model.

It is noteworthy that the discrepancy between Δ_C and Δ_{lw, bulk} of whole leaves, after normalization against Δ_C, did not vary with the ambient humidity despite a difference in leaf transpiration rates (low humidity, 11.5 mmol m⁻² s⁻¹; high humidity, 8.8 mmol m⁻² s⁻¹; Fig. 8). Upon the removal of primary veins, 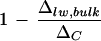is larger at high humidity. In contrast, the Péclet model (Eq. 4) predicts an increasing discrepancy between Δ_lw and Δ_C with increasing transpiration rate, E. That is, a larger 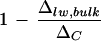is expected at lower humidity. There have been conflicting reports on the existence of such a relationship. Wang et al. (1998) and Roden and Ehleringer (1999) observed no clear dependency of Δ_C − Δ_{lw, bulk} on E, with the former study based on a collection of 90 plant species grown under the same climatic conditions. The positive relationship between Δ_C − Δ_{lw, bulk} and E, illustrated by Wang and Yakir (2000) and Gillon and Yakir (2000), appears to be in agreement with the Péclet model but may well collapse after normalization against Δ_C. Our results show that the discrepancy (Δ_C − Δ_{lw, bulk}) at low humidity is 2.5‰ larger than that at high humidity. This positive correlation with transpiration rate is wiped out upon normalization against Δ_C, as shown in Figure 8. Nonetheless, a positive trend of 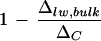with E, consistent with the Péclet model, has been reported (Walker et al., 1989; Flanagan et al., 1994; Barbour et al., 2000). All of the studies mentioned made direct isotopic measurements of extracted leaf water except for that of Barbour and co-workers (2000). The latter demonstrated a convincing positive relationship between 1 − (Δ_sw/Δ_C) and transpiration rate based on the isotopic composition of phloem Suc in castor bean (Ricinus communis), where Δ_sw refers to the deduced isotopic composition of leaf water with which the Suc exchanges. Our conflicting result, a negative relationship between 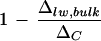and transpiration rate upon the removal of primary veins, requires resolution. First, we cannot rule out the possibility of higher leaf water enrichment by evaporative loss from the cut edges during vein removal at low humidity. Second and perhaps more important, water in the primary veins consistently has lower Δ_vw/Δ_C at low humidity, the difference from that at high humidity being up to 6% (Fig. 2A). In accordance, the removal of primary veins at low humidity would take away a larger proportion of unenriched water, giving a smaller 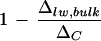value. Because vein water is an intrinsic component of the leaf water enrichment system, we recommend that for comparative studies, bulk leaf water should be extracted from whole leaves without any vein removal. Nonetheless, we could not identify a clear relationship between 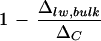and transpiration rate based on the bulk leaf water extraction from whole leaves of cotton.

Applying the String-of-Lakes Model to Leaves for Δ¹⁸O Leaf Water Prediction

Assuming all water pools have equal evaporation rates, the average isotopic content of water in the interconnected pools of the string-of-lakes model should, according to Equation 5, be equivalent to the Craig-Gordon predicted Δ_C. To test this assumption and to check the applicability of the string-of-lakes model in estimating leaf water isotopic content, a weighted mean of measured Δ_lw was computed from the leaf discs sampling. Using a distribution ratio of 4.7:10.7:4.3:1 for regions of margin:intercostal:venous:basal, weighted means of both the measured and modeled leaf water isotopic compositions were obtained (Table II). At low humidity, the weighted mean Δ_lw was 9.2% higher than the weighted mean Δ_C, and 11.8% higher in the case of high humidity. Although we expect the weighted mean of Δ_lw from leaf punches to be larger than Δ_{lw, bulk} because of the exclusion of veins in leaf discs sampling, the weighted mean of Δ_lw being larger than the Craig-Gordon prediction clearly diverged from the expectations of all leaf water models. A higher than expected Δ_lw has previously been encountered (Flanagan et al., 1993; Helliker and Ehleringer, 2000), and the latter group explained their observations by applying the string-of-lakes model, with water pools having variable transpiration rates across the length of the leaf. In our experiment, the sampling of the leaf discs was biased given that the leaf punch could not sample within 1 mm of the major veins without rupturing the veins. Thus, the low degree of enrichment expected in the immediate vicinity of the veins was omitted from our sampling. This may partially account for the higher value of weighted mean Δ_lw compared with Δ_C. It presumably explains the discrepancy with our bulk leaf water measurements, which consistently show enrichment less than the Craig-Gordon prediction.

Table II.

Comparison of the weighted mean of measured Δ_lw and Craig-Gordon predicted Δ_C of cotton leaves in low and high humidities

Time of Sampling	Weighted Mean Δlw	Weighted Mean ΔC	Δlw − ΔC	(Δlw/ΔC) − 1
Low humidity		‰
1115–1500	25.7	23.3	2.4	0.105
1000–1225	27.3	25.1	2.2	0.088
0950–1140	25.9	23.9	2.0	0.082
Mean	26.3	24.1	2.2	0.092
se	0.5	0.5	0.1	0.007
High humidity
1000–1240	18.3	16.9	1.4	0.082
1315–1535	22.0	19.4	2.6	0.135
1015–1330	18.4	16.2	2.2	0.138
Mean	19.6	17.5	2.1	0.118
se	1.2	1.0	0.4	0.018

The vapor pressure deficits of air at low (RH 35%) and high (RH 75%) humidity were 2.8 and 1.0 kPa, respectively. Weighted mean of Δ_lw and Δ_C were calculated from the same data set of Fig. 5A, using a weighting ratio of margin:intercostal:venous:basal = 4.7:10.7:4.3:1. Leaf sampling was carried out on different days.

It has been suggested that most of the discrepancies between modeled and measured leaf water isotopic compositions could be resolved by careful estimation of the kinetic fractionation factor, ε_k (Buhay et al., 1996). As expected from Equation 2, ε_k and consequently Δ_C are sensitive to the boundary layer conductance to water vapor diffusion (g_b), especially at the lower range of g_b (Fig. 9). Increasing g_b from 0.5 to 2.5 mol m⁻² s⁻¹ leads to a calculated enrichment of leaf water by 2‰, whereas a g_b increase from 2.5 to 5.0 mol m⁻² s⁻¹ results in only 0.5‰ enrichment. The degree of uncertainty imposed by ε_k estimation on leaf water isotopic composition will thus be greatly reduced with a highly turbulent boundary layer. In our study, boundary layer conductance in the greenhouse determined by a mass transfer method was 0.52 mol m⁻² s⁻¹. In view of the sensitivity of Δ_C to g_b in this region, the value of g_b was verified by another method based on heat transfer and wind velocity. A value of 0.45 mol m⁻² s⁻¹ was obtained. Because minimal difference was noted between the two methods, an average value of 0.49 mol m⁻² s⁻¹ was used in all Δ_C calculations.

Figure 9.

Relationship of the modeled Δ_C (solid line) and kinetic fractionation ε_k (dashed line) with boundary layer conductance g_b at low and high humidities. Modeled Δ_C and ε_k are calculated using Equations 1 and 2, respectively. Units for g_b and g_s (stomatal conductance) are moles per square meter per second; e_a/e_i refers to the ratio of the vapor pressures in the atmosphere and intercellular spaces.

For a more realistic application of the string-of-lakes model to leaves, Wang and Yakir (1995) proposed that the process of back-diffusion along the string of water elements (a phenomenon clearly supported by the xylem water isotopic pattern) be incorporated into the Gat-Bowser formulation. We envisage back-diffusion of enriched water occurring in two dimensions; along the leaf length in the basipetal direction and diffusion from the evaporative sites into the vein network (radial dimension), which further supplies the enriched water to other series of cells further afield. However, the advective transpiration flux should oppose this diffusion process (Péclet effect), leading to two-dimensional (2-D) gradients of isotopic variation (Fig. 1D). Simulation of a 2-D model of leaf water using a 2-D advection diffusion program was described by Yakir (1998). He modeled the leaf as a square domain having a specified leaf thickness, with water entering from the side and exiting by evaporation from the top, with no flux assumed at other boundaries. The modeled isotopic gradients of leaf water have clear 2-D characteristics that collapse to uni-dimensional during the night when evaporation stops. His findings distinctly exemplify the significant role of transpiration flux in modulating the spatial variation of leaf water enrichment during the day.

Implications of Leaf Water Spatial Heterogeneity

Despite the spatial heterogeneity of leaf water, Barbour et al. (2000) have shown that the isotopic label of sugars exported from castor bean leaves behaves as predicted by the Péclet model. This observation is made from gas exchange leaf chamber experiments under optimum conditions where assimilation rates across the leaf area are most likely uniform. However, for nonuniform assimilation rates across the leaf, spatial heterogeneity of leaf water could pose a challenge to our present applications of leaf water isotopic composition as indicators of plant environment and terrestrial productivity (Yakir, 1998). If assimilation rates are higher, for example, near the leaf tip where leaf water enrichment is higher than the Craig-Gordon prediction, the Δ¹⁸O of retrodiffused CO₂ would be greater and could be misinterpreted as higher terrestrial productivity. Such uneven distribution of assimilation rate would also have implications for the interpretation of the mean isotopic signature of sugars formed from the entire leaf as well as the ¹⁸O content of O₂ produced during terrestrial photosynthesis and the interpretation of the Dole effect (the balance between terrestrial and marine productivity based on the deviation from 23.5‰ in the δ¹⁸O of atmospheric O₂ [Bender et al., 1985, 1994]). Nonuniform assimilation rates are most likely to occur when the amount of light incident on a leaf is inconsistent across the leaf, leading to spatial variations of photosynthetic capacity and ¹³C discrimination, ¹³Δ (Meinzer and Saliendra, 1997). We expect dicotyledoneous leaves, in their natural orientation, to receive more uniform incident rays than long, flagging blades of monocotyledoneous plants. This expectation is supported by the uniform distribution of ¹³Δ across beech (Fagus spp.) leaves (Schleser, 1990) and increasing ¹³Δ from the base to the tip of leaves of sugarcane (Saccharum officinarum; Meinzer and Saliendra, 1997) and maize (Sasakawa et al., 1989). The error introduced by the spatial heterogeneity of leaf water in the applications mentioned will thus be a greater concern in grasslands where their growth humidity is generally low and large isotopic gradients are expected across the leaf, as illustrated in Figure 5.

CONCLUSIONS

The three leaf water models examined in this paper (two-pool model, Péclet model, and string-of-lakes model) are found to be valid in describing the following features of leaf water enrichment. The overestimation of the isotopic enrichment of bulk leaf water by the Craig-Gordon model is well addressed by the two-pool and Péclet models, whereas spatial heterogeneity of leaf water enrichment can be expected from the Péclet and string-of-lakes models. But none of the models on its own could fully account for all of the facets of leaf water enrichment. For example, although a gradient of isotopic enrichment is projected by both the Péclet and the string-of-lakes models, only the latter model correctly predicts the different isotopic enrichment patterns at different humidities. Yet, the latter model could not adequately account for the lower degree of enrichment in bulk leaf water, which the two-pool model and the Péclet model could. Also, the observed partial enrichment of vein xylem water is within expectations of the Péclet model, whereas the other two either assume no enrichment of vein water (two-pool model) or an enrichment equivalent to that at the neighboring evaporative sites (string-of-lakes model). On the other hand, we could not identify a clear relationship between 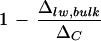and transpiration rate, a correlation expected from the Péclet model.

Our findings acknowledge the presence of capacitance in the ground tissues of vein ribs that are likely to have similar isotopic contents to the vein xylem. This paper also draws attention to the need for modification of the Gat-Bowser formulation of the string-of-lakes model to accommodate continuous, non-discrete evaporating elements and for incorporating Péclet effects along the longitudinal and radial dimensions into the string-of-lakes model.

MATERIALS AND METHODS

Plant Material and Growth Conditions

Seeds of cotton (Gossypium hirsutum L. var Deltapine 90) plants were sown in 4.5-L polyvinylchloride pots containing sterilized garden soil mixture supplied with slow-release fertilizer (Osmote Plus, Scotts-Sierra, Maysville, OH). The plants were grown under full sunlight between late summer and early autumn in two greenhouses at the same temperature (30 ± 1°C day and 22 ± 1°C night) but with different RHs (40% ± 10% and 75% ± 10%) maintained day and night. Tap water was used to water the plants twice daily. All samplings and measurements were carried out on 35- to 55-d-old plants in the greenhouses on cloud-free days during the time period of 11 am to 3 pm when plant photosynthesis was at its maximum and gas exchange was observed to be at steady state.

Gas-Exchange Measurements

Leaf gas-exchange measurements were taken during sunny days using a portable gas-exchange system (model LI-6400, LI-COR, Lincoln, NE) equipped with the standard leaf chamber and the CO₂ injector system for the control of CO₂ concentration. Measurements were made at a photosynthetic photon flux density of 1,200 μmol m⁻² s⁻¹ from an LED light source.

Boundary Layer Conductance Measurements

The boundary layer conductance to water vapor diffusion (g_b) in the greenhouses was first measured using a mass transfer method (Jarvis, 1971). A water-saturated filter paper (No. 1, Whatman, Clifton, NJ) was exposed, and the rate of weight loss from evaporation was recorded. The temperature of the paper leaf model was constantly monitored using an infrared thermometer (Mikron Instrument, Oakland, NJ) with a resolution of 0.1°C. The boundary layer conductance obtained was 0.52 ± 0.04 mol m⁻² s⁻¹. For verification, g_b was also determined using the heat transfer method. The wind speed in the greenhouse, 0.34 ± 0.10 m s⁻¹, was measured using an ultrasonic anemometer (Gill Instruments, Lymington, Hampshire, UK). Using equations given by Ball et al. (1988) for calculating the boundary layer resistance to water vapor based on heat transfer in a forced convection, we obtained a g_b value of 0.45 ± 0.06 mol m⁻² s⁻¹.

Vein Xylem Water Sampling

For sap collection with minimal perturbation, xylem water of an intact leaf was sampled concurrently from primary and secondary veins using a root pressure chamber (Yong et al., 2000). While the whole root system of the plant was enclosed and pressurized in the chamber, a light incision was made on the leaf vein with a sharp razor blade. The pneumatic pressure was adjusted to give a xylem sap flow of about 0.5 μL s⁻¹ exuding from the finer veins. A sample of 0.7 μL of xylem water was directly siphoned off with a pipette (2-μL micro-pipetteman, Gilson Medical Electronics, Middleton, WI) from the water bead formed at the incision point immediately after wiping off the earlier exudate. The collected sap was quickly dispensed into a smooth-walled tin cup (4.5 × 2 mm) and sealed under argon with a modified Carlo Erba liquid encapsulator equipped with a pneumatic actuator. To collect more xylem water for storage, a 10-μL capillary was held steady against the incision, and its ends were immediately sealed with sealing wax after filling. Sampling order followed the general rule of first scoring the vein endings in the vicinity of the leaf margin and gradually moving inwards toward the leaf base where vein diameter progressively increases. This minimized water-flow disruptions to areas yet to be sampled. The petiole of the same leaf was eventually cut to collect petiole water after the completion of vein xylem water sampling.

To determine humidity effects on the isotopic composition of vein xylem water, a step change of humidity was carried out in another experiment. Xylem water was collected from the same vein incision points before and 1 h after the step change of humidity.

Leaf Water and Organic Matter Sampling

To analyze leaf mesophyll water of cotton leaves without the inclusion of vein water, leaf discs (diameter 3 mm) were cut out from an intact leaf (avoiding primary, secondary, and fine veins) with an improved version (Fig. 10) of the purpose-designed leaf punch (Gan et al., 2002). In brief, pressing down the plunger of the leaf punch cuts a leaf disc and also activates a jet of argon that guides the disc to fall directly into a preweighed smooth-walled tin cup (9 × 3.5 mm). The argon jet also flushes out air and hence excludes nitrogen and oxygen from the cup. The filled cup is immediately sealed with the push of a button (pneumatic actuation) and can be directly pyrolyzed before analysis in an Isotope Ratio Mass Spectrometer. Sampling began from the leaf margin and worked inward toward the petiole to minimize water-flow disruptions to the leaf lamina yet to be sampled. Leaf temperature profiles were captured using an IR scanner with a sensitivity of 0.1°C (Thermovision 870, AGEMA, Danderyd, Sweden) after every two to three leaf punches. Regular monitoring of leaf temperature was essential because we noted that leaf temperature in the sampling region would gradually climb by 1°C to 2°C after cutting several leaf discs. After punching out leaf discs from one side of the midrib, leaf temperature was again recorded by the IR scanner before the other one-half was trimmed, avoiding primary veins. The trimmed leaf segments were immediately immersed in toluene (80 mL) for bulk leaf water extraction by azeotropic distillation using a specially designed funnel as described by Revesz and Woods (1990). The leaf-half containing the punch holes was pressed between layers of paper and dried in a 70°C oven. Small dry leaf segments in the vicinity of each punch hole were collected for isotopic analysis of leaf organic matter.

Figure 10.

Cut-away view of the leaf punch device. The punch is hollow with sharp edges to cut a leaf disc and to deliver argon for directing the disc into the tin cup as well as purging the cup. The cup can be immediately sealed with the push of a button that pneumatically operates the pincer arms.

To map spatial isotopic distribution of leaf organic matter, whole leaves of cotton from leaf positions 5 and 7 were harvested from each of three plants. The leaf blades were trimmed into four distinct zones before oven drying. The four zones were (a) margin, for lamina next to the leaf edge; (b) intercostal, for lamina remote from the secondary and primary veins; (c) venous, for lamina adjacent to the primary veins; and (d) basal, for lamina collected at the leaf base within approximately 20 mm of the petiole. Thereafter, the dried leaf segments were ground for isotopic analysis of leaf organic matter. To determine the distribution ratio of the four lamina zones, two fresh leaves were photocopied on paper, and each leaf area was divided into the four zones mentioned. From weighing the paper, the relative ratio of the four zones (margin, intercostal, venous, and basal) was found to be 4.7:10.7:4.3:1, respectively.

For bulk leaf water analysis, whole leaves were sampled, and leaf water was extracted by azeotropic distillation, with some replicates having the primary veins removed. To determine the percentage of water present in the primary veins, leaf fresh weight was first measured, followed by the removal of primary veins. The fresh weights of the remaining lamina and the primary rib skeleton were noted before oven drying. The leaf water content and water associated with the primary ribs were obtained from the difference between the fresh and dry weights of the lamina and primary ribs.

Throughout the period of leaf water sampling, atmospheric water vapor was collected using a dry ice-ethanol cold trap. Over 20 d of leaf water measurements, δ_v = −12.6‰ ± 1.3‰ (sd).

Oxygen Isotope Analysis

Oxygen isotopic analyses of water and dried and fresh leaf samples were all performed using the continuous-flow pyrolysis technique described by Farquhar et al. (1997) with slight modifications. To minimize memory problems, the reaction column was packed with glassy carbon grit (3,150–4,000 μm, HTW, Thierhaupten, Germany) followed by a top layer (0.015 m thick) of nickelized carbon (50% [w/w] Ni, Alpha Resources, Sydney). The same analytical precision of 0.2‰ was achieved after reactor modification. Elemental oxygen standards were beet Suc and ANU-HP water, with the latter (δ¹⁸O = −5.5‰) also serving as the isotopic internal standard for water samples. A standard of beet Suc containing 3% (w/w) nitrogen was used for correcting isotopic composition of dry leaf samples because the latter were found to contain about 3% (w/w) nitrogen. Isotopic calibration agreement between water and organic standards has previously been performed (Gan et al., 2002), and a slope of 1.0027 was obtained over an isotopic range of 90‰. Preparation of liquid samples for pyrolysis was similar to that for leaf xylem water sampling. Dried leaf samples of 1.0 to 1.5 mg were accurately weighed into tin capsules that were then crimped manually. Smooth-walled tin cups containing fresh leaf samples were directly pyrolyzed. The fresh weight of the leaf disc was obtained from the difference between the total weight of the tin cup with the leaf disc and the weight of the empty tin cup. Direct pyrolysis of fresh and dry leaf samples gives the measured values of δ¹⁸O_F and δ¹⁸O_D, respectively. The ¹⁸O ratio of leaf water (δ¹⁸O_lw) from the fresh leaf sample can be calculated by isotopic mass balance,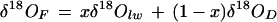

where x refers to the proportion contributed by leaf water in the total oxygen pool of the fresh leaf sample. The value of x was determined from the thermal conductivity detector output of the gas chromatograph in the same acquisition as the ¹⁸O analysis, the calculations of which are detailed in Gan et al. (2002). Overall,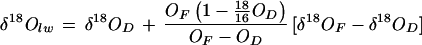

where O_F and O_D are, respectively, the oxygen elemental composition of fresh and dry leaf samples as obtained from the thermal conductivity detector output of the gas chromatograph.

Stomatal Density Distribution

Fresh cotton leaf segments of approximately 0.25 to 0.50 cm² were trimmed from various places on the leaf lamina and placed on carbon paste before being frozen on a metal support precooled in liquid nitrogen. Scanning electron microscope (S-2250N Hitachi, Tokyo) images were taken under standard conditions of 25 kV, 16 mm working distance, and low input of water vapor. To quantify the distribution of stomatal densities over the whole-leaf surface, we targeted four locations: margin, intercostal, venous, and basal. For every location, images of three to four different areas were taken for each abaxial and adaxial surface. Each image represented an area of 0.343 mm² (the field of view at a magnification of 200×). The number of stomata was counted directly from the prints and expressed as number of stomata per mm² of leaf surface.

Analysis of Leaf Vasculature

Leaf pigments and cell contents were cleared by incubating the fresh leaf in methanol at 60°C for 1 h, followed by immersion in warm lactic acid for 5 to 10 min. The venation pattern and density were examined under a light microscope.