Power spectra reveal the influence of stochasticity on nonlinear population dynamics

Abstract

Stochasticity alters the nonlinear dynamics of inherently cycling populations. The power spectrum can describe and explain the impacts of stochasticity. We fitted models to short observed time series of flour beetle populations in the frequency domain, then used a well fitting stochastic mechanistic model to generate detailed predictions of population spectra. Some predicted spectral peaks represent periodic phenomena induced or modified by stochasticity and were experimentally confirmed. For one experimental treatment, linearization theory explained that these peaks represent overcompensatory decay of deviations from deterministic oscillation. In another treatment, stochasticity caused frequent directional phase shifting around a cyclic attractor. This directional phase shifting was not explained by linearization theory and modified the periodicity of the system. If field systems exhibit directional phase shifting, then changing the intensity of demographic or environmental noise while holding constant the structure of the noise can change the main frequency of population fluctuations.

The interactions of stochasticity with nonlinear population dynamics are of major interest in ecology (1–3). Environmental and demographic stochasticity can strongly influence dynamics and can play a key role in the fluctuations of populations (4–12). The influence of stochasticity on deterministic population models with a single stable equilibrium has been analyzed using linear approximations about the equilibrium (13–17). Bjørnstad et al. (18) applied this theory to populations of Atlantic cod and bluefin tuna. Linearization theory has also been applied to nonequilibrium physical systems (19–21). Both bodies of theory use the power spectrum, or simply spectrum (22, 23). However, the spectrum is sometimes not used with population data because estimates of the spectrum based on short time series lack resolution (9).

Our first goal is to propose and test a statistical approach to facilitate the application of the spectrum to the inherent population cycles and nonlinear models of Tribolium flour beetles, which have been used for decades in laboratory studies of population dynamics (11, 24, 25). For Tribolium castaneum, cannibalism plays a major role in dynamics and is represented by nonlinearities in several models (11). The approach proposed combines qualitative biological knowledge with quantitative information in short time series to improve the resolution of estimates of population spectra. We produce detailed, empirically supported, model-based predictions of the spectra of beetle populations. We map the influence of demographic stochasticity on Tribolium dynamics by plotting changes in spectra with gradually increasing stochasticity. This approach may have general utility, not limited to flour beetles.

Our second goal is to show that linear approximation theory sometimes can, and sometimes cannot, explain how stochasticity affects inherently cycling populations. Realistic stochasticity produced frequent unidirectional phase-shifts in population cycling around the deterministic attractor. These phase shifts caused the dominant frequency of the system to shift, invalidating the predictions of linearization theory. We label this effect “directional phase shifting.”

Nisbet et al. (13, 14, 18) concluded that linearization theory is likely to be an effective approximation to the effects of stochasticity on deterministic population models with a single stable equilibrium for all but very small equilibrium populations. For inherently cycling populations, we show that linearization theory will also fail when stochasticity causes substantial directional phase shifting. We give guidelines for determining when shifting may occur and what its effects will be.

Although linearization theory should be tried first in any analysis of interactions between stochasticity and nonlinear dynamics, diverse effects can occur when strong noise renders linearization invalid. We demonstrate such effects and argue that many inherently cycling population systems may be insusceptible to linearization theory because of strong noise. In-depth exploration is needed of interactions between dynamics and strong stochasticity; we present techniques to describe and understand these interactions.

If directional phase shifting occurs in a cycling field population, then changes in the intensity of the environmental or demographic stochasticity affecting that population may alter the main frequency of its oscillations. Such changes in intensity may occur through climate change, geographic variation, or reduced population sizes. Modification of the periodicity of a fluctuating exploited population may affect the exploiting industry; modification of the periodicity of a fluctuating population of disease vectors may affect public health.

Results

Supporting Information.

For further details, see Tables 1–3, Figs. 5–11, and Supporting Text sections 1 and 2, which are published as supporting information on the PNAS web site.

Fit and Predictive Ability of the Lattice Stochastic Demographic Larvae-Pupae-Adult (LSD-LPA) Model.

The LSD-LPA model (Methods) succeeded in fitting well, with the same parameters in both time and frequency domains, all 24 experimental replicates of length 41 (imposed initial conditions plus observations every 2 weeks for 80 weeks). Using model parameters obtained by maximum-likelihood time-domain fitting (Supporting Text 1.1), the frequency-domain fit of the LSD-LPA model with all 24 data replicates was tested (Fig. 1, box 2). The six replicates of length 213 were truncated to length 41 for this purpose. Fit between model and data was good according to our new spectrum distance and shape fit tests (Methods), and was confirmed visually (e.g., Fig. 2 A).

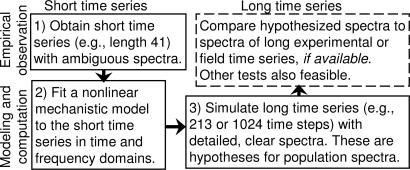
Fig. 1.

The new “spectrum enhancement method” (boxes 1–3, for the three steps of the method) and one way of testing predictions of the method using spectra of long observed time series (fourth box). The method uses biological information contained in a model's functional form to magnify the resolution of predicted spectral estimates. Using this method, the LSD-LPA model accurately magnified spectral resolution; models with incorrect functional forms made incorrect spectral predictions (text). Detailed spectral predictions of well tested models provide biological understanding; predictions of less well tested models provide testable hypotheses.

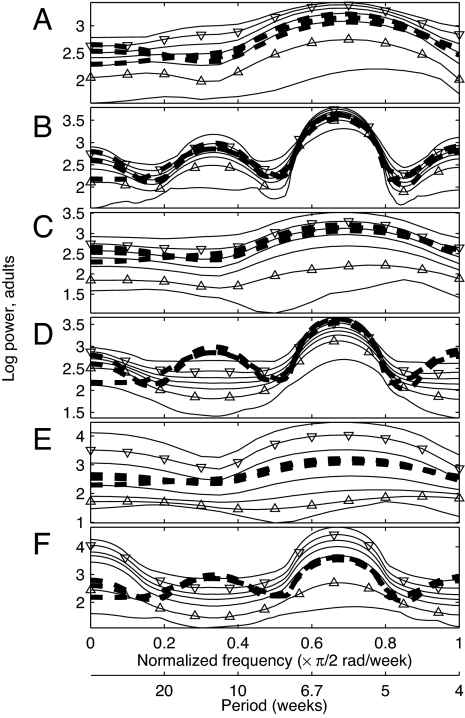
Fig. 2.

Frequency domain fits between models and observed adult population time series of length 41 (A, C, and E) and length 213 (B, D, and F) from the three experimental replicates with c_pa = 0.35. The heavy dashed lines are data log spectra, identical in A, C, and E and identical in B, D, and F. Light solid lines give the minimum, the 5th, 25th, 50th, 75th, and 95th percentiles, and the maximum values at each frequency value of 1,000 log spectra of model-generated time series of length 41 (A, C, and E) and length 213 (B, D, and F). Triangles highlight the 5th and 95th percentiles. Models used were the LSD-LPA model with parameters of Supporting Text 1.1 (A and B), the (intentionally incorrect) constrained LSD-LPA model with c_el = 0 and time-domain-optimized parameters of Supporting Text 2.2 (C and D), and the (intentionally incorrect) constrained LSD-LPA model with c_ea = 0 and time-domain-optimized parameters of Supporting Text 2.2 (E and F). All parameters were optimized for length-41 data. Contrast the good fit in B with the poor fits in D and F. Fit of the constrained LSD-LPA model with no further constraint is similar to A and B and is shown in Supporting Text 2.2. Fits were similar when frequency-domain optimized parameters were used (Supporting Text 2.2). Aliasing of fundamental frequencies of population fluctuation is unlikely to have occurred because the biology of Tribolium suggests that little fluctuation occurs for normalized frequency (nf) >1.

Spectral estimates from length-41 time series lacked resolution. Our new “spectrum enhancement method” allowed detailed spectral analysis by carefully combining data from short time series with a mechanistic dynamical model (Fig. 1). To make higher-resolution predictions, we generated many time series of length 213 using the LSD-LPA model (parameters of Supporting Text 1.1); spectral estimates based on these time series were model-based hypotheses of population spectra (Fig. 1, box 3). We tested the predictive ability of the model and the strategy of this study (Fig. 1, fourth box) by comparing these hypotheses with spectral estimates from the 6 experimental replicates of length 213 (control and c_pa = 0.35 replicates). Hypotheses and data-based estimates agreed qualitatively and quantitatively. A second spectral peak at normalized frequency (nf) 0.33 was predicted by the model and confirmed by the length-213 experimental time series for c_pa = 0.35 (Fig. 2B); see also Supporting Text 2.1. Models that fit well in the time and frequency domains and that accurately represent known biological mechanisms can be effective predictive tools via the spectrum enhancement method.

Testing of the Spectrum Enhancement Method.

As a control on the role of biological information in model predictions, we explored variants of the LSD-LPA model that fitted short population time series, but intentionally made wrong assumptions of biological mechanism. If the spectrum enhancement method is trustworthy, these models should make incorrect spectral predictions. The “constrained LSD-LPA model” had, by definition, diagonal noise covariance matrix Σ (Methods); Σ(3, 3) = 0; c_pa = 0.35; and μ_a = 0.96. It was otherwise the same as the (unconstrained) LSD-LPA model, and was substantially the same as that model, because the off-diagonal entries of Σ were close to zero for the unconstrained model (Supporting Text 1.1). The further constraints c_el = 0 and c_ea = 0 were imposed separately on the constrained LSD-LPA model. These additional constraints correspond to the incorrect assumptions that cannibalism of larvae on eggs, or adults on eggs, respectively, did not occur. We compared the output of all three models with the c_pa = 0.35 experimental time series.

All models fitted acceptably with length-41, truncated versions of the three experimental replicates in the time and frequency domains with the same parameters (Fig. 2 A, C, and E and Supporting Text 2.2). However, only the constrained LSD-LPA model, which correctly specified biological mechanisms, accurately predicted the spectra of long time series (compare the good fit in Fig. 2B with the poor fits in Fig. 2 D and F; Supporting Text 2.2).

Model-Predicted Spectra.

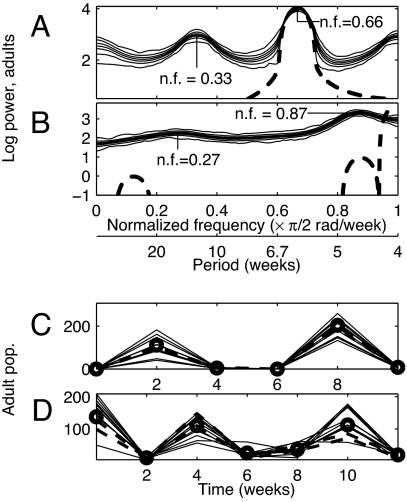
We tested at higher resolution the predictive power of the LSD-LPA model and the spectrum enhancement method by comparing detailed predictions of model-generated spectra with observations for the treatments c_pa = 0 and 0.5. Spectra of model-generated time series of length 1024 are displayed in Fig. 3A and B. For each treatment, the LSD-LPA model predicted a peak that the (deterministic) LPA model did not predict. Both LSD-LPA model peaks are supported by data; they demonstrate the effect of stochasticity on population spectra.

Fig. 3.

Model-predicted power spectra (A and B) and experimental support for predictions (C and D). LSD-LPA model-predicted peaks for c_pa = 0.5 (A) and c_pa = 0 (B) correspond to period 6 time steps (nf 0.33) (A) and period ≈7.4 time steps (nf 0.27) (B). Thin solid lines in A and B give the minimum, 5th, 25th, 50th, 75th, and 95th percentiles, and maximum values at each frequency of 1,000 log spectra of LSD-LPA model-generated adult time series of length 1024. Thick dashed lines give spectra of time series generated by the LPA model with initial conditions on the model attractor. Dashed lines extend below figure axes, but show no important features there. (C) Thin solid lines give 10 repetitions of a length-6 repeating pattern randomly chosen from 129 repetitions isolated from typical length-1024 output of the LSD-LPA model with c_pa = 0.5. Centers of heavy circles are medians of all 129 repetitions. The median pattern was present in experimental data; the best repetition detected in each of the three replicates is shown with a thick dashed line. The pattern caused the smaller LSD-LPA model peak (at nf 0.33) in A. (D) Thin solid lines give 10 repetitions of a length-7 repeating pattern isolated from typical length-1024 output of the LSD-LPA model with c_pa = 0. Centers of heavy circles are medians of these values. The median pattern was detected in data (thick dashed lines). The pattern caused the smaller LSD-LPA model peak (at nf 0.27) in B.

High adult-on-pupae cannibalism.

For c_pa = 0.5, the LSD-LPA model predicted a main spectral peak at nf 0.66 and a secondary peak at nf 0.33 (Fig. 3A). Short LSD-LPA model-generated and experimental time series (of length 41) revealed only the approximate location of the peak at nf 0.66. The LPA model had a stable three-point attractor; it generated length-1024 time series with spectra having only one peak at nf 0.66. This LPA model peak explained the primary peak of the LSD-LPA model, but not its secondary peak.

Experimental data supported the secondary spectral peak predicted by the LSD-LPA model at nf 0.33 (period 6 time steps). Using the “relative lag metric” (Supporting Text 1.4), we extracted an approximately repeating pattern of 6-time-step length from typical length-1024 output of the model. Using the “lag metric” (ref. 9; Supporting Text 1.4), this pattern was then detected in all three experimental replicates with c_pa = 0.5 (Fig. 3C). This repeating pattern appeared more often than would have been expected by chance alone according to permutation tests, <1% significance (Supporting Text 1.5). Detection of this phenomenon in data supported the secondary LSD-LPA model-predicted peak of Fig. 3A. The secondary peak was caused by stochasticity and intensified by lattice effects: the stochastic demographic LPA (SD-LPA) model predicted a peak at nf 0.33 that was smaller than the peak predicted by the LSD-LPA model. Below, we explain how stochasticity produced the peak at nf 0.33.

Zero adult-on-pupae cannibalism.

For c_pa = 0, the main spectral peak hypothesized by the LSD-LPA model occurred at nf 0.87; a smaller peak occurred at nf 0.27 (Fig. 3B). Short model-generated and experimental time series (length 41) revealed only the approximate location of the peak at nf 0.87. The LPA model generated time series of length 1,024 with main, secondary and tertiary spectral peaks at nf 1, 0.877, and 0.123, respectively. The main peak of the LSD-LPA model appeared (wrongly, it turns out) to be related to the secondary peak of the LPA model. However, the secondary peak of the LSD-LPA model could not be explained using the LPA model. Nor could the LPA model explain the absence of LSD-LPA model peaks at nf 1 and 0.123. The peak at nf 0.27 (period 7.41 time steps) was a valid prediction of the LSD-LPA model for c_pa = 0, according to experimental data. Using the lag metrics (Supporting Text 1.4) and permutation tests, an approximately repeating pattern of 7-time-step length was extracted from typical length-1024 output of the LSD-LPA model, was detected in two of the three experimental replicates with c_pa = 0 (Fig. 3D), and was shown to be statistically significant (Supporting Text 1.5). Detection of this phenomenon in data supported the secondary model-predicted peak of Fig. 3B.

The spectrum predicted by the LSD-LPA model was very similar to that predicted by the SD-LPA model: lattice effects did not change the spectrum. Only stochasticity could have caused the differences between the spectra predicted by the LPA and LSD-LPA models. The next section explains how stochasticity rearranged the peaks of the deterministic LPA model to produce the stochastic model peaks.

Deterministic and Stochastic Model Peaks.

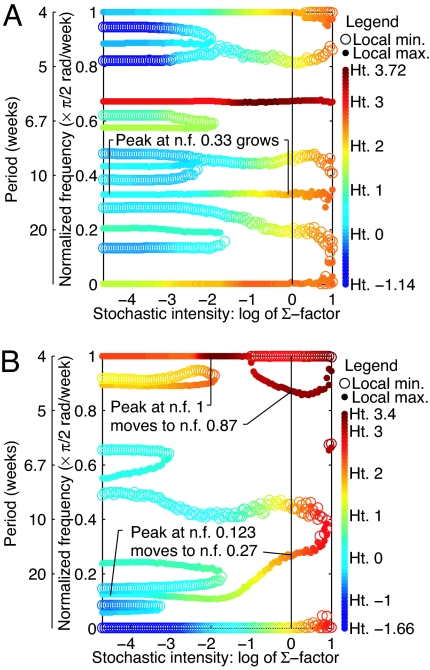
Stochasticity and lattice effects caused the differences between the spectral peaks predicted by the LPA model and by the LSD-LPA model, but the bulk of the differences was caused by stochasticity because the spectra predicted by the LSD-LPA and SD-LPA models were very similar. Lattice effects on the spectrum were minimal for c_pa = 0 and 0.5. To understand differences between LPA- and SD-LPA-model-predicted spectra for c_pa = 0 and 0.5, we mapped how spectral peaks and valleys changed as a function of gradually increasing stochasticity, keeping the form of the stochasticity constant while varying only its magnitude. Some spectral peaks disappeared with increasing stochasticity; others changed location in complex patterns (Fig. 4).

Fig. 4.

Spectral peaks and valleys with increasing intensity of stochasticity in the SD-LPA model for the adult life-stage with c_pa = 0.5 (A) and c_pa = 0 (B). Vertical axes show frequencies of local maxima (filled circles) and minima (open circles) of log spectra. Color shows the heights (Ht.) of local maxima and minima. Horizontal axis shows intensity of stochasticity (scalar multiple of noise covariance matrix; see Methods). Under very low stochasticity (left), spectra were those of the deterministic model. Vertical black lines show experimental stochasticity (Σ factor 1). For these parameter values and Σ factor 1, LSD-LPA, and SD-LPA model spectral predictions were very similar: lattice effects were small. Stochasticity explains the locations of peaks for the LSD-LPA model (Fig. 3 A and B) by explaining the locations of peaks for the SD-LPA model. The smaller peak in Fig. 3A was induced by stochasticity. The smaller peak of Fig. 3B (nf = 0.27) was the nf = 0.123 peak of the LPA model, shifted by stochasticity (and not further shifted by lattice effects). The main peak of Fig. 3B (nf = 0.87) did not come from the deterministic model peak at nf = 0.877, as was expected before this analysis, but was the nf = 1 deterministic model peak, shifted by stochasticity (and not further changed by lattice effects). The deterministic model peak at nf = 0.877 was eliminated by stochasticity. Supporting Text 2.3 shows other life stages. No statistical confidence intervals are given for the locations or heights of peaks and valleys because the variability in these quantities is expected to be small (Supporting Text 1.6 has details of how plots were produced) and no probabilistic conclusions were drawn.

High adult-on-pupae cannibalism.

For c_pa = 0.5, the SD-LPA model-predicted peak at nf 0.33 was stochastically induced: increasing stochasticity gradually increased the power of population oscillations at nf 0.33 (Fig. 4A); without stochasticity, no peak occurred at that frequency (Fig. 3A, dashed line). The growth of the peak at nf 0.33 with increasing stochasticity (Fig. 4A) has a biological interpretation. The LPA model has a stable 3-cycle attractor for c_pa = 0.5; it oscillates among larvae-dominated, pupae-dominated, and adult-dominated life-stage distributions. Stochastic model population fluctuations are similar, but larvae-dominated stage distributions are often alternately heavily and moderately larvae-dominated. Pupae- and adult-dominated distributions alternate in the same way, producing period-6 oscillation overall. With growing stochasticity, the difference between heavily and moderately larvae-dominated (or heavily and moderately pupae- or adult-dominated) distributions grows larger.

Zero adult-on-pupae cannibalism.

For c_pa = 0, the SD-LPA model-predicted peaks at nf 0.27 and 0.87 were stochastically shifted (Fig. 4B). The movements of peaks in Fig. 4B have biological interpretations. With c_pa = 0 and after transients, the LPA model oscillates on alternate time steps between pupae-dominated life-stage distributions (many pupae, few adults, and larvae) and bimodal distributions (many adults and larvae, few pupae). The model has an invariant-loop attractor consisting of two small and widely separated circles, c₁ and c₂, between which it oscillates (Supporting Text 2.4). This oscillation of two-time-step period produces the spectral peak of Fig. 4B at nf 1 for little demographic stochasticity (low Σ factors; see Methods). This peak moves when sufficient stochasticity prevents pupae-dominated distributions from leading unerringly to bimodal distributions, and vice versa. Peak motion from nf 1 to nf 0.87 corresponds to a change in the average number of time steps between pupae-dominated distributions from 2/1 = 2 for low Σ factors to 2/0.87 = 2.30 for experimental levels of stochasticity.

The population state occupied by the LPA model on alternate time steps orbits gradually around c₁. For time steps not spent on c₁, the state orbits around c₂. The result is modulation of the magnitude of the nf 1 population oscillations: the model oscillates between heavily pupae-dominated and heavily bimodal distributions; it then oscillates between moderately pupae-dominated and moderately bimodal distributions, and repeats (Supporting Text 2.4). The frequency of modulation of population variability is nf 0.123. The peak in Fig. 4B at this frequency for low Σ factors depicts the modulation. Motion of this peak from nf 0.123 to nf 0.27 with increasing stochasticity (Σ factor) corresponds to a change in the period of the modulation from 2/0.123 = 16.26 time steps to 2/0.27 = 7.41 time steps.

Patterns of change in spectral peaks other than those observed for c_pa = 0 and 0.5 occurred with increasing stochasticity for other c_pa values (Supporting Text 2.3). The numerical methods of this study allow the model-hypothesized role of stochasticity in establishing the dominant population fluctuations of the beetle system to be explicitly mapped. Developing analytical methods to undergird these numerical methods remains a challenge for the future.

Explanation of Spectral Changes with Stochasticity.

Linearization theory explains interactions between sufficiently weak stochasticity and nonlinear deterministic dynamics with a finite attractor (Supporting Text 1.7). The growth of the peak at nf 0.33 for c_pa = 0.5 can be explained by using linearization theory, as can other aspects of Fig. 4A. In contrast, linearization theory cannot explain the peak motion in Fig. 4B.

High adult-on-pupae cannibalism.

The LPA model, now denoted (L_t+1, P_t+1, A_t+1) = g(L_t, P_t, A_t), was put on the square-root scale: x_t+1 = (l_t+1, p_t+1, a_t+1) = (L_t+1, P_t+1, A_t+1)^1/2 = f(l_t, p_t, a_t) = g(l_t², p_t², a_t²)^1/2. Perturbations due to stochasticity were approximately normally distributed on this scale (Supporting Text 1.1). The model x_t+1 = f(x_t) has stable attractor A = (a₁, a₂, a₃) for c_pa = 0.5. The susceptibility matrices, S₁ = J_a3 J_a2 J_a1, S₂ = J_a1 J_a3, J_a2, and S₃ = J_a2 J_a1 J_a3 (where J_x is the Jacobian of f at x) for this model all have eigenvalues −0.77, 0.65, and 0. The dominant eigenvalue is negative, so theory predicts a component of overcompensatory decay of perturbations from the stable attractor of the square-root-scale model, and a corresponding spectral peak in the adult life stage at nf 1/3 = 0.33 (half the frequency of the deterministic system). The eigenvalue 0.65 is also large, so a component of undercompensatory decay of perturbations from the attractor will also occur, producing a spectral peak at nf 0 for the square-root-scale model. Theory predicts that these peaks will increase in size and prominence with stochasticity increasing from zero. Taking the square root of populations does not affect locations and relative heights of spectral peaks, so theory explains the peaks at nf 0.33 and 0 for the SD-LPA model (Figs. 3A and 4A).

The theoretical mechanism producing the nf 0.33 peak was supported by experimental data on the perturbations of real population vectors from points in the LPA model attractor. Let v_i denote the eigenvector of S_i with eigenvalue −0.77. If the mechanism of overcompensatory decay is correct, then when a square-root-scale population vector x_t deviates slightly from a_i with a component in the direction of v_i, the vector x_t+3 should deviate from a_i with a component in the direction of −v_i. The latter deviation should, on average, be smaller than the former. These patterns held for data (Supporting Text 2.5).

Zero adult-on-pupae-cannibalism.

Linearization theory does not immediately apply for c_pa = 0 because the square-root-scale LPA model with c_pa = 0 has a nonfinite attractor. However, the components of the attractor, c₁^1/2 and c₁^1/2, can substitute for a stable two-point attractor. Making this approximation, we applied linearization theory to the c_pa = 0 treatment (Supporting Text 2.5). Linearization theory predicts, correctly for weak noise, that locations of spectral peaks will not change with increasing stochasticity. The (deterministic) LPA model peaks at 0.123, 0.887 and 1 were not greatly affected by weak demographic stochasticity (log Σ factors less than about −2.5). The prediction is incorrect for stronger noise: peaks shifted unexpectedly for larger Σ factors (Fig. 4B). How can peak motion for higher Σ factors be explained?

The LPA model with c_pa = 0 had an unstable equilibrium, e, about midway between c₁ and c₂. Spectral peaks began to move when stochasticity was strong enough to move population vectors occasionally at least as far from c₁ and c₂ as e (Supporting Text 2.5). Linearization theory failed when this occurred because linearization at points in the attractor does not capture the dynamical behavior of the LPA model at points farther from the attractor than e. For weak stochasticity, the SD-LPA model initialized with a population vector near c_i will produce in one time step a vector nearer c_j (j ≠ i) than c_i. Stronger stochasticity will cause the model to occasionally produce a vector closer to c_i, shifting the phase of the nf 1 oscillation of the system (26). The relative frequency of phase shifting, as a function of the Σ factor, becomes appreciably greater than 0 for the same range of Σ factors at which stochasticity becomes strong enough to move populations further from the attractor than e, and peak motion begins (Supporting Text 2.5).

For experimental levels of stochasticity (i.e., Σ factor 1), a phase shift occurs on ≈12.5% of time steps (Supporting Text 2.5). Whereas the deterministic system switches from c₁ to c₂ or vice versa 100 times in 100 time steps, the stochastic system switches from a neighborhood of c₁ to a neighborhood of c₂ about 100 − 12.5 ≈ 87 times in 100 time steps. This finding corresponds to a ≈12.5% reduction in the primary frequency of the deterministic system, explaining the main peak at nf 0.87 ≈ 1 − 0.125 for the stochastic models and for experimental time series. The percentages of times that each experimental time series phase shifted were 22.5%, 10.0%, and 15.0%; these percentages agreed approximately with those of the simulation (Supporting Text 2.5), but had more scatter because experimental time series had only 40 transitions from one census to the next. Stochastically induced failures to switch at each time step between a pupae-dominated age distribution and a bimodal age distribution caused peak motion in Fig. 4B.

Comparison of High and Zero Adult-on-Pupae Cannibalism.

In contrast to the c_pa = 0 case, phase shifting did not affect the locations of spectral peaks for c_pa = 0.5 (Fig. 4A). In typical length-1024 output of the SD-LPA model, phase shifting occurred about as frequently (on 11.1% of time steps) for c_pa = 0.5 as for c_pa = 0. However, for c_pa = 0.5, two opposite types of phase shifting along the 3-cycle attractor occurred, canceling each other: backward and forward shifting with respect to time evolution of the deterministic system. If the deterministic system moves in one time step from a₁ to a₂, then a forward (backward) phase shift of the stochastic system is movement of the population vector in one time step from a neighborhood of a₁ to a neighborhood of a₃ (a₁). A backward phase shift is a failure to advance to a neighborhood of a₂ (backward compared with the deterministic model). Forward (backward) shifts occurred on ≈8.7% (2.4%) of time steps for c_pa = 0.5. Forward shifts that can be paired with backward shifts at another time do not affect the frequency of oscillation of the system. Forward shifts not cancelled by backward shifts at another time contribute to increasing the frequency of the system; these occurred rarely (on only 6.3% = 8.7 − 2.4% of time steps) for c_pa = 0.5, not enough to have a noticeable effect. In contrast, for c_pa = 0, phase shifting on the approximate 2-cycle comprised of c₁ and c₂ occurred in only one direction; forward and backward shifts on a 2-cycle are the same. Phase shifts could not cancel each other, explaining why peak locations changed for c_pa = 0 but not for c_pa = 0.5, and why linearization theory applied for c_pa = 0.5 but not c_pa = 0.

We call phase shifts that occur predominantly in one direction around an attractor “directional phase shifts.” “Phase dissipation” refers to phase shifts that occur approximately equally in both directions around an attractor. Phase dissipation blunts spectral peaks without changing their location. All phase shifts are directional on a 2-cycle.

Discussion

Linearization theory, which describes the decay of small deviations from a deterministic attractor, predicts that only the magnitudes (not the frequencies) of stochastically induced phenomena change as the magnitude of stochasticity changes. It explains the influence of stochasticity on dynamics for one experimental treatment of this study but fails for another treatment. Ecologically realistic levels of stochasticity can move populations too far from a deterministic attractor for linear approximations rooted at points in the attractor to be valid (27), and can cause directional phase shifting that changes the dominant periodicity of a system. Theory accounting for directional phase shifts and dynamics far from an attractor is needed.

The Tribolium laboratory system is very controlled, but stochasticity (primarily demographic; ref. 24) was still too great for linearization to apply in one case we considered. The intensity of demographic stochasticity relative to population density is proportional to the inverse square root of population size (14, 25, 28). Demographic stochasticity affecting a field system could be stronger or weaker than the stochasticity affecting the Tribolium system according to whether the field system has smaller or larger populations. Both demographic and environmental stochasticity affect field systems. If total stochasticity affecting a field system is comparable to or less than the stochasticity affecting the Tribolium system, linearization theory may apply.

Whether linearization theory explains the effects of stochasticity on a particular nonlinear model also depends on the details of deterministic dynamics (18). If a deterministic model's attractor is close to, for example, unstable equilibria, other attractors, or zero-population boundaries, then low levels of stochasticity may suffice to invalidate predictions of linearization theory. If points of a finite attractor are close together, low levels of stochasticity may cause frequent phase shifting, which may be directional. Phase shifting can also occur for quasiperiodic and chaotic dynamics. Linearization theory will be relatively less useful for weakly stable deterministic models (such as the c_pa = 0 treatment here) for which perturbations from the attractor decay slowly.

Our numerical spectral techniques for examining the biological effects of strong stochasticity (Figs. 1 and 4) may apply to ecological and other systems, and may generalize to continuous-time models, models with a spatial component, and wavelet analysis. How often the spectrum enhancement method gives correct spectral predictions when using a realistic model and how often it gives incorrect spectral predictions when using an unrealistic model remain to be determined.

The strategy of Fig. 1 should be used only with a mechanistic model. A mechanistic model that fits well in the spectral and time domains can be used for detailed spectral analysis even when long experimental time series are lacking (Fig. 1). The additional detail in spectral estimates from long model-generated time series reflects biological hypotheses encoded in the functional form of the model. Detailed estimates are testable hypotheses for population spectra based on all available observations and mechanistic theory (deterministic and stochastic).

Methods

Experiments.

We set adult mortality rate (μ_a) at 0.96, and manipulated effective adult-on-pupae cannibalism (c_pa) to obtain values c_pa = 0, 0.05, 0.10, 0.25, 0.35, 0.50, and 1.00 in seven treatments of three replicates each (29). A control treatment was not manipulated. The larval, pupal, and adult stages were counted (eggs were discarded) every two weeks (one time step) for 80 weeks, giving trivariate time series of length 41 (the initial condition plus 40 time steps). The treatment with c_pa = 0.35 and the controls were continued for 424 weeks, giving six time series of length 213 (24).

Models.

The lattice stochastic demographic LSD-LPA model, a discrete-time discrete-state nonlinear stochastic model, can be constructed in three steps: (i) start with the LPA model, a deterministic model; (ii) include stochasticity (SD-LPA); and (iii) constrain populations to integer values (LSD-LPA).

The LPA model is L_t+1 = bA_t exp(−(c_el/V)L_t − (c_ea/V)A_t), P_t+1 = (1 − μ_l)L_t, A_t+1 = (1 − μ_a)A_t + P_t exp(−(c_pa/V)A_t), where L_t, P_t, and A_t are the numbers of larvae, pupae, and adults at week 2t; b is fecundity per adult per unit time; μ_l, μ_a are mortality rates per unit time per larva and per adult; c_el is the probability that a single larvae encounters and eats a single egg during a small time interval, Δt (24); c_ea and c_pa are similar coefficients for rates of cannibalism per adult on eggs and on pupae, respectively; V is habitat volume in units equal to the volume of 20 g of flour. The initial stage vector (L₀, P₀, A₀) = (250, 5, 100) was used for all experiments and simulations of this study.

The SD-LPA model adds square root scale trivariate normally distributed noise (demographic stochasticity) with covariance matrix Σ after each time step of the LPA model. The LSD-LPA model rounds populations to the nearest integer after each time step of the SD-LPA model. “Lattice” here refers not to a spatial lattice but to the requirement that population counts be integers. For the SD-LPA and LSD-LPA models, stochasticity is modified in intensity by multiplying each entry of Σ by a single positive “Σ factor.” Experimentally, demographic stochasticity relative to population density can be decreased by increasing beetle habitat size (25). The LSD-LPA model is considered the most realistic model of this study. Model parameter values and equations are given in Supporting Text 1.1.

Figures show spectra of adult time series only; spectra of other life-stages are different in detail but had peaks of the same relative heights in the same locations. Frequency-domain fit P values take account of all life stages.

Statistical Tests.

We used new simulation-based statistical tests to see whether nonlinear stochastic models with fixed parameters could generate time series with spectral estimates similar to those of data time series. Two tests give approximate P values to describe the quality of the frequency-domain fit between model and data (see Supporting Text 1.2; see also refs. 22, 30, and 31). The “spectrum distance fit test” measures the sum, across all frequencies, of the squared distances between the mean of log spectra of many model-generated time series and the log spectrum of an experimental time series (this is the squared “L₂ distance”). The test indicates a good fit if the data log spectrum is closer to the mean model log spectrum under the L₂ distance than a large enough percentage of model log spectra. The “spectrum shape fit test” measures the correlation between the mean model log spectrum and the log spectrum of an experimental time series. A good fit occurs if the data log spectrum has shape closer to that of the mean model spectrum than a large enough number of model log spectra. Another technique, similar to techniques applied previously (32–34), provides a visual comparison between spectral estimates from data and distributions of spectral estimates from model-generated time series. These tests reject (or fail to reject) biological hypotheses expressed as stochastic dynamical models.

These spectral fit tests do not use linear approximation. They make no assumptions on the functional form of the spectrum. They have no a priori relationship to traditional time-domain fitting methods (5, 29). A good time-domain fit does not necessarily imply a good frequency domain fit, or vice versa (Supporting Text 1.3; ref. 30).

The fit of a population model should be verified in both domains where feasible (7, 33, 34). A substantially inappropriate model will fail to fit short population time series, for all parameter values, in the frequency and the time domains. A moderately inappropriate model functional form may fit acceptably in both domains, but with different parameter values (examples in Supporting Text 1.3). Such a functional form must be rejected (30). A good model should fit well in both domains with the same parameters.

Abbreviations

SD-LPA

stochastic demographic larvae–pupae–adult

LSD-LPA

lattice SD-LPA

nf

normalized frequency.