Abstract
Many experiments have measured the effect of force on the dissociation of single selectin bonds, but it is not yet clear how the force dependence of molecular dissociation can influence the rolling of cells expressing selectin molecules. Recent experiments using constant-force atomic force microscopy or high-resolution microscopic observations of pause-time distributions of cells in a flow chamber show that for some bonds, the dissociation rate is high at low force and initially decreases with force, indicating a catch bond. As the force continues to increase, the dissociation rate increases again, like a slip bond. It has been proposed that this catch-slip bond leads to the shear threshold effect, in which a certain level of shear rate is required to achieve rolling. We have incorporated a catch-slip dissociation rate into adhesive dynamics simulations of cell rolling. Using a relatively simple model for the shear-controlled association rate for selectin bonds, we were able to recreate characteristics of the shear threshold effect seen most prominently for rolling through L-selectin. The rolling velocity as a function of shear rate showed a minimum near 100 s−1. Furthermore, cells were observed to roll at a shear rate near the threshold, but detach and move more quickly when the shear rate was dropped below the threshold. Finally, using adhesive dynamics, we were able to determine ranges of parameters necessary to see the shear threshold effect in the rolling velocity. In summary, we found through simulation that the catch-slip behavior of selectin bonds can be responsible for the shear threshold effect.
INTRODUCTION
Neutrophils are the most abundant of the leukocytes, found in quantities of ∼5 × 106/mL of blood (1). At sites of inflammation, several types of adhesion molecules, including selectins, are expressed on the blood vessel walls. Neutrophils possess the appropriate counterreceptors and are captured from the blood stream upon bond formation. A captured neutrophil then rolls on the vessel wall as bonds form at the leading edge of the cell and break at the rear. This slow rolling allows signaling events to occur that activate the cell (2,3). Once β2-integrin molecules on the neutrophil are in their active, high-affinity state, the neutrophil firmly adheres to the vessel wall and extravasates between endothelial cells to the tissue where it can eliminate foreign invaders.
The rolling step of the adhesion process has been carefully examined in vitro by allowing cells to flow over and interact with a surface coated in adhesion molecules (either selectins or their ligands). Rolling behavior is characterized by motion of the cells at velocities significantly below that of the free stream. On some molecular surfaces, however, studies at low shear rates have observed that these cells do not readily form adhesive interactions with the surface and do not roll, whereas at higher shear rates, cells are able to roll (2,4–10). This requirement of a high enough level of shear for the cell to roll has been termed the shear threshold effect. Such a requirement may help prevent the undesired accumulation of cells at low-flow sections of the vasculature and aggregation of neutrophils within the blood stream (11,12).
Both P- and L-selectin-mediated rolling have revealed the shear threshold effect (5); however, the effect is most prominent for rolling via L-selectin. A commonly reported trademark of the shear threshold effect is a maximum in the number of rolling cells at an intermediate value of shear stress (4,7,8). For neutrophils rolling via L-selectin bonds on peripheral-node addressin (PNAd), for instance, the number of tethered and rolling cells was zero at low shear stresses, increased to a maximum around 1 dyn/cm2, then decreased again as the shear stress became large (4). There are, however, other interesting manifestations of the shear threshold effect. For example, the average rolling velocity of neutrophils on a low density of soluble P-selectin glycoprotein ligand-1 (sPSGL-1) has been observed to decrease with shear rate to a minimum at ∼100 s−1 before increasing again (10). Also, when stable rolling of a single neutrophil on PNAd was initiated near the optimum shear stress, a sudden drop in flow rate to below the threshold resulted in detachment of the cell after a brief period of continued rolling (2). Another noteworthy observation is that neutrophils did not readily initiate rolling on the CD34 component of PNAd at a high shear stress. However, if rolling was initiated near the optimum shear stress, cells remained bound and rolling even when the flow was suddenly increased (7).
There are two prevailing theories as to the cause of the shear threshold effect: a receptor-ligand on rate that is influenced by shear rate and an off rate that displays catch-bond behavior at low shear rates and slip-bond behavior at high shear rates. Chang and Hammer (13) theorized that the on rate for cell adhesion molecules increases with relative velocity between the cell and substrate surfaces. As the surfaces pass by each other more rapidly, the rate of encounter between adhesion molecules increases, leading to an on rate that increases with shear rate. At the same time, the probability of reaction decreases as the molecules spend less time in proximity of each other, so the on rate plateaus at large relative velocities. In support of this theory of a shear dependent on rate, Dwir and co-workers (14) found that by altering medium viscosity a threshold level of shear rate, not shear stress, was required to initiate stable L-selectin tethers for pre-B lymphocytes on PNAd. It is possible that at low shear rates, and therefore low relative velocity between binding surfaces, the on rate is too low to initiate binding.
Alternatively, a unique off rate could lead to the shear threshold effect. Several flow chamber and atomic force microscopy (AFM) constant-force dissociation experiments have detected a catch-slip bond for selectin molecules in which the off rate initially decreases, then increases with force (9,10,14,15). Measuring the lifetimes of P-selectin/PSGL-1 bonds over a range of forces applied by AFM, Marshall and co-workers (15) found that the off rate of the bonds went through a dramatic minimum at a pulling force of ∼30 pN. However, P-selectin bonds with the antibody G1 revealed an off rate that increased exponentially with force according to the Bell model (16). In another experiment (10), neutrophils were allowed to bind to a sparsely coated surface of sPSGL-1 in a flow chamber. Lifetimes of the transient binding events were measured and a constant force on the bonds was estimated based on the experimental conditions. The off rate of the L-selectin/sPSGL-1 bonds was a function of the force on the bond and showed a minimum at ∼80 pN. Evans and co-workers (17) were able to deduce a possible mechanism for the experimentally detected catch-slip-bond behavior, specifically for the P-selectin/PSGL-1 bond. They postulated that the bond exists in equilibrium between two states. Bond failure can occur via either state, with pathway 1 being fast and pathway 2 being slow. At low forces, state 1 is more populated, so bond dissociation is fast. As the force on the bond increases, state 2 becomes more populated so bond dissociation slows, leading to a catch-bond behavior. Barsegov and Thirumalai suggested a similar two-state model for P-selectin/PSGL-1 bond dissociation (18). Though it has been detected for both, the catch-slip behavior is more prominent for L-selectin than it is for P-selectin bonds, which corresponds to the more prominent shear threshold effect for L-selectin.
Adhesive dynamics is a computational tool developed in our lab to simulate cell adhesion (19). In adhesive dynamics, a model cell is placed in a shear flow and bonds with the surface stochastically form and break in accordance with the association and dissociation rates of the binding molecules. Previous models were able to recreate cell-free rolling behavior using the Bell model for the off rate and a constant on rate (20–25). More recently, deformable microvilli, which greatly improved adhesiveness and rolling, were added to the model (26). Also, activation of model integrins on the cell by selectin ligation recreated the transition from rolling to firm adhesion (27). Although adhesive dynamics has modeled several aspects of cell adhesion, simulations have not yet recreated the shear threshold effect.
By using new kinetic rates in an adhesive dynamics model, we investigate in this work whether the catch-slip bond or shear-induced on rate, or both, is necessary for the shear threshold effect in rolling via L-selectin. We found that though the shear threshold effect was recreated best when both new kinetic rates were used, it was attainable using just the catch-slip off rate with a constant on rate. Later, we explore parameter space to understand how sensitive the shear threshold effect is to parameter values that control the molecular behavior of the system, particularly the catch-slip off rate.
MODEL
The physics of this model is similar to previous adhesive dynamics models of cell rolling, the details of which can be found elsewhere (19,26,28). Briefly, a hard sphere represents the cell in a shear flow over a planar surface coated with PSGL-1 molecules. Protruding from the sphere are randomly distributed microvilli with L-selectin molecules on their tips. Bonds between the cell and surface stochastically form and break based on the bond kinetics, causing the cell to roll. Under the pulling force of a bond, the microvilli stretch according to the rheology described by Shao and co-workers (29). The difference in this model is in the bond kinetics. Instead of the Bell model for the off rate and a simple assumed on rate, a catch-slip bond is used for the off rate with a shear-controlled on rate.
Off rate
Instead of the Bell model, in which the off rate increases exponentially with force, Evans' two-state catch-slip model is used (17). Evans and co-workers deduced the two-state model from a series of dynamic force spectroscopy (DFS) experiments using a biomembrane force probe. When pulled on at a constant loading rate that was slow, all P-selectin/PSGL-1 bonds ruptured at low forces. At an intermediate loading rate, many bonds broke at low forces, but there was also another peak of bond breakage events at a higher force. Finally, at fast loading rates, only a few bonds broke at low forces and the peak of bond breakage events occurred at an even higher force. The peak at high force appeared to follow behavior expected of a single dissociation pathway defined by the Bell model. Enlightening results were obtained from a modification of the simple steady-ramp loading experiments. When the force applied to the bonds was suddenly increased to a value of ∼30 pN, then ramped up at a constant rate, there was no longer evidence of bond breakage at low forces. These jump/ramp experiments suggested that there are two pathways for dissociation. Pathway 1 is very fast and dominates at low forces, which is why bonds broke at low force under slow steady ramps. This pathway was avoided in the jump/ramp experiments because the force was jumped up to a level where the fast pathway was no longer dominant. Pathway 2, as mentioned, is a slower pathway that follows the Bell model and dominates at high forces.
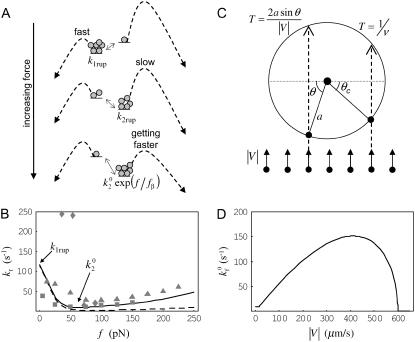
To model this two-pathway dissociation, as depicted in Fig. 1 A, Evans and co-workers (17) assumed that the pathways come from two possible bound states. Dissociation via the two pathways occurs with rates k1rup and k2rup. It was assumed that the off rate for the fast pathway is constant at k1rup. For the slow pathway, on the other hand, dissociation was assumed to follow the Bell model for an exponential increase in off rate with force, so 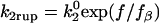 . The unstressed off rate of the slow pathway is given by
. The unstressed off rate of the slow pathway is given by 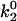 and the force scale for the increase in off rate with force, f, is fβ. The dominant dissociation pathway is determined by the occupancy ratio of the two states. The states were assumed to be in equilibrium at all times (fast equilibration) with a small difference in energy between state 2 and state 1, ΔE21. According to the Boltzmann distribution, this energy difference sets the equilibrium occupancy ratio,
and the force scale for the increase in off rate with force, f, is fβ. The dominant dissociation pathway is determined by the occupancy ratio of the two states. The states were assumed to be in equilibrium at all times (fast equilibration) with a small difference in energy between state 2 and state 1, ΔE21. According to the Boltzmann distribution, this energy difference sets the equilibrium occupancy ratio, 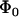 , of state 1 to state 2 at zero force. However, force applied to the bond causes a shift in the energy of each state, resulting in a change in the energy difference between the states. The occupancy ratio of the two states, then, changes exponentially with applied force with a scale of f12. So, although pathway 1 may dominate at low forces where equilibrium favors occupancy of state 1, at higher forces, pathway 2 dominates as equilibrium shifts to favor occupancy of state 2. For bonds exhibiting this type of catch-slip behavior, the off rate is given by (17)
, of state 1 to state 2 at zero force. However, force applied to the bond causes a shift in the energy of each state, resulting in a change in the energy difference between the states. The occupancy ratio of the two states, then, changes exponentially with applied force with a scale of f12. So, although pathway 1 may dominate at low forces where equilibrium favors occupancy of state 1, at higher forces, pathway 2 dominates as equilibrium shifts to favor occupancy of state 2. For bonds exhibiting this type of catch-slip behavior, the off rate is given by (17)
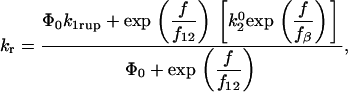 |
(1) |
where 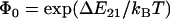 is the equilibrium constant between the two states at zero force.
is the equilibrium constant between the two states at zero force.
FIGURE 1.
Receptor-ligand reaction rates. (A) Depiction of Evans' two-state model for bond dissociation. Bonds can exist in two states. At low forces, state 1 is likely populated and breakage via this state is fast with constant rate k1rup. As the force on the bond increases, state 2 becomes more likely. Breakage via state 2 is slower with rate k2rup, which increases with force according to the Bell model. (B) Base-case and best-case (dashed line) catch-slip off rates as a function of force. Evans' model parameters were chosen as given in Table 1 to correspond to experimental L-selectin off-rate data. The parameters k1rup and 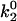 strongly influence the high off rate at low forces and the low off rate at intermediate forces, respectively. Experimental off rates are for L-selectin/PSGL-1 bonds measured by AFM (▪) (9), neutrophils on sparse sPSGL-1 in a flow chamber (▴) (10), and L-selectin-expressing lymphocytes on PSGL-1-derived peptides in a flow chamber (♦) (14). (C) Schematic for shear-controlled on-rate derivation. A molecule of interest is shown with its reactive circle of radius a. A uniform distribution of molecules on the apposing surface approaches the circle with relative velocity |V|. The time T spent in the reactive circle depends on the angle of the entry point, θ. At angles
strongly influence the high off rate at low forces and the low off rate at intermediate forces, respectively. Experimental off rates are for L-selectin/PSGL-1 bonds measured by AFM (▪) (9), neutrophils on sparse sPSGL-1 in a flow chamber (▴) (10), and L-selectin-expressing lymphocytes on PSGL-1-derived peptides in a flow chamber (♦) (14). (C) Schematic for shear-controlled on-rate derivation. A molecule of interest is shown with its reactive circle of radius a. A uniform distribution of molecules on the apposing surface approaches the circle with relative velocity |V|. The time T spent in the reactive circle depends on the angle of the entry point, θ. At angles 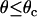 , the molecules are in binding proximity less than the required amount of time, 1/ν, so the probability of those molecules binding is zero. (D) Base-case shear-controlled on rate with parameters given in Table 1. The unstressed on rate increases with relative velocity between surfaces, but then drops to zero when molecules pass by each other too quickly to bind.
, the molecules are in binding proximity less than the required amount of time, 1/ν, so the probability of those molecules binding is zero. (D) Base-case shear-controlled on rate with parameters given in Table 1. The unstressed on rate increases with relative velocity between surfaces, but then drops to zero when molecules pass by each other too quickly to bind.
In Evans' model, there are five parameters that describe the catch-slip behavior of bonds. The equilibration parameters, ΔE21 and f12, control the force at which the change of dominant pathway occurs and the range of force required to complete the switch. The dissociation rate parameters, k1rup and 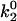 , determine the extremes in the off rate. The constant rate of the fast pathway controls how fast the off rate is at zero force, whereas the unstressed rate of the slow pathway sets the minimum in off rate at an intermediate value of the force. Finally, the force scale for the Bell model, fβ, sets the degree of rate increase with force at high forces. A larger value of fβ corresponds to a more gradual increase in off rate with force.
, determine the extremes in the off rate. The constant rate of the fast pathway controls how fast the off rate is at zero force, whereas the unstressed rate of the slow pathway sets the minimum in off rate at an intermediate value of the force. Finally, the force scale for the Bell model, fβ, sets the degree of rate increase with force at high forces. A larger value of fβ corresponds to a more gradual increase in off rate with force.
Though Evans' model was derived for the P-selectin/PSGL-1 bond, experiments have shown similar catch-slip behavior for L-selectin bonds. Therefore, in this work, Evans' catch-slip model was used to express the off rate as a function of force for L-selectin bonds. Base-case parameters were chosen approximately to give a rate in line with experimental data for L-selectin dissociation from PSGL-1 or sPSGL-1, as shown in Fig. 1 B (9,10,14). The base-case parameters are listed in Table 1. Compared to parameters determined for the P-selectin/PSGL-1 bond (17), the off rates chosen here to represent L-selectin bonds are an order of magnitude faster. This corresponds to the higher velocities observed for L-selectin- compared to P-selectin-mediated rolling (6).
TABLE 1.
Reaction rate parameters
| Parameter | Base case | Best case |
|---|---|---|
| Catch-slip off rate | ||
| k1rup (s−1) | 150 | 150 |
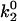 (s−1) (s−1) |
5 | 1 |
| fβ (pN) | 110 | 110 |
| ΔE21 (pN·nm) | 5 | 5 |
| f12 (pN) | 10 | 10 |
| Shear-controlled unstressed on rate | ||
| D (μm2/s) | 0.05 | 0.15 |
| a (μm) | 0.003 | 0.002 |
| kin (s−1) | 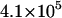 |
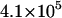 |
| ν (s−1) | 105 | 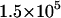 |
| ρligand (sites/μm2) | 100 | 100 |
On rate
The on rate used in this work is a modification of the theory of a shear-induced on rate by Chang and Hammer (13). The on rate was originally derived for the binding of a cell-surface receptor to a ligand-coated surface moving with speed |V| relative to the cell surface. Binding molecules were assumed to be at the ideal binding distance. In this calculation, the binding process was divided into two steps: encounter and reaction. The rate at which molecules encounter each other increases with relative velocity between the surfaces. When |V| is small, however, diffusion of the molecules within their respective membranes is what gives rise to an encounter rate. Thus, the encounter rate, k0, has a diffusive and a convective limit:
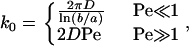 |
(2) |
where D is the relative diffusion coefficient and the Peclet number Pe = |V|a/D. The parameter b is half of the mean distance between ligand molecules and a is the radius of a circle of reactivity around the receptor. Between these two limits, the convective limit provides a good approximation to the true solution of the convection-diffusion equation for encounter.
When a ligand molecule is within the reactive circle of a cell surface receptor, i.e., an encounter has been made, the molecules must then react. The molecules have a probability of reaction, P, which depends on the intrinsic reaction rate and the duration of the encounter as follows:
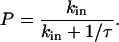 |
(3) |
The intrinsic reaction rate, kin, is assumed to be constant, whereas the average encounter duration, τ, is determined by transport. Using the first-passage-time approach, Chang and Hammer (13) found the diffusion and convection limits of the encounter duration to be:
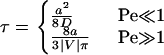 |
(4) |
Again, the convection limit fits the true solution well at intermediate values of Pe.
The overall unstressed forward reaction rate for a cell-surface receptor, considering encounter and probability of reaction, is given by
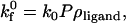 |
(5) |
where ρligand is the density of ligand molecules on the substrate surface. The unstressed on rate of Eq. 5 is adjusted according to the Boltzmann distribution when the distance between molecules deviates from ideal (30). Upon combining Eqs. 2–5 appropriately, the unstressed on rate can be calculated from the following equations in the diffusion and convection limits:
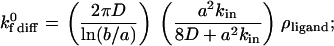 |
(6) |
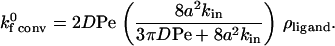 |
(7) |
The transition from the diffusion limit to the convection limit occurs at the value of Pe = Petran, at which the two expressions are equal:
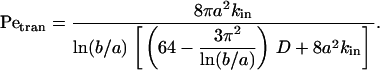 |
(8) |
Notice that for Pe≫1,  in Eq. 7 becomes independent of Pe, i.e., the on rate plateaus as the relative velocity of the binding surfaces increases.
in Eq. 7 becomes independent of Pe, i.e., the on rate plateaus as the relative velocity of the binding surfaces increases.
The equations derived by Chang and Hammer assume that it is always possible for a pair of molecules that have encountered each other to react. However, if the encounter duration is shorter than the time required for the binding molecules to explore conformational space and react, the probability of reaction can become identically zero, causing the on rate to fall off to zero as Pe becomes large (13). As evidence of such an on rate, transient tethering data for cells in a flow chamber report a frequency of binding that decreases as the shear rate becomes large (6,7). To model this “shear-controlled” on rate, a new parameter is necessary: the timescale for exploring conformational space, 1/ν. If a molecule is in the reactive circle for a time too brief compared to 1/ν, its probability of reaction is set to zero. The probability of reaction from Chang and Hammer must be reformulated to account for this new consideration.
It is assumed that the probability of reaction will be significantly affected only in the convective limit, when molecules are passing by each other more quickly. In the convective limit, we can easily calculate the amount of time, T, a molecule will spend in the reactive circle based on only the point (θ) at which the molecule enters the reactive circle, the reactive radius, and the relative velocity with which it is traveling. A schematic of the simplified system is shown in Fig. 1 C. If the time in the reactive circle is less than the timescale for exploration of conformational space, the probability of reaction for that molecule is set to zero. Therefore, the cutoff condition is 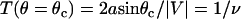 . To calculate an average probability of reaction for molecules passing through the reactive circle at all possible positions, Eq. 3 for the probability is integrated over the appropriate uniform distribution of molecules from
. To calculate an average probability of reaction for molecules passing through the reactive circle at all possible positions, Eq. 3 for the probability is integrated over the appropriate uniform distribution of molecules from 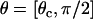 as follows:
as follows:
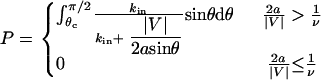 |
(9) |
With this probability in the convective limit that decreases to identically zero, the corresponding on rate initially increases with velocity as the encounter rate increases, but then decreases to zero as the probability of reaction decreases to zero faster. A graph of this shear-controlled on rate for the base-case parameters is shown in Fig. 1 D, and the parameters, selected to be in line with experimentally determined typical values (13), are listed in Table 1. The on rate starts at a constant small value at small velocities while the system is in the diffusion limit. As convection takes over, the on rate increases to a maximum before decreasing to zero when 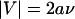 .
.
RESULTS
Adhesive dynamics simulations were used with updated kinetic rates, namely, a catch-slip off rate and a shear-controlled on rate, to recreate the shear threshold effect for L-selectin and to better understand its possible origins. Based on the experimental observations of rolling via L-selectin, there are several properties to look for in simulations of the shear threshold effect. Because heterogeneity of cells is not included in the model, flux measurements are not as meaningful in the simulations, so results will focus on velocity measurements. The characteristics of cell rolling sought in this work are 1), a minimum in average rolling velocity as a function of shear rate; 2), a brief continuation of rolling followed by detachment at shear rates below the threshold when initiated at the optimum shear rate; and 3), continuation of rolling at a high shear rate when initiated at an optimum shear rate, but not when initiated at the high shear rate.
Simulations were started at the given shear rate with the model cell at close apposition to the binding surface. At each set of conditions, five cells were simulated for 10 s each. Average velocities were calculated based on the average distance traveled by the five cells over the last 9 s of the simulation.
Base case
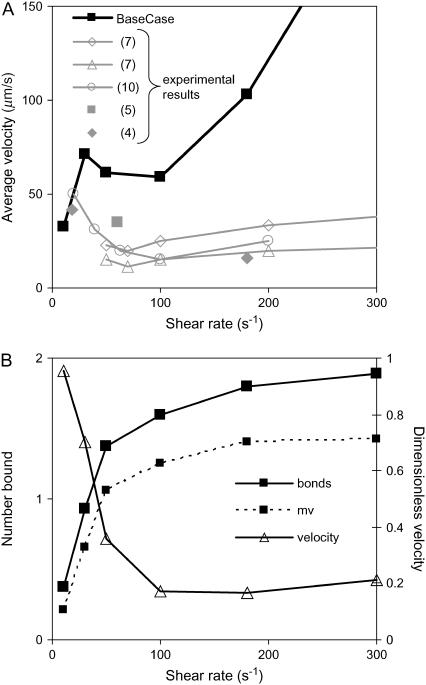
With the initially chosen base-case on rate and off rate discussed in the Model section and given in Table 1, simulations of cell rolling via L-selectin bonds showed a slight minimum in average rolling velocity as a function of shear rate. At very low shear rates (10 s−1), the velocity is small simply because hydrodynamic velocity is small; there is actually no rolling. At very high shear rates (>300 s−1), cells never bind because the on rate drops to zero at these high relative velocities. However, at intermediate shear rates, cells bind to and roll along the surface at velocities significantly below that of the free stream. The minimum in velocity occurs at a shear rate of ∼100 s−1, consistent with experimental results as seen in Fig. 2 A (4,5,7,10).
FIGURE 2.
Base-case results for L-selectin-mediated rolling. (A) Average velocity as a function of shear rate. The base-case simulation shows a minimum in velocity near 100 s−1, similar to experimental results. Experiments are from Puri et al. (7), lymphocytes on CD34 at 50 or 300 sites/μm2; Yago et al. (10), neutrophils on sPSGL-1 at 140 sites/μm2; Lawrence et al. (5) and Finger et al. (4), T-cells on PNAd. (B) Number of bonds and bound microvilli. Also, average velocity normalized by hydrodynamic velocity. The dimensionless velocity decreases with shear rate whereas the number of bonds increases.
It is interesting that over the range of shear rates tested, the average number of bonds and bound microvilli per cell, shown in Fig. 2 B, increases with shear rate. This observation corresponds to the experimental results of Chen and Springer (2), from which they deduce that an increase in bond number with shear rate acts as an automatic braking system and could lead to the shear threshold effect. Related to the increase in bond number, Fig. 2 B also shows that the model predicts that dimensionless velocity normalized by hydrodynamic velocity significantly decreases with shear rate.
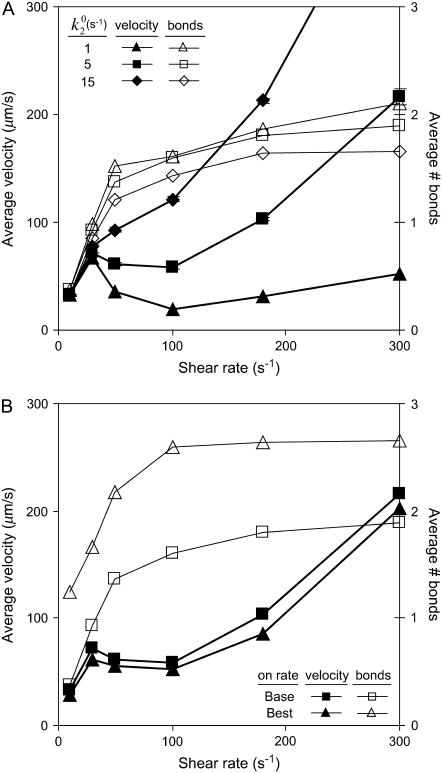
Besides performing the base-case simulations, we explored how different parameters in the rate expressions could affect the appearance of the shear threshold effect. Of particular interest is the effect of the unstressed off rate for pathway 2 of the catch-slip rate, 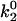 , which gives the minimum in off rate. Fig. 3 A shows that
, which gives the minimum in off rate. Fig. 3 A shows that 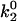 can tune the velocity of the cell when it is rolling at intermediate shear rates; decreasing values of
can tune the velocity of the cell when it is rolling at intermediate shear rates; decreasing values of 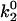 lead to decreases in the minimum in rolling velocity. An additional case to make note of is the modification of the on-rate parameters D, a, and ν to increase the unstressed on rate in the diffusion limit, but decrease it in the convective limit. With these changes in parameters given as the best-case on rate in Table 1, and keeping the base-case off rate, cells depicted in Fig. 3 B rolled at velocities similar to the base case, but at a higher level of bonding to the surface.
lead to decreases in the minimum in rolling velocity. An additional case to make note of is the modification of the on-rate parameters D, a, and ν to increase the unstressed on rate in the diffusion limit, but decrease it in the convective limit. With these changes in parameters given as the best-case on rate in Table 1, and keeping the base-case off rate, cells depicted in Fig. 3 B rolled at velocities similar to the base case, but at a higher level of bonding to the surface.
FIGURE 3.
Average velocity and number of bonds versus shear rate for explorations of rate parameters. (A) Various values of the unstressed off rate (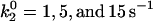 ). The remaining parameters are from the base case. This parameter,
). The remaining parameters are from the base case. This parameter, 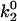 , influences the velocity at intermediate values of shear rate. (B) Different on rates. Results for the base-case on rate are compared to results for the best-case on-rate parameter values D = 0.15 μm/s2, a = 0.002 μm, and ν = 1.5 × 105 s−1, which give a larger rate in the diffusion limit but a smaller rate in the convective limit. The remaining parameters are from the base case. The modified on rate generates more intimate binding to the surface while maintaining rolling velocities similar to the base case.
, influences the velocity at intermediate values of shear rate. (B) Different on rates. Results for the base-case on rate are compared to results for the best-case on-rate parameter values D = 0.15 μm/s2, a = 0.002 μm, and ν = 1.5 × 105 s−1, which give a larger rate in the diffusion limit but a smaller rate in the convective limit. The remaining parameters are from the base case. The modified on rate generates more intimate binding to the surface while maintaining rolling velocities similar to the base case.
Best-case comparison to experiments
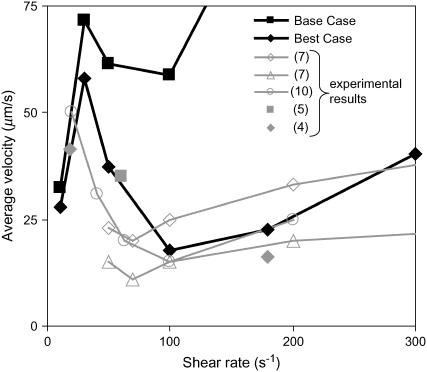
The minimum in velocity that is indicative of the shear threshold effect is apparent in the base case. The minimum occurs near the correct value of shear rate, but the simulated velocities are higher than experimental velocities at intermediate shear rates (see Fig. 2 A). Based on the parameter exploration demonstrated in Fig. 3 A, lowering the value of 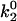 , which lowers the off rate at higher forces, should lead to a better match with experimental data for rolling via L-selectin bonds. This led to the formulation of a “best-case” set of parameters, in which
, which lowers the off rate at higher forces, should lead to a better match with experimental data for rolling via L-selectin bonds. This led to the formulation of a “best-case” set of parameters, in which 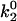 was lowered by a factor of 5. Fig. 4 shows the best-case simulation (best-case parameters are given in Table 1 and the best-case off rate is shown as a dashed line in Fig. 1 B) along with experimental results and the base case for comparison. The minimum in velocity for the best case occurs near the correct value of shear rate, as it does for the base case. The best-case simulation also provides an excellent match to experimental velocities, whereas the base case was less successful.
was lowered by a factor of 5. Fig. 4 shows the best-case simulation (best-case parameters are given in Table 1 and the best-case off rate is shown as a dashed line in Fig. 1 B) along with experimental results and the base case for comparison. The minimum in velocity for the best case occurs near the correct value of shear rate, as it does for the base case. The best-case simulation also provides an excellent match to experimental velocities, whereas the base case was less successful.
FIGURE 4.
Average velocity versus shear rate. For the best case, 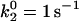 so the off rate is smaller at higher forces. As described in the text, the best-case parameters involve lowering
so the off rate is smaller at higher forces. As described in the text, the best-case parameters involve lowering 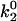 by a factor of 5 relative to the base case, but provide a better match to experimental results (listed in Fig. 2) than the base case does.
by a factor of 5 relative to the base case, but provide a better match to experimental results (listed in Fig. 2) than the base case does.
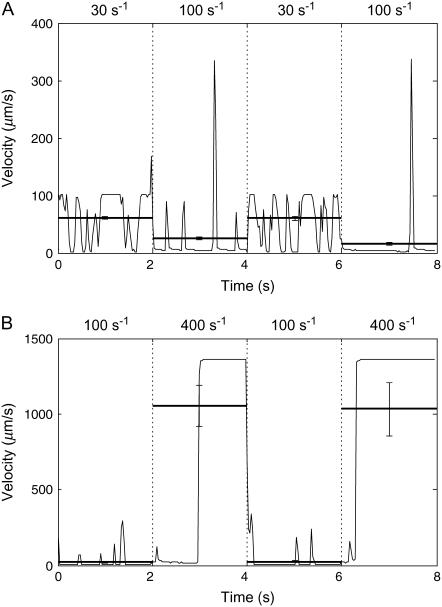
Paralleling several experiments, simulations were performed in which the shear rate was suddenly switched from the optimum of 100 s−1 to above or below that rate. Again, the best-case parameters for the kinetic rates were used. Switching the shear rate from below the threshold (30 s−1) to the optimum and back produced clear changes in velocity. As seen in Fig. 5 A, the simulated cells traveled at an average velocity of ∼60 μm/s when the shear rate was below the threshold for rolling, but when the shear rate was increased to the optimum, the cells slowed down and rolled at an average velocity of ∼20 μm/s. The instantaneous velocity of a single representative cell is also shown in Fig. 5 A. The cell travels near hydrodynamic velocity with a few brief attachments at 30 s−1. At 100 s−1, though, the cell typically travels slowly, with a few spikes in velocity as bonds break during rolling. Finger and co-workers (4) saw similar results in an experiment in which T-cells rolled over a PNAd-coated surface at an average velocity of 16.2 μm/s when the shear rate was at 180 s−1. After a sudden switch to 18 s−1, the cells detached and traveled at the hydrodynamic velocity of 41.3 μm/s. Rolling was restored when the shear rate returned to 180 s−1.
FIGURE 5.
Average and instantaneous velocities during jumps in shear rate. Average velocities were calculated over each 2-s period of constant shear rate and are shown as horizontal lines with the standard error. The instantaneous velocity of a representative cell is also shown over the course of an entire 8-s simulation. (A) The shear rate is changed every 2 s between 30 s−1 and 100 s−1 as indicated in the figure. At 30 s−1, below the threshold shear rate, cells travel near hydrodynamic velocity with only a few brief attachments for an average velocity of ∼61 μm/s. On the other hand, cells roll slowly (∼20 μm/s) at 100 s−1 with only a few spikes in velocity. (B) The shear rate is changed every 2 s between 100 s−1 and 400 s−1 as indicated in the figure. Cells bind and travel slowly with a few spikes in velocity as they roll at 100 s−1. Upon the increase in shear rate to 400 s−1, some cells momentarily maintain bonds and a slow rolling velocity before detaching to the free stream. Therefore, the average velocity at 400 s−1 is below hydrodynamic velocity.
In a similar type of simulation, again using best-case parameters, cells were allowed to roll at the optimum shear rate and then the shear rate was increased to 400 s−1. If initiated at 400 s−1, cells would not form bonds and roll in the simulation because the on rate drops to zero at that shear rate. However, because a significant number of bonds had formed at 100 s−1, some cells continued to roll briefly upon increasing the shear rate to 400 s−1 as illustrated by the instantaneous velocity of a sample cell in Fig. 5 B. This type of result has been demonstrated experimentally for L-selectin-mediated rolling of lymphocytes on CD34 by Puri and co-workers (7). They observed that the number of rolling cells per area peaked at ∼100 s−1, but was nearly zero at a shear rate ∼250 s−1. However, when they initiated rolling at an optimum shear rate, nearly 100% of the rolling cells remained bound as the shear rate was increased up to ∼1000 s−1.
Kinetic-rate sensitivity of the shear threshold effect
Clearly, the combination of a catch-slip off rate and a shear-controlled on rate can reproduce some hallmarks of the shear threshold effect, but which is more important to achieving the characteristic phenomena? To further investigate the importance of the kinetic rates, we explored the sensitivity of the shear threshold effect to each rate systematically.
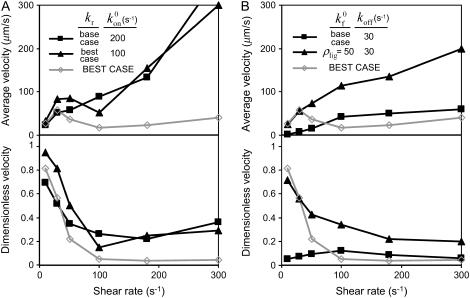
First, as in Fig. 6 A, when the base-case catch-slip off rate was used with an unstressed on rate that was constant at any relative velocity, no minimum in average rolling velocity was apparent when tested over a range of constant on rates (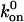 = 10–100 s−1). As a hint of the shear threshold effect, however, the dimensionless velocity did show a significant decrease as the shear rate increased. When the best-case parameters for the catch-slip bond were used (
= 10–100 s−1). As a hint of the shear threshold effect, however, the dimensionless velocity did show a significant decrease as the shear rate increased. When the best-case parameters for the catch-slip bond were used (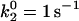 ), a minimum appeared in the velocity as a function of shear rate, even with a constant on rate.
), a minimum appeared in the velocity as a function of shear rate, even with a constant on rate.
FIGURE 6.
Alternative rate combinations. In each panel, the best case, with a catch-slip off rate and shear-controlled on rate, is shown in gray as a reference. (A) Catch-slip off rate with a constant on rate. Average velocities versus shear rate for representative parameters are shown in the upper panel. With the base-case off-rate parameters, there is no dip in velocity, but when the best-case off-rate is used, a minimum becomes apparent. The corresponding dimensionless velocities are shown in the lower panel. There is a significant decrease in dimensionless velocity even with a constant on rate. (B) Shear-controlled on rate with a constant off rate. Average velocities versus shear rate for representative parameters are shown in the upper panel. Neither the base-case on-rate parameters nor an adjusted on rate with half of the base-case ligand density gives a minimum in velocity. The corresponding dimensionless velocities are given in the lower panel. The dimensionless velocity does not monotonically decrease with shear rate for the base-case on rate. With an adjusted on rate, however, the dimensionless velocity does decrease with shear rate, though not sharply, and there is no minimum in velocity.
Alternatively, the base-case shear-controlled on rate was tested with a constant off rate that is not affected by force for a range of off rates (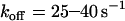 ). As demonstrated in Fig. 6 B, there was no apparent minimum in velocity under these conditions, nor was the dimensionless velocity indicative of the shear threshold effect as it did not sharply decrease with shear rate. We also tested for a minimum in velocity with a constant off rate while varying each parameter of the shear-controlled on rate. Even when the on-rate parameters were adjusted, there was no observable minimum in velocity. In summary, these results suggest that catch-slip bonds are necessary for the shear threshold effect, but the effect is enhanced by a shear-controlled on rate.
). As demonstrated in Fig. 6 B, there was no apparent minimum in velocity under these conditions, nor was the dimensionless velocity indicative of the shear threshold effect as it did not sharply decrease with shear rate. We also tested for a minimum in velocity with a constant off rate while varying each parameter of the shear-controlled on rate. Even when the on-rate parameters were adjusted, there was no observable minimum in velocity. In summary, these results suggest that catch-slip bonds are necessary for the shear threshold effect, but the effect is enhanced by a shear-controlled on rate.
State diagrams
Because of the apparent importance of the catch-slip off rate to the shear threshold effect, we explored some of the interesting parameters of the off rate in the form of state diagrams. Remaining parameters were from the base case. For each set of parameters, simulations were run over a range of shear rates from 10 s−1 to 300 s−1, and the presence or absence of the shear threshold effect was noted. For the purpose of the state diagrams, the shear threshold effect was identified by the following two conditions: 1), the average velocity is >90% of the free-stream hydrodynamic velocity, Vh, at the smallest shear rate of 10 s−1; and 2), there is a local minimum in the average velocity over the range of shear rates tested.
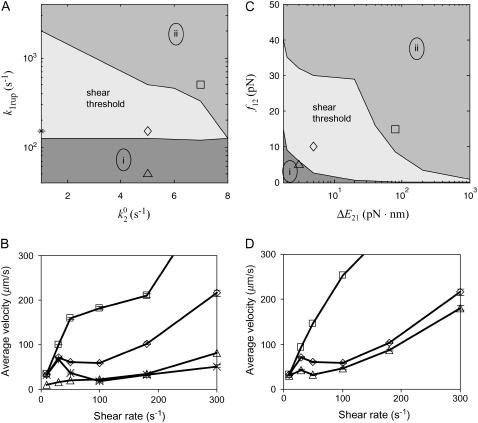
As seen in Fig. 7 A, the first pair of parameters explored was k1rup and 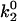 , since these parameters set the difference between the high off rate at low force and the minimum in off rate at intermediate force. At any value of
, since these parameters set the difference between the high off rate at low force and the minimum in off rate at intermediate force. At any value of 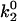 , the lowest possible value of k1rup that permitted the shear threshold effect was ∼125 s−1. For values smaller than this, cells traveled too slowly (<90% Vh) at the lowest shear rate since the unstressed off rate was too small. When either
, the lowest possible value of k1rup that permitted the shear threshold effect was ∼125 s−1. For values smaller than this, cells traveled too slowly (<90% Vh) at the lowest shear rate since the unstressed off rate was too small. When either 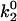 or k1rup was higher than the upper boundary, the dip in velocity disappeared. The larger the minimum off rate (
or k1rup was higher than the upper boundary, the dip in velocity disappeared. The larger the minimum off rate (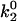 ), the smaller the unstressed off rate (k1rup) had to be in order for the cells to roll slowly enough to produce the minimum in velocity, hence the negative slope for the upper boundary. No shear threshold effect was seen if
), the smaller the unstressed off rate (k1rup) had to be in order for the cells to roll slowly enough to produce the minimum in velocity, hence the negative slope for the upper boundary. No shear threshold effect was seen if 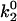 exceeded a critical value. Fig. 7 B exemplifies the average rolling velocity versus shear rate for parameter sets within each region of the state diagram.
exceeded a critical value. Fig. 7 B exemplifies the average rolling velocity versus shear rate for parameter sets within each region of the state diagram.
FIGURE 7.
State diagrams for the shear threshold effect in the space of selected catch-slip bond parameters. Other parameters are base case. In region (i), cells travel at <90% Vh at low shear rates. In region (ii), cells do not achieve a minimum in velocity. (A) State-wise off rate parameter space. When k1rup is too small, cells bind and roll even at very low shear rates. When k1rup is too large, cells do not reach a minimum in velocity. The smaller 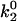 is, however, the larger k1rup can be and still achieve the minimum in velocity. The shear threshold effect can never occur when
is, however, the larger k1rup can be and still achieve the minimum in velocity. The shear threshold effect can never occur when 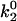 is too large because cells will not bind well enough to achieve a minimum in velocity. (B) Average velocity as a function of shear rate. An example from each region of the state diagram is shown, with parameters given by the corresponding symbols in A. (C) Transition parameter space. When f12 is too small, cells roll at low shear rates since the system quickly switches to the slow pathway. When f12 is too large, on the other hand, the switch to the slow pathway occurs at too high a force, so that cells cannot roll slowly enough to achieve a minimum in velocity. (D) Average velocity as a function of shear rate. An example from each region of the state diagram is shown with parameters given by the corresponding symbols in C.
is too large because cells will not bind well enough to achieve a minimum in velocity. (B) Average velocity as a function of shear rate. An example from each region of the state diagram is shown, with parameters given by the corresponding symbols in A. (C) Transition parameter space. When f12 is too small, cells roll at low shear rates since the system quickly switches to the slow pathway. When f12 is too large, on the other hand, the switch to the slow pathway occurs at too high a force, so that cells cannot roll slowly enough to achieve a minimum in velocity. (D) Average velocity as a function of shear rate. An example from each region of the state diagram is shown with parameters given by the corresponding symbols in C.
Fig. 7 C shows the shear threshold state diagram for the parameters ΔE21 and f12. These parameters affect the transition between states 1 and 2 for bond dissociation. Because ΔE21 gives the difference in energy between states, in combination with the distance between states, Δx12 = kBT/f12, it determines the value of force at which the transition occurs. The two states are occupied equally when the force on the bond is equal to ΔE21/Δx12. The sharpness of this switch is governed by the force scale f12. As seen in the state diagram in Fig. 7 C, the larger the difference in energy, the faster the switch can be and still achieve the shear threshold effect, hence the negatively sloped lines for both boundaries. Below the lower line, the switch is too fast, so the off rate does not stay high and cells travel too slowly at low shear rates. Above the upper line, the switch is too slow and cells cannot roll slowly enough to reach a minimum in velocity. Again, sample velocities as a function of shear rate are shown in Fig. 7 D for each region of the state diagram.
DISCUSSION
In this work, the adhesive dynamics model of cell rolling was updated by the inclusion of revised expressions for the association and dissociation rates of selectin bonds. With a catch-slip bond for the off rate and a shear-controlled unstressed on rate, the essential characteristics of the shear threshold effect for rolling via L-selectin were recreated. The average rolling velocity measured over a range of shear rates reached a minimum value at an intermediate shear rate near the experimentally observed value of ∼100 s−1. This dip in velocity matched experimental measurements well when the best-case rate parameters were used. In addition, a sudden decrease in shear rate to below the shear threshold resulted in detachment of a cell that was previously rolling near the optimum shear rate, as has been observed in experiments. Because the shear-controlled on rate decreases to zero when the relative velocity is very high, cells would not initiate rolling at high shear rates. On the other hand, if a cell was already rolling near the optimum shear rate and the rate was suddenly increased during the simulation, the cell continued rolling briefly before detaching. This observation is also consistent with experiments (7).
In this adhesive dynamics model, the microvilli were allowed to deform according to the rheology measured by Shao and co-workers (29) and described for use in a previous adhesive dynamics model (26). Macroscopic deformation of the whole cell body, on the other hand, was not allowed. We believe that such a simplification is justified because, near the threshold value of shear rate, cell deformation is not expected to significantly affect rolling velocity (31,32). Furthermore, the shear threshold effect has been detected in cell-free systems in which there is no bead deformation. Greenberg and co-workers found a maximum in the flux of sialyl Lewis-coated beads rolling on L-selectin substrates (33). Also, measurements of the rolling velocities of L-selectin-coated beads on sPSGL-1 substrates showed a distinct minimum as a function of the force on the bead due to shear flow (10). These experiments suggest that it is the adhesion molecules that possess a unique property that can give rise to the shear threshold effect.
Based on the simulation results from this model, both a catch-slip bond and a shear-controlled on rate appear to contribute to the minimum in rolling velocity that is distinctive of the shear threshold effect. However, studies that isolate a particular rate showed that a catch-slip off rate seems to make the most important contribution to the shear threshold effect. An exploration of parameter spaces within the context of the catch-slip off rate led to state diagrams for the shear threshold effect. Generally, for this adhesive dynamics model for cell rolling, the shear threshold effect is best achieved by a catch-slip bond with a significant difference between the zero-force and minimum off rates. With such a rate, any bonds that form at low shear rates do not persist long enough for the cells to roll. However, bonds that form at an intermediate shear rate feel a force such that the off rate is low and cells roll. Also, to recreate the shear threshold effect, the switch from the fast to slow dissociation state should not be slow and should occur at an intermediate force within the range of forces felt by a rolling cell. This ensures that the off rate is high when the cells are in low flow and near its minimum when the flow is near the optimum shear rate.
To select parameter values for the dissociation rate used in these simulations, Evans' catch-slip off rate model for P-selectin/PSGL-1 bond dissociation (17) was fit to experimental data for the off rate of L-selectin/PSGL-1 bonds as a function of force (9,10,14). Ideally, Evans' model, which was derived from dynamic force spectroscopy, would have been fit to similar data for L-selectin bonds, but such data showing a catch-slip bond was not available. Instead, the data came from experiments in which the L-selectin bonds were held at a constant force. Based on the distribution of breakage events, the off rate was deduced for each particular force. Such constant-force experiments have revealed catch-slip bond behavior for both L- and P-selectin bonds (9,10,14,15). However, DFS generally gives very different results for both selectin bonds (34–37). The different off rates measured in constant-force and DFS single-bond experiments could be due to a dependence on force history (35). It is also possible that the resolution in DFS is not great enough to definitively detect bonds that break very quickly at low forces on the order of the thermal energy when the loading rate is slow (38,39). Interestingly, the binding frequency has been shown to increase as the loading rate increases, signifying that bonds may be breaking quickly at low loading rates and being counted as nonadhesion events (17,36). To better represent the off-rate kinetics of L-selectin/PSGL-1 bonds according to Evans' model, DFS of the style that detected the catch-slip bond for P-selectin/PSGL-1 should be performed with L-selectin bonds.
The state diagrams for the shear threshold effect in catch-slip bond parameter spaces showed a large region in which the shear threshold effect was detected. At the same time, there are large areas where the shear threshold effect was not achievable. To map out such a state diagram experimentally, L-selectin and its ligand could undergo a series of mutations to create a library of molecular pairs with varying catch-slip bond parameters that would have to be measured experimentally for each mutant. By performing cell-free rolling experiments with molecularly coated beads on an adhesive substrate, a state diagram for the shear threshold effect could be created. It would be interesting to learn experimentally the characteristics of bond kinetics required for the shear threshold effect.
References
- 1.Alberts, B. 2002. Molecular Biology of the Cell. Garland Science, New York.
- 2.Chen, S., and T. A. Springer. 1999. An automatic braking system that stabilizes leukocyte rolling by an increase in selectin bond number with shear. J. Cell Biol. 144:185–200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Simon, S. I., and C. E. Green. 2005. Molecular mechanics and dynamics of leukocyte recruitment during inflammation. Annu. Rev. Biomed. Eng. 7:151–185. [DOI] [PubMed] [Google Scholar]
- 4.Finger, E. B., K. D. Puri, R. Alon, M. B. Lawrence, U. H. von Andrian, and T. A. Springer. 1996. Adhesion through L-selectin requires a threshold hydrodynamic shear. Nature. 379:266–269. [DOI] [PubMed] [Google Scholar]
- 5.Lawrence, M. B., G. S. Kansas, E. J. Kunkel, and K. Ley. 1997. Threshold levels of fluid shear promote leukocyte adhesion through selectins (CD62L,P,E). J. Cell Biol. 136:717–727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Alon, R., S. Chen, K. D. Puri, E. B. Finger, and T. A. Springer. 1997. The kinetics of L-selectin tethers and the mechanics of selectin-mediated rolling. J. Cell Biol. 138:1169–1180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Puri, K. D., S. Chen, and T. A. Springer. 1998. Modifying the mechanical property and shear threshold of L-selectin adhesion independently of equilibrium properties. Nature. 392:930–933. [DOI] [PubMed] [Google Scholar]
- 8.Alon, R., S. Chen, R. Fuhlbrigge, K. D. Puri, and T. A. Springer. 1998. The kinetics and shear threshold of transient and rolling interactions of L-selectin with its ligand on leukocytes. Proc. Natl. Acad. Sci. USA. 95:11631–11636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Sarangapani, K. K., T. Yago, A. G. Klopocki, M. B. Lawrence, C. B. Fieger, S. D. Rosen, R. P. McEver, and C. Zhu. 2004. Low force decelerates L-selectin dissociation from P-selectin glycoprotein ligand-1 and endoglycan. J. Biol. Chem. 279:2291–2298. [DOI] [PubMed] [Google Scholar]
- 10.Yago, T., J. Wu, C. D. Wey, A. G. Klopocki, C. Zhu, and R. P. McEver. 2004. Catch bonds govern adhesion through L-selectin at threshold shear. J. Cell Biol. 166:913–923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Alon, R., R. C. Fuhlbrigge, E. B. Finger, and T. A. Springer. 1996. Interactions through L-selectin between leukocytes and adherent leukocytes nucleate rolling adhesions on selectins and VCAM-1 in shear flow. J. Cell Biol. 135:849–865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Smith, M. J., E. L. Berg, and M. B. Lawrence. 1999. A direct comparison of selectin-mediated transient, adhesive events using high temporal resolution. Biophys. J. 77:3371–3383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Chang, K. C., and D. A. Hammer. 1999. The forward rate of binding of surface-tethered reactants: effect of relative motion between two surfaces. Biophys. J. 76:1280–1292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Dwir, O., A. Solomon, S. Mangan, G. S. Kansas, U. S. Schwarz, and R. Alon. 2003. Avidity enhancement of L-selectin bonds by flow: shear-promoted rotation of leukocytes turn labile bonds into functional tethers. J. Cell Biol. 163:649–659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Marshall, B. T., M. Long, J. W. Piper, T. Yago, R. P. McEver, and C. Zhu. 2003. Direct observation of catch bonds involving cell-adhesion molecules. Nature. 423:190–193. [DOI] [PubMed] [Google Scholar]
- 16.Bell, G. I. 1978. Models for the specific adhesion of cells to cells. Science. 200:618–627. [DOI] [PubMed] [Google Scholar]
- 17.Evans, E., A. Leung, V. Heinrich, and C. Zhu. 2004. Mechanical switching and coupling between two dissociation pathways in a P-selectin adhesion bond. Proc. Natl. Acad. Sci. USA. 101:11281–11286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Barsegov, V., and D. Thirumalai. 2005. Dynamics of unbinding of cell adhesion molecules: transition from catch to slip bonds. Proc. Natl. Acad. Sci. USA. 102:1835–1839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hammer, D. A., and S. M. Apte. 1992. Simulation of cell rolling and adhesion on surfaces in shear flow: general results and analysis of selectin-mediated neutrophil adhesion. Biophys. J. 63:35–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Bhatia, S. K., M. R. King, and D. A. Hammer. 2003. The state diagram for cell adhesion mediated by two receptors. Biophys. J. 84:2671–2690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Chang, K. C., and D. A. Hammer. 2000. Adhesive dynamics simulations of sialyl-Lewis(x)/E-selectin-mediated rolling in a cell-free system. Biophys. J. 79:1891–1902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Chang, K. C., D. F. Tees, and D. A. Hammer. 2000. The state diagram for cell adhesion under flow: leukocyte rolling and firm adhesion. Proc. Natl. Acad. Sci. USA. 97:11262–11267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.King, M. R., and D. A. Hammer. 2001. Multiparticle adhesive dynamics. Interactions between stably rolling cells. Biophys. J. 81:799–813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.King, M. R., and D. A. Hammer. 2001. Multiparticle adhesive dynamics: hydrodynamic recruitment of rolling leukocytes. Proc. Natl. Acad. Sci. USA. 98:14919–14924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.King, M. R., S. D. Rodgers, and D. A. Hammer. 2001. Hydrodynamic collisions suppress fluctuations in the rolling velocity of adhesive blood cells. Langmuir. 17:4139–4143. [Google Scholar]
- 26.Caputo, K. E., and D. A. Hammer. 2005. Effect of microvillus deformability on leukocyte adhesion explored using adhesive dynamics simulations. Biophys. J. 89:187–200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Krasik, E. F., K. L. Yee, and D. A. Hammer. 2006. Adhesive dynamics simulation of neutrophil arrest with deterministic activation. Biophys. J. 91:1145–1155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Chang, K. C., and D. A. Hammer. 1996. Influence of direction and type of applied force on the detachment of macromolecularly-bound particles from surfaces. Langmuir. 12:2271–2282. [Google Scholar]
- 29.Shao, J. Y., H. P. Ting-Beall, and R. M. Hochmuth. 1998. Static and dynamic lengths of neutrophil microvilli. Proc. Natl. Acad. Sci. USA. 95:6797–6802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Dembo, M., D. C. Torney, K. Saxman, and D. Hammer. 1988. The reaction-limited kinetics of membrane-to-surface adhesion and detachment. Proc. R. Soc. Lond. B Biol. Sci. 234:55–83. [DOI] [PubMed] [Google Scholar]
- 31.Jadhav, S., C. D. Eggleton, and K. Konstantopoulos. 2005. A 3-D computational model predicts that cell deformation affects selectin-mediated leukocyte rolling. Biophys. J. 88:96–104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Yago, T., A. Leppanen, H. Qiu, W. D. Marcus, M. U. Nollert, C. Zhu, R. D. Cummings, and R. P. McEver. 2002. Distinct molecular and cellular contributions to stabilizing selectin-mediated rolling under flow. J. Cell Biol. 158:787–799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Greenberg, A. W., D. K. Brunk, and D. A. Hammer. 2000. Cell-free rolling mediated by L-selectin and sialyl Lewis(x) reveals the shear threshold effect. Biophys. J. 79:2391–2402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Evans, E., A. Leung, D. Hammer, and S. Simon. 2001. Chemically distinct transition states govern rapid dissociation of single L-selectin bonds under force. Proc. Natl. Acad. Sci. USA. 98:3784–3789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Marshall, B. T., K. K. Sarangapani, J. Lou, R. P. McEver, and C. Zhu. 2005. Force history dependence of receptor-ligand dissociation. Biophys. J. 88:1458–1466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Fritz, J., A. G. Katopodis, F. Kolbinger, and D. Anselmetti. 1998. Force-mediated kinetics of single P-selectin/ligand complexes observed by atomic force microscopy. Proc. Natl. Acad. Sci. USA. 95:12283–12288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Hanley, W., O. McCarty, S. Jadhav, Y. Tseng, D. Wirtz, and K. Konstantopoulos. 2003. Single molecule characterization of P-selectin/ligand binding. J. Biol. Chem. 278:10556–10561. [DOI] [PubMed] [Google Scholar]
- 38.Evans, E., and K. Ritchie. 1997. Dynamic strength of molecular adhesion bonds. Biophys. J. 72:1541–1555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Lo, Y. S., Y. J. Zhu, and T. P. Beebe. 2001. Loading-rate dependence of individual ligand-receptor bond-rupture forces studied by atomic force microscopy. Langmuir. 17:3741–3748. [Google Scholar]