Abstract
Since the introduction of the induced-fit theory by D. E. Koshland Jr., it has been established that conformational motion invariably accompanies the execution of protein function. The catalytic activity of kinases, specifically, is associated with large conformational changes (∼1 nm amplitude). In the case of guanylate kinase, upon substrate binding, the LID and nucleotide-monophosphate-binding domains are brought together and toward the CORE with large concerted movements about the α3 (helix 3) axis. However, whether the change in conformation mostly affects the catalytic rate or mostly increases binding affinities for one or the other substrate is unclear. We investigate this question using a nanotechnology approach based on mechanical stress. Using an “allosteric spring probe”, we bias conformational states in favor of the “open” (substrate-free) conformation of the enzyme; the result is that the binding constant for the substrate guanosine monophosphate (GMP) is reduced by up to a factor of 10, whereas the binding constant for adenosine triphosphate (ATP) and the catalytic rate are essentially unaffected. The results show that the GMP-induced conformational change, which promotes catalysis, does not promote ATP binding, consistent with previous mutagenesis studies. Furthermore, they show that this conformational change is of the induced-fit type with respect to GMP binding (but not ATP binding). We elaborate on this point by proposing a quantitative criterion for the classification of conformational changes with respect to the induced-fit theory. More generally, these results show that the allosteric spring probe can be used to affect enzymatic activity in a continuously controlled manner, and also to affect specific steps of the reaction mechanism while leaving others unaffected. It is presumed that this will enable informative comparisons with the results of future molecular dynamics or statistical mechanics computations.
INTRODUCTION
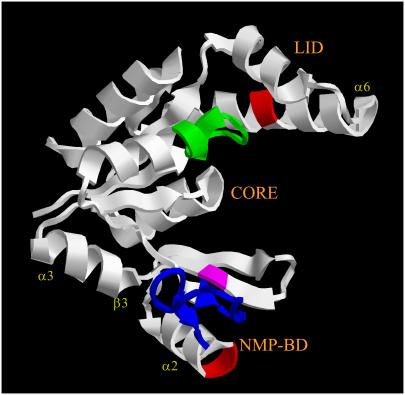
Guanylate kinase (GK) is an essential enzyme that catalyzes the transfer of a phosphate from adenosine triphosphate (ATP) to guanosine monophosphate (GMP) (1). Here, we work with the 24-kDa protein from Mycobacterium tuberculosis. As is evident from the structure (Fig. 1), GK has a clamp-like cavity, where the two lobes of the protein close through an ∼1-nm conformational change upon binding the substrates (2); most of the conformational motion is induced by GMP binding. The substrates GMP and ATP drive this conformational change through several direct and indirect (via water molecules) interactions that bring the LID and nucleotide-monophosphate-binding domain (herein referred to as NMP-BD) nearer and jointly toward the CORE region, the structure closing in a vise-like motion (2,3). In this configuration, the CORE is catalytically active toward phosphoryl transfer, which relies on a residue sequence (the P-loop) that is conserved in kinases (4).
FIGURE 1.
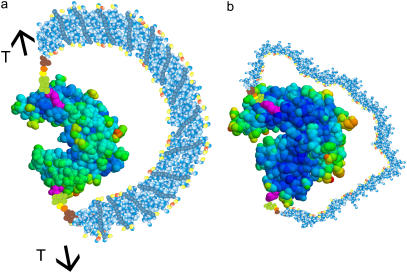
Cartoons of the GK chimera showing the locations of the Cys mutations (magenta). The distance between these two groups is 4.5 nm. (a) The chimera “under tension”: the DNA is in the ds form, and provides a tension across the two lobes of the protein, here shown in the “open” conformation (PDB structure 1EX6). (b) The chimera without tension: the DNA is in the ss state, providing no bias against the closed conformation. The protein is shown in the “closed” conformation (PDB structure 1EX7).
Kinases are generally viewed as examples of the induced-fit mechanism (reviewed in Koshland (5)), so one anticipates that a mechanical stress favoring the “open” conformation of the enzyme would lower the binding affinity for the substrates, the rate of catalysis, or both.
Here, we take a nanotechnology approach to thus controlling protein function. We insert an externally controllable molecular spring on the protein, which we call an “allosteric spring probe” (ASP). Through the ASP, we can affect the static and dynamic conformation of the protein, and watch the effect on specific steps of the reaction mechanism. In the application described here, we bias the statistical weights of the conformational states of GK toward the “open” state, and observe that the binding affinity for one substrate (GMP) is drastically reduced, whereas the binding affinity for the second substrate (ATP) and the catalytic rate are essentially unaffected. This shows that GMP binding is not necessary for, or does not favor, ATP binding, i.e., GMP binding does not allosterically or cooperatively control ATP binding in this molecule. It follows that GMP binding must allosterically control catalysis itself, or at least the ATP hydrolysis step, or else ATP would be hydrolyzed by the enzyme in the absence of bound GMP.
The ASP in this study is realized by covalently coupling a single-stranded (ss) DNA 60mer to the GK (6,7). Using site-directed mutagenesis (Thr-75 → Cys; Arg-171 → Cys) we introduced a cysteine residue on each of the two domains of GK (Fig. 1), establishing specific chemically active sites for coupling of the DNA. The 3′− and 5′-amino modified DNA strand was covalently coupled to GK through a cross-linker, producing the chimera schematically shown in Fig. 1.
This construction allows us to exert a controlled mechanical stress across the two attachment sites on the protein, which presently are located on the LID and NMP-BD (Fig. 2). Namely, the ss DNA 60mer of the chimera is a flexible polymer that exerts essentially no tension on the protein, and leaves the functionality of the enzyme intact. However, upon hybridization with a complementary strand, the DNA substantially rigidifies (the persistence length of ss DNA is ℓss ≈ 1 nm or ∼3 bases (8), whereas ℓds ≈ 50 nm or ∼150 bp for ds DNA (9)), and the semirigid ds DNA has to bend because of the constraint imposed by the attachment points on the protein. Thus, the DNA exerts a mechanical stress on the protein, similar to the tension exerted by a bow on its string.
FIGURE 2.
Relation of the application points of the mechanical stress (the location of the Cys mutations (red)) to the secondary-structure elements mentioned in the text. The GMP binding site is colored blue, the ATP binding site green. Ser-99 (homologous to Tyr-78 in yeast GK) is colored magenta for reference. The GK structure is PDB entry 1S4Q.
This kind of “molecular spring” has been used previously to separate an inhibitor from its docking site on an enzyme, achieving external regulation of enzymatic activity (10). Similarly, external control of an enzyme has been achieved recently by using a light-sensitive polymer to reversibly block the active site (11). More generally, novel experiments using mutagenesis to introduce artificial binding sites for metal ions have obtained remarkable results in controlling enzymes allosterically (12,13).
The novelty of our approach is that we use mechanical stress to control the conformation of the protein. This concept can be applied to virtually any protein, and allows us to study the fundamental mechanisms of allostery from a new perspective. With the ASP, the mechanical stress on the protein is applied in solution, in an ensemble experiment, and can be controlled externally, and semicontinously, by introducing in solution DNA partially or completely complementary to the sequence on the chimera. Here, we report how enzymatic activity is progressively shut off as the mechanical tension is increased by hybridizing longer and longer complementaries to the chimera, and we report detailed measurements of the Michaelis-Menten (MM) constants of the substrates and the catalytic rate, for “large” and “moderate” tensions. These measurements represent the “response function” of the protein's structure to mechanical perturbations.
MATERIALS AND METHODS
Mutagenesis and purification
The Rv1389c gene was amplified by polymerase chain reaction (PCR) using M. tuberculosis H37Rv genomic DNA as the template, forward primer: CCATATGGCTGTGAGCGTCGGCGAGGGACCGGACACCAAGC, which introduced an NdeI site (underlined), and reverse primer: AAGCTTACCTCGTGGTACACCCGGGGAGCCCGGTGCCGTTC, which introduced a HindIII site. The forward primer also inserted an alanine codon (GCT) immediately after the start codon to enhance protein expression, whereas the reverse primer introduced a thrombin recognition sequence to the C-terminus. The PCR product was cloned into pCRBluntII-TOPO (Invitrogen, Carlsbad, CA). After sequence confirmation, the gene was subcloned into pET22b (Stratagene, San Diego, CA), which added a hexa-histidine tag to the expressed protein after the thrombin recognition sequence. The QuikChange Multi Site-Directed Mutagenesis Kit (Stratagene) was used to introduce the T75C and R171C mutations. Further details are given in Supplementary Materials.
GK-DNA complex conjugation
The 5′- and 3′-amino modified 60-base DNA oligomer (Operon, Huntsville, AL) were conjugated to the NHS-ester end of the heterobifunctional cross-linker sulfo-SMCC (Pierce, Rockford, IL). The DNA and sulfo-SMCC were incubated together at 150 μM and 12.5 mM, respectively, for 60–70 min. Quenching of the NHS-ester ends of the free sulfo-SMCC was done by introducing an excess of Tris buffer to the DNA and sulfo-SMCC solution. GK was reduced with dithiothreitol (Sigma, St. Louis, MO) in the presence of EDTA (Sigma) at 80 μM, 50 mM, and 1 mM, respectively, for 30–40 min. Protein desalting spin columns (Pierce) were used to remove excess sulfo-SMCC and dithiothreitol. The other end of the sulfo-SMCC cross-linker, a maleimide group, renders the DNA reactive to sulfhydryls, namely the Cys residues of GK. The solutions of GK and DNA were incubated together (pH ∼6.8) to final concentrations of 65 μM and 50 μM, respectively, for a period of 3–4 h at 20–22° C, followed by an additional 14–16 h at 4° C. Details of the purification are given in Supplementary Materials. From the gels, the measurements below, and the measurements on a different chimera (14), we estimate the yield of correct chimeras in our samples to be somewhere between 50% and 70% depending on the sample. (A yield of 70% is an upper bound (see Supplementary Materials) on correctly constructed chimeras (CCC) due to limitations in the engineering process of the chimera.)
Oligomer sequences
The sequence of the 60mer used for the construction of the chimera was
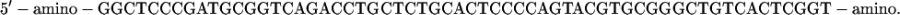 |
The ds hybrid was formed by adding the complementary 60mer in solution. Partial complementaries (L < 60) were complementary to the central tract of the chimera DNA.
Chimera concentrations were quantitated with the Bradford assay.
Assays
Chemoluminescent enzyme activity assay
To measure kinase activity for the GMP titrations, the Kinase-Glo (Promega, Madison, WI) luminescence assay was used, which employs the luciferase catalyzed reaction to measure ATP concentration. The final concentrations of GK-DNA, GMP, ATP, and complementary DNA oligomers used in the assay were 0.75 μM, 6–350 μM, 1.25 μM, and 35 μM, respectively. The reaction time allotted for GK to catalyze phosphoryl transfer was τ = 24 min, whereas the coupled subsequent reaction with the Kinase-Glo reaction buffer was 12 min. The luminescence measurements were performed on a Lumat LB 9507 luminometer.
Spectrophotometric enzyme activity assay
For the ATP titration experiments, kinase activity was analyzed using a pyruvate kinase-lactate dehydrogenase-coupled assay by the method described by Agarwal for GMP kinases (15). This assay measures adenosine diphosphate (ADP) and guanosine diphosphate (GDP) concentrations. For further details see Supplementary Materials.
RESULTS
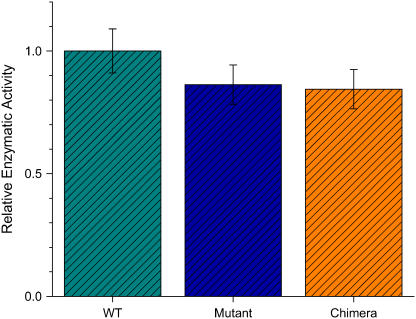
GK activity was measured using the luciferase chemoluminescent assay, which monitors the conversion of ATP (see Methods). A calibration curve was obtained to relate the measured luminescence (in relative light units (RLU)) to the concentration of 100% active GK; in the following, relative enzymatic activity (REA) means RLU transformed into enzymatic activity using the calibration curve. The mutant GK has ∼85% the activity of the wild-type, whereas the activity of the ss chimera is indistinguishable from that of the mutant (Fig. 3). This result, which is far from obvious a priori, is the key to the success of the approach. Namely, it turns out that it is possible to couple an external spring to the protein, indeed a bulky extraneous polymer, without disrupting the function of the protein in the absence of tension.
FIGURE 3.
Effect of the zero-tension ASP construction on the function of the protein: the enzymatic activity (REA) of the mutant GK (turquoise) is ∼85% that of the wild-type (WT, green), and the REA of the ss GK chimera (Chimera, orange) is indistinguishable from that of the mutant (turquoise).
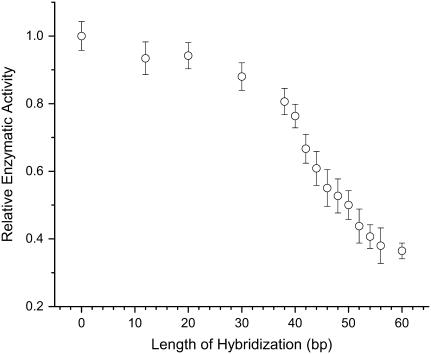
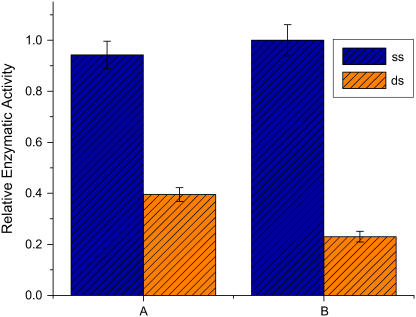
In Fig. 4, we show the regulation of kinase activity by the ASP. By introducing in solution complementary strands of increasing lengths L (from 12 to 60 bases; the ASP on the chimera is 60 bases long), the mechanical stress on the protein, which tends to keep the two domains in the “open” conformation, can be increased semicontinuously. The measured enzymatic activity decreases correspondingly. The data point L = 12 is also a control; it was obtained by introducing in solution a DNA strand of 60 bases in length, of which only a sequence of 12 is complementary to the DNA of the chimera. This strand binds to the DNA of the chimera, but does not cause a mechanical stress. This control shows that the modulation of enzymatic activity in Fig. 4 is not caused by nonspecific steric or charge effects originating from bringing a longer and longer charged polymer in close proximity to the enzyme. The same conclusion can be drawn from Fig. 3. The observed overall effect on enzymatic activity, i.e., the observed dynamic range of ASP control, is limited by the finite yield of correctly constructed chimeras in the samples. Fig. 5 a illustrates that additional purification steps increase the observed dynamic range.
FIGURE 4.
Force-activity curve. This plot shows the response of the protein to increasing mechanical stress. The enzymatic activity (REA) of the GK chimera is plotted versus the length L of the complementary DNA added in solution (i.e., L is the length in bp of the hybridized segment of the ASP). Each point represents the average of four to five independent measurements; the error bars are ±1 SD. The data point L = 12 is also a control; the DNA strand added in solution in this case is actually a 60mer, but only 12 bases are complementary to the DNA of the chimera. This control 60mer sticks to the chimera but does not provide mechanical tension.
FIGURE 5.
Reduction of enzymatic activity under tension. Data are the average of four to five experiments; the error bars are ±1 SD. As the yield of correct chimeras is increased in the samples, the observed dynamic range of control is increased. Sample A shows a twofold effect of the ASP on enzymatic activity, which increases to a fourfold effect (sample B) upon purification on a sulfhydryl column, which retains molecules with unreacted Cys.
The result displayed in Fig. 4 shows that the ASP provides unprecedented fine control over protein conformation, resulting in the ability to control enzymatic activity incrementally. We have shown previously that the mechanical regulation introduced by the ASP is reversible: if the mechanical tension is released (e.g., by cutting the ds DNA), the observed enzymatic activity recovers entirely (7). Those experiments also show that DNA-modifying enzymes can in principle be used on the DNA of the chimera, which leaves open the possibility of adding a second layer of control to this construction.
Detailed insight into the conformational mechanisms associated with the function of this enzyme can be gained by analyzing the effect of mechanical tension on specific steps of the catalytic mechanism. We measure the relevant parameters by titration experiments, analyzed through the Michaelis-Menten description. A single-substrate, two-step catalysis process,
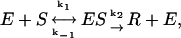 |
(1) |
where E stands for enzyme, S for substrate, ES for the intermediate complex, and R for the product (16), is characterized by the MM constant of the intermediate complex, KM = (k−1 + k2)/k1, and the rate of the catalytic step, k2 (17). The speed of the reaction is
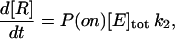 |
(2) |
where P(on) is the probability that the enzyme has a bound substrate,
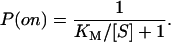 |
(3) |
With two substrates, G (for GMP) and A (for ATP), the same approach (Eqs. 2 and 3) leads to
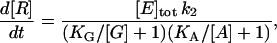 |
(4) |
assuming that binding of one substrate does not influence binding of the other. We show below that our titration experiments (Figs. 6 and 7) are consistent with Eq. 4, and the results obtained with the ASP (namely, that it is possible to disrupt GMP binding without affecting ATP binding) also confirm that ATP binds equally well whether or not GMP is bound.
FIGURE 6.
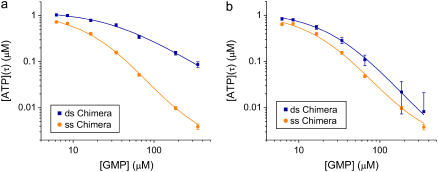
GMP titration experiments. Enzymatic activity (ATP consumption) is monitored with the luciferase assay. We plot the concentration of ATP remaining after a time τ, [A(τ)], versus the initial GMP concentration [G(0)], for the ss and ds chimera. [A(τ)] is a measure of the speed of the enzymatic reaction. Each experimental point represents the average of four to six measurements; error bars are ±1 SD. The ss data are fitted using Eq. 6, the ds data using Eq. 9, with the ss parameters determined by the ss fit. The parameter values extracted from the fits are listed in Table 1. (a) Hybridization with L = 60 (“high tension”). KG is reduced by a factor of 10 under tension (see Table 1). (b) Hybridization with L = 42 (“moderate tension”), corresponding to roughly the midpoint of the force-activity curve (Fig. 5). KG is reduced by a factor of 5.
FIGURE 7.
ATP titration experiments. Enzymatic activity (ADP and GDP formation) is monitored with the Agarwal assay, and the measurements are analyzed using the Eadie-Hofstee plots. The ds chimera activity is shown in red, whereas the ss chimera is shown in black. The slope is the same for the two plots, showing that KA is unaffected by the mechanical stress. The parameters extracted from the linear fits are listed in Table 1.
We performed measurements not of d[R]/dt directly, but instead of the product formed after a time τ, for varying initial GMP concentrations [G(0)] at a fixed initial ATP concentration [A(0)]. More precisely, in the experiments we measure the ATP concentration [A(τ)] remaining after time τ, for the ss and ds chimera (Fig. 6 a). The assay conditions are such that KA/[A] > 1 and there is excess GMP over ATP; with the approximations KA/[A] + 1 ≈ KA/[A], [G] ≈ const. = [G(0)], and since d[R]/dt = −d[A]/dt, Eq. 4 becomes
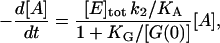 |
(5) |
with the solution
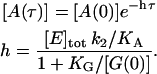 |
(6) |
We use Eq. 6 to fit the ss data in Fig. 6, and extract the parameters 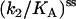 and
and 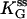 (Table 1). This procedure yields a more robust measurement compared to the method of estimating the initial velocity of the reaction −d[A]/dt (t = 0) from the time course [A](t) and Eq. 5, because Eq. 6 is an integrated (i.e., averaged) measurement. Under these assay conditions it is not possible to extract k2 and KA separately. For the ds chimera, we must take into account that the experimental samples consist of a yield p (0 < p < 1) of correct chimera, plus a fraction of enzymes (1 − p) which is functionally unmodified. Eq. 5 then becomes
(Table 1). This procedure yields a more robust measurement compared to the method of estimating the initial velocity of the reaction −d[A]/dt (t = 0) from the time course [A](t) and Eq. 5, because Eq. 6 is an integrated (i.e., averaged) measurement. Under these assay conditions it is not possible to extract k2 and KA separately. For the ds chimera, we must take into account that the experimental samples consist of a yield p (0 < p < 1) of correct chimera, plus a fraction of enzymes (1 − p) which is functionally unmodified. Eq. 5 then becomes
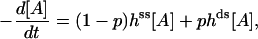 |
(7) |
where
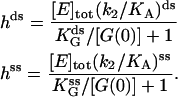 |
(8) |
TABLE 1.
Parameter values extracted from the fits in GMP and ATP titration experiments
| GMP titration experiments | |||
|---|---|---|---|
| Parameter | 60-bp hybrid | 42-bp hybrid | 42-bp hybrid |
| p (yield) | 0.68 | 0.45 | 0.68 |
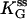 (μM) (μM) |
82 ± 2 | 78 ± 6 | 78 ± 8 |
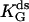 (μM) (μM) |
788 ± 31 | 372 ± 26 | 347 ± 27 |
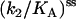 (s·μM)−1 (s·μM)−1
|
0.26 ± 0.03 | 0.17 ± 0.03 | 0.17 ± 0.06 |
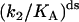 (s·μM)−1 (s·μM)−1
|
0.17 ± 0.02 | 0.23 ± 0.04 | 0.14 ± 0.04 |
| ATP titration experiments | Nuclear magnetic resonance measurements from Li et al. (30) | ||||
|---|---|---|---|---|---|
| Parameter | 60-bp hybrid | 42-bp hybrid | Parameter | WT | Tyr-78 → Phe |
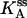 (μM) (μM) |
66.8 ± 9.1 | 61.2 ± 6.9 | KG (μM) | 91 ± 6 | 1800 ± 200 |
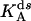 (μM) (μM) |
59.7 ± 5.4 | 56.6 ± 9.4 | KiA (μM) | 80 ± 4 | 160 ± 10 |
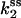 (s−1) (s−1) |
154 ± 18 | 161 ± 21 | k2 (s−1) | 394 ± 15 | 3 ± 0.18 |
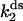 (s−1) (s−1) |
74.2 ± 6.8 | 127 ± 11 | |||
(Upper) Parameters extracted from the GMP titration experiments. The L = 60 and L = 42 hybridizations come from independent chimera batches, so the yields are not necessarily the same; the best fit gives yields p = 0.68 and p = 0.45, respectively, and the values of KG and k2/KA listed. The last column shows how the parameters extracted from the fit change if we fix p = 0.68 (the same value obtained for the 60 bp hybrid) instead. (Lower) KA extracted from the ATP titration experiments, and the corresponding k2, for L = 60. For L = 42, we obtain the same results for KA (no change). Because two different assays are employed for the ATP and GMP titration experiments, for the comparison, the change in the parameters with and without tension is more significant than the absolute values. The NMR values of KG, k2, and KiA are the published results of Zhang et al. (25) and are presented for comparison.
The solution is
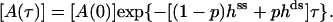 |
(9) |
We use this form (with the ss parameters determined above) to fit the ds data in Fig. 6 a, obtaining the yield p ≈ 0.7 and the ds parameters listed in Table 1 for high tension. The yield p ≈ 0.7 is consistent with bounds from the preparation method, the evidence from the gels, and measurements made on two other proteins (6,7), all of which indicate typical yields of our synthesis in the range 0.3 < p < 0.7. The final result is that the mechanical tension, exerted between Thr-75 and Arg-171 (Fig. 2), i.e., between helices α2 and α6, increases the MM constant for GMP, KG, at least 10-fold, whereas the ratio (k2/KA) decreases by a factor of <2.
It is of interest to repeat these measurements for different values of the mechanical tension, as this is the only method that provides a site-specific but continuously tunable perturbation of the protein. Fig. 6 b shows analogous titration curves obtained at moderate tension, imposed by hybridizing a 42mer complementary to the chimera (this corresponds to about the midpoint of the force-activity curve of Fig. 4). The result is that KG now increases less than fivefold under tension, a smaller effect than for a fully complementary strand. This shows that we can tune the mechanical perturbation so as not to saturate the response of the protein. The result from the best fit of the titration curves (Fig. 6 b) is a slight increase (∼30% increase) in the k2/KA ratio under tension, and p = 0.45 for the yield. Possibly this reflects that under mild tension the ATP binding site is slightly more exposed to solvent. However, if we fix p = 0.68 in the fits (the same value extracted from the fits for the L = 60 experiments; note that the experiments of Figs. 7, a and b, were performed with different batches of chimeras, so p can be different between the two), then we find no change in the (k2/KA) ratio. In conclusion, the ASP in this position has either no effect on k2/KA or it induces a small increase of this ratio at mild tensions.
To measure independently the MM constant for ATP, KA, and thus obtain all three parameters KG, KA, and k2, we performed ATP titration experiments. We used the assay described by Agarwal, which measures GDP (and ADP) presence by coupling to lactate dehydrogenase and pyruvate kinase (see Methods). In Fig. 7, we present the Eadie-Hofstee plot analysis of these experiments, where the slope of the lines is KA (see Eq. 4) and the intercept is proportional to k2/(1 + KG/[G]). With and without tension (ds and ss chimera; hybridization with L = 60), the slope is the same, which shows that KA is the same in the two cases (the value is reported in Table 1). The same plot also shows the decrease in the turnover rate as the chimera changes from ss to ds. Similar ATP titration experiments were carried out for the “mild tension” (L = 42) case, with the same result: KA does not change (Table 1).
Combining the results from the titration experiments (Figs. 6 a and 7), we find that at high tension (L = 60) KG increases by a factor of 10, KA is unaffected, and k2 decreases by a factor of 2.
DISCUSSION
We first summarize the results. We measured the MM constants for the two substrates, KA and KG, and the catalytic rate k2, with and without mechanical stress applied at the specific locations on the protein's surface described in this article. Previously (8), we reported measurements of KG and the ratio k2/KA ; those measurements are reproduced here (Fig. 6 a) to make the article self-contained. Through the new GMP titration experiments (Fig. 7) we measure KA independently, thus obtaining all three parameters, k2, KA, and KG . The results show that with applied mechanical stress, KG is reduced by a factor of 10, KA is unaffected, and k2 is reduced by a factor of 2. The importance of these results, and of measuring all three parameters, lies in part in the specificity with which the mechanical perturbation applied to the protein affects these different parameters. This specificity will presumably allow informative, sharp comparisons with model computations of the response of the protein's structure to this applied force. Had the experiment shown instead that, under stress, all parameters change somewhat, the comparison to future model calculations would hold less promise of generating incisive results.
We also performed measurements at “intermediate” tension (42-bp hybrid in Table 1), which show a decrease in KG by a factor of 5, no change for KA, and a small decrease for k2. These results show that the forces we apply with the molecular spring do not necessarily saturate the response of the protein. Finally, we obtained the remarkable result expressed in Fig. 4. From the biochemical point of view, the figure demonstrates a “semicontinous series” of inhibitory molecules (the complementary strands of increasing lengths), each with a slightly more inhibitory effect than the preceding one in the series. A similar gradual inhibition of enzymatic activity can of course be obtained with “traditional” inhibitors as a function of inhibitor concentration, but for a totally different reason. In the latter case, what changes is simply the average fraction of enzymes with the inhibitor bound. In the case described here, we have actually at our disposal ∼30 different inhibitors (complementary oligomers of lengths from ∼30 to 60 bases) which, when bound under saturating conditions to the chimera, produce 30 gradually different responses.
Several different conceptual frameworks are used to discuss functional conformational changes and more generally allostery. In Koshland's induced-fit theory (5), substrate binding drives a conformational change A → B because the binding energy in the B state is higher than in the A state. In the Cooper-Dryden dynamical mechanism (reviewed in Kern and Zuiderweg (17)), where the focus is on entropic effects, binding of an allosteric regulator alters the spectrum of long-wavelength elastic excitations of the protein; this translates into an entropic contribution to the free energy of substrate binding (18–20). In the “complex energy landscape” approach to protein dynamics, the focus is on the existence of conformational substates (21), where allostery arises because ligand binding alters the energy landscape and thus the statistical weights of the substates (22,23).
These mechanisms are not mutually exclusive. Also, the “complex energy landscape” approach represents really a common language to describe the other mechanisms. For GK, it is known from structural studies (2,3) that substrate binding drives a relative rotation of the two domains about the α3 “hinge”, resulting in the “closed” conformation. Most of this conformational change happens upon GMP binding, not ATP binding. With our measurements, we find that with the molecule, biased in favor of the “open” conformation, KG is dramatically reduced whereas KA is unaffected, which is consistent with the above structural results. More quantitatively, we find (see below) that if the ASP performs a work W against the substrate-induced conformational change, then the binding free energy of GMP is reduced by roughly the same amount W (whereas the binding free energy of ATP is unaffected). We propose this quantitative criterion to classify ligand-induced conformational changes with respect to the induced-fit mechanism, with the results showing that, in the case of GK, GMP binding is of the induced-fit type, whereas ATP binding is not.
Upon substrate binding, in addition to changes in the average conformation of the enzyme, there are also changes in the mobility of the different domains, documented through the Debye-Waller factors in the corresponding structures. Namely, in the closed conformation (with substrates), the NMP-BD and LID domains are more rigid, whereas helix 3 (α3) is more flexible, compared to the open conformation (3,24). Future experiments with the ASP could in principle probe the effects of this entropy flow between the different parts of the molecule, for example by using the molecular spring to rigidify helix 3 and observe the effect on the substrates' binding constants.
The tension in the construct described here can be estimated from the bending modulus of DNA (6); we find that the DNA stores an elastic energy of order W ≈ 25 kTroom and provides a force of order F ≈ 10 pN. This is an upper bound, as it does not take into account force-limiting effects such as, for instance, bubble formation in the DNA.
It is interesting to compare the insights obtained from traditional mutagenesis with the insights obtained from the ASP. In their study of yeast GK, Zhang et al. (25) found that substituting Tyr-78 (which hydrogen-bonds to the phosphate of the bound GMP) with Phe causes KG to increase by a factor of 20, k2 to decrease by a factor of 100, and KA to increase by a factor of 2. This is a measurement of the contribution of the hydrogen bond of Tyr-78 to the free energy of GMP binding (−1.7 kcal/mol), and the stabilization of the transition state, since the structures are unaffected by the substitution.
With the ASP, similarly, we find that we can increase KG by a factor of 10 without affecting KA. This shows that GMP binding does not cooperatively promote ATP binding, in agreement with Zhang et al. (25). Different from the mutagenesis in Zhang et al. (25), the ASP introduces a bias work (W) toward the “open” conformation of GK, where W = F × s, with F being the force applied by the molecular spring and s the conformational motion of the spring attachment points between the open and closed states along the direction of the force (i.e., along the line joining the attachment points). Since s ≈ 1 nm and F ≈ 10 pN according to our estimate, the bias energy is W ≈ 1.5 kcal/mol. The measured factor-of-10 increase in KG corresponds to a change in binding free energy for GMP: ΔG ≈ 1.4 kcal/mol. These measurements directly demonstrate Koshland's induced-fit mechanism in the case of GMP binding to GK. Quantitatively, we find that “reverse biasing” the conformational change that accompanies substrate binding by an amount of work W lowers the binding energy of GMP by the same amount W. On the other hand, the binding energy of ATP is unaffected.
Since the ASP allows direct measurement of the relevant quantities, we are led to the following operational criterion to describe the induced-fit mechanism quantitatively. Suppose binding of a ligand is accompanied by a conformational change, and an ASP is applied which performs the work W against that conformational change. If, as a consequence, the binding energy of the ligand is reduced by an amount ΔG, one can define an index α as follows:
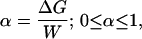 |
(10) |
where small values of α mean that the induced-fit mechanism is not relevant and values of α close to 1 mean that it is, on the contrary, dominant. For example, in the case of GK, we find α ≈ 1 for GMP, but α = 0 for ATP. Note that with W = F × s, and α defined by Eq. 10, for small enough F one will always find α = 1, unless s = 0 (no conformational change), in which case α = 0. That is, in the regime of linear elasticity of the structure, α = 1. On the other hand, in the nonlinear regime, which is probably relevant for functional conformational changes (26), α will depend on F. With quantitative calibration of the force, plus some input on structural deformations from experiments and computations, the ASP may thus allow a quantitative classification of conformational changes vis-à-vis the induced-fit mechanism.
An alternative description of our results is simply that the ASP significantly disrupts the GMP binding site but not the ATP binding site. The catalytically active flexible region (P-loop (3,4)) would not be disrupted because the stress is not directly applied to it. In fact, the key residue in the NMP-BD that participates in catalysis, namely Tyr-78 of yeast GK (25) or, by homology, Ser-99 of tuberculosis GK, is not directly coupled (i.e., through the same secondary-structure element) to the attachment sites of the ASP, perhaps allowing for the residue to remain positioned to aid in catalysis. On the other hand, the residues involved in GMP-binding, Ser-34 or Arg-41 of yeast GK (2) or the homologous Ser-53 and Arg-60 in tuberculosis, are in close proximity to the ASP and could be “unraveled” by the applied tension.
Ultimately, which interpretation is correct must be resolved by direct investigation of the average structural deformation under tension, which could be accomplished experimentally by fluorescence energy transfer or NMR, and computationally by molecular dynamics simulations (27) and statistical mechanics methods (28,29).
In summary, by applying controlled mechanical stresses to GK with the ASP, we quantitatively assess the relevance of the induced-fit theory for this enzyme. We show that the ASP can be used to selectively perturb a specific region or function within a protein, leaving other sites unscathed. This will facilitate comparison with theoretical modeling of the structure's response to applied forces. Distinguishing features of the ASP are the externally controlled and physically defined mechanical tension, which can be continuously modulated, and the possibility of applying the tension between any two chosen points on the protein's surface.
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.
Acknowledgments
We thank the Courey group at University of California, Los Angeles, for use of their luminometer, and the Perry group at University of California, Los Angeles, for use of the Protein Expression Lab facilities.
This work was partially supported by National Science Foundation grant DMR-0405632.
References
- 1.Oeschger, M. P., and M. J. Bessman. 1966. Purification and properties of guanylate kinase from Escherichia coli. J. Biol. Chem. 241:5452–5460. [PubMed] [Google Scholar]
- 2.Sekulic, N., L. Shuvalova, O. Spangenberg, M. Konrad, and A. Lavie. 2002. Structural characterization of the closed conformation of mouse guanylate kinase. J. Biol. Chem. 277:30236–30243. [DOI] [PubMed] [Google Scholar]
- 3.Blaszczyk, J., Y. Li, H. Yan, and X. Ji. 2001. Crystal structure of unligated guanylate kinase from yeast reveals GMP-induced conformational changes. J. Mol. Biol. 307:247–257. [DOI] [PubMed] [Google Scholar]
- 4.Dreusike, D., and G. E. Schulz. 1986. The glycine-rich loop of adenylate kinase forms a giant anion hole. FEBS Lett. 208:301–304. [DOI] [PubMed] [Google Scholar]
- 5.Koshland, D. E., Jr. 1994. The key-lock theory and the induced fit theory. Angew. Chem. Int. Ed. Engl. 33:2375–2378. [Google Scholar]
- 6.Choi, B., G. Zocchi, S. Canale, Y. Wu, S. Chan, and L. J. Perry. 2005. Artificial allosteric control of maltose binding protein. Phys. Rev. Lett. 94:038103–038106. [DOI] [PubMed] [Google Scholar]
- 7.Choi, B., G. Zocchi, S. Canale, Y. Wu, S. Chan, and L. J. Perry. 2005. Allosteric control through mechanical tension. Phys. Rev. Lett. 95:078102–078105. [DOI] [PubMed] [Google Scholar]
- 8.Schellman, J. A., and S. C. Harvey. 1995. Static contributions to the persistence length of DNA and dynamic contributions to DNA curvature. Biophys. Chem. 55:95–114. [DOI] [PubMed] [Google Scholar]
- 9.Strick, T., J.-F. Allemand, V. Croquette, and D. Bensimon. 2000. Twisting and stretching single DNA molecules. Prog. Biophys. Mol. Biol. 74:115–140. [DOI] [PubMed]
- 10.Saghatelian, A., K. M. Guckian, D. A. Thayer, and M. R. Ghadiri. 2003. DNA detection and signal amplification via an engineered allosteric enzyme. J. Am. Chem. Soc. 125:344–345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Shimoboji, T., E. Larenas, T. Fowler, S. Kulkarni, A. S. Hoffman, and P. S. Stayton. 2002. Photoresponsive polymer–enzyme switches. Proc. Natl. Acad. Sci. USA. 99:16592–16597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Marvin, J. S., and H. W. Hellinga. 2001. Conversion of a maltose receptor into a zinc biosensor by computational design. Proc. Natl. Acad. Sci. USA. 98:4955–4962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Liu, H., J. J. Schmidt, G. D. Bachand, S. S. Rizk, L. L. Looger, H. W. Hellinga, and C. D. Montemagno. 2002. Control of a biomolecular motor-powered nanodevice with an engineered chemical switch. Nat. Mater. 1:173–177. [DOI] [PubMed] [Google Scholar]
- 14.Choi, B., and G. Zocchi. 2006. Mimicking cAMP-dependent allosteric control of protein kinase A through mechanical tension. J. Am. Chem. Soc. 128:8541–8548. [DOI] [PubMed] [Google Scholar]
- 15.Agarwal, K. C., R. P. Miech, and R. E. Parks Jr. 1978. Guanylate kinases from human erythrocytes, hog brain, and rat liver. Methods Enzymol. 51:483–490. [DOI] [PubMed] [Google Scholar]
- 16.Cantor, C. R., and P. R. Schimmel. 1980. Biophysical Chemistry. Freeman, New York.
- 17.Kern, D., and E. R. P. Zuiderweg. 2003. The role of dynamics in allosteric regulation. Curr. Opin. Struct. Biol. 13:748–757. [DOI] [PubMed] [Google Scholar]
- 18.Cooper, A., and D. T. Dryden. 1984. Allostery without conformational change. A plausible model. Eur. Biophys. J. 11:103–109. [DOI] [PubMed] [Google Scholar]
- 19.Jusuf, S., P. J. Loll, and P. H. Axelsen. 2003. Configurational entropy and cooperativity between ligand binding and dimerization in glycopeptide antibiotics. J. Am. Chem. Soc. 125:3988–3994. [DOI] [PubMed] [Google Scholar]
- 20.Hawkins, R. J., and T. C. B. McLeish. 2004. Coarse-grained model of entropic allostery. Phys. Rev. Lett. 93:098104–098107. [DOI] [PubMed] [Google Scholar]
- 21.Frauenfelder, H., F. Parak, and R. Young. 1988. Conformational substates in proteins. Annu. Rev. Biophys. Biophys. Chem. 17:451–479. [DOI] [PubMed] [Google Scholar]
- 22.Frauenfelder, H., B. H. McMahon, R. H. Austin, K. Chu, and J. T. Groves. 2001. The role of structure, energy landscape, dynamics, and allostery in the enzymatic function of myoglobin. Proc. Natl. Acad. Sci. USA. 98:2370–2374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Luque, I., S. A. Leavitt, and E. Freire. 2002. The linkage between protein folding and functional cooperativity: two sides of the same coin? Annu. Rev. Biophys. Biomol. Struct. 31:235–256. [DOI] [PubMed] [Google Scholar]
- 24.Muller, C. W., G. J. Schlauderer, J. Reinstein, and G. E. Schulz. 1995. Adenylate kinase motions during catalysis: an energetic counterweight balancing substrate binding. Structure. 4:147–156. [DOI] [PubMed] [Google Scholar]
- 25.Zhang, Y., Y. Li, Y. Wu, and H. Yan. 1997. Structural and functional roles of tyrosine 78 of yeast guanylate kinase. J. Biol. Chem. 272:19343–19350. [DOI] [PubMed] [Google Scholar]
- 26.Miyashita, O., J. N. Onuchic, and P. G. Wolynes. 2003. Nonlinear elasticity, proteinquakes, and the energy landscapes of functional transitions in proteins. Proc. Natl. Acad. Sci. USA. 100:12570–12575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ma, J., P. B. Sigler, Z. Xu, and M. Karplus. 2000. A dynamic model for the allosteric mechanism of GroEL. J. Mol. Biol. 302:303–313. [DOI] [PubMed] [Google Scholar]
- 28.Clementi, C., A. Garcia, and J. N. Onuchic. 2003. Interplay among tertiary contacts, secondary structure formation and side-chain packing in the protein folding mechanism: an all-atom representation study. J. Mol. Biol. 326:933–954. [DOI] [PubMed] [Google Scholar]
- 29.Das, P., C. J. Wilson, G. Fossati, P. Wittung-Stafshede, K. S. Matthews, and C. Clementi. 2005. Characterization of the folding landscape of monomeric lactose repressor: quantitative comparison of theory and experiment. Proc. Natl. Acad. Sci. USA. 102:14569–14574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Li, Y., Y. Zhang, and H. Yan. 1996. Kinetic and thermodynamic characterization of yeast guanylate kinase. J. Biol. Chem. 271:28038–28044. [DOI] [PubMed] [Google Scholar]