Adaptive reconfiguration of fractal small-world human brain functional networks

Abstract

Brain function depends on adaptive self-organization of large-scale neural assemblies, but little is known about quantitative network parameters governing these processes in humans. Here, we describe the topology and synchronizability of frequency-specific brain functional networks using wavelet decomposition of magnetoencephalographic time series, followed by construction and analysis of undirected graphs. Magnetoencephalographic data were acquired from 22 subjects, half of whom performed a finger-tapping task, whereas the other half were studied at rest. We found that brain functional networks were characterized by small-world properties at all six wavelet scales considered, corresponding approximately to classical δ (low and high), θ, α, β, and γ frequency bands. Global topological parameters (path length, clustering) were conserved across scales, most consistently in the frequency range 2–37 Hz, implying a scale-invariant or fractal small-world organization. Dynamical analysis showed that networks were located close to the threshold of order/disorder transition in all frequency bands. The highest-frequency γ network had greater synchronizability, greater clustering of connections, and shorter path length than networks in the scaling regime of (lower) frequencies. Behavioral state did not strongly influence global topology or synchronizability; however, motor task performance was associated with emergence of long-range connections in both β and γ networks. Long-range connectivity, e.g., between frontal and parietal cortex, at high frequencies during a motor task may facilitate sensorimotor binding. Human brain functional networks demonstrate a fractal small-world architecture that supports critical dynamics and task-related spatial reconfiguration while preserving global topological parameters.

Coherent or correlated oscillation of large-scale, distributed neural networks is widely regarded as an important physiological substrate for motor, perceptual and cognitive representations in the brain (1, 2). The topological description of brain networks promises quantitative insight into functionally relevant parameters because their topology strongly influences their dynamic properties such as speed and specialization of information processing, learning, and robustness against pathological attack by disease (3).

The topology of networks can range from entirely random to fully ordered (a lattice). In this spectrum, small-world topology is characteristic of complex networks that demonstrate both clustered or cliquish interconnectivity within groups of nodes sharing many nearest neighbors in common (like regular lattices), and a short path length between any two nodes in the network (like random graphs) (3). This is an attractive configuration, in principle, for the anatomical and functional architecture of the brain, because small-world networks are known to optimize information transfer, increase the rate of learning, and support both segregated and distributed information processing (refs. 4–7; for review, see ref. 8). Small-world properties were recently described empirically in neuroanatomical networks at a microscopic level, e.g., the neuronal network of Caenorhabditis elegans (5), and at the macroscopic level of interregional axonal connectivity of the cat and macaque monkey cortices (9, 10). Neurophysiological networks inferred from patterns of correlated time-series activity in regions of monkey brains (11), regions of human brains (12, 13), and voxels of human functional MRI data also demonstrate small-world topology (14, 15). However, the frequency dependence of small-world brain functional networks, and their sensitivity to different behavioral states, has yet to be determined (16).

To address the issue of frequency, we used a wavelet analysis of magnetoencephalographic (MEG) signals recorded from a set of 275 points overlying the scalp surface, to provide a time–frequency decomposition of human brain activity. This decomposition was followed by a correlation analysis in the wavelet domain to reveal which MEG signals represented similar physiological activity or were functionally connected, in each of six distinct wavelet scales or frequency intervals. Graph theory was applied to describe the topological properties of adjacency matrices derived by a binary thresholding of the continuous wavelet correlation matrices. We used small-world metrics to characterize these undirected graphs representing brain functional networks and to compare network properties across the range of frequency intervals represented by scales of the wavelet transform. We then used these frequency-dependent topological analyses to deduce emergent dynamical properties of the system; specifically, we derived an estimate of the synchronizability of each network.

To address the second issue of state dependency, we extended the analysis to compare the properties of scale-specific networks derived from MEG data recorded with subjects either at rest or performing a simple motor task (visually cued finger tapping). As well as considering the global topological and dynamical parameters of resting and motor task-related networks, we also compared their spatial configurations. For example, we quantified the physical distances between functionally connected nodes, and we mapped the spatial distributions of highly connected “hubs” and topologically pivotal nodes.

Given the limited amount of prior data on small-world properties of human brain functional networks measured by using MEG (or electroencephalography) (12, 17), our hypothetical predictions were modest. We expected to find evidence for small-world brain functional networks in MEG data recorded in both behavioral states. Based on functional neuroimaging studies of finger tapping and timing of motor performance, we also expected to find task-related changes in the connectivity of motor, premotor, prefrontal, and lateral parietal cortical regions (18–26).

Results

Small-World Parameters of Scale-Specific Networks.

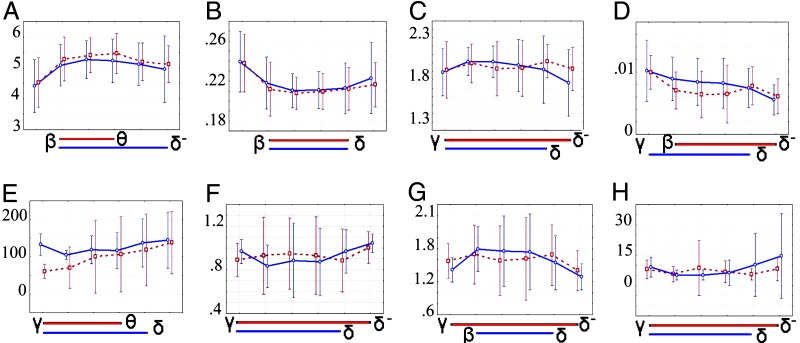
The small-world metric σ ranged between 1.7 and 2.0 (see Table 1 and Fig. 1), but at most scales in both states σ ≈ 1.9, indicating that small-world topology was closely conserved over a wide range of frequencies. In resting networks, the scaling regime for σ was 1.1–75 Hz; in motor task-related networks, the scaling regime was 2.2–75 Hz.

Table 1.

Global topological and dynamical properties of frequency-specific human brain functional networks

Wavelet decomposition level	Frequency range, Hz	Corr	τ	k	L	C	σ	ζ	S (×10−3)
Resting
1	37.5–75	0.18 ± 0.02	0.50 ± 0.05	16.3 ± 5.1	4.5 ± 0.5	0.23 ± 0.02	1.9 ± 0.2	61 ± 14	9.7 ± 1.9
2	18.8–37.5	0.26 ± 0.02	0.74 ± 0.04	12.6 ± 3.1	5.2 ± 0.5	0.21 ± 0.02	1.9 ± 0.1	70 ± 41	8.2 ± 2.3
3	9.4–18.8	0.30 ± 0.03	0.81 ± 0.03	12.4 ± 1.8	5.4 ± 0.4	0.20 ± 0.01	1.9 ± 0.2	100 ± 72	6.3 ± 2.7
4	4.7–9.4	0.30 ± 0.03	0.82 ± 0.03	12.3 ± 2.0	5.4 ± 0.4	0.21 ± 0.01	1.9 ± 0.2	106 ± 75	6.4 ± 3.3
5	2.3–4.7	0.30 ± 0.02	0.81 ± 0.02	12.5 ± 2.0	5.2 ± 0.4	0.21 ± 0.01	2.0 ± 0.1	118 ± 71	7.6 ± 2.9
6	1.1–2.3	0.33 ± 0.05	0.83 ± 0.02	13.7 ± 3.3	5.1 ± 0.4	0.23 ± 0.02	1.9 ± 0.1	137 ± 62	6.0 ± 2.4
Tapping
1	37.5–75	0.18 ± 0.03	0.49 ± 0.09	16.9 ± 5.1	4.4 ± 0.6	0.23 ± 0.02	1.8 ± 0.2	132 ± 21	10.2 ± 3.6
2	18.8–37.5	0.23 ± 0.02	0.69 ± 0.04	13.0 ± 2.6	5.0 ± 0.4	0.21 ± 0.01	2.0 ± 0.1	105 ± 9	9.8 ± 2.7
3	9.4–18.8	0.27 ± 0.02	0.77 ± 0.03	12.2 ± 1.7	5.2 ± 0.4	0.21 ± 0.01	2.0 ± 0.1	118 ± 27	8.4 ± 2.8
4	4.7–9.4	0.28 ± 0.03	0.79 ± 0.02	12.7 ± 2.1	5.2 ± 0.5	0.21 ± 0.01	1.9 ± 0.2	116 ± 35	8.2 ± 2.9
5	2.3–4.7	0.30 ± 0.05	0.81 ± 0.01	13.8 ± 4.9	5.1 ± 0.5	0.21 ± 0.01	1.9 ± 0.2	137 ± 47	7.2 ± 2.6
6	1.1–2.3	0.34 ± 0.06	0.82 ± 0.01	16.7 ± 8.3	4.9 ± 0.8	0.22 ± 0.02	1.7 ± 0.2	144 ± 55	5.2 ± 1.6

Corr, average correlation of the whole brain network before thresholding; τ, threshold applied to wavelet correlation matrices; k, average degree of the network; L, average path length; C, average clustering; σ, small-world scalar value; ζ, characteristic length scale in millimeters; S, synchronizability.

Fig. 1.

Scale-invariance of global topological and dynamical parameters of brain functional networks. Each image summarizes the group mean parameter values over all wavelet scales and in both resting (red) and motor (blue) states; error bars represent 95% confidence interval; blue and red bars below the x axis indicate the extent of the scaling regime for each parameter in both resting (red) and motor (blue) states. (A) Average path length, L. (B) Clustering, C. (C) Sigma, σ. (D) Synchronizability, S. (E) Characteristic length, ζ (mm). (F–H) Parameters of an exponentially truncated power law degree distribution of the form P(k) ≈ A kλ⁻¹e^k/kc. (F) Coefficient, A. (G) Power law exponent, λ. (H), Exponential cut-off degree, k_c.

The mean degree k ≈ 13, the clustering coefficient C ≈ 0.21, and the minimum path length L ≈ 5.2 were also conserved over scales and states (Fig. 1). Although the scaling regimes for these parameters did not include the highest or lowest frequency intervals, they consistently extended from 2 to 37.5 Hz. The γ network was distinguished by higher degree, greater clustering, and shorter path length than the lower-frequency networks in the scaling regime.

Degree Distributions of Scale-Specific Networks.

There was further evidence for scale-invariant topology when we compared the degree distributions of the scale-specific networks in each behavioral state (Fig. 1 F–H). For all networks, the degree distribution was best fit by an exponentially truncated power law, with very similar parameter values at all scales and states [see supporting information (SI) Table 2 for parameter values and SI Fig. 5 for best fits].

Synchronizability of Scale-Specific Networks.

The synchronizability at all scales in both states was at or below the threshold of 0.01 at which systems of various oscillators globally synchronize (see Fig. 1D), suggesting that the brain networks are located dynamically on a critical point of the order/disorder transition (27). There was evidence of scale invariance in synchronizability, with a scaling regime consistently including the frequency range 2–37.5 Hz. It was also notable that synchronizability in both motor and resting states was somewhat higher in the γ band, which reflects the distinctive topological properties (greater density and clustering) of the γ network.

Spatial Configuration of Scale-Specific Networks.

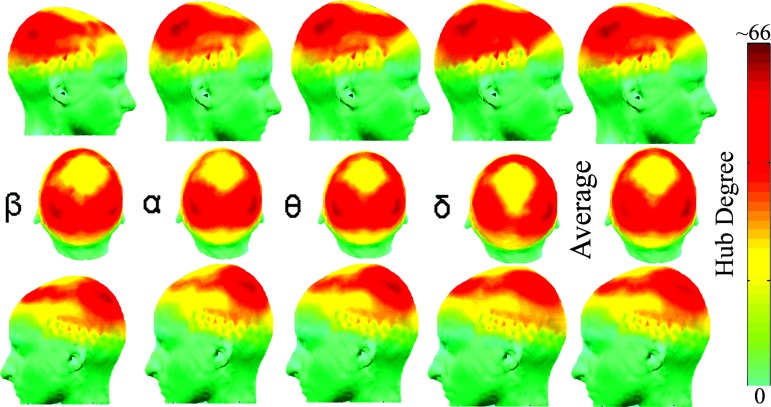
The spatial distribution of network hubs was also broadly similar across scales and states (see Fig. 2 and SI Fig. 5). See SI Fig. 6 for average hub distributions across all scales in both states. However, there were striking differences between scales and states in the physical distance between functionally connected network nodes (see Fig. 3).

Fig. 2.

Self-similarity of spatial distribution of highly connected network nodes or “hubs” in the frequency range 2–38 Hz (64). Each column shows the surface distribution of the degree of network nodes in frequency bands β to δ: red represents nodes with high degree. The last column shows the spatial distribution of degree averaged over these four frequency bands, which emphasizes the similarity of spatial configurations across scales. See SI Fig. 5 for the hub distributions in both states at all frequency bands.

Fig. 3.

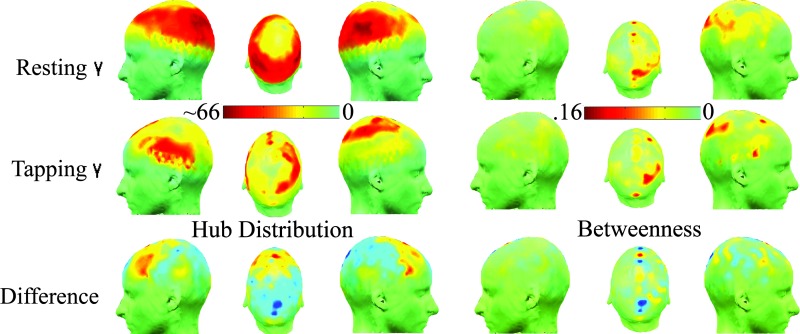
State-related differences in spatial configuration of the highest frequency γ network. The top row shows the degree distribution and betweenness scores for the resting state γ network; the middle row shows the same maps for the motor γ network; the bottom row shows the between-state differences in degree and betweenness. It is clear that motor task performance is associated with emergence of greater connectivity in bilateral prefrontal and premotor nodes, and appearance of topologically pivotal nodes (with high betweenness scores) in medial premotor, right prefrontal, and parietal areas. See SI Fig. 7 for the betweenness distributions in both states at all frequency bands.

In the resting state, long-range functional connectivity between brain regions was stronger at low frequencies. At higher frequencies (β, γ), long-range connectivity was weaker, and most of the edges in the graph represented high-density local connections (see Figs. 1E and 4), shown by the increase in characteristic length scale of network edges ζ, going from high to low frequency scales; and by the increasing number of connector compared with provincial nodes at low frequencies (see SI Fig. 7 for a schematic and SI Fig. 8 for distributions of provincial and connector hubs in both states and all frequency bands).

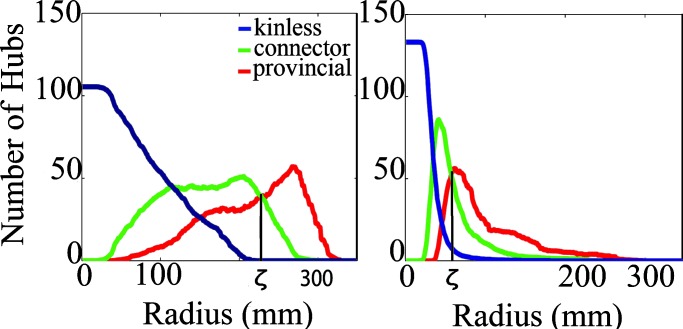
Fig. 4.

Change of provincial, connector, and kinless hubs with neighborhood size. As the radius r is increased, the proportion of provincial nodes is increased, and the proportions of kinless and connector hubs are decreased. The radius at which the proportion of connector and provincial hubs is equal, denoted ζ, is a measure of the characteristic length scale of connections between nodes in the network. (Left) Number of provincial, connector, and kinless hubs as functions of radius r in high-frequency γ networks acquired during motor task performance, ζ ≈ 225. (Right) Number of provincial, connector, and kinless hubs as functions of radius r in high-frequency γ networks acquired during the resting state, ζ ≈ 75. ζ is significantly smaller for the γ, β, and α bands in the resting state than in the tapping state, indicating that performance of the motor task is associated with emergence of longer range connectivity in the brain functional network. See SI Fig. 6 for provincial and connector hub distributions in both states at all frequency bands.

In the finger-tapping state, long-range functional connections emerged more strongly at high frequencies (β, γ), shown by the significant motor task-related increases in characteristic length scale of edges in high-frequency motor networks. It is also represented by the shift from resting-state γ networks dominated by provincial hubs (predominantly connected to locally neighboring regions of bilateral occipital, parietal, and central cortex) to motor γ networks with a larger number of connector hubs in medial premotor and bilateral prefrontal cortex. Some of the new long-range connections engendered by task performance at high frequencies link to topologically pivotal nodes in right medial premotor and prefrontal cortex with high betweenness scores (see Fig. 3; and see SI Fig. 9 for betweenness distributions at all frequencies). This indicates that task performance is associated with reconfiguration of high-frequency networks to favor long-distance connections between prefrontal and premotor sensors not otherwise functionally connected to each other (see SI Fig. 10 for distributions of the length of connections in each state in all frequency bands).

Discussion

We have explored the frequency dependency and task specificity of complex brain functional networks measured in humans by using MEG. We have used the wavelet transform to decompose functional connectivity between spatially remote sources into a hierarchy of scales or frequency intervals; and we have compared scale-dependent profiles of network organization in data acquired with subjects at rest to the same parameters estimated in data acquired with subjects performing a simple motor (finger-tapping) task.

Fractal Brain Networks.

The approximate physiological bandwidth of human brain oscillations is 0.1–100 Hz (four orders of magnitude). Here, we have found that functional brain networks are consistently organized in a small-world topology, with critical dynamics, over the frequency range 1–75 Hz. Several key parameters of global topology and synchronizability were very similar. In particular, there was strong evidence for a scale-invariant or fractal architecture of small-world brain functional networks in the scaling regime 2–37.5 Hz (see Figs. 1 and 2). Scale invariance was evident for classical small-world parameters (such as degree, path length, and clustering) as well as for the parameters of the exponentially truncated power law that provided the best fit to the degree distributions in all scales and states (see Table 1 and SI Table 2).

Fractal properties, i.e., self-similarity over several scales of measurement, have been described in many types of neurobiological data including electroencephalographic and functional MRI time series (28–31), structural MRI measurements of the cortical surface and gray–white matter boundary (32, 33), and microscopic data on neuronal dendritic and cerebrovascular arborizations (34). It is also notable that small-world networks have been generated computationally by a fractal growth process (35) and that adaptive rewiring of initially random networks by neurogenesis may allow development and maintenance of small-world connectivity in the brain (36–40). However, the current data provide the first evidence for self-similarity of global topology and dynamics of large-scale brain functional networks over a range of frequencies.

It is interesting to consider the high- and low-frequency intervals outside this scaling regime. The highest-frequency γ network was distinguished, in resting data, by shorter path length, greater mean degree and clustering, and greater synchronizability than networks in the scaling regime. The resting γ (and β) networks also were associated with relatively short-range distances between functionally connected nodes. Because a major proportion of the brain's energy budget is dedicated to costs of restoring membrane potentials following depolarization (41), and because these costs will be exacerbated by high-frequency oscillations, we conjecture that metabolic or energetic constraints may determine the upper limit on the scaling regime for brain functional networks. The same considerations would not easily explain the lower limit on the scaling regime, but we note that there was high variability of network parameters in the lowest-frequency interval, perhaps due to the relatively short time series segments available for estimation of correlated long-period oscillations. It will be important in future studies to explore the scaling properties of brain functional networks at frequencies <2 Hz in longer time series.

Effects of Motor Task Performance.

There was no evidence for major change in global network parameters as a result of visually cued finger tapping; however, there was extensive spatial reconfiguration of higher-frequency networks during performance of the motor task (see Fig. 3). We propose that small-world brain functional networks may be topologically and dynamically constrained within a narrow window of permissible global parameters, but diversity of function may nevertheless be supported by reconfiguring the set of specific interregional connections that subtend the same global network architecture. In these data, we see this most clearly in the emergence of new long-range connections (see Fig. 1E) and pivotal nodes in frontal and parietal regions in the γ and β networks during motor task performance, although the global topological parameters of these networks were not much affected by the change of behavioral state.

For this to be a plausible model for adaptive reconfiguration of brain functional networks, one would expect the network in any particular state to be sparse, implying that there is a large reserve of alternative connections that could be formed in support of new functions. One might also expect the network's dynamics to be compatible with rapid reconfiguration. Both these conditions are supported by the data. The networks reported here are sparsely connected in both resting and motor states, with an average connection density of 0.095, calculated by the number of connections (≈ k × n = 13 × 274 = 3,562) divided by the possible number of connections between 274 nodes ((n² − n)/2 = 37,401). Moreover, the synchronizability of the networks in all scales and states is close to the threshold of 0.01, which marks the lower limit of the transition zone from globally ordered to disordered behavior in systems of coupled oscillators. The γ network in both states, and the β network in the motor task, both have synchronizability of ≈0.01, implying that higher-frequency networks in particular have critical dynamics “on the edge of chaos,” which would favor their rapid, adaptive reconfiguration in the face of changing environmental demands.

Two experimentally testable predictions arising from this model are, first, that performance of other (nonmotor) tasks should also be associated with emergence of spatially reconfigured but globally constrained small-world networks and, second, that deviation of global topological and dynamical network parameters from the narrow range identified here might be diagnostic of pathological processes, for example, epilepsy might be associated with synchronizability > 0.01 or neurodegenerative disorders might be associated with increased path length and reduced clustering (42).

Temporal Binding Theories of Cognition.

There is a strong prior literature suggesting that correlated oscillations at high frequencies (especially in the γ band) are important as a physiological substrate for sensorimotor binding (43–45). Our data support this view: the emergence of high-frequency, long-distance connections, e.g., between frontal and parietal cortex, was the most salient network change associated with visually cued finger tapping, a task that will depend on rapid temporal integration of sensory cues and motor commands.

Our results further indicate that there is spatially organized coherent oscillation at lower frequencies, and the conservation of small-world topology over the scaling regime 2–37.5 Hz suggests that temporal binding at these frequencies may also be important for distributed information processing. A detailed interpretation of the cognitive significance of this observation is necessarily speculative in the absence of certainty concerning the nature of the neural code. However, it has been argued that frequency may code the channel of communication in neural circuits, and phase modulations may transmit information in specific channels (46). On this assumption, the existence of a scale-invariant small-world topology for brain functional networks might serve as a mechanism for integrating information transmitted in frequency-specific circuits. Correlated oscillations at γ frequencies, which are organized in networks with more critical dynamics, might then be regarded not as the only substrate for temporal binding but as a distributed mechanism for “catalyzing” rapid, state-related changes in spatial configuration of brain functional networks.

Methodological Considerations.

The methods used in this analysis have included wavelet decomposition and correlation analysis of signals and graph theoretic analysis of network properties. Brain processes are both nonstationary and long-memory. Wavelets can be used to produce well behaved covariance estimators of this class of processes (47). Transient objects within the time series can be easily represented by using the natural adaptivity of wavelets, unlike the large amalgamation of sine waves used by the Fourier transform (29). Further, whereas Fourier analysis requires a discrete set of frequencies of interest, the wavelet decomposition sweeps the data through a small set of frequency bands of finite length (48). By using MEG data sampled at 600 Hz, these wavelet frequency bands lie within the well known human brain rhythm bands of electroencephalography and can therefore be compared. Furthermore, the maximum overlap discrete wavelet transform was used instead of the standard discrete wavelet transform both because of its ability to cope with an arbitrary signal length and its superior estimators of wavelet correlation (49).

The present work was performed on MEG data in sensor space, which contains some inherent correlation between magnetic fields on the surface of the brain, which limits anatomical inferences drawn from the data (see SI Supporting Materials and Methods section 2.4 and SI Fig. 11). Although this caveat does not affect our conclusions about global topology and network dynamics, future work will include a source reconstruction of the activity in the brain, which will allow improved extrapolation to anatomical locations.

Conclusion

We have shown that there is a scale-invariant or fractal organization of large-scale brain functional networks in the resting state, which consistently demonstrate small-world properties in the scaling regime 2–37.5 Hz. Performance of a simple motor task was associated with conservation of global topological and dynamical parameters but emergence of long-range connectivity in γ and β bands. We propose that scale-invariant small-world topology may be relevant to temporal binding of information in frequency-encoded channels and that γ networks, which exist in a dynamically critical state, may provide a mechanism for state-related spatial reconfiguration of connections subtending normally conserved global parameters of small-world network organization.

Materials and Methods

Twenty-two healthy right-handed volunteers (12 male, 10 female) with mean age = 31.0 ± 6.5 (SD) years were enrolled in the study. Eleven subjects (6 male, 5 female) performed a finger-tapping task, whereas 11 other subjects matched for age (P = 0.93, t test) and gender were used to procure resting data. MEG data were acquired at the National Institute of Mental Health by using a 275-channel CTF MEG system (VSM MedTech, Coquitlam, BC, Canada) at 600 Hz. For the finger-tapping task, visual stimuli were presented at 1.2 Hz for four trials of 10.24 s each using a custom-built mechanical sensor while motor responses (taps of the right index finger) were registered. In the resting state, data were acquired in a single session while subjects remained quietly immobile with eyes open for 30 min. For the purposes of comparison to the shorter motor task-related data, four data segments of 10.24-s duration were sampled from the resting time series at equally spaced intervals, excluding data acquired in the first 2 or last 2 minutes.

All time series were decomposed by using the maximum overlap discrete wavelet transform (15, 29, 48, 49). Wavelet scales 1–6 collectively represented physiological activity in the frequency range 1–75 Hz, corresponding approximately to the classical electroencephalogram bands: γ (37.5–75 Hz), β (18.7–37.5 Hz), α (9.4–18.7 Hz), θ (4.9–9.6 Hz), high δ (2.4–4.8 Hz), and low δ (1.1–2.2 Hz). To quantify the strength of association at specific frequencies between MEG signals in different brain regions, we calculated the absolute value of the correlation between wavelet coefficients for each pair of sensors at each scale of the transform [see Achard et al. (15) for details]. Correlation matrices were averaged over all four trials. To convert these continuous wavelet correlation matrices to an undirected graph G, we set to zero any correlations with value less than a threshold τ and set to one any correlations greater than τ. This operation transforms each wavelet correlation matrix to a binary adjacency matrix A, which can be graphically represented as a network comprising nodes (brain regions) connected by an edge or line if the wavelet correlation between them was greater than τ.

We chose our threshold τ using three constraints: (i) the false discovery rate (which controls the expected proportion of false positives among suprathreshold correlations) must be <5%; (ii) the average degree must be no smaller than 2 × ln(N) to allow use of graph theory to estimate the small-world scalar σ; and (iii) at least 99% of the nodes of the brain must be connected, because we were interested in global brain dynamics. Within these constraints, we chose the highest threshold possible to optimize the strength and thus biological plausibility of connections (50). A high threshold reduces the number of false-positive edges in the graph and is consistent with the known relative sparsity of anatomical connections in the brain (51).

Small-world parameters including average degree, path length (52, 53), clustering (54), and σ were computed as described (15, 39, 40, 55). Inherent correlations between parameters are discussed in SI Section 2.6 and SI Fig. 12. To exclude the possibility that results were affected by the precise choice of τ, we also estimated σ in networks thresholded with several values of τ and found evidence at all scales of small-world topology σ > 1 in networks thresholded by 0.4 ≤ τ ≤ 0.8.

The distribution of hubs (i.e., nodes with greater than average degree) could further be broken down into provincial (mostly local connections within a radius r), connector (both local and long-range connections), and kinless (mostly long-range connections outside r) hubs as in (56, 57) (see Fig. 4 for hub changes with radius and SI Fig. 7 for a schematic). The characteristic length scale ζ of the network was defined as the radius at which the number of provincial hubs (♯ P) in a network is equal to the number of connector hubs (♯ C). Betweenness nodes showed areas of pivotal topology and were computed as described (58–61) (see Fig. 3 for changes in betweenness distributions in the γ band, SI Fig. 9 for spatial distributions in all bands, and SI Fig. 13 for a numerical distribution). We further considered the general dynamical tendencies of an arbitrary network topology by modeling it as a uniformly coupled system and computing its synchronizability as described (62, 63).

It was clear by preliminary inspection of network parameters estimated at different scales of the maximum overlap discrete wavelet transform that most global topological and dynamical parameters were conserved within narrow bounds over all scales. To define more precisely the scaling regimes for each parameter, we fitted a simple linear regression model for the effect of scale on each of the parameters of interest and tested whether it was significantly greater than 0. If so, we iteratively identified the scale corresponding to largest residuals of the fitted model, removed this scale from the model, and reestimated the model until the effect of scale was not statistically significant. This procedure was used to define the extent of scale invariance, or the scaling regime, for each topological and dynamical parameter in each behavioral state.

Please see SI Supporting Materials and Methods for a more detailed description of materials and methods.

Abbreviation

MEG

magnetoencephalographic.