Functional residues serve a dominant role in mediating the cooperativity of the protein ensemble

Abstract

Conformational fluctuations in proteins have emerged as a potentially important aspect of biological function, although the precise relationship and the implications have yet to be fully explored. Numerous studies have reported that the binding of ligand can influence fluctuations. However, the role of the binding site in mediating these fluctuations is not known. Of particular interest is whether in addition to serving as structural scaffolds for recognition and catalysis, active-site residues may also play a role in modulating the cooperative network. To address this question, we employ an experimentally validated ensemble-based description of proteins to elucidate the extent to which perturbations at different sites can influence the cooperative network in the protein. Applying this method to a database of test proteins, it is found statistically that binding sites are located in regions most able to affect the cooperative network, even for cooperative interactions between residues distant to the binding sites. This indicates that the conformational manifold under native conditions is determined by the network of cooperative interactions within the protein and suggests that proteins have evolved to use these conformational fluctuations in carrying out their functions. Furthermore, because the energetic coupling pattern calculated for each protein is robust and relatively insensitive to sequence, these studies further suggest that binding sites evolved in regions of the protein that are inherently poised to take advantage of the fluctuations in the native structure.

Biological work in living organisms is mediated primarily through the use of protein molecules. Knowledge of the means by which proteins facilitate this work is of paramount importance to an understanding of function as well as the diseases that result from aberrant function. Of particular interest in recent years has been the observation that proteins are highly dynamic molecules that experience dramatic conformational excursions from the canonical high-resolution structure (1–3). In addition, it has also become clear that conformational dynamics play an important role in determining the ability of proteins to perform such diverse tasks as catalysis, allosterism, and signal transduction (4–6).

The observation that protein conformational fluctuations play an important role in function suggests that functional sites in proteins may be uniquely coupled to structural fluctuations (7–9) and thus identifiable by how perturbations at these sites affect the conformational manifold. Here we use an ensemble-based model of the protein to explore this issue. By identifying a statistically significant difference in the response of the ensemble to perturbations at active sites of proteins, as determined from a representative test set, we find that binding sites play a unique role in influencing the cooperative network within proteins. This suggests that binding sites have been preferentially optimized to use conformational fluctuations in the performance of their function.

Results and Discussion

Response of the Ensemble to Perturbations.

The notion that ligand concentration can be used to drive the equilibrium between different conformational states has been widely accepted since Wyman introduced the concept of linked functions (10). However, proteins are conformationally heterogeneous (1–3), and it is not clear that a description of the protein that accounts for only the gross structural differences between two macroscopic thermodynamic states is sufficient to identify the energetic determinants of why a ligand affects a particular equilibrium (7). To address this issue it is necessary to use a variety of experimental (1–6) and computational (7–9) approaches that can provide insight into how functional sites are linked to each of the microscopic states. If proteins have evolved to use conformational fluctuations around the average structure in the performance of their function, as has been suggested from recent NMR relaxation experiments (11), it would follow that functionally important sites on proteins would be coupled in a unique way to the equilibrium distribution of states in the ensemble.

To experimentally investigate the coupling between functionally important residues and the conformational ensemble, one would ideally perturb the energy of each residue, one at a time, and monitor its affect on the distribution of ensemble states (12). As noted previously, this idealized experiment cannot be realistically achieved and can be only approximated by Ala → Gly or Val → Ala mutations at solvent-exposed sites (12, 13). However, with a suitably validated computational model of the conformational ensemble, it is possible to use a computer program to investigate this issue. Here we use such a strategy and propose that the relative impact of functionally important sites on the equilibrium distribution of states in the ensemble can be determined, and that the method can be independently validated by the ability of the algorithm to predict various qualitative and quantitative aspects of cooperative behavior in a model protein.

Ensemble View of Site-to-Site Coupling.

To investigate site-to-site coupling (i.e., cooperativity) in a protein, we have used the COREX algorithm (12–21). COREX models the protein ensemble by approximating structural fluctuations as local order/disorder transitions applied throughout the high-resolution structure. We have previously demonstrated that this approach provides a reliable estimate of the regional stabilities within proteins (14, 17) as well as detailed insight into the cooperative networks that exist within protein structures (12, 16, 18–21).

Within the context of an ensemble, cooperativity can be evaluated by assessing whether two regions of the molecule are thermodynamically coupled. In other words, if the pairwise properties of two residues are consistent in the most probable states, those residues will be coupled; e.g., both residues are in folded (or unfolded) regions or one residue is always in a folded region when the other is an unfolded region. If on the other hand the pairwise properties of two residues are random among the most probable ensemble states, the residues are not coupled. Within the context of the COREX algorithm, the impact of any residue j on all other residues in the protein can be evaluated quantitatively by stabilizing all states in which residue j is folded (12). This perturbation will redistribute the conformational ensemble, and each residue will be perturbed according to the degree of coupling in the most probable states. Two important predictions of this method are the following: (i) distal residues can be coupled in the absence of a visible connectivity pathway (12, 20, 21); and (ii) the coupling between two residues need not be symmetric (the response of residue j to a perturbation at residue k is not necessarily reciprocal) (12, 20).

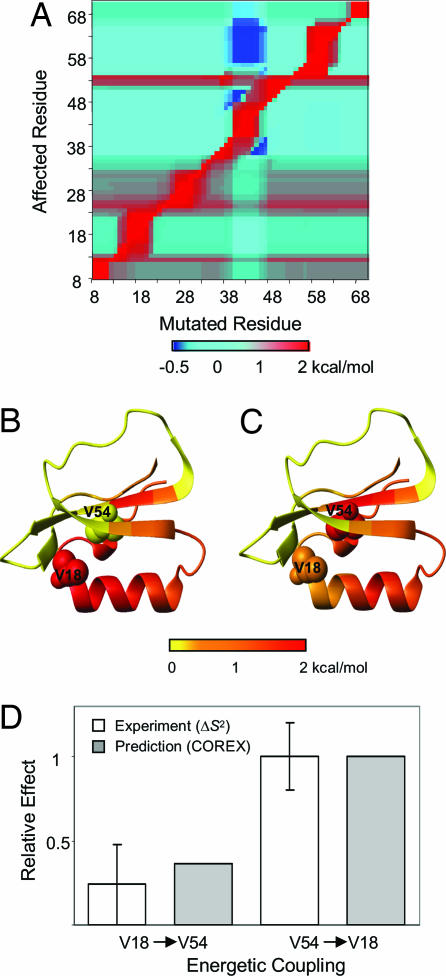
For the present study, the reliability of the cooperativity information obtained by COREX was first established by comparing the calculated results with recently obtained experimental Val → Ala mutations of eglin c (22). The comparison to eglin c is particularly relevant because the experimental results confirm the two unexpected aspects of cooperativity that are well simulated by the COREX algorithm (Fig. 1). First, as found by Lee and colleagues (22), the effects of mutations do indeed propagate to distal sites in the absence of a visible connectivity pathway. Second, and most surprising, cooperativity is not bidirectional (Fig. 1). In the specific case of eglin c, for example, it is found that the quantitative impact of the V18A mutation on V54 is significantly less than the reciprocal mutation (i.e., the effect of the V54A mutation on V18). Although the experimental analysis of eglin c, which involved monitoring the effects of mutations on the NMR-derived relaxation parameters (22), cannot be quantitatively compared with the energetic coupling calculated by COREX, the qualitative agreement demonstrates that the general features of the cooperative behavior in eglin c are captured.

Fig. 1.

Energetic coupling between residues V18 and V54 in eglin c. (A) Influence of a single-site perturbation on all other sites of the protein, as calculated by Eq. 1. (B) Ribbon diagrams of eglin c color-coded according to the magnitude of the influence of the perturbation at V18 on all other sites of the protein. Residues V18 and V54 are shown in CPK. (C) Ribbon diagrams of eglin c color-coded according to the magnitude of the influence of the perturbation at V54. B and C were prepared by using the program MOLMOL (49). (D) Relative effect of the mutation at V18 on V54, and its reciprocal. For a more direct comparison, the predicted and experimental values were normalized [COREX calculations were divided by the influence of the thermodynamic perturbation at V54 on V18, ΔG_f,18^pert,54; the experimental values were divided by the change of S₂^axis at V18 caused by V54A mutation (22)]. The eglin c Protein Data Bank structure used in this analysis was 1CSE.

Global Coupling to the Ensemble.

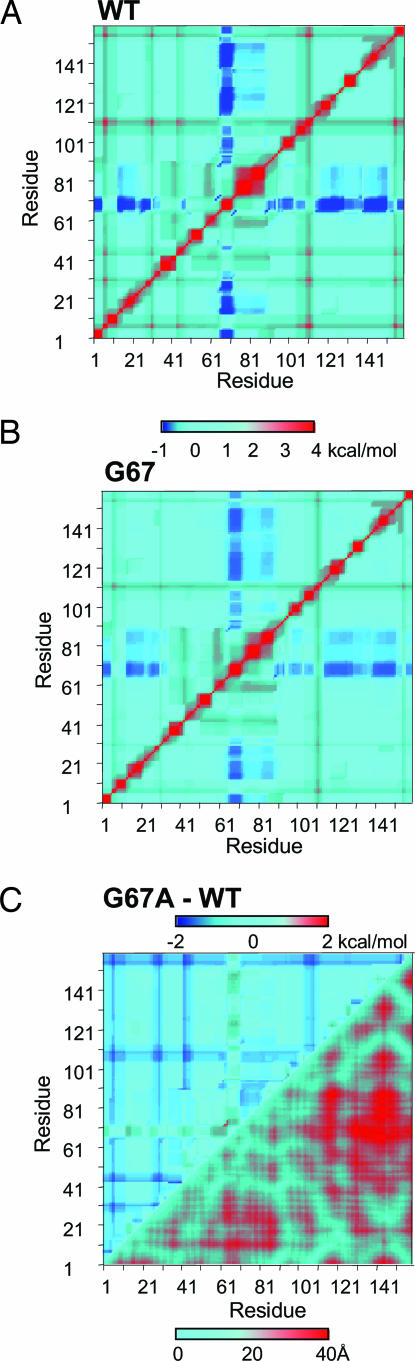
The results for eglin c, as well as previous studies with dihydrofolate reductase (DHFR) (21), suggest that cooperativity information as determined by COREX provides a reasonable description of the actual cooperative network within proteins. To investigate the importance of binding sites in mediating cooperativity, we considered the following. Within the context of an ensemble, cooperativity refers to the susceptibility of each site to a perturbation at another site. For two sites to be coupled, the relevant conformational equilibrium must be suitably poised such that redistributing the ensemble through a perturbation at site j affects the probability that residue k is folded. Thus, we see that the distribution of states in the native state ensemble of a protein is inextricably linked to the cooperativity: the ensemble itself defines the cooperativity (20). It is our hypothesis that if coupling is important to function, then proteins should have evolved so that active-site residues will be important for attenuating the equilibrium and therefore identifiable by how they affect the cooperative network in the protein. To extend our original analyses (12, 21) to challenge this hypothesis, we introduce here the global cooperative response (GCR) (see Methods). We note that because cooperativity is not bidirectional, the GCR must be calculated for each residue pair in such a way as to account for both the effect of residue j on residue k and vice versa. Because, the GCR value is a measure of how a mutation changes the thermodynamic coupling between all residue pairs, it provides a metric of how important a site is to maintaining the cooperative network in the entire protein. This calculation is illustrated in Fig. 2.

Fig. 2.

The GCR is the difference in the cooperativity map between an Ala substitution at each position and the WT structure. (A and B) Energetic coupling between the residues in WT (A) and G67A (B) E. Coli DHFR. A perturbation energy, Δg^pert, of 2 kcal/mol was used to calculate the bidirectional cooperativities (Eq. 2). Red corresponds to a positive coupling of two residues, blue represents a negative coupling, and cyan refers to neutral coupling as indicated by the color bar. (C) Difference in the pairwise cooperativities of WT and G67A E. coli DHFR (upper left) and the distance map between C^α atoms (bottom right). The natural log (Ln) of the GCR values for DHFR range from 7.45 to 9.90, with an average of 8.2. When normalized by the dimensions of the matrix (159 × 159), the average change in energetic coupling per residue pair is 0.14 kcal/mol (with a low of 0.06 kcal/mol and a high of 0.87 kcal/mol) for a 2 kcal/mol perturbation. The Protein Data Bank structure used in this analysis was 7DFR.

First, the thermodynamic coupling between any residue pair in a protein is calculated by evaluating the effect of an energetic perturbation at residue k on residue j and vice versa (Fig. 2A). Inspection of this cooperativity pattern reveals that some regions may show predominantly positive coupling between residue pairs, whereas others demonstrate a negative coupling. Next, point substitutions to Ala are applied to the host protein (labeled as WT in the figure) at each position, one at a time, in such a way as to not perturb the structure (i.e., the Protein Data Bank file is changed only at the mutated residue). Shown in Fig. 2B is the matrix of cooperativity values determined for each residue pair in the pseudomutant G67A of DHFR. Comparison of Fig. 2 A and B reveals that the calculated cooperativity pattern is not significantly affected by the substitution (20). However, despite the similarity in the pattern, the magnitude of the coupling values do change. The difference between the cooperativity matrices of the host and mutant provides a measure of how important that residue is to maintaining the cooperative network (Fig. 2C). Summation over all residue pairs in the difference matrix is defined as the GCR value for position 67 of DHFR. We note that the differences seen (Fig. 2C, upper left) are not merely trivial effects associated with structural changes to residues in the immediate vicinity of the mutation. As the contact map in Fig. 2C reveals, the observed cooperativity changes are independent of the distance between residue 67 and the coupled sites, and indicates that the effect is not mediated by a continuous structural pathway. Repetition of the steps outlined in Fig. 2 for each residue provides the residue-specific GCR (Fig. 3A). Consistent with Fig. 2C, if point mutations are applied only to ensemble states in which the mutation site resides in an unfolded region (i.e., to keep the native contacts identical to that of the WT), essentially identical GCR values are calculated (data not shown), indicating that conformational fluctuations (i.e., unfolding events) are a key determinant of the cooperative behavior in DHFR.

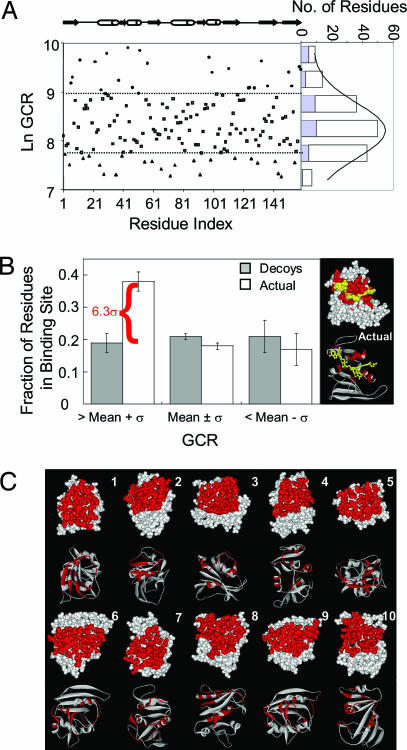
Fig. 3.

GCR values for binding-site residues are higher than for non-binding-site residues. (A) Residue-specific GCR values calculated for E. coli DFHR. The distribution of GCR values are provided in the histogram, with the contribution of binding-site residues highlighted in blue. (B) Fractions of binding-site residues in the high (GCR > mean + σ), medium (mean + σ ≥ GCR ≥ mean-σ), and low (GCR < mean-σ) coupling groups, compared with the average fraction obtained from non-binding-site residues in each category. Error bars indicate one standard deviation. The crystal structure of eDHFR with NADP⁺ and folate is provided in Right. Binding-site residues are colored red, and ligands are colored yellow. (C) Cartoon representations of randomly generated decoy binding sites, also colored red.

Despite the relative robustness of the cooperativity pattern generated for DHFR, some residues are observed to perturb the ensemble to a greater extent than others, with the values following a normal distribution (Fig. 3A). Interestingly, the average GCR value of binding-site residues in DHFR (blue bars in Fig. 3A) is higher than that found for the non-binding-site residues, with a significant fraction of the binding-site values falling outside the standard deviation (σ) of the mean response. This result indicates that binding-site residues in DHFR are statistically more thermodynamically coupled to, and hence more able to impact, the cooperative network in proteins than are non-binding-site residues.

Additional inspection of Fig. 3A, however, reveals that although binding-site positions are often found to be among the group of residues most able to affect the distribution of states (i.e., they are found in the group whose GCR values are more than one standard deviation above the mean), not all binding-site residues are found in this group, and not all residues in this group are binding-site residues. It should be expected that not all binding-site residues contribute equally to a protein's function. Experimentally, it has been observed for several binding sites (23–26) that the different residues comprising each site can contribute vastly different amounts to the functional processes of the protein (i.e., catalysis or allosteric response).

Theoretically, binding sites should have two distinct although not necessarily overlapping properties. First, binding events should elicit a structural response in the protein for an allosteric or enzymatic system. In ensemble terms, this is akin to a redistribution of the probabilities of the states. Second, the binding site should be chemically and topologically compatible to the ligand itself (i.e., have an affinity for the ligand). The method described in this communication attempts only, and in a general manner, to quantify the first property listed above. Given the need for proteins to bind ligands both specifically and with high affinity, it is therefore not surprising that all binding-site residues are not found to be equally coupled to the ensemble.

To determine the uniqueness of the observed coupling for the DHFR binding site, the fraction of binding-site residues in the high coupling group was compared with the fractions obtained from randomly assigned decoy binding sites of similar size to the actual DHFR binding site (Fig. 3C). The uniqueness of the GCR distribution for the actual binding site is shown in Fig. 3B, with the fraction of high coupling residues from the actual binding site being >6σ above the average fraction obtained from the decoy set, whose statistics arise from the non-binding-site residues in each group. This result indicates that the binding site in DHFR has a greater impact on the cooperative network in the protein than any other randomly sampled contiguous region of the protein surface, and by a statistically significant margin.

To investigate the generality of this result with regard to sequence composition, an identical analysis was performed on chicken DHFR (cDHFR), a structural homolog with 30% sequence identity to the Escherichia coli protein and with an additional 30 residues. As seen from Fig. 4A, similar results were obtained for the cDHFR. For this protein, the fraction of binding-site residues in the high coupling group is >5σ above the decoy set. These results indicate that the calculations are a robust property of the DHFR fold and not significantly affected by the precise amino acid sequence or the amino acid composition.

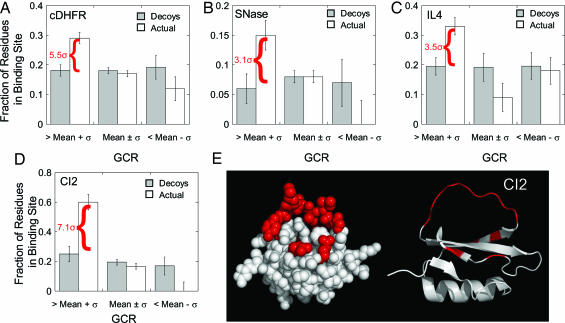
Fig. 4.

High binding-site GCR values are independent of ligand size and type. (A–D) The fractions of binding-site residues in the high (GCR > mean + σ), medium (mean + σ ≥ GCR ≥ mean-σ), and low (GCR < mean-σ) coupling groups for chicken DHFR (cDHFR) (A), staphylococcal nuclease (SNase) (B), interleukin 4 (IL-4) (C), and chymotrypsin inhibitor 2 (CI2) (D). Error bars indicate one standard deviation from the mean for a set of randomly selected decoy sites on each protein, as shown in Fig. 3 for eDHFR. The value shown in red is the number of standard deviations above the decoy set for the fraction of residues in the actual binding site. (E) Actual binding-site residues for CI2, shown in red on space-fill and ribbon representations. Perturbations to binding-site residues affect the cooperativity between all residues throughout the structure, even though the binding site is not situated in a central location in the structure. The Protein Data Bank structures used in this analysis were 8DFR (cDHFR), 1STN (SNase), 1HIK (IL-4), and 2CI2 (CI2). We also note that analysis of eglin c showed similar results to CI2, which is a structural homolog [1.68 Å backbone rms deviation (50)] with 30% sequence identity (data not shown).

To further evaluate the generality of these findings and to establish that the results were not in some way capturing structural properties of the DHFR binding cleft, the analysis was extended to a test set of nonhomologous protein structures that differ in both size and the nature of the biological ligand (Table 1). As was observed for both the E. coli DHFR (eDHFR) and cDHFR proteins, binding-site residues for all proteins tested were also found preferentially in the high coupling group and, on average, the fraction of binding-site residues in the high coupling group was significantly higher than that calculated for a set of randomly assigned decoy sites (Fig. 4). Several important observations can be made from inspection of Fig. 4 and Table 1. First, there is no correlation between the observed statistics and the size of the protein and/or the size and type of ligand. The only caveat is that this analysis was restricted to single-chain, monomeric proteins. Second, the results also appear to be independent of the location and physical attributes of the binding sites. This is demonstrated by comparing the binding site for DHFR (Fig. 3B), which is a cleft in the center of the protein, with the binding site for CI2, which is a loop that protrudes from the molecule (Fig. 4E). Coupled to the observation that there exists no correlation between the impact of a residue on the cooperative network and the distance between that site and any pair of coupled residues (Fig. 2C), these results further indicate that the effects that are being monitored are not trivial consequences associated with changing the structural contacts between two sites.

Table 1.

Monomeric proteins studied

Protein	No. of residues	Interaction partner	Statistical significance
Chymotrypsin inhibitor CI-2	65	Protein (chymotrypsin)	7.1σ
IL-4	129	Protein (IL-4 receptor)	3.5σ
Staphylococcal nuclease	134	Nucleotide (pdTp/Ca2+)	3.1σ
eDHFR	159	Cofactor/substrate NADPH/folate (overall)	6.3σ
		Folate site alone	6.5σ
		NADPH site alone	5.5σ
cDHFR	186	Cofactor/substrate NADPH/folate	5.5σ

Finally, when the statistics for each binding site in DHFR is considered separately (Table 1), the hyperconnectivity is nonetheless maintained, indicating at least for the case of DHFR, that the effect is not regionally distributed within the binding site. It would be of significant interest to determine whether there exist differences between binding sites in multichain proteins that demonstrate allosteric behavior. However, the role of binding sites in maintaining coupling in large multimeric systems awaits further study.

Conclusions

Although the importance of chemical and structural complementarity between protein and ligand are well known, the high intrinsic ability of an active site to affect the coupling throughout a protein (independent of distance) is rather surprising. Proteins are conformationally heterogeneous ensembles that have been shown to use their intrinsic fluctuations to perform their function (11). This means that binding and function are facilitated by many states that are near the minimum in the energy basin around the native structure, a result which is by no means unexpected. However, it appears that proteins have gone further and have evolved to optimize their sensitivity to selectively respond to perturbations at functional sites. Such a sensitivity undoubtedly provides a selective advantage in initiating catalytically important dynamic transitions or transmitting the effects of binding to distal sites.

Equally as important as the existence of this “hyperconnectivity” of active-site residues is the implications it may hold for the evolution of proteins as biological machines. The results presented here reveal that functional sites have unique thermodynamic properties in that they are energetically more coupled to the cooperativity of the ensemble. This opens an intriguing question as to the origins of binding sites in proteins and therefore to the evolution of different folds. One possibility is that the observed hyperconnectivity between the binding site and the ensemble is an intrinsic property of each fold. If this were the case, protein folds could not be viewed as blank scaffolds onto which virtually any function can be evolved, and at any location on the structure. According to this hypothesis, the protein fold would determine the location(s) of the binding site(s) (and possibly the potential range of functions).

Alternatively, the hyperconnectivity could be a property that evolves once a binding site has been selected by nature from among a near limitless number of potential folds and locations within each fold. Although the current analysis does not allow us to distinguish between these two scenarios, it does suggest that thermodynamic criteria, independent of structural, chemical, and topological complementarity, can be established for the identification of putative binding sites on proteins. Such a method awaits further study.

It is interesting to note that the number of possible folds that have been predicted, based on existing fold space, is far less than the theoretical number of potential folds (27). Combined with the fact that several folds have evolved to perform multiple functions at analogous sites (28–32), this observation is consistent with the notion that the putative binding site is coded in the fold [more precisely the energetic balance within the fold (20)], and that not all possible folds will necessarily have the thermodynamic attributes for an effective binding site. If this were the case, folds with little or no potential for a binding site, although possibly appearing at various stages of evolution, may not survive the selection process. The relative ability to design function into novel protein folds (33–35) rather than redesigning function at existing active sites (36–39) may provide significant insight from which to resolve this issue.

Methods

Generation of the Native State Ensemble.

An ensemble of conformational states for each protein was generated by using the COREX algorithm (12, 14, 15, 40). The individual conformations are generated by treating contiguous groups of residues as folding units and generating states where each unit is either folded or unfolded. By systematically varying the boundaries of the folding units and by sampling all possible combinations of multiple groups being unfolded simultaneously, an exhaustive enumeration of conformations is generated. As described in a recent review (16), when a region is considered as unfolded, it is not treated in explicit structural terms. Instead, the average free energy of unfolding that segment is calculated by using a surface area-based parameterization. The Boltzmann weight of each state [K_i = exp(−ΔG_i/RT)] is determined from the calculated Gibbs energy, which has been calibrated previously and tested extensively (41–47). The probability of each state i is determined by P_i = K_i/Σ_iK_i, where summation is over all states in the ensemble.

Calculation of the GCR.

A residue-level description of the stability of the ensemble, which is facilitated through a quantity known as the residue-specific free energy, was defined as ΔG_f,j = −RT × ln κ_f,j = −RT × ln(ΣP_f,j/ΣP_nf,j), where ΣP_f,j and ΣP_nf,j are the summed probabilities of states in which residue j is folded and unfolded (i.e., nf, nonfolded), respectively.

Thermodynamic cooperativity between any residue pair in a protein can be calculated by expanding the above equation to account for changes observed in the folding status of residue j upon an energetic perturbation applied to any other residue k. Specifically, for each state for which residue j is in a folded conformation, a perturbation free energy, Δg^pert,k, is applied which stabilizes that state. As a result, the ensemble of states will be redistributed in a specific way, and the response of the ensemble will provide direct access to the coupling between that residue and every other residue. For any residue j, the effect of an energetic perturbation at k can be calculated as

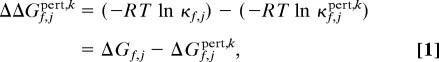where ΔG_f,j^pert,k corresponds to the stability of residue j upon introducing the energetic perturbation to all states in which residue k is folded. Considering that cooperativity between any residues pair is not necessarily bidirectional (12, 22, 48), the above equation is modified to include the reciprocal effect as well:

Shown in Fig. 2A is thus the bidirectional cooperativity of each residue pair (Eq. 2) for the DHFR protein.

To further quantify the importance of any particular position in a protein structure in its ability to transduce structural and energetic perturbations, we systematically substitute each residue to an alanine. Those residues that already were alanine in the host protein were replaced by glycine. The influence of a mutation applied to any residue l on the cooperativity between any residue pair j and k can then be determined by theq difference in cooperativities as calculated by Eq. 2 (ΔG_j,k^pert − ΔG_j,k^pert,mut,l). The overall effect of a mutation at residue l on the cooperative network of a protein, defined here as the global cooperative response (GCR), can then be assessed by GCR_l = Σ_jΣ_k|ΔΔG_j,k^pert − ΔΔG_j,k^pert,mut,l|, where the summations are over all residues in the protein.

Abbreviations

DHFR

dihydrofolate reductase

cDHFR

chicken DHFR

eDHFR

E. coli DHFR

GCR

global cooperative response.