A Free-Rotating and Self-Avoiding Chain Model for Deriving Statistical Potentials Based on Protein Structures

Abstract

Statistical potentials have been widely used in protein studies despite the much-debated theoretical basis. In this work, we have applied two physical reference states for deriving the statistical potentials based on protein structure features to achieve zero interaction and orthogonalization. The free-rotating chain-based potential applies a local free-rotating chain reference state, which could theoretically be described by the Gaussian distribution. The self-avoiding chain-based potential applies a reference state derived from a database of artificial self-avoiding backbones generated by Monte Carlo simulation. These physical reference states are independent of known protein structures and are based solely on the analytical formulation or simulation method. The new potentials performed better and yielded higher Z-scores and success rates compared to other statistical potentials. The end-to-end distance distribution produced by the self-avoiding chain model was similar to the distance distribution of protein atoms in structure database. This fact may partly explain the basis of the reference states that depend on the atom pair frequency observed in the protein database. The current study showed that a more physical reference model improved the performance of statistical potentials in protein fold recognition, which could also be extended to other types of applications.

INTRODUCTION

Knowledge-based statistical potentials, together with semiphysical energy functions and optimization-based potentials, have been widely used in protein structure-related studies. These types of energy functions have been generated for numerous purposes, including fold recognition (1–10), structure prediction (11–16), model validations (17–19), and docking and binding studies (20–23). Knowledge-based statistical potential can be categorized on the basis of different aspects: residue level potentials (1,2,24–30) versus atomic level potentials (3,5,7,8,31–34) or contact-based potentials (4,8,10,24) versus distance-dependent potentials (1–3,7,25). The potential-of-mean-force method involves the derivation of a statistical potential from the atomic spatial distribution in the database by using the Boltzmann formula (25,35). To extract an accurate energy function, the spatial distribution without any atomic interactions, which is considered as the reference state, needs to be defined. In addition, comparison of the real distribution of the atom pairs and the reference state allows for the calculation of the energy functions for all atom pairs. The reliability of this method, however, has been questioned as a result of ambiguous theoretical basis (36–38). The most serious problem, which separates the energy functions from the physical interactions, is that the spatial distribution of an atom pair observed from the database relates to other factors in addition to the interaction within this pair including the geometric confinements and the interactions from other atom pairs in its potential (37). For example, the energy function between two Cα atoms may involve the interaction between the nearby atoms N and O. In this case, the sum of these energy functions may not accurately describe the free energy of the system even with a strictly noninteracting reference state. Thus, defining a reference state that includes the interactions from nearby atoms will render the energy function of every pair more independent and, thereby, more accurate.

Reference states based on the quasi-chemical approximation (5,24), which has been used to extract the Miyazawa-Jernigan potential and knowledge-based potential (KBP), are generally accepted and have been carefully studied (39). Some other reference states, such as Sippl's uniform density reference state (26) and RAPDF (residue specific all-atom probability discriminatory function) (3), were based on the same theoretical assumption as the quasi-chemical reference state. In this kind of reference state, the expected number of atom pairs in a given distance shell is equal or proportional to that observed in the database regardless of atom types. These reference states are referred to as the database-dependent reference state, which implicitly assume that, on average, the atoms in proteins have little or no interaction with each other.

Another newly-developed physical reference state is a distance-scaled, finite ideal gas reference state (DFIRE) (7,40). This reference state differs from previously described states via the use of a distinct physics model that assumes the spatial distribution in the reference state should be scaled as r^α. Additionally, this method, which partially cuts the long-range tail caused by the statistics bias, assumes that all atom pairs beyond a distance cutoff are noninteracting. The DFIRE potential exhibits an improved performance in fold recognition by the unique physical reference state and the use of the cutoff.

Nevertheless, these two types of reference states suffer from different problems. The reference states based on atom spatial distribution involve some energy information and, thus, cannot reflect absolutely zero interaction. For example, the extremely low frequency of database-dependent reference state from 0 to 2.5 Å, which may indirectly decrease the score for atom collision, is attributable to the van der Waals force between atoms. On the other hand, the distance-scaled, finite ideal gas reference state neglects to incorporate factors other than interaction that contribute to the spatial distribution of the atoms in the reference state. As the atoms in proteins are not weakly interacting particles in the gas phase, the proximity of two atoms may not result from an attractive interaction but from a bond restriction. Moreover, the influence from nearby interactions cannot be eliminated from the DFIRE potential. Thus, this potential differs from the actual physical interaction. The chain connectivity and the nearby interactions represent intrinsic constraints, which may partially determine the distance distribution for the atom pairs and should be involved in the reference state. Therefore, a more reasonable reference state to extract the actual physical interaction is a chainlike model (41).

A Gaussian random coil reference state was applied to calculate the contact probability in proteins (39), but the real contact probability between atom or residue pairs is related to the sequence distance. As a result, a more precise chainlike reference state should be a sequence distance-dependent model. In the current work, two different sequence distance-dependent chainlike reference states were developed to exclude the intrinsic constraints and to simultaneously achieve zero interaction. The potentials based on these two states were applied to the fold recognition decoy sets. These two reference states implicitly achieve our two goals simultaneously for atom pairs with long sequence distance. In addition, these reference states deal with atom pairs with short sequence distances in different ways: 1), the first reference state is the free-rotating chain reference state that results in a local noninteracting model while maintaining the geometric restrictions in protein structures to achieve local zero interaction; and 2), the second reference state is the self-avoiding chain reference state that incorporates the van der Waals interaction into the local model to partially exclude interference of other atoms from the pairwise potential.

METHODS

Factors included in the reference state

Each polypeptide backbone is restricted by bond length, bond angle, and bond rotation. In a chain model, the spatial distance of two atoms depends on their sequence distance or sequence length. Here, the sequence length was measured by the number of bonds between these two atoms, and sequence distance was measured by residues. For a given atom pair with fixed sequence distance, the reference state is a chain that links the two atoms with the same geometric restriction as the peptide, assuming that the atoms on the chain have no interaction with each other. Due to the solvent confinement and crystal packing effect, the chain linking the atom pair should be depicted as a chain confined in a finite region. To simplify this model, we defined the reference state as a chain confined in a hard sphere. For the two atoms being studied (the two terminals of the chain), one was defined as fixed in the center of the sphere and the other as floating in the sphere. Under this assumption, two different circumstances can occur:

1. When the sequence distance is short enough to guarantee that the farthest end-to-end distance is less than the radius of the sphere and that the solvent confinement cannot influence the structure of the chain, the two terminals of the chain are considered a local atom pair.

2. When the sequence distance is long enough and the distance distribution in the sphere is not influenced by bond restriction, the two terminals of the chain are considered a nonlocal atom pair.

After the delimitation of the two circumstances (see Supplementary Material), we defined the atom pairs with sequence distances <5 as local atom pairs and all other atom pairs as nonlocal atom pairs. Each of these cases warrants its own statistics and reference states. The local reference state is a sequence distance- and spatial distance-dependent reference state while the nonlocal reference state is only spatial distance-dependent. These two states generate two distinct potentials, the nonlocal potential (sequence distance-independent potential) and the local potential (sequence distance-dependent). The full potential is the sum of these two parts.

This model has taken the bond restriction and the solvent confinement into account. Under these circumstances, the expected distance distribution for nonlocal atom pairs is related to the square of the distance and is independent of the sequence length. As the atoms in proteins are not weakly interacting particles, interaction between atoms could partially influence the spatial distribution of other atoms. Accepting the two factors described above causes the extracted energy function for a given atom pair to incorporate the interaction from other atom pairs. Here, we defined orthogonal potential as the potential in which the energy function for each atom pair does not include the influence or energy from other pairs. In addition, the process to generate the orthogonal potential is termed “orthogonalization.” To achieve orthogonalization, the influence from the other atoms should be precluded as much as possible; however, the depiction of all interactions from other atoms in a reference state for pairwise potential is difficult. Thus, the van der Waals force, which is the interaction that all varieties of atom pairs share, is incorporated. This interaction is simplified to a short-range hard sphere interaction. When an atom is fixed, the atoms with a few bonds linked to the fixed atom are obliged to remain nearby and occupy space via their pump volume, and thus, little neighboring space remains available to other atoms. Consequently, the atoms with longer sequence distances are more inclined to occupy the space in a farther distance bin so as to avoid those local atoms. In this case, the volume of remaining space (the nonlocal reference state) to locate the nonlocal atom would change more notably than the square of distance.

Consequently, if the expected distance distribution is scaled as the square of the distance and the method was applied to atoms on a self-avoiding lattice chain, the energy function for the hard sphere potential would have a long tail. Therefore, for nonlocal atom pairs, the self-avoiding effect should be taken into account in the reference state. However, it should be noted that the self-avoidance between the two atoms under examination is part of the potential and cannot be incorporated into the reference state.

The confined free-rotating chain state

Based on the factors presented above for the local reference state, the bond restrictions, including bond length and bond angle, primarily determine the expected distance distribution for local atom pairs. Local self-avoidance is not included. In the nonlocal reference state, the intensity of self-avoidance influenced the distance distribution. Locally, the chain is a short free-rotating chain without solvent confinement whose end-to-end distance distribution obeys the Gaussian distribution. Therefore, the expected probability of the atom pair i and j between the spatial distances r−Δr and r+Δr is governed by the algebraic expression

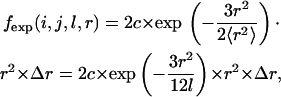(1)

where c is the normalization constant, which does not affect the distribution factually, l is the sequence length of pair i and j with a sequence distance (d) <5, and 〈r²〉 is the root mean-square end-to-end distance of reference state (RMSED) determined by the sequence length l. With the backbone geometric features, we found that 〈r²〉 ≈ 6l (see Supplementary Material). As the RMSED is determined by the sequence length, the distance distribution varies for different sequence distances for a given atom pair.

In the nonlocal range, the probability is virtually independent of the sequence distance and, thus, could be simplified as a spatial distance-dependent function. In DFIRE (7), this probability was assumed to be directly proportional to the spatial distance to the power of 1.61 (a fitted value). In our method, an atom is fixed in the center of the sphere. Therefore, the possibility should be directly proportional to the square of the spatial distance without the self-avoiding effect; however, the self-avoiding effect, which acts like a repulsive force, renders the same exponent parameter >2. Therefore, the probability of atom pairs between r−Δr and r+Δr is

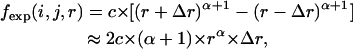(2)

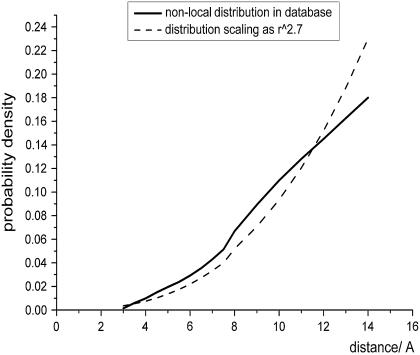
where c is the normalization constant and the value of the power exponent α is the power parameter >2 that represents the intensity of nonlocal self-avoidance and is obtained from the scaling behavior of the atom distance distribution in the database. While an α-value approximating two indicates that the self-avoiding effect of other atoms does not considerably alter the end-to-end distance distribution, an α-value >2 indicates that the exclusive volumes of other atoms occupy a large proportion of space that could have contained the nonlocal atoms. These effects influence the distance distribution of nonlocal atom pairs and can be obtained from protein structure database analysis. To evaluate the self-avoiding effect on other atoms, we fit the distribution to Eq. 2 and only applied the probability distribution between 3 and 15 Å as the probability densities within 3 Å are attributable to the van der Waals potential between the two atoms under examination, which is not involved in the reference state. Moreover, the linear relation between the logarithm of the expected probability and the logarithm of the distance only occurs when the spatial distance is >3 Å. Thus, the value of α from the distribution beyond 3 Å (Fig. 1) can be determined from the distance distribution of nonlocal pairs:

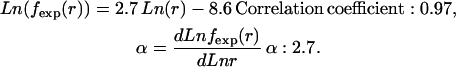Thus, we assigned the value of α to 2.7, and 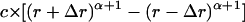was applied as the expected probability of nonlocal reference state. The values from 2.2 to 3.5 were also used to verify that the potential performs best at 2.7 and is not much sensitive to the parameter change.

FIGURE 1.

Scaling behavior of the distance distribution of nonlocal atom pairs.

In the confined free-rotating chain state, the nonlocal spatial distribution is similar to the distribution in the database (Fig. 1), while the distance distribution predicted by a Gaussian distribution does not coincide with the actual distribution in proteins as it fails to incorporate local self-avoidance in the reference state. Although self-avoidance is regarded as a nonlocal effect in general, ignoring it would cause a deviation from the actual distribution. Additionally, a local free-rotating reference state cannot orthogonalize the local potential. To study the relationship between the self-avoiding effect and the local potential, we applied a new method to establish a completely self-avoiding chain reference state.

The confined self-avoiding chain state

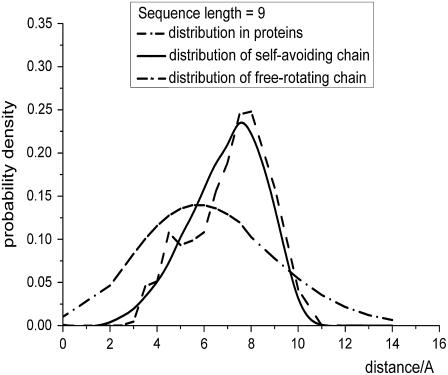
To thoroughly incorporate the self-avoidance in the second reference state (both local and nonlocal), we constructed a database of artificial peptides via Monte Carlo simulation. At each sequence length, we generated 200,000 self-avoiding chains for each sequence length from 3 to 100 with different backbone dihedral angles (different conformations). In these self-avoiding chains, the hard-sphere contact radii of heavy atoms was used in some classical work (42) and was defined as collisions that occur when two atoms are closer than 2.75 Å. Here, the collision distance is set slightly less than the average distance to include the possibility of hydrogen bonds and weak collisions. The bond lengths and angles used in simulation are the same as the parameters in the free-rotating chain (see Supplementary Material). Solvent confinement was defined as a sphere with a radius equal to 20 Å, which contains the chain (also applied to the free-rotating chain). This definition does not affect the performance of the potential as the local distribution is nearly free of the solvent confinement. A strict self-avoiding chain completely excludes the existence of atom collision and strong hydrogen bonds. The collision and hydrogen bond between the two terminals (the atoms in question), however, are included in the potential, and this collision is not included in the reference state. Consequently, we suppose that the fixed terminal cannot collide with all the atoms on the chain, including the floating terminal. This assumption implicitly permits the collision and hydrogen bonds between the atoms and the fixed terminals, and the other atoms on the chain, including the floating terminal, must avoid each other. After simulation, the end-to-end distance distribution of this self-avoiding chain is determined, and this distribution is used as the new expected distance distribution. Comparison of the distribution in protein structures and those expected by the two local reference states (Fig. 2) indicates that the self-avoiding chain assumes a much better fit with the protein structures as this chain takes more properties of the real polypeptide into account.

FIGURE 2.

Comparison of the spatial distribution of local atom pairs derived from databases, distribution derived from self-avoiding chain simulation, and distribution predicted by free-rotating chain, when the sequence lengths between the atom pairs were fixed to 9.

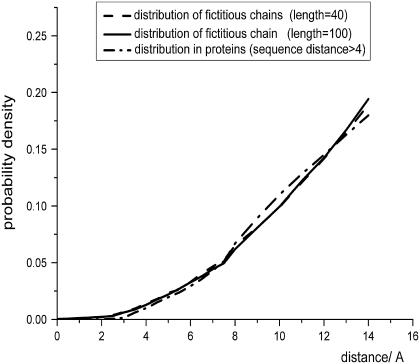
In addition to the similarities of the distance distributions for local atom pairs, similarities between the self-avoiding chain and the proteins exist for the nonlocal pairs as well (Fig. 3). In the self-avoiding chain, the sequence length does not influence the nonlocal distribution curve, and the scaling behavior is similar to that observed from databases. Both curves share the same scaling behavior after 3 Å. This similarity explains why database-dependent reference states (e.g., KBP and RAPDF) also produce decent potentials even though these reference states do not explicitly claim zero interaction and orthogonalization of their potentials. In the simulated self-avoiding chains, the natural logarithm of the expected probability is also linearly proportional to that of spatial distance,

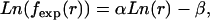where α ranges from 2.4 to 2.8 stochastically with correlation coefficients >0.98 when the sequence length of the chain is no less than 40. This finding coincides with the 2.7 derived from the nonlocal distribution in the database. These two reference states share the same nonlocal distribution (α 2.7), and thus, the two reference states have the same nonlocal potential. The two local potentials based on the two reference states were named free-rotating chain-based potential (FRCBP) and self-avoiding chain-based potential (SACBP).

FIGURE 3.

Comparison between the spatial distribution of nonlocal atom pairs and the distribution derived from self-avoiding backbone simulation (sequence lengths of 40 or 100).

In these reference states, the expected number of pairs of atoms i and j between the spatial distances r−Δr and r+Δr under different circumstances (local or nonlocal) is derived from the reference state. The knowledge-based potential functions can be written as

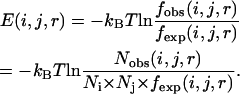(3)

Cutoff of the potentials

Most knowledge-based potentials, including the potential derived from the Sippl's approximation (25), the RAPDF (3), the KBP (5), and the DFIRE (7), have a tail when the distance is >10 Å. The DFIRE potential performed better on the decoy sets by using 15 Å as a cutoff and setting the potential before 15 Å as

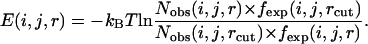(4)

In our method, the bin between 14 and 15 Å was also selected as the cutoff. Thus, for some local atom pairs with a maximum distance of <14 Å, the greatest distance bin was employed as the cutoff distance. Theoretically, interactions beyond 10 Å quickly approach zero, and the tail of the potential in this long range may, in fact, camouflage or exaggerate the real interactions between the atoms. This long-range tail may be attributed to different reasons. The local atom pair at a given sequence distance always corresponds to a secondary structure. The high frequency of secondary structures renders the chains between atomic pairs unlikely to exist as an extended state, and thus, the low frequency in long-distance bins generates an energy platform in energy function. For nonlocal atom pairs, the potential between atoms in two hydrophobic residues may have either a repulsive or an attractive tail after 10 Å, even if no electrostatic interaction exists (37). Generally, the long-range tail of local and nonlocal potentials both begin from 8 to 10 Å. Therefore, in our potential (both local and nonlocal), we calculated the energy within 10 Å by Eq. 4 and ignored the effects of the energy beyond 10 Å.

In other words, when the distance was <10 Å,

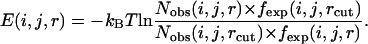When the distance was >10 Å,

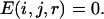The variation in the long-range potential improves the measurement in a decoy-independent manner and enhances the average Z-score of all the decoy sets by 5%. The bin width and cutoff have not been further optimized, although changes in these parameters may offer an enhanced performance of this method.

Training set and test sets

We employed the structural database used in the DFIRE method (7). This database was based on databases selected by Hobohm et al. (43) and contained 1011 proteins with resolution <2 Å and sequence identity <30%. To assess the potential, three groups of decoy sets were tested:

1. The first group was comprised of five single decoy sets from the Prostar website (http://prostar.carb.nist.gov) including: misfold (44), asilomar (45), pdberr (46), sgpa (46), and ifu (47). In the “Asilomar” decoy set, the native structure of protein NDK was replaced by the structure of PDB code 1nue (48). Eight decoys were excluded from the original set due to mismatched sequences: crabpi_vriend, edn_biosym, edn_weber, mchpr_vihinen, ndk_abagyan, ndk_vihenen, p450_abagyan, p450_weber (7).

2. The second group was comprised of five multiple decoy sets (4state_reduced (49), fisa (12), fisa_casp (12), lmds (50), and lattice_ssfit (51)) from the Decoys ‘R’ Us website and included 32 proteins.

3. The third group comprised a multiple decoy set Rosetta (52) from the Baker laboratory website. This set included 41 proteins with corresponding x-ray crystal structures.

Here, we compared FRCBP and SACBP with three atomic detailed potentials that have a physical reference state (RAPDF, KBP, and DFIRE) and two other potential with different methods (McConkey's potential and DFIRE-side-chain center-of-mass (SCM)).

Atom types and bin procedure

FRCBP and SACBP only include the interaction between heavy atoms and use the residue-specific heavy atom type to distinguish different atoms. Thus, 167 types of atoms are taken into account.

In the bin procedure, we divide the distances into 0.5 Å bins from 2 Å to 8 Å, into 1 Å bins from 8 Å to 15 Å, and included the distances <2 Å in a separate bin. The interaction in each bin was obtained using Eq. 4. When the frequency of the atom pair i, j in a distance bin was zero, the value of the interaction was set to 10 k_BT to ensure that these “impossible” interactions have higher potential than possible collisions. Additionally, we excluded the extremely local contacts (including the contacts between atoms within the same residue or in neighboring residues) from the scoring, as a reference state based merely on the backbone geometrical features may not be accurate in these circumstances and these contacts do not contribute much to the folding.

RESULTS

Decoy group 1 (single decoy sets)

Publicly available decoy sets were used to test FRCBP and SACBP. In the first group, each native structure has one or more incorrect decoys and different potentials were applied to discriminate the native ones. For the first four decoy sets in this group, most atom-level potentials achieved 100% correct identification. The fifth decoy set “ifu” (independent folding units) was more difficult as the correct conformations of these isolated peptide fragments were differentiated by a small number of atom pairs (3). The best performance on this set was previously achieved by the Ron Elber's potential T32S3 (10) with an 80% discrimination rate (or success rate), while the other three potentials, which were made by similar methods, only achieved a success rate of 71% on average. In this decoy set, the performance of FRCBP was slightly better than the other potentials with an 82% discrimination rate, while the 75% success rate of SAVBP was similar to the other potentials (Table 1).

TABLE 1.

Discrimination rate by different potentials for the first group decoy set

Source	RAPDF*	KBP*	DFIRE (7)	T32S3 (10)	FRCBP	SAVBP
Misfold	100%	100%	100%	100%	100%	100%
Pdberr, sgpa, and asilomar	100%	100%	100%	NA	100%	100%
Ifu	73%	75%	75%	80%	82%	75%

^*These results were calculated based on the same database as DFIRE to compare the performance of RAPDF, KBP, and DFIRE (7).

Decoy group 2 (Decoy ‘R’ Us)

The second group of decoy sets is a group of multiple decoys, which are widely used in the assessment of potentials. In multiple decoy sets, each native structure has a set of approximate conformations. The two primary criteria to evaluate the ability of a potential to discriminate the native structures are success rate and Z-score. The success rate indicates the percentage of first-ranked native structures in the decoy sets. The Z-score is defined as 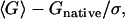where 〈G〉 and σ denote the mean and standard deviation of the free energy values of the decoys, and G_native denotes the free energy of the native structure. Here, we did not include the quaternary structures in our scoring to facilitate comparison with the original atom-level potentials that did not incorporate the quaternary structures. The performance of FRCBP was slightly better than other potentials with a better success rate of 87.5% (28/32) and a comparable average Z-score of 4.5. The structures, which were not identified correctly, include: 1fc2(fisa), 1bba(lmds), 1fc2(lmds), and 3icb(4state). The performance of SACBP was comparable to the other potentials with a Z-score of 4.7 and a success rate of 81.3% (26/32, Tables 2 and 3).

TABLE 2.

Targets in the second group decoy set missed by FRCBP and SACBP

Source	Target (PDB ID)	Target missed by FRCBP	Target missed by SACBP
4state	1ctf, 1r69, 1sn3, 2cro, 3icb, 4pri, 4rxn	3icb	3icb
Fisa	1fc2, 1hdd-C, 2cro, 4icb	1fc2	1hdd-C, 1fc2
fisa_casp	1bg8-A, 1bl0, 1jwe
Lmds	1b0n-B, 1bba, 1fc2, 1ctf, 1dtk, 1igd, 1shf-A, 2cro, 2ovo, 4pti	1bba, 1fc2	1bba, 1fc2
lattice_ssfit	1bco, 1ctf, 1dkt-A, 1fca, 1nkl, 1pgb, 1trl-A, 4icb

TABLE 3.

Success rates and Z-scores for the second group decoy set

	RAPDF*		KBP*		DFIRE (7)		FRCBP		SACBP
Source	Z-score	Rank 1	Z-score	Rank 1	Z-score	Rank 1	Z-score	Rank 1	Z-score	Rank 1
4state	3.0	7/7	3.2	7/7	3.5	6/7	3.4	6/7	3.4	6/7
Fisa	1.3	1/4	1.2	0/4	4.8	3/4	3.1	3/4	2.7	2/4
fisa_casp	4.1	3/3	2.1	0/3	5.4	3/3	5.8	3/3	5.6	3/3
Lmds	−0.5	3/10	0.5	3/10	0.9	7/10	3.7	8/10	3.8	7/10
lattice_ssfit	7.2	8/8	6.6	8/8	9.5	8/8	6.7	8/8	7.5	8/8
Total	2.8	22/32	2.9	18/32	4.5	27/32	4.5	28/32	4.7	26/32

^*These results were calculated based on the same database as DFIRE to compare the performance of RAPDF, KBP, and DFIRE (7).

The incorrect sets included the four decoy sets missed by FRCBP and 1b0n-B in lmds and 1hdd-C in fisa. Among these structures, the performances of SACBP on 3icb, 1b0n-B, and 1hdd-C were much better with Z-scores of 2.0, 2.2, and 2.5 and ranks of native structures of 2, 2, and 4, respectively. The other three proteins are all short chains that other potentials also failed to recognize without quaternary structures. The recognition of the local conformations may be attributed to their contacts with larger subunits.

Decoy group 3 (Rosetta decoys)

The proteins in the third group are associated with ∼1000 alternative structures (except 1acf with 2000 decoys) generated by the Rosetta structure prediction method (Table 4). In this group, the FRCBP and SACBP outperformed all the other atomic detailed potentials. The success rate of SACBP was 78% while the percentage of decoy sets with a Z-score of >1 was 93% (Table 5). The nine missed decoys include 1ajj, 1cc5, 1gvp, 1msi, 1nxb, 1orc, 1ptq, 2erl, and 2fdn. The success rate of FRCBP was 76% while the missed decoys include the nine presented above and 1tul.

TABLE 4.

Targets in the third group decoy set missed by FRCBP and SACBP

Source	Target (PDB ID)	Target missed by FRCPB	Target missed by SACPB
Rosetta	1aa2, 1acf, 1aho, 1ajj, 1bdo, 1cc5, 1csp, 1ctf, 1eca, 1erv, 1gvp, 1hle, 1kte, 1lfb, 1lis, 1mbd, 1msi, 1mzm, 1nxb, 1orc, 1pal, 1pdo, 1pgx, 1ptq, 1r69, 1ris, 1tul, 1utg, 1vls, 1who, 2acy, 2erl, 2fdn, 2fha, 2gdm, 2sn3, 4fgf, 5icb, 5pti	1ajj, 1cc5, 1gvp, 1msi, 1nxb, 1orc, 1ptq, 1tul, 2erl, 2fdn	1ajj, 1cc5, 1gvp, 1msi, 1nxb, 1orc, 1ptq, 2fdn, 2erl

TABLE 5.

Success rates and Z-scores for the third group decoy set

	RAPDF*		KBP*		DFIRE (7)		FRCBP		SACBP
Source	Z-score	Rank 1	Z-score	Rank 1	Z-score	Rank 1	Z-score	Rank 1	Z-score	Rank 1
Rosetta	3.2	24/41	3.2	23/41	3.9	31/41	4.9	31/41	4.7	32/41
2 and 3	3.0	46/73	3.1	41/73	4.1	58/73	4.7	59/73	4.7	58/73

^*These results were calculated based on the same database as DFIRE to compare the performance of RAPDF, KBP, and DFIRE (7).

DISCUSSION

Comparison with other potentials

McConkey's potential (8) is an atom-atom and atom-solvent contact scoring function that performs well on the Decoy 'R' Us and Rosetta decoy sets. We tested FRCBP and SACBP on the reduced multiple decoy sets used in their assessment (see Table 1(a) in Supplementary Material). Our two potentials slightly outperformed McConkey's potential for Z-scores with a similar success rate. The DFIRE-SCM (29) is a coarse-grained potential based on the distance-scaled, finite ideal gas reference state with 20 residue types located at the side-chain center of mass (SCM). The performance of this potential on groups 2 and 3 was even better than DFIRE-all-atom and was comparable to SACBP and FRCBP (see Table 1(b) in Supplementary Material).

In comparison with the atom-level potentials that are based on physical reference states, the FRCBP had the highest success rate and average Z-scores of all of these potentials. The SACBP is performed better than DFIRE and only slightly worse than FRCBP with respect to Z-scores. The ability of FRCBP and SACBP to recognize native structures is comparable to those potentials, which have been considered to perform well. The two physical reference states presented here yield good performances with reasonable physical models. Comparing FRCBP and SACBP, FRCBP performed slightly better even though the latter orthogonalizes the local potential. Our attempt to involve the local self-avoidance did not, however, improve the performance significantly. There are two possible reasons:

1. The potential of the mean force method could be based on nonorthogonal pairwise potential and, thus, does not require orthogonalization;

2. The orthogonalization is not thorough enough to cause an effect.

Improvement of the potentials would occur only when most interference has been eliminated without the loss of true potential.

Comparison between the local and nonlocal potentials

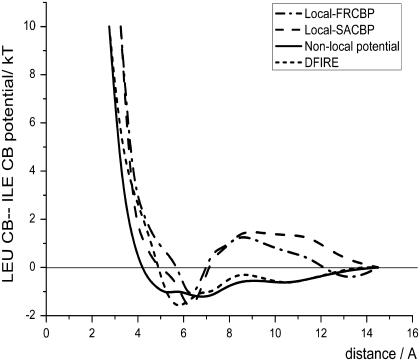
As the real physical interaction between two atoms is a function of the spatial distance (except when the distance is extremely short or the interaction also relates to orientation), the potential of a given atomic pair should be independent of the sequence distance. That is, the local atomic pairs and the nonlocal atomic pairs should have the same potential in the same distance bin. The local potentials with different sequence distances are distinct from the nonlocal potentials for two reasons. First, the energy functions for some atom pairs suffer from the lack of statistics. Second, the local potential might incorporate more sequence information, and this difference causes the potential to differ from the real physical interaction. The high frequency of regular secondary structure in proteins results in the high frequency of local atom pairs at a fixed distance. The potential well generated by this high frequency may be partially attributed to the stability of the secondary structures. This stability may deepen the minimum on the energy curve. As a result, the fluctuations of local energy functions are generally more drastic than those of nonlocal functions. Comparing to DFIRE, a potential derived from the same database, our nonlocal potential was smoother while the local potentials (both FRCBP and SACBP) seemed to amplify the fluctuation on DFIRE (Fig. 4). Another significant difference between these two local potentials and DFIRE is that the local potentials only had one obvious minimum. In DFIRE, the two minima could be attributed to the two leading types of secondary structures; however, in local FRCBP and SACBP, the minimum corresponding to the β-sheets was smoothed by the local reference states. In fact, as the nonlocal interactions always dominantly contribute to the stability of β-sheets, the local potential should not possess a minimum corresponding to β-sheet.

FIGURE 4.

Distance dependence of the nonlocal potential, local FRCBP (sequence distance of 4), local SACBP (sequence distance of 4), and DFIRE between C_β atoms in ILE and LEU residues.

α-value

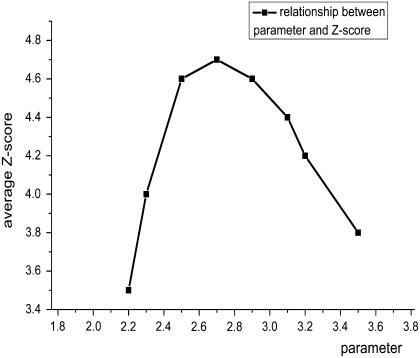
In Eq. 2, the exponent α is a key parameter for the nonlocal potential. From the linear fit statistically derived from the database, we set the α-parameter to 2.7 to match the distribution in proteins. This assumption was also supported by our simulation using a self-avoiding chain. The extent that the performance of the nonlocal potential relies on the α-value remains unknown. In addition, it is not known whether the parameter that fit the statistics best would render the best performance. This question is important for determining whether a more accurate reference state results in a more accurate potential. Therefore, α was varied from 2.2 to 3.5 to study the performance of the potential (Fig. 5). To quantify this relationship, the average Z-scores of the multiple decoy sets were applied as the criteria for the performance of the potential. These new nonlocal potentials cooperated with the local potential FRCBP in scoring. No difference occurs when the new potentials were used with the SACBP. The best performance coincided with the most reasonable parameter, but the performance did not rely heavily on the value of parameter α. When α lies in the range between 2.3 and 3.3, the average Z-score is >4 (85% of the highest Z-score). Conversely, the dependence of DFIRE on α was stronger as the Z-score declined to 3.88 (86%) as α decreased from 1.61 to 1.50. The weaker reliance on this parameter is attributed to the influence of the local potentials, which were derived from theoretical calculations (FRCBP) or Monte Carlo simulation (SACBP).

FIGURE 5.

The average Z-score of the second and third groups of decoy sets using different α-values.

Additionally, the value of α is a symbol of the self-avoiding effect. At an α of 2.7, the reference state has incorporated nonlocal self-avoidance and ruled out the influence from the potential. At an α of 2, the reference state did not include this effect and incorporated the influence of avoidance in the potential. In the case presented here, when α is 2, the average Z-score is 2.4, which is less than for all other potentials. Therefore, the incorporation of nonlocal self-avoidance in the reference state obviously improves the performance of the potential, and the attempt to orthogonalize the nonlocal potential seems successful.

Comparison of two types of reference state

The spatial distribution predicted by the self-avoiding chain is similar to the distribution obtained from our database (Fig. 2); however, several details indicate that the distribution observed in proteins might not represent a noninteracting state. We focused on the spatial distribution of atom pairs with a sequence length of 9. The distribution curve of the self-avoiding chain was smoother than that of proteins, since the distribution curve of the self-avoiding chain reflects one probability barrier and that of proteins reflects three barriers. The other two barriers correspond to the structure features in the proteins. An artificial local potential was used to represent the mean of all pairwise interactions from the distribution regardless of atomic types while the self-avoiding chain was used as a reference state (see Fig. 1 in Supplementary Material). On the distribution curve for proteins (Fig. 2), the probability barrier between 2.5 and 3.5 Å generates a potential minimum in this bin, which coincides with the occurrence of a hydrogen bond. The probability barrier between 4 and 5 Å causes a potential well, and this distance relates to the occurrence of α-helices as the distance between two atoms on an α-helix with a sequence length of 9 is ∼4.5. As a result, the existence of these probability barriers is attributed to the protein structure preference and also reflects the frequency of α-helix and hydrogen bonds; <3 Å indicates a van der Waals interaction at short range. Thus, the distribution at a certain length is not completely independent of energy, although the distribution is independent of atomic types. The database-dependent reference states in many methods may not be an absolute noninteracting state. However, potentials based on database-dependent reference states exhibits an acceptable performance, as the mean interaction is relatively insignificant compared to the interaction of a given atom pair.

Incompatibility in reference state

Even though our work has incorporated new factors into the reference state and the performance on protein fold recognition was acceptable, our theory also deliberately neglected some important factors to make the model understandable. The solvent atoms were simplified to a hard sphere, which indicates that the potential cannot include the interaction with solvent like in other previous studies (8,53). In addition, the influence from quaternary structures or the environment, which might contribute to the local conformation, is not considered (8,53). The potentials are only dependent on distance and have no orientation information (54,55). The performance of these two potentials may be better due to the combination of physical effective energy (56). Incorporating these factors may improve the potentials both theoretically and practically. Besides, our attempts to include some neighboring influences in the reference state to eliminate them from potentials were not particularly successful. The potential for an atom pair is still the combination of the true potential and statistical bias and does not reflect the real interaction independent of other pairs (37). To generate an orthogonal potential, the reference state should consider the statistical bias or the outside influence on each atom pair. A uniform density reference state may cause difficulty in achieving this goal. Perhaps, only the reference state involving detailed information about the atoms is able to exclude influences such as interactions with other atoms, distribution inclination, etc. For example, atoms in hydrophobic residues are often buried in the center of proteins, and this location may result in potentials with a repulsive tail in the long range (3,7,37). An absolutely orthogonal potential requires the reference state for atoms in hydrophobic residues to have a hydrophobic distribution inclination, and only with this reference state can the potential cut the long-range repulsive tail.

Such a reference state implicitly contains some energy information and thus cannot reflect absolutely zero interaction. If the reference state of hydrophobic atoms is a peptide inclined to cluster at the center, the reference state has inevitably possessed interaction with solvent. Therefore, the reference state focused on orthogonalization may not be strictly zero interaction at the same time. As a typical example, the self-avoiding chain reference state, which intends to orthogonalize the local potential, certainly contains a little more energy information than the free-rotating chain. Generally, the reference state based on the distribution observed in proteins may do more in orthogonalization and less in zero interaction. From this point of view, orthogonalization and zero interaction cannot be completely achieved at the same time. In our work, we attempted to maximize the orthogonalization and zero interaction as much as possible. The results showed that the orthogonalization of the nonlocal potential obviously improves the performance of the potential. The FRCBP and SACBP achieved the highest Z-score when the parameter represented the intensity of the self-avoiding effect while the incorporation of the local self-avoiding effect did not significantly influence the behavior of the potential.

Compared with other physical reference states, SACBP and FRCBP identified more native structures with higher Z-scores as these two reference states are more complete and accurate. In fact, these two reference states do not differ and also have some relation with former physical reference states. A comparison between the reference states demonstrates that the physical model of finite ideal gas reference state is close to the free-rotating chain-based reference state while the self-avoiding chain reference state, which is derived from simulation, has some similarities with the database-dependent reference states.

These similarities could, in part, explain why the potential of mean force, an energy function quite different from the real physical interaction, could be widely applied to protein studies. Our study also shows that focusing on the orthogonalization as well as on zero interaction in the reference state improves the performance of potentials. Thus, a reference state, which can simultaneously achieve zero interaction and orthogonalization at the largest extent, would likely contribute to great progress in the study of statistical potential, fold recognition, and other protein.

SUPPLEMENTARY MATERIAL

A more detailed description of the method and comparison results with other potentials can be found on the journal website. The numerical values of the two potentials can be downloaded at ftp://mdl.ipc.pku.edu.cn/pub/software/SACBP-FRCBP/SACBP-FRCBP.tar.gz.