Abstract
Evolution of protein structure from random coil to native is first represented topologically by its time-dependent sequences of discretized Ramachandran basins occupied by successive backbone residues. Introducing energetic and entropic criteria at each instant of observation transforms the description from a structurally ambiguous topological representation to an unambiguous geometric picture of the folding process. The method is applied with success to folding of β-lactoglobulin, traditionally perplexing because of its reputed nonhierarchical folding pattern. This molecule passes through a stage, ca. 0.1 μs duration, of transient, “flickering” α-helical structure, until a bit of tertiary structure forms that stabilizes the system long enough to allow it to pass to its native β-sheet.
The changes in the dihedral angles Φ and Ψ at the α-carbon atoms of the peptide backbone dominate protein folding. Next in importance are the evolving interactions of hydrophobic and hydrophilic side chains. Dihedral angles of residues engaged in secondary and tertiary structures vary much more slowly than those not engaged in such structures. Also, thermalization times within a basin of attraction in the Ramachandran map of each residue are typically much shorter than the rate of interbasin hopping. These considerations led us to a coarse-grained, symbolic model of the evolving topology of proteins as they fold (1–3). By “topology” we mean a vector of assignments of Ramachandran basins (R-basins) within a model endowed with a grammar for pattern recognition and rules for the time-evolution of such patterns. This paper extends that method by connecting the topology at each step to a specific geometry, and applies it to the folding of a particularly perplexing example. The link to geometry is achieved by estimating energetic and entropic changes for the structures consistent with the pattern generated in each stage of the statistical search process, and then, at that stage, eliminating all but the most favored geometry on the basis of free energy change. The method is intended as a first step, to be followed by a more sophisticated treatment in which all thermodynamically probable structures are retained as long as they are viable. The method demonstrates the collapse-inducing nucleation and folding to the native state of β-lactoglobulin, the object of a most relevant experimental study that appeared as this work was being completed (4).
The heart of the topological model is the time-evolving “local topological map”, or LTM, a two-row matrix whose columns are the N amino acids of the sequence. The time-dependent first row of the matrix indicates in which of the allowed R-basins each successive residue lies at each time step; the (constant) second row indicates the hydrophobic, hydrophilic, or amphiphilic character of the side chain of each residue. This latter is used to evaluate the acceptability of nonbonded contacts to form a pattern that can be associated with a secondary or tertiary structure. Thus, the description is topological insofar as the torsional states are discretized according to their R-basins. In all but the simplest cases (such as bovine pancreatic trypsin inhibitor), the inference of structures from the LTM may depend on the algorithm one uses to read the LTM. This, plus the multiplicity of structures compatible with an assignment of basins, leads to an ambiguity both in how to carry out the next steps of the dynamics and in the structural interpretation of the LTM pattern. Here, we show how to remove this difficulty and apply the method to a protein whose folding process has been problematic, β-lactoglobulin.
The dihedral variables “flip” randomly at a mean rate representing local changes occurring at 1011 s−1, until a sequence of six or more residues occupy R-basins compatible with a significant structural feature, such as a loop, an α-helix, a β hairpin or reverse turn, a β strand, etc. The rates of the dihedral flips are drawn from a Gaussian distribution around their mean. The recognition steps occur every 64 ps, the time for a discernible minimal pattern to form (5). When a secondary structure feature is recognized, the hopping rate among R-basins slows for that group of residues to a mean 107 s−1, the typical time for local restructuring of a helix, as detectable in proton exchange. When a tertiary motif appears, the mean flipping rate slows further to 103 s−1, the NMR time scale (6). In our previous work, the accessible R-basins were allotted equal probability; here, we give them probabilities proportional to their areas at the energy of the lowest saddle in the R-map. As soon as a geometry has begun to establish itself, we use a more explicit free energy criterion, described below, for acceptance or rejection of each new, putative 64-ps-advanced form of the LTM.
Structures need not be perfect; in fact, some tolerance to errors, to both torsional incongruities and contact mismatching, is necessary if the model is to predict folding rates and native structures at this coarse level (1–3). In accord with nucleation theory (7) and inferences from experiments (8, 9), secondary and tertiary structures dismantle if they develop bubbles of “wrong” torsional states that constitute about 33% of the consensus window. The rate of each elementary folding step at the optimum tolerance level, together with microscopic reversibility, make it possible to use the detailed balance principle to infer topographies of mean thermalized optimal folding paths and a coarse description of the cross section of the protein's potential energy surface (3, 10).
The principal limitation preventing application of the topological approach to systems of over 100 residues has been the ambiguity arising from the multiplicity of possible geometric assignments consistent with a given vector of R-basins of the backbone. Here, we describe a method to eliminate that ambiguity and associate a single structure, or a set of possible structures in a rank order of probability. The method is based on thermodynamic considerations of the potential energy, both local and residue-residue interactions, and the configurational entropies of the R-basin sequences. To infer entropies from areas of the R-basins, we assume that we can replace canonical with microcanonical entropies and that internal motions faster than the backbone dihedral flips equilibrate thermally between the instants when the backbone chain is examined. We describe the method briefly, and then discuss how it predicts the folding of β-lactoglobulin (β-LG). Elsewhere, we shall compare this with the folding of ubiquitin, which may or may not be hierarchical (11–13). This analysis indicates that β-lactoglobulin folds nonhierarchically insofar as some regions of the molecule pass rapidly in and out of “flickering” helical structures until some tertiary structure stabilizes the helical structure of this region enough for the entropically driven kinetics to carry it into its stable native β-sheet motif (13–16).
After each topological “search,” the pattern generated by the LTM dynamics is interpreted and assigned an unambiguous geometric description thus: First, because several geometries may correspond to the same LTM, we determine a distribution of geometries consistent with the current LTM. At each step, only the newly introduced ambiguities need resolution. A set of assignments of the dihedral angles at each α-carbon, Φ and Ψ, for these geometries are obtained from the PROCHECK probability distribution of plotted Φ, Ψ points for each residue (17), a distribution derived from the high-resolution structures of 162 proteins. The density of sample values used in this procedure typically yields about 700 structures. (We take six sample points in basin 1, four in basin 2, and only one in basin 3, for each residue.)
Next, we eliminate all of the possible new structures but one. (We intend to refine this step later to allow a few favored structures to be followed in parallel.) In this, the “reading” stage, we reject all allowable geometries consistent with the latest LTM except that with the lowest free energy. “Reading” the LTM means identifying the corresponding CM. “Reading” requires evaluation of side chain enthalpies and entropies; the allowable structure with the lowest free energy is the only one retained at this point, to be used as the starting geometry for the next stage of evolution. This includes the entropies and enthalpies of the side chain interactions, and the enthalpic contributions from large-scale organizations. These determine the geometric realization of each LTM and thereby, through its time scaling, its further evolution.
Next is the step to the new stage of the LTM. Each putative LTM transition is accepted or rejected based on the free energy change of its optimized geometry according to a Metropolis-like criterion: accepted if the free energy drops, accepted or rejected by a Boltzmann-weighted probability if the free energy increases. The free energy change is computed from contact energies (Lennard–Jones, effective hydrophobic, and Coulombic), the microcanonical entropy change associated with any change in R-basins and the side-chain entropy change. (This is estimated for formation of a contact as ΔSsc = R ln q−x, where q ≈ 2 is the torsional restriction factor and x is the number of sigma bonds beyond the β-carbon in the lateral chain.)
Application of the detail balance principle makes accessible the difference in thermalized energies (averaged over LTM patterns), ΔU(1,2), between any two consecutive topologies (1–3) along the folding pathway (17). Thus ΔU(1,2) = RTln[D(2)r(2,1)/(D(1)r(1,2)], where D(1) and D(2) are the degeneracies of the LTMs, equal to the products of their R-basins areas; r(1,2) and r(2,1), respectively, represent Zwanzig's mean first passage rates for the 1→2 transition and its reverse. For example, the rate at which L units fall into the “correct” R-basin to yield a 1→2 constructive transition is r(1,2) = f × L × 2−L, where f is the mean hopping frequency assigned by the renormalization operation to the L residues in topology 1. Thus, inversion of the coarse kinetics data reveals coarse topographical features of the potential energy surface (3, 7).
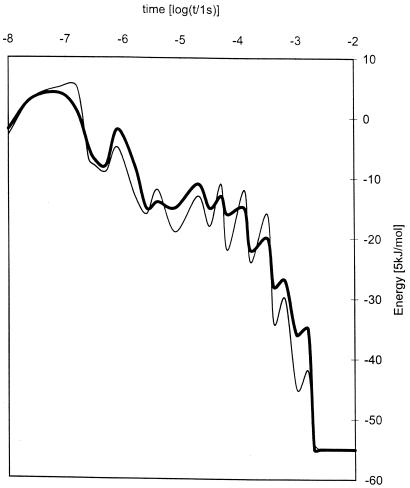
Now, we apply this method to β-lactoglobulin. This system is said to be a nonhierarchical folder because it is reported to pass through an α-helical stage on its way to its native structure made primarily of β-sheets (13–16). Fig. 1 shows the time history of the energy along the most and least reproducible folding paths that yield the native state. Fig. 2 shows a sequence of contact maps at selected times along the most reproducible folding path. These were based on runs at 318 K in which the prolines were fixed in their native, trans conformation.
Figure 1.
Time evolution of the mean thermalized energies for β-lactoglobulin along the most frequent folding path (heavy curve) and the least reproducible path to the native structure (light curve).
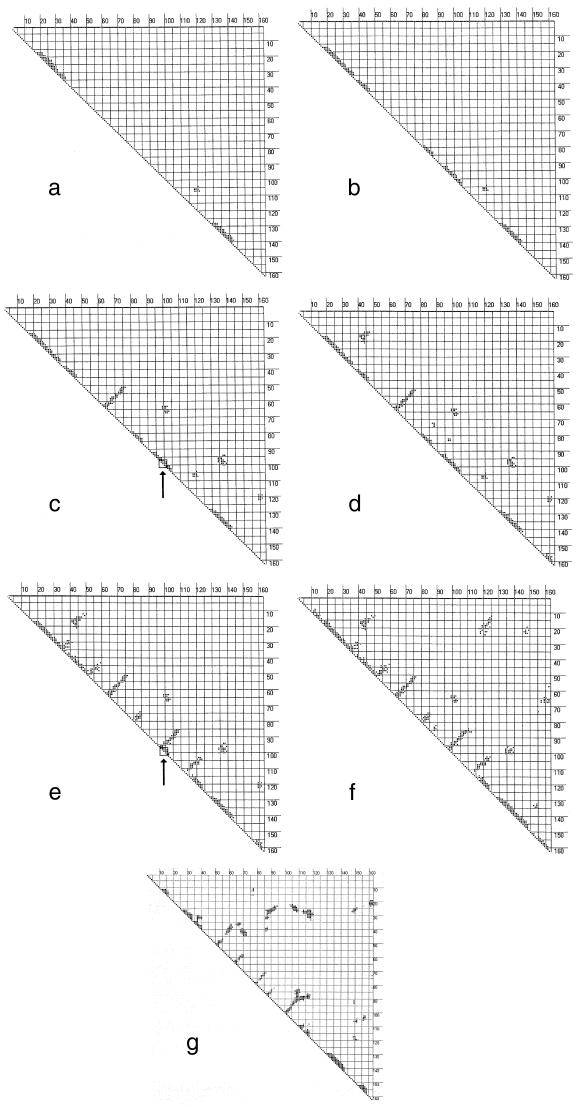
Figure 2.
Seven snapshots in the time evolution of the contact matrix for β-lactoglobulin obtained respectively (a–g) at 6.4 × 10−8, 3.0 × 10−7, 7.9 × 10−7, 1.8 × 10−5, 5.2 × 10−4, 1.0 × 10–3 s, and essentially the contact matrix for the native structure. The arrows in c and e indicate regions that show local topological invariance but structural multiplicity; that is, the relevant torsion angles remain in the same R-basins but change geometries.
In the time range to about 0.1 μs, the low entropy barriers produce kinetics inducing the system to organize helical regions of up to about four turns, with virtually no long-range structure. The specific structures tend to be transient, but there is a significant amount of helical structure, of order 30–40%, at most times throughout this period. In other words, the observations are consistent with this model, that there is indeed a significant fraction of helical structure in the protein throughout this period. However the topological results are also consistent with the observations that there is no persistent early structure with a sizeable percent of the structure in α-helices. A time-varying display of the contact map for each recognition step shows that large parts of the helical structure come and go with almost every new image. At about 1 μs, budding tertiary interactions appear, and, with them, some β-sheet forms in a previously unstructured region. This seems to be an important stabilizing stage of the folding process, probably associated with a downward step along the staircase of the potential surface (18), because little or no reversal of this step is found in the simulations. This trend continues for ca. 10 μs, with just a little more tertiary structure growing in. Then, after about 0.5 ms, the system reaches another, larger staircase drop along the path down the potential surface; at this point, several single-turn β-sheets appear where there previously were helical structures. As in atomic clusters (18), the sharp drops of the staircase arise from the formation of nuclei for structure formation, in this case the structure associated with hydrophobic collapse.
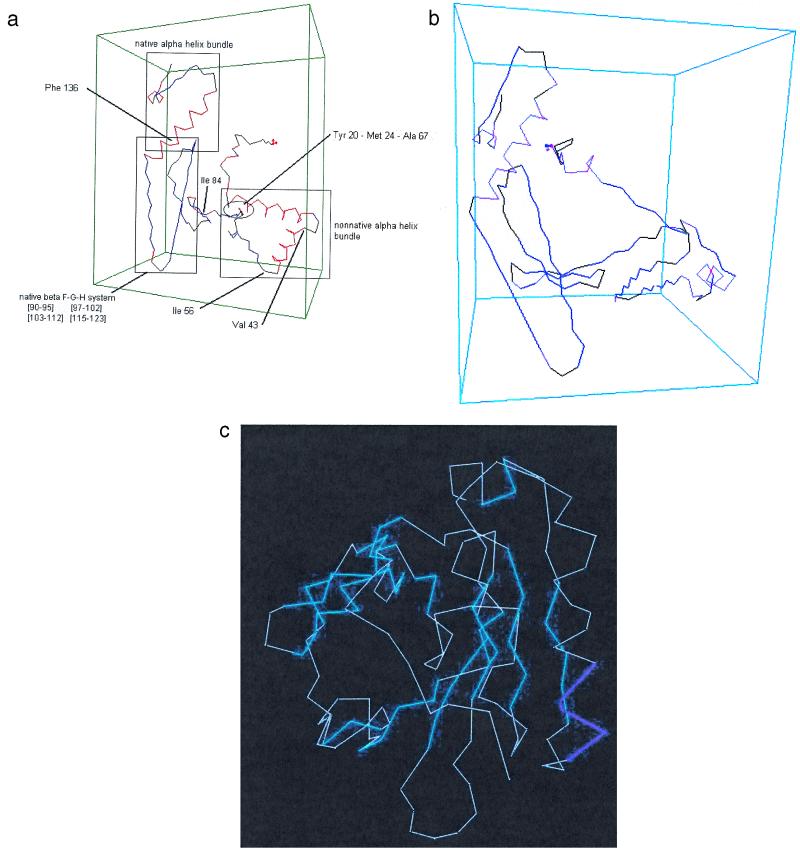
During these transformations, the relevant torsion angles of the turns remain in their same R-basins. Torsion angles of residues that go from α-helical to β-strand configurations must change R-basins, but the concomitant increases of configurational entropy assist those changes. When this is accompanied by enthalpic stabilization of tertiary scaffolding, the two effects can compensate for the enthalpy loss from dismantling the helical regions. Otherwise, the entropic gain alone would not be sufficient to stabilize the new structure, and the system could simply pass readily back and forth between the helix and the β-sheet. The formation of the β-sheets from the α-helices is apparent in the transition from Fig. 2d, at 18 μs, to Fig. 2e, at 520 μs. The geometry corresponding to Fig. 2e, as determined by the procedure described above, is shown in Fig. 3a. Later steps carry the β-lactoglobulin to the contact map of Fig. 2f, corresponding to the schematic structure of Fig. 3b, and eventually to the native structure, essentially Fig. 2g. The region designated as “nonnative α-helix” in Fig. 3a becomes a set of β-strands in Fig. 3b: the A-strand, 17–27, the B-strand, 41–49, and the C-strand, 52–59. The D-strand, 67–74, does not quite come out perfectly but, among the β-features, it is the first to form. The E-strand, 81–84, appears rather more helical than β-strand in Fig. 2e, but the model does take this segment into the correct β-structure eventually, as shown in Fig. 2 f and g. The β-strands F (90), G (102), and H (118), as well as the helix (136) are already properly established in the first 0.5 ms, as both Fig. 2e and Fig. 3a show.
Figure 3.
Structures found for β-lactoglobulin at stages along the folding path of the contact maps of Fig. 2: (a) the structure corresponding to e; (b) the structure corresponding to f, not yet the native structure but after the transition from helical to β-structure in the 18–57 region. Sections shown in red are α-helices; sections in blue are β-structures. Sections in black are turns or random coils.
It is especially relevant to compare these results with the experimental findings of ref. 4, which appeared as this work was being completed. There are differences in the details: the theoretical model has the D-β-strand forming first among the β-features, whereas the kinetics of protection against proton exchange show the G and H strands forming first and the C-strand, soon thereafter. However the theoretical model establishes almost all of the same groups to be protected as is found in the experiments. The theoretical model deals with events to milliseconds; the shortest possible times measurable in the experiments are in this range. Hence the kinetics are not truly comparable. It is appropriate to compare the structural features of the two approaches. The model clearly shows the “overshoot” of α-helical structure, as seen in many experiments (15), and the transience of this structure. The F-G-H β-barrel clearly protects the amide protons of that portion of the system within about a millisecond, in the model. (The time scales of model and experiment cannot be compared directly because of the differences in conditions chosen for each.)
In ref. 4, the authors raised possibility that the folding of β-lactoglobulin could, under some conditions, involve cis-trans isomerization of prolines. Because the appearance of that article, they carried out “double-jump” experiments, starting with folded, native β-lactoglobulin, unfolding it and, in a time too brief to permit trans → cis isomerization, refolded the protein. The results show that it is unnecessary to invoke cis proline to interpret the folding kinetics adequately. Our theoretical model, does not allow cis -proline configurations. Hence these new experimental results provide reassurance for the validity of the model.
This method differs from previous approaches (e.g., refs. 19–22) in several ways. It is not a mechanical model using molecular dynamics and thus is not restricted to brief intervals, nor does it restrict the system to a lattice. Rather, it pursues the evolution of folding by following the constraints that develop as patterns of occupancy of Ramachandran basins appear. No prior assumptions, apart from what occupancy patterns are compatible with secondary and tertiary structures, appear in the fundamental model. Explicit structural interpretation is a second step, derived from PROCHECK and the areas of the basins. Furthermore, the recent stopped-flow experiments of Goto et al. (refs. 14 and 15, and personal communication), measuring circular dichroism and proton-deuteron exchange, demonstrate how the results of this method can be compared with observations along the folding pathways, not only at points where particularly stable forms appear. The predictions of intermediate, partly folded structures can be made and compared with such experiments without recourse to mutations that may lead to substantial changes in the potential surface.
We summarize that the nonhierarchical character of this protein emerges from the model, insofar as it shows that “on-path” formation of locally structured but nonnative regions, especially the transient helices in this instance, may be necessary steps in the folding process. However, the formation of such intermediate secondary structures is certainly not sufficient to induce the requisite hydrophobic collapse that takes the system to its native structure. Some long-range organization is necessary in this system to carry it from its kinetically determined helical structure to its ultimate form. At present, this method is only able to describe the behavior of the backbone as the folding process goes on; with the inclusion of the new structural information, it will be possible to extend the procedures to take into account the roles of side groups.
Acknowledgments
We thank Robert Huber, Konstantin Kostov, Jerome Percus, and Tobin Sosnick for helpful comments and suggestions. This research was supported by the National Research Council of Argentina and the National Science Foundation.
Abbreviations
- R-basin
Ramachandran basin
- LTM
local topological map
Footnotes
This paper was submitted directly (Track II) to the PNAS office.
Article published online before print: Proc. Natl. Acad. Sci. USA, 10.1073/pnas.260359997.
Article and publication date are at www.pnas.org/cgi/doi/10.1073/pnas.260359997
References
- 1.Fernández A. Phys Chem Chem Phys. 1999;1:861–869. [Google Scholar]
- 2.Fernández A, Berry R S. J Chem Phys. 2000;112:5212–5222. [Google Scholar]
- 3.Fernández A, Kostov K, Berry R S. Proc Natl Acad Sci USA. 1999;96:12991–12996. doi: 10.1073/pnas.96.23.12991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Forge V, Hoshino M, Kuwata K, Arai M, Kuwajima K, Batt C A, Goto Y. J Mol Biol. 2000;296:1039–1051. doi: 10.1006/jmbi.1999.3515. [DOI] [PubMed] [Google Scholar]
- 5.Zwanzig R. Proc Natl Acad Sci USA. 1995;92:9801–9804. doi: 10.1073/pnas.92.21.9801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Brooks C L, Petitt L M, Karplus M. Proteins: A Theoretical Perspective of Dynamics, Structure and Thermodynamics. New York: Wiley; 1988. [Google Scholar]
- 7.Fernández A, Colubri A. Phys Rev E. 1999;60:4645–4651. doi: 10.1103/physreve.60.4645. [DOI] [PubMed] [Google Scholar]
- 8.Bai Y M, Englander S W. Proteins Struct Funct Genet. 1996;24:145–151. doi: 10.1002/(SICI)1097-0134(199602)24:2<145::AID-PROT1>3.0.CO;2-I. [DOI] [PubMed] [Google Scholar]
- 9.Hilser V J, Gomez J, Freire E. Proteins Struct Funct Genet. 1996;26:123–133. doi: 10.1002/(SICI)1097-0134(199610)26:2<123::AID-PROT2>3.0.CO;2-H. [DOI] [PubMed] [Google Scholar]
- 10.Fernández A, Kostov K, Berry R S. J Chem Phys. 2000;112:5223–5229. [Google Scholar]
- 11.Khorasanizadeh S, Peters I D, Roder H. Nat Struct Biol. 1996;3:193–205. doi: 10.1038/nsb0296-193. [DOI] [PubMed] [Google Scholar]
- 12.Krantz B A, Moran L B, Kentsis A, Sosnick T R. Nat Struct Biol. 2000;7:62–71. doi: 10.1038/71265. [DOI] [PubMed] [Google Scholar]
- 13.Sabelko J, Ervin J, Gruebele M. Proc Natl Acad Sci USA. 1999;96:6031–6036. doi: 10.1073/pnas.96.11.6031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Shiraki K, Nishikawa K, Goto Y. J Mol Biol. 1995;245:180–194. doi: 10.1006/jmbi.1994.0015. [DOI] [PubMed] [Google Scholar]
- 15.Hamada D, Kuroda Y, Tanaka T, Goto Y. J Mol Biol. 1995;254:737–746. doi: 10.1006/jmbi.1995.0651. [DOI] [PubMed] [Google Scholar]
- 16.Ragona L, Confalonieri L, Zetta L, De Kruif K G, Mammi S, Peggion E, R, Longhi R, Molinari H. Biopolymers. 1999;49:441–450. doi: 10.1002/(SICI)1097-0282(199905)49:6<441::AID-BIP2>3.0.CO;2-A. [DOI] [PubMed] [Google Scholar]
- 17.Laskowski P A, MacArthur M W, Moss D S, Thornton J M. J Appl Crystallogr. 1993;26:283–291. [Google Scholar]
- 18.Ball K D, Berry R S, Kunz R E, Li F-Y, Proykova A, Wales D J. Science. 1996;271:963–966. [Google Scholar]
- 19.Dill K A, Chan H S. Nat Struct Biol. 1997;4:10–19. doi: 10.1038/nsb0197-10. [DOI] [PubMed] [Google Scholar]
- 20.Bryngelson J, Onuchic J N, Socci N D, Wolynes P G. Proteins Struct Funct Genet. 1995;21:167–195. doi: 10.1002/prot.340210302. [DOI] [PubMed] [Google Scholar]
- 21.Munoz V, Eaton W. Proc Natl Acad Sci USA. 1999;96:11311–11316. doi: 10.1073/pnas.96.20.11311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Alm E, Baker D. Proc Natl Acad Sci USA. 1999;96:11305–11310. doi: 10.1073/pnas.96.20.11305. [DOI] [PMC free article] [PubMed] [Google Scholar]