Polyelectrostatic interactions of disordered ligands suggest a physical basis for ultrasensitivity

Abstract

Regulation of biological processes often involves phosphorylation of intrinsically disordered protein regions, thereby modulating protein interactions. Initiation of DNA replication in yeast requires elimination of the cyclin-dependent kinase inhibitor Sic1 via the SCF^Cdc4 ubiquitin ligase. Intriguingly, the substrate adapter subunit Cdc4 binds to Sic1 only after phosphorylation of a minimum of any six of the nine cyclin-dependent kinase sites on Sic1. To investigate the physical basis of this ultrasensitive interaction, we consider a mean-field statistical mechanical model for the electrostatic interactions between a single receptor site and a conformationally disordered polyvalent ligand. The formulation treats phosphorylation sites as negative contributions to the total charge of the ligand and addresses its interplay with the strength of the favorable ligand–receptor contact. Our model predicts a threshold number of phosphorylation sites for receptor–ligand binding, suggesting that ultrasensitivity in the Sic1–Cdc4 system may be driven at least in part by cumulative electrostatic interactions. This hypothesis is supported by experimental affinities of Cdc4 for Sic1 fragments with different total charges. Thus, polyelectrostatic interactions may provide a simple yet powerful framework for understanding the modulation of protein interactions by multiple phosphorylation sites in disordered protein regions.

Cellular regulatory networks have evolved finely tuned responses, disruption of which can result in aberrant development or uncontrolled growth, as in cancer. Signaling events are often triggered by posttranslational modifications, such as protein phosphorylation, and subsequent interaction of the modified protein with a binding partner (1). In many cases, signaling proteins are phosphorylated on multiple sites (2). Multiple phosphorylations offer several possible mechanisms to fine-tune signaling events. For example, different kinases may be required for the phosphorylation of different sites on a protein, often by means of “priming” events, in which phosphorylation at one site enables recognition by a subsequent kinase that phosphorylates another site (3). In some instances, multiple phosphorylations can lead to graded regulation of a binding interaction (4). Of particular interest to the present study is the requirement for multiple phosphorylations of a disordered protein by the same kinase to bind to its target. This behavior can lead to a highly sensitive response by transforming a graded input (the kinase concentration, [kinase]) into a sharply thresholded output (5, 6), even in a simple steady-state setting without the presence of ultrasensitive changes in the phosphorylation level entailed by open-system chemistry (7–9). In the simple case with independent phosphorylation sites in the presence of a counteracting phosphatase, this is because the output of an effect that requires n phosphorylations varies approximately as [kinase]ⁿ before the output level is saturated. Hence, when the value of n is sufficiently larger than one, output stays at an insignificantly low level and increases sharply only when [kinase] attains a certain threshold.

However, the biophysical origin of phosphorylation thresholds, mandating a minimum number of phosphorylations to effect certain biological events, remains to be deciphered. A mathematical formalism for understanding such processes has been proposed (10), but the underlying physics of molecular interactions has not been elucidated. Here we address the physicochemical forces that might enable a multiphosphorylated protein to bind with high affinity to a partner above a certain phosphorylation threshold, even though the binding affinity of each individual phosphorylated epitope might be very weak.

A model ultrasensitive system that involves a single receptor site and a polyvalent ligand is the interaction of the cyclin-dependent kinase inhibitor Sic1 with the SCF ubiquitin ligase subunit Cdc4 in yeast. When Sic1 is phosphorylated on any six (or more) of nine sites [termed Cdc4 phosphodegrons (CPDs)], it binds to a WD40 domain in Cdc4 with concomitant ubiquitination and degradation of Sic1 (11, 12). The phosphorylation-dependent degradation of Sic1 in the late G₁ phase of the cell cycle enables the development of B-type cyclin–cyclin-dependent kinase activity and the onset of DNA replication (13–15). It has been demonstrated that the phosphodegrons of Sic1 consist of suboptimal binding motifs for binding to the WD40 domain. Although a single high-affinity CPD motif is sufficient for recruitment of Sic1 to Cdc4, because the threshold is absent, premature onset of degradation of Sic1 leads to genome instability (11).

Sic1 is an intrinsically disordered protein (11). Multisite phosphorylation often regulates the function of intrinsically disordered proteins, such as Sic1 (see, e.g., ref. 16); moreover, the sequence patterns of regions adjacent to phosphorylation sites are often very similar to those of intrinsically disordered regions (17). As the key roles of intrinsically disordered proteins in cellular processes are recognized, the study of this class of proteins is flourishing (18–22). Thus, it has become increasingly clear that biology has made use of the manifold polymeric states available to a polypeptide chain (18). Even for proteins that can be folded, in view of recent advances in the study of possible noncooperative “downhill” folding (23–25), the traditional notion of cooperative folding as a functional requirement for globular proteins seems an oversimplification (26). For many tasks involved in cellular function, intrinsically disordered proteins offer several unique attributes. For instance, disordered regions can be flexible linkers or thermodynamic tethers (27) and “entropic springs” (28). Conformational plasticity may also allow such regions to bind to multiple partners and thus serve as hubs in protein–protein interaction networks (29, 30). It has also been suggested that because intrinsically disordered proteins can encode larger intermolecular interfaces with smaller protein sizes compared with folded proteins, they may allow for more economical genome and cell sizes (21). By sampling a larger volume, conformational disorder may lead to enhanced capture rates for a protein (31) and serve to better exclude other competing proteins from interacting with its binding partners, as illustrated for example by the entropic barrier formed by the unstructured FG repeats of the nuclear pore (32). Some intrinsically disordered proteins undergo disorder-to-order transitions to adopt stable structures upon binding to their partners (22, 33, 34), but some remain largely disordered, even when bound, or only undergo a limited disorder-to-order transition of a short binding motif (21, 22). Our knowledge of the thermodynamics of disordered proteins is limited. But such knowledge is important to account for these binding mechanisms and their biological implications.

In this study, we investigate electrostatic interactions as a component of the physical mechanism that leads to phosphorylation-dependent ultrasensitive binding of intrinsically disordered ligands. In general, there are more charged residues and fewer hydrophobic residues in intrinsically disordered proteins than in globular proteins (35). Thus, electrostatic interactions are expected to play a more prominent role in conformationally flexible (36), intrinsically disordered proteins than in globular proteins. To emphasize that our proposed electrostatic effects encompass all of the charged phosphorylated sites of the ligand, regardless of whether they are in close proximity to the receptor site, we term these interactions “polyelectrostatic.” We construct a simple analytical mean-field model of the binding of a folded, charged receptor protein to a disordered ligand protein with variable phosphorylation levels. This model rationalizes the behavior of phosphorylation-dependent binding under different solvent and phosphorylation conditions and provides insights into an energetic design of this class of highly cooperative protein–protein interactions. Experimentally determined affinities of Cdc4 for a series of peptide fragments from Sic1 with different net charges are consistent with the predictions of the polyelectrostatic model.

Results and Discussion

Statistical Mechanics of Binding.

We first outline a basic formulation for describing the interactions between folded proteins and disordered polyvalent ligands. The present work takes an equilibrium modeling approach to address data from experiments performed under equilibrium conditions, although we note that ultimately nonequilibrium analyses (7–9) will be needed to address processes in living cells. Here we consider a system of N_r identical receptor molecules and N_l identical ligands in an aqueous solution of volume V. To address Cdc4–Sic1 interactions, we focus on the case in which each folded protein molecule (corresponding to Cdc4) contains one binding (receptor) site, whereas each ligand contains n possible binding regions (corresponding to the CPDs of Sic1) that can bind to the single receptor site on the folded protein. We further assume that, for n ≥ 1, each ligand can bind to at most one receptor protein at a time. This condition holds readily if the concentration of receptor protein is sufficiently low. We note that, although Cdc4 is known to dimerize, dimerization does not affect its affinity for Sic1 because the two binding sites in the dimer are well separated (J. Tang, S. Orlicky, Z. Lin, A. Willems, D. Neculai, D. Ceccarelli, F. Mercurio, B. Shilton, F. Sicheri, and M.T., unpublished data). In other words, we consider the binding process r + l ⇌ r·l with the dissociation constant

where r, l, and r·l represent, respectively, free (unbound) receptor, free ligand, and bound receptor–ligand complex; and […] denotes concentration.

To relate the dissociation constant to microscopic interactions, we start with the standard statistical mechanical description of this system in terms of a total partition function, Q_tot, which is a product of contributions from the partition functions for a free disordered ligand protein (Q_l^(f)), a free folded receptor protein (Q_r^(f)), and a bound receptor-ligand complex (Q_c^(b)):

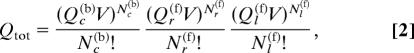where V is the volume of the solution in a certain unit (the size of which is immaterial to the present analysis); Q_l^(f), Q_r^(f), and Q_c^(b) are partition functions for the respective individual molecules in the free state or for the complex with a given center-of-mass position; N_c^(b) is the number of bound receptor–ligand complexes; N_r^(f) and N_l^(f) are, respectively, the number of free receptor and free ligand molecules, hence N_r^(f) = N_r − N_c^(b), N_l^(f) = N_l − N_c^(b), [r] = N_r^(f)/V, [l] = N_l^(f)/V, and [r·l] = N_c^(b)/V. Because the conformational diversity of each individual molecule or complex has already been factored into their respective partition functions, the factorials in Eq. 2 account for the fact that the N_c^(b) bound receptor–ligand complexes are indistinguishable and that the same applies to the N_r^(f) free receptors and to the N_l^(f) free ligands.

The total partition function is the sum of statistical weights of all possible configurations of the receptor/ligand system. Accordingly, the free energy of the system A = −k_BT ln Q_tot, where k_BT is Boltzmann's constant times absolute temperature. Using Eq. 2 for Q_tot, we determined the most probable physical configuration by minimizing the free energy A [see supporting information (SI) Appendix 1]. This calculation allows the fraction of ligand bound, θ = N_c^(b)/N_l, to be expressed in terms of (i) the partition functions Q_c^(b), Q_r^(f) and Q_l^(f) for individual bound complex and free molecules, (ii) the receptor to ligand concentration ratio γ = N_r/N_l, and (iii) the total ligand concentration ρ_l = N_l/V:

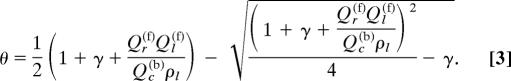This formulation also provides the concentration of free ligand, ρ_l^(f) = (1 − θ)ρ_l, and free receptor, ρ_r^(f) = (γ − θ)ρ_l, as functions of the fraction of ligand bound:

Because each ligand can bind to only one receptor, the fraction of ligand bound, θ, varies between 0 and a maximum value θ_max = γ for γ ≤ 1, and between 0 and θ_max = 1 for γ ≥ 1. Thus, we may normalize θ by θ_max and consider θ/θ_max as an order parameter for binding. We have computed and compared results for θ_max = 1 and θ_max < 1 for several test cases. The general trend of dependence of θ/θ_max on the other variables of the model are very similar (data not shown). For simplicity, numerical results below will be presented for γ = 1. The dissociation constant, K_d, can now be obtained as the concentration of free receptor, ρ_r^(f), when θ = 1/2:

which, when substituted into Eq. 1 with [r] = ρ_l(γ − θ), [l] = ρ_l(1 − θ), and [r·l] = ρ_lθ, can readily be checked to yield Eq. 3 for θ. Eq. 5 is a general relation valid for all values of Q and γ. The number of binding regions or phosphorylated sites, n, of the disordered peptide does not appear explicitly in this equation. We now explore how possible physical interactions determine the values for Q and consequently lead to a dependence of K_d on n.

Model of Electrostatic Interactions.

We examine how the electrostatic interactions between the receptor and the multiple phosphorylated sites might lead to ultrasensitivity. Because the effect of phosphorylation is to add two negative charges to a residue and because electrostatic interactions likely play a significant role (37, 38) in the structural consequences of phosphorylation (39), an obvious candidate for the physical basis of ultrasensitivity is changes in electrostatic interactions. As a first step in our investigation, we consider a physical picture in which the charges of the disordered ligand are dynamically distributed in a diffuse manner, as illustrated in Fig. 1. In other words, we adopt an equilibrium, mean-field perspective (40, 41) in which the electrostatic interactions are not specific, recognizing that such interactions can be biologically functional, for example, in the association of peripheral proteins to cell membranes (42).

Fig. 1.

Schematic of a conformationally disordered ligand (yellow) with both positive (blue) and negative (red) charges (for a total charge, q_l) that is bound to a receptor (green) with a binding site having charge q_r. The distance 〈r〉 is between the binding site of the receptor and the center of mass of the disordered ligand.

Our approach is based on the following simplifying assumptions. (i) The conformational shape and the overall charge distribution of the disordered ligand are not significantly affected by binding. (ii) The electrostatic interaction between the receptor and a bound, disordered ligand can be described approximately as a screened Coulombic interaction between two charges (q_r on the receptor and the total net charge on the ligand, q_l) separated by an effective distance 〈r〉 (Fig. 1). The present treatment does not distinguish between enthalpic contributions and possible entropic contributions from counterion release (43). (iii) The binding of the disordered ligand and the receptor entails, in addition to the electrostatic interaction, a favorable contact energy E_b comprised of van der Waals and other energetic terms that derive from the short-range contacts within the binding interface. We further assume that E_b is independent of whichever one of the n possible binding regions of the disordered ligand is in contact with the binding site on the receptor. (iv) This favorable contact interaction and the electrostatic interaction are absent when the disordered ligand is unbound.

It follows from assumption i that the partition function for a complex is proportional to the product of the partition functions of its two constituent parts, Q_c^(b) ∝ (δV) Q_r^(f) Q_l^(f), because the respective internal degrees of freedom of the receptor and the disordered ligand in the complex are taken to be roughly the same as when they are individually free. The factor (δV) is a volume of tolerance delineating the range of variation of the separation between the centers of mass of the two constituent molecules in the complex (44). This factor sets the volume (and concentration) scale in the formulation. Assumptions ii and iii further imply that

where ε_d is the dielectric constant and α is a Debye–Hückel screening parameter. The number n of possible binding regions on the ligand appears as an overall multiplicative factor because it corresponds to the number of distinguishable ways of forming the complex, assuming that, to a first approximation, they are equally likely to bind. Thus, by combining Eqs. 5 and 6, it follows that the dissociation constant

which depends on n explicitly in the overall 1/(nδV) factor as well as implicitly by means of q_l in the exponential factor (see below).

Obviously, this formulation is a highly simplified caricature of the real system. For instance, in reality, the conformational shape of the ligand could change upon binding, and the electrostatic interactions are more accurately described by the Coulombic attractions and repulsion between individual charges than by net charges and an effective separation 〈r〉. Incorporation of these effects would likely lead to tighter binding, as discussed below and in SI Appendix 1. The present treatment also assumes that receptor interaction with different binding sites of the disordered ligand entail the same favorable contact energy E_b. However, in reality it is known that the CPD sequences on Sic1 differ from one another, with various degrees of mismatch to the canonical CPD consensus sequence (11). In addition, the current model addresses only the thermodynamics but not the kinetics of binding (10). Assuming no interaction between the receptor and the ligand in the unbound state means that there is little or no kinetic driving forces for the binding interaction other than diffusion; this might not be realistic. Despite these limitations, in our estimation, this model captures much of the essential physics of interest. It also offers a practical means to study qualitatively or even semiquantitatively the interplay between ligand net charge q_l (see below) and other solvent variables. For example, the effects of salt concentration on binding may be explored by noting that α ≈ $\sqrt{I}$ where I is the ionic strength of the solution, as in previous mean-field theories of biopolymers (40). In this regard, to a first approximation, addition of salt is expected to weaken the polyelectrostatic interactions.

Ultrasensitivity as a Consequence of Cumulative Ligand–Receptor Electrostatic Interactions.

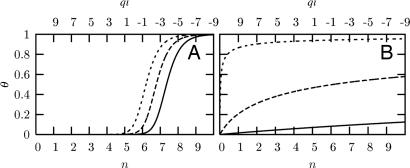
Based on this modeling setup, Fig. 2 examines the origin of ultrasensitivity in our model. The number of phosphorylation sites enters into our formalism (i) as an overall multiplicative factor for the partition function Q_c^(b) of the bound complex, as noted above, and (ii) as a multiplicative factor on a negative contribution to the net charge q_l of the ligand in Eq. 6:

where q_l⁰ is the charge of the unphosphorylated ligand and c is the charge contribution per phosphorylation; c is taken to be 2 at pH 7. The strength of the electrostatic interaction depends on the dielectric constant ε_d, which is ≈80 for bulk water and approximately 2–4 for the interior of a folded protein molecule (45). Because the ligand is disordered in both the free and bound state, the numerical results in Fig. 2 are presented for an intermediate value of ε_d = 20. We have performed calculations by using other values of ε_d (5 ≤ ε_d ≤ 80); the general trend of the results are similar (data not shown).

Fig. 2.

Fraction of bound ligand θ as a function of the net charge (q_l) and the number of phosphorylations (n) on the ligand. (A) Variation of θ for different ligand concentrations in the mean-field model with E_b = −10 k_BT, q_r = 3, q_l⁰ = 11 and 〈r〉 = 12 Å. Ligand concentrations, ρ_l, equal [in units of (δV)⁻¹] 10⁻⁶ (short-dashed line), 10⁻⁷ (long-dashed line), and 10⁻⁸ (solid line). (B) Variation of θ for different numbers of binding motifs, n, for an alternate model in which K_d = (nδV)⁻¹ exp(E_b/k_BT), with E_b values −12 (solid line), −15 (long-dashed line), and −20 (short-dashed line) k_BT, and ρ_l = 10⁻⁷ (δV)⁻¹. The parameters n and q_l are shown as continuous variables; however, only integer numbers of n and the corresponding values of q_l are of physical interest. Numerical results presented in this and subsequent plots are for γ = 1, as discussed in the text, and T = 298 K.

Fig. 2A depicts ultrasensitive behavior in our model. The fraction θ of ligands bound undergoes a steep sigmoidal transition from θ ≈ 0 at n = 5 to θ ≈ 1 at n = 7 or 8. Hence, it is a sharp binding transition that is triggered by a threshold value of n and also displays switch-like properties (46). The threshold n value increases with decreasing total ligand concentration, ρ_l. However, the dependence of threshold n value on ρ_l is not strong. In this example, the threshold n changes only from 6 to 7 for a variation of ρ_l over two orders of magnitude. Although the exact threshold n value in the model depends on the choice of parameters, Fig. 2A demonstrates clearly that ultrasensitivity arises readily from polyelectrostatic interactions, provided that these interactions are sufficiently strong. This is a direct consequence of a linear increase in favorable ligand–receptor interaction strength with the number n of phosphorylated sites, because q_l decreases linearly with n (see Eq. 8 and Eq. 6 for Q_c^(b)).

In contrast, Fig. 2B illustrates a hypothetical scenario in which ultrasensitivity does not emerge. Here the ligand–receptor interaction strength is assumed to be independent of the number of phosphorylated sites; i.e., the exponential term in the Q_c^(b) expression in Eq. 6 is set to a constant. In that case, the only dependence of θ on n is a configurational entropic contribution from the overall multiplicative factor of n in Eq. 6 that accounts for the number of ways the ligand can bind. Fig. 2B shows that such an interaction scheme cannot produce ultrasensitivity. Although θ increases with n, either there is no non-zero threshold n value (for more negative E_b) or the increase in θ with n is gradual (for less negative E_b). There is no sign of a sigmoidal transition when the only dependence of Q_c^(b) on n is in the form of Q_c^(b) ∼ n.

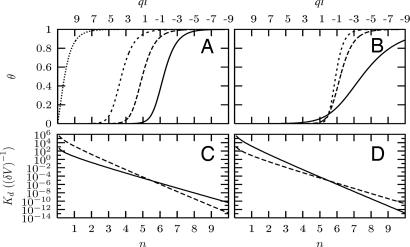
Fig. 3A underscores the interplay between the short-range contact energy E_b and the longer-range polyelectrostatic effect in ultrasensitive behavior. It shows that the threshold n value decreases with more favorable (more negative) E_b. For example, the threshold n reduces to one when E_b = −35 k_BT in the model. In other words, a strongly favorable ligand–receptor contact interaction at the binding site can abolish the electrostatically driven ultrasensitive effects. This result rationalizes the experimental finding that suboptimal CPD sequences are necessary for ultrasensitive binding (11). In addition, the model provides an explanation for the lowering of the threshold from a requirement for six phosphorylations to only three with a Cdc4 K402A/R443D double mutant that increases the affinity (with a more negative E_b) for the suboptimal CPD sequences containing basic residues C-terminal to the phosphorylation site (12).

Fig. 3.

Binding curves and binding constants as a function of the net charge (q_l) and the number of phosphorylations (n) on the ligand for mean-field models, with q_l⁰ = 11, ε_d = 20 as in Fig. 2, and ρ_l = 10⁻⁶ (δV)⁻¹. (A) θ vs. n for different contact energies. E_b = −35 (dotted line), −20 (short-dashed line), −15 (long-dashed line), −10 (solid line) k_BT. q_r = 3, and 〈r〉 = 12 Å. (B) θ vs. q_l for different effective charges on the receptor. q_r = 5 (short-dashed line), 3 (long-dashed line), and 1(solid line). E_b = −5 k_BT, and 〈r〉 = 12 Å. (C) K_d vs. n for different charges on the receptor. q_r = 2 (solid line), and q_r = 3 (dashed line). E_b = −10 k_BT, and 〈r〉 = 12 Å. (D) K_d vs. n for different effective distances for the polyelectrostatic interaction between the receptor and the ligand. 〈r〉 = 12 Å (solid line), 〈r〉 = 14 Å (dashed line), q_r = 3, and E_b = −10 k_BT.

Fig. 3 B–D provides several predictions of our model, which we included because these results should be amenable to future experimental tests. Fig. 3B shows that the sharpness of the θ transition with respect to the net charge q_l on the ligand increases with an increasingly positive charge on the receptor. Fig. 3 C and D shows the variation of the dissociation constant with the number n of phosphorylated sites on the disordered ligand for different charges on the receptor and for different ligand sizes.

Experimental Sic1 Fragment-Binding Data Support the Polyelectrostatic Hypothesis.

To provide an initial test of our model, we used fluorescent titration spectroscopy to determine the Cdc4 binding affinities of short Sic1 peptides containing phosphorylation sites and with different net charges (Fig. 4). The small size of these peptides, illustrated in Fig. 4A, might have consequences for the possible charge distributions of the bound states, an issue that is largely beyond the scope of this work but that is briefly explored in SI Appendix 1. To compare the present model with experiment, rough estimates were made for some of the variables in the expression for K_d, as follows. First, the binding pocket of Cdc4 contains three arginine residues. Thus we have used q_r = 3 in Fig. 4B. The presence of additional positive charges on Cdc4 at positions immediately adjacent to the binding pocket may warrant a larger value for this parameter but will not affect our conclusions below. Second, the value of 〈r〉 for the peptide was motivated by the end-to-end distance ≈$\sqrt{N}$ b, where N is the number of residues and b is the average distance between two adjacent residues if the conformational ensemble is modeled as a Gaussian chain (47). With ≈10 residues for each peptide and a C_α–C_α distance of ≈3.8 Å, we take 〈r〉 = 12 Å. Third, the value of E_b cannot be determined from current experimental data. Here we set E_b to −15 k_BT to ensure favorable binding. Because E_b always appears together with the concentration scale δV, the chosen E_b value will affect the δV value estimated from experiment (see below). Fourth, the Debye–Hückel screening parameter α is taken to be 0.12 Å⁻¹, corresponding to a screening length of 8.2 Å for a 0.15 M univalent salt buffer (48) used in the experiment. Fifth, because the peptides are short, their electrostatic interactions with the receptor protein are mediated more by bulk water (and less by the peptides themselves). Taking this into consideration, it is reasonable that an ε_d = 44 value, which is higher than that in Figs. 2 and 3, was found to provide a better account of the experiment. Finally, with these parameters, if the concentration scale δV is tuned to roughly fit the experiment, we arrive at δV ≈ (1.3 Å)³. Considering the sizes of the ligand and receptor molecules, this δV value is a reasonable volume of tolerance for the variation of the center-of-mass position of the bound ligand relative to that of the receptor.

Fig. 4.

Sic1 peptide binding to Cdc4. (A) Schematic of a short peptide fragment bound to a receptor protein. (B) Binding constants vs. ligand net charge (q_l) in the mean-field model, with q_r = 3.0, E_b = −15 k_BT, 〈r〉 = 12 Å, and ε_d = 44. K_d values are shown for n = 1 (solid line), 2 (dashed line), and 3 (dotted line). (C) Peptide fragment sequences. Blue (red) background corresponds to positively (negatively) charged residues. pS and pT denote phosphorylated serine and threonine, respectively. (D) Experimental dissociation constants vs. ligand net charge for peptide fragments shown in C. The line is a least-square fit of log(K_d) vs. q_l. Error bars are one standard deviation of the results from three independent titrations. The number labels for the fragment sequences correspond to those in C.

The Sic1 peptides used in our experiment were Sic1 1–10, 30–38, 42–50 and 66–85; in addition, we considered also the 42–50 peptide with two glutamic acid residues and with two lysine residues added (sequences 1, 2, 3, 4, 5, and 6, respectively, in Fig. 4C). The numbers of phosphodegrons, n, in these peptides vary from one to three. Accordingly, theoretical binding curves for n = 1, 2, or 3 are provided in Fig. 4B, which shows that, for a given q_l, the variation in K_d among the plotted n values is quite small. The experimental binding affinities as a function of peptide net charge are shown in Fig. 4D. The dependence of K_d on the net charge is to a good approximation exponential (linear in the logarithmic scale shown), which is in close agreement with the model predictions in Fig. 4B.

These experimental results lend support to our hypothesis that polyelectrostatic interactions are a significant driving force for ultrasensitivity in the Sic1/Cdc4 system. In this regard, it should be noted that although the model δV parameter in Fig. 4B was tuned to mimic the experimental results, the linear dependence of logK_d vs. net charge is a robust feature of the model. From the slope of logK_d vs. Sic1 peptide net charge in Fig. 4D, we may estimate a binding free energy change of 0.77 k_BT per unit charge. This estimation means a free energy change of 1.54 k_BT, and hence an ≈4.7-fold increase in K_d per phosphorylation. Assuming a similar charge dependence for the binding of 90-residue Sic1 (1–90), this significant difference in predicted affinity between n-fold and (n + 1)-fold phosphorylated peptide is consistent with the experimental findings of significant degradation of 6-fold but not 5-fold phosphorylated Sic1 (12) and the ability of Cdc4 to “capture” 6-fold but not 5-fold phosphorylated Sic1 (11). The relationship between K_d and the ligand net charge also depends on the detailed charge distribution and ligand length. In SI Appendix 1, we explore this relationship in terms of polyampholyte polarizability and show how longer ligands can compensate for unfavorable electrostatic interaction by conformational rearrangements and that this effect depends on charge distribution and ligand flexibility.

Conclusions

We have investigated the mathematical and physical requirements for ultrasensitivity in a simple polyvalent ligand–single receptor system. The observation of a switch-like change in binding affinity places constraints on how the population of bound complex or the fraction of ligand bound, θ, depends on the number, n, of phosphorylated sites. It is not sufficient for θ to increase linearly with n. But ultrasensitivity can be a consequence of θ increasing exponentially with n (Fig. 2). This requirement is formally similar to that for other cooperative transitions in biology, such as protein folding (26).

Such an exponential dependence was also postulated in a previous mathematical model for ultrasensitivity (10), although this earlier study did not provide a physical mechanism. A recent proposal argues that multiple phosphorylation events can in principle favor binding by reducing the conformational entropy of a disordered ligand when binding is coupled with a high degree of conformational ordering of the ligand (49). However, for the Sic1–Cdc4 system, the available experimental evidence suggests that phosphorylation on multiple sites does not lead to substantial decrease in the conformational disorder of Sic1 (11) (T.M., W.-Y. Choy, S. Orlicky, F. Sicheri, L. Kay, M.T., and J.D.F.-K., unpublished data).

Noting the obvious fact that phosphorylation increases negative charges on a ligand, here we show that a viable physical mechanism for ultrasensitivity is readily supplied by the increasingly favorable electrostatic interactions between a positively charged receptor protein and a disordered ligand protein with an increasing number of phosphorylated sites. This formulation satisfies the above mathematical condition because the electrostatic interaction energy naturally enters into the exponential factor of the Boltzmann weights. Our hypothesis appears consistent with existing data and the experimental data reported in this work.

The present model highlights the important interplay between the more specific, spatially short-range contact interactions in and around the binding pocket and the less specific, spatially long-range polyelectrostatic interactions between the binding partners. Consistent with experiments on the Sic1–Cdc4 system (11), polyelectrostatic interactions can lead to ultrasensitivity only when the strength of the specific contact interactions (E_b in our model) is not too strong (Fig. 3). In other words, the specific contact interactions must be insufficient for binding in the first place such that cumulative charge interactions, e.g., by increasing the number of phosphorylations for the Sic1/Cdc4 case, can tip the balance toward favorable binding. Because our model is rather generic, this effect should be applicable to a broad class of polyvalent intrinsically disordered ligands. For example, the F-box protein Grr1 engages in a multisite phosphorylation-dependent interaction with a disordered region in its substrate the G₁ cyclin Cln2 (50) and a phosphorylation-independent interaction with an acidic degron sequence of another substrate, Mks1 (51). Notably, and unlike Cdc4, Grr1 does not appear to have a dedicated phosphoepitope binding pocket but instead interacts with substrates by means of a cationic surface on its leucine-rich repeat domain (52). These disordered polyelectrostatic interactions contrast with interactions involving a disorder-to-order transition upon binding (22), for which the specific contact interactions involving the phosphate leads to significant structural stabilization. In addition, there are certain to be other mechanisms of binding interactions involving phosphorylation of disordered proteins that do not lead to ultrasensitivity, as in the phosphorylation of an unstructured region of the transcription activator Ets-1, which results in a graded DNA binding affinity essentially as a “rheostat” rather than a switch (4).

Finally, we emphasize that the polyelectrostatic perspective put forth in this work is more general than the simple mean-field model used to illustrate it here. The present treatment considers only the screened electrostatic interaction between a pair of effective point charges, one representing the receptor, the other representing the ligand, without accounting for charge distribution. However, it is also clear from the formal development that the trends predicted by our model are readily generalizable, e.g., to cases for which there are multiple specific contacts instead of only one specific contact region between the intrinsically disordered ligand protein and the receptor protein. By incorporating more structural and energetic details, our perspective can potentially address many more subtle phenomena, as exemplified by the brief exploration of the impact of polyampholytic charge polarization (53–55) in the disordered ligand (SI Appendix 1). In this context, it would be fruitful to investigate the effects of charge distribution on the receptor side as well. There is no shortage of intriguing fundamental biological questions for which the polyelectrostatic perspective would be of relevance.

Experimental Procedures

The binding measurements of Sic1 fragments to Cdc4 were carried out by using an ATF 105 spectrometer (AVIV Instruments, Lakewood, NJ) equipped with an automatic titrator. The binding of the peptide fragments were monitored by using intrinsic tryptophan fluorescence with an excitation wavelength of 298 nm and an emission wavelength of 366 nm. All measurements were performed in 50 mM Hepes/150 mM NaCl/5 mM DTT, pH 7.5, at 22°C. The concentration of Cdc4 was 0.5 μM for all measurements. The Cdc4 concentrations were determined by using UV absorption at 280 nm in 6 M guanidine hydrochloride. The concentrations of the peptide fragments were assessed by BCA assays and amino acid analysis.

Cdc4 used for binding assays was the same monomeric Cdc4–Skp1 complex used for crystallography with Cdc4 encompassing residues 263–744 (12). It was expressed and purified as reported before (12). Phosphopeptides were obtained from Genscript and the Advanced Protein Technology Centre at the Hospital for Sick Children, and purified by reversed-phase chromatography on a C18 column. The identity and proper phosphorylation of the peptides were confirmed by amino acid analysis and MALDI mass spectrometry.

Abbreviation

CPD

Cdc4 phosphodegron.