Abstract
We used dynamic force spectroscopy (DFS) to explore the energy landscape of interactions between a chelated uranyl compound and a monoclonal antibody raised against the uranyl-dicarboxy-phenanthroline complex. We estimated the potential energy barrier widths and the relevant thermodynamic rate constants along the dissociation coordinate. Using atomic force microscopy, four different experimental setups with or without the uranyl ion in the chelate ligand, we have distinguished specific and nonspecific binding in the binding affinity of the uranyl compound to the antibody. The force loading rates for our system were measured from 15 to 26,400 pN/s. The results showed two regimes in the plot of the most probable unbinding force versus the logarithm of the loading rate, revealing the presence of two (at least) activation barriers. Analyses of DFS suggest parallel multivalent binding present in either regime. We have also built a molecular model for the variable fragment of the antibody and used computational graphics to dock the chelated uranyl ion into the binding pocket. The structural analysis led us to hypothesize that the two regimes originate from two interaction modes: the first one corresponds to an energy barrier with a very narrow width of 0.5 ± 0.2 Å, inferring dissociation of the uranyl ion from its first coordination shell (Asp residue); the second one with a broader energy barrier width (3.9 ± 0.3 Å) infers the entire chelate compound dissociated from the antibody. Our study highlights the sensitivity of DFS experiments to dissect protein-metal compound interactions.
INTRODUCTION
Uranium salts may cross biological membranes and cause a large range of toxic effects in cells and organs (1). These effects can be divided into radiation and heavy metal toxicology. The radiation toxicity of uranium compounds might be considered as low while the prominent chemical toxicity of uranyl ions (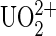 ) in different organs has been demonstrated (2). The initial step for rationalizing developments of new bioremediations is to understand the mechanism by which the uranyl ion exerts deleterious effects at cellular and molecular levels (3). Consequently, information on chemical properties of uranyl ions is of great significance. Due to scarcity and toxicity of uranium compounds, many efforts have gone to computational developments of quantum chemistry and modeling of metal chelates. However, an adequate description of electron correlation effects and incorporation of the large relativistic effects remain challenging for the existing theoretical approaches on actinide metals (4). To directly gain insight on how the uranyl ion binds to biological systems, we have investigated the binding reaction at a molecular level of chelated
) in different organs has been demonstrated (2). The initial step for rationalizing developments of new bioremediations is to understand the mechanism by which the uranyl ion exerts deleterious effects at cellular and molecular levels (3). Consequently, information on chemical properties of uranyl ions is of great significance. Due to scarcity and toxicity of uranium compounds, many efforts have gone to computational developments of quantum chemistry and modeling of metal chelates. However, an adequate description of electron correlation effects and incorporation of the large relativistic effects remain challenging for the existing theoretical approaches on actinide metals (4). To directly gain insight on how the uranyl ion binds to biological systems, we have investigated the binding reaction at a molecular level of chelated 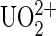 with the monoclonal antibody, namely Mab U04S, raised against UO2-DCP (UO2-2,9-dicarboxy-1,10-phenanthroline, (5)) using the mouse hybridoma technique (C. Vidaud, in preparation). We attempt to determine relevant kinetic parameters that are useful for modeling and to better understand the chemical properties of uranium-containing molecules like peptides or proteins. It is generally agreed that the thermodynamic parameter to best describe the affinity of a ligand with a protein is the kinetic dissociation constant.
with the monoclonal antibody, namely Mab U04S, raised against UO2-DCP (UO2-2,9-dicarboxy-1,10-phenanthroline, (5)) using the mouse hybridoma technique (C. Vidaud, in preparation). We attempt to determine relevant kinetic parameters that are useful for modeling and to better understand the chemical properties of uranium-containing molecules like peptides or proteins. It is generally agreed that the thermodynamic parameter to best describe the affinity of a ligand with a protein is the kinetic dissociation constant.
In this study, we combined both experimental and theoretical techniques to investigate the interactions of UO2-DCP and Mab U04S. For the experimental part, we adopted a single molecule manipulation technique using atomic force microscopy (AFM) (6). AFM has been used to correlate the binding strength between a ligand and a receptor with an applied force that pulls the ligand out of the receptor environment (7). The force at which the bond breaks depends on the loading rate, i.e., a larger bonding force can be measured at higher loading rates. This unbinding process has been recognized as a thermally activated decay of a metastable state. Therefore, it can be described in the framework of the reaction theory, referred to as an irreversible or far from equilibrium reaction (8). The first kinetic model was proposed by Bell (9) and refined later by Evans and Ritchie (10). Recently, a general formalism for the AFM study on thermodynamic stability was formed by Tinoco and Bustamante (11) to compare the data of single molecule(s) and that of bulk solutions. This type of AFM experiment is also termed dynamic force spectroscopy (DFS) (12). DFS has been carried out to study kinetic behaviors of several systems (13–18) including antigen-antibody systems (19–21).
In this article, we present the first, to our knowledge, direct DFS study on binding kinetics of an immobilized heavy metal and a macromolecular receptor. Force-displacement curves in DFS measurements have been found highly convoluted and to include signals from both specific and nonspecific interactions that complicate analysis of raw force-displacement data. Therefore, we have used the previously developed software to analyze data throughout this work (22). To avoid confusion on the terms specific and nonspecific used in our article, we have reserved the use of “specific” for the interaction of our interest, i.e., those between the uranyl chelate (UO2-DCP) and Mab U04S, whereas “nonspecific” refers to interactions between other constituents of the system.
For the theoretical part, we used the comparative modeling technique, an extremely useful tool to dissect the function role of surface residues in proteins (23), to build a molecular model of the variable fragment of Mab U04S. A UO2-DCP compound model was docked in the binding pocket of Mab U04S. Structural analysis of the bound complex was made in light of DFS results that led us to hypothesize a dissociation mechanism for this molecular system.
MATERIALS AND METHODS
Experimental setups and sample preparations
A Dimension 3100 AFM microscope with a Nanoscope IV controller (Digital Instrument Veeco, Santa Barbara, CA) was used for measuring unbinding forces of the molecular system. The experiments were carried out using the force mode of AFM that produces force-displacement curves. The external force applied through the cantilever tip to the system follows Hooke's law as a product of the cantilever spring constant, kc, and the deflection distance, dc. We independently determined the spring constants of all the gold-coated tips (Olympus Biolever, Olympus, Melville, NY; Veeco NPG), as previously described elsewhere (22). We measured standard error deviations on cantilever spring constants to be ∼10–25% for soft tips (<10 pN/nm) and 7–15% for stiff tips. The smallest detectable force of these cantilevers was 10 pN. Calibration of a new tip was routinely performed after every chemical treatment during the course of an AFM experiment. We obtained a wide range of loading rates by controlling either the retracting speed of the piezo scanner or the spring constant of the cantilever. For instance, a loading rate of 80,000 pN/s is obtained using the cantilever with a spring constant kc = 100 pN/nm and a vertical scanning frequency of 1 Hz (to approach and retract) over the ramp size of the piezo scanner at 400 nm.
Functionalization of gold-coated glass slides
The probed surface was prepared according to an adapted method of Brogan et al. (24) on an ultraflat gold-coated glass slide (generously provided by Pr. Joël Chopineau), as shown in Fig. 1 A. The glass slide was functionalized by a Protein A (ProtA) before linking Mab U04S to the surface (25). The gold-coated surface was pretreated with 10 nM mercapto-undecanoic acid in ethanol. After three rinses, the slide was incubated for 10 min in an aqueous solution v/v of 75 mg/mL ethyl-N-[3-diethylaminopropyl]carbodiimide and 11.5 mg/mL N-hydroxysuccinimide (NHS), followed by three rinses with acetate buffer and then submerged in 1 nM ProtA in 10 mM sodium acetate buffer (pH 4.8) followed by three rinses. Mab U04S was then added as drops of 0.1 ∼ 1.0 nM protein solutions in 10 mM phosphate buffer, pH 7.5 for 15 min. The final step was cross-linking of ProtA and Mab U04S via a bifunctional cross-linker using 1 μM dimethyl adipimidate (DMA, Pierce, Rockford, IL) for 15 min in 10 mM triethanolamine buffer, pH 8, followed by three rinses in 10 mM phosphate, 50 mM KCl buffer, pH 7.5. Finally, the slide surface was saturated with bovine serum albumin (BSA) (10 μg/ml) for 30 min in 10 mM phosphate buffer, at pH 7.5 (26). Loosely bound proteins were removed by rinsing with 10 mM phosphate, 50 mM KCl buffer, pH 7.5.
FIGURE 1.
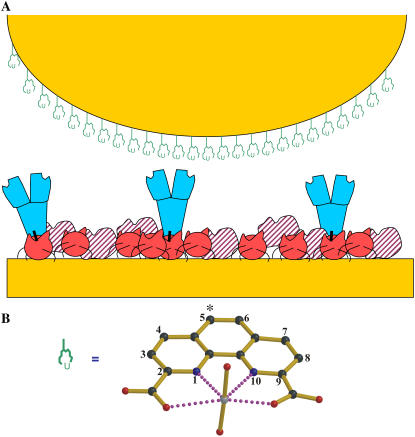
(A) A cartoon sketch displaying the distributions of chelated compounds over the functionalized tip and protein molecules deposited on the substrate surface in the four experimental setups (systems 1–4) for this study. The tip is represented by an orange half-sphere, and the gold-coated glass slide to support the substrate surface is drawn as an orange rectangle at the bottom; all molecules are described as follows: UO2-DCP compound is expressed as a schematic chemical representation, Mab U04S is blue and Y-shaped, protein A is red filled, BSA is in red-hashed shapes, and a chemical linking agent that covalently couples antibodies and protein A is represented by a vertical black bar. System 1: UO2-DCP attached on the tip, Mab U04S-protein A on the BSA saturated substrate surface with protein A attached on the surface. System 2: Only DCP on the tip, protein A-Mab U04S on the substrate surface as described for system 1. System 3: UO2-DCP on the tip, the substrate surface lacks Mab U04S. System 4: DCP linked to a PEG spacer that is attached on the tip, protein A-Mab U04S on the substrate surface as described for system 1. (B) Compound model of 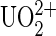 ion chelated by DCP, UO2-DCP. The coordination bonds between U and nitrogen or oxygen are indicated by purple dotted lines. In this model, one or two oxygens from Mab U04S may fulfill the first coordination sphere of the uranium metal. The symbol (*) indicates the atom to which the DCP is coupled to the tip.
ion chelated by DCP, UO2-DCP. The coordination bonds between U and nitrogen or oxygen are indicated by purple dotted lines. In this model, one or two oxygens from Mab U04S may fulfill the first coordination sphere of the uranium metal. The symbol (*) indicates the atom to which the DCP is coupled to the tip.
Functionalization of the tip coupled with DCP and [UO2-DCP]
The gold-coated tip was activated with 10 nM 5-thiouredoethanethiol-DCP or DCP-thiol (ERAS Labo, St. Nazaire les Eymes, France) in dimethyl formamide (DMF) at room temperature (RT) for 30 min, then rinsed in 10 mM HEPES solution, 150 mM NaCl buffer at pH 7.4. To ligate the 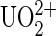 ion to DCP, the tip was loaded with
ion to DCP, the tip was loaded with 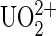 ions by incubating in 100 nM uranyl phosphate solutions at RT for 30 min. In case the functionalization failed, we first measured systematically unbinding events of our system without the
ions by incubating in 100 nM uranyl phosphate solutions at RT for 30 min. In case the functionalization failed, we first measured systematically unbinding events of our system without the 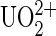 ion on the cantilever tips. At low occurrence of nonspecific unbinding events, the
ion on the cantilever tips. At low occurrence of nonspecific unbinding events, the 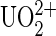 ion was then added to the tip and measurements proceeded.
ion was then added to the tip and measurements proceeded.
Functionalization of the tip coupled with DCP through a PEG spacer
The hetero bifunctional polyethylene glycol (PEG) spacer, NHS-PEG-MAL (Nektar Therapeutics, San Carlos, CA), which contains an activated ester group at one end and a maleimide group at the other end, was attached to the gold-coated tip. The gold-coated tip was pretreated with 50 μM cysteamine in water (Fluka-Sigma-Aldrich, St-Quentin Fallavier, France) at RT for 30 min followed by three rinses in HEPES (pH 8.2). The hetero bifunctional PEG spacer (10 nM in 10 mM HEPES buffer, pH 8.2) was incubated on the tip surface for 1 h at RT. After three rinses in phosphate buffer (10 mM, 50 mM KCl, pH 7.5), the tip was incubated with 10 nM DCP-thiol in DMF for 30 min. Excess of DCP was removed by rinsing the tip three times with 10 mM phosphate buffer, 50 mM KCl at pH 7.5.
Distribution density of molecules on glass slides
The height images of antibody deposited surfaces was obtained using the AFM tapping mode with a Nanoscope IIIA controller (Digital Instrument Veeco). Measurements were recorded at a frequency of 0.5 ∼ 1 Hz along the scanning line (512 × 512 pixels) and processed for flattening and plane correction using the Nanoscope software (Veeco). The oscillation amplitude of the cantilever tip was kept at the set-point value. All experiments were carried out at RT in air with humidity around 30%. The height images were determined by minimizing the interaction between the tip and the probed surface (27). Further improvements were made using the Fourier filtering option in the SPIP software (version V3.3.2.0, Image Metrology A/S, Lingby, Denmark). By analyzing the height images, we estimated the average distribution density of protA-Mab U04S complexes ∼2000/μm2 (Fig. 2). The substrate surface appeared completely covered, though nonuniformly, by a molecular assembly 4-nm high on average (Fig. 2).
FIGURE 2.
Height image of the substrate surface with coupled protein A-Mab U04S and BSA saturated as described in system 1. The image was obtained using the AFM tapping mode. The average of measured height is ∼4 nm; the scale bar on the bottom left represents 500 nm. The image depicts a completely protein-covered surface as judged by the indentation of the molecular layer at the center. In the picture, large white areas correspond to protein accumulation provoked by the indentation (contact mode), and smaller clearer spots represent single proteins.
Kinetics of [UO2-DCP]-Mab U04S binding
According to Bell's model, we assumed that dissociation of our molecular complex under an external force can be described in the transition state theory (8–11,28,29). Combining with the van't Hoff relation, the rate constant of the metal compound dissociated from the protein complex is accordingly expressed as
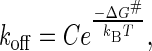 |
where ΔG# represents the activation free energy of the metal-protein complex; kB is the Boltzmann constant, T is the temperature, and C is the preexponential factor. In the absence of the applied force (F = 0), koff = k0 and ΔG# = ΔG0 for a dissociation reaction under the natural condition. The activation free energy under an external force along the dissociation coordinate was proposed in this form: ΔG# = ΔG0 − Fγ. The parameter γ is interpreted as the width to climb up the energy barrier to the transition state. The measured force is obtained from the required deflection distance dc to rupture the bond. To manifest the influence of applied force on the rate constant koff, we reexpressed koff as
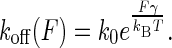 |
Consider the applied force as a linear function of time with the loading rate r as the proportional constant, then the dependence of koff at time t on force is solely reflected on the dependence of r. In a standard fashion of the kinetic theory, one may straightforwardly derive the formula for the most probable unbinding force as
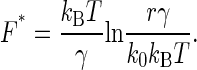 |
In turn, we may obtain the value of γ by plotting F* against ln(r) as well as k0 from the slope of the line fitting.
Force-displacement curve treatments
Force-displacement curves were first calibrated using the YieldFinder software (22). We determined the experimental loading rate, re, based on a multiple parallel bond system as (30)
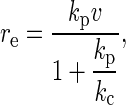 |
where v is the scan rate, kc corresponds to the spring constant of the cantilever, and kp represents the spring constant of proteins attached on the substrate and was obtained by the following relationship with the observed loading slope of the rupture event keq:
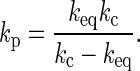 |
Corrected loading rates were assembled into 11 groups characterized by an averaged standard deviation of ∼7% for each group. On average each group is composed of 115 values. Then, the distribution of rupture forces was clustered into several bins ranging from 3 pN for small loading rates to 50 pN for large loading rates. Gaussian curves were used to fit each peak of the force distribution, allowing us to extract the most probable rupture forces, F*.
Three-dimensional models of UO2-DCP, Mab U04S, and their complex
The variable region of Mab U04S has been sequenced (T. Bessou, unpublished). We used the comparative modeling technique to build the three-dimensional structure of the recombinant variable fragment of Mab U04S (31,32). We identified the anti-Thermus aquaticus DNA polymerase antibody TP7 as the best template to model U04S. The sequence identity was ∼83% without insertions or deletions. The crystal structure used (Protein Data Bank (PDB) code 1AY1) for both light and heavy chains was determined at 2.2-Å resolution (33). Side chains were replaced, optimized (23), and refined by a computational graphic procedure that takes advantage of a database of well-known antibody structures (34). All atomic positions were energy minimized using X-PLOR (35) with the CHARMM22 force field parameters (36). The model quality was evaluated by PROCHECK (37) with 82.3% of φ,ψ dihedral angles in the most favorable regions.
The structure of DCP was obtained from the Cambridge Structural Database (code XAMHOJ, (38)), with a Ni atom coordinated and several bound water molecules around. We replaced the Ni atom and two axial water molecules by uranyl and two uranium-bound oxygen atoms with the U-O bond length of 1.8 Å. Then this modeled compound was used in computational visual graphics docking. Chelated UO2 preferentially binds to carboxylic groups in proteins (39). Only three aspartic acids are present in antibody CDRs: in CDRL2, CDRH1, and CDRH3. The AspH-30A in CDRH1 is located on the top of the antibody fragment (Fab) and could not make direct interactions with a ligand bound in the binding pocket. The other two constitute potential coordination residues to ligate with UO2. Accordingly, two molecular models were made with different CDRH3 conformations. In model A, the CDRH3 conformation was inherited from the template antibody 1AY1, the predicted coordinating residue with UO2 was AspH-100 (Kabat numbering). In model B, the CDRH3 conformation was modified to enable AspL-50 (Kabat numbering) to coordinate with UO2.
RESULTS
For convenience, we have notated the different combinations of experimental setups as system 1, UO2-DCP chelate on the tip, protein A-Mab U04S on the gold-coated glass slide (substrate) saturated with BSA; system 2, only DCP compound on the tip, protein A-Mab U04S on the substrate saturated with BSA; system 3, UO2-DCP chelate on the tip, the substrate lacks the antibody Mab U04S; system 4, only DCP compound attached on the tip through a PEG spacer, protein A-Mab U04S on the substrate saturated with BSA. Fig. 1 presents a schematic picture describing compounds and molecules distributed over the tip and the substrate. The structure of the experimental system was shown to be a uniform monolayer as confirmed by the height image of the substrate in Fig. 2.
Interactions between UO2-DCP and Mab U04S
Interactions between the UO2-DCP chelate complex and Mab U04S were measured using DFS on system 1. A total of 5198 unbinding events was performed on system 1 over 11 different loading rates. The averaged separation distance between tip and sample surface was 16.8 and 23.4 nm for the measurements performed at the loading rate of 1002 ± 120 and 2060 ± 210 pN/s, respectively. From crystallographic data, the heights of Fc and Fab fragments are known as 7 and 8 nm, respectively. Besides, a flexible linker between the Fc and Fab as well as the flexibility of protein A underneath the antibody may also contribute to distance lengthening. Taken all together, it implies that the measured separation distance (∼20 nm) is in good agreement with our experimental setups.
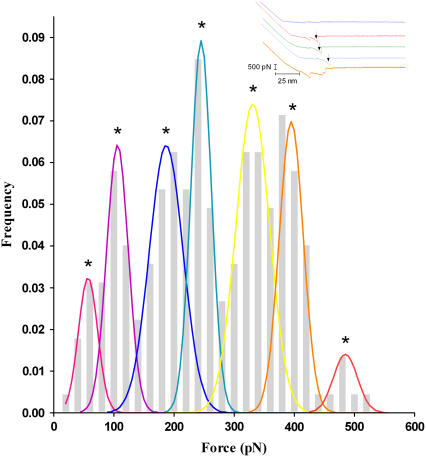
Among identified unbinding events, 1263 isolated rupture peaks from the force-displacement curves for analysis (Fig. 3, inset) were selected using our in-house software YieldFinder (22). The isolated rupture peak was defined as the one starting and ending near the baseline. A typical distribution of unbinding forces for specific interactions, at a given loading rate of 2060 pN/s, is displayed in Fig. 3. As shown in Fig. 3, a distribution of multiple unbinding populations is also observed at each tested loading rate.
FIGURE 3.
Frequency histograms of unbinding events obtained at the loading rate of 2060 pN/s. The bin size of unbinding force is 20 pN. Peaks in the histograms were fitted using Gaussian functions, as described in previous work (22). The maximum value of each Gaussian curve corresponds to the most probable unbinding forces F*. Inset shows typical experimental force-displacement measurements. The top curve indicates no occurrence of unbinding events. Unbinding peaks were selected only if they are well isolated; i.e., starting and ending near the baseline, for example those indicated by a black arrow in the blue, green, and red curves. No peak was considered in the orange curve.
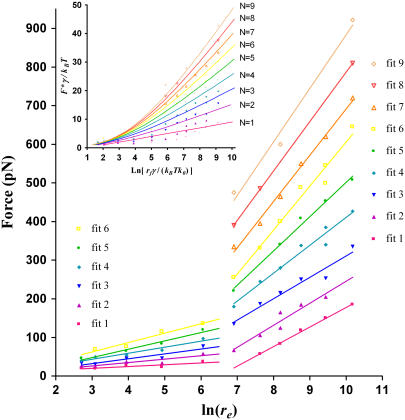
To obtain the interaction parameters of [UO2-DCP]-Mab U04S binding, we determined the most probable rupture forces (F*) from the maximum of the fitting curves in Fig. 3, then we plotted F* with respect to the logarithm of the experimental loading rate. Fig. 4 shows the results over the range of loading rate from 15 to 2.64 × 104 pN/s. Two regimes could be determined in the plot: one located in the region of low loading rates (<665 pN/s) and the other one in the region of high loading rates (>665 pN/s). The detailed procedure of obtaining multiple regression lines in Fig. 4 has been described elsewhere (22). Briefly, one parent regression line that fits all the data points was drawn first. Then, we generated lines parallel to the parent regression line in such a manner that each line can fit as many points as possible. Finally, the points associated with each line were used to compute the corresponding regression line. We obtained values >0.74 and >0.95 of the correlation coefficient for regression line at low and high loading rates, respectively. Interaction parameters γ and k0 (see Materials and Methods) were derived from these regression lines (Table 1). Standard errors were obtained using the fitted curve equations as given in the GraphPad Prism software (GraphPad, San Diego, CA). Clearly, errors are greater for the extrapolated k0 values than for the slope-derived γ values.
FIGURE 4.
Plots of the most probable unbinding forces F* versus the natural logarithm of the experimental loading rate on the biochemical bonds. Due to multiplicity of F* at one loading rate, we have drawn multiple linear regression lines for multiple populations of forces (see text for details). Six fits were present in the low loading rate region (<665 pN/s); whereas nine fits were found in the high loading rate region (>665 pN/s). Inset indicates fitting lines (normalized coordinates) of the normalized distribution of F* versus normalized loading rates, according to the Williams model of rupture force of multiple attachments loaded in parallel using a γ = 0.19 nm and k0 = 0.13 s−1 (49).
TABLE 1.
Kinetic parameters characterizing the interactions between UO2-DCP and Mab U04S
| Fit 1 | Fit 2 | Fit 3 | Fit 4 | Fit 5 | Fit 6 | Fit 7 | Fit 8 | Fit 9 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| High loading rate* | γ (nm) | 0.08 ± 0.00‡ | 0.07 ± 0.01 | 0.07 ± 0.01 | 0.06 ± 0.01 | 0.05 ± 0.00‡ | 0.04 ± 0.00‡ | 0.03 ± 0.00‡ | 0.03 ± 0.00‡ | 0.03 ± 0.00‡ |
| k0 (s−1) | 13.2 ± 6.0 | 5.2 ± 3.0 | 1.4 ± 3.9 | 1.0 ± 1.8 | 0.9 ± 0.8 | 1.5 ± 1.3 | 0.6 ± 0.3 | 0.4 ± 0.3 | 0.3 ± 0.8 | |
| Low loading rate† | γ (nm) | 0.89 ± 0.39 | 0.47 ± 0.16 | 0.33 ± 0.09 | 0.26 ± 0.04 | 0.19 ± 0.03 | 0.17 ± 0.03 | NO§ | NO | NO |
| k0 (s−1) | 0.06 ± 0.2 | 0.11 ± 0.4 | 0.12 ± 0.4 | 0.08 ±0.09 | 0.10 ± 0.12 | 0.06 ± 0.1 | NO | NO | NO |
1002–26400 pN/s.
14–428 pN/s.
<0.005.
Not observed.
Nonspecific interactions in force-displacement measurements
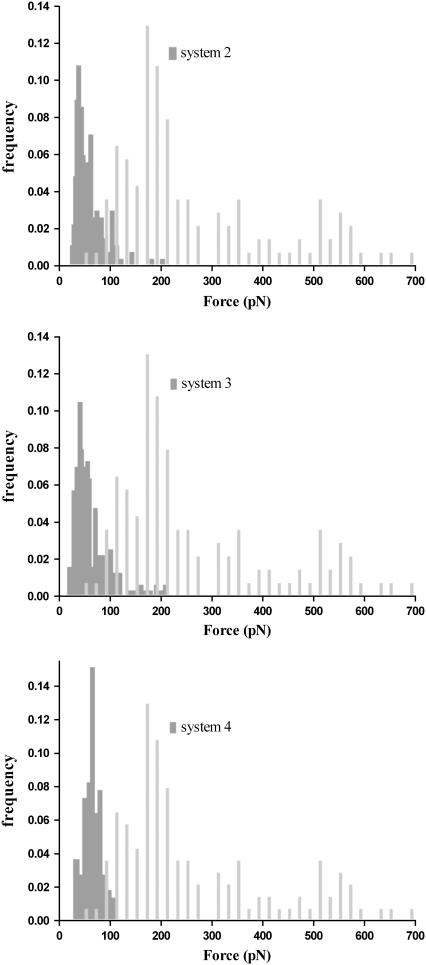
Nonspecific interactions have been measured experimentally by removing one component from system 1 (either the uranyl or the antibody, systems 2 and 3, respectively). It was suggested that adding a linker between the tip and a ligand should produce less nonspecific interactions. We have used a PEG linker (system 4) to perform measurements for studying nonspecific interactions. Contrary to specific unbinding events observed in system 1, the distribution of unbinding events corresponding to systems 2–4 at high loading rates are described by a single population, shown in Fig. 5. Similar findings were observed in the same systems at low loading rates (data not shown). In both conditions, most unbinding events occur at a force <120 pN. This can be further illustrated by superimposing the histograms of event frequencies from specific (system 1) and nonspecific (systems 2–4) interactions. Fig. 5 reveals that nonspecific rupture forces slightly overlap with rupture events obtained at low forces. The overlapping rupture events correspond to those identified in the first fits in Fig. 4. It indicates that nonspecific interactions can be characterized with a very weak binding strength. Concerning the effect of a PEG linker on the distribution of nonspecific interactions, it appears that the added flexibility did not markedly alter the measurements (Fig. 5). These results highlight the robustness of determination of nonspecific unbinding events in our system.
FIGURE 5.
Distribution of frequency histograms of unbinding events obtained between nonspecific and specific interactions. Specific interactions were measured at 6400 pN/s and are presented in light gray-filled bars. The dark gray-filled histograms from top to bottom correspond to systems 2, 3, and 4 at the applied loading rate of 5580, 2900, and 5600 pN/s, respectively. The bin size for nonspecific unbinding force is 3 pN. The selection of isolated unbinding peaks leads from force-displacement curves to a noteworthy reduction of nonspecific noises.
Three-dimensional model of Mab U04S
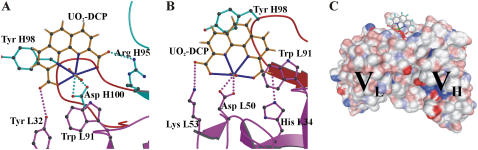
A comparative model of Mab U04S was performed using standard antibody modeling protocols (23,32). The sequence identity between the selected template antibody 1AY1 and Mab U04S is ∼83% across both the light and heavy chains. The root mean-square deviation between Cα atoms of the template and the U04S model is 0.12 Å, over a total of 222 out of 227 residues excluding the five residues from the CDRH3. Uranyl ions are usually tightly coordinated with five or six oxygen atoms in the equatorial plane (Fig. 1 B). A recent survey of chelated uranyl ions in proteins revealed that the most frequent ligating residues are aspartic and glutamic acid (39). There are only three aspartic acids available among the six hypervariable loops in Mab U04S: AspL-50 in CDRL2, AspH-30A in CDRH1, and AspH-100 in CDRH3. The one in CDRH1 is not appropriate for making close contact toward a bound ligand. Thus, two molecular models, A and B, were built in which UO2-DCP were positioned so that the carboxyl groups of aspartic acids fulfilled the coordination sphere of UO2 in a bidentate manner (Fig. 6, A and B). The two aspartic acids are located in a solvent-exposed region; the binding site in each model is rather shallow (shown in Fig. 6 C). Such a “flat” binding pocket is reminiscent of the template antibody 1AY1, an antiprotein antibody. The location of the antigen binding site in either model is very close to each other. Both of them share a common list of interacting residues such as TyrH-98, TyrL-32, and TrpL-91. Residues TyrH-98 and TrpL-91 flank the UO2-DCP compound. In both models, atom C5 of DCP, used to graft the DCP onto a carrier protein, is completely solvent exposed. On the contrary, model A reveals one carboxyl group of DCP forming a salt bridge with ArgH-95 (Fig. 6 A), whereas model B illustrates this carboxyl group making the salt bridge with LysL-53 (Fig. 6 B).
FIGURE 6.
Three-dimensional model of Mab U04S variable fragment. The light chain (VL) is colored in magenta and the heavy chain (VH) is in cyan. (A) The CDRH3 conformation (red) is similar to the template antibody 1AY1. The uranium atom is chelated with DCP (orange sticks) through navy blue bonds. An interaction between the  and Mab U04S (magenta and cyan sticks) is made through coordination bonds between the uranium atom and the antibody residue AspH-100. AspH-100 is located at the center of CDRH3, near the bottom of the binding pocket. In this model, DCP makes hydrogen bonds with ArgH-95 (CDRH3) and TyrL-32 (CDRL1). (B) The CDRH3 conformation was remodeled so that the uranium atom can be coordinated with AspL-50 (CDRL2). In this model, DCP forms a hydrogen bond with HisL-34 (CDRL1) and a salt bridge with LysL-53 (CDRL2). In both models A and B, the UO2-DCP compound is sandwiched between TyrH-98 (CDRH3) and TrpL-91 (CDRL3) and is solvent exposed in such a manner that a linkage through a protein carrier is allowed. The figures were constructed using Molscript (60) and rendered using Raster3D (61). (C) Molecular surface of Mab U04S variable fragment. Colorization is according to the DG scheme using the PMV software (62). The picture illustrates a shallow depth of the binding pocket of Mab U04S toward UO2-DCP (colored balls and sticks) estimated as γ ≈ 4 Å for the outer activation barrier from DFS results.
and Mab U04S (magenta and cyan sticks) is made through coordination bonds between the uranium atom and the antibody residue AspH-100. AspH-100 is located at the center of CDRH3, near the bottom of the binding pocket. In this model, DCP makes hydrogen bonds with ArgH-95 (CDRH3) and TyrL-32 (CDRL1). (B) The CDRH3 conformation was remodeled so that the uranium atom can be coordinated with AspL-50 (CDRL2). In this model, DCP forms a hydrogen bond with HisL-34 (CDRL1) and a salt bridge with LysL-53 (CDRL2). In both models A and B, the UO2-DCP compound is sandwiched between TyrH-98 (CDRH3) and TrpL-91 (CDRL3) and is solvent exposed in such a manner that a linkage through a protein carrier is allowed. The figures were constructed using Molscript (60) and rendered using Raster3D (61). (C) Molecular surface of Mab U04S variable fragment. Colorization is according to the DG scheme using the PMV software (62). The picture illustrates a shallow depth of the binding pocket of Mab U04S toward UO2-DCP (colored balls and sticks) estimated as γ ≈ 4 Å for the outer activation barrier from DFS results.
DISCUSSION
In the study of force-induced bond rupture, the unbinding process of a ligand-receptor pair is governed by a force applied in the direction of the dissociation coordinate. Exploiting the stochastic characteristics of unbinding event measurements, the thermodynamic parameters in bulk solutions can be derived from samplings of single-molecule kinetics (11,40,41). Very few systems for ligand-receptor unbinding are described and none dealt with metal-protein unbinding. To highlight difficulties in DFS experiments, one might notice that even the most studied case (avidin-biotin) is still subject to many theoretical refinements (42,43). In this work, we performed detailed analysis on the interaction between a UO2 chelate and a Mab. A great advantage of single-molecule study is the low impact of inactive molecules on measurements compared to bulk solution measurements (44). Provided with different combinations of interacting pairs, we have measured explicitly the nonspecific interactions, which allowed us to estimate their influence on the specific interactions.
Treatments of nonspecific interactions
Mab U04S shows no detectable affinity for DCP; therefore we used the DCP-functionalized tips (systems 2 and 4) as a reference to distinguish nonspecific unbinding events. Data analysis of force-displacement measurements revealed that the distribution of rupture events is slightly overlapped with specific and nonspecific interactions. However, nonspecific unbinding events show marginal dependence of F* on the loading rate (data not shown) and appear in the force-rupture distribution as a single population (Fig. 5). Thus, we cannot exclude the possibility that rupture force measurements do correspond to nonspecific interactions, at least for the first population in the force distribution (Figs. 3 and 5). It was suggested that nonspecific unbinding events can be reduced by covalently coupling the ligand or receptor to a flexible spacer (21,45–47). We have tested this suggestion using system 4, where DCP was covalently coupled to a PEG spacer that was directly attached to the tip. Although the distribution of nonspecific unbinding events appeared to be more uniform in system 4 (Fig. 5), the values of F* were in the same range as that in systems 2 and 4.
Detection of multivalent interactions
Avidity is a natural and important property in antigen-antibody interactions, leading to accrued complexity in antibody systems. That is, antibodies can bind antigens through either one or both paratopes. In system 1, the AFM tip attaching UO2-DCP compounds may interact with multiple antibodies on the substrate due to the small size of the chelate. This has already been observed in a system of divalent metal and polyhistidine peptides (48). Unfortunately, the dependency of F* on the loading rate was not further analyzed for that system. From the distribution of F* at various loading rates, we gained insight into multivalent interactions of [UO2-DCP]-Mab U04S complex. At low loading rates (<665 pN/s), we have fitted the plot of F* versus ln(re) to six straight lines, whereas at higher loading rates, nine lines were required (Fig. 4). The multiple fitting lines characterize an unbinding process of multiple “bonds”. To confirm our findings, we modeled our data as the rupture of multiple identical bonds in parallel, according to a recent development that assumes each binding attachment sharing the applied force equally and the time to break N attachments equal to the sum of the time breaking each attachment (49). The relationship between the measured loading rate, rf, and the measured rupture force, F*, can be described by the following equation:
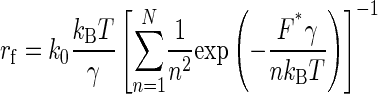 |
Using normalized forces and loading rates (21), the predicted loading rate, rf, in function of the force rupture, F* (Fig. 4 inset), reveals the presence of multiple parallel bonds. Fig. 4 (inset) shows the maximum number of parallel bonds equal to nine that is in accord with the fitted lines observed in Fig. 4. As a result, our system has six and nine parallel bonds corresponding to three to four antibodies since each antibody has two antigen binding fragments (Fabs). This is also consistent with a geometric estimation of the cantilever tip surface. With a radius 40 nm of the tip that penetrates into the substrate layer at maximum by 4 nm, a surface area of spherical cap equals 1005 nm2. The coating density of our system 1 is ∼2 antibodies per 1000 nm2, in close agreement with the maximum number of observed multiple parallel bonds (three to four antibodies).
Very interestingly, Williams's scheme for parallel bonds (49) does not simultaneously resolve the rupture forces into different interaction modes among the range of loading rates, as shown in Fig. 4 with two slopes. By applying Bell's model, the results are very informative in revealing the presence of two energy barriers in the energy landscape.
Affinity of chelated metal-antibody interactions
Based on Bell's model (9,12), we obtained a biphasic plot of F* against ln(re) over a range of loading rate (up to 103) similar to what was used in other antigen-antibody systems (19–21). However, we avoided employing a higher speed to prevent the tip and sample from alterations and limited the maximum contact force to several hundred piconewtons (50).
Since we have shown the specific interaction between UO2 and Mab U04S, we expect that the uranyl plays a major role in the binding process. Knowing that the uranyl preferentially binds to acidic side chains of proteins, we modeled the interaction between DCP-UO2 and Mab U04S such that UO2 is able to fulfill its first coordination sphere with negatively charged residues (Fig. 6). A structural analysis was performed on the molecular model of [UO2-DCP]-Mab U04S complex at an atomic level. From Fig. 6, the UO2-DCP compound was inserted into the shallow binding pocket of Mab U04S in such a way that the atom U is coordinated with a solvent exposed residue, AspL-50 in model A and AspH-100 in model B, and the DCP ligand enhances the binding strength by forming a putative salt bridge with LysL-53 and ArgH-95 in model A and B, respectively. A similar interaction pattern can be found in the MOAD binding database (51) where a chelate compound strongly interacts with the antibody (PDB code 1IND (52)). In their system, the chelate compound contains an indium ion coordinated with an EDTA derivative. The coordination of the indium ion is completed by a histidine residue in CDRH3, whereas most of the carboxylic groups of EDTA make salt bridges with positively charged residues in the binding pocket. It has been shown that these salt bridges play an important role in the affinity of metal compound-antibody complex (53). Likewise, DCP in our antibody complex is in direct contact with Mab U04S at the atomic level.
The biphasic pattern observed in the plot of F* versus the logarithm of the loading rate has been interpreted as characteristic of an inner and outer activation barrier (15,18,54), though still under debate (55–57). Supported by our molecular modeling data, we interpret the inner activation barrier as to rupture the coordination bonds of UO2 with antibody residue (AspL-50 or AspH-100), a process with a very narrow barrier width (γ < 1 Å). The outer activation barrier corresponds to detaching the entire chelate compound UO2-DCP from the antibody binding pocket through nonbonded interactions such as salt bridges (>3 Å), a process characterized with a broader barrier width (γ > 1 Å).
The kinetic information about [UO2-DCP]-Mab U04S dissociation under the natural condition (without external forces) is provided in Table 1. The values of the kinetic dissociation constant k0 at zero force range from 0.3 to 13.2 s−1 at high loading rates and 6.0 × 10−2 to 0.12 s−1 at low loading rates. The decreasing k0 toward higher rate populations in Fig. 4 is strongly supportive of multivalency in [UO2-DCP]-Mab U04S interactions. Assuming a value of 3 × 105 M−1s−1 for kon (58), the equilibrium affinity constant was evaluated in the order of 1.0 × 106 M−1 to 2.3 × 104 M−1 at high loading rates and 5 × 106 M−1 to 2.5 × 106 M−1 at low loading rates. The estimated value is in the range comparable to another chelated-metal-antibody system that the affinity constant was measured experimentally as from 5 × 107 to 103 M−1 (59).
Acknowledgments
We thank L. Reisser for preparing and purifying antibodies, S. Coullet for sequencing U04S, and A. Lorphelin and O. Pible for helpful discussions.
This work has been supported by the program for environmental nuclear toxicology of the Commissariat à l'Énergie Atomique (CEA), France.
Michael Odorico and Jean-Marie Teulon contributed equally to this work.
Editor: Jane Clarke.
References
- 1.Foulkes, E. C. 2000. Transport of toxic heavy metals across cell membranes. Proc. Soc. Exp. Biol. Med. 223:234–240. [DOI] [PubMed] [Google Scholar]
- 2.Craft, E., A. Abu-Qare, M. Flaherty, M. Garofolo, H. Rincavage, and M. Abou-Donia. 2004. Depleted and natural uranium: chemistry and toxicological effects. J. Toxicol. Environ. Health B Crit. Rev. 7:297–317. [DOI] [PubMed] [Google Scholar]
- 3.Vidaud, C., A. Dedieu, C. Basset, S. Plantevin, I. Dany, O. Pible, and E. Quemeneur. 2005. Screening of human serum proteins for uranium binding. Chem. Res. Toxicol. 18:946–953. [DOI] [PubMed] [Google Scholar]
- 4.Kaltsoyannis, N. 2003. Recent developments in computational actinide chemistry. Chem. Soc. Rev. 32:9–16. [DOI] [PubMed] [Google Scholar]
- 5.Blake, I. R., A. R. Pavlov, M. Khosraviani, H. E. Ensley, G. E. Kiefer, H. Yu, X. Li, and D. A. Blake. 2004. Novel monoclonal antibodies with specificity for chelated uranium(VI): isolation and binding properties. Bioconjug. Chem. 15:1125–1136. [DOI] [PubMed] [Google Scholar]
- 6.Binnig, G., C. F. Quate, and C. Gerber. 1986. Atomic force microscope. Phys. Rev. Lett. 56:930–933. [DOI] [PubMed] [Google Scholar]
- 7.Florin, E. L., V. T. Moy, and H. E. Gaub. 1994. Adhesion forces between individual ligand-receptor pairs. Science. 264:415–417. [DOI] [PubMed] [Google Scholar]
- 8.Guthold, M., R. Superfine, and R. M. Taylor. 2001. The rules are changing: force measurements on single molecules and how they relate to bulk reaction kinetics and energies. Biomed. Microdev. 3:9–18. [Google Scholar]
- 9.Bell, G. I. 1978. Models for the specific adhesion of cells to cells. Science. 200:618–627. [DOI] [PubMed] [Google Scholar]
- 10.Evans, E., and K. Ritchie. 1997. Dynamic strength of molecular adhesion bonds. Biophys. J. 72:1541–1555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Tinoco, I. Jr., and C. Bustamante. 2002. The effect of force on thermodynamics and kinetics of single molecule reactions. Biophys. Chem. 101–102:513–533. [DOI] [PubMed] [Google Scholar]
- 12.Merkel, R., P. Nassoy, A. Leung, K. Ritchie, and E. Evans. 1999. Energy landscapes of receptor-ligand bonds explored with dynamic force spectroscopy. Nature. 397:50–53. [DOI] [PubMed] [Google Scholar]
- 13.Fritz, J., A. G. Katopodis, F. Kolbinger, and D. Anselmetti. 1998. Force-mediated kinetics of single P-selectin/ligand complexes observed by atomic force microscopy. Proc. Natl. Acad. Sci. USA. 95:12283–12288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Baumgartner, W., P. Hinterdorfer, W. Ness, A. Raab, D. Vestweber, H. Schindler, and D. Drenckhahn. 2000. Cadherin interaction probed by atomic force microscopy. Proc. Natl. Acad. Sci. USA. 97:4005–4010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Yuan, C., A. Chen, P. Kolb, and V. T. Moy. 2000. Energy landscape of streptavidin-biotin complexes measured by atomic force microscopy. Biochemistry. 39:10219–10223. [DOI] [PubMed] [Google Scholar]
- 16.Chen, S., and T. A. Springer. 2001. Selectin receptor-ligand bonds: formation limited by shear rate and dissociation governed by the Bell model. Proc. Natl. Acad. Sci. USA. 98:950–955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zhang, X., and V. T. Moy. 2003. Cooperative adhesion of ligand-receptor bonds. Biophys. Chem. 104:271–278. [DOI] [PubMed] [Google Scholar]
- 18.Li, F., S. D. Redick, H. P. Erickson, and V. T. Moy. 2003. Force measurements of the alpha5beta1 integrin-fibronectin interaction. Biophys. J. 84:1252–1262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Schwesinger, F., R. Ros, T. Strunz, D. Anselmetti, H. J. Guntherodt, A. Honegger, L. Jermutus, L. Tiefenauer, and A. Pluckthun. 2000. Unbinding forces of single antibody-antigen complexes correlate with their thermal dissociation rates. Proc. Natl. Acad. Sci. USA. 97:9972–9977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kienberger, F., G. Kada, H. Mueller, and P. Hinterdorfer. 2005. Single molecule studies of antibody-antigen interaction strength versus intra-molecular antigen stability. J. Mol. Biol. 347:597–606. [DOI] [PubMed] [Google Scholar]
- 21.Sulchek, T. A., R. W. Friddle, K. Langry, E. Y. Lau, H. Albrecht, T. V. Ratto, S. J. Denardo, M. E. Colvin, and A. Noy. 2005. Dynamic force spectroscopy of parallel individual mucin1-antibody bonds. Proc. Natl. Acad. Sci. USA. 102:16638–16643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Odorico, M., J.-M. Teulon, O. Berthoumieu, S.-w. W. Chen, P. Parot, and J.-L. Pellequer. 2007. An integrated methodology for data processing in dynamic force spectroscopy of ligand-receptor binding. Ultramicroscopy. In press. [DOI] [PubMed]
- 23.Chen, S.-w. W., and J. L. Pellequer. 2004. Identification of functionally important residues in proteins using comparative models. Curr. Med. Chem. 11:595–605. [DOI] [PubMed] [Google Scholar]
- 24.Brogan, K. L., J. H. Shin, and M. H. Schoenfisch. 2004. Influence of surfactants and antibody immobilization strategy on reducing nonspecific protein interactions for molecular recognition force microscopy. Langmuir. 20:9729–9735. [DOI] [PubMed] [Google Scholar]
- 25.Dammer, U., M. Hegner, D. Anselmetti, P. Wagner, M. Dreier, W. Huber, and H. J. Guntherodt. 1996. Specific antigen/antibody interactions measured by force microscopy. Biophys. J. 70:2437–2441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Allen, S. 1997. Detection of antigen-antibody binding events with the atomic force microscope. Biochemistry. 36:7457–7463. [DOI] [PubMed] [Google Scholar]
- 27.San Paulo, A., and R. Garcia. 2000. High-resolution imaging of antibodies by tapping-mode atomic force microscopy: attractive and repulsive tip-sample interaction regimes. Biophys. J. 78:1599–1605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Strunz, T., K. Oroszlan, I. Schumakovitch, H. Guntherodt, and M. Hegner. 2000. Model energy landscapes and the force-induced dissociation of ligand-receptor bonds. Biophys. J. 79:1206–1212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Friedsam, C., A. K. Wehle, F. Kühner, and H. Gaub. 2003. Dynamic single-molecule force spectroscopy: bond rupture analysis with variable spacer length. J. Phys. Cond. Mat. 15:1709–1723. [Google Scholar]
- 30.Erdmann, T. 2005. Stochastic dynamics of adhesion clusters under force. Thesis in Theoretische Physik. Universität Potsdam, Potsdam, Germany. 155.
- 31.Pellequer, J. L., B. Zhao, H.-I. Kao, C. W. Bell, K. Li, Q. X. Li, A. E. Karu, and V. A. Roberts. 2000. Stabilization of bound polycyclic aromatic hydrocarbons by a π-cation interaction. J. Mol. Biol. 302:691–699. [DOI] [PubMed] [Google Scholar]
- 32.Pellequer, J.-L., S.-w. W. Chen, Y.-s. Keum, A. E. Karu, Q. X. Li, and V. A. Roberts. 2005. Structural basis for preferential binding of non-ortho-substituted polychlorinated biphenyls by the monoclonal antibody S2B1. J. Mol. Recogn. 18:282–294. [DOI] [PubMed] [Google Scholar]
- 33.Murali, R., M. Helmer-Citterich, D. J. Sharkey, E. R. Scalice, J. L. Daiss, M. A. Sullivan, and H. M. Krishna Murthy. 1998. Structural studies on an inhibitory antibody against Thermus aquaticus DNA polymerase suggest mode of inhibition. Protein Eng. 11:79–86. [DOI] [PubMed] [Google Scholar]
- 34.Roberts, V. A., J. Stewart, S. J. Benkovic, and E. D. Getzoff. 1994. Catalytic antibody model and mutagenesis implicate arginine in transition-state stabilization. J. Mol. Biol. 235:1098–1116. [DOI] [PubMed] [Google Scholar]
- 35.Brünger, A. T. 1992. X-PLOR, version 3.1. A system for x-ray crystallography and NMR. Yale University Press, New Haven, CT.
- 36.MacKerell, A. D., D. Bashford, M. Bellott, R. L. Dunbrack Jr., J. D. Evanseck, M. J. Field, S. Fisher, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher III, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiorkiewicz-Kuczera, D. Yin, and M. Karplus. 1998. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B. 102:3586–3616. [DOI] [PubMed] [Google Scholar]
- 37.Laskowski, R. A., M. W. MacArthur, D. S. Moss, and J. M. Thornton. 1993. PROCHECK: a program to check the stereochemical quality of protein structures. J. Appl. Crystallogr. 26:283–291. [Google Scholar]
- 38.Xie, Y.-B., J.-R. Li, and X.-H. Bu. 2005. The synthesis and structure of the NiII complex of 1,10-phenanthroline-2,9-dicarboxylate: a three-dimensional network via hydrogen bonding interactions. J. Mol. Struct. 741:249–253. [Google Scholar]
- 39.Pible, O., P. Guilbaud, J.-L. Pellequer, C. Vidaud, and E. Quéméneur. 2006. Structural insights into protein-uranyl interaction: towards an in-silico detection method. Biochimie. 88:1631–1638. [DOI] [PubMed] [Google Scholar]
- 40.Keller, D., D. Swigon, and C. Bustamante. 2003. Relating single-molecule measurements to thermodynamics. Biophys. J. 84:733–738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Neumann, R. M. 2003. On the precise meaning of extension in the interpretation of polymer-chain stretching experiments. Biophys. J. 85:3418–3420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Pincet, F., and J. Husson. 2005. The solution to the streptavidin-biotin paradox: the influence of history on the strength of single molecular bonds. Biophys. J. 89:4374–4381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Schlierf, M., and M. Rief. 2006. Single-molecule unfolding force distributions reveal a funnel-shaped energy landscape. Biophys. J. 90:L33–L35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Azimzadeh, A., J. L. Pellequer, and M. H. V. Van Regenmortel. 1992. Operational aspects of antibody affinity constants measured by liquid-phase and solid-phase assays. J. Mol. Recogn. 5:9–18. [DOI] [PubMed] [Google Scholar]
- 45.Hinterdorfer, P., W. Baumgartner, H. J. Gruber, K. Schilcher, and H. Schindler. 1996. Detection and localization of individual antibody-antigen recognition events by atomic force microscopy. Proc. Natl. Acad. Sci. USA. 93:3477–3481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Willemsen, O. H., M. M. Snel, K. O. van der Werf, B. G. de Grooth, J. Greve, P. Hinterdorfer, H. J. Gruber, H. Schindler, Y. van Kooyk, and C. G. Figdor. 1998. Simultaneous height and adhesion imaging of antibody-antigen interactions by atomic force microscopy. Biophys. J. 75:2220–2228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Idiris, A., S. Kidoaki, K. Usui, T. Maki, H. Suzuki, M. Ito, M. Aoki, Y. Hayashizaki, and T. Matsuda. 2005. Force measurement for antigen-antibody interaction by atomic force microscopy using a photograft-polymer spacer. Biomacromolecules. 6:2776–2784. [DOI] [PubMed] [Google Scholar]
- 48.Schmitt, L., M. Ludwig, H. E. Gaub, and R. Tampe. 2000. A metal-chelating microscopy tip as a new toolbox for single-molecule experiments by atomic force microscopy. Biophys. J. 78:3275–3285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Williams, P. M. 2003. Analytical descriptions of dynamic force spectroscopy: behaviour of multiple connections. Anal. Chim. Acta. 479:107–115. [Google Scholar]
- 50.Hinterdorfer, P., and Y. F. Dufrene. 2006. Detection and localization of single molecular recognition events using atomic force microscopy. Nat. Methods. 3:347–355. [DOI] [PubMed] [Google Scholar]
- 51.Hu, L., M. L. Benson, R. D. Smith, M. G. Lerner, and H. A. Carlson. 2005. Binding MOAD (Mother Of All Databases). Proteins. 60:333–340. [DOI] [PubMed] [Google Scholar]
- 52.Love, R. A., J. E. Villafranca, R. M. Aust, K. K. Nakamura, R. A. Jue, J. G. Major Jr., R. Radhakrishnan, and W. F. Butler. 1993. How the anti-(metal chelate) antibody CHA255 is specific for the metal ion of its antigen: x-ray structures for two Fab'/hapten complexes with different metals in the chelate. Biochemistry. 32:10950–10959. [DOI] [PubMed] [Google Scholar]
- 53.Meyer, D. L., M. Fineman, B. W. Unger, and J. M. Frincke. 1990. Kinetics of the dissociation of indium-(p-substituted-benzyl)ethylenediaminetetraacetic acid hapten analogues from the monoclonal anti-hapten antibody CHA255. Bioconjug. Chem. 1:278–284. [DOI] [PubMed] [Google Scholar]
- 54.Zhang, X., E. Wojcikiewicz, and V. T. Moy. 2002. Force spectroscopy of the leukocyte function-associated antigen-1/intercellular adhesion molecule-1 interaction. Biophys. J. 83:2270–2279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Derenyi, I., D. Bartolo, and A. Ajdari. 2004. Effects of intermediate bound states in dynamic force spectroscopy. Biophys. J. 86:1263–1269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Marshall, B. T., K. K. Sarangapani, J. Lou, R. P. McEver, and C. Zhu. 2005. Force history dependence of receptor-ligand dissociation. Biophys. J. 88:1458–1466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Neuert, G., C. Albrecht, E. Pamir, and H. E. Gaub. 2006. Dynamic force spectroscopy of the digoxigenin-antibody complex. FEBS Lett. 580:505–509. [DOI] [PubMed] [Google Scholar]
- 58.Pellequer, J.-L., and M. H. V. Van Regenmortel. 1993. Measurement of kinetic binding constants of viral antibodies using a new biosensor technology. J Immunol. Meth. 166:133–143. [DOI] [PubMed] [Google Scholar]
-
59.Shreder, K., A. Harriman, and B. L. Iverson. 1996. Molecular recognition of a monoclonal antibody (AC1106) cross-reactive for derivatives of
 and
and 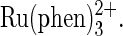 J. Am. Chem. Soc. 118:3192–3201. [Google Scholar]
J. Am. Chem. Soc. 118:3192–3201. [Google Scholar] - 60.Kraulis, P. J. 1991. MOLSCRIPT: a program to produce both detailed and schematic plots of protein structures. J. Appl. Crystallogr. 24:946–950. [Google Scholar]
- 61.Merritt, E. A., and D. J. Bacon. 1997. Raster3D: photorealistic molecular graphics. Meth. Enzymol. 277:505–524. [DOI] [PubMed] [Google Scholar]
- 62.Sanner, M. F. 1999. Python: a programming language for software integration and development. J. Mol. Graph. Model. 17:57–61. [PubMed] [Google Scholar]