Abstract
Allelic association provides a means to map disease genes that, in a dense map of polymorphic markers, has considerably higher resolution than linkage methods. We describe here a composite likelihood estimate of location for a disease gene against a high-resolution marker map by using allele frequencies at linked loci. Data may be family-based, as in the transmission disequilibrium test, or from a case-control study. χ2 tests, logarithm of odds, standard errors, and information weights are provided. The method is illustrated by analysis of published cystic fibrosis haplotypes, in which ΔF508 is more accurately localized than by other association studies. This differs from current approaches by adopting a more general Malecot model for isolation by distance, where distance here is between marker and disease locus, allowance for errors in the map and model, and freedom from assumptions about demography, systematic pressures, and the ratio of physical to genetic distance. When these assumptions are introduced the number of generations since the original mutation may be estimated, but this is not required to determine location and its standard error, so that evidence from allelic association may be efficiently combined with linkage evidence to identify a region for positional cloning of a disease gene.
Keywords: disease gene mapping, Malecot model, cystic fibrosis
Dependence of allele frequencies at two loci is called allelic association, linkage disequilibrium, or gametic disequilibrium. We shall use the first term. Spurious allelic association is not characteristic of the population, but is either a type 1 error or is induced by biased sampling or typing. Real allelic association can be confirmed in multiple samples. Allelic association mapping depends on the association of specific marker alleles with a disease mutation and the expectation of greater association as the disease locus is approached. The strength of the association depends on pressure to disrupt haplotypes of linked loci by recombination and mutation and the effects of selection and drift. Data may be family-based or a case control study of individuals without close relationship. Linkage mapping requires cosegregation of marker and disease alleles within a family and can involve any allele at the marker locus. Allelic association provides a means to map genes for disease susceptibility that is independent of linkage evidence and, in favorable cases, has greater resolution. To exploit this we require an integrated map that combines genetic and physical evidence, an estimate of location on the same scale for linkage and association, and efficient weights by which they may be combined to give a single, optimal estimate and test of significance that in principle are the same as for two linkage samples. Here we show how such an analysis may be performed by the allass program for testing, estimating, and mapping allelic association. allass is written in C and is available from http://cedar.genetics.soton.ac.uk/public_html/.
Association ρ
Assuming that recombination dominates systematic pressure of mutation, selection, and long-range migration (with which it is confounded), the natural measure of allelic association is
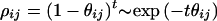 |
1 |
where θij is the recombination rate per gamete per generation between loci I and J, t is the number of generations during which the population has been approaching equilibrium, and ρij is the (coefficient of) association between I and J (1). Neglecting stochastic variation because of finite population size, the expected frequency of haplotypes with allele u at locus I and allele v at locus J is
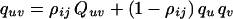 |
2 |
where qu, qv are the marginal gene frequencies (assumed constant in time) and Quv was the corresponding haplotype frequency among founders t generations ago (u = 1,.., U and v = 1,.., V).
Attempts to apply this theory encounter the problems that the founder haplotype frequencies Quv are unknown and the model is greatly simplified. Therefore, ρ has been neglected in favor of kinship ϕ, a metric based on χ2 with (U − 1) (V − 1) degrees of freedom that does not require estimation of Quv (2). Usually the power of parsimonious models, even if approximate, is greater than for models with many degrees of freedom (3). Illustrations of this principle in genetics include tests of Hardy–Weinberg equilibrium (4) and of oligogenic linkage (5). We therefore conjectured that maximum likelihood estimation of a single value of ρ for each marker locus, where applicable, would provide the most reliable inference about allelic association and therefore about the location of disease genes. Models with multiple values of ρ, measuring the association between each marker allele and the disease locus, imply an equal number of unknown values of Quv, and no general theory has been developed that is biologically meaningful and efficiently estimable (6). However, the special case of a 2 × 2 haplotype table has proven manageable and useful. The cells of each table give counts for a given marker allele where a represents disease haplotypes with the allele, b gives disease haplotypes without the allele, and c and d represent the corresponding normal haplotypes. Given a two-allele disease locus, the only practical problem is to reduce a U-allele marker locus to two alleles.
Merging Associated Marker Alleles
We reduce U 2 × 2 tables for disease allele × marker allele by merging associated alleles through a stepwise process. The allele with the largest value of χ2 is taken to be associated, whether χ2 is significant or not. Thus, at each marker there is at least one allele in the “associated” class (and this association may be positive or negative). For each table, if the determinant ad − bc is negative, this corresponds to a (possibly spurious) protective marker allele, and only similar protective alleles will be pooled into the associated class. A positive value of ad − bc corresponds to a (possibly spurious) susceptibility allele to be pooled with similar susceptibility alleles. Then for U > 2, the selected allele is excluded and the test is repeated on the remainder, only significant association being accepted. We define significance as χ12 with Yates’ correction >5 without a Bonferroni correction for the number of tests. In our experience this gives an acceptable balance between type I and type II errors. This process is continued until only one allele remains or no remaining allele is significant. Table 1 defines the final haplotype counts as 2 × 2 tables for each marker. Formally this procedure is the same as has been used to designate founders in a phylogeny (7), but here the associated alleles are pooled into one class and the remaining alleles are pooled into the second class. When a marker has both positively and negatively associated alleles, it is treated as two loci with the same location, one with positively associated alleles versus the rest, the other with negatively associated alleles versus the rest. In the latter case, a and b are interchanged, as are c and d, so that ρ > 0. As with any assumption, the equality of ρ for different alleles and for positive and negative associations may be questioned. “Protective” marker alleles reflect haplotypes in which few disease mutations have occurred, but recombination is the same as for positively associated alleles at the same locus. For a diallelic locus the absolute values are equal. Although no model can include all possible deviations, the analysis makes allowance for errors by separating the estimation of ρ for each marker locus (Table 1) from its expected value. The disease frequency determines an enrichment factor ω as the ratio of the number of cases to controls divided by the ratio of disease frequency to normal in the population of haplotypes. Introduction of ω makes it unnecessary to approximate the associated marker allele frequency R in the population by its frequency among controls (6). This approximation is poor unless Q ≪ R.
Table 1.
Haplotype frequencies by population
| Disease | Population | Marker
|
Total | |
|---|---|---|---|---|
| Disease-associated allele + | Nonassociated allele − | |||
| Disease allele | Founders | Q | 0 | Q |
| + | Equilibrium | QR | Q (1 − R) | Q |
| Cohort | Qρ + QR (1 − ρ) | (1 − ρ) Q (1 − R) | Q | |
| Case-control | f11 = ωQ [ρ + R (1 − ρ)]/Σ | f12 = ω (1 − ρ) Q (1 − R)/Σ | ωQ/Σ | |
| Observed (counts) | a | b | ||
| Normal allele | Founders | R − Q | 1 − R | 1 − Q |
| − | Equilibrium | R (1 − Q) | (1 − R) (1 − Q) | 1 − Q |
| Cohort | (R − Q) ρ + R (1 − Q) ( 1 − ρ) | (1 − R) [ρ + (1 − Q) (1 − ρ)] | 1 − Q | |
| Case-control | f21 = [(R − Q) ρ + R (1 − Q) (1 − ρ)]/Σ | f22 = (1 − R) [ρ + (1 − Q) (1 − ρ)]/Σ | (1 − Q)/Σ | |
| Observed (counts) | c | d | ||
| Total (except case-control) | R | 1 − R | 1 | |
Σ = 1 + (ω − 1) Q
For the ith marker locus all parameters are subscripted by i. lnlk = a ln f11 + b ln f12 + c ln f21 + d ln f22; Q = disease gene frequency; R = disease-associated marker allele frequency; ω = sample enrichment factor; ρ = association.
In passing we make obvious extensions. If a quantitative trait is substituted for a disease dichotomy, the regression of the trait on the number 0, 1, or 2 of marker alleles is proportional to ρ. In the transmission disequilibrium test at least one parent is heterozygous for a marker allele associated with the disease. Therefore, the marker allele has frequency r = 0.5. The test uses only affected offspring, controls are omitted, and the transmission frequency from a marker heterozygote to affected children is (1 + ρ)/2 (8).
Location SD
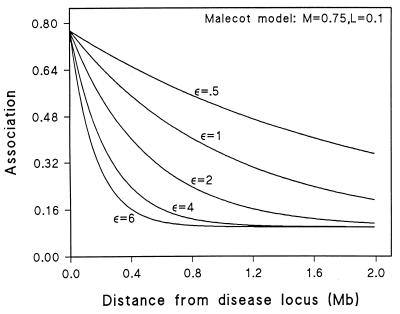
Because alleles have been dichotomized by disease association, we may simplify the notation by letting ρ̂i be the maximum likelihood estimate of association between disease and the ith marker locus with information Ki given in the Appendix. Assuming that allelic association is declining from a higher level in founders, association plausibly follows the Malecot model for isolation by distance (1),
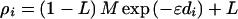 |
3 |
The Malecot model was derived to describe kinship as a function of distance between populations. We adapt it here to represent distance between marker and disease locus. The general characteristics of the Malecot model are illustrated in Fig. 1. The parameter M reflects a monophyletic or polyphyletic origin of susceptible haplotypes and is 1 if there is a unique susceptible haplotype and marker mutation is negligible, and less than 1 otherwise; ɛ > 0 is dependent on the number of generations during which the haplotypes have been approaching equilibrium and the pressure to disrupt them by recombination, mutation, and perhaps selection; L is the bias due to spurious association in the sample resulting from the constraint ρ̂i > 0, and di ≥ 0 is the distance between disease locus and the ith marker locus (9). Departures from the model including mutational heterogeneity, errors in the map, disproportion between physical distance and recombination, failure to report nonsignificant values of ρ, and neglect of associated alleles other than the most significant can distort estimates of M and L.
Figure 1.
Association is described as a function of distance from disease to marker locus in megabases and parameters, with ɛ reflecting the number of generations since the original mutation, M reflecting mono- or polyphyletic origin of the mutation, and L representing bias introduced by assuming at least one associated allele per marker. Curves illustrate the decline of association with distance for a range of values of ɛ assuming M = 0.75 and L = 0.1.
To apply the Malecot model we suppose that a small region contains m ordered markers G1,.., Gm and perhaps a disease locus D. The physical locations Sl,.., Sm of markers are assumed to be known without error. It is convenient to take the distance from marker i to the disease locus as di = δi (Si − SD), where
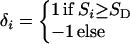 |
4 |
so that the derivative of the composite likelihood takes the appropriate sign. We assume that the Si are measured in Mb from G1 (so that S1 = 0). The logarithmic likelihood of the multiple pairwise observations summed over marker loci is
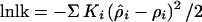 |
5 |
Goodness of fit is tested by χ2 = −2 lnlk with m-n degrees of freedom, where m is the number of marker loci and n is the number of parameters estimated. The logarithm of odds (lod) for allelic association is derived from the difference between total χm2 (Table 2) and χm−n2 for the accepted model, which is itself a χ2 with n degrees of freedom (see Appendix). At this point objection could be raised that the terms in a composite likelihood (Eq. 5) are not independent but positively correlated, a fact neglected in other multiple pairwise analyses of allelic association. This tends to make the χ2 test conservative, given exact weights and an exact model. A nominally significant χ2 must be accommodated in the analysis, conventionally by the empirical information we propose.
Table 2.
The CRTR region [12; 14]
| Probe | Enzyme | Locus | Location S, Mb | Association, ρ̂ | Information, K | χ2 |
|---|---|---|---|---|---|---|
| metD | BanI | MET | 0 | .5850 | 82 | 27.98 |
| metD | TaqI | MET | .009 | .6125 | 10 | 3.79 |
| metH | TaqI | MET | .024 | .4582 | 40 | 8.33 |
| E6 | TaqI | D7S340 | .524 | .3410 | 23 | 2.69 |
| E7 | TaqI | D7S340 | .534 | .4159 | 25 | 4.35 |
| pH131 | HinfI | D7S122 | .554 | .6511 | 124 | 52.66 |
| W3D1.4 | HindIII | D7S122 | .569 | .6440 | 118 | 48.86 |
| H2.3A | TaqI | WNT2 | .594 | .8242 | 31 | 21.10 |
| EG1.4 | HincII | WNT2 | .614 | .9740 | 66 | 62.24 |
| EG1.4 | BglII | WNT2 | .619 | .9746 | 69 | 65.18 |
| JG2E1 | PstI | D7S23 | .654 | 1.0000 | 69 | 68.80 |
| E2.6 | MspI | D7S23 | .684 | 1.0000 | 43 | 43.07 |
| H2.8a | NcoI | D7S399 | .709 | 1.0000 | 55 | 55.46 |
| E4.1 | MspI | D7S399 | .744 | 1.0000 | 43 | 43.07 |
| J44 | XbaI | D7S399 | .779 | 1.0000 | 44 | 43.98 |
| 10-1X.6 | AccI | CFTR | .859 | .9793 | 103 | 98.65 |
| IVS8CA+ | CFTR | .866 | .9518 | 2,019 | 1,828.83 | |
| IVS8CA− | CFTR | .866 | .9814 | 1,956 | 1,884.05 | |
| 10-1X.6 | HaeIII | CFTR | .869 | .9798 | 108 | 103.23 |
| ΔF508 | — | CFTR | .880 | — | — | — |
| T6/20 | MspI | CFTR | .889 | .9394 | 20 | 17.81 |
| H1.3 | NcoI | CFTR | .899 | 1.0000 | 58 | 57.96 |
| IVS17BTA | CFTR | .926 | .9313 | 1,090 | 944.97 | |
| IVS17BCA | CFTR | .926 | .9284 | 549 | 472.98 | |
| CE1.0 | NdeI | CFTR | .949 | 1.000 | 6 | 6.49 |
| J32 | SacI | D7S424 | 1.599 | .2970 | 92 | 8.13 |
| J3.11 | MspI | D7S8 | 1.669 | .3653 | 69 | 9.16 |
| J29 | PvuII | D7S426 | 1.769 | .3729 | 77 | 10.74 |
| Totals | 6,988 | 5,994.57 |
χ12 from 2 × 2 table for each marker.
Maximum likelihood estimates of SD and the significant nuisance parameters M, L, and ɛ give conditional information about location as KD = 1/K−1SS, where K−1SS is the corresponding element in the covariance matrix. To obtain a maximum likelihood estimate of SD, efficient combination with linkage as Σ KD SD/Σ KD is straightforward regardless of which is more informative (5). If residual χ2 is significant, the corresponding KD should be divided by χ2/df. This allowance for errors in the model is essential if evidence on linkage and allelic association is to be pooled and a minimal region is to be defined for positional cloning.
ΔF508—A Monophyletic Allele
Polyphyletic minor genes with a long history are a difficult and perhaps insuperable problem for disease mapping by allelic association unless the markers are within a candidate locus. We therefore look first at monophyletic major genes, which have a short history. The cystic fibrosis transmembrane conductance regulator (CFTR) locus that determines cystic fibrosis is “the best example of the utility of linkage disequilibrium in mapping disease genes” (10). The locus spans 250 kb between the restriction fragment length polymorphisms (RFLPs) D7S23 and D7S8 (11). On the map of Kerem et al. (12) CFTR occupies the interval from 0.78 Mb to 1.03 Mb distal to MET, with ΔF508 at position 0.88 (Table 2). Kerem et al. reported 23 RFLPs defining 77 haplotypes with ΔF508 and 149 other haplotypes. To secure monophyletic origin we merged non-ΔF508 alleles with the control sample. Tsui (13) estimated the European gene frequency of ΔF508 as .014. These observations imply ω = (.986) (77)/(.014) (149) = 36.4. Other data have been reported on this interval. The allass program gives for each dataset and its specific ω an intermediate output with S, ρ̂, K, and χ2 for each marker. These files may be pooled, with partition of homogeneity χ2 by dataset if overall heterogeneity is significant. To illustrate this approach we included the three intragenic microsatellites of Morral et al. (14), of which IVS8CA has negatively associated alleles (14, 15, 16, 18) in addition to the positively associated ones (17, 23). By our convention this generates two markers at the same location. Estimates of association are consistent with surrounding RFLPs (Table 2).
Association declines more rapidly distal to CFTR, with a 650-kb gap before the three most distal markers. For all 27 markers the best fit is at M = 1, L = 0, but a slightly smaller value of M and larger value of L are not excluded (Table 3). ΔF508 is positioned below its accepted location at 0.834 Mb (Table 4), but the difference when ΔF508 is positioned at the actual location (0.88) gives a χ12 = 5.38, which is not significant at the .001 level used by Terwilliger (6) or the .01 level of Devlin et al. (15). Significance tests in multiple pairwise mapping are approximate. To explore this further we made two other analyses. When the three most proximal and most distal markers are omitted, χ12 is reduced to 3.77. When the number of markers is reduced to 13 by adopting the 9 regions of Kerem et al. (12), χ12 is 2.75. The effect on the estimate of location is very small and χ2 values for the various hypotheses and datasets correspond quite well with degrees of freedom. In no analysis is the estimate of M less than 1 nor the estimate of L significantly different from 0. We expect M to be 1 for a monophyletic allele and L to be small. Because the expected value of χ12 is 1 on the null hypothesis, the bias induced by taking ρ to be positive is about 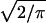 /
/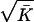 for diallelic markers, where K̄ is the mean value of K per marker. In this example the bias is .050. When M is 1 and ɛ is estimated, virtually identical values of χ2 are obtained for L = 0 and .050.
for diallelic markers, where K̄ is the mean value of K per marker. In this example the bias is .050. When M is 1 and ɛ is estimated, virtually identical values of χ2 are obtained for L = 0 and .050.
Table 3.
The ΔF508 allele of CFTR: Tests of hypotheses
| Hypthesis | 27 loci
|
Medial 21 loci
|
13 regions
|
|||
|---|---|---|---|---|---|---|
| χ2 | df | χ2 | df | χ2 | df | |
| M = 1, L = 0, S = .88 | 29.44 | 26 | 22.69 | 20 | 12.54 | 12 |
| M = 1, L = .050, S = .88 | 29.47 | 26 | 22.71 | 20 | 12.42 | 12 |
| M = 1, L = 0 | 24.06 | 25 | 18.92 | 19 | 9.60 | 11 |
| M = 1, L = .050 | 24.20 | 25 | 18.99 | 19 | 9.58 | 11 |
| M = 1 | 24.06 | 24 | 18.92 | 18 | 9.58 | 10 |
| M = .99 | 24.96 | 24 | 19.40 | 18 | 9.63 | 10 |
Parameters fixed by hypothesis are given. Values of estimated parameters (ɛ, S, and L) are not shown. χ2, goodness of fit to Malecot model with df (degrees of freedom).
Table 4.
The ΔF508 allele of CFTR: Estimates of lods, parameters, and information
| 27 loci | Medial 21 loci | 13 regions | |
|---|---|---|---|
| m | 27 | 21 | 13 |
| Total χm2 | 5,994.57 | 5,926.43 | 5,578.08 |
| χm−32 | 24.06 | 18.92 | 9.58 |
| χ32 for association | 5,970.51 | 5,907.51 | 5,568.50 |
| Z1 for association | 1,292.70 | 1,279.02 | 1,205.43 |
| SD | 0.834 | 0.836 | 0.836 |
| KD | 5,660 | 5,119 | 4,365 |
| ɛ | 1.019 | 0.986 | 1.051 |
| σɛ | 0.112 | 0.171 | 0.171 |
Parameters ɛ, L, and S estimated, M = 1. Z1, lod corresponding to χ32 for association; SD, estimated location of ΔF508; KD, information about location.
The lod Z1 for allelic association, calculated as in the Appendix, is similar in the three analyses and overwhelmingly significant (Table 4). It dwarfs the evidence on location from linkage, which was necessary but not sufficient for positional cloning. The interval between MET and D7S8 was too small for reliable mapping by linkage at the time when CF was recognized through recessive disease, hence the interest in developing allelic association to localize the gene. By allelic association Terwilliger (6) placed ΔF508 at 0.77 Mb, with a 13.8 support interval for χ2 corresponding to a lod of 3 from 0.69 to 0.87, overlapping the CFTR locus but not including ΔF508. Devlin et al. (15) localized ΔF508 at 0.81 Mb. Using a subset of the Kerem sample, Xiong and Guo (16) estimated error by their method as 75 kb. Using the same subset of the data by this method gives an identical error. The capability of allass to pool different studies allows greater precision. For the combined Kerem and Morral samples we place ΔF508 at 0.834 Mb (Table 4), within 50 kb of its physical location.
Discussion
In the location database ldb the sex-average distance between MET and D7S8 is 0.8 cM (17), compared with a physical distance of 1.67 Mb. The ratio z is twice as great as the rule of thumb that equates 1 Mb to 1 cM. The estimated duration of ΔF508 is 100 zɛ, or 209 generations, but this would be an underestimate if the allele persisted for a long time in a small population that later expanded. The highest frequency of ΔF508 is found north of the Alps in the region settled by Celtic and Germanic tribes, but substantial frequencies occur in Turkey, Russia, and Israel, suggesting dispersal during the Neolithic as proposed by Serre et al. (18). Our estimated duration, although obtained by an entirely different method, is in close agreement with their estimate of 100–200 generations. Morral et al. (14) estimated a duration an order of magnitude greater at 2,627 generations, assuming a gametic mutation rate of 3.3 × 10−4 or less. If the ancestral haplotype was 17–31-13, the frequency of substitutions is .513, .330, and .021. Neglecting multiple substitutions and recombination, the number of generations at the assumed mutation rate is 1,555, 1,000, and 63. These estimates are variable, the gametic mutation rate is uncertain, and neglect of recombination and selection may not be justified. The highly significant value of ɛ in the pooled data is evidence that recombination is of greater magnitude than mutation over the interval from MET to D7S8. Allelic association gives much less information about the age of ΔF508 than about its location.
Terwilliger (6) applied multiple pairwise analysis to conditional likelihood when a single, positively associated allele is specified a priori at each marker locus. He assumed that all markers were positioned exactly on a genetic map that could be equated to a physical map by the 1 cM = 1 Mb rule of thumb. The problem of testing for association and the resulting bias L were not addressed, and negative associations were excluded. Multiple associated alleles were considered in Table 3, which does not model approach to equilibrium under recombination. Because no test was provided for goodness of fit, there was no allowance for errors in the model.
Devlin et al. (15) drew attention to the fact that multiple pairwise mapping (19) uses composite likelihood for which useful mathematical theory has been developed (20). They assume two alleles at each marker locus, but do not consider how a larger number could be dichotomized. They introduce the approximation R − Q ∼ R and assume L = 0, M = 1 to approximate ɛ with no test for errors in the model. We allow explicitly for case-control sampling and make minimal evolutionary assumptions. Perhaps as a consequence, there is no evidence of heterogeneity in this example.
Sham and Curtis (21) introduced Monte Carlo tests for disease association with alleles at a single marker locus. They recognized that alleles should be combined in a way that preserves the evidence for association. Xiong and Guo (16) developed ingenious composite likelihood methods that incorporate parameters for mutational age, population growth, and recurrent mutation, unfortunately not known with any precision. When the physical location is given, ad hoc assumptions can be introduced to improve the estimate from allelic association. In the more relevant case of unspecified physical location, there is little basis for choice of unknown parameters that may make the estimate from allelic association better or worse. Testing for associated alleles, the difference between genetic and physical maps, and allowance for errors in the model are not considered. They gave several examples in which their method worked better than earlier methods. For the CFTR locus their estimated error using 19 markers selected from the reported 23 (12) was 75 kb. Using the same subset of the data with our method we obtain exactly the same error. With the full set of 27 markers the error is reduced to only 46 kb.
We have not yet attempted to map a disease locus in complex inheritance, where marker gene frequencies in cases and controls provide reduction to 2 × 2 tables but the locus cannot be haplotyped. This must be a severe constraint on the power of allelic association, as is the small interval in which allelic association can sometimes be detected (2). Efficient combination with linkage allows the same family material to be used for both tests. Although isolated cases are easier to collect than familial cases, they are more likely to be phenocopies and are usually less informative for linkage.
The lod score required for reliable detection of a candidate locus, which is as much as 9 when each marker locus is tested individually (22), is minimized by partitioning the genome into regions of 10 or more megabases (Mb), within which only a single candidate is sought. Then there is only one degree of freedom for disease location, regardless of the total number of alleles in the region. If markers are sufficiently dense, a combination of few tests and high power justifies the canonical lod of 3, and evidence from linkage and allelic association may be used to give a single, optimal location and test of significance. It remains to be seen how this approach performs with multiple disease mutations and complex inheritance.
ABBREVIATIONS
- CFTR
cystic fibrosis transmembrane conductance regulator
- lod
logarithm of odds
Numerical Analysis
In Table 1 let Uγ = ∂ lnlk/∂γ for γ = Q, R, ρ, with corresponding information matrix [kγγ′] that reflects sampling from the current population but not drift over generations. Newton–Raphson iteration gives ρ̂. Under Ho the score for ρ is U = (ad − bc) n/(a + c)(c + d) with conditional information K = n (a + b) (b + d)/(a + c)(c + d), where n = a + b + c + d and ρ = U/K, and U2/K is the usual χ2 for a 2 × 2 contingency table. An apparently significant χ2 is reduced by Yates’ correction, deducting n/2 from |ad−bc| . Trial values are Qo = (a + b)/[(ω − 1) (c + d) + n], ρ0 = (ad − bc)/(a + b) d and R0 = c/(c + d). At ρ̂ = 1 only R is estimated. Because of the instability of kρρ, the information Ki about ρ̂ for the ith marker is taken as the lesser of K and χ2/ρ̂2.
For Eq. 5 the information matrix is calculated by exact second derivatives after convergence under a variable metric algorithm (23).
To compute the lod Z1 with 1 degree of freedom that has the same significance level as χ2 with m degrees of freedom a numerical recipe to obtain the corresponding probability ρ (23) was modified to return the natural logarithm (ln p), and the Hastings approximation to the corresponding normal deviate χp was used with
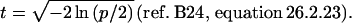 |
Then Z1 = χp2/(2 ln10).
References
- 1.Malecot G. Les Mathématiques de l’Hérédité. Paris: Maison et Cie; 1948. [Google Scholar]
- 2.Morton N E, Wu D. Am J Hum Genet. 1988;42:173–177. [PMC free article] [PubMed] [Google Scholar]
- 3.Agresti A. Categorical Data Analysis. New York: Wiley; 1990. [Google Scholar]
- 4.Morton N E. Revista di Antropologia. 1997;74:1–9. [Google Scholar]
- 5.Lio P, Morton N E. Proc Natl Acad Sci USA. 1997;94:5344–5348. doi: 10.1073/pnas.94.10.5344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Terwilliger J D. Am J Hum Genet. 1995;56:777–787. [PMC free article] [PubMed] [Google Scholar]
- 7.Morton N E, Lew R, Hussels I E, Little G F. Am J Hum Genet. 1972;24:277–289. [PMC free article] [PubMed] [Google Scholar]
- 8.Spielman R S, McGinnis R E, Ewens W J. Am J Hum Genet. 1993;52:506–516. [PMC free article] [PubMed] [Google Scholar]
- 9.Morton N E, Klein D, Hussels I E, Dodinval P, Todorov A, Lew R, Yee S. Am J Hum Genet. 1973;25:347–361. [PMC free article] [PubMed] [Google Scholar]
- 10.Kaplan N L, Hill W G, Weir B S. Am J Hum Genet. 1995;56:18–32. [PMC free article] [PubMed] [Google Scholar]
- 11.Anand R, Ogilvie D J, Butler R, Riley J H, Finniear R S, Powell S J, Smith J C, Markham A F. Genomics. 1991;9:124–130. doi: 10.1016/0888-7543(91)90229-8. [DOI] [PubMed] [Google Scholar]
- 12.Kerem B, Rommens J S, Buchanan J A, Markiewicz D, Cox T K, Chakravarti A, Buchwald M, Tsui L-C. Science. 1989;245:1073–1080. doi: 10.1126/science.2570460. [DOI] [PubMed] [Google Scholar]
- 13.Tsui L-C. Hum Mut. 1992;1:197–203. doi: 10.1002/humu.1380010304. [DOI] [PubMed] [Google Scholar]
- 14.Morral N, Bertranpetit J, Estivill X, Nunes V, Casals T, et al. Nat Genet. 1994;7:169–175. doi: 10.1038/ng0694-169. [DOI] [PubMed] [Google Scholar]
- 15.Devlin B, Risch N, Roeder K. Genomics. 1996;36:1–16. doi: 10.1006/geno.1996.0419. [DOI] [PubMed] [Google Scholar]
- 16.Xiong M, Guo S-W. Am J Hum Genet. 1997;60:1513–1531. doi: 10.1086/515475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Collins A, Frezal J, Teague J, Morton N E. Proc Natl Acad Sci USA. 1996;93:14771–14775. doi: 10.1073/pnas.93.25.14771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Serre J L, Simon-Bouy B, Morret E, Jaume-Roig B, Balassopoulou A, Schwartz M, Taillander A. Hum Genet. 1990;84:449–454. doi: 10.1007/BF00195818. [DOI] [PubMed] [Google Scholar]
- 19.Morton N E. Human Gene Mapping 4 (1977): Fourth International Workshop on Human Gene Mapping. Basel: S. Karger; 1978. pp. 15–36. [Google Scholar]
- 20.Lindsay B G. Contemporary Mathematics. 1988;80:221–239. [Google Scholar]
- 21.Sham P C, Curtis D. Ann Hum Genet. 1995;59:97–105. doi: 10.1111/j.1469-1809.1995.tb01608.x. [DOI] [PubMed] [Google Scholar]
- 22.Risch N, Merikangas K. Science. 1996;273:1516–1517. doi: 10.1126/science.273.5281.1516. [DOI] [PubMed] [Google Scholar]
- 23.Press W H, Teukolsky S A, Vetterling W T, Flannery B P. Numerical Recipes in C. 2nd Ed. Cambridge, U.K.: Cambridge Univ. Press; 1992. [Google Scholar]
- 24.Abramowitz M, Stegun A. Handbook of Mathematical Functions. New York: Dover; 1965. [Google Scholar]