Quantitative characterization of cell synchronization in yeast

Abstract

Metabolic oscillations in baker's yeast serve as a model system for synchronization of biochemical oscillations. Despite widespread interest, the complexity of the phenomenon has been an obstacle for a quantitative understanding of the cell synchronization process. In particular, when two yeast cell populations oscillating 180° out of phase are mixed, it appears as if the synchronization dynamics is too fast to be explained. We have probed the synchronization dynamics by forcing experiments in an open-flow reactor, and we find that acetaldehyde has a very strong synchronization effect that can account quantitatively for the classical mixing experiment. The fast synchronization dynamics is explained by a general synchronization mechanism, which is dominated by a fast amplitude response as opposed to the expected slow phase change. We also show that glucose can mediate this kind of synchronization, provided that the glucose transporter is not saturated. This makes the phenomenon potentially relevant for a broad range of cell types.

A remarkable example of cell synchronization is found in yeast cells showing glycolytic oscillations. In this system, cell suspensions with billions of yeast cells show synchronized oscillations in NADH fluorescence with a period around one half minute (1, 2). A manifest demonstration of this phenomenon occurs when two suspensions oscillating 180° out of phase are mixed. Just after mixing, the macroscopic oscillations disappear momentarily, but the two subpopulations synchronize within 5 min (i.e., <10 times the period of the oscillations) and the macroscopic oscillations reappear with full amplitude (3–5). This indicates active in-phase synchronization. It is believed that the synchronization is mediated by simple metabolites related to glycolysis (1, 4, 5), and as such it is an example of cell–cell communication that does not depend on any highly specialized signaling molecules or receptors. A similar synchronization mechanism could be operative in any oscillatory cell type, possibly through other metabolic signaling channels. Therefore, the understanding of the mechanism for glycolytic cell synchronization in yeast is important for the general understanding of cellular dynamics and interactions. Acetaldehyde (Aca) has been proposed as mediator of the synchronization (5). If this is the true mechanism of the phenomenon, then this understanding should allow us to explain it not only qualitatively but also quantitatively correct. It has been questioned whether the amount of Aca produced by the yeast cells is enough to cause synchronization (1), and several attempts have been made to account quantitatively for the synchronization process by using mathematical models based on biochemical descriptions (6–8). None of these have, however, been successful in explaining all experimental facts. In all cases, the synchronization process is one order of magnitude too slow, and in some cases the models even predict out-of-phase synchronization instead of the in-phase synchronization seen experimentally.

A necessary condition for a chemical species to act as a synchronizer is that it can penetrate the cell membrane, and that an instantaneous change in its concentration will influence the oscillations and give rise to an amplitude or phase change. Many different substances known to pass the cell membrane have been tested for this property. Proper responses are observed with Aca (3, 5, 9, 10), O₂ (11), and (when the glucose transporter is not saturated) glucose (10). From these experiments, quantitative data are available on O₂- and Aca-induced phase shifts, and on dynamic quenchings of the oscillations by perturbations with Aca and glucose. Substances that have been tested, but without proper responses, are H⁺ (3), K⁺ (3), Mg²⁺ (4), ethanol (4, 10), phosphate (4), cyanide (10), and glycerol (7). Pyruvate shows a proper response at pH 4.6 (9) but not at the higher pH values normally used (3, 10).

Another necessary condition for a species to act as a synchronizer is that it oscillates in the extracellular medium as a result of periodic excretion or absorption by the cells. This condition excludes O₂ as a synchronizer in anaerobic experiments or experiments where respiration is inhibited (4, 5, 12), so we are left with Aca, glucose, and possibly unknown substances as chemical synchronizer candidates. Indeed, Aca oscillations have been reported in the literature (5): the phase of the Aca oscillations is +200° relative to the NADH fluorescence signal, and the amplitude is reported as 5–8 μM when the correction given in ref. 13 is taken into account.

Our recent analysis of the cause of the glycolytic oscillations showed that the instability leading to oscillations is caused by the allosteric regulation of phosphofrutokinase in combination with increasing flux through the glycolytic pathway that is autocatalytic in ATP (i.e., ATP is invested in the upper part of glycolysis, and twice the amount of ATP is released in the lower part). A way to increase glycolytic flux is to increase the temperature, and when the flux is increased, the yeast cells produce more heat. Hence, temperature oscillations is another possible means of cell synchronization. Because the ATP-linked flux-instability is central to the glycolytic oscillator, one could expect that even small temperature oscillations might be enough for synchronization to occur.

Following these considerations, we set out to quantify the synchronization properties of heat, glucose, and Aca. Specifically, we consider whether these synchronizer candidates are able to account quantitatively for the mixing experiment observations (5) or, alternatively, whether yet unknown synchronizers are involved.

Results

Temperature Oscillations and Temperature Sensitivity.

The possibility that temperature variations might be involved in cell synchronization was tested by measuring the temperature variations associated with glycolytic oscillations. In our setup, we find temperature oscillations of 1–2 mK. These oscillations match the oscillations in the fluorescence signal; the temperature maximum is found just after the maximum in NADH fluorescence. Supporting information (SI) Fig. 4 shows the temperature dependence of the oscillatory period. (These results are in agreement with those reported in ref. 14.) The observed temperature amplitude can only give rise to a frequency change of <0.2‰. Hence, it is very unlikely that temperature variations contribute significantly to the rapid synchronization observed in the mixing experiments.

Resonant Forcing of Glycolytic Oscillations.

We cannot obtain online measurements of the remaining two candidates, Aca and glucose. Instead, we assess their synchronizer properties by phase-shift experiments. We force yeast cell suspensions with either glucose or Aca. We use resonant forcing, i.e., the forcing frequency is set to the natural frequency of the yeast cell oscillations (SI Fig. 5). This mimics as far as possible the natural entrainment process. When the NADH oscillations have been entrained at a stable phase relative to the forcing signal, we shift the phase of the external forcing by 180° and record the dynamics of the re-entrainment. If the forcing has a strong effect on the yeast cell oscillators, then there will be a large immediate effect of the phase shift, and the re-entrainment will be fast.

Dynamics of Glucose-Mediated Synchronization.

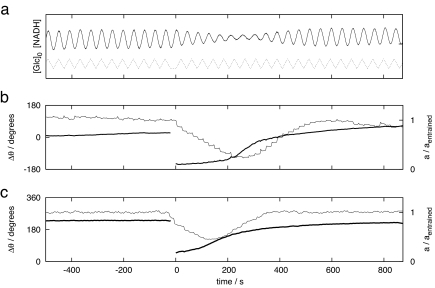
Yeast cells have a fast and strong glucose response as long as their glucose transport systems are not saturated but are insensitive to changes in the extracellular glucose concentration when the glucose transporters are saturated (10, 15). When a glucose phase-shift experiment is performed with a measured average extracellular glucose concentration of [Glc] = 2.4 mM, which is close to the K_M value of the HXT7-encoded glucose transporter K_M = 1.7 mM (16), then the amplitude is transiently reduced to 25% of the entrained amplitude, and the re-entrainment is complete within 13 oscillatory periods (Fig. 1 a and b). The entrainment phase of the glucose forcing coincides with the quenching angle of extracellular glucose (10). When a similar experiment is done at a measured extracellular glucose concentration of [Glc] = 4.5 mM, we see a weak amplitude response of a_min/a_entrained = 0.75 and a slow phase re-entrainment (SI Fig. 6a). At an extracellular glucose concentration of [Glc] = 19 mM, we see no amplitude response and no re-entrainment (SI Fig. 6b). These experiments show that glucose-mediated cell synchronization is possible at low extracellular glucose concentrations but that it cannot be involved in the cell synchronization of the mixing experiments, because these experiments are performed at relatively large extracellular glucose concentrations (10–20 mM).

Fig. 1.

180° phase-shift experiments. Yeast cell populations are forced with either glucose (a and b) or Aca (c) at their natural frequency. Once the phase difference between the external forcing and the yeast cell oscillations is stable, the forcing phase is shifted 180° at time t = 0 s. (a) Fluorescence signal (solid line), which is proportional to [NADH], and the mixed flow glucose concentration with an average value of 19 mM and a half amplitude of 0.12 mM. The actual average glucose concentration is measured to 2.4 mM. (b) Time courses of the amplitude (thin line) and phase (heavy line) in the same experiment. (c) Time courses of the amplitude (thin line) and phase (heavy line) in a phase-shift experiment with Aca forcing at a forcing amplitude of a_[Aca]0 = 2.0 μM. We report the phase relative to the phase of the forcing, Δθ = θ_forcing − θ_NADH, so that the phase is positive if the maximum of the forcing precedes the maximum of the NADH signal. The amplitude is reported relative to the amplitude of the entrained oscillations.

Dynamics of Acetaldehyde-Mediated Synchronization.

The synchronizer properties of Aca are also probed with phase-shift experiments. These experiments are performed at saturating glucose concentrations. In addition, it turned out that to observe oscillations with the additional Aca flow used for the forcing, the mixed-flow cyanide concentration had to be increased. This is consistent with the idea that cyanide (in addition to the inhibition of respiration) reacts with Aca to form lactonitrile (4, 17). As was the case with glucose forcing, the entrainment phase of the resonant Aca forcing is close to its quenching angle (10).

We performed 180° phase-shift experiments with varying amplitudes of the Aca forcing. An example of such an experiment is shown in Fig. 1c. We quantified the responses to the phase shifts in terms of the minimum relative amplitude a_min/a_entrained observed during the re-entrainment, and in terms of the amplitude relaxation time 1/(−k_amp) seen in the last part of the amplitude decay. As discussed below, these two measures can be compared with the mixing experiment. In addition, we quantified the relaxation time of the last part of the phase relaxation curve. The measures are defined in Methods, and the results are shown in Table 1.

Table 1.

Quantitative characterization of the re-entrainment after 180° phase shifts in the resonant Aca forcing

Forcing period, s	Forcing amplitude,† μM [Aca]0	Minimum amplitude,†amin/aentrained	Relaxation time
			Amplitude,† s	Phase,† s
39	0‡	1	∞	∞
39	0.28	0.66	830	1,300
39	0.60	0.80	170	1,000
39	1.2	0.55	270	550
39	1.4	0.41	88	230
39	1.5	0.61	47	320
39	2.0	0.45	51	220
38	2.2	0.15	61	180
39	2.3	0.20	53	300

^†These measures are defined in Methods.

^‡Forcing with pure water.

Quantitative Comparison with the Mixing Experiment.

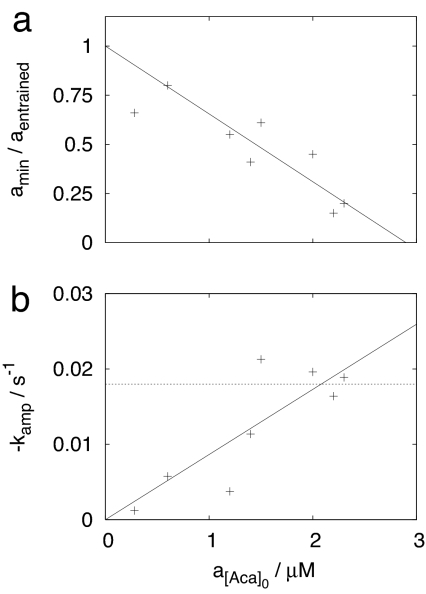
A quantitative comparison with measures obtained from the mixing experiment of ref. 5 is performed by extrapolating the re-entrainment measures in Table 1 to the corresponding values of the mixing experiment. The minimum amplitude observed in the mixing experiment is a_min/a_full = 0, as expected when two populations 180° out of phase are mixed. Fig. 2a shows the linear extrapolation of the minimum amplitudes (Table 1): a 180° phase shift will quench the oscillations at a mixed flow Aca amplitude of a_[Aca]0 ≈ 2.9 μM. If we assume that the oscillations disappear because the Aca oscillation produced by the yeast cells is balanced by the forcing, then this is an estimate of the Aca amplitude (in a mixed flow sense) produced by the yeast cell population. From the data in ref. 5, we determine an amplitude decay rate of k_amp = −0.018 s⁻¹ in the mixing experiment. As seen from Fig. 2b, this corresponds to the mixed flow Aca amplitude a_[Aca]0 ≈ 2.1 μM. In this last part of the amplitude relaxation time trace of the phase-shift experiment, however, the Aca signal is composed of both the external forcing and the Aca produced by the yeast cells. This is different in the mixing experiment, where the Aca signal is produced solely by the yeast cells. Our estimate of the amplitude of the Aca signal needed to produce the fast resynchronization observed in the mixing experiment will therefore depend on the phase difference between the Aca signal from the yeast cells and from the forcing. This gives an estimate of between 2.1 and 2.1 μM + 2.9 μM = 5.0 μM (all mixed flow), in good agreement with the 2.9 μM mixed flow amplitude estimated from minimum amplitudes.

Fig. 2.

Comparison of a mixing experiment (5) and the responses to 180° phase shifts in the resonant Aca forcing. (a) Linear extrapolation (solid line) of the minimum amplitudes to the zero value of the mixing experiment. (b) Linear interpolation (solid line) of the amplitude decay rate determined in the last part of the phase-shift experiment. In b, the dashed line indicates the corresponding amplitude decay rate of the mixing experiment.

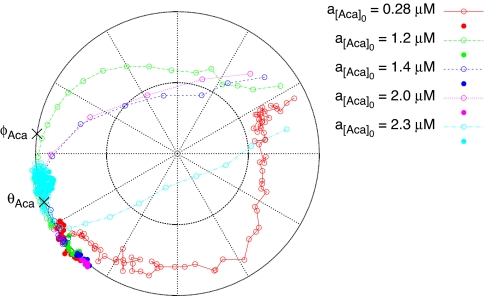
An extracellular Aca amplitude of 5–8 μM (ref. 5, taking into account the correction given in ref. 13) has been measured at a cell density four times higher than that used for the mixing experiment in ref. 5. Hence, in the mixing experiment the actual Aca concentration amplitude is 1–2 μM. Because extracellular Aca is removed not only via outflow from the reactor but also in a reaction with cyanide, this is in reasonable agreement with our estimate of the minimum Aca amplitude needed to explain the fast resynchronization of the mixing experiment. Quantitatively, our calculations show that a [Aca]₀ sinusoidal oscillation with a mixed flow amplitude of a_[Aca]0 = 2.1 μM results in [Aca] oscillations with an actual concentration amplitude of a_[Aca] = 1.5 μM, if the extracellular Aca is removed at a rate of 10 min⁻¹ as previously estimated (S. De Monte, F. d'Ovidio, S.D., and P.G.S., unpublished data). We conclude that the observed Aca concentration amplitude is sufficiently large to account quantitatively for the cell synchronization dynamics of the mixing experiment. That Aca is the mediator of the cell-synchronization is further supported by the finding that the phase at which the yeast cells are entrained by the Aca forcing coincides with the phase of Aca oscillations in nonforced yeast cells (5) (Fig. 3).

Fig. 3.

Phase and amplitude responses as seen in the 180° Aca phase-shift experiments (Table 1). The plot is a polar plot; the distance from the center indicates the NADH amplitude a relative to the fully entrained NADH amplitude a_entrained, and the angle indicates the phase difference Δθ between the forcing and the NADH signal. Different experiments are indicated by color-coding. Filled symbols are states observed before the phase shift, and open symbols indicate states observed after it. The states in the plot are separated in time by 39 s, equivalent to one oscillation period. Hence, the distance between adjacent points on a trajectory indicates the speed along it. The phase of Aca oscillations θ_Aca observed in nonforced yeast cell populations (5) and Aca's quenching phase φ_Aca (10) are indicated by ×. For clarity, response curves are only drawn for a subset of the experiments.

Synchronization Mechanism.

The phase-shift experiments differ from the mixing experiments in that they provide insights into both the amplitude and the phase responses of the yeast cells. This information is visualized in the polar plot in Fig. 3. It is seen that the yeast cells respond to the Aca phase shift with a fast and pronounced amplitude response; stronger forcing leads to a stronger and faster amplitude response. This amplitude response is responsible for most of the re-entrainment. The final part of the re-entrainment, however, is a relatively slow phase response, which occurs when the yeast cell population has regained full amplitude (see also Table 1 and Fig. 1c). We conclude that the yeast cells respond to changes in the extracellular Aca oscillations as “soft” 2D limit-cycle oscillators, and not as “stiff” pseudo-1D phase oscillators. This notion is further supported by the off-resonance forcing experiment presented in SI Fig. 7. The data also indicate that Aca has an almost immediate effect on the glycolytic dynamics, despite the fact that Aca is distant to the core of the glycolytic oscillator (19–22). This behavior fits a scenario where the glycolytic oscillators are close to a Hopf bifurcation (10), and the Aca membrane transport kinetics is fast compared with the time scales of the glycolytic oscillator (S. De Monte, F. d'Ovidio, S.D., and P.G.S., unpublished data).

Discussion

If an Aca-based mechanism can account quantitatively for the synchronization of the yeast cells, then why do mathematical models predict synchronization dynamics that are at least an order of magnitude too slow? Our data on the combined phase and amplitude responses of the yeast cells (Fig. 3) provide a possible answer to this question. The re-entrainment transients show that the yeast cells respond to the extracellular Aca signal through a combined phase and amplitude response, and that the amplitude response is fast. This indicates that the oscillators are soft 2D oscillators, and that the Aca membrane transport kinetics transport are fast.

Comparing with existing models (6, 7), we can now see why these were unable to account for the fast synchronization: The glycolysis model in ref. 6 does not show such soft sinusoidal oscillations. Instead, it is a stiff relaxation-like oscillator, which does not have the fast amplitude response but only a slow phase response (6). The glycolysis model in ref. 7 is a soft 2D oscillator, but the Aca membrane transport kinetics is too slow to make the model able to account for the fast synchronization dynamics. This is in agreement with our previous theoretical analysis of the synchronization process of this model (8, 23). The actual construction of a revised model will be presented in a future publication.

These findings have implications for our understanding of the mixing experiment and of the loss of oscillations observed at low cell densities (S. De Monte, F. d'Ovidio, S.D., and P.G.S., unpublished data) (24). The transient loss of macroscopic oscillations seen in the mixing experiment is not simply due to averaging of two oscillatory signals 180° out of phase. Rather, the glycolytic oscillations in the two subpopulations lose most (or all) of their amplitudes in a fast amplitude response. This resets the phases of oscillation, and the reappearance of the oscillations is governed by the instability of the stationary state and the attraction of the limit cycle, precisely as the recovery following a dynamic quenching (10). As expected, the time scales involved in the recovery from a mixing experiment and from a quenching are comparable (compare refs. 5 and 10). When the cell density is decreased toward the critical point where oscillations can no longer be observed, then the amplitude of the extracellular Aca oscillations will also decrease because of a larger extracellular volume per yeast cell. Our experiments indicate that such a decrease in the extracellular Aca amplitude will result in a decrease in the amplitude of the intracellular oscillations. Hence, it is likely that the loss of oscillations at the critical cell density is due to loss of oscillations in each of the yeast cells, as opposed to loss of synchrony. This explanation is consistent with the observation that a single, noninteracting yeast cell does not show spontaneous glycolytic oscillations under conditions where dense populations do (25), and it is further supported by work recently carried out in our laboratory (S. De Monte, F. d'Ovidio, S.D., and P.G.S., unpublished data).

Going beyond yeast, we note that even though a glucose-based synchronization mechanism is not essential for the synchronization of yeast glycolytic oscillations, our glucose forcing experiments in conditions where the glucose transporters are not saturated (Fig. 1 a and b) show, however, that glucose can act as a potent synchronizer. Cells can tune their sensitivity to an external glucose signal by changing the affinity of their glucose transporters, and glycolysis is an important part of energy metabolism of almost all cell types. Therefore, this effective cell synchronization mechanism has been evolutionary accessible for most cell types, so it does not seem unlikely that it plays a functional role in some. Most metabolic systems are temperature-sensitive, but no example of temperature-mediated cell synchronization has been reported.

Methods

Measurements of Cellular Dynamics.

Yeast cells (Saccharomyces cerevisiae X2180) were grown at 30°C in batch culture in a rotary shaker to the point of glucose depletion as described in ref. 26. The yeast cells were washed twice in 0.1 M potassium phosphate buffer, diluted to the desired cell density, and kept at 2–4°C until they entered the reaction chamber. The metabolic state of the cells was recorded by means of NAD(P)H autofluorescence measurements as described in refs. 10 and 18. Forcing experiments were carried out in a thermostated (25°C) continuous-flow stirred-tank reactor (CSTR) with inflows of cell suspension, glucose solution, cyanide solution, and sometimes Aca solution as described in ref. 10 but with minor modifications.

External Forcing of Cellular Dynamics.

Forcing with glucose or Aca was done by changing the flow of the corresponding computer-controlled stepper-motor-driven burette periodically. For the first half of the forcing period, the specific flow rate was set to j_m −a, and for second half forcing period, it was set to j_m + a such that the average flow j_m is unchanged from the corresponding unforced system. Calculation of the resulting forcing profile is described in SI Text. No effect was seen when similar forcing experiments were carried out with water.

Phase-shift experiments were performed by first allowing the yeast cells to synchronize with a forcing with the same frequency as nonforced yeast cells. Then the phase of the forcing was changed by 180°, and the re-entrainment of the yeast cells by the forcing was recorded. The phase-shift responses were characterized by three measures (Table 1): the minimum amplitude a_min reached during the transient (reported relative to the amplitude of the entrained signal a_entrained), the amplitude relaxation rate k_amp, and the phase relaxation rate k_phase. The relaxation rates are the exponential decay rates toward the stable entrained amplitude and the stable phase of entrainment, respectively. Only the last parts t > t* of the phase-shift transients are used for determination of relaxation rates. Specifically, we define t* as the time point where half of the amplitude has been regained, i.e.,

and

In the glucose forcing experiments, the total specific flow of the CSTR was j₀ = 0.05 min⁻¹, the mixed flow cyanide concentration was [CN⁻]₀ = 5.7 mM, and the cell density was 14 (mg of dry weight)/ml ≈ 1.4 × 10⁹ cells per ml. When Aca was used for the forcing, the CSTR operating parameters were j₀ = 0.06 min⁻¹, [Glc]₀ = 60 mM, and [CN⁻]₀ = 5.9 mM, the mixed flow Aca concentration had a time-average of [Aca]₀ = 0.32 mM, and the cell density was 11 (mg dry weight)/ml.

Transient Experiments.

Transient experiments were conducted with all flows turned off. The oscillations were induced by pulse addition of 30 mM glucose followed by a 5 mM pulse of KCN once the glucose-induced damped oscillations had disappeared. The oscillatory period was determined in the most stable part of the train of oscillations following the cyanide addition.

Additional Methods.

Information about calculation of the forcing profile, temperature measurements, glucose measurements, and chemicals can be found in SI Text.

Abbreviation

Aca

acetaldehyde.