Protein-induced Local DNA Bends Regulate Global Topology of Recombination Products

Abstract

The tyrosine family of recombinases produces two smaller DNA circles when acting on circular DNA harboring two recombination sites in head-to-tail orientation. If the substrate is supercoiled, these circles can be unlinked or form multiply linked catenanes. The topological complexity of the products varies strongly even for similar recombination systems. This dependence has been solved in the current study. Our computer simulation of the synapsis showed that the bend angles, ϕ, created in isolated recombination sites by protein binding before assembly of the full complex, determine the product topology. To verify the validity of this theoretical finding we measured the values of ϕ for Cre/loxP and Flp/FRT systems. The measurement was based on cyclization of the protein-bound short DNA fragments in solution. Despite the striking similarity of the synapses for these recombinases, action of Cre on head-to-tail target sites produces mainly unlinked circles, while that of Flp yields multiply linked catenanes. In full agreement with theoretical expectations we found that the values of ϕ for these systems are very different, close to 35° and 80°, respectively. Our findings have general implications in how small protein machines acting locally on large DNA molecules exploit statistical properties of their substrates to bring about directed global changes in topology.

Introduction

Site-specific recombination is utilized by a great variety of organisms for well defined genomic rearrangements.^{1; 2; 3} Various recombination systems attracted much attention over the last two decades, and were studied by using different methods. Among these methods, in vitro studies of the recombination reactions have been particularly important in revealing their various attributes, including mechanisms (reviewed in refs. (1; 4; 5)). Such studies usually make use of circular plasmid substrates harboring a pair of specific target sites. In the case of several members of the tyrosine family site-specific recombinases, the subject of this paper, the substrate can carry the target sites in either head-to-head (inversion substrate) or head-to-tail (deletion substrate) orientations. The recombination products from deletion substrates are two smaller circles which can be unlinked, or form torus links that differ in linking number, Ca. Similarly, the products from the inversion substrates can be unknotted circles, or knots with a range of crossing numbers. The topological complexity of the products varies strongly depending on a particular recombination system, DNA supercoiling, plasmid size and the distance along the DNA contour between the target sites. While it has been understood, at least qualitatively, how the latter three factors affect the product topology,^{1; 4; 5; 6} large difference in the topological complexity of products, observed for various systems of the tyrosine family recombinases, has remained a puzzle. Solving this puzzle was the goal of this study.

Over the years, topology of the recombination products has been widely used to deduce conclusions about structure of the synapses, pathways of their assembly, and dynamic DNA conformations governing the process.^{1; 4; 5} It was understood that different types of juxtaposition of the recombination sites are responsible for the topological complexity of recombination products.^{7; 8; 9; 10} These types of site juxtapositions in supercoiled substrate were named “random collisions” and “slithering” (Figure 1). The former represents juxtaposing by 3-D diffusion of the superhelix branches, while the latter process can be considered as 1-D diffusion of the specific sites along the interwound superhelix. Figure 1 illustrates how the synapse resulting from the branch collision traps supercoils and produces linked DNA circles, while the synapse formed by the site collision inside the same branch of the interwound superhelix gives unlinked circular molecules.

Figure 1.

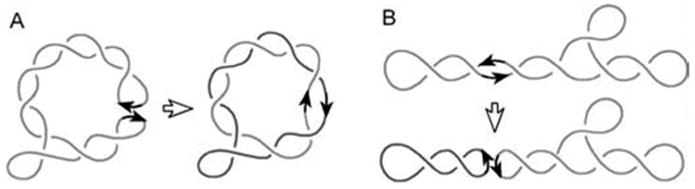
Two types of juxtaposition of the recombination sites and resulting recombination products. (A) The juxtaposition by 3-D diffusion of superhelix branches. The synapse traps four supercoils in the diagram and produces DNA circles with Ca = 4. (B) The site juxtaposition results from 1-D diffusion of the specific sites along the interwound superhelix. In this case recombination gives two unlinked circles.

Thus, it has been understood how recombination products of various topological complexity can be produced from a supercoiled substrate DNA. This does not explain, however, why synapsis in some site-specific recombination systems proceeds by one way, and by a different way in other systems. This difference in the complexity of product topology is especially pronounced for the Cre/loxP and Flp/FRT systems. The systems have striking similarities in their overall reaction mechanism, and still form products of different topological complexity. The theoretical part of our study implicitly addresses these simple systems, although the idea derived in this part has much wider implications. In the second, experimental part of the work, we used Cre/loxP and Flp/FRT systems to test the theoretical finding.

Results

Computer Simulations of Synapsis: Effect of Pre-synaptic DNA Bend on Product Topology

To address the problem of product topology, we undertook computer simulations of the recombination process. Since the product topology is completely specified at the moment the synaptic complex is assembled, we have, first of all, to simulate synapsis. It has been shown for Cre and Flp recombinases that the synapsis occurs through collision of preassembled halves of the synaptic complex,^{11; 12; 13; 14} and our simulation was based on the corresponding model. Thus, we treated synapsis as a collision of two properly oriented halves of the complex (Figure 2). Each half is assumed to consist of a specific site bound by two recombinase monomers. We also introduced a DNA bend by angle ϕ in each protein-bound DNA target site. This is consistent with the gel electrophoresis data for the isolated halves.^{15; 16} It is important to emphasize that the bend angles observed in the X-ray structures of the synapses^{17; 18; 19} and those present in the pre-synaptic halves need not be identical. We used a well-tested way to construct equilibrium sets of DNA conformations, modeling circular DNA molecules as a closed discrete wormlike chain consisting of rigid cylinders (see Methods for details). The chain had both bending and torsional rigidity, making possible simulation of supercoiled DNA molecules. The bent conformations of the specific sites were assumed to be rigid during the simulation procedure. Typical simulated conformations of the chain are shown in Figure 3 (panels A and B). From the constructed set we selected conformations in which the specific sites were properly juxtaposed to form the synaptic complex. For all such conformations, we modeled the recombination reaction, and determined topology of the resulting products (Figure 3, panel C and D).

Figure 2.

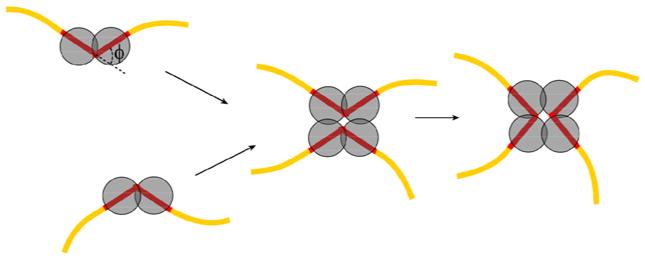
The model for the assembly of the synaptic complex by tyrosine family recombinases. A key element of the model is that formation of the recombinase-bound DNA partners is a necessary first step in synapsis. DNA structure in the ‘pre-synaptic’ halves is assumed to be bent by angle ϕ. The value of ϕ can be different from the value of the corresponding angle in the mature synaptic complex.

Figure 3.

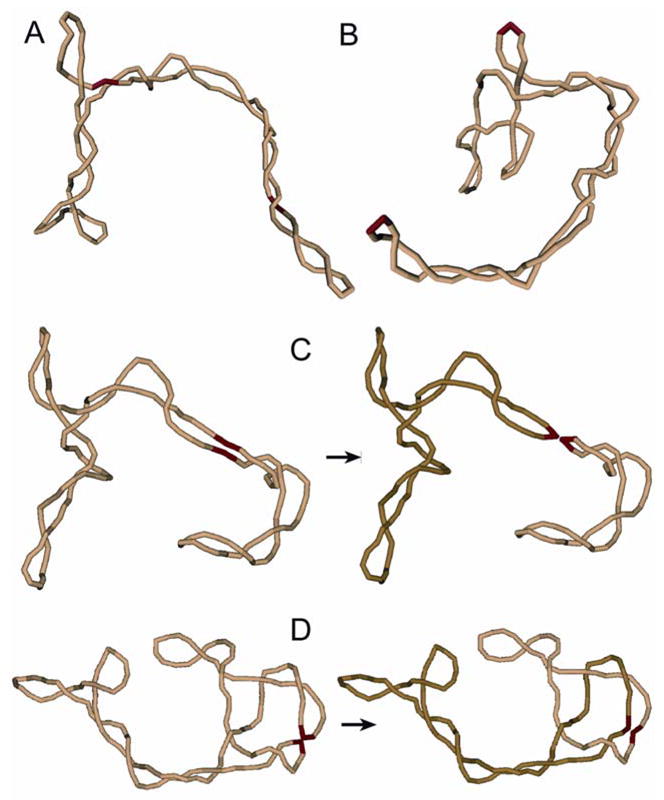
Monte Carlo simulation of the recombination reaction. (A, B) Typical simulated conformations of supercoiled DNA with different locations of the specific sites (shown by red) are presented. Conformations of the specific sites are assumed to be bent by bound proteins. Each cylindrical segment of the model chain corresponds to 30 bp of the double helix. (C) A conformation of the model chain with juxtaposition of the recombination sites within the same superhelix branch is shown. This type of juxtaposition usually occurs if the bend angle, ϕ, in the sites is small. The recombination products are unlinked in this case. (D) A conformation of the model chain with juxtaposed recombination sites which are located at superhelix apices is displayed. This type of juxtaposition is typical for large values of ϕ. The synapsis traps a few supercoils in such cases and the recombination products form torus links. The value of Ca equals 2 for the shown case.

In the course of the simulation we found that the bend of the protein-bound recombination sites before their juxtaposition determines the distribution of Ca of the recombination products formed from directly oriented sites (or the distribution of knots for inversely oriented sites). If the bend angle, ϕ, is small, the collisions of the complex halves mainly occur in one branch of supercoiled DNA (Figure 3C). The recombination event gives unlinked circles in this case. When ϕ increases, the synapse geometry is not incorporated smoothly in one superhelix branch. Therefore, properly juxtaposed protein-bound sites are located more often at different branches, so the complex traps a few supercoils. The recombination products are mainly linked in this case. At even larger ϕ, the bent DNA segments tend to be located at superhelix apices where the double helix has to be bent in any case (see Figure 3B). Such location of bent DNA segments has been demonstrated both experimentally and theoretically.^{20; 21} In this case, the synaptic complexes result from the juxtaposition of the superhelix apices. This type of synapsis traps even more supercoils, further increasing the product Ca (Figure 3D). The value of ϕ depends on a particular recombination system.^{22; 23} Therefore, different systems produce products of different topological complexity.

The simulated distributions of Ca are presented in Figure 4 (the upper two rows) for different values of ϕ. For ϕ < 30° the recombination products are mainly unlinked. We see from the figure, however, that the fraction of linked circles increases rapidly for 30° < ϕ < 50°, and very few unlinked circles appear for ϕ = 60°. Correspondingly, Ca of the catenanes increases monotonically with increase in ϕ. Although the distributions shown in the figure correspond to a particular length of the substrate circular DNA (4.1 kb) at a superhelix density of −0.05 and a fixed separation between the recombination sites (1.4 kb), they illustrate well the general picture.

Figure 4.

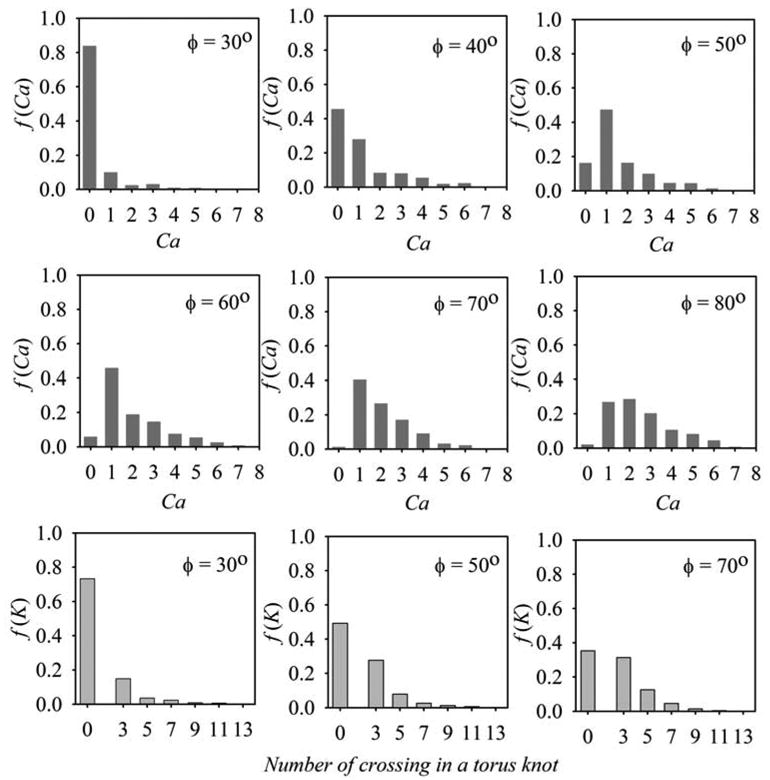
Computed distributions of recombination products for different values of the bend angle in the recombination sites. The fractions of products with different topologies, were computed for supercoiled substrate DNA 4.2 kb in length with specific sites separated by 1.4 kb. The distributions of the product linking number, Ca, are shown for DNA containing two target sites in direct orientation (rows 1 and 2). The fraction of unlinked circles corresponds to Ca = 0. The distributions of different torus knots and unknotted circles, which are formed from DNA with inverted orientation of the recombination sites, are shown in row 3. The topology of recombination products was specified by the minimum number of crossings in knot projection. The unknotted circles correspond to zero crossings. The DNA superhelix density in all these simulations was equal to −0.05.

We also simulated the distribution of recombination products for the substrate DNA with inversely repeated recombination sites (the bottom row in Figure 4). In this case the recombination produces unknotted circles or torus knots which can be specified by the minimal number of crossings on their projection. One can see from the figure that as ϕ increases, so does the product topological complexity.

It should be noted that the simulation results shown in Figure 4 were obtained for σ of −0.05, although the substrate DNAs used in our study have σ of −0.06 (see below). We found that our Monte Carlo simulation procedure is a few times more efficient for σ of −0.05 than for σ of −0.06, so much more computational time is required to obtain the same statistical error for the latter value of σ. However, the computations for ϕ of 30° and 50° performed for both these values of σ showed very close distributions of recombination products.

Differences between Flp and Cre in Product Topology Suggest Distinct Pre-synaptic Bends in the Target Sites

In order to test the effect of ϕ on product topology, as predicted by the simulation, we used the related Cre/loxP and Flp/FRT recombination systems. Despite the striking similarity of the synaptic complexes for these systems,^{18; 24; 25} they give very different distributions of the recombination products on supercoiled substrates. The Cre/loxP system produces mainly unlinked circles and a small amount of the singly linked catenanes in the deletion reaction.^{10; 26} The Flp/FRT system produces primarily multiply linked catenanes.²⁷ We confirmed this sharp difference in the product topology between the two systems for our reaction conditions and substrate DNAs with σ = −0.06 (Figure 5C, D). This difference disappears for nicked substrates (Figure 5A, B), in full agreement with the computer simulation which predicts formation of mainly unlinked circles regardless of the value of ϕ when the substrate DNA is relaxed (data not shown). By comparing these experimentally observed product distributions for supercoiled substrate with our computational data we concluded that ϕ should be close to 30° for Cre/loxP complex and larger than 60° for Flp/FRT complex (see Figure 4).

Figure 5.

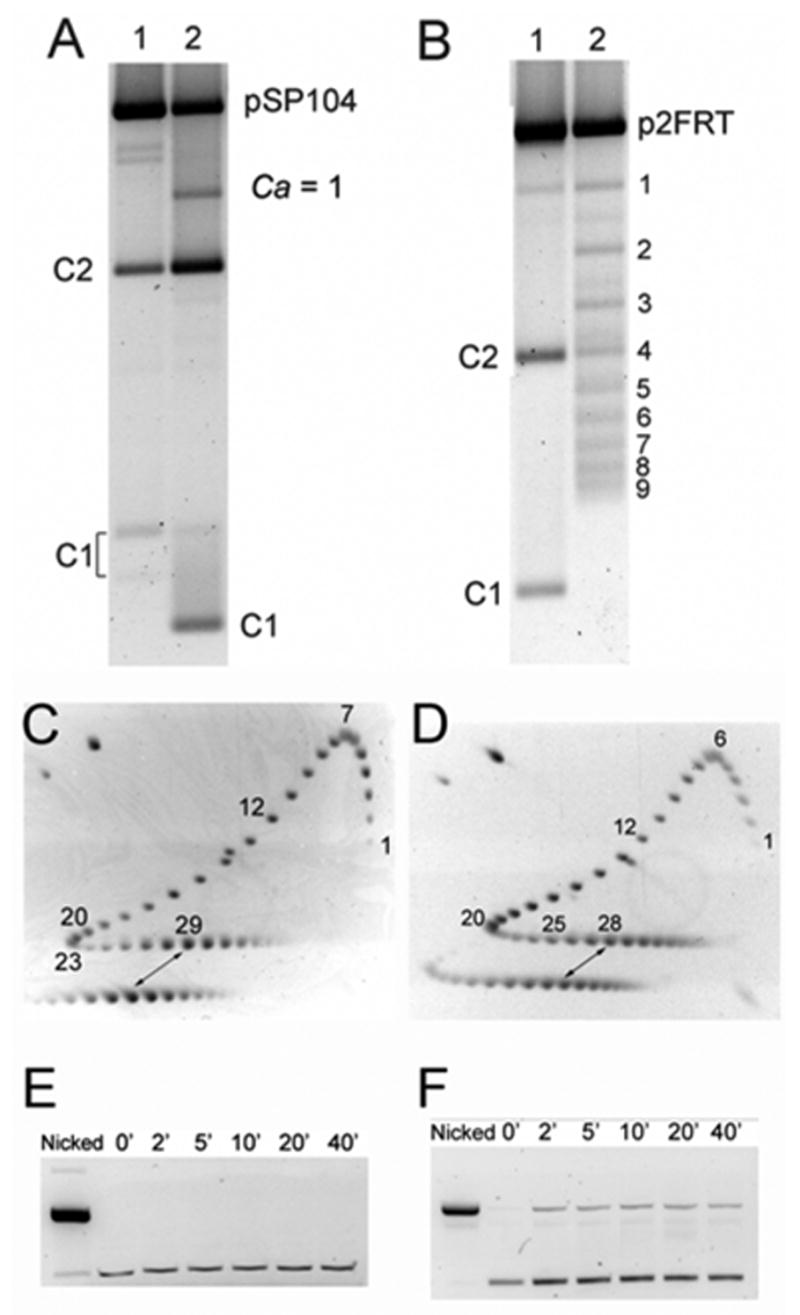
The recombination and strand cleavage reactions by Cre and Flp. The products from the recombination reactions were separated by agarose gel electrophoresis. C1 and C2 are small and large circular deletion products formed by recombination. Catenanes are indicated by their respective linking number value. (A) Lane 1, nicked plasmid pSP104 treated with Cre; lane 2, the same plasmid in supercoiled form treated with Cre. (B) Lane 1, nicked plasmid p2FRT treated with Flp; lane 2, the same plasmid in supercoiled form treated with Flp gives catenanes with different values of Ca. DNA from reactions with supercoiled plasmids (lanes 2) was nicked with N.BstNBI prior to electrophoresis. C1 of lane 2 in panel A escaped nicking because it lacks the enzyme cut site; this increased the mobility of the circle and C1/C2 catenane (Ca =1). (C, D) Determination of the plasmid superhelix density by 2D gel electrophoresis (see ‘Materials and Methods’ for details). The reference mixture of topoisomers (the upper numbered patterns) and the substrate plasmids used in the recombination assays (the lower patterns) were run in the first and second dimensions (indicated by arrows) in the absence and presence of 1.5μg/ml chloroquine, respectively (see ‘Materials and Methods’ for details). To avoid overlap, the reference sample was loaded in a separate well with a time delay. The distance between the wells accounts for the horizontal shift between corresponding topoisomers of the reference and experimental samples. The estimated σ values for pSP104 and p2FRT, corrected for the ionic strength of the recombination buffer, were −0.061 and −0.060, respectively. (E, F) Analysis of DNA cleavage by Cre and Flp in the isolated halves of the recombination complexes. Low concentration of plasmids with single loxP (E) or FRT (F) sites were used in the analysis which was performed as detailed under ‘Materials and Methods’. The band of nicked DNA, seen in panel F, originates from the covalent intermediates between Flp and FRT site of the plasmid.

Since there are very few linked circles formed by Cre from the supercoiled substrate, it is possible, in principle, that the difference in the topological complexity of products between Cre and Flp results from strand cleavage and supercoiling relaxation in the Cre complexes before synapsis. In light of this caveat, we studied the cleavage of DNA substrate by Cre under our experimental conditions. A plasmid bearing one loxP site and Cre were incubated in the recombination buffer over a period of 40 min. After inactivation and digestion of the protein, the DNA molecules were analyzed by agarose gel electrophoresis. The result demonstrated that Cre does not generate any noticeable amount of nicked DNA (Figure 5E) and, therefore, does not relax supercoiling in substrate DNA. This finding is in agreement with the recent work of Ghosh et al.²⁸ suggesting that recombination is not initiated by the assembly of pre-cleaved Cre-loxP intermediates. In a similar assay with a plasmid containing one FRT site, roughly 20% of the total DNA was in the nicked form (Figure 5F); this percentage remained constant from 2 min to 40 min. The cleavage result confirms the earlier conclusion²⁹ that a Flp dimer bound to an FRT site can induce single-stranded nicks with covalent attachment of a Flp monomer to the 3’-end of the broken DNA. It is important to note that the transient break-rejoin cycles mediated by Flp do not result in the relaxation of supercoils. As a simple proof, the deletion reaction by Flp yields very little free circles (Figure 5B). Furthermore, Flp does not exhibit an intrinsic topoisomerase activity, presumably because the steric constrains within the FRT-Flp dimer complex impedes free strand rotation.³⁰ It is only when the interaction between Flp monomers is relaxed under artificial conditions that a weak topoisomerase activity of Flp can be elicited.

Experimental Determination of ϕ for Flp and Cre Systems

Clearly, the conformations of the isolated pre-synaptic protein-bound sites can differ from the halves of the full synaptic complexes. There is only limited information on the structures of Cre-bound loxP site or Flp-bound FRT site before they form the synaptic complex. The circular permutation analysis showed a 55° DNA bend in Cre/loxP complex, and >140° DNA bend in Flp/FRT complex.^{15; 16}However, the method provides only semiquantitative data on protein-induced bends.³¹

Therefore, we have re-investigated the DNA bends, induced by Cre and Flp recombinases, by using a DNA cyclization assay. The assay relies on the measurements of the cyclization efficiencies of DNA fragments, in the presence of DNA ligase, and comparing them with theoretical values.^{32; 33; 34; 35} Quantitatively the cyclization efficiency is characterized by the j-factor, the effective concentration of one end of the fragment in the vicinity of the other end. Changes of the double helix flexibility or presence of DNA bends strongly affect the values of j-factors.^{34; 36; 37} In an earlier study we have developed a modified version of the cyclization assay by using gapped DNA as the substrates.³⁷ The introduction of a 4-nucleotide single-stranded gap region in DNA makes all torsional orientations of DNA ends equally probable, which greatly simplifies the data analysis. With gapped DNA, it is possible to measure an unknown DNA bend by using only one DNA length, instead of conducting the experiments on ten fragments to cover the length of one DNA helical repeat. We used gapped DNA fragments 200 bp in length for all cyclization experiments in this study. The gap was located near one end of the fragments and separated by half of the fragment contour length from either loxP or FRT sites.

The j-factor can be determined from a cyclization experiment as

$$j=2M_0\underset{t\to 0}{lim}C(t)/D(t)$$ (1)

where M₀ is the DNA concentration, t is the ligation time, C(t) is the amount of circular monomers (CM), D(t) is the total amount of linear and circular dimers (LD and CD).^{34; 36} Since the dimerization rate is not affected by the protein binding, the j-factor change resulting from the protein binding should correspond to the change in the cyclization rate. Therefore, in this work we compared the cyclization rates for Cre- and Flp-bound DNA fragments with the cyclization rate of the same fragments in the absence of the recombinases. We also kept in mind that the ligation experiments for the j-factor determination must be performed at sufficiently low concentration of DNA ligase, when accumulation of the reaction products is proportional to the ligase concentration.^{32; 33; 38} Under this condition the values of C(t) and D(t) can be measured at different ligase concentrations where a product accumulation occurs in time scale convenient for the measurements. Comparison of the cyclization rates has to be normalized on the ligase concentrations.

First, we analyzed the binding of Cre with the loxP-containing DNA fragments. We showed, by gel retardation analysis, that for protein concentration between 20 and 200 nM more than 91% of the fragments form cII complexes, containing two monomers of the recombianse bound per loxP site (see Fig 6A). Similar gel retardation analysis showed that for the same range of the protein concentration more than 82% of the FRT-containing fragments form cII complexes (Figure 6B). The results of the assay are in general agreement with the published data.^{14; 39}

Figure 6.

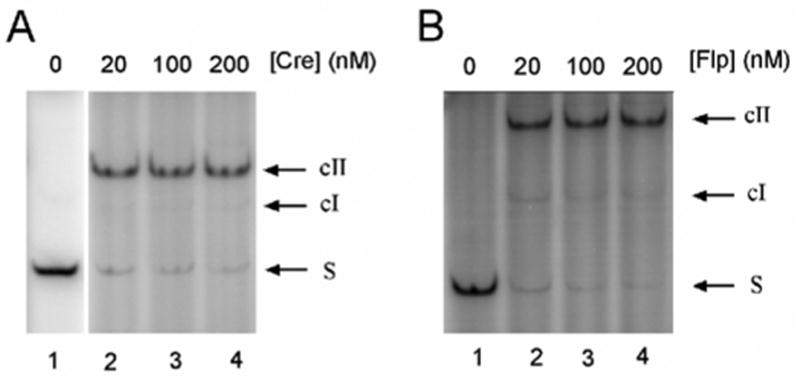
Electrophoretic mobility shift assay for DNA-protein binding. (A) 1nM of lox1 DNA was incubated with indicated amounts of Cre protein under the conditions described under ‘Methods’. cI and cII, DNA-protein complexes bound with one and two Cre molecules, respectively, at the loxP site. About 91% and 93% of the DNA were in cII when [Cre] was varied from 20nM to 200nM. (B) 1nM FRT1 DNA was incubated with indicated amounts of Flp protein. cI and cII, DNA-protein complexes bound with one and two Flp molecules, respectively, at the FRT site. About 83% and 91% of the DNA formed cII complex when [Flp] was varied from 20nM to 200nM.

We performed the cyclization experiments at both 20 and 200 nM of Cre. It should be noted that even at the highest concentration of Cre there was only one molecule of the protein per 400 bp, since 50 ng/μl of sonicated salmon sperm DNA was always included in the ligation mixture. We also found that 200 nM concentration of Cre does not change the j-factor of FRT-containing fragments (data not shown). Therefore, nonspecific binding of Cre with 200 bp gapped DNA fragments did not disturb the assay. The reaction was initiated by adding DNA ligase to Cre-bound DNA fragments. Aliquots of the ligation products were collected over the reaction time-course to analyze the accumulation of circular DNA molecules by gel electrophoresis. The values of the cyclization rate constants obtained for two concentrations of Cre did not differ by more than 15%. The result of one of these experiments is shown in Figure 7A.

Figure 7.

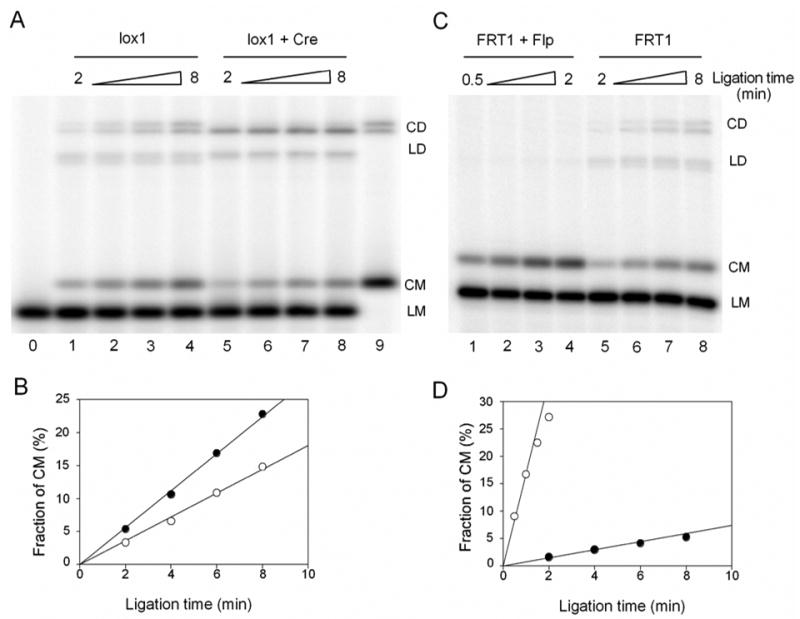
Cyclization experiments of 200bp gapped DNA and their complexes bound with Cre or Flp recombinases. (A) 1nM lox1 in the absence of Cre (lanes 1–4) and in the presence of 20nM Cre (lanes 5–8) was ligated simultaneously (but in separate reactions) by the same amount of T4 DNA ligase. Aliquots of the ligation mixture were quenched after 2, 4, 6, 8 minutes of the reaction. Lane 0 and 9 are unligated and completely ligated lox1 samples. CD, circular dimer; LD, linear dimer; CM, circular monomer; LM, linear monomer. (B) The accumulations of CM for lox1 DNA with (○) or without (●) bound Cre. Fraction of CM was calculated as the ratio of CM to the DNA substrate for each lane from the phosphorimages. For the experiment shown here, the cyclization rate of the Cre-bound DNA (○) was 64% of that of the protein-free fragment (●). (C) 1nM FRT1 in the presence (lanes 1–4) and in the absence of 20nM Flp (lanes 5–8) was ligated simultaneously (but in separate reactions) by T4 DNA ligase. The ligase concentration during the ligation of the Flp-bound fragment was 2.5 times lower than that for the protein-free fragment, to produce proper amounts of CM for quantitation. Also note that the time course in lanes 1–4 was 4 times shorter than in lanes 5–8. (D) The accumulations of CM for FRT1 DNA with (○) or without (●) bound Flp. The fraction of CM in the second plot (●) has been normalized to compensate for the 2.5 fold difference in the actual ligase concentrations. For the experiment shown here, the rate of cyclization of the Flp-bound fragment was 22 times higher than the corresponding rate for protein-free fragment.

We also found that a notable amount of dimers quickly formed during the early stage of the ligation, but it increased slowly afterwards. Normally, the accumulation of dimers should be proportional to the ligation time if the percentage of ligated DNA is small. A likely explanation to the unusual dimer accumulation is that a small fraction of Cre-bound DNA fragments formed synapses under the ligation conditions. In this case the sticky ends of the two DNA fragments would be brought into close vicinity of each other, so that the fragments can be easily ligated to dimers. This process did not disturb, however, the cyclization of the Cre-bound fragments which remained proportional to the ligation time (Figure 7A).

Similar experiments with FRT-containing fragments bound with Flp showed that the fragment cyclization is very fast, indicating a large bend angle induced in the fragments by Flp binding. For accurate measurements of C(t) at the initial stage of ligation, we reduced both the ligase concentration and the ligation time course, so only a small fraction of dimers was observed in these experiments (Figure 7B). Within statistical error of the experiments, the same values of C(t) were obtained for 20 and 200 nM of Flp in the ligation mixture.

The results obtained for both Cre- and Flp-bound fragments are summarized in Table 1. The data show that the j-factor of the Flp-bound fragment is approximately 25 times larger than that for the Cre-bound fragment. The only possible interpretation of this result is that the bend of loxP site induced by Cre is much smaller than the bend of FRT site induced by Flp binding. To determine these bend angles we needed to compare the measured j-factors with the computations based on an appropriate model of the fragments. In our case the base of the model is homogeneous discrete wormlike chain, commonly used to describe DNA conformational properties.^{38; 40} A short flexible stretch of the model chain accounted for 4 nucleotide gap in the fragments.³⁷ To account for the protein-induced bending, the model chain included a stretch, corresponding to the length of loxP or FRT site, with an equilibrium bend angle ϕ and a higher bending rigidity than the bending rigidity of the protein-free double helix, g. The latter factor was introduced since protein binding makes the corresponding DNA segment much more rigid. Indeed, the complex is approximately 2 times thicker than the double helix, and the bending rigidity of a homogeneous rod is proportional to the cube of its diameter.⁴¹ Of course, this higher bending rigidity of protein-bound DNA stretch reduces the fragment j-factor and only sufficiently large induced DNA bend can compensate this reduction. We do not know the bending rigidity of these complexes, so we needed to make an assumption regarding this value. Since the complexes are not as densely packed as the double helix per se, the increase of the bending rigidity should be smaller than the 8-fold increase expected for a homogeneous rod. Thus, we assumed that the protein-bound DNA stretch has the bending rigidity between 2g and 8g. We also found that the j-factors of the bent fragments are hardly changed if the rigidity of the bent stretch increases above 8g. Although this uncertainty in the bending rigidity of the protein-bound DNA site increased the error bar for the determination of the induced bend angle, ϕ, it remains within reasonable limits. Comparing the measured values of j-factors with the computed j(ϕ) , we found that the Cre-induced bend equals 35° ± 8° while the Flp-induced bend equals 78° ± 4° (Figure 8). The computed distributions of the recombination products for these values of ϕ (Figure 4) show that the products of Cre-mediated recombination should be mainly unlinked circles, while Flp should produce highly linked catenanes. The conclusion is in agreement with the experimentally observed product distributions for these recombinases (Figure 5A, B).

Table 1.

The values of j-factors and bend angles for the protein-bound and protein-free DNA fragments. The data represent the average values obtained over a few independent measurements performed for different concentrations of recombinases (see the text for details).

Fragment	j-factor, nM	j / j0	Bend angle, degrees
Cre-bound	5.7 ± 1.0	0.67	32 ± 8
Flp-bound	150 ± 30	17.5	78 ± 4
Protein-free, j0	8.5 ± 0.2	1	0

Figure 8.

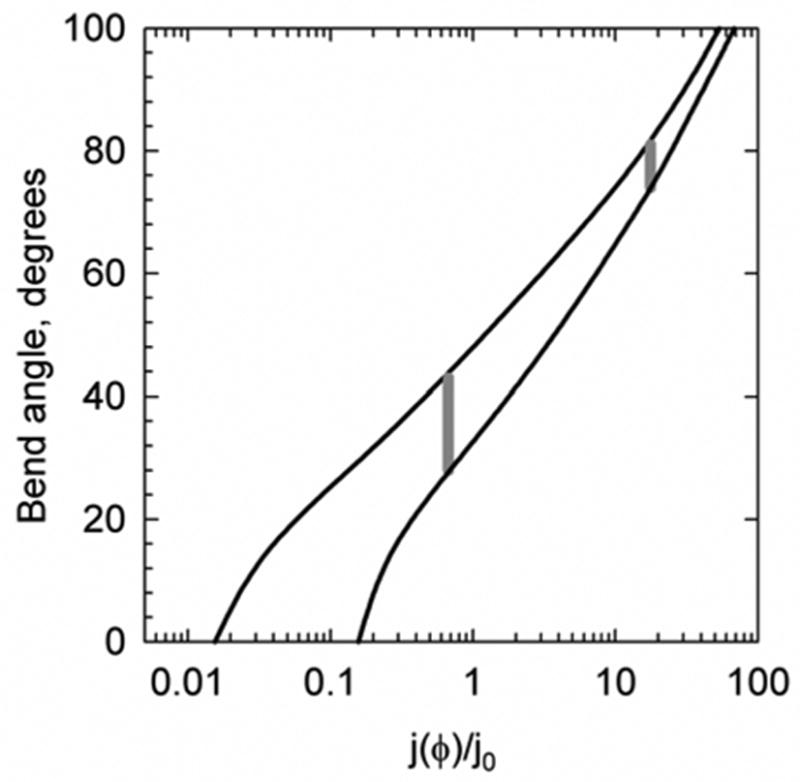
The relation between j-factor of a 200 bp gapped DNA fragment and the bend angle in this fragment. The computed dependence of j-factor on bend angle assumes that protein binding increases the bending rigidity of the binding site, 34 bp, by a factor of 2 (the lower curve) or 8 (the upper curve). Further increase in the site bending rigidity has a negligible effect on the dependence. The value of j₀ corresponds to the j-factor of the protein-free gapped DNA fragment 200 bp in length, which is equal to 8.5 nM. The measured j-factors for the fragments bound with Cre and Flp are shown by gray vertical lines.

Discussion

Topological Divergence and the Protein-Induced DNA Bends

The topological complexity of recombination products varies strongly even for similar systems of the tyrosine family of recombinases. We found in computer simulations that the bend angles in the separated halves of recombination complex strongly affect the synapsis pathway and, consequently, the topology of the recombination products produced from supercoiled substrate DNA. According to the simulation, the topological complexity of deletion products increases dramatically, from nearly 100% of unlinked circles to nearly 100% of multiply linked catenanes, when the angle changes from 30° to 60°. The corresponding increase of the product topology was predicted for knot formation from inversion substrate as well. This theoretical finding has a simple qualitative explanation. Strongly bent and properly juxtaposed specific sites cannot be easily incorporated into one superhelix branch without significant disturbance of its typical conformation. Instead, such properly juxtaposed sites are more often located at different apices of the interwound superhelix. Correspondingly, the synapsis traps a range of supercoils (Figs. 1A and 3D), and the recombination produces linked DNA circles (knotted circles in the case of the inversion substrate). The sites with small bends are mainly juxtaposed across the same superhelix branch and the synapse produces unlinked DNA circles (Figs. 1B and 3C). Although the quantitative picture will be different for more complex systems of the tyrosine family which include accessory proteins, the general principle found in this study should be valid for such systems as well.

The major assumption of our theoretical analysis concerns the mode of synapsis, namely, that it is preceded by assembling the halves of the recombination complex (Figure 2). This mode has been established experimentally, however, for at least some of the well characterized tyrosine family of recombinases. Other features of the actual system which are not included in the modeling, cannot affect the conclusion of our computational analysis. For example, there is no need to account for the possibility that recombination occurs only in a fraction of synaptic complexes, since it affects the recombination rate but does not change distribution of recombination products. Similarly, there is no need to account for two possible directions of DNA bend in the isolated protein-bound recombination sites,³ as long as the bend angles in the both directions are the same. We assumed that the synapsis is not a diffusion limited process, so the probability of synapse with a particular DNA conformation is specified by the equilibrium conformational distribution. This is a common assumption in theoretical analysis of protein assisted DNA looping.⁴² In particular, the assumption is supported by the fact that the average time before the first collision of DNA sites is a few orders of magnitude smaller than the time of synapsis.^{14; 43} We assumed in our theoretical analysis that the orientation of the specific sites in the synapses is antiparallel. The alternative assumption, that the sites have parallel orientation in the synaptic complex, should not change our results notably. We did not analyze this alternative quantitatively since the great majority of available structural and biochemical data on tyrosine recombinases convincingly prove the antiparallel orientation of recombination sites in the synapses,^{17; 18; 24; 25; 44; 45; 46} while only two studies based on electron and atomic force microscopy argue for the parallel orientation.^{47; 48}

Overall, our finding regarding the relationship between the protein-induced bend angle ϕ and the topological complexity of recombination products is a direct consequence of synapsis occurring between two pre-bent target sites, each bound by a recombinase dimer. Furthermore, to confirm the finding we have experimentally established the correspondence between the product topology and angle ϕ for two well-studied systems, Cre/loxP and Flp/FRT. Cre recombination produces mainly unlinked circles during the deletion reaction, while Flp gives highly linked torus catenanes with different values of Ca (see Figure 5). The simulated distributions of the recombination products calculated for the experimentally measured values of ϕ are in very good agreement with the measured product distributions.

A few earlier studies had indicated that the yield of linked circles from Cre mediated deletion reactions can vary from a small fraction to nearly 50% of the total products.^{10; 26; 49} It was also observed that product topology is modulated strongly by pH: a small fraction of linked recombination products at neutral pH increases markedly at higher pH.⁵⁰ These variations are not inconsistent with our model, according to which the bend angle in the separated halves of the synapse determines the topological complexity of the recombination products. Under the reaction conditions employed in our assays, this angle is close to 30°; on the other hand, it is close to 90° in the crystal structure of the Cre-loxP synaptic complex.²⁴ So, the angle can change and we believe that it does so, on changing solution conditions. It is apparent therefore that the Cre-bound loxP sites can exist in more than one conformation under different contexts. The solution conditions may thus determine the magnitude of the bend angle between the loxP arms.

A few Flp mutants have been described in literature that create a smaller bend angle compared to wild type Flp ^{51; 52}. The changes, however, are relatively small. The mutant proteins are not inactive in recombination, although some of them are severely compromised in their catalytic efficiency. According to our simulation results, the decrease in bend angle even in the worst affected among the mutants will not be sufficient to change the product topology from complex to simple.

Distinct Pre-Synaptic Bends in Related Recombination Systems: Biological Implications

It is interesting that, while the measured bend angle for Flp-bound FRT site is in a good correspondence with the synapse crystal structure,¹⁸ the angle in isolated Cre-bound loxP site is much smaller than that in Cre synaptic complex.^{24; 25} Our finding that the angle affects the product complexity suggests an explanation for the difference between two mechanistically similar systems. Indeed, the major role of Cre is thought to be in resolving replication dimers of bacteriophage P1 DNA to monomeric circles to ensure that each daughter cell receives one copy during cell division. Thus, it is clearly desirable for the phage to have these circles unlinked. The Cre structure could be evolutionary selected to introduce a small bend angle in loxP site upon binding. The increase of the DNA bend in the Cre-loxP synapse must result from the interaction between Cre monomers bound to separate sites. A similar feature could be useful for other prokaryotic recombinases that reduce chromosome or plasmid dimers to monomers for facilitating equal segregation. Furthermore, recombinases responsible for DNA excision may also benefit from this strategy. However, the absence of unconstrained supercoiling in eukaryotic cells⁵³ makes any adjustment of the bend angle by natural selection in these cells nearly impossible. So, it is not surprising that the bend angle for Flp-bound FRT site is close to that in the synapse crystal structure. Furthermore, the function of Flp is in the copy number amplification of the 2 micron yeast plasmid by a replication-coupled recombination reaction.^54;55 Flp has not been demonstrated to play a role in plasmid segregation, the decatenation of replicated plasmid molecules being promoted almost entirely by topoisomease II.⁵⁶ Thus the differences in the bend angles introduced by Cre and Flp into their respective target sites, and the attendant contrast in the topological complexities of their respective recombination products, may reflect the distinct physiological purposes to which these two mechanistically related enzymes are employed in their native contexts.

Local DNA Bends Have Global Consequence on its Topology

Topology is a global property of circular DNA molecules, and it is impossible to design a machine which could ascertain topology by using only a local interaction with these long molecules. Enzymes are very small compared with DNA molecules, so they definitely belong to the category of such locally acting machines, although they can interact simultaneously with two or more DNA segments separated along the molecular contour. It turns out, however, that enzymes can change DNA topology in a desired direction by using internal statistical properties of DNA molecules rather than by ascertaining their topology. The idea appeared for the first time when it was suggested that complex synaptic structures assembled by the serine family recombinases provide topological selectivity of the recombination products.^{57; 58} Another example of such action is topology simplification below equilibrium by type II DNA topoisomerases, where a protein-induced DNA bend is combined with unidirectional segment transfer.^{59; 60}

In this study, we provide an explanation for how directed topological transformation is accomplished by the site-specific recombinases. Both type II DNA topoisomerases and the recombinases introduce local bends into short DNA segments, and these bends affect the statistical conformational properties of circular DNA molecules. The enzymes make use of these statistical properties to reach their topological goal. This is not the same as topology ascertainment, since the result of each topological transformation remains to be random. However, the local bends can dramatically change the probabilities of different outcomes of these transformations.

Materials and Methods

Protein preparations

The 6xHis-tagged Cre was purified as described previously.⁶¹ The protein was overexpressed in E. coli BL21(DE3)pLysS strain, induced by 1 mM IPTG. It was purified by Ni-NTA Superflow columns (Qiagen), followed by buffer exchange through Econo-Pac 10DG column (Bio-Rad). Cre protein used in the study was >95% pure as judged by SDS-PAGE analysis. The 6xHis-tagged variant of Flp protein, commonly known as Flpe,⁶² was purified by a similar method in E. coli DH10B strain, induced by 0.2% L-arabinose. The purity of the Flpe protein was >85% by SDS-PAGE analysis. Flpe is more thermostable than native Flp, and exhibits wild type recombination activity. All purified proteins were free of nuclease activity. The recombination activities of the proteins were assayed on supercoiled plasmids carrying loxP or FRT sites. The protein concentrations were determined by Quick Start Bradford assay (Bio-Rad) using BSA as the standard. The proteins were stored in small aliquots at −80 °C.

DNA preparations

Lox1 and FRT1, the 200 bp DNA substrates for cyclization assays, were prepared by the method described by.³⁷ lox1 carries the 34 bp loxP sequence, and FRT1 carries the truncated 34 bp FRT sequence. Both lox1 and FRT1 were cloned into the HindIII site of pUC19 plasmid vector and transformed into DH5α cells. The constructed plasmids, pLOX1 and pFRT1, were purified by mini-prep kit (Qiagen). The gap in the 200 bp DNA fragments were generated by nicking enzymes N.BbvCIA and N.BstNBI (New England Biolabs), followed by the removal of the short tetra-nucleotides. The DNA concentrations were determined by measuring UV absorbance at 260 nm.

The DNA substrates for the gel mobility shift assay or the cyclization assay were generated by HindIII restriction, and subsequently end-labeled by [γ-³²P] ATP in the exchange reaction with T4 polynucleotide kinase. The enzymes were heat inactivated at 65°C for 20min.

Plasmid pSP104 of 4.1 kb with 2 loxP sites in direct orientation separated by 1.4 kb was constructed for Cre recombination. The plasmid p2FRT of 4.3 kb with 2 FRT sites in direct orientation separated by 1.5 kb was constructed for Flp recombination.

Determination of superhelix densities of plasmids used in the recombination assays

For each plasmid, a broad mixture of the topoisomers was prepared by nicking and successive ligation of the plasmid in the presence of different concentrations of chloroquine (0, 40, 100, 200, 350, 500, 600 μg/ml). The untreated plasmid was also added to the mixture. This reference mixture and the substrate plasmid were subjected to 2D gel electrophoresis⁶³ in agarose gel in TBE buffer at 3 volts/cm at room temperature. To avoid overlapping of the topoisomers from the two sources the reference mixture was loaded in the gel with a 1 hour delay. The first and second dimensions were run in the absence of chloroquine and in the presence of 1.5μg/ml chloroquine, respectively, for 12 hours in each direction. The separated individual topoisomers in the reference mixture were sequentially numbered, in order to calculate the linking number difference, ΔLk, for each topoisomer. The ΔLk of each topoisomer of the substrate DNA was read off from the correspondence to the reference topoisomers. The values of ΔLk were corrected to account for the ionic conditions of the recombination buffer.⁶⁴

Recombination assays

2 nM nicked or supercoiled pSP104 plasmid was incubated with 10 nM Cre enzyme in the buffer used for cyclization experiment at pH 7.1, 22 °C, except that the salmon sperm DNA and ATP were omitted. Reaction was terminated after 5 min by heating at 65 °C for 20 min. The supercoiled 4.1 kb substrate and the 2.8 kb circular product (C2) were relaxed by treatment of N.BstNBI nicking endonuclease (NEB). The residual Cre was digested by Proteinase K in the presence of 0.1% SDS prior to gel electrophoresis.

The recombination of p2FRT plasmid (10nM) by 2nM Flp was carried out in Flp binding buffer at pH 7.1 and 22 °C for 5 min. The reaction was terminated by heating at 65 °C for 20 min. The supercoiled p2FRT substrate and both circular products (C1 and C2) were relaxed by N.BstNBI. The residual Flp was digested by Proteinase K in the presence of 0.1% SDS.

The recombination products were separated by 0.8% SeaKem LE agarose (Cambrex) gel electrophoresis in TAE buffer at 2V/cm for 16 hours. DNA bands were visualized by VistraGreen staining, and quantified by digital photography and ImageQuant software (Amersham).

DNA cleavage assays

1 nM of plasmids pLOX1 or pFRT1, containing a single copy of loxP or FRT, respectively, were incubated in recombination buffer with 20 nM of the corresponding recombinases for 2, 5, 10, 20, and 40 minutes at 22°C. The recombinases were then inactivated by adding 1% SDS and heating the reaction mixtures at 65°C for 20 min. Following proteinase K treatment at 37°C for 1hour, the DNA molecules were analyzed by agarose gel electrophoresis.

DNA-protein binding assays

Binding of the recombinases with 200 bp fragments containing specific sites was followed by gel retardation analysis. Cre/lox1 assays were conducted at 22 °C in 60 mM Tris, pH 7.1, 53 mM NaCl, 3 mM MgCl₂, 0.1 mg/ml BSA, 50ng/μl sonicated salmon sperm DNA, 1 mM ATP, 2% (v/v) glycerol. The binding reactions were started by the addition of the Cre protein. Flp/FRT1 binding reactions were incubated under the same conditions, except that the binding buffer contained a higher concentration of NaCl (120 mM) and an additional 2 mM of 2-mercaptoethanol. After 30min of incubation, a dye solution was added to each binding reaction, which brought the glycerol to 5%, xylene cyanol and bromophenol dye to 0.01%. The samples were electrophoresed in 5% nondenaturing polyacrylamide gels in 0.5x TBE buffer (45 mM Tris-Borate, pH8.3, 1 mM EDTA) at 4°C. The gels were pre-run for one hour prior to sample loading.

Cyclization experiments

1 nM of gapped DNA substrate was incubated with recombinase under the conditions described in DNA-protein binding experiments. A final recombinase concentration of 20 or 200 nM was used in the cyclization reactions. Cyclization was initiated by adding freshly diluted T4 DNA ligase to the binding mixture. The ligase concentrations were 80 units/ml for Cre, and 30 units/ml for Flp reactions. In order to eliminate the variations in ligase activity, ligation of the recombinase-free DNA samples were carried out in parallel for each cyclization experiment. Aliquots of the ligation mixture were taken and quenched immediately with 40mM EDTA and 0.1% SDS. The samples were heated at 65 °C for 10 min, and then treated with Proteinase K at 37 °C for 30 min. The unreacted radioactive ATP in the samples was removed by Sephadex G-50 spin columns. The ligation products were electrophoresed in 2.0% MetaPhor agarose (Cambrex) at 5 V/cm for 8 hrs in TBE buffer.

The gels were air-dried and recorded on storage phosphor screen. The screen was scanned by a Storm PhosphorImager (GE Healthcare). The results were processed using the ImageQuant software.

Computer simulation of synapsis in supercoiled DNA

Circular DNA was modeled as a discrete worm-like chain consisting of N rigid cylinders of equal length l (see Figs. 3–5).⁶⁵ The values of the model parameters corresponded to a solution of 0.2 M NaCl: DNA persistence length of 50 nm, torsional rigidity of 3.0 × 10⁻¹⁹ erg·cm, and DNA effective diameter of 5 nm.⁶⁵ The length of a straight segment was equal to 10 nm, so each cylinder of the chain corresponded to 30 bp. It has been shown that further reduction of the segment length does not change the simulation results.⁶⁵ Each recombination site, assumed to be bound with two recombination proteins, was modeled by two adjacent segments. The induced bend angle between the two segments, ϕ, did not fluctuate during the simulation. In accordance with the experimental part of the work, the recombination sites had head-to-tail orientation and were separated by 1440 bp; the total length of the circular DNA was 4200 bp. We used the Metropolis procedure to simulate the equilibrium ensemble of DNA conformations.⁶⁵ From this set of conformations, those with properly juxtaposed sites were taken for the analysis of the recombination product topology.

The equilibrium sampling, which corresponds to the described model, does not provide sufficient number of chain conformations where the specific sites are juxtaposed in the proper orientation. To enrich the sampling by conformations with the properly juxtaposed sites, we used a biased sampling procedure, based on adding an artificial potential to the system:⁴⁵

$$U=A·\left[{\left(\frac{r_0}{r}\right)}^{2q}-2{\left(\frac{r_0}{r}\right)}^q\right]·exp\left(-\frac{{\varphi }^2+{\theta }^2+{\varsigma }^2}{2{\sigma }^2}\right),$$ (2)

where r , ϕ, θ and ς are variables whose definitions are explained in the legend to Figure 9. The values for the parameters A, q, r₀ and σ in the computations were:

Figure 9.

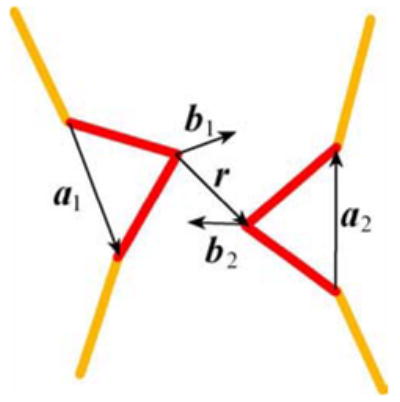
Monte Carlo simulations of synapsis. The diagram shows variables that define the mutual orientation of the recombination sites (shown by red). The variables are used in the potential specified by Eq. (2) and for the definition of the synapsis. Vectors b₁ and b₂ are perpendicular to a₁ and a₂, respectively, and are in the planes of the sites. The angles which appear in Eq. (2) are defined as: $\varphi =arccos\left[\frac{-({\mathit{a}}_1{\mathit{a}}_2)}{a_1{a}_2}\right],\theta =arccos\left[\frac{-({\mathit{b}}_1{\mathit{b}}_2)}{b_1{b}_2}\right]\hspace{0.17em}\text{and\hspace{0.17em}}\varsigma =arccos\left[\frac{({\mathit{b}}_1\mathit{r})}{b_{1}r}\right]$.

A = 17k_BT, q = 0.8, r₀ = 0.6l and σ² = 1, where k_BT is the Boltzmann temperature factor. Although the potential disturbs the whole distribution, it does not affect the conformational distribution among the states with juxtaposed sites.

The specific sites were considered properly juxtaposed if r was less than 0.8l and angles ϕ and θ were smaller than 20°. We tested that further tightening this conditions does not change the simulation results.

The simulations were performed for DNA superhelix density of −0.05. We chose this superhelix density since the statistical averaging was too slow for higher values of supercoiling. A few billions of elementary moves of the Metropolis procedure⁶⁵ were performed for each value of ϕ. 10⁹ moves take approximately one hundred hours on G5 PowerMac processor.

j-Factor Calculation

The algorithm based on a set of conditional probabilities was used for the j-factor calculation.⁶⁶ The corresponding program, jfm2full.c, and a sample data file, jfm2full.data, are available at http://crab.chem.nyu.edu/jfactor/index.html. The program makes it possible to perform fast and accurate calculations of the j-factor values for a chain consisting of segments of equal lengths. The program assumes that the bending, torsional rigidities and the minimal energy orientation of adjacent segments are specified for each segment independently. We found that for 200 bp fragments the calculated values of j-factor do not depend on the segment length if one segment corresponds to less than 10 bp. For the calculations presented in the paper, one straight segment of the chain corresponded to 5 bp. The persistence length the double helix was equal to 48.5 nm. The gap of 4 nt was modeled by 1 segment with the same length, 1.7 nm, 11.4 times lower bending rigidity and zero torsional rigidity. The latter value of the gap bending rigidity was obtained by fitting the computed and measured values of j-factor (see ref. (37) for details). A stretch of 7 segments modeled the 34 bp protein-bound site. The stretch had a higher value for the bending rigidity, specified under ‘Results’, and an intrinsic bend uniformly distributed over the stretch. It has been shown that the distribution of the intrinsic bend along a stretch of this length does not affect the j-factor value.³⁷