Scaffold proteins confer diverse regulatory properties to protein kinase cascades

Abstract

The assembly of multiple signaling proteins into a complex by a scaffold protein guides many cellular decisions. Despite recent advances, the overarching principles that govern scaffold function are not well understood. We carried out a computational study using kinetic Monte Carlo simulations to understand how spatial localization of kinases on a scaffold may regulate signaling under different physiological conditions. Our studies identify regulatory properties of scaffold proteins that allow them to both amplify and attenuate incoming signals in different biological contexts. These properties are not caused by the well established prozone or combinatorial inhibition effect. These results bring coherence to seemingly paradoxical observations and suggest that cells have evolved design rules that enable scaffold proteins to regulate widely disparate cellular functions.

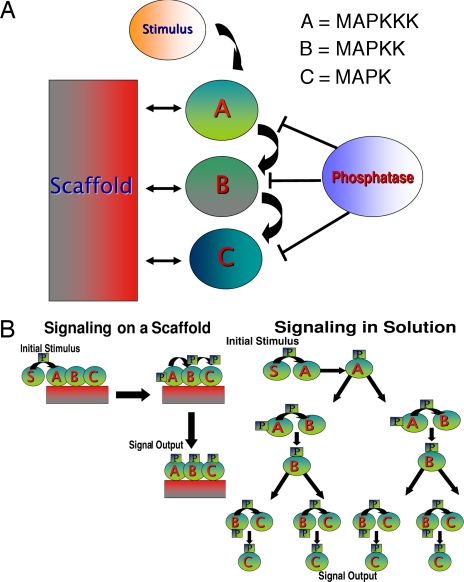
The sequential activation of multiple protein kinases constitutes a highly conserved intermediate step in eukaryotic cell signaling pathways and is crucial for the regulation of numerous cellular decisions (1–3). Common explanations for the ubiquity of these multileveled kinase cascades include the possibility that they amplify signaling and incorporate additional regulatory checkpoints that may improve the specificity and fidelity of the signal output (4–6). In many instances (e.g., in several MAPK cascades), these kinase cascades are associated with scaffolding proteins that assemble multiple components of the signaling cascade in sequence (Fig. 1A) (7–10).

Fig. 1.

Computer simulations model the effects of scaffolding a kinase cascade. (A) In a model kinase cascade such as the MAPK cascade, an initial stimulus, S* (e.g., Ras-GTP), is recruited to and activates kinase A (MAPKKK). An active A (MAPKKK) in turn activates a B kinase (MAPKK), which then can activate kinase C (MAPK). Phosphatases are present that can encounter and deactivate activated kinases. (B) Schematics are shown for the sequence of signaling events in solution and on a scaffold in our model. For a chemical reaction to occur in solution, the appropriate species must first come into contact with its substrate and then overcome a thermal energy barrier to model catalysis. When assembled on a scaffold, active kinases need only overcome the thermal energy barrier to activate their downstream target. Phosphatases are allowed to interact with active kinases that are bound to the scaffold. Excluding phosphatases from interacting with scaffold-bound proteins is also considered.

The general principles underlying how scaffold proteins function to influence signaling in protein kinase cascades are still poorly understood. Scaffold proteins are believed to be involved in many regulatory processes such as intracellular trafficking and pathway sequestering, and several factors have been shown to influence their signaling function (8). For example, the relative concentration of scaffolding proteins has been shown to be a key variable that modulates signal output in many instances (11, 12). Indeed, one signature of a scaffold protein is believed to be the appearance of a “bell-shaped” protein titration curve.

Recent reports also indicate that certain scaffolding proteins, such as Ste5 involved in the MAPK pathway of the yeast mating response, can catalytically activate a MAPK upon binding by inducing autophosphorylation of the threonine residue in the TxY motif in the MAPK, Fus3 (13). More complexity is added by suggestions that some scaffolds may recruit phosphatases to their scaffold-bound substrates (8) or, in contrast, protect scaffold bound kinases from phosphatase-mediated deactivation (12, 14).

Although functions such as catalysis could be important for specific systems, the ubiquity of scaffolds suggests that the physical effects of tethering members of the cascade to a scaffold may have a functional role. It is difficult to ascertain that specific effects (e.g., catalysis or feedback) are absent in an experimental system. Therefore, it is problematic to study this potentially more generic function of scaffolds. Furthermore, a systematic variation of the many factors that may influence mechanisms through which spatial localization of kinases on a scaffold may affect signal propagation is currently not tractable. It would therefore be very useful to identify the most influential variables on which experiments should focus. For these reasons, we carried out computer simulations to study whether, how, and under what conditions assembling a sequence of kinases on a scaffold affects signal propagation through a multitiered kinase cascade.

We investigated how scaffolds can influence protein motion, phosphorylation of downstream kinases by an active kinase, and phosphatase-mediated deactivation of kinases. The signaling module that we studied (Fig. 1) can be characterized by the following small number of parameters: the rate at which an active kinase can phosphorylate a downstream kinase, the rate at which phosphatases can remove a phosphate group from a kinase, the binding affinity of kinases to the scaffold or exchange rate, the relative concentration of scaffolds and kinases, and the parameters characterizing the mobility of the various protein kinases. We studied how scaffolds influence signal propagation for different physiological conditions determined by values of these parameters. Schematics of how signaling occurs in solution and on a scaffold are shown in Fig. 1B. Other important issues that we examined with this model are the consequences of whether kinases bound to the scaffold can phosphorylate downstream kinases that are in solution and whether phosphatases in solution can act on proteins bound to the scaffold.

The simple model we studied (with a relatively small number of parameters) allows us to meticulously study these different scenarios in depth. Yet, it provides enough relevant features to allow the mechanisms extracted from this model to be biologically meaningful. Results from our simulations indicate that, depending on cellular conditions, the spatial organization of kinases on scaffold proteins can either enhance or inhibit signal propagation through a kinase cascade. Specifically, scaffolds enhance signal propagation when prevailing conditions would lead to attenuation. Conversely, scaffolds inhibit the propagation of signals that would otherwise be greatly amplified. We discuss how these results provide a conceptual framework that sheds light on available observations and suggest further experiments that could help elucidate the role of scaffolds in cell signaling processes further.

Model Development and Key Variables

We simulated a model multileveled protein kinase cascade such as the MAPK. An initial stimulus, S*, (e.g., Ras-GTP) can interact with a MAPKKK to activate it. The activated MAPKKK can then activate a MAPKK. The MAPKK, in turn, activates a MAPK. Finally, the MAPK activates a downstream species. The following sequence of signaling events,

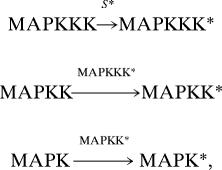where * denotes a fully activated kinase, is also described in Fig. 1. Each of these above signaling events is modeled as an elementary chemical reaction. Each activated kinase can be deactivated by phosphatase-mediated catalysis. For notational convenience, MAPKKK will hereon be referred to as kinase A, MAPKK as kinase B, and the MAPK as kinase C.

Space is discretized on a 100 × 100 × 100 lattice [supporting information (SI) Fig. 6]. If we assume a lattice spacing of 10 nm, a typical diameter of a protein, the concentration of kinases in our simulation box is ≈1 μM for kinase A and kinase B and ≈5 μM for kinase C. In a physiological context, assuming the radius of the cell is ≈10 μm, these values approximately correspond to ≈10⁵ molecules of kinases A and B and a copy number of ≈5 × 10⁵ for kinase C in our simulation. These relative numbers are commensurate with reported kinase concentrations (15). Six hundred generic phosphatases are also present, giving a 1:1 ratio of kinases to phosphatases. As described in SI Text and SI Fig. 7, in most cases, our qualitative results are not sensitive to variations of these numbers. For the results presented, all events occur in the cytosol but the consequences of restricting reactions to a membrane are also considered (SI Text).

One important variable is the time it takes for an active kinase to encounter its substrate; our studies focused on experimentally relevant encounter times as diffusion constants (16), and aforementioned kinase concentrations were chosen accordingly (SI Text and SI Fig. 8). For most results, we consider the activation of protein kinases and phosphatase-mediated deactivation to occur through a single reactive collision involving reactants making contact and then overcoming a thermal energy barrier. The results are qualitatively similar in many cases for catalytic mechanisms (SI Text and SI Fig. 8).

The model as defined above involves the following biophysical parameters: E, the energy barrier for disassociation of a bound species from a scaffold; E₂, the energy barrier for association of a kinase to a scaffold; E₃, the energy barrier for activation of a kinase by an appropriate target enzyme, and E₄, the energy barrier for deactivation of a kinase by a neighboring phosphatase. The amplitude of the initial stimulus is an important quantity in cell signaling. We define a variable, σ ≡ [S*]/[A]₀ (the amplitude of initial stimulus scaled to a characteristic density of protein kinase, [A]₀). Other important variables are: λ ≡ P_Diffusion/P_Reaction (the ratio of probabilities for attempting diffusion and reaction moves in the simulations), which is a measure of protein mobility and ξ ≡ [Scaffold]/[A]₀, which is the ratio of scaffold density to a characteristic density of kinases.

To quantify how signals propagate along the cascade, we define an amplification factor, φ, that measures the fractional change in activated signaling species as the signal propagates through the cascade (i.e., the ratio of the numbers of an activated downstream kinase at the end of the cascade relative to that of the first kinase); φ ≡ 〈C*/A* − 1〉, where * denotes a fully activated species, and the brackets indicate an average over many simulations (analogous to a population average over many cells). φ is positive if the signal is amplified as it propagates along the cascade, and it is negative if it is attenuated. The absolute magnitude of the signal, θ ≡ 〈C*/[A]₀〉, is also considered.

Sensitivity amplification (17), 〈d(lnC*)/d(lnS*)〉, another metric often used for studying signaling cascades and their input–output characteristics, is not considered here, because our study focuses mainly on the propagation of a signal's amplitude: how scaffold proteins could shape the dose–response (i.e., input–output characteristics) of a signaling system has been studied theoretically (7, 12, 14). It has been suggested that for cases when enzymes are saturated in solution, scaffolds would decrease the sharpness of the dose–response curves and can even convert switch-like to graded responses.

We compute the quantities of interest by using a kinetic Monte Carlo algorithm (18, 19) that is described in Methods and SI Text. For reasons mentioned therein, a signaling model using ordinary differential equations was not used.

Results

Scaffold Proteins Amplify Signals That Are Attenuated in the Absence of a Scaffold.

We first considered the situation where basal phosphatase activity is high, making the cascade intrinsically difficult to activate. In this circumstance, weak signals are rapidly attenuated and do not propagate regardless of whether a scaffold is present (data not shown). Also, in the absence of scaffolds, strong signals (σ ∼ 1) are attenuated (φ < 0). We obtained this result by taking the affinity of kinases to the scaffold to be sufficiently weak so that, on average, these proteins are not bound to the scaffold.

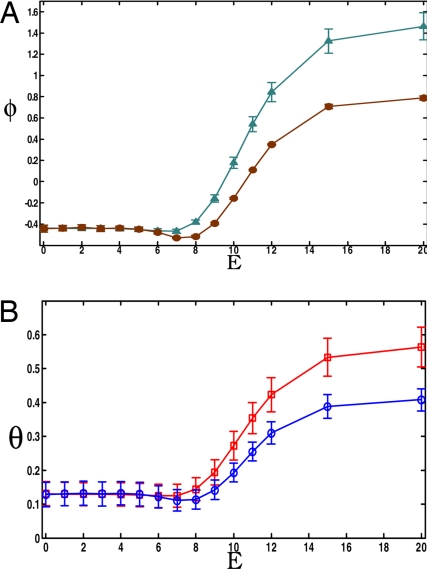
When the affinity of the kinases to the scaffold increases, kinases begin to assemble onto the scaffold. When the affinity is sufficiently strong, available kinases are bound to their corresponding binding sites on the scaffold, and this scenario can be interpreted as having a scaffold present. We find that, when phosphatase activity is high, and the initiating stimulus is strong, assembling kinases onto the scaffold results in a sharp increase in the number of active kinases as the signal propagates along the cascade (Fig. 2A). In this circumstance, assembling kinases on a scaffold allows for significant signal amplification. For reasonable parameter values, a ≈100% increase in signal output (ϕ ∼ 1) with respect to the first member of the cascade can result. Amplification is also evident in the absolute magnitude of the signal output (Fig. 2B). Thus, when phosphatase activity is sufficiently high, a scaffold allows for the effective propagation of a signal that would otherwise be significantly quenched. Note that this amplification of signal propagation occurs even when phosphatases can act on scaffold-bound kinases.

Fig. 2.

Scaffold proteins can amplify signals that would otherwise attenuate. The case of high basal phosphatase activity, E₄ = 0. Shown are calculated values of signal amplification, ϕ, φ ≡ 〈C*/A* − 1〉 (A) and signal magnitude, θ, θ ≡ 〈C*/[A]₀〉 (B) for increasing values of the kinase-scaffold binding affinity E. The A (MAPKKK) and B (MAPKK) concentrations equal that of the scaffold, whereas the concentration of C (MAPK) is five times larger (other situations are described in SI Text and SI Fig. 7). A strong stimulus, σ = 1 (σ ≡ [S*]/[A]₀), is used. Two cases are considered: a “constrained” case, where species bound to the scaffold cannot activate species in solution (diamonds in A and circles in B) and an “unconstrained” case, where species bound to the scaffold can activate species in solution (triangles in A and squares in B).

Scaffold Proteins Can Suppress Signals That Are Amplified in the Absence of a Scaffold.

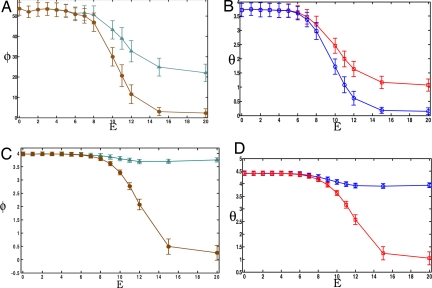
Now we consider situations in which basal phosphatase activity is low, rendering the cascade easy to activate. In this circumstance, strong (σ ∼ 1) and weak (σ ≪ 1) signals are strongly amplified in the absence of a scaffold as there is little to impede the propagation of signals (Fig. 3 A and B). The magnitude of φ is much larger compared with the situation where phosphatase activity is high because, in this case, the signal is amplified exponentially as each activated kinase can activate many downstream targets.

Fig. 3.

Scaffold proteins attenuate signals that would otherwise strongly amplify. Low basal phosphatase levels are considered (E₄ = 6). Signal amplification ϕ, φ ≡ 〈C*/A* − 1〉 (A and C), and signal magnitude θ, θ ≡ 〈C*/[A]₀〉 (B and D) are considered as a function of scaffold binding affinity, E. Two cases are shown: a weak stimulus (σ ≪ 1, σ ≡ [S*]/[A]₀) of small amplitude and low basal phosphatases levels (E₄ = 6) (A and B) and a stimulus of large amplitude (σ = 1, σ ≡ [S*]/[A]₀) (C and D). All other conditions are the same as those reported in Fig. 2. As shown in these plots, assembling signaling components onto a scaffold by increasing E results in significantly lower amplification and signal output. Again, in each panel, two cases are considered: a constrained case, where species bound to the scaffold cannot activate species in solution (diamonds in A and C and circles in B and D), and an unconstrained case, where species bound to the scaffold can activate species in solution (triangles in A and C and squares in B and D).

In striking contrast to the situation where phosphatase levels are high, for low phosphatase activity, assembling kinases on a scaffold greatly suppresses signaling and limits signal amplification (Fig. 3). For weak signals, this effect is accentuated if scaffold-bound kinases can only interact with downstream kinases that are also attached to the scaffold (Fig. 3). Although signal amplification still occurs, our simulations demonstrate that the extent to which amplification occurs is severely limited (and approaches nonexistence) when scaffold-bound kinases are constrained to interact only with other scaffold-bound kinases.

If scaffold-bound kinases are allowed to activate their downstream targets that are not bound to the scaffold, scaffolds have only a small effect on the propagation of strong signals when phosphatase activity is low (Fig. 3 B and D). The slight dampening of the signal in this case is largely caused by a smaller frequency of collisions between proteins bound to the scaffold and those in solution compared with that of mobile proteins in solution.

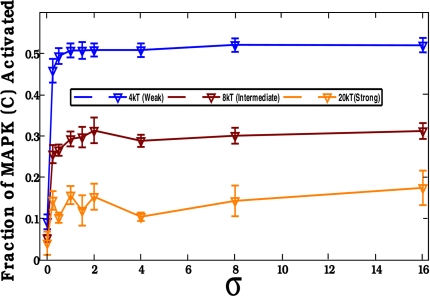
The ability of scaffolds to limit amplification can also be manifested in other interesting ways. Our calculations show that, provided phosphatase activity is sufficiently low and scaffold-bound kinases cannot activate free kinases, increasing the exchange rate (i.e., lowering the energy barrier for disassociation) characterizing the binding of the last kinase (kinase C) to the scaffold can result in more efficient signal propagation (Fig. 4). This result suggests that the observed (A.S.S., unpublished results) low affinity of Erk to KSR (a scaffold associated with a MAPK module in mammalian cells) may serve to enhance signal propagation. It is also tempting to suggest that this factor could be one (of many) factor(s) underlying the recent observation that a mutation, which blocks binding of the MAPK, Fus3, to the scaffold, Ste5, but keeps the docking site to the MAPKK, Ste7, intact, results in greater signaling output in the yeast mating response (13) as this could effectively increase the exchange rate.

Fig. 4.

Serial engagement of the last kinase can greatly influence signal output in a MAPK cascade. We consider the scenario where the first two kinases, A and B (MAP3K, MAP2K) bind tightly (E₂ = 20) and the binding affinity C (MAPK) is varied as follows: weak (E₂ = 4), intermediate (E₂ = 8), and strong (E₂ = 20) disassociation energies. The ordinate represents the fraction of activated C (MAPK) proteins (a measure of signal output), and the abscissa is the scaled strength of signal, σ, σ ≡ [S*]/[A]₀. The signal output is largest when kinase C (MAPK) is allowed to rapidly disassociate (E₂ = 4) from the scaffold. Data presented are for a 1:1:10:1 ratio of A/B/C/scaffolds.

Mechanism Underlying Why Scaffolds Can both Amplify and Limit Signal Propagation.

A unified conceptual framework explaining why scaffolds can both enhance and attenuate signaling emerges from our study. Suppose a kinase such as kinase A in Fig. 1A is activated. In the absence of a scaffold, the number of molecules, N, of the downstream kinase (kinase B) that it could potentially phosphorylate must be enclosed in a volume that grows with the diffusion coefficient of the upstream kinase (kinase A) and the time (τ_p) it takes phosphatases to deactivate it. Scaffolds impose a stoichiometric constraint that limits the number of molecules (N_scaf) of the inactive downstream target (kinase B) that can potentially be phosphorylated, to those that are bound to the scaffold. When N > N_scaf, an activated kinase (kinase A) can phosphorylate more of its substrates (kinase B) in the absence of the scaffold. This is the situation when phosphatase activity is low (τ_p is large), and so a scaffold limits signal amplification (Fig. 3). However, when phosphatase activity is high, N can be less than N_scaf; i.e., signal propagation in the absence of a scaffold is limited by the short time available for encounters between kinases before phosphatases inactivate them. Now, scaffolding results in amplification (Fig. 2) because the spatial proximity of kinases on a scaffold reduces the encounter time, and this effect dominates over the inhibitory stoichiometric constraint.

More precisely, N, must be contained in the volume, Ω ∼ (Dτ_p)^d/2, where D is the diffusion constant, d is the spatial dimension (d = 2 for a cell membrane, and d = 3 for signaling in the cytosol or on an endosome). Then,

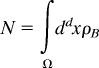where ρ_B is the concentration of inactive B kinases. If proteins are assembled onto a scaffold, the only molecules of the inactive B that can potentially be phosphorylated by an active A molecule are those that are on the scaffold [i.e., they are enclosed within a volume, Ω ∼ (L_scaf)^d], where L_scaf is the distance between kinase B and kinase A on the scaffold. The number of kinase B that could be potentially activated is then

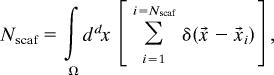where δ(x⃗) is the Dirac delta function, and N_scaf is the number of kinases that can be activated on the scaffold (one in our case). When kinases in solution can exchange with scaffold-bound kinases, the effective N_scaf in the sum can be larger. When the system is characterized by conditions such that N > N_scaf, an activated A can phosphorylate more B proteins in the absence of the scaffold because the stoichiometric constraint imposed by scaffolding is inhibitory. This is the situation when phosphatase activity is low (τ_p, Ω, and N are large), and so a scaffold limits signal amplification (Fig. 3). However, when phosphatase activity is high, N can be less than N_scaf because τ_p and Ω are small; i.e., signal propagation in the absence of a scaffold is limited by the short time available for encounters between kinases before phosphatases inactivate them. In these circumstances, scaffolding results in amplification (Fig. 2).

Also, under these conditions, significant signal amplification occurs even when there are equimolar concentrations of signaling components bound to the scaffold. The time it takes for a scaffold-bound downstream kinase to be activated by a scaffold-bound upstream kinase is much shorter than the time required for the stimulus, S*, to be recruited to the complex and activate the first kinase in the sequence. Therefore, when phophatases render kinases inactive on the scaffold, the kinases further down the cascade become reactivated on average much more quickly than those at the beginning of the cascade. This causes scaffolds to influence kinase activation in a hierarchical fashion. If a scaffold-bound B* or C* is deactivated, a scaffold bound A* or B* quickly reactivates B or C. However, if A* is deactivated, a much longer time is required for a reactive collision with S*. One then notices a positive gradient of active signaling molecules when moving along the cascade. Our simulations suggest that this effect can potentially be very significant, allowing for many-fold changes in signal output with reasonable parameter values. This effect can be seen in the positive values of ϕ; in Fig. 2A, for example, ϕ ∼ 1, implying a ≈100% increase in active molecules of C as compared with A.

The Network of Interactions Between Phosphatases and Their Target Kinases Can Influence the Function of Scaffold Proteins.

Although phosphatases are in general believed to play a crucial role in regulating kinase cascades, the precise ways in which phosphatases interact with members of kinase cascades in different contexts are not fully understood and are currently the subject of intense study (21, 22). Some have also suggested that, because of steric constraints, phosphatases may not be able to interact with activated kinases that are bound to a scaffold (12, 14). In these theoretical studies, phosphatases were prevented from acting on scaffold-bound kinases, which enhanced signaling.

We have studied the consequences of different scenarios by which phosphatases can interact with scaffolded kinase cascades (SI Fig. 9). We find that when individual kinases are protected from deactivation when bound to a scaffold, qualitative behavior in the signal amplitude does not change (SI Fig. 9 a and b). Similar results are obtained when all three kinases are protected from deactivation when bound to the scaffold. Alternatively, if certain kinases, upon activation, are never deactivated by phosphatases, then some qualitative findings can change as discussed in SI Text.

For instance, in SI Fig. 9c, when phosphatases cannot deactivate kinase C, assembling kinases on the scaffold with a high affinity reduces signal output. In the absence of a scaffold and if phosphatases cannot act on kinase C, each of these kinases would eventually become activated. However, binding to a scaffold and preventing kinases from activating substrates in solution prevents the kinase C molecules that reside in solution from being activated even when phosphatases do not act on them. This effect is removed when kinases that are bound to the scaffold can interact with their substrates in solution. For these cases (SI Fig. 9c), such perturbations result in scaffolds having little to no effect on the signal output.

Importance of Scaffold Concentration.

One signature of a scaffold protein is believed to be the presence of nonmonotonic behavior (bell shape) in a scaffold protein titration curve. If scaffolds are essential for activation, then too few scaffolds results in reduced output; alternatively, at high concentrations, scaffolds also would inhibit signaling because molecules that are activated in sequence are less likely to be bound to the same scaffold (i.e., the prozone effect) (7). So, we considered how our results depend on scaffold concentration under conditions of high (SI Fig. 10a) and low (SI Fig. 10b) basal phosphatase activity. We find a bell-shaped curve for high phosphatase activity (SI Fig. 10a) when “titrating” along the relative scaffold concentration, ζ. For conditions of low phosphatase activity (SI Fig. 10b), the nonmonotonic behavior in signal output that appears in SI Fig. 10a is no longer present, because, in this case, both the low phosphatase, inhibitory regime that characterizes the scaffold-mediated signaling and the prozone effect are at work.

Finally, many parameters governing the behavior of cell signaling pathways, such as diffusion coefficients, binding affinities, and catalytic rate constants, are unknown and are likely to greatly differ in individual physiological contexts. It is therefore essential that we understand how our results depend on unknown parameter values. We performed extensive sensitivity analysis with respect to all relevant parameters to examine the robustness of the qualitative behavior to parameter values. Our results demonstrate that in most cases (SI Text) the qualitative function of assembling kinases onto a scaffold described above is insensitive to variations over wide ranges of these parameters.

Discussion

A unified conceptual framework that explains why scaffolds can both enhance and attenuate incoming signals, and why this is biologically important, emerges from our findings; a summary of the key findings is given in Fig. 5. Our results suggest that a robust system that is resistant to spurious noise but needs to respond vigorously to a strong stimulus should be designed with high basal phosphatase activity and scaffolds. An example is provided by T cells where discriminating between minute amounts of antigenic stimulus and spurious noise is critical. Basal phosphatase activity is high in T cells [phosphatases have been shown to interact with MAPK components in mammalian cells (21, 22)], and the KSR scaffold (23, 24) is known to amplify signaling through the MAPK pathway as measured by ERK activation.

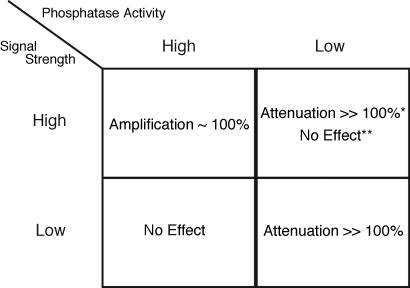
Fig. 5.

Summary of different regimes that characterize scaffold-mediated signal transduction. The characterization of four regimes of scaffold-mediated signal transduction: (i) high signal strength and high phosphatase activity, (ii) high signal strength and low phosphatase activity, (iii) low signal strength and high phosphatase activity, and (iv) low signal strength and low phosphatase activity. * indicates the case when kinases bound to a scaffold cannot phosphorylate their downstream substrates that remain in solution. ** indicates the case when kinases can interact with their downstream targets that are present in the solution. The absence of * or ** indicates that the effect occurs regardless of whether scaffold bound proteins can activate downstream targets in solution. These results summarize our findings when phosphatases are allowed to act on scaffold-bound kinases and reflect the balance between stoichiometric constraints and removal of transport limitations by scaffolds. As described in Results and SI Fig. 9, preventing phosphatases from acting on scaffold-bound kinases does not alter these results substantially.

Conversely, a system that needs to be highly sensitive to stimuli should be designed such that the cascade is intrinsically easy to activate (e.g., low phosphatase activity). Such a system would be overwhelmed, however, if exposed to a strong stimulus. Scaffolding kinase components can limit signal amplification and prevent the potentially catastrophic consequences of amplifying strong stimuli in this case. Signal integration during phototransduction requires a response to a few photons, and this is facilitated by a cascade that is easy to activate. Scaffolding such a cascade using INad (25) inhibits signal amplification in Drosophila.

Our results suggest that scaffold proteins can intrinsically amplify strong signals that would otherwise not propagate efficiently, but in other instances, they can insulate kinase cascades from propagating signals that would otherwise be strongly amplified with potentially deleterious consequences. As signaling often results in the up-regulation of phosphatase expression, it is interesting to speculate that the role of scaffolds may change with time; scaffolds could take on positive and negative regulatory functions at different time points in the course of signal transduction. By amplifying attenuating signals when phosphatases are up-regulated and abating amplifying signals when phosphatases are down-regulated, signaling specificity and fidelity, to some extent, could then be obtained by having the scaffold provide the right balance of positive and negative control of the signal amplitude. Scaffold proteins would then confer additional, intrinsic feedback mechanisms to an already carefully regulated, highly evolved, complex cellular process. The diverse consequences of spatially organizing kinases on a scaffold revealed by our studies would be further modulated by processes such as catalytic modifications and feedback control.

Our results highlight the dual positive and negative regulatory properties that scaffold proteins confer to kinase cascades. Such properties are predicted to have consequences on shaping the input–output characteristics of the signaling cascade. Because scaffolds limit signal amplification when phosphatase levels are low, the model predicts that, under these conditions, dose–response curves would appear less sharp in the presence of scaffolds. This is because each stimulating molecule has the ability to activate many more than one downstream target in solution, whereas the scaffold limits this number. Conversely, under conditions in which signals attenuate in solution (high phosphatase levels), scaffolds increase the sharpness of the dose–response curve only slightly. Such scenarios presuppose that the kinases are not operating in saturating or “zero-order ultrasensitive” conditions in solution. The latter situations would allow scaffolds to change the dose–response from an “all or none” to a graded response, as has been suggested (7, 12, 14).

We hypothesized that scaffold-mediated signaling could be influenced by the rate at which kinase C (the MAPK) exchanges with the scaffold as this would permit a scaffolded signaling complex to generate many activated C species. Therefore, we investigated the effects of the affinity of the third member of the cascade to the scaffold. We found that in some situations decreasing the binding affinity of kinase C to the scaffold can result in a larger response. This result follows from the ability of each signaling complex to potentially activate many of its downstream substrates when the substrate can quickly exchange with the scaffold. We noted that this prediction could explain the observed low affinity of ERK to the KSR scaffold (A.S.S., unpublished results). We also speculated that this result may underlie recent data that demonstrates that mutating the docking site of Fus3 to the scaffold Ste5 results in a larger signal output because it reduces the strength of interaction of this kinase with the scaffold (13). However, such simple explanations for these observations may be confounded by specific features of importance to particular signaling mechanisms. Yet, in light of our results, it is tempting to suggest that the affinity between the MAPK and the scaffold may be a crucial parameter that has been evolutionarily fine-tuned for specific systems.

We also investigated how the topology of the kinase/phosphatase interaction network affects signal output. When kinases are protected from phosphatases only when bound to the scaffold, qualitative results (SI Fig. 9 a and b) are the same as when phosphatases can act on scaffolded kinases (Figs. 2 and 3). But, in some instances (SI Fig. 9c), changes to the network topology (i.e., preventing phosphatase action on certain members of the kinase cascade regardless of whether or not they are attached to the scaffold) can change the functional role of assembling kinases onto a scaffold.

Finally, we studied how our results depend on scaffold concentration. For high basal phosphatase activity, we found a bell-shaped titration curve. This finding is consistent with previous work (12), which, however, did not consider the potentially inhibitory role of scaffolds revealed by our studies of situations where basal phosphatase activity is low (Fig. 3). When scaffolds limit signal propagation, no such nonmonotonic behavior was seen (SI Fig. 10b). Instead, signal output decreases monotonically with increasing scaffold concentration.

Our computational studies suggest general molecular mechanisms for how scaffold proteins can regulate signal transduction in diverse ways. Thus, our results provide possible clues for why scaffolds are involved in so many critical cellular pathways and how their improper regulation can lead to disastrous phenotypic outcomes (20, 26, 27). We hope that our attempt to elucidate some general principles that govern scaffold function provides conceptual guidelines for future experimentation.

Methods

Simulation Methodology.

We simulate a model protein kinase cascade such as the MAPK cascade (Fig. 1A) in the presence and absence of a scaffold with a Metropolis-based kinetic Monte Carlo algorithm (18, 19). The Monte Carlo simulations (SI Fig. 6) allow us to monitor the relevant stochastic processes that occur in cell signaling. Proteins are represented as discrete objects, occupying a site on a lattice of dimensions 100 × 100 × 100. Reflecting (i.e., hard-wall) boundary conditions exist at each of the faces of the cubic lattice. The system is not periodically replicated. Proteins can diffuse (i.e., translate on the lattice in random directions), bind and unbind, and undergo state transformations according to a prescribed reaction network (Fig. 1). Protein motion is subject to excluded volume (steric) constraints in that no two proteins can occupy the same site on the lattice. Chemical (state) transformations and binding events are modeled as thermally activated processes with associated energy barriers, E_i, for activation, inactivation, binding, and unbinding reactions.

In a Monte Carlo step, n trials are attempted, where n is the number of proteins in the simulation. For a given trial, a protein is first chosen at random with uniform probability. A displacement move in a particular direction is then attempted with probability, P(diffusion) = $P(diffusion)=\frac{1}{6}{P}_{diffusion}\min \{1,\exp (-E_{\infty })\}$, where P_diffusion is the probability of attempting a diffusion move. Excluded volume is accounted for by imposition of an infinite energy barrier, E_∞, located at sites containing other proteins but is zero everywhere else. Upon considering all possible nearest-neighbor interactions, reaction moves, as determined by the network topology, are tried with probability, P(reaction) = P_reactionmin{1,exp(−E_i)}, where P_reaction is the probability of attempting a reaction move, E_i is the energy barrier for the ith reaction scaled with respect to k_BT (Boltzman's thermal energy).