Rapid Detection of Positive Selection in Genes and Genomes Through Variation Clusters

Abstract

Positive selection in genes and genomes can point to the evolutionary basis for differences among species and among races within a species. The detection of positive selection can also help identify functionally important protein regions and thus guide protein engineering. Many existing tests for positive selection are excessively conservative, vulnerable to artifacts caused by demographic population history, or computationally very intensive. I here propose a simple and rapid test that is complementary to existing tests and that overcomes some of these problems. It relies on the null hypothesis that neutrally evolving DNA regions should show a Poisson distribution of nucleotide substitutions. The test detects significant deviations from this expectation in the form of variation clusters, highly localized groups of amino acid changes in a coding region. In applying this test to several thousand human–chimpanzee gene orthologs, I show that such variation clusters are not generally caused by relaxed selection. They occur in well-defined domains of a protein's tertiary structure and show a large excess of amino acid replacement over silent substitutions. I also identify multiple new human–chimpanzee orthologs subject to positive selection, among them genes that are involved in reproductive functions, immune defense, and the nervous system.

A point mutation is under positive or directional selection if it confers a fitness benefit. Natural selection favors its bearer and will thus increase its frequency. To identify genes subject to positive selection is as difficult as it is important. First, such identification can find genes responsible for species differences, such as the differences between humans and chimpanzees (Kreitman 2000; Johnson et al. 2001; Clark et al. 2003; Akey et al. 2004; Vallender and Lahn 2004; Nielsen et al. 2005a; Wang et al. 2006). Second, positively selected genes may connect ecological change to molecular change (Watt 1977, 1983; Watt et al. 1983). Third, identification of genes subject to positive selection can help answer whether genetic differences between populations have adaptive significance (Smith and Eyre-Walker 2002; Andolfatto 2005). For human populations, candidates include genes mediating adaptations to UV exposure or pathogens, such as malaria. Fourth, on the level of individual genes, positive selection is often restricted to small regions of a gene. Its identification may point to functionally important regions of a gene and is thus of potential interest to protein engineers who alter proteins to produce new functions.

Two broad classes of approaches exist to identify positive selection (Kreitman 2000; Bamshad and Wooding 2003). They both rely on predictions made by the neutral theory of molecular evolution (Kimura 1983). The first approach compares the incidence of two different classes of genetic change within genes (Li 1997; Kreitman 2000), synonymous (silent) changes, which are likely to be neutral, and nonsynonymous or amino acid replacement changes, which are more likely subject to selection. Specifically, the ratio N/S of the number of nonsynonymous (N) to synonymous (S) changes per gene, or the ratio K_a/K_s of the fraction of nonsynonymous (K_a) to synonymous changes (K_s) per nonsynonymous and synonymous site, can give an indication of positive selection. A ratio K_a/K_s significantly greater than one, for example, indicates an excess of amino acid replacement substitutions over (neutral or weakly selected) silent substitutions. It indicates positive selection. Many variations of this class of test exist. They differ in the amount of sequence data and computational resources required (Suzuki and Gojobori 1999; Suzuki 2004; Massingham and Goldman 2005; Pond and Frost 2005; Zhang et al. 2005). The second class of tests relies on predictions made by the neutral theory for allele or haplotype frequencies (Kreitman 2000; Bamshad and Wooding 2003) within and among populations. For example, in a genomic region where positive selection has swept a mutation to high frequency, one would expect a low amount of sequence diversity, an excess of rare alleles, and a greater amount of linkage disequilibrium than predicted by the neutral theory (Bamshad and Wooding 2003). Selection acting on one population but not others can lead to a greater than expected degree of population differentiation. Test statistics, such as Tajima's D, Fu's W, Wright's F_ST, and many others, exploit information in these patterns (Fu 1996; Tajima 1989; Kreitman 2000). The distinction between such tests is not sharp, and some tests (McDonald and Kreitman 1991) arguably fall into both categories.

Application of the available battery of tests to different genes and genomes has produced a large number of well-corroborated cases of positive selection (Hughes and Nei 1988; McDonald and Kreitman 1991; Shyue et al. 1995; Hughes and Yeager 1998; Nurminsky et al. 1998; Ting et al. 1998; Tsaur et al. 1998; Zhang et al. 1998; Watt and Dean 2000; Wyckoff et al. 2000; Sabeti et al. 2002; Smith and Eyre-Walker 2002; Bamshad and Wooding 2003; Clark et al. 2003; Mundy and Cook 2003; Presgraves et al. 2003; Akey et al. 2004; Vallender and Lahn 2004; Bustamante et al. 2005; Nielsen et al. 2005a,b; Zhu et al. 2005; Wang et al. 2006). One prominent class of positively selected genes is implicated in male reproduction. Such genes are affected by sexual selection or sperm competition. They include the Drosophila genes Odysseus (Ting et al. 1998) and Acp26Aa (Tsaur et al. 1998) and the human protamine genes (Wyckoff et al. 2000). A second class of genes is involved in a host's immune response to pathogens, or in a pathogen's evasion of this response. They include the human major histocompatibility complex (MHC) locus (Hughes and Nei 1988), the gene encoding eosinophil-cationic protein (Zhang et al. 1998), and many others. In primates, additional classes of positively selected genes are involved in vision and olfaction, neural development, and metabolism (Vallender and Lahn 2004).

The two classes of available tests for positive selection have two limitations. First, many tests that rely on differences between nonsynonymous and synonymous changes do not systematically take into account that positive selection often acts only on small regions of a gene product. Examples include the human MHC locus and the env gene of the human immunodeficiency virus 1 (HIV-1). Both are examples in which selection has favored diversity. Its action is restricted to the antigen-recognition site in MHC and to the hypervariable regions in the env gene (Holmes et al. 1992; Hughes and Yeager 1998; Nielsen and Yang 1998). In particular the K_a/K_s test is extremely conservative in assessing positive selection, because it averages over the entire length of a gene. To be sure, this limitation can be readily overcome, but at the price of additional data (entire phylogenies instead of sequence pairs) and often considerable computational cost. Second, demographic history may generate spurious signatures of positive selection in tests that compare allele frequencies (Bamshad and Wooding 2003). For example, population bottlenecks, which can be associated with speciation events, lead to relaxed selection. The resulting increased rate of amino acid sequence divergence may create a false appearance of positive selection when comparing amino acid replacements within and among species. Conversely, a rapidly expanding population like the human population, may spuriously generate some of the sequence signatures (excess of rare alleles, etc.) characteristic of positive selection. Reconstructions of population history are often difficult and controversial, so this limitation is likely to stay with us.

I here propose a simple test that is complementary to existing approaches and that overcomes some of the mentioned limitations. It is not subject to the vagaries of population histories, yet sensitive to selection acting on a small region of a molecule, requires only pairs of sequences, and is thus sufficiently rapidly executed to be applied to all genes in a genome. It detects variation clusters of aggregated nucleotide substitutions that are too closely spaced to be observed by chance alone and that thus violate the predicted distribution of substitution spacing for neutral variation.

METHODS

Variation clusters under the Poisson null hypothesis:

Consider m amino acid replacement substitutions in a protein-coding region that comprises n codons. Denote as 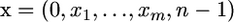the array that comprises (i) all the positions x_i of the m mutations, which can range from zero to n − 1, (ii) the position of the beginning (0), and (iii) the position of the end (n − 1) of this region. Denote as 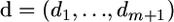the array of distances between these positions, where d₁ = x₁, d_i = x_i − x_i−1 (2 ≤ i ≤ m), d_m+1 = (n − 1) − x_n. If the substitution positions are Poisson distributed, an assumption that is appropriate if there is only a moderate number of mutations, one can estimate the parameter λ of this distribution simply as λ = m/n. Consider now k consecutive mutational positions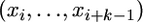. I call such a group a k-cluster or variation cluster. The length of this variation cluster is d_i,k = x_i+k−1 − x_i . One can show (Wagner 1997) that d_i,k has a Pearson type III distribution, whose probability density is equal to 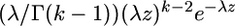, where 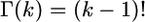is the gamma function. This means that the probability P(d_i,k) that the number of codons spanned by a k-cluster is smaller than d_i,k is equal to

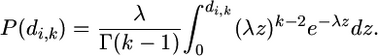(1)

The statistical measure P_p that I use for aggregation under this Poisson null hypothesis is the minimum of this probability over all possible k-clusters for all values of k (k ≤ 2 ≤ m), that is, 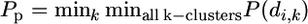. Put differently, this measure identifies the cluster of k whose length is most unlikely to be observed by chance alone. If P_p < 0.05, then there exists at least one k and one k-cluster with length significantly shorter than expected by chance alone. Efficient routines to evaluate (1) are available (Press et al. 1992).

I note that the estimate of λ implicitly accounts for variation in mutation rates or amounts of variation in different genomic regions. Among two genomic regions of the same lengths, the region with a higher mutation rate will have a larger expected value of m, and thus also a greater estimated value of λ. This, in turn implies that a variation cluster of a given length and number of substitutions will have a lower P_p in the region with more overall variation, simply because it is more likely to observe this cluster by chance alone when there are more substitutions to begin with.

Variation clusters under the uniform null hypothesis:

The null hypothesis here is that the m substitutions in a coding region of length n codons follow a uniform distribution. As a test statistic, I use the sample variance 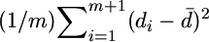. I first determine this variance for a coding region and call it 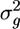. I then generate a large number (>10⁴) of arrays x whose entries follow a uniform distribution on the interval (0, n − 1) and determine the corresponding distance array d and the variance 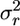. I then determine the fraction P_u of these random samples in which 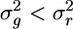. If this fraction is small (e.g., P_u < 0.05), then the variance 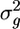is significantly greater than expected by chance alone. P_u indicates significantly increased variance of mutational position spacing. It thus is an indicator of aggregation.

I note that P_u is a global measure of aggregation that indicates whether the mutated codons of a gene, when taken together, show evidence of aggregation. If only a small subgroup of codons are highly aggregated, P_u may fail to detect this pattern. In contrast P_p is a local measure of aggregation that identifies the group of mutated codons that show the best indication of aggregation. By definition, it will not fail to find a subgroup of highly clustered mutations.

Clustering in the protein tertiary structure:

To determine whether a group of k amino acid replacements in a protein with known tertiary structure is significantly more clustered than expected by chance alone, I first identified all protein structure files in the protein data bank (PDB; http://www.rcsb.org/pdb/) that are associated with the protein. For each of these files, I then carried out the following procedure. I extracted the atomic coordinates of all α-carbon atoms for each peptide chain that the file contained. I then aligned the protein-coding sequence of interest with the protein-coding sequence of each of these chains. I chose those chains that showed the highest sequence similarity (typically 100% or close to it) to the protein-coding sequence of interest and asked whether structural data were available for all k amino acid residues in the variation cluster. If so, I determined the average pairwise distance

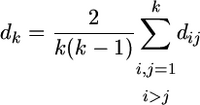of all α-carbon atom coordinates of amino acids in the k-cluster, where 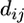denotes the Euclidian distance of the α-carbon atom coordinates of atoms i and j. I then randomly and uniformly sampled k amino acids from the peptide chain and determined the mean pairwise distance d_r of their α-carbon atoms analogously. I repeated this random sampling at least 10⁴ times and determined the fraction P_3D of the random samples in which d_k > d_r. If this fraction is small (e.g., P_3D < 0.05), then d_k is smaller than expected by chance alone. P_3D is thus analogous to P_u but in three dimensions. Where more than one protein structure was associated with a protein-coding region, I repeated this procedure for all available structures and used the smallest P_3D value for further analysis.

Data sources:

I obtained information on 13,454 unambiguous human–chimpanzee gene orthologs, as well as their location, K_a and K_s, from Mikkelsen et al. (2005, Supplementary Table S23). I obtained the coding region sequence of all chimpanzee and human genes in this data set from the Ensembl database (Hubbard et al. 2005) (http://www.ensembl.org/Multi/martview; National Center for Biotechnology Information [NCBI] build 35), and from NCBI (http://www.ncbi.nlm.nih.gov/) in October 2005. For each human gene with an unambiguous human–chimpanzee ortholog, I used the human coding nucleotide sequence to query a database of all chimpanzee coding sequences using BLAST (Altschul et al. 1997). The highest-scoring sequence pair was retained for further analysis only if the alignment of this pair involved the entire length of the query sequence and if the amino acid identity among the two sequences was greater then 90% (as a filter to avoid analyzing recombination products). From these alignments I determined the number and positions of all codons in which synonymous and nonsynonymous changes had occurred. Codon pairs where one codon had suffered an insertion or deletion (indicated by an alignment gap) were excluded from this count, even in the part of the study that considered gapped alignments. For complexity filtering I used a stand-alone version of the program seg (Wootton and Federhen 1996, obtained from http://www.ncbi.nlm.nih.gov/Ftp/), which I applied with default parameters to the amino acid sequence of the human proteins of interest.

To analyze protein tertiary structures, I first obtained a list of all human genes associated with a PDB structure file from Ensembl. Subsequently, I obtained all relevant human PDB files from the Research Collaboratory for Structural Bioinformatics (ftp://ftp.rcsb.org/pub/pdb/data/structures/divided/pdb/). For each human protein-coding region and each associated PDB file that contained structural information from either X-ray crystallography or nuclear magnetic resonance (NMR) experiments, I then carried out the following steps. First, I extracted the amino acid sequence of each peptide chain for which the structure file contained information from the ATOM entry describing the spatial coordinates of an amino acid's α-carbon atom. For NMR data, which are given as multiple measurements or “models” of protein structure for a thermodynamic ensemble of conformations, I chose the first model in the PDB file for this extraction. Second, I aligned the human protein-coding region with each of the extracted peptide chains that exceeded a length of 20 amino acids, using a Needleman–Wunsch global alignment as implemented in ClustalW (Thompson et al. 1994). Third, I retained for further analysis those alignments where more than 30% of the coding region sequence could be aligned to a peptide chain, and where the resulting overall amino acid identity exceeded 90%. Among these alignments, I chose the chain with the highest match to the coding region, or, if there was more than one such chain (e.g., in the case of a homomultimeric protein), I chose the chain with the lowest alphanumerical index. For all structures shown here, and for most sequences analyzed, peptide chains filtered for analysis in this way showed 100% sequence identity to the human protein-coding sequence over their alignable length, notable exceptions being experimentally mutagenized proteins. Fourth, I determined for each protein whether structural information was available for all protein regions in which amino acid changes had occurred between humans and chimpanzees, and included only such proteins for further analysis. The fourth step eliminates a large number of proteins from further analysis, because structural information is often available only for a small region or domain of a protein. Finally, for the remaining proteins, I determined whether changed amino acid residues showed significant clustering in the tertiary structure, using the statistical test described above.

RESULTS

Assaying significant variation clusters:

Consider two DNA or protein molecules that shared a common ancestor at some time in the recent past. If they evolve neutrally, that is, if all preserved changes in them are neutral changes, then each nucleotide or amino acid position in them has the same probability of having changed. (Deleterious changes may have occurred but would not have been preserved.) With suitable precautions, strong deviations from this neutral prediction, in the form of nonuniform substitution spacing (variation clustering), can indicate positive selection.

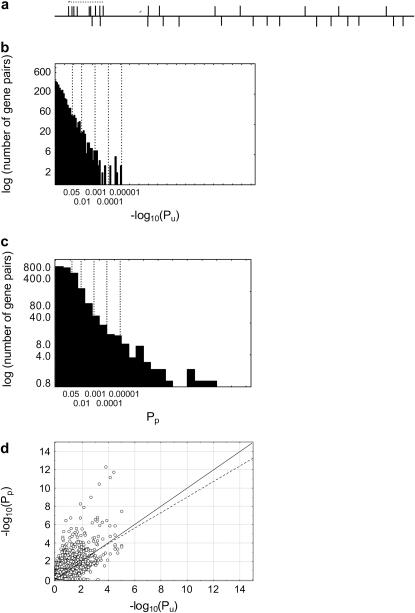
I first applied two tests for variation clustering (see methods) in coding regions to 5251 known human genes that had well-curated annotation (Pruitt et al. 2005) and their unambiguous orthologs in chimpanzees (Mikkelsen et al. 2005). The first test rests on the null hypothesis of a uniform distribution of mutational changes across the coding region. Small values of the test statistic P_u mean that the null hypothesis is rejected and that the mutations as a whole are aggregated, clumped, or clustered in the coding region. The second, complementary, test rests on a null hypothesis of Poisson-distributed mutational changes in the coding region. Small values of the second test statistic, P_p, indicate that there is at least one group of k consecutive amino acid changes (out of m total changes in a coding region) that show clustering (Figure 1a). In contrast to the first test, the second test is also able to detect highly clustered amino acid changes in a small region of a protein.

Figure 1.—

Many genes have highly significant variation clusters. (a) Schematic of a variation cluster. The horizontal line represents the protein-coding region of a gene. Bars above the line indicate amino acid changes in the coding region. Bars below the line indicate silent nucleotide changes. The dotted line indicates a highly significant variation cluster, an accumulation of too many amino acid changes in a short region to be seen by chance alone. (b) Histogram of significance P_u (note the logarithmic scale) of the deviation of amino acid substitution spacing from a uniform distribution. (c) Histogram of significance P_p of deviation of amino acid substitution spacing from a Poisson distribution for 2896 human–chimpanzee gene pairs that could be aligned over the full length of the human gene. For ease of viewing, the horizontal axis in both b and c extend only to P < 10⁻¹⁵. However, there are three values of P_p smaller than 10⁻¹⁵, which are not shown on the histogram in b. Also, because estimation of P_u involved a computationally expensive randomization approach, P_u was estimated only for values greater than 10⁻⁵. Values smaller than 10⁻⁵ are set to zero and do not appear on the histogram in c. There are 15 genes with P_u < 10⁻⁵. (d) Scatterplot of –log₁₀(P_u) and –log₁₀(P_p). The solid line indicates –log₁₀(P_u) = –log10(P_p), and the dashed line is a linear regression line. P_p and P_u are highly correlated (Spearman's s = 0.51; n = 2896; P < 10⁻¹⁷), but –log10(P_p) > –log10(P_u) for most genes.

Figure 1, b and c shows distributions of P_u and P_p for the genes analyzed here, indicating various significance thresholds. A total of 440 genes (15.2%) have P_u < 0.05. One would expect that 95% of the statistical tests significant at P < 0.05 correctly rejected the null hypothesis of no variation clustering. Eighteen genes (0.62%) have P_u < β = 0.05/2896 = 1.7 × 10⁻⁵, which is the excessively conservative Bonferroni-corrected threshold for the total number of 2896 gene pairs with two or more amino acid replacement substitutions examined here. Fifteen of these 18 genes have a P_u too small (<10⁻⁵) to be detected by the randomization approach I used. (These genes do not appear on Figure 1b.) A total of 962 genes (33.2%) have P_p < 0.05 and 44 (1.51%) have P_p < β. The smaller number of significant values for P_u indicates its lower sensitivity for small groups of highly clustered substitutions. The true number of genes with significantly aggregated amino acid changes likely lies between the two extremes observed here (0.5–33%). Even though P_p and P_u show a highly significant positive statistical association (Spearman's s = 0.51; n = 2896; P < 10⁻¹⁷; Figure 1d), only 10 of the 44 gene pairs with P_p < β also have P_u < β. In other cases, some group of substitutions shows clumping but all the substitutions as a whole do not. Overall, for 75.6% (2190) of gene pairs P_p < P_u. Taken together, these observations indicate that P_p is more sensitive to detect variation clustering.

Although genes that have experienced strong positive selection need not experience a N/S > 1 or K_a/K_s > 1 over the length of the whole gene, one would expect that these ratios are greater in positively selected genes than in other genes. P_p does indeed show a highly significant association with either ratio (−log₁₀(P_p) − N/S: Spearman's s = 0.27, n = 2742, P < 10⁻¹⁷; −log₁₀(P_p) − K_a/K_s; s = 0.09, n = 2803; P < 5.3 × 10⁻⁶). The association is modest in absolute value, underlining that K_a/K_s is a weak indicator of positive selection. In contrast, for P_u this association is weaker or even weakly negative. (−log₁₀(P_p) − N/S: Spearman's s = 0.06, n = 2727, P = 0.0026; −log₁₀(P_u) −K_a/K_s; n = 2790; s = −0.06, P = 0.001). Qualitatively identical patterns exist for the associations with N and K_a itself (not shown). These observations, and the greater sensitivity of P_p to detect variation clusters motivate my focus on P_p for the rest of this contribution.

Variation clusters comprise multiple amino acid changes in a small fraction of a gene's length:

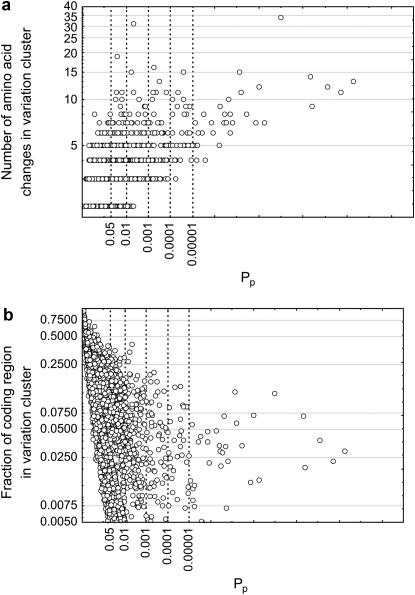
Figure 2a shows the number of amino acid changes k in the most highly significant variation cluster for all gene pairs with P_p < 0.05. The mean k is 3.82 (±0.09 SEM) for all these genes and increases to 9.71 (±1.13) for genes with P_p < β. There is overall a strong statistical association between P_p and the number of amino acids in the most highly significant cluster (Spearman's s = 0.52, n = 2896; P < 10⁻¹⁷). Genes with the most highly clustered amino acid changes thus have more such changes in a cluster. The total length of the most highly significant variation cluster spans only a small fraction of the coding sequence (Figure 2b). This fraction decreases with increasing significance of P_p (Spearman's s = −0.75; n = 2896; P < 10⁻¹⁷), meaning that the most highly significant clusters are most concentrated in the smallest regions of the protein. Their mean length comprises a fraction 0.05 (±1.8 × 10⁻³) of the coding sequence length for genes with P_p < 0.05 and a fraction 0.035 (±4 × 10⁻³) for genes with P_p < β. Given that the mean length of the coding regions in the analyzed data set is 427 amino acids, this means that the most highly significant variation clusters do not span large protein regions that could comprise entire protein domains, but very small patches of fewer than 25 amino acids.

Figure 2.—

Highly significant variation clusters contain multiple substitutions in a small region. The horizontal axes show the significance P_p of deviation from a Poisson distribution for 2896 human–chimpanzee gene pairs. Note the logarithmic scale. (a) The vertical axis shows the number of amino acid changes observed in the most highly significant variation cluster. (b) The vertical axis shows the fraction of the protein-coding region's length spanned by this cluster. As P_p, increases, more and more amino acid changes become concentrated in a smaller and smaller region.

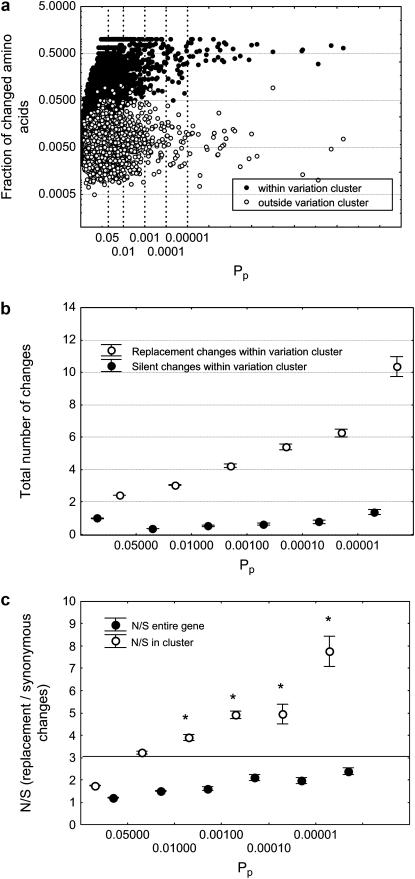
A complementary perspective on variation clusters can be obtained by separating each protein-coding region into two parts, one part comprising the most significant variation cluster and another part comprising the remainder of the coding region. Figure 3a displays the fraction of codons that underwent amino acid replacement substitutions within and outside the variation cluster as a function of P_p. (Note the logarithmic scale on the vertical axis, which shows the fraction of affected codons.) For genes with P_p < 0.05, in the region outside the substitution cluster a mean fraction 7.6 × 10⁻³ (±3.5 × 10⁻⁴) of codons underwent an amino acid changing substitution. Because each codon consists of three nucleotides, and because the vast majority of these amino acid replacement substitutions are caused by single nucleotide changes, this corresponds to an overall nucleotide sequence divergence of 7.6 × 10⁻³/3 = 2.5 × 10⁻³ that caused the observed amino acid differences. This is very close to the mean K_a = 2.88 × 10⁻³ for all the gene pairs analyzed here and to the mean K_a=2.45 × 10⁻³ estimated for human–chimpanzee orthologs (Mikkelsen et al. 2005). In addition, the genes with P_p < 0.05 do not evolve much faster overall at synonymous sites than the remainder of the genes analyzed here (genes with P_p < 0.05, K_s = 1.47 × 10⁻² ± 4 × 10⁻⁴; other genes, K_s = 1.38 × 10⁻² ± 1.76 × 10⁻⁴). Thus, the genes with P_p<0.05 do not evolve especially rapidly over their entire sequence.

Figure 3.—

Variation clusters contain many more replacement changes than silent changes. (a) The horizontal axis shows P_p on a logarithmic scale, and the vertical axis shows the fraction of amino acids changed inside the most highly significant variation cluster (solid circles) and in the remainder of the protein-coding region (open circles). Note the logarithmic scale on the vertical axis, which shows that the fraction of amino acids changed is orders of magnitude higher inside a cluster than in the remainder of the gene. (b) Gene pairs are binned according to P_p, as shown on the horizontal axis. Open and solid circles indicate the mean number of replacement changes and silent changes, respectively, inside the most highly significant variation clusters in the n = 2896 gene pairs examined. Whiskers indicate one standard error of the mean. While the number of amino acid changes increases dramatically with increasing cluster significance, the number of synonymous changes does not. (c) Open circles indicate the mean ratio N/S of the number of replacement changes to silent changes for the most highly significant variation clusters in the n = 2896 gene pairs examined. Solid circles indicate the same mean ratio, but for the gene pair as a whole. Whiskers indicate one standard error of the mean. The horizontal line indicates the ratio N/S = 3:1, which is somewhat greater than the ratio expected by neutral evolution (see main text) and renders the analysis conservative. Means labeled with an asterisk (*) are significantly greater than the 3:1 ratio (10⁻³ < P_p < 10⁻²: n = 62, P = 1.06 × 10⁻³; 10⁻⁴ < P_p < 10⁻³: n = 28, P = 3 × 10⁻⁶; 10⁻⁵ < P_p < 10⁻⁴: n = 12, P = 4.6 × 10⁻²; P_p < 10⁻⁵: n = 23, P = 1.65 × 10⁻³; t-test for single means).

This normal overall divergence stands in stark contrast to the substitution pattern within a variation cluster. For genes with P_p<0.05, a mean fraction 0.4 (±1.1 × 10⁻²) of codons has undergone an amino acid replacement change within a substitution cluster. This is more than a factor 52 higher than the rate of substitutions in the remainder of the coding region (0.4/7.6 × 10⁻³ > 52). It corresponds to an overall nucleotide divergence of 0.4/3 = 0.13 that caused the observed amino acid differences. This is more than a factor 10 higher than the overall sequence divergence between humans and chimpanzees (1.23 × 10⁻²) (Mikkelsen et al. 2005). Most of the overall divergence in coding regions is due to synonymous divergence, which accumulates at a 5-fold faster rate than amino acid replacement divergence, because of purifying selection (K_a/K_s = 0.23 for human–chimp orthologs (Mikkelsen et al. 2005)), rendering the 10-fold excess in the amino acid divergence even more conspicuous. Not surprisingly, the situation is even more extreme in substitution clusters with P_p < β. There, almost half of all amino acids (0.58 ± 0.034) have undergone substitution, raising the amino acid substitution rate a factor 76 above that for the genes overall.

Variation clusters are not caused by high mutability of CpG-rich regions:

The test statistic P_p takes into account that different genomic regions may have different mutation rates, by estimating the sole parameter of the Poisson distribution based on the overall variation found in the genomic region to be analyzed (see methods). In doing so, however, it cannot exclude the possibility that highly significant variation clusters preferably exist in small patches of DNA with elevated mutation rates that occur within a genomic region. The most prominent determinant of dramatically elevated mutation rates is the content of the dinucleotide CpG, because both transitions and transversions at CpG dinucleotides are an order of magnitude higher than at other sites (Nachmann and Crowell 2000). To find out whether the mutability of CpG dinucleotides causes highly significant variation clusters, I estimated the fraction of CpG dinucleotides within variation clusters, i.e., the fraction of dinucleotide positions where the human gene, the chimpanzee gene, or both had a CpG dinucleotide. This fraction is small, with a mean of 0.05 (±2 × 10⁻³). Importantly, the fraction of mutated CpG dinucleotides, where the human gene or the chimpanzee gene but not both had a CpG dinucleotide, is even smaller within variation clusters (mean 0.03 ± 7 × 10⁻⁴). This dinucleotide content is also small for the substitution clusters with the highest significance (P_p < β; fraction of CpG: 0.04 ± 6 × 10⁻³; fraction of mutated CpG: 0.02 ± 2 × 10⁻³). These numbers show that CpG mutability cannot explain the existence of highly significant variation clusters.

Little overlap between variation clusters and low complexity regions:

The key question regarding variation clustering is whether it is due to positive or relaxed selection. The similar rates at which genes with highly significant variation clusters and genes without such clusters evolve show that the clusters do not simply reflect relaxed selection over the genes harboring them as a whole. However, this does not exclude the possibility that selection is dramatically relaxed in the clusters themselves. At its most extreme, such relaxed selection would correspond to neutral evolution and imply that the extent of variation in a cluster is similar to that expected in neutrally evolving genomic regions. I carried out several analyses that speak to this question. The simplest such analysis is to examine proteins for low complexity regions if they show a highly significant variation cluster (Wootton and Federhen 1996), because low complexity regions are known to be associated with regionally relaxed selection. I find generally very little overlap between variation clusters and low complexity regions. For example, for only 13.6% (6/44) of genes with the most highly significant variation cluster (P_p < β) does the cluster overlap with a high complexity region. All but one of these six cases concern genes where insertions or deletions have occurred in a gene. In no case is the variation cluster entirely contained within a low complexity region. In a random sample of the same number of genes where the most significant cluster had P_p > 0.05, the cluster overlapped with a low complexity region in a greater number of genes (34% or 15 of 44) than it did in genes with P_p < β, a difference that is marginally significant (χ² = 5.07; P = 0.02). This means that highly significant variation clusters do not overlap more but slightly less with low complexity regions than one might expect. This observation excludes low sequence complexity as a prominent cause of highly significant variation clusters.

Variation at fourfold degenerate codons suggests that relaxed selection does not cause highly significant variation clusters:

The above analysis of low complexity regions is inconclusive with respect to the role of relaxed selection in variation clustering, because high complexity regions may also be subject to relaxed selection. To analyze how much variation might be expected under relaxed selection or neutral evolution, I focused on the amount of synonymous variation seen in fourfold degenerate codons, because it is the variation within coding regions that is least affected by selection. I first identified all (1.05 × 10⁶) aligned pairs of fourfold degenerate codons that encode the same amino acid in the human–chimpanzee gene pairs analyzed here. A fraction 0.0129 of their third positions showed a synonymous change. This fraction serves as a benchmark of the divergence to be expected under relaxed selection or neutral evolution. I then asked whether the amount of variation observed in a significant variation cluster could be expected by chance alone, given this degree of synonymous divergence. To this end, I employed an exact (one-tailed) binomial test, which determines the probability P_b that the number of nucleotide differences is equal or greater to the observed number of nucleotide differences in a cluster, using a probability that two nucleotides are different by 0.0129 (taken from the divergence of fourfold degenerate codons). Small values of this binomial probability P_b indicate that the degree of divergence observed in an actual cluster is not to be expected by chance alone for regions that evolve at a rate characteristic of fourfold degenerate codons. Importantly, for all variation clusters that are significant at P_p < 0.05, P_b is typically also smaller than 0.05. Specifically, for clusters with 0.01 < P_p < 0.05, median (mean, standard error of the mean) P_b = 0.002 (0.045, 0.005), for 10⁻³ < P_p < 10⁻², P_b = 0.0012 (0.02, 0.007), for 10⁻⁴ < P_p < 10⁻³, P_b = 3.2 × 10⁻⁵ (0.003, 1.6 × 10⁻³), and for 10⁻⁵ < P_p < 10⁻⁴, P_b = 1.2 × 10⁻⁵ (0.0067, 5.6 × 10⁻³). For more than 90% of the clusters with the highest significance of P_p < β, P_b is even smaller than P_p. As far as divergence at fourfold degenerate sites is an indicator of relaxed selection, this implies that the vast majority of variation clusters leading to amino acid changes cannot be attributed to relaxed selection.

Excess of replacement over silent substitutions in variation clusters:

In a third analysis aimed at excluding relaxed selection, I examined the number of synonymous changes inside a variation cluster. The greatly increased number of amino acid changes observed in a variation cluster could be explained by relaxed selection, if the number of synonymous changes showed a concomitant increase. The data in Figure 3b demonstrate that this is not the case. The figure shows means and standard errors for the number of synonymous and amino acid replacement changes in a variation cluster, for gene pairs binned according to P_p. There is clearly a dramatic increase in the number of amino acid replacement changes, but only a slight change in synonymous changes with increasing significance –log₁₀(P_p).

Figure 3c shows the actual ratio N/S of amino acid replacement to silent changes for entire gene pairs and within variation clusters. In asking whether this ratio is in excess of that expected by neutral evolution, I needed to assume some ratio N/S characteristic of neutrally evolving DNA. Among neutrally evolving genes, this ratio can vary substantially, depending on the base composition and codon composition of a coding region. For the genes analyzed here, I thus estimated the distribution of this ratio by introducing 1000 random mutations with a transition:transversion bias of 2:1 into each human gene analyzed here and determined N/S for these mutations. This analysis yielded a distribution of N/S with a mean of 2.53 (±0.003 standard error). Only 3.05% of genes had an expected neutral N/S ratio greater than 3. In addition, there is no statistical association between this neutrally expected ratio N/S and the significance P_p of the most significant variation cluster in a gene (Spearman's s = −0.02; P = 0.34). This means that genes with highly significant variation clusters do not have a higher expected value of N/S under neutral evolution. For these reasons, I used in the analysis of the data in Figure 3c an average N/S ratio of 3:1 (horizontal line in the figure), which renders my results conservative. Specifically, I asked whether genes in the categories shown in Figure 3c show a significant excess of nonsynonymous to synonymous change over this neutrally expected ratio. Starting with P_p < 0.01 all groups of genes examined showed such a significant excess (10⁻³ < P_p < 10⁻²: n = 62, P = 1.1 × 10⁻³; 10⁻⁴ < P_p < 10⁻³: n = 28, P = 3 × 10⁻⁶; 10⁻⁵ < P_p < 10⁻³: n = 13, P = 4.6 × 10⁻²; P_p < 10⁻⁵: n = 23, P = 1.6 × 10⁻³; t-test for single means). This means that variation clusters contain more amino acid changing substitutions than can be expected under neutral evolution. I note that only variation clusters with S > 0 can be considered for analyses of the ratio N/S, but there are many such clusters where S = 0, such that the excess of N over S is even higher than shown here.

When studying the ratio N/S, it is also instructive to analyze clusters of synonymous change. In a large data set comprising thousands of genes, some degree of clustering is expected for all kinds of genetic change, including synonymous change. As opposed to what is observed for clusters of amino acid changing substitutions, however, the ratio N/S should, however, not be elevated in such clusters. This is indeed the case. For instance, the ratio N/S is small and actually slightly lower in synonymous variation clusters with P_p < 0.05 than in clusters with P_p > 0.05 (N/S = 0.18 ± 0.007 vs. N/S = 0.08 ± 0.008).

Taken together, all these observations exclude relaxed selection and confirm that genes with highly significant variation clusters evolve under the influence of positive selection.

The data I analyzed thus far allowed insertions or deletions (indels) between the human and chimpanzee orthologs, which manifest themselves as sequence alignment gaps. I ignored codons that included such gaps. Indels that cause the open reading frame to shift will most likely have deleterious effects. On rare occasions, however, they might survive and perhaps even have beneficial effects. The sequence signature of such an indel may be a contiguous stretch of apparently changed amino acids, which would give high P_p values. Such frameshifting indels are not very frequent, because they would imply a near absence of synonymous changes in a large cluster, which is not generally the case (results not shown). Nonetheless, I repeated all of the above analyses with only those gene pairs that could be aligned without gaps. The results are qualitatively identical to those above (Figures S1–S3 at http://www.genetics.org/supplemental/).

Variation clusters in a coding region are also highly localized in protein tertiary structure:

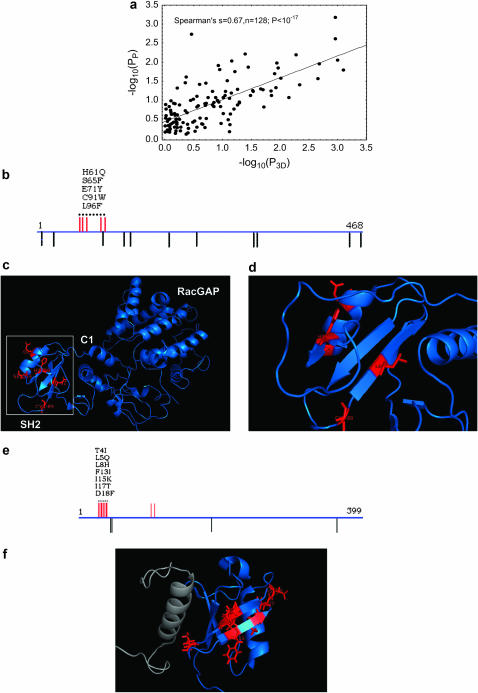
Do significant amino acid variation clusters in a gene also translate into three-dimensional variation clusters in a protein's tertiary structure? To address this question, I used pairwise distances of amino acid α-carbon atoms from known X-ray or NMR crystal structures. I determined the significance of a variation cluster in three-dimensional space through a test-statistic P_3D that is analogous to P_u (see methods). If P_3D is small (e.g., P_3D < 0.05) then amino acid changes are significantly clustered in three-dimensional space. One-dimensional clustering of variation, as indicated by P_p is highly associated with three-dimensional clustering (Figure 4a; s = 0.67, P < 10⁻¹⁸).

Figure 4.—

Clustering of amino acid changes in protein tertiary structure. (a) The horizontal axis shows –log₁₀(P_3D), calculated only for the amino acids in this variation cluster; the vertical axis shows –log₁₀(P_p). P_3D indicates to what extent the amino acid changes that occurred in a protein are significantly clustered in the protein's tertiary structure (Spearman's s = 0.67, P < 10⁻¹⁸). (b) Amino acid and silent variation in the gene encoding human β2-chimaerin. The horizontal line represents the protein-coding region (468 amino acids). Red bars above the line indicate amino acid changes in the coding region. Black bars below the line indicate silent nucleotide changes. The dotted line indicates the most highly significant variation cluster. Amino acid changes in this cluster (from left to right) are indicated by lettering (from top to bottom). (c) Tertiary structure of the protein in blue with amino acid changes indicated in red (from PDB file 1XA6; Canagarajah et al. 2004). The three protein domains are lettered in white. Note that all the amino acid changes occurred in the SH2 domain. (d) The SH2 domain boxed in white, magnified. Note that even though amino acid changes may be highly clustered, the side chains of the affected amino acids are not necessarily in immediate contact. (e) Amino acid variation in the coding region of HHR23B (399 amino acids), which is involved in spermatogenesis. (f) NMR tertiary structure (blue, PDB file 1UEL; Ryu et al. 2003) of the N-terminal ubiquitin-like domain (91 amino acids) of the protein encoded by HHR23B complexed with the protein S5A (gray), involved in protein degradation. Amino acid changes in the most significant variation cluster are labeled in red.

As an example, Figure 4b shows mutational changes in the protein-coding region of the human β2-chimaerin protein (CHN2), which is a signaling molecule. Upon binding of the second messenger diacylglycerol, this protein activates the small GTPase Rac (Leung et al. 1994). The protein has three domains, an SH2 domain, which can interact with phosphotyrosines on activated protein kinases. Its physiological partner is unknown. The second and third domain are a protein kinase C homology-1 (C1) domain, necessary for diacylglycerol binding and a RacGAP domain necessary for Rac activation (Canagarajah et al. 2004). The molecule has been implicated in the formation of some cancers such as high-grade gliomas (Yuan et al. 1995). Amino acid replacement residues are highly clustered both in the coding region (P_p = 6.6 × 10⁻⁴) and in the crystal structure (P_3D = 1.1 × 10⁻³). The five amino acid substitutions in the highly significant variation cluster (Figure 4b, dashed line) are the only amino acid substitutions in the molecule. Only one silent change occurs inside the variation cluster, and all remaining 10 changes outside the cluster are silent. As can be seen from the crystal structure (Figure 4, c and d), all of the amino acid changes are concentrated in the SH2 domain, one of them (S65F) being immediately adjacent to the phosphotyrosine binding pocket. Figure S4 at http://www.genetics.org/supplemental/ shows a second example, human ribonuclease L (RNASEL), which is involved in the immune response to viral infections. Here, some of the highly clustered change occurs in a protein domain known to be in contact with a small-molecule activator (Floyd-Smith et al. 1981; Wreschner et al. 1981; Tanaka et al. 2004).

Genes with the strongest evidence for positive selection:

Table S1 at http://www.genetics.org/supplemental/ shows the 35 genes with ungapped alignments and the most highly significant P_p, which represents a (potentially small) subset of genes subject to positive selection. The average variation cluster in this set spans only 4.4% of the coding region's length. Sixteen of the 35 genes do not have a single synonymous change in the variation cluster. Fourteen of the remaining 19 genes show a ratio N/S > 3, as would be expected for positive selection. This large number of genes (85%) with evidence for selection independent of P_p contrasts with the small number of genes (12%) that show N/S > 3 over the whole length of the gene. Among intriguing genes in this list are previously established cases of positive selection, such as the human breast cancer gene BRCA1 (Huttley et al. 2000; Hurst and Pal 2001; Fleming et al. 2003) (P_p = 5.1 × 10⁻⁵), where N:S = 9:0 in the variation cluster. Its variation cluster lies in the region where BRCA1 interacts with RAD51, a human recombinase (Fleming et al. 2003). Another previously studied example is the vomeronasal receptor gene VN1R1 (P_p = 7.8 × 10⁻⁵; N:S = 5:0) (Mundy and Cook 2003), which plays a role in mammalian mating and pheromone communication (Wysocki and Meredith1987; Del Punta et al. 2002).

Novel candidates for positive selection include the human homolog of the yeast protein RAD23 (HHR23B; P_p = 1.34 × 10⁻⁶). This protein is involved in DNA repair and protein degradation. Its N-terminal Ubiquitin-like (UbL) domain also interacts with the human protein S5A (Ryu et al. 2003), which carries proteins marked for degradation to the proteasome. The coding region for this protein contains a highly significant variation cluster spanning 14 codons and involving 7 amino acid changing substitutions (Figure 4, e and f). The cluster contains zero silent substitutions; thus N:S = 7:0. In contrast, N:S is merely 9:5 = 1.8 over the whole gene. The gene-wide K_s = 0.0123 (K_a/K_s ≈ 0.2), very similar to the genome-wide average for human–chimpanzee gene pairs. The gene as a whole thus does not evolve especially rapidly: Only 2% of amino acids changed over the length of the whole gene. In contrast, 50% of all amino acids have changed in the substitution cluster. Structural information from NMR is available for the UbL domain complexed with S5A (Ryu et al. 2003). It reveals a closely spaced cluster of amino acids in a structurally well-defined protein region. The protein is involved in spermatogenesis where ubiquitin-dependent proteolysis is highly active (Sutovsky et al. 2001; Huang et al. 2004). The protein is thus associated with reproductive functions. A splice variant of it is highly expressed in human testes and in ejaculated spermatozoa (Huang et al. 2004). In mice, its absence leads to male sterility (Ng et al. 2002).

Other genes with strong evidence of positive selection include MAPK14 (P_p = 4.37 × 10⁻¹¹), encoding a mitogen-activated protein kinase involved in the immune system, ADAM29 (P_p = 4.5 × 10⁻¹²), implicated in spermatogenesis, CLN8, which functions in the nervous system (P_p = 7.5 × 10⁻⁶), and FYN, which is a protein kinase implicated in myelination and learning (P_p = 3.42 × 10⁻⁸). These genes are exemplary of three broad classes of genes found to be under positive selection in many studies (Hughes and Nei 1988; McDonald and Kreitman 1991; Shyue et al. 1995; Hughes and Yeager 1998; Nurminsky et al. 1998; Ting et al. 1998; Tsaur et al. 1998; Zhang et al. 1998; Wyckoff et al. 2000; Sabeti et al. 2002; Smith and Eyre-Walker 2002; Bamshad and Wooding 2003; Clark et al. 2003; Mundy and Cook 2003; Presgraves et al. 2003; Akey et al. 2004; Vallender and Lahn 2004; Bustamante et al. 2005; Nielsen et al. 2005a,b; Wang et al. 2006). These classes include genes associated with immune functions (represented here by RNASEL, discussed above, MAPK14, and LRMP from Table S1 at http://www.genetics.org/supplemental/). Positive selection is also rampant among genes with reproductive functions, where sexual selection and sperm competition can exert strong selection pressures (ADAM29, RAD23B discussed above, VN1R1). Apoptosis is important for spermatogenesis and apoptotic genes are often positively selected (Nielsen et al. 2005a). Table S1 also includes apoptotic genes (MAPK8, MAP3K5). A third class is associated with neuronal functions (CNTN2, LPHN2, FYN, CABP1). Further classes of genes represented in Table S1 include metabolic genes (selection due to dietary change) and likely transcription factors (GPT2, ZFYVE26). Thus, the approach I proposed identifies multiple genes subject to positive selection whose function is consistent with known classes of genes affected by positive selection.

DISCUSSION

In sum, the test to detect positive selection I propose relies on a simple null hypothesis: In neutrally evolving protein-coding sequences, amino acid changes would follow a Poisson distribution. Highly aggregated amino acid changes in protein-coding regions violate this null hypothesis. In principle, a variation cluster could also be explained by nonuniform purifying selection on a protein: Over most of a gene's coding regions, amino acid changes might accumulate according to a Poisson distribution, whereas in small, less important regions, relaxed selection might allow faster evolution. However, four lines of evidence speak against this possibility. First, highly significant variation clusters show an acceleration of evolutionary rates much greater than expected under neutral evolution or relaxed selection. Second, they are associated with a great increase in the number of nonsynonymous but not synonymous changes. Third, in such clusters the rate of amino acid change significantly exceeds that of synonymous change. Fourth, variation clusters occur in structurally well-defined and functionally important protein domains of high sequence complexity. Their one dimensional clustering in the coding region also corresponds to three-dimensional clustering in the protein tertiary structure.

The method overcomes several limitations of existing approaches. First, the method overcomes the excessive statistical conservativism of the K_a/K_s test. It is also statistically more rigorous than approaches that determine the ratio K_a/K_s in short windows sliding across an alignment and provides an easily interpreted P-value for variation clustering. Second, it does not require polymorphism data. This can be an advantage, because such data are readily available only for a small number of model organisms such as humans and Drosophila. The method thus also avoids the difficulties of distinguishing positive selection from demographic effects (Bamshad and Wooding 2003; Akey et al. 2004; Stajich and Hahn 2005). Third, the method accommodates varying mutation rates among the genomic regions it analyzes by estimating its sole free parameter λ from the extent of local variation. Fourth, the method is conceptually very simple, computationally rapid, and allows automatic identification of variation clusters for thousands of genes in mere seconds. This feature distinguishes it from other approaches that originated in molecular systematics where variation in substitution rates can lead to erroneous inference of phylogenetic trees (Goldman and Yang 1994; Nielsen and Yang 1998; Yang 1996; Yang and Nielsen 2000, 2002). The methods to correct this problem can also be applied to detect positive selection (Nielsen and Yang 1998; Yang and Nielsen 2002; Clark et al. 2003; Nielsen et al. 2005b). These methods are extremely useful, but also computationally intensive, and make a series of assumptions about how many classes of nucleotides in a coding region evolve at different rates.

I emphasize that the approach I propose is complementary and not always superior to existing approaches. For example, methods that take advantage of all the information in population genetic data will be better at detecting selection within a species, and especially very recent positive selection. Candidate genes found with this approach may thus be very different from candidate genes found with other approaches, as exemplified by a recent article reviewing 91 human genes previously reported to be subject to positive selection (Sabeti et al. 2006), many of which were based on population genetic data. Only two of these genes (BRCA1 and VN1R1) are among the best candidates proposed here, an observation that highlights how different approaches can detect very different genes subject to positive selection.

Each existing method for detecting positive selection has limitations. One limitation of the proposed method is that for some genes under positive selection, amino acid replacements may be dispersed in the coding region. To estimate this fraction of false-negative genes would be an important task of future work. A second possible limitation is that it is not clear how extreme demographic events such as severe bottlenecks may affect substitution patterns. However, it is difficult to see how some of the observations made above, such as the great excess of amino acid changes over silent changes, could be mere artifacts of demography. A third limitation of the proposed method is that it applies only to moderately diverged sequences. If two sequence pairs are so highly diverged that the Poisson assumption does no longer hold, and that a large number of multiple substitutions at each site have occurred, application of the method is inappropriate. In practice, it should not be applied to sequences that show more than 10 percent amino acid divergence (Sokal and Rohlf 1981). However, in such situations, the method can be applied to internal branches of a densely sampled phylogenetic tree, where pairwise divergences are lower. I note that in sequences of low divergence, there may be too few substitutions in a variation cluster to rigorously test for an excess of replacement over silent changes. In such situations, the method I propose is particularly valuable, because it relies on a complementary null hypothesis and uses substitution spacing itself as an indication of selection.