Abstract
We performed numerical simulations of DNA chains to understand how local geometry of juxtaposed segments in knotted DNA molecules can guide type II DNA topoisomerases to perform very efficient relaxation of DNA knots. We investigated how the various parameters defining the geometry of inter-segmental juxtapositions at sites of inter-segmental passage reactions mediated by type II DNA topoisomerases can affect the topological consequences of these reactions. We confirmed the hypothesis that by recognizing specific geometry of juxtaposed DNA segments in knotted DNA molecules, type II DNA topoisomerases can maintain the steady-state knotting level below the topological equilibrium. In addition, we revealed that a preference for a particular geometry of juxtaposed segments as sites of strand-passage reaction enables type II DNA topoisomerases to select the most efficient pathway of relaxation of complex DNA knots. The analysis of the best selection criteria for efficient relaxation of complex knots revealed that local structures in random configurations of a given knot type statistically behave as analogous local structures in ideal geometric configurations of the corresponding knot type.
INTRODUCTION
Type II DNA topoisomerases transiently cut double-stranded DNA (dsDNA) and then actively pass another dsDNA segment from the same or other DNA molecule through the transient cut. After the passage, the original connectivity of the cut DNA molecule is re-established (1). The possibility of inter-segmental passages greatly facilitates such vital processes as DNA replication or chromosome segregation (2,3). However, random inter-segmental passages occurring within long DNA molecules in living cells would create DNA knots and these are known to be noxious for cells (4,5). One way to decrease the risk of DNA knotting is to perform topoisomerase-mediated passages in such a way that the creation of knots out of unknots is restricted, while the passages occurring within already knotted DNA molecules preferentially unknot them. Indeed, in vitro reactions where long circular dsDNA molecules (10-kb long) were used as substrate for type II DNA topoisomerases revealed that the level of DNA knotting at the steady-state level of these reactions was up to 50times lower than the topological equilibrium resulting from random inter-segmental passages occurring within freely fluctuating circular DNA molecules of the same length (6). Maintaining the level of DNA knotting below the topological equilibrium is thermodynamically possible since type II DNA topoisomerases use the energy of ATP hydrolysis for each inter-segmental passage (1). However, it is still unclear how these enzymes interacting with a small portion of the knotted circular DNA molecule can recognize whether a given inter-segmental passage will lead to a simplification rather than to a complication of the DNA topology. Over the years, several different mechanisms have been proposed to explain how DNA topoisomerases can keep the level of DNA knotting below the topological equilibrium (6–12). While early models were very complex (6,7), a recent strikingly simple proposal invoked only the enzyme binding preference for inter-hooked arrangements of juxtaposed segments before performing the inter-segmental passage between those segments (12). Indeed, very recent simulation studies that used random polygons confined to a cubic lattice revealed that selection of inter-hooked arrangements of opposing segments as sites of inter-segmental passage can cause a 50-fold reduction of the steady-state knotting probability as compared to the topological equilibrium in this system (13). These studies and similar ones investigating unlinking of catenated chains (14) provided therefore a proof of principle that a preference for certain geometry of juxtaposed segments can lead DNA topoisomerases to perform very efficient unknotting. However, random polygons confined to a cubic lattice show orders of magnitude lower knotting probability than random polygons in free space with the same number of segments (15,16). Therefore, it is questionable whether the observed reduction of the knotting probability of random polygons in the cubic lattice adequately reflects the situation resulting from the selection of inter-hooked juxtapositions in DNA molecules freely fluctuating in solution. A model that reflects more accurately the knotting probability of long DNA molecules consists of freely jointed equilateral chains where each segment represents the Kuhn's statistical segment [i.e. 300 bp in the case of dsDNA (17)]. The freely jointed chain model is especially suited to reproduce conditions where the DNA effective diameter is very small or even close to zero due to the presence of sufficient concentration of counterions neutralizing the DNA charge (18–20) and in fact such conditions are believed to operate within living cells. We therefore used an equilateral chain model to investigate the effect of the selection of specific segment–segment arrangements as sites of inter-segmental passages on the steady-state knotting probability for modelled DNA molecules that undergo intramolecular DNA–DNA passages. We quantitatively measured the effects of changing various geometrical parameters of hooked juxtapositions on the topological outcomes of inter-segmental passage reactions and checked whether the same selection rule that can ensure efficient unknotting of simple knots could also explain how type II DNA topoisomerases can unknot more complex knots directly into unknots without passing through other possible pathways of knot's relaxation. In addition, our studies allowed us also to investigate what are the average arrangements of segments within different topological domains in random knots of a given type.
METHODS
Polygons with 32 segments statistically correspond to ∼10-kb long DNA, for which biochemical data on topology simplification by type II DNA polymerases exist (6). In our simulations 32-segment long equilateral polygons forming a given knot type were randomized by crank-shaft rotations of 2- to 20-segment long subchains while controlling that segments do not cross each other and therefore keep the same knot type. This was achieved by a procedure that checks whether a surface of revolution drawn by the rotated subchain does not intersect with the remaining portion of the chain (21). Only the moves (rotations) that do not produce any intersections were accepted. After every 200 accepted moves, the polygon was checked for the presence of pairs of vertices at a distance smaller than one segment length. If one or more of such pairs were detected, one of them was chosen at random and the chosen vertices and their adjacent segments were characterized in geometrical terms (see Figure 1 where the chosen vertices are denoted as A1 and A2). The analysed polygon was then projected in the direction very close to the line connecting the chosen vertices to produce a diagram containing the information about under- and over-passing segments at every crossing. Subsequently, the under-pass to over-pass change (13,22) was performed at a crossing formed by a projection of one of the segments flanking vertex A1 with one of the segments flanking vertex A2. The topological consequence of this change was then analysed by calculation of the HOMFLY polynomial (23). This procedure was then repeated at least 3 million times for every analysed knot type i.e. for unknots (01), left-handed trefoil knots (31L) and left-handed version of five nodded twist knot (52L) knots (see Figure 2 for schematic drawings of these knots).
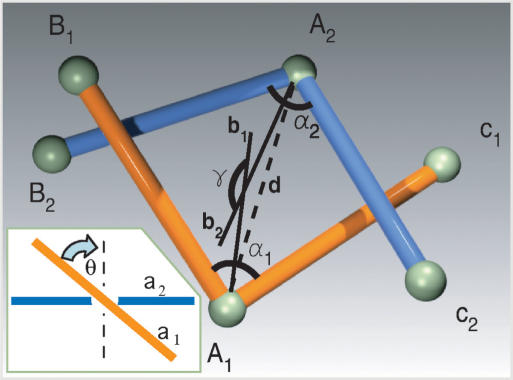
Figure 1.
Geometry of juxtapositons. Juxtaposition of two two-segment-long subchains with central vertices A1 and A2. To describe the geometry of the juxtapositions we use the distance d, the opening angles α1 and α, the facing angle γ (between the bisectrices b1 and b2) and the geometrical chirality angle θ between unoriented tangential lines passing through the vertices A1 and A2 (see the Inset). To consider juxtapositions as inter-hooked the following three conditions have to be fulfiled: (i) each subchain intersects with a sector of the plane extending from angle a defined by the other subchain. (ii) The angle γ > 105°. (iii) the mean opening angle (α1 + α2)/2 < 22.5°. Inset: Geometric chirality between two unoriented lines in space. The two lines are projected on the plane that is parallel to both the lines while the projection conserves the information which of the lines was closer and which was further from the observer. Perpendicular lines are considered as achiral while the geometric chirality angle is the smallest angle of rotation applied to the overlying line in order to make it perpendicular to the underlying line. In the case of positive (right-handed) chirality, a clockwise rotation of the overlying line is required to make it perpendicular to the underlying line (shown), while a counterclockwise rotation would be required for lines with negative (left-handed) geometric chirality. The bigger the angle of the rotation, the higher the absolute value of the geometric chirality.
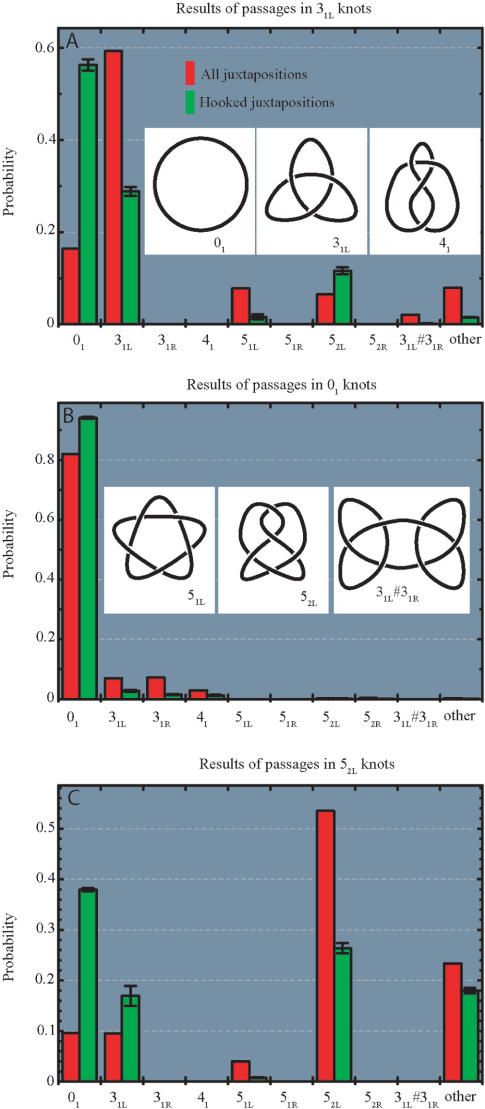
Figure 2.
Topological consequences of strand-passage reaction for random and hooked juxtapositions in trefoil knots (A) unknots (B) and 52 knots (C). Insets show standard diagrams of simple knots analysed here. As a notation, we use a modification of Alexander–Briggs designation where the main number indicates the minimal number of crossings a given knot can have in a projection and the subscript number indicates the tabular position of a given knot among knots with the same minimal crossing number in standard tables of knots (48,49). The R and L letters indicate left- or right-handed form of a given chiral knot. The observed topological outcomes were consistent with the theoretically predicted strand-passage distances between various knots (50,51). The error bars denote the SD (in case of all juxtapositions, the big statistical sample resulted in error bars smaller than the thickness of the lines demarking the histogram bars).
RESULTS
Geometry of juxtapositions at sites of strand passage
Buck and Zechiedrich (12) proposed that if type II DNA topoisomerases were able to recognize specifically inter-hooked juxtapositions as sites of strand passages, then the steady-state level of knotting maintained by type II topoisomerases could be diminished as compared to completely random strand passages. Liu et al. (13) defined the criteria of inter-hooking for portions of random polygons in the cubic lattice, where due to the lattice constraint each subchain involved in an inter-hooked juxtaposition needs to have at least four segments. For polygons in free space, inter-hooked juxtaposition can be already formed by two subchains composed of two segments each. Figure 1 illustrates what geometric characteristics of juxtapositions of two subchains composed of two segments each were analysed by us. It is somewhat arbitrary to decide what geometry of inter-segmental juxtaposition should be considered already as inter-hooked and where the limit is. To illustrate the possible effect of inter-hooking, the data in Figure 2 show a topological difference between passages at random juxtapositions and these that fulfiled the following three conditions: (i) each subchain intersects with a sector of the plane extending from angle α defined by the other subchain; (ii) the facing angle γ > 105°; (iii) the mean opening angle (α1 + α2)/2 < 22.5° (Figure 1). The mean opening angle of 22.5° (i.e. the deflection angle of 157.5°g) might seem to be very high, however recent experimental studies of DNA cyclization demonstrated that DNA fragments as short as 94 bp efficiently circularize and therefore show a cumulative deflection angle of 360° (24). Those results have lead to a conclusion that sharp kinks form spontaneously in the DNA (24). While the presence of spontaneous DNA kinks in DNA is presently a matter of debate (25,26) our modelling results can be equally well applied to strong bends resulting from localized kinks or strong bends resulting from the cumulative bending angle of ca. 150° that is redistributed over the length of 40 bp or so.
In the Methods section, we provided a detailed description how we generated random configurations of knots and how we analysed the effects of varying geometry of juxtapositions on the topological outcome of inter-segmental passages performed at these juxtapositions. In brief, we randomly picked generated configurations of knotted or unknotted chains that showed one or more approaches between non-neighbouring segments. Then one juxtaposition per simulated configuration was randomly picked and upon its geometrical characterization we determined what would be the resulting knot type if the strand passage occurred at this juxtapositions. The analysed chains were composed of 32 segments since this number statistically corresponds to DNA chains of 10 kb.
Stimulation of unknotting by action on inter-hooked juxtapositions
Figure 2A shows the effect of the selection of inter-hooked juxtapositions (green bars), as compared to random juxtaposition (red bars) as sites of strand passage within random configurations of trefoil knots (the analysed configurations were limited to left-handed versions of trefoil knot and are therefore denoted as 31L knots). It is visible that a passage at inter-hooked juxtaposition has 3.6 times higher probability to result in unknot as compared to a passage at a random juxtaposition. Figure 2B shows how the topological consequences of strand-passage reactions within unknots depend on whether the selected juxtaposition was inter-hooked or just random. The observed inhibition of the formation of trefoil knots for passages at inter-hooked juxtapositions as compared to random juxtapositions was of the order of 3.9. Combining the data from Figure 2A and B, one can conclude that the selection of inter-hooked configurations as sites of inter-segmental passages is expected to decrease the steady-state ratio of trefoils to unknots by about 14 times (3.9 × 3.6) as compared to random passages, provided that the frequency ratios between random and inter-hooked configurations is the same in trefoil knots and unknots. However, our analysis revealed that the ratio of inter-hooked to random configurations is 1.65 times higher in trefoil knots than in unknots. The rate of the strand-passage reaction in unknotted and trefoil-forming molecules can be assumed to be proportional to the frequency of appearance of recognized juxtapositions within unknots or trefoils, respectively (8). Therefore, the selection of inter-hooked juxtapositions (with the cutoff parameters described above) as sites of strand passage would be expected to diminish the level of knotting by more than 23 times (14 × 1.65) below the topological equilibrium in this system. This is 2-fold less than the effect observed in biochemical experiments performed by Rybenkov et al. (6) who revealed a 50-fold reduction of the knotting level in DNA molecules with a size closely corresponding to 32 statistical segments. To reach this level of knotting reduction in simulation studies, one would need a more strict selection of inter-hooked juxtapositions, requiring a smaller mean opening angle (α1 + α2)/2 or a bigger facing angle γ, for example. Alternatively, the knotting reduction level could be further increased by introducing a modification of a kinetic proofreading mechanism proposed by Yan et al. (7). This mechanism assumes that type II topoisomerases have a strong binding preference for inter-hooked juxtapositions, but after first binding to DNA, the energy of ATP is used to liberate the bound juxtaposition without performing the passage reaction but instead activating the enzyme for a passage during a short time period. If during this short activation time a juxtaposition with the preferred geometry is bound by the enzyme it is used for the inter-segmental passage. If no juxtaposition with preferred geometry is bound within the short time after the first binding, the activation state decays and the entire cycle has to be repeated. The mechanism of kinetic proofreading is based on the fact that inter-hooked juxtapositions are more frequent in knotted than in unknotted molecules and it essentially squares the probability that a passage happens in a knotted DNA molecule rather than in unknotted one (7). After introducing a kinetic proofreading factor, we observed that the same selection criteria for inter-hooked juxtapositions (as described above) caused a ca 40-fold knotting reduction.
Selection of a specific pathway of knot's relaxation
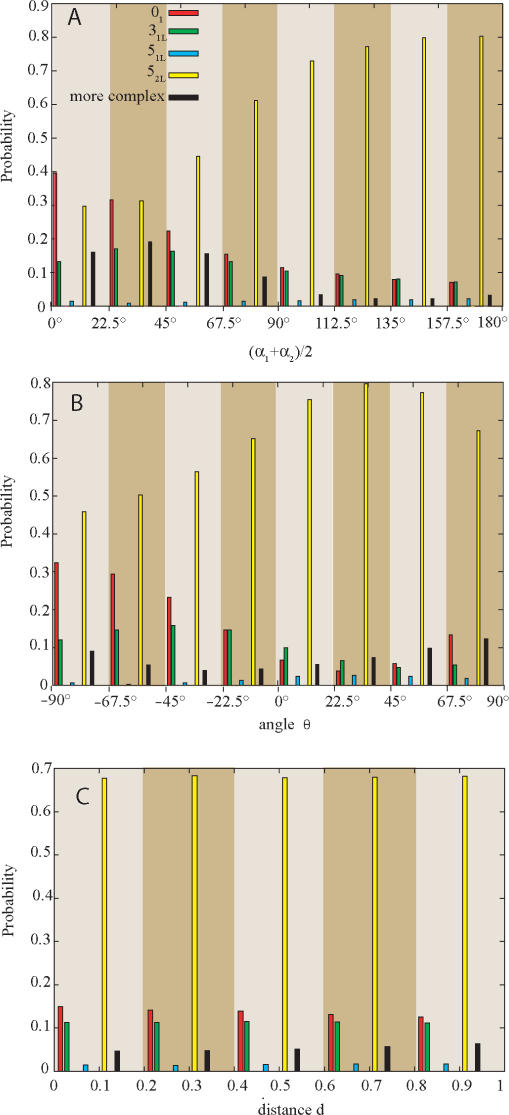
Type II DNA topoisomerases were shown not only to be able to maintain the knotting level below the topological equilibrium but also to choose a specific pathway of relaxation of more complex knots (27). The chosen pathway maximized the efficiency of unknotting by selecting the passages that lead to direct unknotting instead of progressive relaxation through knots with intermediate level of knotting (27). To investigate the effect of selection of inter-hooked juxtapositions on the topological outcomes of strand passages in more complex knots we studied topological transitions in left-handed version of 52 knots (52L) since left-handed twist knots arise naturally as result of intermolecular passages in negatively supercoiled DNA molecules (28,29) and these DNA knots were used in experiments that demonstrated selective pathway of knots’ relaxation (27). Figure 2C shows that random passages within 52L knots result in roughly equal proportions of unknots and 31L knots (ca. 10% each), and in a high proportion of strand passages that maintain the original topology (>50%). Selection of inter-hooked juxtapositions, however, greatly stimulates knots simplification and preferentially leads to events that cause unknotting (∼40% of events) rather than to forming trefoil knots (<20% of events). Mann et al. (27) observed that human topo II acting on 52 knots showed high selectivity for passages that directly lead to formation of unknots, while passages to 31 knots were hardly observed. In order to understand the possible basis of this specificity we investigated how the selection of specific geometry of the juxtaposition affects the topological consequences of the strand passages occurring within 52L knots. Figure 3A shows how the mean opening angle [(α1 + α2)/2], calculated for both two-segment subchains forming juxtapositions (Figure 1), influences the efficiency of unknotting and of other topological transitions resulting from a strand passage at these juxtapositions. It is visible that the narrower the mean opening angle the more efficient the unknotting. The unknotting approaches 40% frequency for the juxtapositions with the mean opening angle between 0° and 22.5° and it remains below 7% for the mean opening angle between 157.5° and 180°. The probability of not changing the knot type after a strand passage has the opposing tendency. For juxtapositions with the mean opening angle <22.5° only 30% of passages maintained the topology of 52L knot, while for the mean opening angles between 157.5 and 180° ∼80% of passages did not change the knot type. The observations that strongly hooked juxtapositions (with small opening angle) are likely to give rise to simpler knots upon strand passage while weakly hooked juxtapositions (with large opening angle) result in a passage that does not change the topology are consistent with the proposal by Buck and Zechiedrich (12) and with the simulations studies by Liu et al. (13). In general, inter-hooked juxtapositions are more likely to be encountered in the knotted portion of a random chain. Therefore, passages occurring at such juxtapositions are likely to result in a simplification of the knot. Unhooked juxtapositions are more likely to occur between subchains that are not prompted to bend over each other as those in a trivial loop. Therefore, strand passages at such juxtapositions are more likely to result in no change of the topology. More difficult to explain is the observation that the ratio of passages to unknots versus those to 31 knots strongly decreases (from three to one) as the mean opening angle increases. Apparently, the portion of the knot (topological domain) where passages between opposing segments lead to formation of unknots is more bent and has the opposing segments more inter-hooked with each other than the topological domain within which inter-segmental passage leads to creation of trefoil knots. More detailed description of topological domains of various knots can be found in Ref. (30).
Figure 3.
Effects of various geometric characteristics of juxtapositions on the topological outcome of strand passages occurring at these juxtapositions in 52L knots. Notice the qualitative difference between effects of mean opening angle (A), the geometric chirality (B) and the distance between the vertices A1 and A2 (C).
Figure 3B shows the effect of the geometric chirality of the juxtaposition on the topological outcomes of passages occurring at these juxtapositions. The concept of geometric chirality is explained in the inset to Figure 1. To characterize the geometric chirality of juxtapositions we measure it for the two unoriented tangential lines a1 and a2 passing through the vertices denoted as A1 and A2 on Figure 1. In contrast to Figure 3A, where unknotting frequency of inter-segmental passages is progressively decreasing with the increase of the mean opening angle, the unknotting dependence on the geometric chirality of juxtapositions is more complex. Formation of unknots is strongly favoured by inter-segmental passages at juxtapositions with strong right-handed geometric chirality while it is least efficient for juxtapositions that are achiral or show weak left-handed chirality. Interestingly, the formation of unknots increases again for juxtapositions with strong left-handed chirality. Formation of trefoil knots is more efficient than that of unknots for juxtapositions that are achiral or show a weak left-handed chirality. Apparently, the juxtapositions that after a passage lead preferentially to creation of 31 knots frequently show weak geometric chirality, while the juxtapositions leading to the preferential formation of unknots are usually strongly chiral. Figure 3C shows the dependence of the topological outcomes on the distance between the two central vertices A1 and A2 of each subchain forming the juxtapositions (Figure 1). Interestingly, the distance of approach does not influence significantly the topological consequences of strand passages occurring at these juxtapositions. Notice though that all juxtapositions analysed in Figure 3 were pre-selected to be weakly hooked, i.e., have the γ angle >90° and satisfy the criteria that one subchain pierces the sector of plane defined by the other subchain (Figure 1).
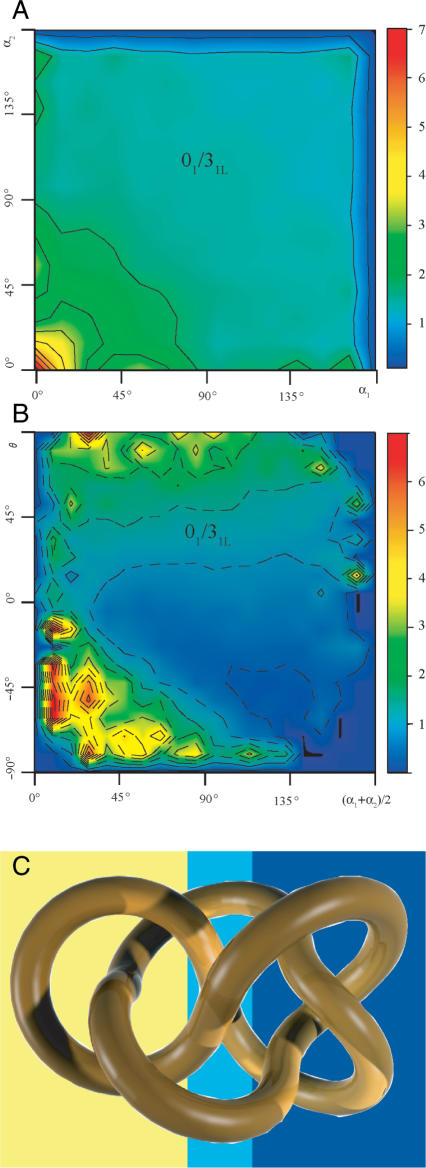
We have shown above that the selection using just one criterion, like the mean opening angle (Figure 3A) or the geometric chirality angle, can result in up to 3-fold higher conversion rate to unknots than that to 31 knots. However, the steric selectivity of DNA topoisomerases for the geometry of juxtapositions is most likely a combination of several criteria. Figure 4A and B show how the ratio of passages from 52L knots to unknots versus those from 52L knots to 31L knots depends on various pair-wise combinations of selection criteria. Figure 4A uses a colour code to show how the combination of opening angles (α) at both subchains forming the selected juxtaposition (Figure 1) affects the topological consequences of the reaction. It is visible that the 01/31 ratio can reach a value as high as six depending on the combination of opening angles α. The majority of the configuration space where the transitions to unknots are highly favoured over those to 31 knots, are in the region where both opening angles α are small (<25°). However, the 01/31 ratio also reaches a moderate value in a region of the configurations space where one subchain has a very small opening angle (<10°) and the other has a large opening angle of (130–170°). This would correspond to a situation where a strongly bent subchain is hooked over a rather straight subchain. Figure 4B illustrates how the combination of the mean opening angle and the geometric chirality angle affects the 01/31 ratio resulting from passages at the corresponding juxtapositions. The ratio between passages to unknots and those to 31 knots exceeds six for juxtapositions with strong negative geometric chirality and having in addition small average opening angle. The examples shown in Figure 4 demonstrate that steric selectivity can very well lead to a situation where the great majority of topoisomerase-mediated passages in 52L knot could result in unknots (27). Specific combinations of more than two criteria are likely to define a portion of the configurations space where juxtapositions would result in a still higher bias toward passages to unknots than those shown in Figure 4A and B. Although we do not know yet what the rules of steric selection are in the case of human topoisomerase II we should be able to find out what are the steric properties of 52L knots that could be used to guide the topoisomerase to convert it into unknots rather than into trefoils.
Figure 4.
Inferring local geometric characteristics of random configurations of knots from the topological consequences of intersegemental passages. (A and B) 01/31 ratio arising from intersegmental passages within 52L knot as a function of the opening angle at both subchains forming the juxtaposition at which the strand passage occurs (A) or the mean opening angle and the chirality of the juxtaposition (B). (C) Ideal configuration of 52L knot with indicated topological domains within which intersegmental passages lead to unknotting (dark blue background) or to formation of 31L knots (yellow background) and to the formation of 51L knots (light blue background).
Random knots and ideal knots
Looking at standard diagrams of 52L knot (Figure 2) one sees no reasons why low geometrical chirality of juxtapositions should favour passages to 31L knots. However, standard minimal diagrams of knots may not reflect the average 3D structure of a random chain forming a given knot. It was shown earlier that ideal geometric configurations of a given knot reflect certain global statistical properties of corresponding random knots of a given type (31). Thus, for example, the writhe of ideal knots had practically the same value as the average writhe of randomly fluctuating knotted chains forming the same knot type (31,32) or even random knots of the corresponding type formed on a cubic lattice (33). We decided therefore to have a closer look at the ideal configuration of the 52L knot hoping to see some hints why the selection of inter-hooked juxtapositions favours specifically transitions to unknots. Figure 4C shows the ideal geometric representation of the knot 52L. Inter-segmental passages between opposing segments in a region presented on a yellow background would lead to formation of trefoil knots and it is visible that the two big loops forming this region are not inter-hooked but rather point in the same direction (if both loops were reduced to two segment subchains, the bisectrices would point in both cases in the same direction i.e. toward right of the figure). Inter-segmental passages between opposing segments in a portion of the knot that is drawn on dark blue background (Figure 4C) would lead to formation of unknots. Interestingly, the opposing regions there are inter-hooked. Therefore, if random configurations of knots retain some characteristics of ideal knots then selection of inter-hooked juxtapositions in 52L knots is more likely to cause unknotting than a change to 31L knot. Can ideal configurations also explain the data presented in Figure 4A and B? From the data presented in Figure 4A, we can conclude that in the portion of 52L knot where passage between opposing segments leads to the creation of unknots, the juxtapositions of highly bent subchains are much more likely to be present. Indeed, our measurements of local radius of curvature in the ideal geometric configuration of 52L knot revealed that regions where passages between opposing segments leads to formation of unknots are significantly more bent than the regions where inter-segmental passages lead to formation of trefoil knots (data not shown). Similar observations can also be made for chirality. The opposing segments in the domain in which a strand passage leads to formation of 31L knots (yellow background) are practically perpendicular to each other and thus show low chirality. Strong negative chirality is however observed within a domain in which passage between opposing subchains leads to formation of unknots (shown on dark blue background). Our analysis suggests, therefore, that ideal geometric configurations of knots reflect not only global statistical properties of random knots of a given type such as time-averaged writhe (31,34) but also such local characteristics like the curvature and chirality (35) within corresponding topological domains of a given knot.
DISCUSSION
The presented simulation study has dealt only with the unknotting activity of type II DNA topoisomerases, however the same selection principle is also expected to greatly favour the decatenation activity of type II DNA topoisomerases (12). Simulation studies using polygons confined to a cubic lattice have in fact demonstrated that the selection of hooked juxtapositions strongly stimulate both unknotting and decatenation of modelled DNA rings (13,14). Until recently, a much higher biological importance was attributed to the decatenation activity of type II DNA topoisomerases than to their unknotting activity, since catenated and pre-catenated rings are normal intermediates of DNA replication process (36,37) and it is essential to remove all interlinking between daughter DNA molecules before the completion of the cell division (3,38). A very recent study showed however that unknotting activity is also of very high biological importance as the presence of knots in DNA was shown to promote severe replicon dysfunctions and induced high mutation rate (39).
For the description of the selection model to be more complete, one needs to consider at which point of the reaction the energy gained from ATP hydrolysis is used by type II DNA topoisomerases. It is important to realize that topoisomerase-mediated strand cleavage and re-sealing are isoenergetic, reversible reactions, as the energy of the hydrolysed phosphodiester bond in the DNA is maintained in a phosphodiester bond between the active tyrosine residue of the protein and the phosphate group of the DNA. Therefore, type I topoisomerases do not depend on the energy gained from ATP hydrolysis to perform efficient relaxation of supercoiled DNA. However, relaxation reactions mediated by type I DNA topoisomerases can only diminish the free energy of DNA substrates and therefore can be considered as driven by the DNA relaxation. For thermodynamic reasons the catalytic action of topoisomerases that is not coupled to ATP hydrolysis cannot move the system out of topological equilibrium (40). To understand better the energetic requirements of the reaction let us consider what could happen if type II DNA topoisomerases with high affinity for hooked juxtapositions were not able to use the energy gained from ATP hydrolysis. Without ATP hydrolysis the enzyme can bind very efficiently to hooked juxtapositions as this step of the reaction is driven by the binding energy. Subsequently, the enzyme can perform the inter-segmental passage from inside to the outside of the inter-hooked juxtaposition, provided that the affinity of the enzyme for the DNA arrangement after the passage is higher than to the DNA arrangement before the passage. In fact, all these steps of the reaction can be performed by type II topoisomerases when ATP is replaced by non-hydrolysable analogues (41–43). For all these steps of the reaction to proceed in a correct order without the need of ATP hydrolysis, it is necessary that the energy of the system progressively diminishes and this means that the complex between the topoisomerase and the DNA after the passages should be very stable. As a consequence, at the end of the reaction one would need the energy to dissociate this very stable complex so that the DNA and topoisomerase could function again. In biochemical experiments that established that type II DNA topoisomerases can perform one cycle of the reaction without ATP hydrolysis, the ‘dead-end’ complexes between the enzyme and the DNA were disrupted by SDS and proteinase K (41) and this was equivalent to providing the energy to dissociate those stable complexes. In reactions performed in the presence of ATP, the energy gained from ATP hydrolysis is used by the enzyme for its resetting for next rounds of the reaction. In principle, the energy of ATP hydrolysis occurring at just one point of the catalytic cycle can be stored in form of a mechanical stress that can be then used stepwise to induce a cascade of conformational changes required during several distinct steps of a complex enzymatic reaction. Observations showing that, in the presence of non-hydrolysable analogues of ATP, type II topoisomerases can perform one round of the reaction but are unable to perform another round (41–43) indeed suggested that ATP hydrolysis only happens after the strand passage is complete. However, more recent studies suggested that two ATP molecules bound in quasi-symmetrically located regions of the dimeric enzyme are hydrolysed sequentially at two specific points during each catalytic cycle of type II topoisomerases (44,45). The first hydrolysis precedes the phase of inter-segmental transport and therefore could be directly coupled to the active transfer (45) or to the kinetic proofreading mechanism (7). Since the complete strand passage happens also without the ATP hydrolysis it is likely that the energy gained from the hydrolysis at this point just speeds up of the reaction or is used for quality control. The second hydrolysis happens at the end of the reaction (45), which is consistent with the earlier proposal that ATP hydrolysis serves to dissociate the enzyme from the DNA after inter-segmental passage and is used for resetting the enzyme for another binding and cleavage cycle of the reaction (43,46). The principle of using the energy of ATP hydrolysis to dissociate stable complexes formed between the enzyme and DNA products of the reaction is frequently encountered in biological systems and RecA protein, for example, uses its ATPase activity to release itself from the stable complex formed with the DNA after the strand-exchange reaction is completed (47).
CONCLUSIONS
We have demonstrated that local geometry of segment juxtapositions contains not only the information that can be used by type II DNA topoisomerases to keep the level of DNA knotting below the topological equilibrium but also the information required to select the most efficient way of relaxation of more complex knots. Presumably, the evolutionary pressure to keep the DNA knotting level very low was the driving force for the selection of topoisomerase II-DNA-binding mechanism that has led to very efficient selection of passages toward unknots (39). It is hard to imagine that DNA topoisomerases can always recognize the most efficient way of relaxation of complex knots, however, for the knots that are frequently encountered in living cells as for example left-handed twist knots (28,29), such a specific recognition had a chance to evolve. At this point, we do not know yet which are the actual geometric parameters selected by topoisomerases to guide them to perform most efficient knots relaxation. High-resolution structural studies of various topoisomerases while interacting with DNA will be needed to answer this point. Simulations performed by us showed what are the potential possibilities of the selection and what would be their expected effects.
ACKNOWLEDGEMENTS
A.S. thanks Andrew Bates, Jacques Dubochet, Anthony Maxwell and Alexander Vologodskii for discussions on DNA topology simplification by type II DNA topoisomerases. We thank Chris Soteros, Mariel Vazquez, Joaquim Roca, Eric Rawdon, Jennifer Mann and Lynn Zechiedrich for their comments on the manuscript. We also thank Kenneth Millett and Eric Rawdon for making available their program for the calculation of HOMFLY polynomial. This work was supported in part by Swiss National Science Foundation grants 3100A-103962 and 3100A0-116275. Funding to pay the Open Access publication charges for this article was provided by Swiss National Science Foundation.
Conflict of interest statement. None declared.
REFERENCES
- 1.Maxwell A, Costenaro L, Mitelheiser S, Bates AD. Coupling ATP hydrolysis to DNA strand passage in type IIA DNA topoisomerases. Biochem. Soc. Trans. 2005;33:1460–1464. doi: 10.1042/BST0331460. [DOI] [PubMed] [Google Scholar]
- 2.Bates AD, Maxwell A. DNA Topology. Oxford: Oxford University Press; 2005. [Google Scholar]
- 3.Schvartzman JB, Stasiak A. A topological view of the replicon. EMBO Rep. 2004;5:256–261. doi: 10.1038/sj.embor.7400101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Portugal J, Rodriguez-Campos A. T7 RNA polymerase cannot transcribe through a highly knotted DNA template. Nucleic Acids Res. 1996;24:4890–4894. doi: 10.1093/nar/24.24.4890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Olavarrieta L, Martinez-Robles ML, Sogo JM, Stasiak A, Hernandez P, Krimer DB, Schvartzman JB. Supercoiling, knotting and replication fork reversal in partially replicated plasmids. Nucleic Acids Res. 2002;30:656–666. doi: 10.1093/nar/30.3.656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Rybenkov VV, Ullsperger C, Vologodskii AV, Cozzarelli NR. Simplification of DNA topology below equilibrium values by type II topoisomerases. Science. 1997;277:690–693. doi: 10.1126/science.277.5326.690. [DOI] [PubMed] [Google Scholar]
- 7.Yan J, Magnasco MO, Marko JF. A kinetic proofreading mechanism for disentanglement of DNA by topoisomerases. Nature. 1999;401:932–935. doi: 10.1038/44872. [DOI] [PubMed] [Google Scholar]
- 8.Vologodskii AV, Zhang W, Rybenkov VV, Podtelezhnikov AA, Subramanian D, Griffith JD, Cozzarelli NR. Mechanism of topology simplification by type II DNA topoisomerases. Proc. Natl Acad. Sci. USA. 2001;98:3045–3049. doi: 10.1073/pnas.061029098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Roca J. Varying levels of positive and negative supercoiling differently affect the efficiency with which topoisomerase II catenates and decatenates DNA. J. Mol. Biol. 2001;305:441–450. doi: 10.1006/jmbi.2000.4307. [DOI] [PubMed] [Google Scholar]
- 10.Klenin K, Langowski J, Vologodskii A. Computational analysis of the chiral action of type II DNA topoisomerases. J. Mol. Biol. 2002;320:359–367. doi: 10.1016/S0022-2836(02)00447-3. [DOI] [PubMed] [Google Scholar]
- 11.Trigueros S, Salceda J, Bermudez I, Fernandez X, Roca J. Asymmetric removal of supercoils suggests how topoisomerase II simplifies DNA topology. J. Mol. Biol. 2004;335:723–731. doi: 10.1016/j.jmb.2003.11.011. [DOI] [PubMed] [Google Scholar]
- 12.Buck GR, Zechiedrich EL. DNA disentangling by type-2 topoisomerases. J. Mol. Biol. 2004;340:933–939. doi: 10.1016/j.jmb.2004.05.034. [DOI] [PubMed] [Google Scholar]
- 13.Liu Z, Mann JK, Zechiedrich EL, Chan HS. Topological information embodied in local juxtaposition geometry provides a statistical mechanical basis for unknotting by type-2 DNA topoisomerases. J. Mol. Biol. 2006;361:268–285. doi: 10.1016/j.jmb.2006.06.005. [DOI] [PubMed] [Google Scholar]
- 14.Liu Z, Zechiedrich EL, Chan HS. Inferring global topology from local juxtaposition geometry: interlinking polymer rings and ramifications for topoisomerase action. Biophys. J. 2006;90:2344–2355. doi: 10.1529/biophysj.105.076778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Janse van Rensburg EJ, Whittington SG. The knot probability in lattice polygons. J. Phys. A: Math. Gen. 1990;23:3573–3590. [Google Scholar]
- 16.Yao A, Matsuda H, Tsukahara H, Shimamura MK, Deguchi T. On the dominance of trivial knots among SAPs on a cubic lattice. J. Phys. A: Math. Gen. 2001;34:7563–7577. [Google Scholar]
- 17.Rybenkov VV, Cozzarelli NR, Vologodskii AV. Probability of DNA knotting and the effective diameter of the DNA double helix. Proc. Natl Acad. Sci. USA. 1993;90:5307–5311. doi: 10.1073/pnas.90.11.5307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Shaw SY, Wang JC. Knotting of a DNA chain during ring closure. Science. 1993;260:533–536. doi: 10.1126/science.8475384. [DOI] [PubMed] [Google Scholar]
- 19.Adrian M, Ten Heggeler-Bordier B, Wahli W, Stasiak AZ, Stasiak A, Dubochet J. Direct visualization of supercoiled DNA molecules in solution. EMBO J. 1990;9:4551–4554. doi: 10.1002/j.1460-2075.1990.tb07907.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Bednar J, Furrer P, Stasiak A, Dubochet J, Egelman EH, Bates AD. The twist, writhe and overall shape of supercoiled DNA change during counterion-induced transition from a loosely to a tightly interwound superhelix. Possible implications for DNA structure in vivo. J. Mol. Biol. 1994;235:825–847. doi: 10.1006/jmbi.1994.1042. [DOI] [PubMed] [Google Scholar]
- 21.Flammini A, Maritan A, Stasiak A. Simulations of action of DNA topoisomerases to investigate boundaries and shapes of spaces of knots. Biophys. J. 2004;87:2968–2975. doi: 10.1529/biophysj.104.045864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hua X, Nguyen D, Raghavan B, Arsuaga J, Vazquez M. Random state transitions of knots: a first step towards modeling unknotting by type II topoisomerases. Topol. Appl. 2007;154:1381–1397. doi: 10.1016/j.topol.2006.05.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ewing B, Millett KC. Progress in Knot Theory and Related Topics Herman, Paris. Vol. 56. Herman: Paris Press; 1996. pp. 51–68. [Google Scholar]
- 24.Cloutier TE, Widom J. Spontaneous sharp bending of double-stranded DNA. Mol. Cell. 2004;14:355–362. doi: 10.1016/s1097-2765(04)00210-2. [DOI] [PubMed] [Google Scholar]
- 25.Du Q, Smith C, Shiffeldrim N, Vologodskaia M, Vologodskii A. Cyclization of short DNA fragments and bending fluctuations of the double helix. Proc. Natl Acad. Sci. USA. 2005;102:5397–5402. doi: 10.1073/pnas.0500983102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Wiggins PA, Nelson PC. Generalized theory of semiflexible polymers. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2006;73:031906. doi: 10.1103/PhysRevE.73.031906. [DOI] [PubMed] [Google Scholar]
- 27.Mann JK, Deibler RW, Sumners DW, Zechiedrich EL. Unknotting by type II topoisomerases. Abstracts of papers presented to the American Mathematical Society. 2004;25:994-992–187. [Google Scholar]
- 28.Wasserman SA, Cozzarelli NR. Supercoiled DNA-directed knotting by T4 topoisomerase. J. Biol. Chem. 1991;266:20567–20573. [PubMed] [Google Scholar]
- 29.Sogo JM, Stasiak A, Martinez-Robles ML, Krimer DB, Hernandez P, Schvartzman JB. Formation of knots in partially replicated DNA molecules. J. Mol. Biol. 1999;286:637–643. doi: 10.1006/jmbi.1998.2510. [DOI] [PubMed] [Google Scholar]
- 30.Flammini A, Stasiak A. Natural classification of knots. Proc. R. Soc. A. 2006;463:569–582. [Google Scholar]
- 31.Katritch V, Bednar J, Michoud D, Scharein RG, Dubochet J, Stasiak A. Geometry and physics of knots. Nature. 1996;384:142–145. doi: 10.1038/384122a0. [DOI] [PubMed] [Google Scholar]
- 32.Cerf C, Stasiak A. A topological invariant to predict the three-dimensional writhe of ideal configurations of knots and links. Proc. Natl Acad. Sci. USA. 2000;97:3795–3798. doi: 10.1073/pnas.97.8.3795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Janse van Rensburg EJ, Orlandini E, Sumners DW, Tesi MC, Whittington SG. The writhe of knots in the cubic lattice. J. Knot Theor. 1997;5:31–44. [Google Scholar]
- 34.Katritch V, Olson WK, Pieranski P, Dubochet J, Stasiak A. Properties of ideal composite knots. Nature. 1997;388:148–151. doi: 10.1038/40582. [DOI] [PubMed] [Google Scholar]
- 35.Plunkett P, Piatek M, Dobay A, Kern J, Millett KC, Stasiak A, Rawdon EJ. Total curvature and total torsion of knotted polymers. Macromolecules. 2007;40:3860–3867. [Google Scholar]
- 36.Sundin O, Varshavsky A. Terminal stages of SV40 DNA replication proceed via multiply intertwined catenated dimers. Cell. 1980;21:103–114. doi: 10.1016/0092-8674(80)90118-x. [DOI] [PubMed] [Google Scholar]
- 37.Peter BJ, Ullsperger C, Hiasa H, Marians KJ, Cozzarelli NR. The structure of supercoiled intermediates in DNA replication. Cell. 1998;94:819–827. doi: 10.1016/s0092-8674(00)81740-7. [DOI] [PubMed] [Google Scholar]
- 38.Zechiedrich EL, Cozzarelli NR. Roles of topoisomerase IV and DNA gyrase in DNA unlinking during replication in Escherichia coli. Genes Dev. 1995;9:2859–2869. doi: 10.1101/gad.9.22.2859. [DOI] [PubMed] [Google Scholar]
- 39.Deibler RW, Mann JK, Sumners DW, Zechiedrich L. Hin-mediated DNA knotting and recombining promote replicon dysfunction and mutation. BMC Mol. Biol. 2007;8:44. doi: 10.1186/1471-2199-8-44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Bates AD, Maxwell A. Energy coupling in type II topoisomerases: why do they hydrolyze ATP? Biochemistry. 2007;46:7929–7941. doi: 10.1021/bi700789g. [DOI] [PubMed] [Google Scholar]
- 41.Osheroff N, Shelton ER, Brutlag DL. DNA topoisomerase II from Drosophila melanogaster. Relaxation of supercoiled DNA. J. Biol. Chem. 1983;258:9536–9543. [PubMed] [Google Scholar]
- 42.Williams NL, Howells AJ, Maxwell A. Locking the ATP-operated clamp of DNA gyrase: probing the mechanism of strand passage. J. Mol. Biol. 2001;306:969–984. doi: 10.1006/jmbi.2001.4468. [DOI] [PubMed] [Google Scholar]
- 43.Roca J, Wang JC. DNA transport by a type II DNA topoisomerase: evidence in favor of a two-gate mechanism. Cell. 1994;77:609–616. doi: 10.1016/0092-8674(94)90222-4. [DOI] [PubMed] [Google Scholar]
- 44.Harkins TT, Lewis TJ, Lindsley JE. Pre-steady-state analysis of ATP hydrolysis by Saccharomyces cerevisiae DNA topoisomerase II. 2. Kinetic mechanism for the sequential hydrolysis of two ATP. Biochemistry. 1998;37:7299–7312. doi: 10.1021/bi9729108. [DOI] [PubMed] [Google Scholar]
- 45.Baird CL, Harkins TT, Morris SK, Lindsley JE. Topoisomerase II drives DNA transport by hydrolyzing one ATP. Proc. Natl Acad. Sci. USA. 1999;96:13685–13690. doi: 10.1073/pnas.96.24.13685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Sugino A, Higgins NP, Brown PO, Peebles CL, Cozzarelli NR. Energy coupling in DNA gyrase and the mechanism of action of novobiocin. Proc. Natl Acad. Sci. USA. 1978;75:4838–4842. doi: 10.1073/pnas.75.10.4838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Rosselli W, Stasiak A. Energetics of RecA-mediated recombination reactions. Without ATP hydrolysis RecA can mediate polar strand exchange but is unable to recycle. J. Mol. Biol. 1990;216:335–352. doi: 10.1016/S0022-2836(05)80325-0. [DOI] [PubMed] [Google Scholar]
- 48.Rolfsen D. Knots and links. Berkeley, CA: Publish or Perish Press; 1976. [Google Scholar]
- 49.Adams CC. The Knot Book. New York: W.H. Freeman and Company; 1994. [Google Scholar]
- 50.Darcy IK, Sumners DW. In: Knots '96: Proceedings of the Fifth International Research Institute of Mathematical Society of Japan. Suzuki S, editor. Singapore: World Scientific; 1997. pp. 267–278. [Google Scholar]
- 51.Darcy IK, Sumners DW. Rational tangle distance on knots and links. Math. Proc. Cambridge Philos. Soc. 2000;128:497–510. [Google Scholar]