Toward high-resolution prediction and design of transmembrane helical protein structures

Abstract

The prediction and design at the atomic level of membrane protein structures and interactions is a critical but unsolved challenge. To address this problem, we have developed an all-atom physical model that describes intraprotein and protein–solvent interactions in the membrane environment. We evaluated the ability of the model to recapitulate the energetics and structural specificities of polytopic membrane proteins by using a battery of in silico prediction and design tests. First, in side-chain packing and design tests, the model successfully predicts the side-chain conformations at 73% of nonexposed positions and the native amino acid identities at 34% of positions in naturally occurring membrane proteins. Second, the model predicts significant energy gaps between native and nonnative structures of transmembrane helical interfaces and polytopic membrane proteins. Third, distortions in transmembrane helices are successfully recapitulated in docking experiments by using fragments of ideal helices judiciously defined around helical kinks. Finally, de novo structure prediction reaches near-atomic accuracy (<2.5 Å) for several small membrane protein domains (<150 residues). The success of the model highlights the critical role of van der Waals and hydrogen-bonding interactions in the stability and structural specificity of membrane protein structures and sets the stage for the high-resolution prediction and design of complex membrane protein architectures.

Approximately 30% of naturally occurring proteins are predicted to be embedded in biological membranes. These proteins perform essential signaling and transport functions but are very difficult to study experimentally. To date, only 125 unique high-resolution membrane protein structures have been solved. The development of membrane protein structure prediction methods is therefore of considerable interest. Past prediction efforts have generally focused on the coarse-grained modeling of large polytopic membrane proteins (1–3). All-atom modeling has been limited to the prediction of the conformations of transmembrane (TM) peptides or to computationally expensive refinement of 7-TM helical bundles by molecular dynamics simulations (4–10). The efficient, all-atom modeling of polytopic membrane protein structures would be greatly facilitated by a fast, accurate and general method that recapitulates the physical and structural properties of these complex assemblies at the atomic level.

The biogenesis of α-helical polytopic membrane proteins involves membrane insertion followed by folding (11). In the second stage, assembling and reorienting TM segments established during the insertion step generates tertiary and quaternary structures. An accurate description of this stage requires an understanding of the energies of interactions inside the protein and between the protein and its anisotropic environment. van der Waals (VDW) packing, hydrogen bonding, solvation, and electrostatics are thought to be the main forces that stabilize TM helix (TMH) assemblies (12). However, their magnitude and relative importance has not been clearly established, and no current method has been shown to quantitatively and efficiently capture the energetics that govern the stability and orientation of complex membrane protein assemblies in lipid bilayers. To address these limitations, we have developed an all-atom physical model that efficiently recapitulates protein interatomic and protein–solvent interactions in the anisotropic membrane environment. The model describes interactions between protein residues at atomic detail whereas the water, hydrophobic core, and lipid head group regions of the membrane are treated by using continuum solvent models. We have also developed a methodology for the efficient sampling of helical distortions that occur frequently in membrane proteins. In this paper, we describe the validation of the model and sampling methods in computational membrane protein design, docking, and structure prediction experiments.

Results

In this section, we (i) give a brief overview of the physical model, (ii) describe in silico tests of the model, (iii) analyze the contribution of individual components to the success of the model, (iv) describe the sampling of TMH distortions, and (v) describe the application of the method to ab initio structure prediction.

Overview of the Physical Model.

Our computational model is based on an energy function that describes membrane intraprotein interactions at the atomic level and membrane protein/lipid interactions implicitly. Hydrogen bonds (hbonds) are treated explicitly, including weak CHO hbonds and bifurcated hbonds in which a carbonyl oxygen accepts more than one hydrogen atom [supporting information (SI) Fig. 3]. As shown below, the model recapitulates a wide range of hbonding interaction networks observed in native membrane proteins. The energy function is summarized in Materials and Methods, and a detailed description of all force field parameters is presented in SI Materials and Methods.

Validation of the Physical Model.

In this section, we describe the validation of the model using a battery of structure prediction and design tests.

Side-chain conformation recovery test.

The ability of the model to predict side-chain conformations was assessed by simultaneously repacking side-chains on fixed protein backbones derived from 18 high-resolution crystal structures. As shown in SI Table 3, the method predicts the correct combination of chi1 and chi2 dihedral angles for 73% of the buried positions, a value that compares well with that obtained for water-soluble protein–protein interfaces (13). The recovery is higher in regions embedded in the membrane hydrophobic core, consistent with a higher degree of packing in these regions compared with those facing the lipid head groups.

Amino acid recovery test.

The energy function was tested in redesign experiments in which sequence space is searched for the combination of amino acids that minimizes the free energy of the protein structure. In tests with soluble proteins, design calculations recover a significant fraction of the amino acid native identities, suggesting that native sequences are close to optimal for their structures (14). Table 1 and SI Table 4 show the level of recovery for individual amino acids embedded in both the hydrophobic core and the lipid head group regions of the membrane. The method selected the native amino acids at >45% of buried and almost 35% of all positions. These values compare well with those previously obtained for water-soluble proteins (14). For both lipid and water soluble proteins, the recovery is higher for nonpolar than for polar residues, consistent with the latter being often selected by nature for function instead of stability.

Table 1.

Amino acid sequence recovery in computational design experiments

Residue	Total		Core		Interface
	All	Buried	All	Buried	All	Buried
Apolar	42	50	45	53	41	48
Polar	14	21	16	22	13	20
All	34	43	39	46	31	40

Computational design methods were used to find the lowest-energy amino-acid sequence for 18 membrane proteins. Values are the percentage of positions that have the same amino acid in the native and designed sequences. The total, core, and interface columns correspond to the results obtained for all regions, the regions facing the hydrophobic core of the membrane bilayer, and the regions facing the lipid head groups, respectively. In each of these categories, the results are shown for all and buried positions.

The gradient in amino acid polarity between the hydrophobic core and the lipid head group regions is another important property of native membrane proteins that was well recovered in our design experiments (SI Fig. 4a). SI Fig. 4b shows that the distributions of amino acids in the designed sequences agree reasonably well with those observed in native proteins in both regions of the membrane.

Native TMH docking test.

Monte Carlo simulations using fixed backbone but flexible side chains were used to dock single TMHs on their protein templates to generate diverse sets of near-native and nonnative conformations (15). The native and near-native docked arrangements were significantly lower in energy than nonnative conformations (as indicated by the Z score values in column 3 of Table 2 and in SI Fig. 5). The significant energy gap observed for most complexes is a validation of the energy function because the native docked arrangement is almost certainly the lowest in energy.

Table 2.

Native TMH docking tests

Protein	Docked residues	Zlrms
		Full	No weak/bif HB
Glycophorin A	All	3.26	1.02
Glycerol channel	39–55	2.56	1.89
Glycerol channel	234–245	3.59	2.87
PsaL subunit of PSI	5–15	2.22	1.82
Halorhodopsin	1–29	2.37	1.73
Halorhodopsin	204–232	1.71	1.66
Calcium ATPase	764–775	2.35	1.97
Cytochrome c oxidase	76–89	2.87	2.63
Photosynthetic reaction center	572–582	2.22	2.01
Photosynthetic reaction center	659–672	2.3	1.89
Mean ± SD	—	2.55 ± 0.55	1.95 ± 0.51

The energy gap among native, near-native (N), and nonnative (NN) docked complexes was assessed by using Z_lrms = (〈E〉_NN − 〈E〉_N)/σ_E^NN (see Materials and Methods). The contribution of the membrane-specific hbonding term to the energy gap between native and nonnative docked complexes was analyzed: full membrane potential (Full), potential without membrane-specific side-chain–backbone bifurcated and side-chain–side-chain, backbone–side-chain weak hbonds (no weak/bif HB). ΔZ_lmrs is the difference between the Z score values obtained with and without the weak/bif HB potential. Successful discrimination is defined as a Z score >1. PSI, Photosystem I; —, not applicable.

Analysis of the Contribution of Individual Terms in the Model.

Solvation.

The solvation term is dominated by the free-energy cost of transferring polar groups and the free-energy gain of transferring nonpolar groups from water into the lipid bilayer. There is a lesser contribution associated with their transfer from the lipid environment into the protein interior (SI Materials and Methods). The anisotropy of the membrane bilayer plays an important role in the amino acid distribution in membrane proteins. Accordingly, the removal of the solvation potential from the energy function led to a 25% decrease in the total sequence recovery and to the loss of the amino acid polarity gradient along the membrane normal. By penalizing suboptimal membrane embeddings, the solvation potential also increases the discrimination of near-native from nonnative TMH interfaces that have rmsd values of >5 Å to the native structures (results not shown). However, it does not play a major discriminative role for decoys closer to the native structures.

VDW and hbonding interactions.

Short-range VDW and hbond interactions contribute to the discrimination between TMH interfaces that have smaller structural discrepancies to the native structures (Table 2 and SI Fig. 5). Upon addition of the bifurcated and weak CHO hbond terms, the energy gaps between native and nonnative docked conformations increased by 31% on average (Table 2). This highlights their role in stabilizing tightly packed interfaces involving glycine zippers as in the glycerol channel and glycophorin A or interfaces accommodating small polar residues (i.e., Ser and Thr). The incorporation of the bifurcated and weak CHO hbond terms in the energy function improved the recovery of polar amino acids, especially Thr and Ser (by 13%) (SI Fig. 3) and produced an increase of nearly 2% in overall sequence recovery in regions embedded in the membrane hydrophobic core. No significant increase in sequence recovery was obtained with a pure electrostatic treatment (5) of these interactions (results not shown), arguing for the importance of modeling the orientational dependencies of their energies.

Efficient Sequence-Based Modeling of Distorted TMHs.

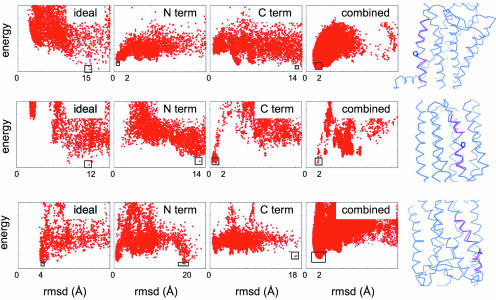
We have simplified the sampling of TMH distortions by identifying from sequence the location of the kinks and by modeling the regions away from the predicted hinges with ideal helices. Most TMH distortions occur at Pro residues or at positions where kinks initiated by Pro residues were later stabilized by tertiary interactions during evolution (16). The deformation of the polypeptide chain generally propagates up to four residues N-terminal to the residue responsible for the bend (17). We hypothesized that the native conformation of the distorted helix could be identified by modeling the chain away from the bend-induced hinges by ensembles of pairs of ideal helix fragments with a range of orientations (see Materials and Methods). This approach was tested by docking ideal helix fragments to native protein templates and selecting the pairs with the lowest nonlocal interaction energy with other TMHs. The distortions analyzed here encompass most of the deformations observed in membrane protein structures: regular Pro-induced hinges, larger kinks induced by combination of small polar residues with Pro residues (18) and Pro-like hinges stabilized by tertiary interactions (16). Fig. 1 and SI Fig. 6 summarize the results obtained on such distorted TMHs in halorhodopsin and bovine rhodopsin. Control experiments where ideal helices defined for the entire length of the native helices were docked on the protein templates confirmed that native tertiary interactions cannot be recapitulated with ideal backbone geometries (Fig. 1 and SI Fig. 6, left plot). Native conformations could also generally not be identified by individual ideal helix fragments defined away from the bend (Fig. 1 and SI Fig. 6, middle plots). However, when filtered based on the observed range of kink angles and distances between the peptides (SI Fig. 7), the resulting pairs of docked peptides defined an energy funnel toward near-native conformations. In all these experiments, the lowest-energy filtered pairs of ideal peptide conformations had combined rmsd values of <2 Å to the native conformation (rightmost plots in Fig. 1 and SI Fig. 6).

Fig. 1.

Modeling of TM distorted helices with ideal helix fragments defined around hinges predicted from sequence. Single distorted helices were cut away from membrane protein structures, and the cut-away region was docked back onto the remainder of the structures by using flexible side-chain rigid backbone docking with one of several representations for the backbone. In the leftmost plots, a single ideal helix was docked; in the two center plots (N term and C term), the regions N- and C-terminal to the kink were represented by short ideal helices and docked independently; the rightmost plots (combined) show compatible N- and C-terminal ideal helix pairs with distances and angles within the ranges predicted based on the sequence of the kink (Materials and Methods and SI Fig. 7). Each plot shows the energy (y axis) versus rmsd to the native structure (x axis) for structures generated in independent Monte Carlo docking calculations; the lowest-energy structure generated is indicated by a black box. Also shown are superpositions between the lowest-energy structure (magenta) from the “combined” plots with the native structure (blue). (Top) Bovine rhodopsin TMH kinked at Pro-53 with a kink angle of 17.1°. (Middle) Halorhodopsin kinked at Pro-94 with a kink angle of 30.4°. (Bottom) Halorhodopsin with a Pro-like kink at Thr-92 and a kink angle of 38.9°.

Structure Prediction.

De novo prediction of interface-bound peptide structures.

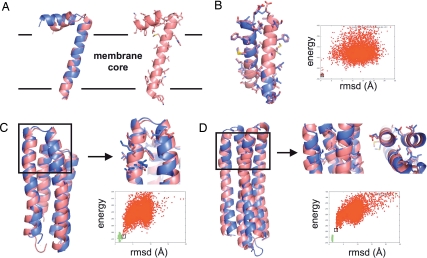
Domains lying parallel to the membrane bilayer in the interface region are recurrent in membrane-embedded polypeptides. We performed a prediction from sequence of the structure of the fd-coat protein. Its structure was determined experimentally in oriented lipid bilayers by high-resolution solid-state NMR (19) and is composed of one TM and one interfacial helix segment. Coarse-grained models, generated by the low-resolution ROSETTA membrane protocol (3) were refined and relaxed with the all-atom energy function (see Materials and Methods). The lowest-energy structure had a rmsd of 2.4 Å from the NMR structure with the orientation of the TM and interfacial regions correctly predicted (Fig. 2A). The model contains characteristic atomistic features of membrane interface-embedded peptides with hydrophobic and polar residues snorkeling in and out of the membrane lipid bilayer, respectively.

Fig. 2.

Structure prediction. (A) fd-coat protein. (Left) Backbone superposition of the experimental structure determined by solid-state NMR (19) (blue) and the lowest-energy decoy generated by ROSETTA (pink) starting from an extended chain. The rmsd over 30 C^α atoms is 2.4 Å. (Right) All-atom representation of the lowest-energy decoy generated by ROSETTA. The boundaries predicted by ROSETTA between the hydrophobic core and the interface regions of the membrane are represented with a black solid line. (B) Glycophorin A. Isolated monomers were docked with the ROSETTA protein–protein docking protocol and the all-atom membrane force field. The superposition between the native (blue) and the lowest-energy predicted structure (pink) is represented. The rmsd over 45 C^α atoms is 0.65 Å. (C and D) Ab initio structure prediction of polytopic membrane proteins. Native polytopic membrane protein conformations define a narrow energy basin in the all-atom conformational energy landscape. When near-native topologies are generated at the coarse-grained level, all-atom relaxed decoys define a funnel toward the native basin and the lowest-energy predicted structures have near-atomic resolution structures. In the energy versus rmsd plots, nonnative (red points) (generated from sequence by the ROSETTA coarse-grained structure prediction mode) and native conformations (green points) were relaxed by sampling the conformational degrees of freedom of all backbone and side-chain atoms. Cartoons show superposition between the native (blue) and the lowest-energy predicted structure (pink). Boxed areas show regions where close to native side-chain packing arrangements were obtained. The rmsd values are 2.1 Å over 111 C^α atoms for BRD4 (C) and 2.4 Å over 139 C^α atoms for VATP (D).

Prediction of TMH oligomeric interfaces by docking.

Many functions of membrane proteins are driven by oligomerization and accurately predicting the structures of these assemblies is a current challenge. Fig. 2B shows that the native dimeric structure of glycophorin A can be predicted by docking randomly oriented monomers without enforcing the symmetry of the homodimer. The lowest-energy conformation has a rmsd of only 0.65 Å to the native structure determined by high-resolution NMR techniques (20). This approach should prove useful for the structure prediction of membrane protein oligomers starting from monomeric structures.

De novo prediction of polytopic membrane protein structures.

To be observed experimentally, native structures must be significantly lower in free energy than nonnative conformations. A force field that recapitulates such an energy gap is therefore critical for high-resolution structure prediction. Coarse-grained models were generated by using the low-resolution ROSETTA membrane protocol (3) and then refined with the all-atom energy function. The energies of these refined ab initio models were compared with those of native structures relaxed by the same protocol. Fig. 2 and SI Fig. 8 show that the relaxed native structures of 3- to 7-helix integral membrane proteins define a deep and narrow energy funnel and are lower in energy than nonnative structures. The narrow width of the native basins is consistent with a rugged conformational energy landscape dominated by short-range interactions in which native-like side-chain packing can be disrupted by relatively small backbone perturbations. When near-native topologies (<4 Å) are generated at the coarse grained level, the all-atom refinement protocol produces structures that define a funnel toward the native basin (Fig. 2 C and D). The lowest-energy predicted structures have near-atomic resolution with rmsd of 2.1 Å over 111 atoms and 2.4 Å over 139 atoms for the 4-helix bundles BRD4 and VATP, respectively. Close to native side-chain packing arrangements can be observed in the best predicted regions (Fig. 2 C and D).

Discussion

The prediction and design of membrane protein structures is an important but difficult challenge. To address this problem, we have developed a model that recapitulates efficiently and at atomic resolution the physical and local structural properties of membrane proteins in the membrane bilayer. The model was validated by using a wide range of in silico design and structure prediction tests. Seventy-three percent of side-chain rotamers (chi1 and chi2) and 35% of all native residues of diverse polytopic membrane proteins were recovered in computational design experiments (Table 1 and SI Table 3). Other important properties of membrane proteins, e.g., anisotropy in amino acid distribution, gradient in polarity, and interfacial peptide conformations were also well recovered (Fig. 2 and SI Fig. 4). Large energy gaps were predicted between native and nonnative conformations of TMH interfaces and polytopic membrane proteins (Table 2, Fig. 2, and SI Figs. 5 and 8).

The physical model focuses on intraprotein short-range VDW and hbond interactions and treats protein/lipid interactions implicitly with a continuum solvent model. The good recovery of amino acid anisotropic distribution, gradient in polarity, and interfacial peptide conformations indicates that our continuum solvent model captures the main solvation properties of the membrane bilayer. The success of our model in the prediction and design tests suggests that short-range VDW and hbond interactions are essential for the stability and structural specificity of TMH bundles. These results also are consistent with the predominant role of hydrophobic and uncharged polar residues in the large majority of intramembrane interactions away from polar pore-lining regions. The importance of bifurcated and weak hbonds to membrane protein stability and structural specifity is demonstrated by the increase in Z scores (measure of structural determination in structure prediction tests) and in the recovery of small, uncharged polar residues when these terms were included in the energy function (SI Figs. 3 and 5 and Table 2). Unlike other potentials (5, 21) that only model the electrostatic character of polar interactions, our energy function explicitly models the orientational dependencies of their energies, which was found to be critical in our sequence recovery tests (results not shown). With the incorporation of detailed hbonding interactions, our model goes beyond that used recently to very successfully design specific nonpolar TMH interfaces (22).

The structural diversity of TMH proteins is increased by the presence of kinks and bends in helices (12). For example, all G protein-coupled receptors share the same 7-helix bundle topology but are predicted by sequence to have different kink patterns and therefore different structures (16). A systematic search around each residue for such deviations from ideal helix geometry would be computationally prohibitive, making the efficient modeling of these structural properties an important challenge. Fortunately, ≈90% of distortions in TMHs induce localized deformations (17) and can be predicted from sequence (16). Modeling distorted TMHs away from the bend-induced hinges identified by sequence with ideal helix fragments can therefore reduce the complexity of the search in conformational space. This simple strategy recapitulates a large spectrum of observed helical distortions (Fig. 1 and SI Fig. 6) and enables the efficient modeling of structural diversity in TMH bundles; this will be of particular relevance for the prediction of G protein-coupled receptor structures.

Finally, near-atomic-resolution ab initio structure predictions (<2.5 Å) were achieved for three membrane protein domains whose sizes range from 45 to 145 residues (Fig. 2). This level of accuracy compares well with that of the predictions obtained on small water-soluble protein domains (<85 residues). These results suggest that, when coarse-grained decoys with near-native topologies (<4 Å) are generated, high-resolution structural properties of membrane proteins can be predicted from sequence. The main challenge for carrying out such predictions on larger systems is to develop conformational sampling strategies that consistently generate near-native topologies at the coarse-grained level.

Our results suggest that the present model captures the essential physical properties that govern the solvation and stability of membrane proteins. It is clear, however, that more sophisticated models of the membrane will be needed to predict the effects at the molecular level of membrane deformations and specific lipid/amino acid interactions that are involved in the regulation of membrane protein structures and functions (12, 23). A more accurate treatment of electrostatics accounting for induced polarization effects and shifts in ionization constants (24) may also be necessary to model functional properties involving networks of buried charged residues or water/ion-solvated regions in channels and transporters. Our model sets the stage for the high-resolution prediction and design of polytopic membrane protein structures. Direct applications involve the structure prediction of small membrane protein domains and interfaces, the prediction of disease-related mutational effects, the generation of atomic-resolution models from low-resolution experimental data and the design of new membrane proteins.

Materials and Methods

Energy Function.

The free energy function is an extension of the ROSETTA full-atom potential developed previously for water-soluble protein structure prediction and design calculations (14). This force field consists of a linear combination of a Lennard–Jones potential that models VDW attractive and repulsive atomic forces, a backbone torsional term that accounts for the different local structural propensities of the amino acids, a knowledge-based pair interaction term that approximates electrostatic interactions between protein side chains, 20 reference energies that control the overall amino acid composition, an implicit atomic solvation term based on the model developed by Lazaridis and Karplus (25), and an orientation-dependent hbonding term (26). Both the solvation and the hbond potentials were modified to account for the anisotropic membrane environment.

The membrane environment is described by using three continuum phases: two isotropic phases (water and the hydrophobic core of the lipid bilayer) and one anisotropic phase in between (lipid head group region of the membrane). An implicit atomic solvation potential was derived for the hydrophobic phase based largely on experimental transfer free energies of peptides from water to cyclohexane (5). The atomic solvation energies in the water phase are identical to those used in the energy function for water-soluble proteins (25). The atomic solvation energies in the membrane interface region are derived by interpolating the solvation properties from the two adjacent phases based on the depth of each atom in the membrane (see SI Materials and Methods).

The previously developed ROSETTA hbond potential (26) was modified to model the effect of the membrane environment on the strength of the hbonds (see SI Materials and Methods). The hbond potential also was further developed to explicitly model weak (CHO) (SI Materials and Methods and SI Fig. 9) and bifurcated side-chain/backbone hbonds (in which a backbone oxygen accepts more than one hydrogen) (see SI Fig. 3), which play important roles in inducing helical distortions and stabilizing polar residues in membrane proteins (see SI Materials and Methods).

As described previously (14), the weights for each term of the energy function were optimized to recover the native amino acid identities of membrane proteins in a set of 18 membrane protein crystal structures (see SI Materials and Methods and SI Table 5). Each energetic term was evaluated for all rotamers of all amino acids by using a backbone-dependent rotamer library expanded by additional rotamers placed at plus or minus one standard deviation of the statistically determined minima (27).

Amino Acid Sequence and Side-Chain Conformation Recovery.

In conformation recovery experiments, the backbone structure was kept fixed to the crystallographic coordinates and the side chains were repacked simultaneously. Side-chain dihedral angles were considered correctly predicted if they were within 40° of the crystallographically determined values. In sequence recovery experiments, the backbone structure also was held constant and sequence space was searched for the combination of amino acids that minimizes the free energy of the system (see SI Materials and Methods).

TMH Docking and Protein Structure Prediction.

Native TMH docking.

Single TMHs were stripped off from polytopic membrane proteins and docked on the remaining protein template with the ROSETTA docking protocol (15). The backbone rigid-body and interfacial side-chain conformational degrees of freedom were sampled in these calculations. The same decoys were ranked by the membrane protein all-atom energy function with or without membrane-specific hbond terms. The discrimination between decoys was assessed by computing the energy gap (Z score) between the near-native and nonnative conformations. The low rmsd (in C^α coordinates from the native structure) Z score (Z_lrms, discriminating near-native from nonnative conformations) is defined as

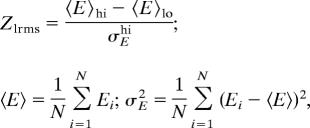where the averages and the standard deviation are computed over decoys with high (hi) and low (lo) rmsd, as indicated. Low rmsd (near-native) decoys are the lowest 5% of the rmsd distribution.

Full-atom structure relaxation.

Coarse-grained models were generated with the low-resolution ROSETTA membrane ab initio structure prediction method (3) and then refined with the all-atom energy function. Structure refinement in the all-atom conformational energy landscape combines Monte Carlo minimization of backbone and side-chain degrees of freedom with discrete side-chain optimization. Each move in this landscape involves a random perturbation of backbone torsion angles followed by discrete optimization of side-chain rotamers and then by gradient-based local minimization on all conformational degrees of freedom (28). The energy of these refined decoys were compared with the energy of the native structures relaxed with the same protocol.

Modeling of Distorted Helices by Ideal Helix Fragment Docking.

The presence of kinks was predicted at Pro residues or at positions where Pro residues could be identified in multiple sequence alignments (16). The majority of Pro-hinged TMHs have hinge locations between positions (i − 4) and i (where the Pro residue is at position i) (17). Therefore, ideal helix fragments were defined away from the predicted hinges, i.e., from position i − 4 to the N terminus of the TMH (N fragment) and from position i to the C terminus of the TMH (C fragment). Docked conformations of pairs of helix fragments were filtered based on two metrics (SI Fig. 7): (i) the range of kink angles expected for Pro-induced hinges with or without small polar residues at positions i − 1 to i − 3 (17, 18) and (ii) the range of distances between the C^α values of the C-terminal positions of the N fragment and the C^α values of the N-terminal positions of the C fragment derived from statistical analysis of distorted TMHs in high-resolution structures of polytopic membrane proteins (SI Fig. 7C). For each possible pair of docked ideal helical fragments, the above-mentioned kink angle and distances were computed. If either angle or distances were not found within the predicted values plus or minus one standard deviation, this particular pair was discarded from the population of docked helix pairs. After this filtering step, the remaining pairs were analyzed, and the modeling was considered successful when the filtered pairs of ideal helix conformations with the lowest total energy were also low in rmsd.

Abbreviations

TM

transmembrane

TMH

TM helix

VDW

van der Waals

hbond

hydrogen bond.