Ionic Current Blockades from DNA and RNA Molecules in the α-Hemolysin Nanopore

Abstract

We characterize the substate structure of current blockades produced when single-stranded polynucleotide molecules were electrophoretically driven into the α-hemolysin protein pore. We frequently observe substates where the ionic current is reduced by ∼50%. Most of these substates can be associated with a molecular configuration where a polymer occupies only the vestibule region of the pore, though a few appear related to a polymer occupying only the transmembrane β-barrel region of the pore. The duration of the vestibule configuration depends on polymer composition and on which end of the polymer, 3′ or 5′, subsequently threads into the narrowest constriction and initiates translocation. Below ∼140 mV a polymer is more likely to escape from the vestibule against the applied voltage gradient, while at higher voltages a polymer is more likely to follow the voltage gradient by threading through the narrowest constriction and translocating through the pore. Increasing the applied voltage also increases the duration of the vestibule configuration. A semiquantitative model of these trends suggests that escape has stronger voltage dependence than threading, and that threading is sensitive to polymer orientation while escape is not. These results emphasize the utility of α-hemolysin as a model system to study biologically relevant physical and chemical processes at the single-molecule level.

INTRODUCTION

Individual single-stranded DNA or RNA molecules can be detected as they are driven electrophoretically through a nanometer-scale pore (1,2). During translocation, polynucleotide molecules impede the flow of small ions and cause a transient blockade of the ionic current through the pore. These blockade events contain a wealth of information about the composition and concentration of polynucleotide molecules in the vicinity of the pore (3–7). This has motivated a growing interest in nanopore-based molecular detection technologies (2,4–6,8–12). The original and most widely used pore for polynucleotide detection is the Staphylococcus aureus α-hemolysin (αHL) protein pore (13). The αHL system is a sensitive probe of DNA structure (14) and basepairing kinetics (15–18), DNA-protein interactions (19), the physics of confined polymers (20), and the physics of ion permeation (21). The blockade events produced during the interaction of DNA with αHL allow the rare combination of high-throughput, real time, single-molecule observations. The composition of the polynucleotide molecules can be easily manipulated, and the structure and composition of pore interior are known (13) and can be engineered (10,22,23). Finally, the temperature, applied voltage, and buffer composition can be controlled and characterized with a high degree of precision. These properties make the αHL system a particularly attractive platform for engineering nanopore-based biosensors and an excellent system for developing and testing theoretical models of nanoscale biological processes (24–29).

Individual current blockade events observed during the interaction between single-stranded polynucleotide molecules and αHL often demonstrate multiple substates of distinct conductance (6,14,30). A Deep state where the current is reduced to ∼0–30% of the unobstructed Open state is generally associated with translocation of a polynucleotide molecule through the pore (1,5,9,10,19,30,31). The dependence of the duration, depth, and frequency of occurrence of the Deep state on polymer length, applied voltage, temperature, and polymer composition have been experimentally characterized (1,3,5,7,19,31). A growing amount of theoretical work has sought to develop a model that can encompass as many of these observations as possible (24–28,32,33). A Mid state where the current is reduced to ∼30–85% of the Open state is also often observed (6,14,30). Previous studies with double-stranded DNA constructs (9,15) indicate that a Mid state can be produced when a polynucleotide molecule is resident only in the vestibule portion of the pore. The dynamics of single-stranded polynucleotide molecules in the αHL vestibule have been investigated in simulation studies (33,34), but the detailed characteristics of Mid states produced by these polymers have not yet been investigated experimentally. In this article, we analyze the substate structure of current blockade events produced by single-stranded polynucleotide molecules in the αHL pore. We focus primarily on the vestibule-associated Mid state, exploring how its characteristics depend on polymer composition, polymer orientation, and applied voltage.

MATERIALS AND METHODS

Homogeneous ssDNA oligonucleotides dA₅₀, dC₅₀, and dT₅₀ were synthesized by Integrated DNA Technologies (Coralville, IA) and homogeneous RNA oligonucleotides rA₅₀, rC₅₀, and rU₅₀ were synthesized by Dharmacon RNA Technologies (Lafayette, CO). None of these synthetic oligonucleotide constructs were phosphorylated at either the 5′ or 3′ end. All samples were PAGE-purified by the suppliers. We resuspended the oligonucleotide samples in the experimental buffer and stored them at −20°C until immediately before use.

Horizontal diphytanoyl-PC/hexadecene bilayers (Avanti Polar Lipids, Alabaster, AL) were formed across a ∼20 μm diameter aperture in Teflon. Monomeric αHL (EMD Biosciences, San Diego, CA) was added to one side of the bilayer (cis side) at a concentration of ∼50 μg/ml. The cis side was grounded and positive voltage was applied to the trans side of the bilayer. With 120 mV applied across the bilayer, insertion of a single αHL pore was marked by an abrupt jump in the current from 0 to ∼120 pA. RNA or ssDNA was then added to the cis compartment to a concentration of 1–2 μM. In this configuration, the αHL pore was oriented such that polynucleotide molecules were driven into the pore through its extramembranous vestibule region. All experiments were performed at 21 ± 2°C in 1 M KCl, 10 mM HEPES/KOH buffered at pH 8.

We used an Axopatch-1B patch-clamp amplifier (Axon Instruments, Union City, CA) to apply voltage across the bilayer and to measure the ionic current flowing through the pore. The analog signal was low-pass filtered at 50 kHz with a four-pole Bessel filter. The amplified, filtered signal was digitized at 250 kHz with a NI PCI-6014 DAQ card (National Instruments, Austin, TX). Data acquisition was controlled with custom software written in LabWindows/CVI (National Instruments). Data analysis was implemented in MatLab (The MathWorks, Natick, MA).

RESULTS AND DISCUSSION

Blockades demonstrated rapid transitions between well-defined conductance states

Entry of individual polynucleotide molecules into the αHL nanopore caused current blockade events with two primary conductance states; a Mid state where the ionic current was between 30% and 85% of the unobstructed Open state, and a Deep state where the current was between 0% and 30% of the Open state (Fig. 1). The rise time of Open state to Mid state or Mid state to Deep state transitions was generally comparable to the 7-μs limit imposed by our 50 kHz antialiasing filter. We thus modeled the structure of each event as a sequence of Mid and Deep conductance states. Using typical threshold-based nanopore event detection algorithms (3,4,31), we defined an Open Threshold at I_OS-2σ_OS and a Deep Threshold at 0.3*I_OS, where I_OS is the average Open state current and σ_OS is the RMS noise of the Open state (Fig. 1). Mid states were identified as periods when the ionic current was between the Open and Deep Thresholds, and Deep states were identified as periods when the ionic current was below the Deep Threshold. We parameterized each event by the durations and average currents of its constituent substates, and we required that a substate have a duration of 30 μs or longer to be included in our description of the event.

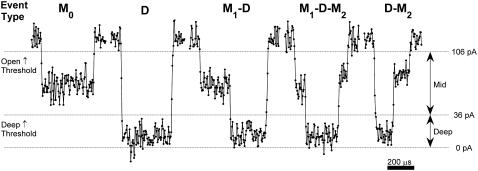
FIGURE 1.

Example of ionic-current traces illustrating the substate structure of polynucleotide-induced current blockade events. These traces are from an experiment with dT₅₀ at 120 mV. The horizontal lines show the zero current level and the thresholds used to subdivide events into constituent Mid and Deep states. We defined three kinds of Mid states: M₀ states occur in the absence of a Deep state, M₁ states directly precede a Deep state, and M₂ states directly follow a Deep state. All Deep states were abbreviated as D. We classified each event by its sequence of states. Our names for the various blockade event types appear above the corresponding traces.

We focused our analysis on the five types of events shown in Fig. 1. We defined a Mid state that occurred in the absence of a Deep state as an M₀ state, a Mid state that directly preceded a Deep state as an M₁ state, and a Mid state that directly followed a Deep state as an M₂ state. All Deep state signals were defined as D-states. We classified events according to their sequence of states. Table 1 lists the percentages of event types observed for different polymers in experiments with 120 mV applied across the bilayer. M₀, M₁-D, and D were the most common types of events for all six polymers we investigated. Events with M₂ states occurred with small but appreciable frequency only for rA₅₀, dT₅₀, and rU₅₀. Events that were not well described by any of the five event types shown in Fig. 1 were identified by one or more of the following characteristics:

1. The Mid state had an excursion into the Deep state that was longer than 22 μs but shorter than 30 μs, too long to be attributed to electronic noise but too short for characterization as a Deep state;

2. The RMS noise of one of the states was larger than twice the RMS noise of the Open state; and

3. The event demonstrated more than one Deep state signal.

TABLE 1.

Distributions of event types for the six polymers we investigated

Polymer	M0	D	M1-D	M1-D-M2	D-M2	Other
dA50 (6)	43 ± 4	28 ± 1	27 ± 4	<1	<1	2
dC50 (8)	19 ± 4	66 ± 5	7 ± 2	<1	<1	7 ± 2
dT50 (8)	39 ± 5	15 ± 1	38 ± 3	3	1	4
rA50 (7)	42 ± 2	14 ± 1	32 ± 2	2	1	9 ± 3
rC50 (5)	20 ± 6	62 ± 7	12 ± 1	<1	<1	6 ± 1
rU50 (3)	37 ± 8	31 ± 4	12 ± 3	3 ± 1	5 ± 2	12 ± 1

The five explicit event types are illustrated in Fig. 1. Other-type events are those that were not well described by any of the five explicit types. Values are given as percentages of the total number of events, averaged over repeated experiments. Uncertainties give the standard error of the mean, and the number of times each experiment was repeated is shown after the polymer name. M₀, D, and M₁-D type events were by far the most common types of blockades, and M₂ states occurred with nonnegligible frequency only in experiments with dT₅₀, rA₅₀, and rU₅₀.

Molecular interpretation of blockade substates

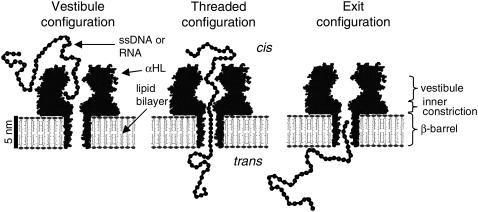
The known structure of the αHL pore (13) is central to a physical interpretation of the different types of ionic current blockades. Fig. 2 shows a schematic cross section of an αHL pore in a lipid bilayer. On the cis side of the bilayer the pore entrance narrows to a diameter of ∼2.5 nm before opening into the internal vestibule region. The vestibule region widens to a maximum diameter of ∼4.6 nm before narrowing down and joining a short, ∼1.5-nm-diameter inner constriction. The inner constriction leads into a ∼5-nm-long, ∼2-nm-diameter β-barrel that spans the bilayer and opens into the trans compartment. All our experiments were configured such that ssDNA and RNA molecules were driven into αHL from the cis side of the bilayer.

FIGURE 2.

Molecular interpretation of the structure of the blockade events shown in Fig. 1. We hypothesize that the vestibule configuration produces both M₀ and M₁ states and that the threaded configuration produces Deep states. We also suggest that either retraction from the threaded configuration back into the vestibule configuration or pausing of a polymer in the exit configuration could produce M₂ states.

Knowledge of the structure of αHL combined with a crude volume-exclusion model for the obstruction of current through αHL leads to a simple physical interpretation (Fig. 2) of the various event types shown in Fig. 1 (35). When a polymer occupies only the vestibule region of the pore, it reduces the current to the Mid state. This vestibule configuration leads to M₀ events if the polymer escapes back into the cis compartment. Alternatively, one end of the polymer may thread through the inner constriction of the pore and into the β-barrel, impeding the passage of ions enough to reduce the current to the Deep state. If the polymer continues threading through the β-barrel, it will eventually exit on the trans side of the bilayer. This translocation scenario accounts for M₁-D type events if the vestibule configuration persists long enough to produce a resolvable Mid state (longer than our 30-μs temporal resolution). We interpret D-type events as translocations where the vestibule configuration persisted for <30 μs. It is also possible, in principle, for a polymer that has threaded into the inner constriction to retract back into the vestibule configuration. In the last two traces of Fig. 1, a well-resolved Mid state is observed after the Deep state. It is clear how retraction from the threaded configuration back into the vestibule configuration followed by escape into the cis compartment could account for these M₂ signals. However, if the Deep state corresponds to translocation, then the subsequent M₂ state could result if the polymer's progress through the pore is arrested in a configuration where its trailing end occupies part of the β-barrel, but is no longer threaded through the inner constriction. We refer to this hypothetical configuration as the exit-configuration.

The association of the vestibule configuration with reduction of the current to the Mid state and the threaded configuration with further reduction of the current to the Deep state is supported by results from previous investigations. Howorka et al. investigated the binding of free oligonucleotides to complementary strands that were tethered to the interior of the αHL vestibule (36). When the transient, double-stranded DNA constructs had sufficiently long single-stranded overhangs, they produced current blockades that fluctuated between Mid and Deep conductance states. Complexes with shorter overhangs produced blockades that only demonstrated Mid states. Similar data and interpretations have been given for experiments with hairpin DNA having variable length duplex regions (9,37). These results strongly support the association of the Mid state with the vestibule configuration and the association of the Deep state with the threaded configuration. Further, a recent simulation study that simultaneously computed the time evolution of a single-stranded polymer interacting with the αHL pore and the corresponding modulation of the ionic current was able to reproduce this relationship between molecular configurations and degrees of current obstruction (33).

Homogeneous single-stranded DNA and RNA polymers are highly flexible, so it is more difficult to infer their particular arrangement in the αHL vestibule than for the more rigid double-stranded DNA constructs. We suggest two distinct ways in which a polymer may enter the vestibule from the cis compartment. One possibility is that entrance is initiated by fluctuation of an end segment into the vestibule, and the other possibility is that an internal segment of the polymer forms a transient loop that fluctuates into the vestibule and initiates polymer entrance. The result of Vercoutere et al. (9), where ssDNA constructs with hairpins at both the 3′ and 5′ ends did not cause resolvable Mid state blockades, argues against loop-initiated entrance. We also note two potential arrangements of the polymer in the vestibule configuration. Either the entire 50-mer is drawn inside the vestibule, or only part of the 50-mer is in the vestibule while the rest of the polymer remains in the cis compartment. The latter possibility is illustrated in Fig. 2. In the duplex DNA experiments, the αHL vestibule accommodated up to ∼24 nucleotides and still demonstrated Mid states (36), suggesting that at least half of a 50-nucleotide-long ssDNA or RNA molecule could be drawn into the vestibule. Jung et al. estimated that the accessible volume of the αHL vestibule, corrected for hydration of the vestibule surface, is ∼32,600 ų (38). Deamer et al. estimated a molecular volume of ∼290 ų for a single Adenylic nucleotide (39). Assuming that each nucleotide is accompanied by four water molecules leads to a rough estimate of ∼17,000 ų for the volume occupied by a hydrated dA₅₀ molecule. These calculations indicate that the vestibule is, in principle, large enough to hold an entire ssDNA or RNA 50-mer. While it is energetically favorable for the entire polymer to enter the vestibule, the entropic contribution to the free energy is quite complex. As the polymer enters the vestibule there are entropic costs associated with removing each monomer from the bulk cis volume (26) and from packing additional monomers into the confining vestibule (40). However, there is also entropic benefit associated with moving the polymer from a partially filled state, where a segment is restricted to the entrance, to a completely filled state where the polymer is free to reorient within the confining vestibule (20). It is not clear, a priori, which of these effects dominate in our experiments. We will return to the question of how much of the polymer is drawn into the vestibule after presenting our data.

Deep state statistics

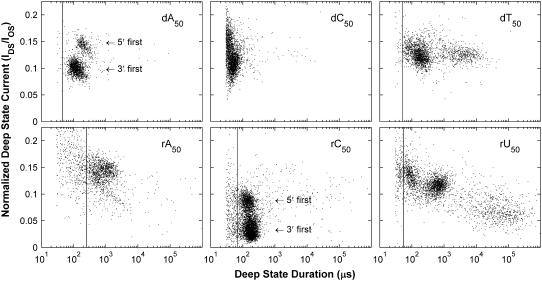
Each point in Fig. 3 gives the duration and average current of one Deep state. The panels show representative data from one experiment at 120 mV for each of the six polymers we investigated. We display the data on a log-linear scale to allow visualization of the Deep state duration distributions across many orders of magnitude. Clear grouping behavior is observed in all of the panels. Most of these groups correspond to local maxima in the two-dimensional distributions of Deep state durations and currents. However, the groups of long duration states in the dT₅₀ and rU₅₀ panels do not correspond to local maxima, but appear as groups because of the logarithmic scaling of the duration axis. Previous work strongly suggests that the signals in the maxima-associated groups arise from translocation of polymers through the pore (1,14,31). The general characteristics we observed for these maxima-associated signals are in good agreement with previously reported results (1,3,14,19,30,31). These references present extensive characterization and discussion of the Deep state. In this report, we focus only on the aspects of the Deep state that are important to our characterization and interpretation of blockade structure.

FIGURE 3.

Distributions of Deep state durations and currents. Each point corresponds to the duration and normalized average current of one Deep state. Data were acquired with 120 mV applied across the bilayer. We display the data on a semilogarithmic scale to allow visualization of the Deep state distributions across many orders of magnitude in duration. The vertical lines give the locations of minima in the duration distributions (see Fig. 5). We only associate signals longer than these minima with translocation of polymers through the pore. The longest duration groups of signals in the dT₅₀ and rU₅₀ panels do not correspond to local maxima in the distributions. These long signals are well described by exponential distributions with time constants of ∼3.7 ms for dT₅₀ (Fig. 4) and ∼94 ms for rU₅₀. They appear as groups because of the logarithmic scaling of the duration axis. Previous work found that the two groups in the dA₅₀ and rC₅₀ distributions were related to 3′- or 5′-first translocation.

The durations of the Deep states in the translocation-associated groups for the five homopolymers other than dC₅₀ were appreciably longer than our 30-μs cutoff, suggesting that we were able to detect nearly all translocation events in experiments with these polymers at 120 mV. It is clear from the dC₅₀ panel that many translocation-associated signals were shorter than our 30-μs cutoff time. Events demonstrating these short translocation signals were classified as Other, and we hypothesize that fast translocation accounts for a significant fraction of dC₅₀ Other-type events listed in Table 1. The two groups in the dA₅₀ and rC₅₀ distributions have previously been shown to arise from translocation of polymers in either of two possible orientations, 3′-first or 5′-first (28,30). We will utilize this orientation information in our subsequent analysis of the Mid state.

The long-duration Deep states in the dT₅₀ and rU₅₀ panels have not been previously reported. For dT₅₀, Deep states with duration longer than 4 ms constitute ∼20% of the total number of signals shown in the panel and their distribution is well described by a single exponential with a ∼3.7-ms time constant (Fig. 4). Analogously for rU₅₀, Deep states with duration longer than 10 ms constitute ∼21% of the total and their distribution is well described by a single exponential with a ∼94-ms time constant. Previous analysis of Deep state data found a 10–100-μs exponential time constant for the fall-off of the Deep state duration distribution in the vicinity of the maxima (3). However, this analysis did not take into account these extremely long events. The characteristics of the Mid states before and after the long Deep states are similar to those of the translocation-associated signals, suggesting that the long signals also represent translocation. To explain these long Deep states, we hypothesize that during translocation a polymer's forward progress can be significantly inhibited or even stopped entirely for relatively long periods of time. Tangling of the polymer at the neck or binding of one or more bases to the residues lining the β-barrel are two possible causes of such a stoppage. The Deep state would then persist until untangling or unbinding occurred, allowing normal translocation to resume and the subsequent exit of the polymer from the pore into the trans compartment.

FIGURE 4.

Duration distribution of the extremely long dT₅₀ Deep states. These signals appear as the rightmost group in the dT₅₀ panel of Fig. 3. As is clear from this plot, the group of long dT₅₀ Deep states does not correspond to an additional maximum in the dT₅₀ Deep state duration distribution. The long signals constitute ∼20% of the total number of signals in the dT₅₀ panel of Fig. 3 and are well described by an exponential distribution with a time constant of ∼3.7 ms (dashed curve).

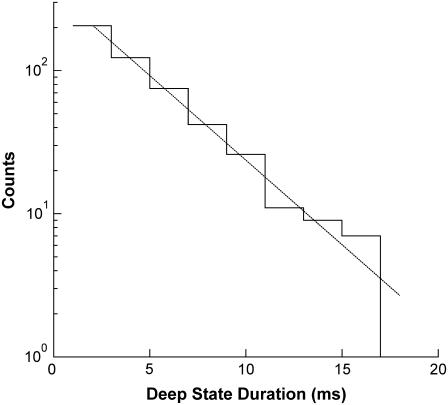
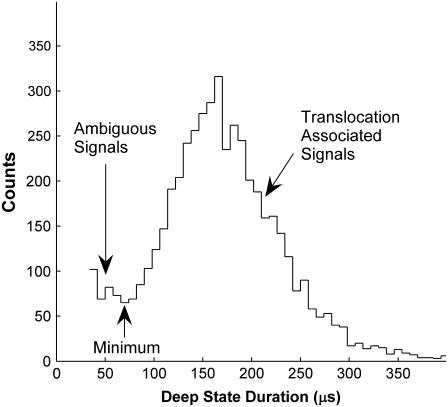
A final important feature in the Deep state distributions is that, with the exception of dC₅₀, we observed minima in the duration distributions between our 30 μs experimental cutoff time and the first maxima (Fig. 5). These minima are not readily apparent in Fig. 3 due to the logarithmic scaling, but their locations are given by the solid vertical lines. The rise in the distribution for durations shorter than these minima is not consistent with a simple picture of translocation, wherein one expects a monotonic decrease in probability for durations shorter than the most probable duration (24). Similar minima in Deep state duration distributions have been previously reported (1,30). Signals shorter than the minima were attributed to multiple possible effects such as retraction from the threaded configuration back into the vestibule configuration, very rapid translocation, or translocation of short polynucleotide fragments. Due to the ambiguity in the interpretation of these short Deep states, we only designated Deep states with durations longer than the minima as translocations (Fig. 5). If some of these short signals represent retraction, then we would expect to find events with multiple Deep states. Such events are often observed in experiments with short double-stranded DNA constructs in the αHL vestibule (36,37,41). We occasionally observed such events in experiments with dT₅₀ and rA₅₀, but their frequency of occurrence was difficult to quantify because they were rare and difficult to identify with our simple data analysis algorithm. Multiple Deep state events in experiments with the other four polymers were almost never observed. The existence of events with multiple Deep states suggests that retraction from the threaded configuration back into the vestibule configuration can occur and be resolved in our experiments. However, this process seems quite rare and it remains unclear to what extent it can account for the short, ambiguous Deep states.

FIGURE 5.

rC₅₀ Deep state duration distribution. This distribution shows the same data as the rC₅₀ panel of Fig. 3, but the signals have been binned in duration and are displayed on a linear scale. There is a clear minimum in this duration distribution between our 30-μs experimental cutoff time and the translocation-associated maxima. We observed similar minima in the Deep state duration distributions of other polymers we investigated (Fig. 3, solid vertical lines). We designated signals longer than the minima as translocation-associated Deep states and those shorter than the minima as ambiguous Deep states.

Mid state statistics

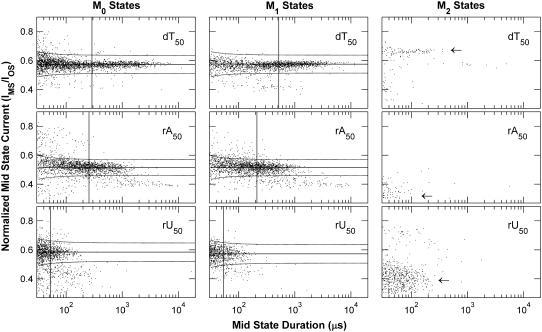
Fig. 6 shows the durations and currents of the three types of Mid states, M₀, M₁, and M₂, from experiments at 120 mV with dT₅₀, rA₅₀, and rU₅₀. Each distribution displays a characteristic current, I_M, around which the majority of the signals are clustered. We quantified this characteristic current with a Gaussian fit to the largest peak in a weighted distribution of the currents of the Mid states. The duration of each signal was used as the weighting factor, and the longest 5% of signals in each data set were excluded so that the peak location was not dominated by a minority of extremely long signals. I_M values for the distributions in Fig. 6 are shown as solid horizontal lines. We focused our analysis on Mid states of similar current by defining a primary group with boundaries at I_M ± (w + 2*σ_OS/sqrt(n_obs)). The term w is an empirical width factor that we set to 7.5 pA. The term 2*σ_OS/sqrt(n_obs) accounts for the expected increased statistical variation in the estimated average current of shorter signals, where σ_OS is the RMS noise observed in the Open state and n_obs is the number of samples of the ionic current time series used to estimate the average current of a given Mid state. The dashed curves in Fig. 6 show the boundaries defining the primary groups of signals. We used the average duration of the Mid states in the primary group, t_M, to parameterize the Mid state duration distributions. Again, the longest 5% of Mid states within the primary group were excluded from the calculation of t_M to prevent the statistic from being dominated by a minority population of very long signals. The t_M values for each data set are shown as solid vertical lines in each panel of Fig. 6. M₀ and M₁ data for dA₅₀, dC₅₀, and rC₅₀ followed the same general patterns as the data shown in Fig. 6, while the occurrence of M₂ signals was negligible in experiments with these polymers. Table 2 summarizes the average values of I_M and t_M at 120 mV for all six of the polymers we investigated.

FIGURE 6.

Distributions of Mid state durations and currents. Each point gives the duration and normalized average current of one Mid state. Rows show representative data from one experiment at 120 mV with the indicated polymer. Columns correspond to different types of Mid states (see Fig. 1). The solid horizontal lines show the characteristic Mid state current, I_M, and the solid vertical lines show t_M, the average duration of the Mid state signals contained within the dashed curves. We associate M₀ and M₁ states with the presence of a polymer in the αHL vestibule. Arrows in the M₂ panels point out signals in the M₂ distributions that have different normalized currents than the M₀ or M₁ signals. We hypothesize that these differing M₂ states are produced when a polymer is held in a configuration where it still occupies part of the β-barrel but is no longer threaded through the neck of the pore (Fig. 2). Table 2 summarizes I_M and t_M values for the six polymers we investigated.

TABLE 2.

Summary of Mid state characteristics for different polymers with 120 mV applied across the bilayer

Polymer	Signal type	IM/IOS	tM (μs)	Escape probability
dA50	M0	0.59 ± 0.01	75 ± 3	0.60 ± 0.05
	M1	0.57 ± 0.01	69 ± 2
dC50	M0	0.65 ± 0.01	54 ± 6
	M1	0.64 ± 0.01	57 ± 6
dT50	M0	0.58 ± 0.01	288 ± 27	0.48 ± 0.05
	M1	0.58 ± 0.01	605 ± 83
	M2	0.63 ± 0.01	122 ± 12
rA50	M0	0.50 ± 0.01	171 ± 17	0.59 ± 0.03
	M1	0.50 ± 0.01	154 ± 12
rC50	M0	0.60 ± 0.02	61 ± 4	0.57 ± 0.07
	M1	0.59 ± 0.01	59 ± 7
rU50	M0	0.58 ± 0.02	53 ± 1	0.69 ± 0.09
	M1	0.57 ± 0.02	55 ± 1
	M2	0.40 ± 0.01	67 ± 2

Values are averages from repeated experiments, and uncertainties are the standard error of the mean. The number of repeated experiments for each polymer is given in Table 1. We do not quote an escape probability for dC₅₀ because rapid translocation of these polymers made it difficult to accurately estimate the number of translocations. We do not parameterize the rA₅₀ M₂ distribution because it does not demonstrate a well-defined group of signals.

In comparing the first two columns of Fig. 6, one sees that for a given polymer there is a strong similarity between the M₀ and M₁ distributions. This similarity is also reflected in the I_M and t_M values in Table 2 (except for the dT₅₀ t_M values). These observations are consistent with the association of both M₀ and M₁ signals with a polymer in the vestibule configuration. Since we interpret M₀ signals as escape from the vestibule configuration back into the cis compartment, we define an escape probability as N(M₀)/(N(M₀)+N(M₁)), where N(M₀) and N(M₁) are the number of signals in the primary groups of the M₀ and M₁ distributions, respectively. Average escape probabilities for experiments at 120 mV are listed in Table 2 and range between ∼0.5 and ∼0.7. This indicates that at 120 mV, a homogeneous, 50-nucleotide long DNA or RNA molecule residing in the vestibule configuration is slightly more likely to escape against the voltage gradient back into the cis compartment than to follow the voltage gradient and translocate through the pore.

The majority of the M₂ signals demonstrate current levels that are clearly distinct from M₀ and M₁ current levels (Fig. 6, arrows). Assuming that the Deep states preceding these M₂ signals indicate translocation, we hypothesize that these Mid states occur when a polymer's exit into the trans compartment is hindered while it still occupies part of the β-barrel but is no longer threaded through the inner constriction of the pore (Fig. 2). The mechanism that hinders polymer exit could also occur at a previous stage in the translocation process, when the polymer was still threaded through the inner constriction of the pore and blocking the current at the Deep state. In this case, one might expect that polymers demonstrating longer, more frequent M₂ signals would also demonstrate longer Deep states. This correlation is found in our experiments as dT₅₀ and rU₅₀ produce the longest Deep states and the most frequent M₂ states. The M₂ distributions in Fig. 6 also show a few signals with current levels similar to the characteristic current levels in the M₀ and M₁ distributions. These M₂ signals are consistent with the hypothesis that a polymer can retract from the threaded configuration back into the vestibule configuration. We interpret these signals in the same way we interpret the existence and rarity of events with multiple Deep states—retraction of a threaded polymer back into the vestibule configuration can be observed, but only very rarely.

For the six homopolymers we investigated, the Mid state characteristics are moderately sensitive to polymer composition. M₀ and M₁ states for dA₅₀, dT₅₀, rC₅₀, and rU₅₀ all show a normalized residual current of I_M/I_OS ≈ 0.59, whereas dC₅₀ signals show a slightly larger residual current and rA₅₀ signals show a significantly smaller residual current. The characteristic durations of M₀ and M₁ states for rA₅₀ and dT₅₀ are significantly longer than those of the other four polymers. The largest escape probability was 0.69 for rU₅₀, and the smallest was 0.48 for dT₅₀, with the escape probabilities of the remaining polymers more or less evenly distributed between the two extreme values. These polymer-specific differences in Mid state characteristics could enhance the ability of αHL to analyze and distinguish polynucleotide samples. However, further work is needed to understand the molecular origins of these differences. For example, the large difference between the Mid state characteristics of dA₅₀ and rA₅₀ suggests that specific interactions between Adenine bases and the residues lining the vestibule are not the primary factors determining the Mid state characteristics of a given polymer.

Voltage dependence of the vestibule configuration

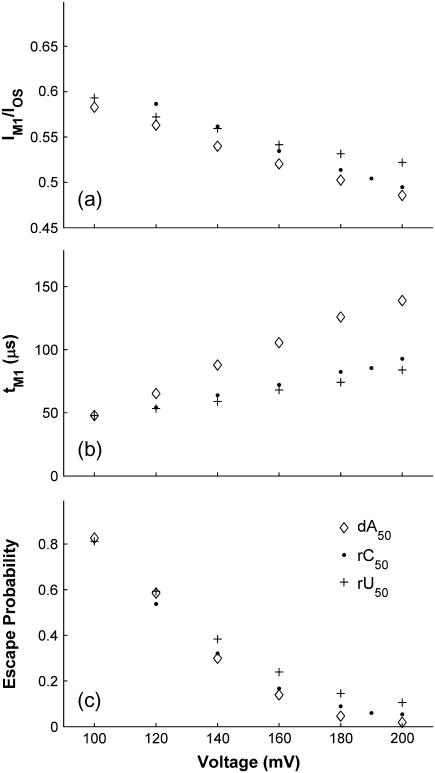
We conducted experiments at a variety of voltages over the range of 100–200 mV. Data obtained at each voltage were analyzed as described in the previous section. Fig. 7 shows the voltage dependencies of I_M/I_OS, t_M, and the escape probability for dA₅₀, rC₅₀, and rU₅₀. The I_M/I_OS and t_M values in Fig. 7 were derived from the M₁ distributions as opposed to the M₀ distributions because we observed a large number of M₁ signals for all polymers at all voltages. As we increased the voltage we saw a moderate but clear decrease in the normalized M₁ current level (Fig. 7 a), a substantial increase in the typical M₁ duration (Fig. 7 b), and a substantial decrease in the escape probability to near zero at 200 mV (Fig. 7 c). Voltage curves for dC₅₀, dT₅₀, and rA₅₀ are not shown, though their trends are qualitatively the same as those shown in Fig. 7.

FIGURE 7.

Voltage dependence of the vestibule configuration for dA₅₀, rC₅₀, and rU₅₀. (a) Normalized M₁ current. (b) Mean duration of the primary group of M₁ states. (c) Escape probability. The escape probability reflects the likelihood that a polymer which has inserted into the vestibule will escape back into the electrically negative compartment. It was calculated as the ratio of the number of M₀ states to the sum of the number of M₀ and M₁ states. Voltage-dependent data for dC₅₀, dT₅₀, and rA₅₀ shows the same trends as the data in this figure, but we do not display it here.

The general voltage-dependent trends shown in Fig. 7 provide further evidence supporting the hypothesis that M₀ and M₁ signals correspond to a polymer in the vestibule configuration. If a higher applied positive voltage on the trans side pulls more negatively charged bases from the cis side into the vestibule, then the volume exclusion mechanism of current obstruction accounts for the decrease in the normalized Mid state current (Fig. 7 a). This simple mechanism can explain the general trend in the data, but a variety of additional factors may also contribute to the observed Mid state current (42). The trends in Fig. 7, b and c, can be explained by a simple kinetic model wherein escape from the vestibule and threading of a polymer end from the vestibule into the inner constriction would be described as activated processes with associated rate-constants β and γ, respectively. If the vestibule configuration obeyed such simple kinetics, its duration would be exponentially distributed with a time constant of τ_M = (β + γ)⁻¹, and the escape probability would be given by β/(β + γ). The trends in t_M and the escape probability shown in Fig. 7 could then result if 1), escape is favored at low voltages, while threading is favored at high voltages (β > γ below ∼140 mV, γ > β above ∼140 mV); 2), the escape rate constant, β, decreases with increasing voltage; and 3), escape has a stronger voltage dependence than threading (over the range 100–200 mV, |∂β/∂V| > |∂γ /∂V|).

Polymer orientation and the vestibule configuration

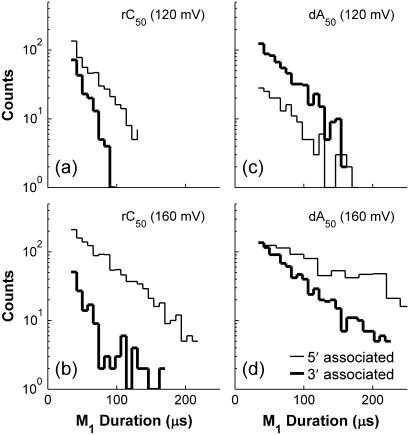
Before making a more detailed comparison between our data and this kinetic model of the vestibule configuration, we must consider the effects of polymer orientation. We previously demonstrated that translocation of an rC₅₀ polymer in a 3′→5′ orientation produced stronger obstruction of the ionic current than translocation in a 5′→3′ orientation (30), and Mathe et al. found an analogous effect for poly-dA translocation (28). This orientation-dependent Deep state conductance leads to the two well-resolved groups of signals in the rC₅₀ and dA₅₀ panels of Fig. 3. We utilized this effect to distinguish M₁ states that were followed by 3′-first translocation from those that were followed by 5′-first translocation. The resulting M₁ duration distributions are shown in Fig. 8. These distributions indicate that 5′-associated M₁ states tend to be longer than 3′ states, and that this difference is enhanced as the voltage increases. Application of the kinetic model we have proposed requires that the duration distributions of 3′ and 5′-associated vestibule configurations be individually well described by single exponentials. Single-exponential fits accurately represent the dA₅₀ data for both orientations and the rC₅₀ data for 5′-associated M₁ states. These fits were determined using the maximum likelihood method. M₁ states followed by 3′-first translocation for rC₅₀ were rare and short, making it difficult to assess the exponential character of these data. The existence of orientation-dependent differences in the duration of the vestibule configuration for the other four polymers is suggested by the observation that, at voltages above ∼140 mV, their overall M₁ duration distributions are better described using two exponentials rather than a single exponential.

FIGURE 8.

M₁ state duration distributions grouped by polymer orientation. Panels a and b show data for rC₅₀ and panels c and d show data for dA₅₀. Data in top row were obtained at 120 mV while the data in the bottom row were obtained at 160 mV. The correlation between Deep state characteristics and polymer orientation shown in Fig. 3 enabled us to group these M₁ states by orientation.

The correlation between translocation orientation and vestibule configuration lifetime suggests that there are two distinct vestibule configurations, one for each orientation of the polymer in the vestibule. This could occur if only part of the polymer resides in the vestibule, with one end remaining in the cis compartment. Alternatively, if the entire polymer resides in the vestibule then its conformational freedom must be so restricted that it cannot reorient itself within the vestibule. While it remains unclear how much of the polymer resides in the vestibule, it nonetheless seems appropriate to use separate sets of rate constants to model 3′- and 5′-associated vestibule configuration kinetics.

Kinetic model of vestibule configuration

We are able to compare our dA₅₀ data to a kinetic model with the characteristics described above because its 3′- and 5′-associated M₁ states can be distinguished and the orientation-dependent M₁ duration distributions are individually well described by single exponentials (Fig. 8). However, because we cannot distinguish between 3′- and 5′-associated M₀ signals, we are unable to estimate orientation-specific 3′- and 5′-associated escape probabilities and use them to derive estimates for the escape and threading rate constants directly from our data. We can estimate the overall escape probability, which is a weighted average of the orientation-specific escape probabilities. It is then possible to make a semiquantitative analysis of the vestibule configuration kinetics by assuming a particular model for the voltage dependence of the rate constants and then assessing that model's ability to reproduce our voltage-dependent τ₃, τ₅, and escape probability data (Fig. 9). We assume a very simple model where the 3′- and 5′-associated escape rate constants, β₃ and β₅, are identical and decrease exponentially with voltage (Eq. 1), while the threading rate constants, γ₃ and γ₅, are different but are both independent of voltage (Eqs. 2 and 3):

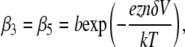(1)

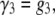(2)

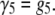(3)

In Eq. 1, b is the escape rate constant with zero applied voltage, e is the elementary charge, z is the effective charge of a phosphate on the polynucleotide backbone after taking into account the effects of counterions, n is the number of phosphates resident in the vestibule during the transition state for escape, δ is the fractional voltage drop in the vestibule, V is the applied voltage, k is the Boltzmann constant, and T is the temperature. The values g₃ and g₅ are the voltage-independent rate constants for threading of a polymer-end through the neck of the pore. This model is a simplified implementation of the Woodhull formalism (43). A similar approach has previously been used to describe the kinetics of polypeptides in the αHL pore (44). To simplify our notation we define a characteristic escape voltage V_E ≡ [eznδ/kT]⁻¹. This leads to the following expressions for the exponential time constants and the overall escape probability:

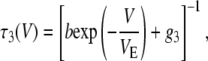(4)

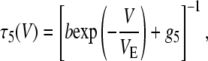(5)

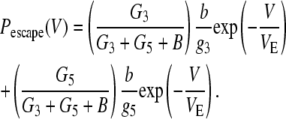(6)

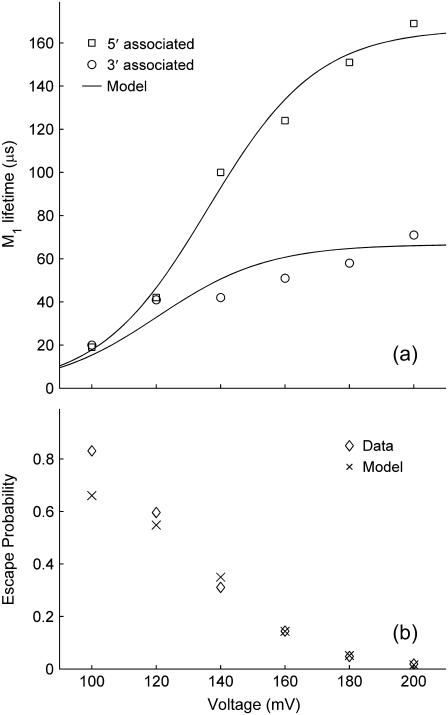
G₃ and G₅ are the observed numbers of 3′- and 5′-associated M₁ signals, and B is the total number of observed M₀ signals. The parameter values g₃ = 0.016 μs⁻¹, g₅ = 0.006 μs⁻¹, b = 18 μs⁻¹, and V_E = 17 mV give reasonable agreement between this model and our data (Fig. 9). These values were found by minimization of the total sum-squared deviation between the data in Fig. 9 and model of Eqs. 4–6. Weighting factors were set such that the contributions to the total sum-squared deviation were approximately equal for the three curves.

FIGURE 9.

Voltage-dependent dA₅₀ data compared to a kinetic model with voltage-dependent rate constants (Eqs. 4–6). M₁ lifetimes at each voltage were derived from exponential fits to the 3′ and 5′ associated M₁ duration distributions. The escape probability data in the bottom panel (⋄) is the same as the dA₅₀ escape probability data shown in Fig. 7 c, while the model values (×) were derived from Eq. 6. The model for the escape probability cannot be shown as a continuous curve because it requires experimental data (the observed numbers of 3′- and 5′-associated M₁ signals). The model curves and values were generated with the parameters g₃ = 0.015 μs⁻¹, g₅ = 0.006 μs⁻¹, b = 18 μs⁻¹, and V_E =17 mV in Eqs. 4–6.

Introducing voltage dependence into the threading rate constants as γ = gexp(V/V_Th) required very weak voltage dependence (V_Th > 1000 mV) to give a reasonable description of our data. We found that a variety of other five-parameter models were also able to give reasonable descriptions of our data, but none did appreciably better than the four-parameter model of Eqs. 1–3. We also explored additional four-parameter models, one where the orientation dependence arose from differing voltage-independent factors in the escape rate constants (β₃ = b₃exp(−V/V_E), β₅ = b₅exp(−V/V_E), and γ₃ = γ₅ = g), and another where the orientation dependence arose from differing 3′- and 5′-associated escape voltages (β₃ = bexp(−V/V_E3), β₅ = bexp(−V/V_E5), and γ₃ = γ₅ = g). Neither of these four-parameter models gave acceptable descriptions of our data.

Interpretation of vestibule configuration model

The model specified by Eqs. 1–3 strongly supports the assertion that over the range V ∼ 100–200 mV, the escape process is much more sensitive to voltage than the threading process. The relatively weak voltage dependence of threading may be related to a small voltage gradient within the vestibule (36) and the lack of negatively charged terminal phosphate groups at both the 3′ and 5′ ends of our synthetic polymers. The arrival of a polymer end at the neck may therefore be a diffusive process which is little biased by the applied voltage. Furthermore, insertion of the uncharged sugar/base portion of the terminal nucleotide far enough into the pore neck to allow the charged phosphate to experience the high electric field could also be a relatively voltage-insensitive step in the threading process. Another aspect of the vestibule configuration suggested by our model is that the orientation dependence of the vestibule configuration lifetime (Fig. 8) can be primarily attributed to different rate constants for 3′ vs. 5′ threading. Specifically, 3′ threading is easier than 5′ threading. This finding is consistent with the results of Mathe et al. (28), where experiments showed that poly-dA segments passed more rapidly through the αHL inner constriction when they moved in the 3′→5′ direction as compared to the 5′→3′ direction. In the same report, molecular dynamics simulations of a polydA molecule threaded through the αHL pore also found that 3′→5′ passage was faster than 5′→3′ passage. These simulations revealed a microscopic mechanism for the orientation asymmetry. When the polymer was confined in a tube with diameter <1.5 nm, the DNA bases tilted toward the 5′ end of the polymer. Because initial threading of a polymer and passage of a threaded polymer through the neck are very similar processes, we expect that the confinement-induced tilt is what makes 3′ threading easier than 5′ threading. Because the pore entrance that connects the vestibule to the cis compartment is ∼2.5 nm in diameter, we do not expect an asymmetric tilting of the bases to be important to the escape process. Our finding that the voltage-independent factor in the escape rate constant (b in Eq. 1) need not depend on orientation is consistent with this expectation. The orientation independence of escape also suggests that z, n, and δ in Eq. 1, the microscopic factors that determine the voltage sensitivity of escape, do not depend strongly on polymer orientation. Finally, we note that assumptions z = 0.3, n = 20, and δ = 0.2 lead to the estimate V_E = 20 mV, indicating that our crude experimental value of 17 mV is physically plausible. The kinetic model we have presented is quite simple, but it gives a very reasonable description of our data and it suggests a number of interesting properties of the behavior of a polynucleotide molecule when it is confined in the αHL vestibule.

CONCLUSIONS

We presented an analysis of the current blockades produced by single-stranded polynucleotide molecules in the αHL pore that takes into account their substate structure. We modeled the structure of each blockade as a sequence of Mid (current at ∼50% of unobstructed level) and Deep (current <∼30% of unobstructed level) conductance states. There appear to be two distinct configurations of the polymer in the pore that cause a Mid state. Our data are consistent with the interpretation that the most common Mid state occurs at the beginning of the polymer/pore interaction, when part of a polymer enters the αHL vestibule from the cis compartment. The ionic current remains in the Mid state until the polymer either 1), escapes back into the cis compartment, causing a return to the Open state current; or 2), threads through the inner constriction of the pore and blocks the current at the Deep state. For some polymers, up to ∼80% of the observed current blockade events demonstrated resolvable signals indicative of a polymer in the vestibule configuration. Occasionally we observed Mid states that followed Deep states and demonstrated a different amount of residual current than the vestibule-associated Mid states. We attribute these Mid states to a configuration where the trailing end of the polymer occupies part of the β-barrel region of the pore, but is no longer threaded through the pore's inner constriction. These β-barrel signals were much less frequent than the vestibule-associated signals, occurring in between 3% and 8% of the blockade events for three of the polymers we investigated (rA₅₀, rU₅₀, and dT₅₀), and almost never occurring for the other three polymers (dA₅₀, dC₅₀, and rC₅₀). We observed clear statistical differences in the Mid state characteristics of different polymers, indicating that Mid state analysis could enhance the capability of αHL as a single-molecule analytical device. Simulation studies of these polymer-specific differences could provide much needed insight into their molecular origins, and accurate prediction of these differences would provide very strong validation of the simulation methodology.

We focused particular attention on the signals indicative of the vestibule configuration because they are a very prominent but little studied component of the current blockades produced by polynucleotide molecules in the αHL pore. To gain insight into the general physics of the vestibule configuration, we analyzed vestibule configuration data at a variety of voltages between 100 and 200 mV. We observed a clear decrease in the normalized current with increasing voltage. This may be the result of crowding as more bases are pulled into in the vestibule at higher voltages. We also found that the characteristic duration of the vestibule configuration increased with increasing voltage while the probability of polymer-escape from the vestibule back into the electrically negative volume decreased. A simple kinetic picture where the rate constant for escape decreases strongly with voltage while the rate constant for threading has much weaker voltage dependence qualitatively explains these trends. This simple picture was slightly complicated by the observation that the duration of the vestibule configuration depended on which end of the polymer, 3′ or 5′, subsequently threaded into the inner constriction. We found that a kinetic model with the following characteristics gave a very nice description of our orientation and voltage-dependent dA₅₀ data: 1), the escape rate constant decreases exponentially with voltage but does not depend on orientation; and 2), 3′- and 5′-threading have different rate constants that do not depend on the applied voltage. From this semiquantitative analysis we conclude that, for our unphosphorylated ssDNA and RNA 50-mers, threading has much weaker voltage dependence than escape, threading is sensitive to polymer orientation, and escape is insensitive to polymer orientation. The intricate molecular details revealed by this analysis make an important contribution to the overall understanding of the interaction between single-stranded polynucleotide molecules and the αHL pore. Further, the vestibule configuration represents an additional aspect of the αHL system that can be used to study the physical characteristics of nucleic acids. While our data support the conclusion that there are two distinct vestibule configurations, one for each orientation of the polymer, we are presently unable to make any more detailed inferences into the arrangement of the polymer in the vestibule. Experiments with polymers of various lengths will likely give insight into this question, possibly allowing identification of a characteristic polymer length below which the entire polymer is drawn into the vestibule and above which part of the polymer remains in the cis compartment. This information may give new insight into the flexibility and packaging properties of single-stranded polynucleotide molecules on nanometer length scales.