Abstract
Cardiac hypertrophy is a known risk factor for heart disease, and at the cellular level is caused by a complex interaction of signal transduction pathways. The IP3-calcineurin pathway plays an important role in stimulating the transcription factor NFAT which binds to DNA cooperatively with other hypertrophic transcription factors. Using available kinetic data, we construct a mathematical model of the IP3 signal production system after stimulation by a hypertrophic α-adrenergic agonist (endothelin-1) in the mouse atrial cardiac myocyte. We use a global sensitivity analysis to identify key controlling parameters with respect to the resultant IP3 transient, including the phosphorylation of cell-membrane receptors, the ligand strength and binding kinetics to precoupled (with GαGDP) receptor, and the kinetics associated with precoupling the receptors. We show that the kinetics associated with the receptor system contribute to the behavior of the system to a great extent, with precoupled receptors driving the response to extracellular ligand. Finally, by reparameterizing for a second hypertrophic α-adrenergic agonist, angiotensin-II, we show that differences in key receptor kinetic and membrane density parameters are sufficient to explain different observed IP3 transients in essentially the same pathway.
INTRODUCTION
Pathological cardiac hypertrophy has been identified as a major risk factor leading to heart failure (1). An understanding of the biological pathways involved in cardiac hypertrophy may yield benefits in understanding the progression of, and the development of therapies for, cardiac disease.
A range of signal transduction pathways are implicated in hypertrophy, including the inositol 1,4,5-trisphosphate (IP3)-calcineurin pathway, the mitogen-activated protein kinase p42/p44, mitogen-activated protein kinase p38, jun N-terminal kinase, and the phosphoinositide 3-kinase-wingless-related mouse mammary tumor virus integration (PI3K-Wnt) pathways (2–10). In vivo, none has a monopoly on hypertrophic effects and many pathways interact (3), the details of which have yet to be fully elucidated experimentally.
The role of the IP3-calcineurin pathway in cardiac hypertrophy was discovered during the 1990s and, despite some initial controversy, calcineurin's role has now been accepted. Extracellular agonists stimulate Gq-family G-protein-coupled receptors (GPCRs). On stimulation, the G-protein α-subunit activates phospholipase C (PLC) (11,12), and causes hydrolysis of membrane-bound phosphatidyl inositol-4,5-bisphosphate (PIP2). This forms the secondary messenger IP3. IP3 production causes an increase in the intracellular calcium concentration ([Ca2+]i), which in turn activates the phosphatase calcineurin. Calcineurin activation leads to changes in gene expression by facilitating translocation to the nucleus of cytosolic transcription factors of the nuclear factor of activated T cells (NFAT) family. There such factors bind to nuclear DNA cooperatively with transcription factors from the other hypertrophic pathways to facilitate transcription (13). NFAT's ability to act as a signal integrator for hypertrophy (14) in this manner is a key reason that the IP3-calcineurin pathway is significant.
These findings have motivated the use of existing immunosuppressive calcineurin inhibitors (such as Cyclosporin A and FK506) as experimental attenuators of hypertrophy. The results of that approach have been conflicting, with similar rodent models exhibiting no effect, attenuation, or even complete prevention of hypertrophy, and occasionally lethal side-effects from the immunosuppressors (15). Thus, a more detailed understanding of the pathways for hypertrophy is necessary for the development of practical therapeutic treatments.
The biological processes of the IP3 production system represent only a tiny proportion of the activities within a cell, yet even these are complex with many players and diverse interactions. For such systems a computational model is a useful tool (16), bringing together quantitative and qualitative data to allow interactive exploration of our understanding. Currently no mathematical model for the IP3-calcineurin pathway exists in the cardiac myocyte.
This work focuses on modeling the signal transduction pathway from extracellular agonist to the production of IP3 by the extracellular agonists endothelin-1 (17) (ET-1) and angiotensin-II (18) (Ang-2). The responses of IP3 to the two agonists are different, despite the signal transduction pathway being almost identical. We construct the first mathematical model of the IP3 production and degradation signal transduction system in the mouse atrial cardiac myocyte, as stimulated by the hypertrophic agonist ET-1. Sensitivity analysis was undertaken to determine which parameters are significant in determining features of the IP3 transient. We investigate possible causes of the different IP3 response from stimulation with Ang-2, and show that the differences in system behavior are explainable in terms of receptor kinetics.
METHODS
We constructed a mathematical model of the IP3 production system as stimulated by the α-adrenergic agonist ET-1 in the atrial cardiac myocyte. Since experimental processes are often time consuming and costly, it is important to assess from current knowledge what the most influential parameters are that determine properties of the system. We applied a global sensitivity analysis (the Morris Method) to determine the important parameters of the system by their influence on five characteristics of stimulated IP3 transients.
Using the ET-1 model as a baseline, we then refined the model to stimulation with the alternative agonist Ang-2. Ang-2 is a hormone produced via the angiotensin-renin system, and also produced locally on stretch of the cardiomyocyte (18,19). Ang-2 signals are received by two main isoforms of the Ang-2 receptor-Type 1 (AT-1) and Type 2 (AT-2). Cells from different animals contain different proportions of each although the proportion is approximately equal in rodents such as the rat (20). There is evidence linking AT-1 receptors to PLCβ, IP3 production, and calcium release via Gq family GPCRs (21–23). Transients resulting from stimulation with Ang-2 are much shorter-lived than those from ET-1, despite the fact that the same pathway is activated in both cases. We sought to determine whether the different transient behavior between the two agonists can be explained in our model by altering key parameters of the receptor alone. We found that the necessary changes to the model could be both motivated and understood by considering the results of the previously completed sensitivity analysis.
Model construction
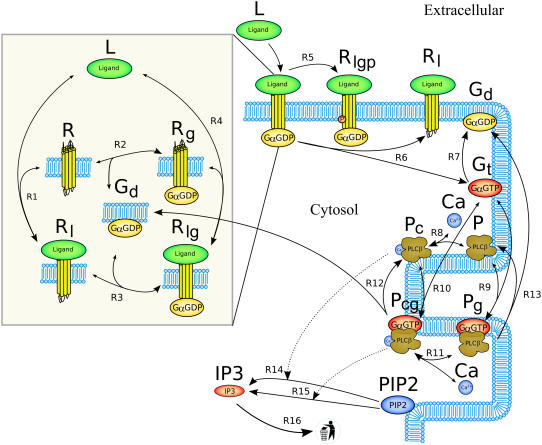
We developed a mathematical model of the significant biological processes relating to the transduction of extracellular ligand signals through Gq family receptors and subsequent IP3 production in the mouse atrial cardiac myocyte. A reaction scheme of the model is shown in Fig. 1. The model encompasses the extracellular ligand (L), the GPCRs (R), activation of phospholipase Cβ (P) by GαGTP (Gt) subunits, and both the basal and stimulated hydrolysis of PIP2 to form IP3. Conceptually, the model can be divided into three modules:
GPCR cycling, dealing with ligand, receptors, and diffusible Gα messengers.
PLCβ cycling, dealing with the activation of PLCβ.
IP3 production and degradation, concerned with the hydrolysis of IP3 from PIP2, and the background consumption of IP3.
The mathematical model was formulated using mass action kinetics, and implemented as a system of ordinary differential equations. For convenience, the model was encoded into the computer-readable protocol Cellular modeling Markup Language (CellML) (24). A complete list of the model equations, and a list of model parameters and initial conditions are provided in Tables 3 and 4, respectively. This signal transduction pathway involves interactions between membrane-bound and freely diffusing cytosolic species. Cytosolic species are represented by concentration (in μM) while membrane-bound species are given as area densities (number per unit of membrane area, in μm−2). The model is also available as CellML code in the online CellML Repository (http://www.cellml.org/models).
FIGURE 1.
Reaction scheme of the IP3 production system. The extracellular ligand (L) binds to receptors (R), whether precoupled with GαGDP (Gd, yielding Rlg) or not (Rl). Fully activated receptors (Rlg) release GαGTP (Gt), which, along with calcium (Ca), stimulates PLCβ (P). In the unstimulated state, PLCβ-Ca2+ (Pc) hydrolyzes PIP2 to produce IP3 via reaction R14. When stimulated, PLCβ-Ca2+-GαGTP (Pcg) hydrolyses PIP2 at a faster rate via reaction R15. Free IP3 is degraded via reaction R16.
TABLE 3.
IP3 model equations
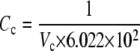 |
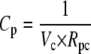 |
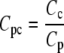 |
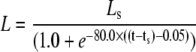 if if 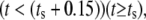 Ls; if Ls; if 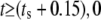 otherwise. otherwise. |
| kr,1=kf,1 × Kd,1 |
| J1=kf,1 × R × L − kr,1 × Rl |
| kr,2=kf,2 × Kd,2 |
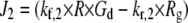 |
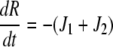 |
| J3 = kf,3 × Rl × Gd − kr,3 × Rlg |
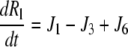 |
| kr,4 = kf,4 × Kd,4 |
| J4 = kf,4 × L × Rg − kr,4 × Rlg |
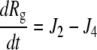 |
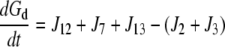 |
| J5=kf,5 × Rlg |
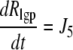 |
| J6=kf,6 × Rlg |
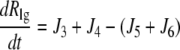 |
| J7=kf,7 × Gt |
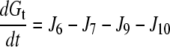 |
| J9=kf, 9 × P × Gt − kr,9 × Pg |
| J8=kf, 8 × P × Ca − kr,8 × Pc |
| J10=kf,10 × Pc × Gt − kr,10 × Pcg |
| kr,11=kf,11 × Kd,11 |
| J11=kf,11 × Pg × Ca − kr,11 × Pcg |
| J12=kf,12 × Pcg |
| J13=kf,13 × Pg |
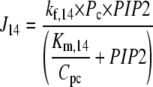 |
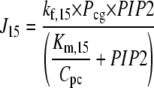 |
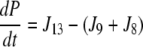 |
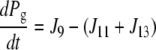 |
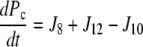 |
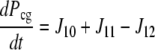 |
| J16=kf,16 × IP3 |
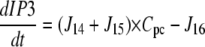 |
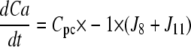 |
TABLE 4.
Model parameters and initial conditions
| Symbol parameters | Description | Units | Value | Source |
|---|---|---|---|---|
| kf,1 | R1 forward rate constant | μM−1 s−1 | 3.00 × 10−4 | (fitted value)* |
| Kd,1 | R1 dissociation constant | μM | 3.00 × 10−5 | Bers (28) |
| kf,2 | R2 forward rate constant | μm2 s−1 | 2.75 × 10−4 | Lukas (25) |
| Kd,2 | R2 dissociation constant | μm−2 | 27,500 | Lukas (25) |
| kf,3 | R3 forward rate constant | μm2 s−1 | 1.00 | Lukas (25) |
| kr,3 | R3 reverse rate constant | s−1 | 1.00 × 10−3 | Lukas (25) |
| kf,4 | R4 forward rate constant | μM−1 s−1 | 3.00 × 10−1 | (fitted value)† |
| Kd,4 | R4 dissociation constant | μM | 3.00 × 10−5 | Bers (28) |
| kf,5 | R5 forward rate constant | s−1 | 4.00 × 10−4 | (fitted value)‡ |
| kf,6 | R6 forward rate constant | s−1 | 1.00 | Lukas (25) |
| kf,7 | R7 forward rate constant | s−1 | 1.50 × 10−1 | Lukas (25) |
| kf,8 | R8 forward rate constant | μM−1 s−1 | 1.67 × 10−2 | Lukas (25) |
| kr,8 | R8 reverse rate constant | s−1 | 1.67 × 10−2 | Lukas (25) |
| kf,9 | R9 forward rate constant | μm2 s−1 | 4.20 × 10−3 | Lukas (25) |
| kr,9 | R9 reverse rate constant | s−1 | 1.00 | Lukas (25) |
| kf,10 | R10 forward rate constant | μm2 s−1 | 4.20 × 10−2 | Lukas (25) |
| kr,10 | R10 reverse rate constant | s−1 | 1.00 | Lukas (25) |
| kf,11 | R11 forward rate constant | μM−1 s−1 | 3.34 × 10−2 | See discussion under PLCβ Cycling |
| Kd,11 | R11 dissociation rate constant | μM | 1.00 × 10−1 | Lukas (25) |
| kf,12 | R12 forward rate constant | s−1 | 6.00 | Lukas (25) |
| kf,13 | R13 forward rate constant | s−1 | 6.00 | See discussion under PLCβ Cycling |
| kf,14 | R14 forward rate constant | s−1 | 4.44 × 10−1 | See discussion under IP3 Production and Degradation |
| Km,14 | R14 Km value | μM | 19.8 | Bhalla and Iyengar (49) |
| kf,15 | R15 forward rate constant | s−1 | 3.80 | (fitted value)§ |
| Km,15 | R15 Km value | μM | 5.00 | Bhalla and Iyengar (49) |
| kf,16 | R16 forward rate constant | s−1 | 1.25 | DOQCS1 database (50) |
| Ls | Ligand stimulation concentration | μM | varies | User-defined |
| PIP2 | PIP2 density | μm−2 | 4000 | Xu et al. (51) |
| ts | Time of stimulation | s | varies | User-defined |
| Vc | Cytosolic volume | μm3 | 2549.3 | Leri et al. (52), Bers (28) |
| Initial conditions | ||||
| Ca | Cytosolic Ca2+ concentration | μM | 1.00 × 10−1 | Bers (28) (steady state) |
| Gd | GαGDP density | μm−2 | 10,000 | Lukas (25) (steady state) |
| Gt | GαGTP density | μm−2 | 0.00 | (unstimulated) |
| IP3 | IP3 concentration | μM | 0.015 | See discussion under IP3 Production and Degradation |
| L | Ligand concentration (extracellular) | μM | 0.00 | (unstimulated) |
| P | PLCβ density | μm−2 | 90.9 | Lukas (25) (steady state) |
| Pc | PLCβ-Ca2+ density | μm−2 | 9.09 | Lukas (25) (steady state) |
| Pg | PLCβ-GαGTP density | μm−2 | 0.00 | (unstimulated) |
| Pcg | PLCβ-Ca2+-GαGTP density | μm−2 | 0.00 | (unstimulated) |
| R | Noncoupled receptor density | μm−2 | 13.9 | Kobayashi (53) (steady state) |
| Rg | Precoupled receptor density | μm−2 | 5.06 | Kobayashi (53) (steady state) |
| Rl | Ligand-bound receptor density | μm−2 | 0.00 | (unstimulated) |
| Rlg | Active receptor density | μm−2 | 0.00 | (unstimulated) |
| Rlgp | Phosphorylated receptor density | μm−2 | 0.00 | (unstimulated) |
| Rpc | Plasma membrane/cytosolic volume ratio | μm−1 | 4.61 | Bers (28) |
GPCR cycling
Extracellular ligand (L) binds to cell-surface receptors (R), shown by reversible reactions R1 and R4 in Fig. 1. For Gq family receptors, this binding causes a conformational change which replaces GDP with a GTP on an at-tached G-protein's α-subunit. This causes the Gα subunit to dissociate (reaction R6) and stimulate other proteins inside the cell. For a receptor to transduce the ligand signal across the membrane, it requires both an attached G-protein and a ligand-binding event. The model utilizes the receptor components from a nonexcitable cell model of Lukas (25) that uses the precoupled-receptor concept (26): should the Gα subunit bind first (as shown in reaction R2), then the receptor is known as precoupled (Rg), and exhibits a higher affinity for the ligand than if Gα had bound after the ligand (via reaction R3). Only the state where both ligand and Gα subunit are bound is considered an activated receptor (Rlg). Active receptors are targeted for phosphorylation and eventual invagination and recycling by the cellular machinery. Once phosphorylated, the receptor is no longer available for further signal transduction. For the purposes of the model, this is abstracted into a one-time phosphorylation step (reaction R5).
The model is designed to simulate experiments where the cell is initially unstimulated. At a predetermined stimulation timepoint (ts), ligand is added, which is represented by a (smoothed) Heaviside step function to the desired stimulation concentration (Ls). The amount of ligand bound to receptors is assumed negligible compared to the total amount of ligand available, hence the concentration of free ligand in the model does not decrease as ligand binds to the receptors.
All reactions were modeled as kinetic fluxes following the Law of Mass Action. For example, the flux (J1) for reaction R1
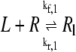 |
is given by the flux expression
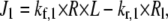 |
where R is the receptor area density in μm−2, L is the extracellular ligand concentration in μM, Rl is the density of receptors with ligand bound in μm−2, and kf,1 and kr,1 are rate constants measured in μM−1 s−1 and s−1, respectively. J1 is therefore a flux measured in μm2 s−1.
Endothelins bind to their receptors with high enough affinity for the reaction to be considered irreversible under physiological conditions (27), hence it seems likely that when the active Gα subunit dissociates during reaction R6, the ligand and receptor complex (Rl) remains together.
PLCβ cycling
The active GαGTP messenger (Gt) released from stimulated receptors binds to the enzyme PLCβ (P), shown in Fig. 1 as the reversible reactions R9 and R10. This binding can be considered independently from the binding of the costimulatory calcium ions (Ca) shown in reversible reactions R8 and R11. Free GαGTP degrades to GαGDP via a self-GTPase activity of the α-subunit, removing its ability to stimulate PLCβ, represented as reaction R7. This activity in PLCβ-bound GαGTP and dissociation from PLCβ is assumed for modeling purposes to occur in the same step and is shown by reactions R12 and R13 depending on whether Ca2+ is also bound or not. When bound to PLCβ, this step is assumed to occur at the same rate, irrespective of the additional presence or absence of bound calcium (from Pcg or Pg, respectively).
The formulation of the reactions R7-R13 follows the same form described in GPCR cycling above, although for some reactions an additional conversion factor is required: Ca2+ is a cytosolic species, measured in μM whereas the membrane-associated fluxes such as J1 above are membrane density fluxes (μm−2 s−1). To convert to concentration fluxes, it is convenient to define a conversion factor
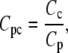 |
(1) |
where Cc is a conversion factor from a number of particles to a cytosolic concentration (μM), and Cp is a conversion factor from a number of particles to a density on the cell's plasma membrane (μm−2). Together they give a conversion factor that can be applied to the appropriate density fluxes to give the corresponding concentration fluxes for cytosolic products, or vice versa.
A number of parameters were taken from the existing model by Lukas (25), where appropriate. For the binding of Ca2+ to PLCβ-GαGTP (Ca binding to Pg in reaction R11) only the dissociation constant (Kd,11) was known. We have made the assumption that the forward rate constant for reaction R11 is twice that of the similar reaction R8, due to the binding of GαGTP. From this assumption the reverse rate constant for reaction R11 was calculated.
The resting level of calcium in the cardiac myocyte was assumed to be 100 nM (28).
IP3 production and degradation
The species PLCβ-Ca2+ (Pc) and PLCβ-Ca2+-GαGTP (Pcg) act as hydrolyzers, converting the substrate PIP2 to IP3, shown by reactions R14 and R15 in Fig. 1, respectively. These catalytic reactions were modeled using Michaelis-Menten kinetics according to the quasi-steady-state approximation, their equations therefore being of the form (J14 is shown as an example)
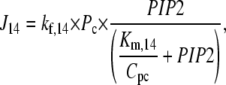 |
where the Km of the reaction is scaled by the conversion factor Cpc (see Eq. 1).
IP3 binds to IP3 receptors (IP3Rs) in the cell, which are also regulated by calcium. It was assumed that the amounts of both IP3 and calcium bound are negligible compared to their cytosolic concentrations, and therefore IP3Rs do not effect the concentrations of those small species. IP3R activation causes a minor cytosolic calcium spike from intracellular stores, followed by a much larger sustained calcium influx from outside the cell—this latter phenomenon being known as capacitative calcium entry (29). In the protocol of interest to this work, the extracellular entry does not occur, and the minor initial spike is assumed to have little effect on the model calcium. The IP3Rs, having no effect on the rest of the model, are therefore not included in this formulation.
The hydrolysis of PIP2 also produces the membrane-bound diacylglycerol species, but that is not considered in this model.
PIP2 is manufactured by the cell, and resupplied after use to the plasma membrane via the breakdown of inositol phosphates (30). Since there is no evidence that the level of PIP2 is rate-limiting (31), in the model PIP2 is fixed at its initial value.
A degradation reaction (R16) encompasses the dephosphorylation or phosphorylation of IP3 to form inositol bisphosphate and inositol tetraphosphate, respectively. For the purposes of this model, the metabolic recycling of IP3 from those products is not considered. The basal level of IP3 is therefore a balance between the basal production and the degradation rates (reactions R14 and R16, respectively).
A published report (32) of a ∼30 nM peak in IP3 on stimulation by 100 nM of ET-1, together with estimates of the peak-to-basal ratio of ∼2:1 (33,34), suggest that the basal concentration of IP3 in the mammalian myocyte is ∼15 nM. This is the estimate used in this model. The kinetics of the basal IP3 production reaction (via kf,14) were adjusted to provide this value. The balancing degradation rate was known with more confidence and kept as in the literature (25).
Morris analysis
The model was refined to simulate the response to ET-1 stimulation (see Results for a comparison of model behavior to experimental data). We then sought to determine which parameters controlled the IP3 transient produced by the system by undertaking a global sensitivity analysis following the Morris method (35). The Morris method is a screening algorithm: it ranks the parameters of the model, by their average effect on a particular model simulation output, over a given range of parameter values. The global nature of the analysis is applicable given the system's high nonlinearity (36) and the method has been shown to be as efficient as commonly-used variance based techniques in detecting factors of low sensitivity. It is also computationally cheaper than such techniques (37) as the required number of model evaluations varies linearly with the number of model factors.
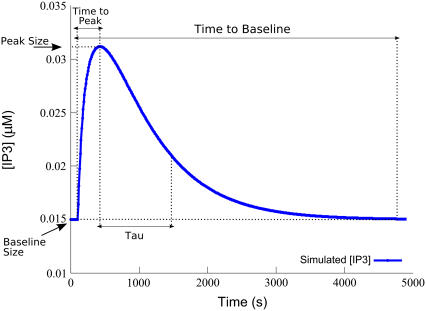
The method yields a score for each parameter of the model estimating the partial differential of an objective function with respect to that parameter. We chose five objective functions to analyze the model by, to capture the behavior of the resulting IP3 transient (these measures are illustrated graphically on a representative IP3 transient in Fig. 4):
Baseline Concentration. The basal concentration of IP3 established at steady state before stimulation.
Time-to-Peak. Time in seconds from the stimulation time to the peak IP3 concentration.
Peak Concentration. The maximum concentration of IP3 during the transient.
Tau-to-Tail Ratio. The ratio of the time after the peak at which the tail of the transient dips below 1/e of its peak amplitude, to the length of the tail (from the peak to the return to baseline as in the next objective function). Flatter transients have a higher Tau-to-Tail Ratio, closer to 1.0.
Time-to-Baseline. The time in seconds, since stimulation, for the return to baseline concentration. Since returning transients can approach the baseline asymptotically, we measured returning to baseline as occurring when the amplitude of the transient had dropped below 10% after the peak.
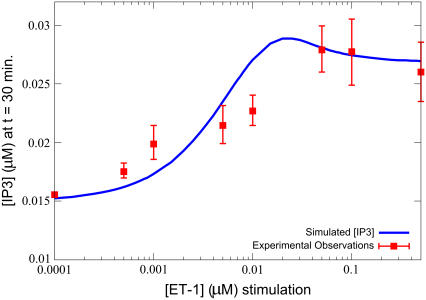
FIGURE 4.
IP3 dose-response curve on ET-1 stimulation. The model also closely matches experimental observations (40) for the concentration of IP3, after 30 min, on stimulation by various concentrations of ET-1. Simulations were performed with the equations as in Table 3 and the parameters and initial conditions as in Table 4. Additionally, ts = 100 s, and the model was run until (t − ts) = 1800 s (30 min of stimulation) for each of Ls = 1 × 10−4, 5 × 10−4, 1 × 10−3, 5 × 10−3, 1 × 10−2, 5 × 102, 1 × 10−1, and 5 × 10−1 μM.
To determine the sensitivity of these measures to the model parameters, we define for each parameter a range of values over which it can vary. These may vary widely, whether by virtue of the very different quantities which they represent, or simply by different physiological constraints. The amount of variation of a parameter inside a particular range is normalized to a fraction of that range, designated δ. The parameter ranges defined for our analysis are listed in Table S1 in the Supplementary Material. Parameter ranges were normalized and parameters allowed to take one of 16 equally spaced values (Morris parameter p = 16). For each parameter, changes in each of the objective functions were measured for a δ change over the range defined, where δ is (38)
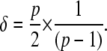 |
This yields a sliding window of 53.3% of each parameter's range. Parameters therefore begin each of a series of analysis trajectories at one of 16 values within their defined range, and at each step of each trajectory, one parameter is varied by 53.3% of that range, and the subsequent effect on each the objective functions are measured.
Parameter change effects are divided by δ, to give an estimate for the parameter's effect on each objective measure, over the parameter's entire defined range. We ran two sets of 8000 trajectories as described by Morris (35) for each parameter over the five objective functions (Morris parameter r = 8000), as we found this gave repeatable clustering and ordering (unless parameters were very similar in significance) results between the two sets.
For each test, the model was run to achieve steady state before agonist stimulus was applied. Up to a further 130,000 s was simulated (∼36 h) to allow IP3 to peak and resume the baseline level again for all parameter sets tested.
We then combined both sets of tests to give an overall population for each parameter of 16,000 sensitivity measures, and used the Campolongo extension (38) of the method to calculate the mean absolute effect (μ*) as a direction-independent measure of sensitivity of the defined normalized ranges.
Tables S2–S6 in the Supplementary Material show the parameters ranked by their effects thus calculated, for each of the five objective functions.
Angiotensin-II refinement
We sought to determine whether the different IP3 transient produced by Ang-2 (as opposed to ET-1) stimulation could be explained by receptor-related parameters alone. A number of model parameters were therefore adjusted to match known published kinetics for the Ang-2 receptors. It is known that the rodent Ang-2 receptor has a larger dissociation constant than the ET-1 receptor: ∼1.5 nM in rat and ferret, and that the receptor density is much lower than that for ET-1, being approximately one-fifth (see Table 25 in (28)). These literature-motivated parameter changes alone were not sufficient to explain the differences in the resulting IP3 transient. We therefore investigated the most significant remaining receptor-related parameters.
We used the results of the sensitivity analysis to identify the 10 most significant parameters with respect to the IP3 transient (see Table 1). Two of these (kf,4 and kf,5) relate to kinetics associated with the receptors themselves, and hence are likely to be different between ET-1 and Ang-2 receptors.
TABLE 1.
Ten most significant model parameters
| Rank | Parameter | Meaning |
|---|---|---|
| 1 | kf,5 | Rate constant for the phosphorylation of active receptor. |
| 2 | Ls | Full-strength ligand concentration during stimulation. |
| 3 | kf,4 | Rate constant for the binding of ligand to precoupled receptor. |
| 4 | kf,16 | Rate constant for the degradation of IP3. |
| 5 | Rpc | Ratio of plasma membrane surface area to cytosolic volume. |
| 6 | Gd | Area density of free inactive G-protein. |
| 7 | Kd,2 | Dissociation constant for the precoupling of receptor. |
| 8 | kf,14 | Rate constant for the nonstimulated IP3 production reaction. |
| 9 | kf,8 | Forward rate constant for the binding of calcium to PLCβ. |
| 10 | kr,8 | Reverse rate constant for the binding of calcium to PLCβ. |
Experimental research by Abdellatif et al. (39) measured accumulation of IP3 in cultured rat neonatal ventricular cardiac myocytes on stimulation of 100 μM Ang-2, using ion-exchange chromatography. During fitting to this data, we determined predicted new values for those significant receptor parameters using the Levenburg-Marquardt algorithm (implemented as the “levmar” nonlinear least-squares fitting package obtained from http://www.ics.forth.gr/∼lourakis/levmar). Multiple runs were conducted in an attempt to evade local minima, and a close fit with the experimental data was obtained. Varying additional parameters did not significantly increase the goodness-of-fit.
RESULTS
IP3 transients in response to ET-1 stimulation
Model parameters were refined to the mouse atrial myocyte by fitting the IP3 transient resulting from stimulation at various ET-1 strengths to experimental data from Jiang et al. (40). Based on the available data, we performed the fit based on IP3 transient observations. To our knowledge data on the ET-1 stimulated responses of proteins upstream of IP3 do not currently exist. Model parameters were adjusted until the output from the model closely matched the experimental observations, to match the mouse atrial myocyte on stimulation by the specific extracellular ligand ET-1.
To achieve the fit, several parameters' values had to be changed from those derived from other sources. These changes are presented in Table 4.
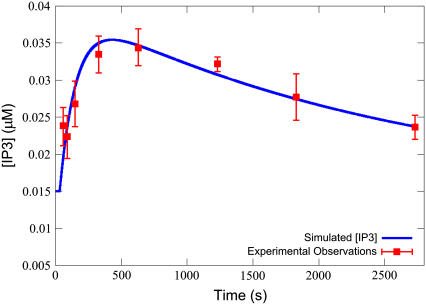
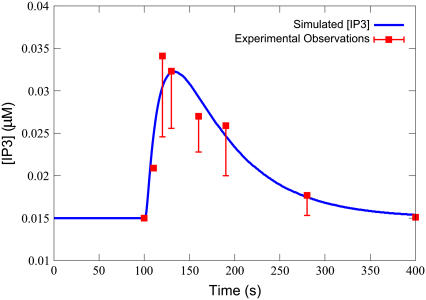
A comparison of an IP3 transient from the model with experimentally determined IP3 time-course data from Jiang et al. on 100 μM of ET-1 stimulation is shown in Fig. 2. Simulation results were generated from the model defined in Table 3, with the parameters defined in Table 4, and Ls = 0.100 μM, ts = 30.0 s, to match the experimental protocol. The numerical solver used was an implicit Runge-Kutta method based on Radau quadrature, as described by Hairer and Wanner (41). Absolute and relative error tolerances were set at 10−9. As can be seen, the model behavior closely matches experimental results.
FIGURE 2.
IP3 transient-based objective measures. Graphical depiction of the measures used to define the objective functions for the sensitivity analysis. Tau is the time point at which the transient dips beneath 1/e × amplitude.
A further comparison with IP3 transient data is shown in Fig. 3. Jiang et al. measured the IP3 concentration in cells 30 min after stimulation with various concentrations of ligand. To simulate this, the model's ligand stimulation strength (Ls) was varied at regular intervals from 1 × 10−4 μM to 1.0 μM, and the concentration of IP3 measured 1800 s (30 min) after ligand addition. Figs. 2 and 3 demonstrate that appropriate IP3 transient behavior is produced by the model.
FIGURE 3.
IP3 transient curve on ET-1 stimulation. The simulated IP3 transient closely matches experimental observations (40) on application of 100 nM ET-1. Simulations were performed with the equations as in Table 3 and the parameters and initial conditions as in Table 4. Additionally, ts = 30 s, and Ls = 0.100 μM.
Key drivers of the IP3 transient
The most significant parameters in terms of impact on the IP3 transient are listed in Table 1. Parameters were sorted by summing their proportional significance for each objective measure. A complete list of all model parameters and their significance scores can be found in Table S7 in the Supplementary Material.
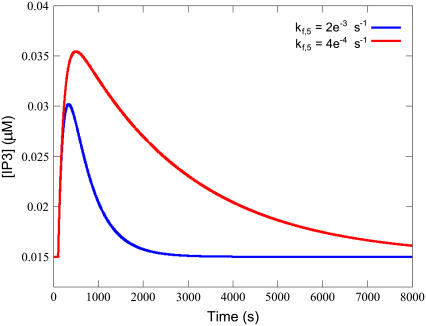
The single most important parameter is the receptor phosphorylation rate constant (kf,5). The quantity kf,5 governs the reaction that terminates the signal by reducing the total available receptor density, and thus reducing the possibility of sarcolemmal signal transduction in response to extracellular hormonal stimulation. It is of critical importance for setting the Time-to-Baseline, as without a phosphorylation step the system would simply equilibrate based on the stimulation concentration of ligand and the transient would be constant. Decreasing the phosphorylation rate via the kf,5 parameter increases the tail as shown in Fig. 5. As can also be seen in that figure, a higher kf,5 reduces the Time-to-Peak. While lowering kf,5 increases the length of the transient's tail it also increases Tau. This is to be expected, however the increase in Tau is proportionally less than the increase in the tail length. Hence, over the range tested, the Tau-to-Tail Ratio reduces as kf,5 increases. These three effects make the phosphorylation rate of the receptors crucial to determining the transient's behavior.
FIGURE 5.
Decreased kf,5 results in a higher peak and a longer time-to-baseline from peak. Simulations were performed with the equations as in Table 3 and the parameters and initial conditions as in Table 4. Additionally, ts = 100 s, Ls = 0.100 μM, and kf,5 was varied as depicted in the legend.
The following two parameters—the ligand strength (Ls) and the rate constant for the binding of ligand to precoupled receptor (kf,4)—have virtually identical effects across all objective function measures (see Table S7 in the Supplementary Material for quantitative details). We consider each in turn.
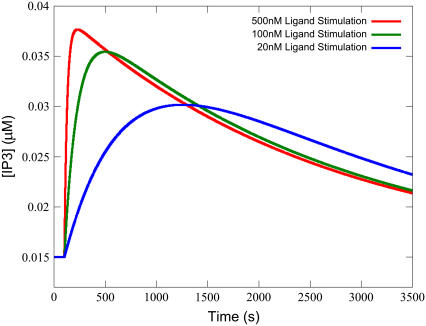
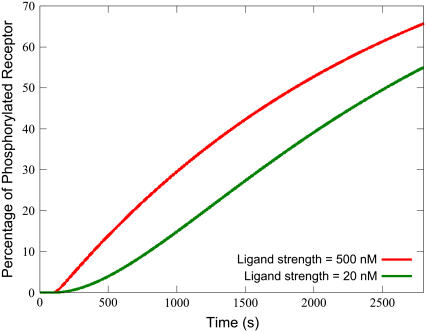
It might be expected that the applied ligand concentration (Ls) is significant in determining the response. Ls is significant largely due to its effect on the Time-to-Peak, which is demonstrated in Fig. 6. For stimulation with lower ligand concentration, the transient flattens and takes longer to achieve its maximum. This is due to the effect that ligand concentration has on the phosphorylation of available receptor. With higher ligand concentration, more active receptor is immediately available for phosphorylation, which turns off the signal faster. For low ligand strength, less IP3 signal amplitude is achieved, but the receptor pool is not consumed as quickly. This can be seen from a plot of the percentage of phosphorylated receptor over time, as shown in Fig. 7 for the highest and lowest ligand strengths in Fig. 6.
FIGURE 6.
Decreasing ligand strength strongly effects Time-to-Peak. Lower ligand strength produces a slower rate of active receptor production, thus the transient takes more time to achieve its maximum. Simulations were performed with the equations as in Table 3 and the parameters and initial conditions as in Table 4. Additionally, ts = 100 s and Ls was varied as depicted in the legend.
FIGURE 7.
Higher ligand strength more readily increases phosphorylated receptor density. Although the long-term gradients for phosphorylated receptor density are similar for both high and low concentrations of ligand strength, a higher strength yields a much larger initial gain. Simulations were performed with the equations as in Table 3 and the parameters and initial conditions as in Table 4. Additionally, ts = 100 s and Ls was varied as depicted in the legend.
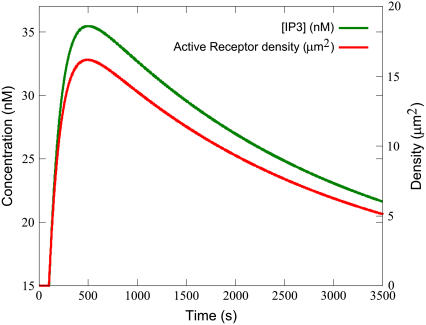
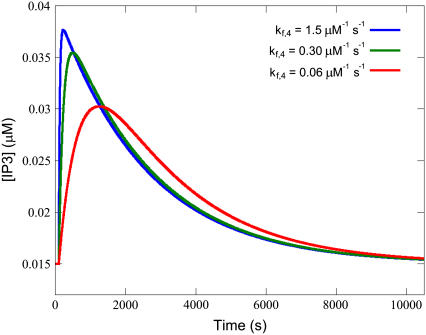
The forward rate constant for the binding of ligand to precoupled receptor (kf,4) also heavily influences the formation of activated receptors. This parameter has a large effect on the Time-to-Peak. Examination of the changes in the membrane density of various species reveals that the IP3 transient closely follows the shape of the density curve on the active receptors (the product of reaction R4) (see Fig. 8). The parameter kf,4's effect on Time-to-Peak can thus be explained by its influence on the production of active receptor, which in turn leads to the peak for IP3.
FIGURE 8.
The IP3 transient follows the active receptor transient. Simulations were performed with the equations as in Table 3 and the parameters and initial conditions as in Table 4. Additionally, ts = 100 s and Ls = 0.100 μM.
Both parameters also significantly influence the Time-to-Peak and the Tau-to-Tail Ratio. A higher peak due to high active receptor formulation (as increased by kf,4, Ls and also the parameter Gd) leads sooner to a more rapidly decreasing transient, as receptors are more readily available to be phosphorylated faster. This gives a sharper peak earlier, with a longer post-peak tail and therefore a lower Tau-to-Tail Ratio, compared to a flatter transient with a longer time to peak, a shorter tail, and higher Tau-to-Tail Ratio when those parameters are lower. This is illustrated for kf,4 specifically in Fig. 9. The same effect occurs when Ls or Gd are decreased (not shown).
FIGURE 9.
Higher kf,4 reduces the Tau-to-Tail Ratio. Increased kf,4 gives sharper peaks, but longer tails from the peak, and a lower Tau-to-Tail Ratio compared to flatter transients with a higher ratio when kf,4 is decreased. Simulations were performed with the equations as in Table 3 and the parameters and initial conditions as in Table 4. Additionally, ts = 100 s, Ls = 0.100 μM, and kf,4 was varied as depicted in the legend.
The next most important parameter is the forward rate constant (kf,16) for the degradation of IP3, which is the main consumer of IP3 in this system. The ratio of sarcolemmal surface area to cytosolic volume (Rpc) is also important as it determines the cytosolic flux in IP3 concentration resulting from a given surface area on the plasma membrane (a smaller cytosolic volume would yield a higher concentration change for the same IP3-producing sarcolemmal surface area). Hence this parameter has a direct effect on the concentration of IP3 produced for a given stimulus. Both these parameters mainly effect the IP3 Baseline Concentration and the Peak Concentration—one parameter affecting via IP3 degradation and the other affecting production, respectively.
The top five parameters together represent the most important determinants for each of the five objective functions—kf,5 for Time-to-Baseline, Ls and kf,4 both equally for each of Time-to-Peak and Tau-to-Tail Ratio, and both kf,16 and Rpc for each of Baseline and Peak Concentration.
The value Gd represents the densities of a species required to form that mobile messenger—the amount of free GαGDP. Gd's effects on Tau-to-Tail Ratio and Time-to-Peak is similar to the effect of kf,4 or Ls, as has already been discussed, being a multiplicative factor in the forward rates of both reactions R2 and R3, which form active receptors.
Kd,2 has similar but less pronounced effects to Gd, which is due to it being a determinant of the rate of precoupled receptor formation, and therefore influences the rate of production of active receptors.
The basal IP3 production forward rate constant (kf,14) is also important, largely for its effect on the Baseline Concentration. This is expected since the basal IP3 concentration is a balance of reaction R14 and the degradation rate as previously discussed.
The next two parameters of importance are the forward and reverse rate constants for the binding of calcium to PLCβ. The PLCβ-Ca2+ so produced is the only enzyme capable of producing IP3 in this system without ligand stimulation. Hence their effect on Baseline and Peak Concentrations, while less than that of other parameters such as kf,16 and Rpc, is notable.
Together these are the most significant control parameters of the IP3 model. They are also, therefore, the key parameters to be determined experimentally for a species of interest, as they have the strongest effect on the time course of the IP3 transient after stimulation of the Gq protein-coupled receptors.
Angiotensin-II stimulation
The literature-derived and refinement-fitted parameter changes required to adjust the model (as discussed in Methods) for Ang-2 cell stimulation are shown in Table 2. A graph of the experimental observations together with the fitted IP3 transient is shown in Fig. 10.
TABLE 2.
Parameters altered during refinement to angiotensin experimental data
| Symbol | Meaning | ET-1 value | Ang-2 value | Source |
|---|---|---|---|---|
| Kd,1 | Dissociation constant for the binding of ligand to the receptor with no attached G-protein. | 3.00 × 10−5μM | 1.50 × 10−3μM* | Bers (28) |
| Kd,2 | Dissociation constant for the binding of unbound receptor to G-protein. | 2.75 × 104μm2 | 2.74 × 104μm2† | |
| Kd,4 | Dissociation constant for the binding of ligand to the receptor with attached G-protein. | 3.00 × 10−5μM | 1.50 × 10−3μM* | Bers (28) |
| kf,4 | Forward rate for the binding of ligand to precoupled receptor. | 3.00 × 10−1μM1 s−1 | 6.02 × 10−1μM−1 s−1 | (fitted value) |
| kf,5 | Receptor phosphorylation rate. | 4.00 × 10−4 s−1 | 6.22 × 10−2 s−1 | (fitted value) |
| kf,6 | G-protein dissociation rate from the activated receptor. | 1 s−1 | 22.2 s−1 | (fitted value) |
| R | Density of noncoupled receptors. | 13.9 μm−2 | 2.93 μm−2 | Bers (28) |
| Rg | Density of receptors coupled with G-proteins. | 5.06 μm−2 | 1.07 μm−2 | Bers (28) |
In keeping with the ET-1 model, Kd,1 and Kd,4 retain their equality to one another.
Due to rounding for the values of R and Rg, the kinetic constant Kd,2 also had to be adjusted as the precise figure was closer to 27,400 than 27,500 μm−2, to achieve the same steady-state levels of R and Rg.
FIGURE 10.
Simulated fit to the observations of Abdellatif et al. (39). The simulated transient matches the observations (39) for stimulation with 100 nM of Ang-2. Simulations were performed with the equations as in Table 3 and the parameters and initial conditions as in Table 4, and the Ang-2 values listed in Table 2. Additionally, Ls = 100 μM and ts = 100 s.
Three parameters were adjusted during the refinement. An increase in kf,5 is needed to reduce the length of the transient to the shorter Ang-2 response. A minor adjustment to kf,4 (less than an order of magnitude) was also made. A third parameter was also modified—for forward rate constant for the dissociation of the messenger GαGTP from active receptors (kf,6). This modification was necessary due to the increased kf,5, which results not only in a shorter tail, but a lower peak. By increasing kf,6, more signal can be transferred to the PLCβ module via the messenger GαGTP, raising the IP3 transient peak without greatly increasing the tail. This combination of parameter changes, in concert with those derived from the literature, was sufficient to explain the experimental data.
Thus, once we allow for different receptor densities and known kinetic differences, the difference between the ET-1- and Ang-2-induced IP3 transients can be explained solely in terms of additional receptor kinetic changes in the phosphorylation rate (via rate constant kf,5), the binding of extracellular ligand to the precoupled receptor (kf,4) and the release of active G-protein (kf,6).
DISCUSSION
We have presented the first model of the IP3 production system in the atrial cardiac myocyte. We used this model to 1), assess the key drivers of the IP3 transient system; and 2), hypothesize the kinetic mechanism that allows two different receptors to provoke different behaviors in the same downstream pathway.
The IP3 system
The sensitivity analysis showed that several parameters that we expected to be important were in fact significant, increasing our confidence in the model. It also rated some parameters unexpectedly high—indications which have led to further insights on the functioning of the IP3 production system.
That the phosphorylation rate of the receptor (via kf,5) is of high importance is expected. There are two other switch-off points for the stimulated IP3 transient—the GαGTP self-hydrolysis to GαGDP when mobile (via kf,7), or when bound to PLCβ-Ca2+ (via kf,12 and kf,13). The fact that the phosphorylation rate of the receptor is more important than these highlights the importance of the interface of the cell to the surroundings above the internal mechanisms, at least in this system.
It is also intuitive that the ligand strength (Ls) is important. What is perhaps less obvious but shown by the sensitivity analysis is that this effect seems to be due largely to the ligand's effect on precoupled receptor density as opposed to its effect on noncoupled receptor density. The impact of Ls is identical to that of the forward rate constant for the binding of that ligand to precoupled receptor. This is explainable by both being multiplicative factors in that reaction (R4). It is such reaction that is important for the formation of active receptors (Rlg) on stimulation by ligand. The noncoupled reaction (R1) is less important on the stimulation of ligand as a further reaction must then be carried out (reaction R3) for the GαGDP to bind to the ligand-receptor complex before the receptor is active. In the precoupled state, the receptor becomes active much more readily and determines the responsiveness of the system far more significantly.
It seems likely that the effect on precoupled receptor density is also why the amount of GαGDP and the dissociation constant for receptor precoupling (Kd,2) are significant at numbers six and seven in the top 10—which may have at first seemed puzzling. GαGDP is a reactant for the formation of precoupled receptors (Rg), which in turn are reactants for that important reaction R4.
That the degradation rate of IP3 (via kf,16) and geometric ratio of membrane area-to-cytosolic volume (Rpc) are important is also expected when their role in the degradation and production of IP3, respectively, is considered, as was noted above. That the parameters (kf,8 and kr,8) related to the formation of the basal PIP2-hydrolyser (Pc) and the subsequent hydrolysis reaction (kf,14) are important is not surprising, given that the Baseline Concentration was one of the objective functions. The availability of Pc influences the resulting stimulated transient also, as mass of PLCβ is conserved when forming the stimulated hydrolyser Pcg, and kf,14 influences the difference between Pc activity and Pcg activity, having implications for the tail of the IP3 transient. Hence overall these are among the more significant parameters of the system.
Of the top seven parameters, five relate to the receptor kinetics. This highlights again the importance of the cell/environment interface in this system and indicates how a change in receptor density and kinetics from ET-1 to Ang-2 can alter the resulting IP3 transient to the extent observed experimentally.
Drivers of the angiotensin-II IP3 transient
Taken together, only parameters relating to the receptor kinetics and density have been altered to yield the fits to experimental data. Hence the model is consistent with the idea that a shorter IP3 transient from Ang-2 compared to ET-1 can be produced simply by a change in the type and number of receptors without the need for any other mechanisms.
The change in phosphorylation rate of active receptor (via constant kf,5) is consistent with the observation that the receptor phosphorylation rates differ even between subtypes of the same receptor (42). As discussed above, this phosphorylation rate is the most important factor in determining the time for the transient to reach the baseline level again after stimulation. Therefore in determining the possible differences in receptor kinetics between ET-1 and Ang-2 binding receptors, an increase in the phosphorylation rate (to reduce the transient's time length) for Ang-2 receptors seems likely.
The increase required in the dissociation rate of active G-protein subunits from the receptor (kf,6) suggests that, in cardiomyocytes, along with an increased phosphorylation rate (compared with endothelin receptors), the AT-1 receptor may also have an increased rate of GαGTP dissociation from the activated receptor compared to that of the ET-1A receptor. This prediction, and the increase in the rate of binding of ligand to precoupled receptor (kf,4), could be investigated experimentally.
We also refined the model to a second Ang-2 dataset from rat neonatal ventricular myocytes, that of Sadoshima and Izumo (43), which measured IP3 transients at two different concentrations of Ang-2. The experimental observations were too coarsely grained for our purposes to be confident about the peak of the transient, but best fits were achieved with similar values for kf,5 and kf,6 (0.0421 s−1 compared with 0.0622 s−1 and 14.9 s−1 compared with 22.2 s−1, respectively), increasing our confidence in the roles of the receptor phosphorylation and active G-protein dissociation rates.
The importance of the receptor phosphorylation rate, as evidenced both by the sensitivity analysis and its role in the fitting of the Ang-2 dataset, highlights the value of experimental measurement of this parameter for receptors of interest. Often experiments focus on determining the binding constants to certain ligands. As we have shown, for signal transduction the resulting intracellular signal is heavily influenced by the temporal dynamics of receptor activation, which is a balance between the binding of the ligand and the molecular events that switch-off active receptors. For the purposes of signal transduction, the determination of kinetic parameters pertaining to signal termination events may be even more important than the traditional focus on binding rates (kf,5 was overall the most important parameter).
Future directions
We have concluded that the rate of receptor deactivation is crucial for determining the behavior of the stimulated transient. In vivo the signal is stopped by several receptor desensitization mechanisms, including phosphorylation, binding of an inhibitor protein to the receptor, and receptor internalization. The details of exactly which process leads to desensitization differ depending on cell and receptor type. For example, phosphorylation may not play a role in the internalization of β-2 adrenergic receptors, but may play a role in muscarinic acetylcholine receptors (44). Also, with respect to the path the receptor takes once internalized, even different isoforms of the same receptor can take different routes. For example, in Chinese hamster ovary cells, endothelin isoform A (ET-A) receptors were found to be routed to a recycling compartment while endothelin isoform B (ET-B) receptors appeared to be destroyed in internal lysosomes (45). It is also possible that recycling can occur via multiple pathways with different timescales, as it appears to do for the human V2 vasopressin receptor (46). The full desensitization-sensitization cycle of ET-A receptors in the cardiac myocyte is not completely understood. Therefore, in this work, receptor desensitization is modeled simply as a phosphorylation step. Experimentally, ET-A phosphorylation appears to be correlated with desensitization (27). There is, however, some evidence (42) that ET-A desensitization occurs via internalization rather than phosphorylation, hence what in the model is called phosphorylation may in reality be internalization.
While for the purposes of model functionality both abstractions are largely identical (being essentially a removal of receptors from availability), it may be useful to extend the model with details of this internalization and recycling, once known. This would allow the model to respond to multiple stimuli, as receptors could then get replenished post-phosphorylation. The question of how the longer timescale process of receptor recycling influences hypertrophic signaling could then also be explored.
This model assumes a resting level of calcium, similar to that employed in the experiments of Jiang et al. (40). In a beating heart, the calcium levels oscillate. From the sensitivity analysis the parameter Ca corresponding to cytosolic calcium concentration ranked 11th overall, due to its effects on Baseline and Peak Concentration of the IP3 transient, and hence is likely to have a minor but measurable effect. It will therefore be interesting to explore the behavior of the model during a calcium oscillation and eventually couple to models of cell electrophysiology and excitation-contraction coupling (47,48). Comparing model results to experimental observations of IP3 transients in beating cells would extend our understanding of calcium handling in this system as it impacts on signal transduction.
The signal transduction pathway is complex and there are many kinetic parameters that could be measured. We present the top 10 parameters as those most likely to influence the IP3 transient formed in response to extracellular ligand. To confirm our understanding of this pathway in the cardiac myocyte it would be helpful to make experimental observations of these parameters and compare them to modeled values, thus refining the model as such data becomes available.
A further source of refinement would be transient data post ET-1 stimulation in the mouse atrial myocyte for proteins upstream of IP3; for example, free GαGTP or calcium-bound PLCβ. To our knowledge no such data exists, but such data could be used to constrain the model and refine its accuracy for behavior upstream of the IP3 transient.
The model predictions for the Ang-2 refinement are perhaps limited by the fact that we used data from rat ventricular myocyte, whereas the ET-1 stimulated model was developed in the mouse atrial myocyte. It is assumed that the Ang-2 induced IP3 transient would be sufficiently similar between the two cell types. To improve the validity of the refinement, it would be advantageous to conduct measurements of the Ang-2 induced IP3 transient in the mouse atrial myocyte and check that a similar refinement can be performed.
SUPPLEMENTARY MATERIAL
To view all of the supplemental files associated with this article, visit www.biophysj.org.
Supplementary Material
Acknowledgments
P.H. and E.J.C. thank the Maurice Wilkins Center for Molecular Biodiscovery.
M.C. was supported by the Foundation for Research, Science and Technology of New Zealand through a Bright Futures Doctoral Scholarship.
Editor: Raimond L. Winslow.
References
- 1.Heineke, J., and J. D. Molkentin. 2006. Regulation of cardiac hypertrophy by intracellular signaling pathways. Nat. Rev. Mol. Cell Biol. 7:589–600. [DOI] [PubMed] [Google Scholar]
- 2.Molkentin, J. D., J.-R. Lu, C. L. Antos, B. Markham, J. Richardson, J. Robbins, S. R. Grant, and E. N. Olson. 1998. A calcineurin-dependent transcriptional pathway for cardiac hypertrophy. Cell. 93:215–228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Sugden, P. H. 1999. Signaling in myocardial hypertrophy: life after calcineurin? Circ. Res. 84:633–646. [DOI] [PubMed] [Google Scholar]
- 4.Bare, D. J., C. S. Kettlun, M. Liang, D. M. Bers, and G. A. Mignery. 2005. Cardiac type 2 inositol 1,4,5-trisphosphate receptor: interaction and modulation by calcium/calmodulin-dependent protein kinase II. J. Biol. Chem. 280:15912–15920. [DOI] [PubMed] [Google Scholar]
- 5.Hardt, S. E., and J. Sadoshima. 2002. Glycogen synthase kinase-3β: a novel regulator of cardiac hypertrophy and development. Circ. Res. 90:1055–1063. [DOI] [PubMed] [Google Scholar]
- 6.Yamazaki, T., and Y. Yazaki. 2000. Molecular basis of cardiac hypertrophy. Zeitschrift fr. Kardiologie. 89:1–6. [DOI] [PubMed] [Google Scholar]
- 7.Passier, R., H. Zeng, N. Frey, F. J. Naya, R. L. Nicol, T. A. McKinsey, P. Overbeek, J. A. Richardson, S. R. Grant, and E. N. Olson. 2000. CaM kinase signaling induces cardiac hypertrophy and activates the MEF2 transcription factor in vivo. J. Clin. Invest. 105:1395–1406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wilkins, B. J., and J. D. Molkentin. 2002. Calcineurin and cardiac hypertrophy: where have we been? Where are we going? J. Physiol. (Lond.). 541:1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kohno, M., and J. Pouyssegur. 2003. Pharmacological inhibitors of the ERK signaling pathway: application as anticancer drugs. Prog. Cell Cycle Res. 5:219–224. [PubMed] [Google Scholar]
- 10.Crabtree, G. R. 1999. Generic signals and specific outcomes: signaling through Ca2+, calcineurin, and NFAT. Cell. 96:611–614. [DOI] [PubMed] [Google Scholar]
- 11.Ju, H., S. Zhao, P. S. Tappia, V. Panagia, and I. M. C. Dixon. 1998. Expression of Gqα and PLC-β in scar and border tissue in heart failure due to myocardial infarction. Circulation. 97:892–899. [DOI] [PubMed] [Google Scholar]
- 12.Taylor, S. J., H. Z. Chae, S. G. Rhee, and J. H. Exton. 1991. Activation of the β1 isozyme of phospholipase C by α subunits of the Gq class of G-proteins. Nature. 350:516–518. [DOI] [PubMed] [Google Scholar]
- 13.Wilkins, B. J., and J. D. Molkentin. 2004. Calcium-calcineurin signaling in the regulation of cardiac hypertrophy. Biochem. Biophys. Res. Commun. 322:1178–1191. [DOI] [PubMed] [Google Scholar]
- 14.Crabtree, G. R., and E. N. Olson. 2002. NFAT signaling: choreographing the social lives of cells. Cell. 109:S67–S79. [DOI] [PubMed] [Google Scholar]
- 15.Leinwand, L. A. 2001. Calcineurin inhibition and cardiac hypertrophy: a matter of balance. Proc. Natl. Acad. Sci. USA. 98:2947–2949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Crampin, E. J., M. Halstead, P. Hunter, P. Nielsen, D. Noble, N. Smith, and M. Tawhai. 2004. Computational physiology and the physiome project. Exp. Physiol. 89:1–26. [DOI] [PubMed] [Google Scholar]
- 17.Kakita, T., K. Hasegawa, E. Iwai-Kanai, S. Adachi, T. Morimoto, H. Wada, T. Kawamura, T. Yanazume, and S. Sasayama. 2001. Calcineurin pathway is required for Endothelin-1-mediated protection against oxidant stress-induced apoptosis in cardiac myocytes. Circ. Res. 88:1239–1246. [DOI] [PubMed] [Google Scholar]
- 18.Sadoshima, J., Y. Xu, H. S. Stayter, and S. Izumo. 1993. Autocrine release of angiotensin II mediates stretch-induced hypertrophy of cardiac myocytes in vitro. Cell. 75:977–984. [DOI] [PubMed] [Google Scholar]
- 19.Lijnen, P., and V. Petrov. 1999. Renin-angiotensin system, hypertrophy and gene expression in cardiac myocytes. J. Mol. Cell. Cardiol. 31:949–970. [DOI] [PubMed] [Google Scholar]
- 20.Goutsouliak, V., and S. W. Rabkin. 1998. Comparison of angiotensin II type-1 and type-2 receptor antagonists on angiotensin II-induced IP3 generation in cardiomyocytes. Gen. Pharmacol. 30:367–372. [DOI] [PubMed] [Google Scholar]
- 21.Touyz, R., and C. Berry. 2002. Recent advances in angiotensin II signaling. Braz. J. Med. Biol. Res. 35:1001–1015. [DOI] [PubMed] [Google Scholar]
- 22.Hua, B., L.-L. Wu, D.-Q. Xing, J. Liu, and Y.-L. Zhao. 2004. Angiotensin II induced upregulation of Gαq/11, phospholipase Cβ3 and extracellular signal-regulated kinase 1/2 via angiotensin II type 1 receptor. Chin. Med. J. 117:88–93. [PubMed] [Google Scholar]
- 23.Mehta, P. K., and K. K. Griendling. 2007. Angiotensin II cell signaling: physiological and pathological effects in the cardiovascular system. Am. J. Physiol. Cell Physiol. 292:C82–C97. [DOI] [PubMed] [Google Scholar]
- 24.Lloyd, C. M., M. D. B. Halstead, and P. F. Nielsen. 2004. CellML: its future, present and past. Prog. Biophys. Mol. Biol. 85:433–450. [DOI] [PubMed] [Google Scholar]
- 25.Lukas, T. J. 2004. A signal transduction pathway model prototype I: from agonist to cellular endpoint. Biophys. J. 87:1406–1416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Shea, L., and J. J. Linderman. 1997. Mechanistic model of G-protein signal transduction determinants of efficacy and effect of precoupled receptors. Biochem. Pharmacol. 53:519–530. [DOI] [PubMed] [Google Scholar]
- 27.Freedman, N. J., A. S. Ament, M. Oppermann, R. H. Stoffel, S. T. Exum, and R. J. Lefkowitz. 1997. Phosphorylation and desensitization of human endothelin A and B receptors. Evidence for G-protein-coupled receptor kinase specificity. J. Biol. Chem. 272:17734–17743. [DOI] [PubMed] [Google Scholar]
- 28.Bers, D. M. 2002. Excitation-Contraction Coupling and Cardiac Contractile Force, 2nd Ed. Kluwer Academic Publishers, New York.
- 29.Hunton, D. L., L.-Y. Zou, Y. Pang, and R. B. Marchase. 2004. Adult rat cardiomyocytes exhibit capacitative calcium entry. Am. J. Physiol. Heart Circ. Physiol. 286:H1124–H1132. [DOI] [PubMed] [Google Scholar]
- 30.Haugh, J. M., A. Wells, and D. A. Lauffenburger. 2000. Mathematical modeling of epidermal growth factor receptor signaling through the phospholipase C pathway: mechanistic insights and predictions for molecular interventions. Biotechnol. Bioeng. 70:225–238. [PubMed] [Google Scholar]
- 31.Willars, G. B., S. R. Nahorski, and R. A. Challiss. 1998. Differential regulation of muscarinic acetylcholine receptor-sensitive polyphosphoinositide pools and consequences for signaling in human neuroblastoma cells. J. Biol. Chem. 273:5037–5046. [DOI] [PubMed] [Google Scholar]
- 32.Remus, T. P., A. V. Zima, J. Bossuyt, D. J. Bare, J. L. Martin, L. A. Blatter, D. M. Bers, and G. A. Mignery. 2006. Biosensors to measure inositol 1,4,5-trisphosphate concentration in living cells with spatiotemporal resolution. J. Biol. Chem. 281:608–616. [DOI] [PubMed] [Google Scholar]
- 33.Takanashi, M., and M. Endoh. 1992. Concentration- and time-dependence of phosphoinositide hydrolysis induced by endothelin-1 in relation to the positive inotropic effect in the rabbit ventricular myocardium. J. Pharmacol. Exp. Ther. 262:1189–1194. [PubMed] [Google Scholar]
- 34.Parkinson, P. A., H. Parfenova, and C. W. Leffler. 2000. Phospholipase C activation by prostacyclin receptor agonist in cerebral microvascular smooth muscle cells. Proc. Soc. Exp. Biol. Med. 223:53–58. [DOI] [PubMed] [Google Scholar]
- 35.Morris, M. D. 1991. Factorial sampling plans for preliminary computational experiments. Technometrics. 33:161–174. [Google Scholar]
- 36.Campolongo, F., S. Tarantola, and A. Saltelli. 1999. Tackling quantitatively large dimensionality problems. Comput. Phys. Commun. 117:75–85. [Google Scholar]
- 37.Campolongo, F., J. Cariboni, A. Saltelli, and W. Schoutens. 2004. Enhancing the Morris Method. In Sensitivity Analysis of Model Output. K. M. Hanson, and F. M. Hemez, editors. SAMO 2004, Santa Fe, New Mexico.
- 38.Saltelli, A., S. Tarantola, F. Campolongo, and M. Ratto. 2004. Sensitivity Analysis in Practice—A Guide to Assessing Scientific Models. Wiley, New York.
- 39.Abdellatif, M. M., C. D. Neubauer, W. J. Lederer, and T. B. Rogers. 1991. Angiotensin-induced desensitization of the phosphoinositide pathway in cardiac cells occurs at the level of the receptor. Circ. Res. 69:800–809. [DOI] [PubMed] [Google Scholar]
- 40.Jiang, T., E. Pak, H. Zhang, R. P. Kline, and S. F. Steinberg. 1996. Endothelin-dependent actions in cultured AT-1 cardiac myocytes: the role of the ∫ isoform of protein kinase C. Circ. Res. 78:724–736. [DOI] [PubMed] [Google Scholar]
- 41.Hairer, E., and G. Wanner. 1996. Solving ordinary differential equations. II. Stiff and differential-algebraic problems. In Springer Series in Computational Mathematics, Vol. 14, 2nd Ed. Springer, New York.
- 42.Cramer, H., W. Muller-Esterl, and C. Schroeder. 1997. Subtype-specific desensitization of human endothelin ETA and ETB receptors reflects differential receptor phosphorylation. Biochemistry. 36:13325–13332. [DOI] [PubMed] [Google Scholar]
- 43.Sadoshima, J., and S. Izumo. 1993. Signal transduction pathways of angiotensin II–induced c-fos gene expression in cardiac myocytes in vitro. Roles of phospholipid-derived second messengers. Circ. Res. 73:424–438. [DOI] [PubMed] [Google Scholar]
- 44.Ferguson, S. S. G., J. Zhang, L. S. Barak, and M. G. Caron. 1998. Molecular mechanisms of G-protein-coupled receptor desensitization and resensitization. Life Sci. 62:1561–1565. [DOI] [PubMed] [Google Scholar]
- 45.Bremnes, T., J. D. Paasche, A. Mehlum, C. Sandberg, B. Bremnes, and H. Attramadal. 2000. Regulation and intracellular trafficking pathways of the endothelin receptors. J. Biol. Chem. 275:17596–17604. [DOI] [PubMed] [Google Scholar]
- 46.Innamorati, G., C. Le Gouill, M. Balamotis, and M. Birnbaumer. 2001. The long and the short cycle. alternative intracellular routes for traffick-ing of G-protein-coupled receptors. J. Biol. Chem. 276:13096–13103. [DOI] [PubMed] [Google Scholar]
- 47.Noble, D., and Y. Rudy. 2001. Models of cardiac ventricular action potentials: iterative interaction between experiment and simulation. Philos. Trans. Roy. Soc. London A Math. Phys. Eng. Sci. 359:1127–1142. [Google Scholar]
- 48.Crampin, E. J., and N. Smith. 2005. A dynamic model of excitation-contraction coupling during acidosis in cardiac ventricular myocytes. Biophys. J. 90:3074–3090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Bhalla, U. S., and R. Iyengar. 1999. Emergent properties of networks of biological signaling pathways. Science. 283:381–387. [DOI] [PubMed] [Google Scholar]
- 50.Sivakumaran, S., S. Hariharaputran, J. Mishra, and U. S. Bhalla. 2003. The database of quantitative cellular signaling: management and analysis of chemical kinetic models of signaling networks. Bioinformatics. 19:408–415. [DOI] [PubMed] [Google Scholar]
- 51.Xu, C., J. Watras, and L. M. Loew. 2003. Kinetic analysis of receptor-activated phosphoinositide turnover. J. Cell Biol. 161:779–791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Leri, A., S. Franco, A. Zacheo, L. Barlucchi, S. Chimenti, F. Limana, B. Nadal-Ginard, J. Kajstura, P. Anversa, and M. Blasco. 2003. Ablation of telomerase and telomere loss leads to cardiac dilatation and heart failure associated with p53 upregulation. EMBO J. 22:131–139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Kobayashi, T., T. Miyauchi, S. Sakai, M. Kobayashi, I. Yamaguchi, K. Goto, and Y. Sugishita. 1999. Expression of endothelin-1, ETA and ETB receptors, and ECE and distribution of endothelin-1 in failing rat heart. Am. J. Physiol. Heart Circ. Physiol. 276:H1197–H1206. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.