Stochastic inhibitor release and binding from single-enzyme molecules

Abstract

Inhibition kinetics of single-β-galactosidase molecules with the slow-binding inhibitor d-galactal have been characterized by segregating individual enzyme molecules in an array of 50,000 ultra small reaction containers and observing substrate turnover changes with fluorescence microscopy. Inhibited and active states of β-galactosidase could be clearly distinguished, and the large array size provided very good statistics. With a pre-steady-state experiment, we demonstrated the stochastic character of inhibitor release, which obeys first-order kinetics. Under steady-state conditions, the quantitative detection of substrate turnover changes over long time periods revealed repeated inhibitor binding and release events, which are accompanied by conformational changes of the enzyme's catalytic site. We proved that the rate constants of inhibitor release and binding derived from stochastic changes in the substrate turnover are consistent with bulk-reaction kinetics.

The emergence of new assays for studying enzymes at the single-molecule level has profoundly extended our view of enzyme mechanisms. Whereas stochastic molecular behaviors are hidden by using bulk methods, single-molecule experiments have revealed that, in a population of enzymes, such as lactate dehydrogenase (1), phosphatase (2), or β-galactosidase (3), the catalytic rates of individual enzyme molecules are heterogeneous and do not interconvert quickly. Furthermore, it has been shown that the substrate turnover of individual β-galactosidase (4), cholesterol oxidase (5), or lipase (6) molecules undergoes dynamic fluctuations in sequential catalytic cycles. These two variations in enzyme activity are referred to as static and dynamic heterogeneity, respectively, and have both been attributed to different conformational states of the enzyme. Despite such heterogeneity, the Michaelis–Menten model derived from bulk enzyme experiments still holds for single-molecule experiments once a stochastic perspective is adopted (4, 7, 8).

Traditionally, one of the most important tools to elucidate an enzyme's catalytic mechanism has been to study the enzyme in the presence of inhibitors. Here, we set out to correlate inhibition mechanisms established in bulk enzyme studies with single-enzyme molecule experiments. To date, inhibitors have been used in single-molecule studies to obtain information about conformational dynamics. Ha et al. (9) showed that it is possible to distinguish between free and inhibitor-bound states of a single-staphylococcal nuclease enzyme molecule. The binding of an inhibitor imposed a conformational constraint on the enzyme molecule resulting in a change of single-molecule polarization and intramolecular single-pair FRET. In this article, we report the direct observation of inhibitor release and binding from single-enzyme molecules by monitoring their substrate turnover.

Modeling Single-Enzyme Molecule Inhibition.

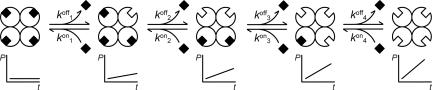
In the presence of an inhibitor, only the free enzyme is catalytically active; however, because most enzymes are oligomeric (10), there is often more than one “on” and “off” state. A tetrameric enzyme can be in one of five different states, depending on how many molecules of inhibitor are bound to it as depicted in Scheme 1. According to conventional enzymology, the degree of inhibitor saturation should result in a discrete rate of product formation by the remaining free catalytic sites.

Scheme. 1.

Inhibitor release and binding from a tetrameric enzyme molecule.

Considering only the dissociation of the enzyme inhibitor complex in the upper half-reaction of Scheme 1, each apparent dissociation rate constant k_1–4^off should be different because, although there are four possibilities for a completely occupied tetramer to release an inhibitor, there are only three possibilities for a tetramer with three bound inhibitors and so on. If the four catalytic sites are independent, the apparent dissociation constants are equal to the intrinsic dissociation constant k_p^off of a protomer multiplied by the statistical factors 4, 3, 2, and 1. Taking the forward and back reactions together, the apparent equilibrium constants are K₁ = 4 K_p, K₂ = 3/2 K_p, K₃ = 2/3 K_p, and K₄ = 1/4 K_p (11).

In a bulk inhibition experiment, an inverse hyperbolic dependence of the enzyme velocity v on the inhibitor concentration [I] is given by Eq. 1:

where v₀ is the velocity without inhibitor, and K_i is the inhibition constant; K_i is essentially the same as K_p if the protomers are independent. In this case, plotting 1/v versus [I] yields a linear Dixon plot (12).

In contrast to bulk experiments, a single-molecule inhibition experiment records the stochastic change in substrate turnover of the interconverting inhibition states of an individual enzyme molecule, and enables the probability density for a transition to another state to be calculated. If an inhibitor, with [I] = K_i, is added to a single-tetrameric enzyme, the five possible activity states are in equilibrium. Ideally, each transition to another inhibition state will be reflected in a 25% change of substrate turnover. It is known, however, that the individual activities of different enzyme molecules can vary by up to a factor of four, even without inhibitor (1, 3), and it is possible that the activity of an individual enzyme may fluctuate upon inhibitor binding and release. In this case, it would not be possible to distinguish the different states of inhibition depicted in Scheme 1 by comparing the substrate turnover d[P]/dt.

To circumvent this complication, the enzyme can be preincubated and equilibrated with an excess amount of inhibitor and subsequently highly diluted to [I] ≪ K_i. Under this pre-steady-state condition, the reaction sequence depicted in Scheme 1 can only proceed sequentially from left to right, whereas the reverse reaction will be negligible. Thus, the first inhibitor dissociation from the enzyme, k₁^off, can be determined independently of the actual activity of the first free protomer.

In a steady-state experiment, the rate constant of enzyme conversion between different inhibition states can be calculated by the autocorrelation function of the turnover rates of single-enzyme molecules

where the brackets indicate averaging along a trajectory, T(t) denotes the substrate turnover at time t, and δT(t) is the deviation of the substrate turnover from the average. The decay rate of the autocorrelation function, k^c, is composed of the sum of the association and the dissociation rates (5). Eq. 3 shows the case of a monomeric enzyme

For a tetrameric enzyme with four independent subunits and five different states of activity, the autocorrelation function should be multiexponential and exhibit a stretched exponential decay; e.g., the substrate turnover of an enzyme with four bound inhibitor molecules will still be positively correlated to the substrate turnover of an enzyme with three bound inhibitors. However, there is no sequential correlation if the enzyme has bound two inhibitors and an activity near the average turnover.

To obtain k^on in the absence of substrate, Eq. 3 must be corrected for competitive substrate binding (13). Thus, k^on can be calculated as

Because k^off and k^on become apparent as separate terms in steady-state inhibition experiments with single-enzyme molecules, the autocorrelation analysis is more comparable to bulk kinetics under pre-steady-state conditions than to bulk kinetics under steady-state conditions, which can only reveal the equilibrium constant K_i.

Measurement of Single-β-Galactosidase Molecules.

Escherichia coli β-galactosidase is a large 464-kDa tetrameric enzyme of four identical subunits that has been extensively characterized (14, 15). β-galactosidase is active only as a tetramer (16) and catalyzes the hydrolysis of lactose and other β-d-galactopyranosides (17). β-galactosidase was the first enzyme to be used for single-molecule kinetic experiments (18). In our investigation, we used the substrate resorufin-β-d-galactopyranoside that generates fluorescent resorufin upon hydrolysis (Fig. 1). The kinetic constants for this enzyme-substrate pair are K_M = 380 μM and k_cat = 730 s⁻¹ (19), which were also derived from single-enzyme molecule experiments (4).

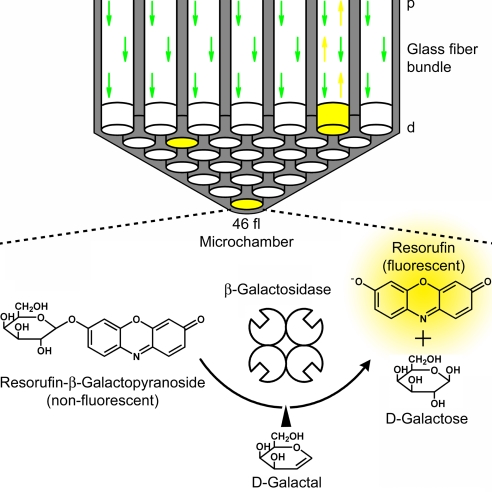
Fig. 1.

Single-enzyme substrate turnover in microchambers. A schematic section with a 2-mm-diameter glass optical fiber bundle containing 50,000 fibers in total is shown in Upper. Forty-six-femtoliter (46 μm³) microchambers were etched homogenously into the distal end (d) of the fibers. The fiber core is shown in white, and the cladding is shown in gray. The fiber bundle was mounted on a custom-built upright epifluorescence microscope, and the reaction progress was monitored through the proximal side (p) of the fiber bundle after the chambers had been sealed by a silicone gasket (gasket not shown). The probability P(x) that exactly x enzyme molecules are entrapped in a certain microchamber is given by the Poisson distribution Pμ(x) = e^−μ × μ^x/x!, where μ is the mean number of enzymes per microchamber. An enzyme concentration of 3.6 pM in a volume of 46 fl yields a probability of only one β-galactosidase molecule in every 10 microchambers (24). These single-enzyme molecules convert nonfluorescent resorufin-β-d-galactopyranoside substrate to fluorescent resorufin (yellow chambers). This process is inhibited if the reaction intermediate analog d-galactal binds to β-galactosidase.

The strong inhibition of β-galactosidase by d-galactal was elucidated through bulk experiments (13, 20–22). d-galactal is not a classical competitive inhibitor as it forms a glycosyl-enzyme transition state that decomposes very slowly to 2-deoxygalactose (13). This process is accompanied by a conformational change of the enzyme, as demonstrated by the difference in the ultra-violet absorbance spectra between the free and inhibited enzyme (21). To date, all attempts to demonstrate the formation of a second conformational enzyme state during the hydration of d-galactal by kinetic means have failed (22). The very slow binding and release rates [2.7 × 10² M⁻¹ s⁻¹ and 4.6 × 10⁻³ s⁻¹, respectively (13)] of d-galactal, however, render it particularly useful for single-enzyme experiments, because β-galactosidase inactivation due to inhibitor binding can be clearly distinguished from the waiting times between adjacent substrate turnovers. These fluctuating waiting times have been observed and characterized with a single-β-galactosidase molecule experiment and typically occur for a few milliseconds but can persist for up to 10 s (4).

Enclosing single-enzyme molecules and their catalysis products in very small reaction containers is a straightforward method that requires no enzyme immobilization and ensures a constant reaction volume without evaporation (23, 24). In this work, we captured single-β-galactosidase molecules with 100 μM resorufin-β-d-galactopyranoside in an array of 5 × 10⁴ ultra small reaction microchambers located on the end of an optical fiber bundle (Fig. 1) (24, 25). A droplet of the enzyme and substrate solution was sandwiched between the distal face of an etched optical fiber bundle and a silicone gasket, and the chambers were tightly sealed under mechanical pressure. The enzyme concentration in the droplet was calculated with the Poisson equation such that either one or zero enzyme molecules would be present in each microchamber. The developing fluorescent product in the microchambers that contained a single-enzyme molecule was excited and monitored through the proximal face of the fiber, using a custom-built upright epifluorescence microscope.

Results and Discussion

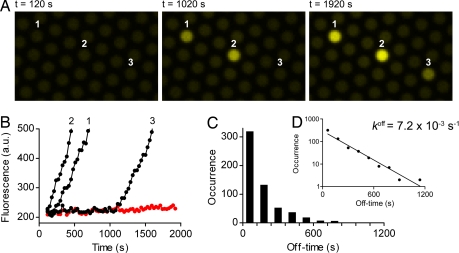
All single-enzyme molecules in the microchambers turned over substrate without delay if no inhibitor was added, and each individual enzyme showed a distinct turnover rate. In contrast, when β-galactosidase was equilibrated with an excess amount of d-galactal and subsequently highly diluted to [I] ≪ K_i before enclosing the enzyme in the microchambers, there was a delay in the onset of substrate turnover of the single-enzyme molecules because of the slow dissociation rate of d-galactal. Fig. 2 shows the stochastic nature of inhibitor dissociation. It should be noted that the onset of substrate turnover indicates the dissociation of the first inhibitor molecule from the enzyme and gives a digital readout, with each enzyme molecule converting from an inactive to an active state. The frequency distribution of off-times (Fig. 2D) shows a first-order inhibitor release with a dissociation rate constant k₁^off = (7.2 ± 0.3) × 10⁻³ s⁻¹. k^off values determined with bulk experiments were 4.6 × 10⁻³ s⁻¹ (13) or 2.5 × 10⁻³ s⁻¹ (22), respectively. As k₁^off = 4 × k^off, the rate constant from the single-enzyme experiment is somewhat lower than the previous reports suggest.

Fig. 2.

Time-dependent inhibitor release from single-enzyme molecules in a pre-steady-state experiment. β-galactosidase (3.6 nM) was preincubated with 100 μM d-galactal (≈5 × K_i) for 20 min and then diluted 1,000-fold into 100 μM resorufin-β-d-galactopyranoside. The diluted solution was enclosed in 46-fl chambers within 2 min, and sequential fluorescence images of single-enzyme substrate turnovers were taken every 30 s with low illumination and an exposure time of 2 s (SI Movie 2). (A) A sequence of these images recorded after closing the chambers (Left) and after 1,020 s (Middle) and 1,920 s (Right) shows a delayed onset of substrate turnover that we attribute to stochastic inhibitor release events. (B) Trajectories of fluorescence increase in the indicated microchambers. An empty chamber shows a constant background (red curve). (C) Distribution of off-times (bars) derived from 581 turnover trajectories and four independent experiments. The stochastic event when the enzyme started to turn over substrate was determined by eye. Off-times of every 2 min were binned. (D) The line is an exponential fit to the data, giving a rate constant k₁^off = (7.2 ± 0.3) × 10⁻³ s⁻¹ (best fit ± asymptotic SEM). The semilogarithmic plot illustrates a first-order release of inhibitor.

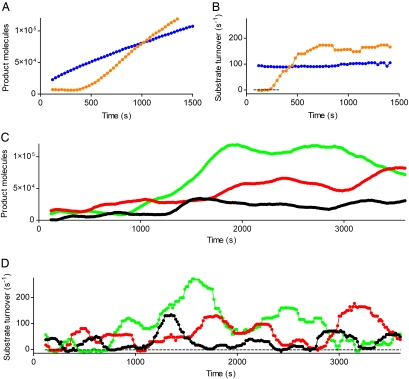
We then investigated quantitatively how inhibitor interactions affect the substrate turnover of a single-enzyme molecule. The derivative of the fluorescence increase with time yields the substrate turnover of a single-enzyme molecule and indicates its state of inhibitor binding [Fig. 3 and supporting information (SI) Movie 1]. The classical static model of inhibitor interaction would be characterized at the single-enzyme level by two features. First, the five inhibition states depicted in Scheme 1 should be observed as five distinct and equally spaced substrate turnover rates that should interconvert with time. No intermediate rates among these distinct states should occur. Second, if the four catalytic sites are independent, as suggested in ref. 17, all transitions between the off-state and full activity would pass through all intermediate states.

Fig. 3.

Quantitative measurement of substrate turnover. (A) Trajectories of fluorescent product increase from an experiment without inhibitor (blue circles) and a pre-steady-state experiment (orange circles) as described in Fig. 2. (B) Substrate turnover calculated by taking the time derivative of the trajectories (A) and compensating for resorufin photobleaching (see Substrate Turnover Calculation). Without inhibitor, there is only a single state of enzyme activity, whereas in a pre-steady-state experiment, the activity jumps from a state of no activity quickly to its maximum activity. (C) Steady-state experiment. β-galactosidase (3.6 pM) was enclosed with 20 μM d-galactal and 100 μM resorufin-β-d-galactopyranoside in 46-fl chambers and sequential fluorescence images of single-enzyme product formation were taken every 15 s with low illumination and an exposure time of 2 s. Three representative trajectories (black, red, and green circles) of several hundred from multiple arrays are shown. (D) Substrate turnover of C. In a steady-state experiment, several distinct states of activity can be distinguished.

To test the first assumption of the static model, steady-state experiments that allow the enzyme to undergo repeated inhibitor binding and release events were performed. We incubated single-β-galactosidase molecules with 20 μM d-galactal, based on previous reports of the bulk K_i (13, 20, 22), and 100 μM resorufin-β-d-galactopyranoside. Differences in the turnover rates can only be attributed to the inhibitor if the substrate concentration remains relatively constant over time. Because the average substrate turnover of a single-β-galactosidase molecule in equilibrium with inhibitor was 65 turnovers per s and the 46-fl microchambers each contained 2.8 million substrate molecules, <10% of the substrate was depleted over the entire 1-h experiment. Consequently, although the reaction volume of each microchamber is small enough to isolate single-enzyme molecules and to accumulate a readily detectable concentration of product molecules, it is also large enough to contain a sufficient amount of substrate molecules to prevent depletion. It has been shown that the amount of active β-galactosidase molecules decays exponentially in very dilute solutions because of tetramer dissociation (4). From the interrupted trajectories of inactivated enzyme molecules in the absence of inhibitor, we calculated the half-life of β-galactosidase to be 6.1 ± 1.1 h (mean ± SD), which is consistent with the previous report of 5.6 ± 0.7 h. Thus, during a 1-h experiment, only 10% of the individual enzymes will be inactivated.

It is possible to distinguish inhibitor-induced changes in the turnover rates from dynamic heterogeneity of single-enzyme molecules by determining the coefficients of variation of several hundred individual turnover rates in the presence (140 ± 56%) and absence (34 ± 10%) of d-galactal (mean ± SD). A statistical analysis of the coefficients of variation confirmed that the substrate turnover changes were significantly higher in the presence of the inhibitor (two-tailed, unpaired t test, P < 0.0001). Fig. 3 C and D show in detail for three of several hundred enzyme molecules that individual enzymes underwent a state of inactivity because of inhibitor binding that was never observed in the absence of inhibitor or in a pre-steady-state experiment (Fig. 3 A and B).

We have observed that individual β-galactosidase molecules differ in their distinct activities even without any inhibitor present (unpublished data). Because of this intrinsic distribution of enzyme activity, it was not possible to correlate the highest state of activity to a completely uninhibited enzyme, and thus, to define the five distinct states of substrate turnover. The only state that is clearly defined is the completely inactive state. Even if a trajectory does not pass through a fully active enzyme, all other states should be “quantized,” however, this observation could not be made in the experiments discussed here. From this result, we conclude that d-galactal binding and release events are accompanied by conformational changes such that the enzyme does not necessarily return to the same state of activity after inhibitor release. This observation is consistent with a previous report in which conformational changes induced by d-galactal binding were characterized by the difference in the ultra-violet absorbance spectra between the free and inhibited enzyme (21). With our single-enzyme approach, we demonstrate that inhibitor binding to an enzyme induces conformational changes that result in a different enzyme activity each time the inhibitor dissociates. Thus, static heterogeneity, as defined by kinetically distinct individual enzymes in an enzyme population, is intrinsically dynamic. Because the rate constant of d-galactal binding is approximately four orders of magnitude slower than k_cat/K_M for galactoside hydrolysis, it was noted in ref. 13 that β-galactosidase inhibition occurs with an activation barrier much higher than any barrier encountered during the hydrolysis of galactosides. Crossing this activation barrier may result in a conformational rearrangement that leads to a different catalytic activity when the inhibitor is released. An important implication of this observation is that the rate constant for inhibitor release from β-galactosidase, k^off, should have both a temporal dimension, as traditionally assumed in kinetic experiments, and a quantitative dimension defined by the substrate turnover of the new conformation. These two dimensions are essentially unresolvable in bulk experiments.

For the second assumption of the static model, data from bulk reactions are contradictory concerning whether an independent or nonindependent inhibitor binding and release mechanism is operative. β-galactosidase inhibition with d-galactal was first reported to yield a nonlinear Dixon plot (20), indicating an allosteric interaction of the four catalytic protomers, whereas linear relationships were reported later (13, 22), implying no allosteric interaction. In our single-molecule pre-steady-state experiment, the lifetime of an inactive enzyme with four bound inhibitors, which could last for up to 20 min, should be the shortest compared with the lifetime of an enzyme with three, two, or one bound inhibitor molecules if there are no interactions between protomers (Scheme 1). These intermediate states of inhibitor binding should be observable by three different states of enzyme activity. The majority of enzymes, however, showed only a one-step jump from no activity to the highest state of activity, as shown in the representative example of Fig. 3B. It is interesting to note in Fig. 3B that the activity of a previously inhibited enzyme can be even higher than the activity of an enzyme that has never been in contact with the inhibitor. This observation is consistent with the broad activity distribution of β-galactosidase.

The instantaneous change from no activity to maximum activity renders it unlikely that the four catalytic sites release the inhibitor independently. A nonindependent or cooperative inhibitor release means that the apparent rate constant k₁^off derived from Scheme 1 is essentially the same as that of k^off, because all four inhibitor molecules dissociate from a single-enzyme molecule simultaneously.

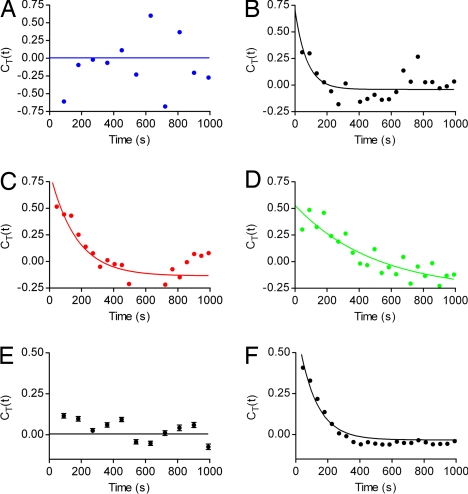
With this information about cooperative inhibitor binding and release mechanism, the autocorrelation function can be calculated as for the case of a monomeric enzyme according to Eq. 2. Because C_T(t) contains the combined information of repeated binding and release events along the entire time course of a single-enzyme molecule, it reflects the on and off rates more accurately than the observable changes in the turnover rates shown in Fig. 3D. The autocorrelation function of the single-enzyme molecules plotted in Fig. 3 was calculated and is shown in Fig. 4. Whereas no correlation between adjacent turnover rates is observable in the absence of inhibitor (Fig. 4A), a correlation can be seen for the three single-β-galactosidase molecules incubated with 20 μM d-galactal (Fig. 4 B–D). The data points fit to a single-exponential decay, but the rate constants, k^c, vary by one order of magnitude. A plot assembled from hundreds of individual autocorrelation functions yields a better curve fit and a more accurate value for k^c (Fig. 4F). Again, a clear distinction can be made between the autocorrelation function of enzymes incubated without (Fig. 4E) and with inhibitor (Fig. 4F). The data points in Fig. 4F can be fitted to a single-exponential decay with k^c = (8.9 ± 0.2) × 10⁻³ s⁻¹. According to Eq. 4, k^c and k^off, determined with the pre-steady-state experiment, can be used to calculate k^on = 1.1 × 10² s⁻¹ M⁻¹, which is in the same range as the literature values of 2.7 × 10² s⁻¹ M⁻¹ (13) or 4.5 × 10² s⁻¹ M⁻¹ (22). If the literature values of k^off (13, 22) are used with k^c, k^on is 2.7 × 10² s⁻¹ M⁻¹ or 4.1 × 10² s⁻¹ M⁻¹, which comes even closer to the reported values. These differences indicate that k^c can be calculated from the autocorrelation function with an even higher accuracy than that of k^off from the pre-steady-state experiment.

Fig. 4.

Autocorrelation functions of single-enzyme substrate turnover trajectories (see Substrate Turnover Calculation) calculated with Eq. 2. The solid lines show the fit of the data points to a single-exponential decay: C_T(t) = C_T (0) exp(−k^c × t). (A) Substrate turnover autocorrelation of the enzyme shown in Fig. 3B that was incubated without inhibitor. (B–D) Steady-state substrate turnover autocorrelations of the enzymes shown in Fig. 3D. The autocorrelation plots are shown in the same color as the substrate turnover trajectories in Fig. 3. The decay constants are (13.7 ± 8.4) × 10⁻³ s⁻¹ (B), (6.1 ± 1.9) × 10⁻³ s⁻¹ (C), and (2.0 ± 0.9) × 10⁻³ s⁻¹ (D) (best fit ± asymptotic SEM). (E) Assembled autocorrelation of 433 substrate turnover trajectories incubated without inhibitor. The autocorrelation of every substrate turnover trajectory was calculated, and each time lag was averaged. Error bars indicate the SEM. There is no correlation of adjacent substrate turnover rates. (F) Assembled autocorrelation function of 944 substrate turnover trajectories with inhibitor as described in E. Because of the high number of averaged substrate turnover trajectories, the error bars are too small to be visible. The rate constant k^c is (8.9 ± 0.2) × 10⁻³ s⁻¹.

Additionally, the single-exponential fit shown in Fig. 4F was compared with a model of a stretched exponential decay: C_T(t) = C_T (0) exp[−(k^c × t)^β]. We observed a better fit with β = 1 compared with all smaller values for β. Because distinct turnover rates that could be attributed to the five inhibition states depicted in Scheme 1 would result in a stretched exponential decay of the autocorrelation function, the single-exponential decay further indicates that β-galactosidase exists predominantly in two states, either free or completely occupied with four d-galactal molecules.

Conclusion

We have shown that segregating individual enzyme molecules in a large array of ultrasmall reaction containers on the surface of an optical fiber bundle is a powerful tool for studying inhibition kinetics at the single-enzyme level. Inhibited and active states of an enzyme can be clearly distinguished and the large array size provides good statistics from only a few experiments. The scope of our method, however, is not limited to a digital readout. Rather, it allows for the quantitative detection of substrate turnover changes over long time periods that can be related to repeated inhibitor binding and release events accompanied by conformational changes of the enzyme's catalytic site. The abrupt transition from no activity to maximum activity and the autocorrelation analysis indicate that d-galactal binding and release are cooperative. We demonstrated that the rate constants of inhibitor release and binding can be determined from stochastic changes in the substrate turnover trajectories of single-enzyme molecules and are in good agreement with the rate constants of bulk reaction kinetics.

Methods

Materials.

β-galactosidase from E. coli (grade VIII) was purchased from Sigma–Aldrich (St. Louis, MO) and reconstituted to 2 μM in PBS/MgCl₂ (2.7 mM KCl/1.5 mM KH₂PO₄/136 mM NaCl/8.1 mM Na₂HPO₄/1 mM MgCl₂, pH 7.3). The aliquoted enzyme was snap-frozen with liquid N₂ and stored at −80°C. Stock solutions of 100 mM d-galactal (1,5-anhydro-2-deoxy-d-lyxo-hex-1-enitol) (Sigma–Aldrich) in PBS/MgCl₂, of 100 mM resorufin-β-d-galactopyranoside (Invitrogen, Carlsbad, CA) in DMSO, and of 180 mM resorufin sodium salt (Invitrogen) in DMSO were aliquoted and stored at −20°C.

All experiments were conducted in PBS/MgCl₂ with 0.05 mg/ml BSA (Sigma–Aldrich) and 0.005% Tween 20 (Sigma–Aldrich) at room temperature. The enzyme stock solution was diluted just before experimentation.

Microchamber Array Fabrication.

Glass optical fiber bundles (2-mm diameter) with 50,000 individually cladded fibers (4.5-μm diameter) were purchased from Schott (Elmsford, NY) and cut to ≈4.5 cm in length. Both ends of the fibers were sequentially polished on an automated fiber polisher (Ultra-tec, Santa Ana, CA), using lapping films with a grid size of 30, 12, 9, 3, 1, and 0.3 μm (Mark V Laboratory, East Granby, CT). The cladding and core material of the optical material are both composed of silica but are doped with different materials. This way, the core could be selectively etched for 115 s with 0.025 M HCl under stirring to create an array of 50,000 2.9-μm-deep microchambers with a volume of 46 fl (μm³).

Microchamber Sealing.

Nonreinforced gloss silicone sheeting material (0.25-mm thickness) (Specialty Manufacturing, Saginaw, MI) was cut into pieces of ≈1 cm² and thoroughly cleaned by using soapy water followed by extensive rinsing with deionized water. For preparing a gasket, the silicone sheet was put on an equally sized, clean microscope slide.

The fiber bundle with the femtoliter array faced downwards was locked in the custom-built stage of an upright epifluorescence microscope. The gasket (silicone sheet upside) was placed under the fiber bundle on a mechanical platform, and ≈25 μl of solution was placed on the silicone sheet. The microchambers were filled with the solution by bringing the solution in contact with the array and repeatedly moving the platform with the silicone sheet up and down. Finally, the microchambers were tightly sealed by pressing the silicone sheet vertically against the fiber bundle.

Imaging System.

Fluorescence signals were recorded with an upright Olympus (Tokyo, Japan) BX61 microscope equipped with a short arc mercury lamp (Ushio, Tokyo, Japan), an appropriate filter set with λ_ex = 571 nm and λ_em = 584 nm (Chroma Technology, Rockingham, VT), and a CCD camera (Sensicam QE; Cooke Optics, Romulus, MI). Images were taken every 15 or 30 s with low illumination and an exposure time of 2 s through a ×10 objective lens. The fluorescence light is totally internally reflected in the cores of the fiber bundle because of the higher refractive index of the core material compared with the cladding material. Thus, the light beams are focused on the proximal face of the fiber bundle and can be allocated individually to the microchambers. IPLab software (Scanalytics, Fairfax, VA) was used for fluorescence signal analysis and adding pseudocolor.

Substrate Turnover Calculation.

The photobleaching rate of the fluorescent product was determined by enclosing 10 μM resorufin in the microchambers and monitoring the fluorescence decrease every 15 s with an exposure time of 2 s over 1 h. An exponential fit of the data yielded a photobleaching rate, k_ph, of 10⁻³ s⁻¹. To obtain a calibration factor for the product, resorufin standard solutions were enclosed and measured in the microchambers. The raw fluorescence intensities of the trajectories (Fig. 3 A and C) were multiplied with the calibration factor and background corrected. The substrate turnover was calculated by S(t) = F′(t) + k_ph × F(t), where S(t) is the substrate turnover of a single-enzyme molecule in the microchamber, F(t) is the fluorescence intensity as a function of time, F′(t) is its time derivative, and k_ph is the photobleaching rate. Experiments with measurement intervals of 30 s were corrected with k_ph/2.

An average and median filter of length 9 was used for Fig. 3 to smooth F(t) and F′(t), respectively. With a recording interval of 15 s, the effective time resolution in Fig. 3 is ≈2 min. For the calculation of the autocorrelation functions in Fig. 4, unsmoothed turnover rates were used. Instead, the fluorescence intensities of three adjacent time points were binned.