Measurement of bond vector orientations in invisible excited states of proteins

Abstract

The focus of structural biology is on studies of the highly populated, ground states of biological molecules; states that are only sparsely and transiently populated are more difficult to probe because they are invisible to most structural methods. Yet, such states can play critical roles in biochemical processes such as ligand binding, enzyme catalysis, and protein folding. A description of these states in terms of structure and dynamics is, therefore, of great importance. Here, we present a method, based on relaxation dispersion NMR spectroscopy of weakly aligned molecules in a magnetic field, that can provide such a description by direct measurement of backbone amide bond vector orientations in transient, low populated states that are not observable directly. Such information, obtained through the measurement of residual dipolar couplings, has until now been restricted to proteins that produce observable spectra. The methodology is applied and validated in a study of the binding of a target peptide to an SH3 domain from the yeast protein Abp1p and subsequently used in an application to protein folding of a mutational variant of the Fyn SH3 domain where ¹H-¹⁵N dipolar couplings of the invisible unfolded state of the domain are obtained. The approach, which can be used to obtain orientational restraints at other sites in proteins as well, promises to significantly extend the available information necessary for providing a site-specific characterization of structural properties of transient, low populated states that have to this point remained recalcitrant to detailed analysis.

Solution NMR spectroscopy is a powerful technique for the study of biomolecular dynamics spanning a range of time scales from picoseconds for bond vector librations to many hours for hydrogen exchange in the buried interiors of proteins (1, 2). One very important approach, based on the concept of a “spin-echo” that was first described by Hahn in 1950 (3), is called the Carr–Purcell–Meiboom–Gill (CPMG) relaxation dispersion method (4, 5). This class of experiment provides a window into processes with conformational exchange on the millisecond time scale (6), a time regime that is often the relevant one for the lifetimes of bound ligands (7, 8), protein folding events (9), or molecular rearrangements that are important for the control of enzyme function (10–13). For systems in which the ground state exchanges with a minor conformer populated at 0.5% or higher and with exchange rates on the order of a hundred to a few thousand per second, the CPMG dispersion experiment provides a sensitive measure of the exchange dynamics (6). Rates of exchange, populations of exchanging states, and chemical shifts of nuclear spins in minor states can be obtained from fits of dispersion profiles to the appropriate model of exchange. Most importantly, information from potentially every residue is obtained in states that are often invisible in even the most sensitive of NMR spectra.

Fig. 1a illustrates a simple case in which a loop of a protein, highlighted in green, exchanges between two states for which distinct ¹⁵N chemical shifts are obtained (Fig. 1b). Typically, the states may have very different populations and lifetimes so that peak intensities are highly skewed, to the point where the minor state is not observed (Fig. 1b Inset). The chemical shifts of the invisible excited state can be reconstructed from CPMG relaxation dispersion measurements, where the widths of peaks of the observable state, R_2,eff, are measured as a function of the frequency of application of radio-frequency pulses, ν_CPMG, that quench the effects of the chemical exchange event(s) (6) [see supporting information (SI) Text]. This is possible because the resulting dispersion profiles (R_2,eff vs. ν_CPMG) are sensitive to Δν, the difference in chemical shifts between ground and excited states (in hertz). In favorable cases, the derived chemical shifts of the excited state can be interpreted to provide structural information (9). Although exciting developments in using chemical shifts as the sole probes of structure have been forthcoming (14), the relation between chemical shifts and high-resolution structure remains empirical. In solution NMR studies of proteins for which well resolved, high-resolution spectra can be recorded, chemical shifts supplement distance constraints measured from NOE spectra (15), dihedral angle constraints from scalar couplings (16), and orientational restraints in the form of residual dipolar couplings (17, 18) that are combined to generate three-dimensional structures.

Fig. 1.

Measurement of amide bond vector orientation in invisible excited protein states. (a) Energy level diagram for a two-state exchanging system, where the loop (green) can exist in two conformations. (b) Resulting ¹H-decoupled ¹⁵N spectrum for a single amide probe of conformational exchange between two states whose populations are highly skewed. In weakly aligning media (c) and without ¹H decoupling, each line is split by the sum of ¹H-¹⁵N dipolar and scalar couplings (J_NH ∼ −93 Hz). Spectra resulting from the ¹H in the down and up spin-states are shown in d in red and blue, respectively. (e and f) Separate ¹⁵N CPMG relaxation dispersion experiments monitor exchange between ground and excited state conformations that are separated by Δν (black), Δν − 0.5ΔD_NH (red), or Δν + 0.5ΔD_NH (blue), from which ΔD_NH can be extracted. There is a small contribution to the chemical shift that results from alignment (19) so that ν_A and ν_B are shifted slightly (≤5 Hz for the alignment parameters of the systems considered here at a field of 800 MHz) between b and d (not included for clarity). Thus, values of Δν include contributions from incomplete averaging of the anisotropic chemical shift, as described in the text. In f, intrinsic relaxation rates, R_2,∞, have been subtracted from the dispersion profiles to emphasize their differences, ΔR₂ = R_2,eff − R_2,∞. Note that the relative magnitude of TROSY and anti-TROSY dispersion profiles reverses with the sign of the product Δν × ΔD_NH.

Measuring Residual Dipolar Couplings in Invisible States

Residual dipolar couplings are a particularly valuable probe of structure because they relate bond vector orientations in a molecular frame and in this sense provide long-range information that is lacking from other NMR observables (17, 18). In isotropic solution such couplings average exactly to zero, but they can be reintroduced into spectra by dissolving the molecule of interest into a medium that produces weak alignment (18). This leads to peak splittings that can be quantified and related to orientation, so long as the peaks themselves can be observed in spectra. Fig. 1 c and d illustrates the situation for an amide bond vector attached to a protein dissolved in alignment media. As before, the protein undergoes exchange between major (“A”) and minor (“B”) conformations; resonance lines for the major and minor states are split into two, with the displacement given by the sum of the scalar coupling, J_NH, assumed invariant between conformers, and the dipolar coupling, D_NH, that is related to the bond orientation in each state and that in general will be different for corresponding bond vectors in states A and B. In Fig. 1d, the spectrum of the minor state is shown (along with the major state) but, in general, will not be observed. Yet, it is still possible to measure dipolar couplings of the “invisible,” minor state by using suitably designed CPMG relaxation dispersion experiments. In a “typical” relaxation dispersion NMR experiment, conducted in isotropic solution, exchange is measured between major and minor states that are separated by Δν, and this type of experiment can be performed on fractionally aligned proteins with the appropriate NMR scheme [Fig. 1e (black) and SI Fig. 5]. In the case of an aligned system, Δν = Δν_isotropic + Δν_anisotropic, where the first term is the isotropic shift difference and the second term arises from the incomplete averaging of the anisotropic chemical shift due to alignment (19). Fig. 1f (black) shows the resultant relaxation dispersion profile that derives from the time-dependent modulation of chemical shift by the exchange event(s).

It is also possible to measure conformational exchange in a spin-state selective manner by using amide probes where the ¹⁵N spin is coupled to its directly attached ¹H in the down (red) or up (blue) spin-state, corresponding to exchange between states separated by Δν − 0.5ΔD_NH and Δν + 0.5ΔD_NH, respectively, where ΔD_NH = D_NH^A − D_NH^B is the difference between ¹H-¹⁵N dipolar couplings in states A and B, and D_NH^K is given by an expression in the literature [see equation 3e of Bax et al. (20)]. As described above, Δν consists of contributions from both isotropic and anisotropic interactions, but because the orientation-dependent shift contributions are independent of ¹H spin-state, they do not interfere with the extraction of accurate ΔD_NH values. Experiments for measuring ΔD_NH can be performed in a straightforward way by selecting for TROSY (transverse relaxation optimized spectroscopy; Δν − 0.5ΔD_NH) (21) or anti-TROSY (Δν + 0.5ΔD_NH) magnetization components during CPMG elements in experiments that build on the elegant TROSY-dispersion experiment developed by Palmer and coworkers (22) that is used for measurements in isotropic solution. In the same way that a time-dependent modulation of chemical shift leads to a relaxation dispersion profile (Fig. 1f, black), so too can the modulation of dipolar couplings that arises from exchange between states. As expected, dispersion profiles that derive from exchange between states separated by Δν ± 0.5ΔD_NH are distinct (Fig. 1f, blue and red). Thus, by measuring these three classes of dispersion experiment, all under conditions where the system of interest is weakly aligned, and fitting the data simultaneously, it is possible to extract |Δν| and |Δν ± 0.5ΔD_NH| (dispersion experiments are invariant to the sign of the shift difference). The sign of the dipolar coupling can be resolved, however, by measuring the sign of Δν, achieved by monitoring the variation of peak positions in spectra recorded at different static magnetic field strengths (23).

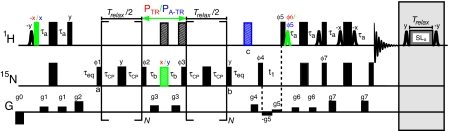
Fig. 2 shows ¹⁵N TROSY- and anti-TROSY-based CPMG relaxation dispersion pulse schemes that have been developed for the quantification of ¹H-¹⁵N dipolar couplings in invisible states of proteins [details of the experiments are provided in SI Text, along with a dispersion experiment for measuring |Δν| (SI Fig. 5)]. Central to the dispersion experiments is the constant-time CPMG pulse train of duration T_relax. In the case of the TROSY scheme, only the TROSY components that are present during the CPMG element are selected and recorded during (t₁, t₂). In contrast, in the anti-TROSY scheme a ¹H 180° pulse is inserted at point c that interconverts TROSY and anti-TROSY magnetization components, with the TROSY components subsequently selected. Thus, cross-peaks in “anti-TROSY” spectra are of the TROSY variety but report on exchange between anti-TROSY components during the CPMG pulse element. This leads to clear improvements in resolution and sensitivity over schemes that maintain the anti-TROSY components throughout.

Fig. 2.

Pulse schemes of ¹⁵N constant-time TROSY and anti-TROSY CPMG relaxation dispersion experiments for measurement of ΔD_NH in protein systems undergoing millisecond-time-scale exchange dynamics. All ¹H and ¹⁵N 90° (180°) radiofrequency pulses are shown as narrow (wide) black bars and are applied at the highest possible power level, with the exception of the ¹⁵N refocusing pulses of the CPMG element, along with the 90° sandwiching pulses, which are applied at a slightly lower power level (≈6 kHz). Composite 180° pulses (34) are represented by “striped” rectangles. All pulse phases are assumed to be x, unless indicated otherwise. N can be any integer. Differences in the TROSY/anti-TROSY schemes are highlighted (in red and blue for TROSY and anti-TROSY, respectively; the 180° pulse at point c is omitted in the case of the TROSY experiment). Water-selective 90° ¹H pulses (shaped pulses) are rectangular (≈1.6 ms). The phase cycling used is as follows (Varian): φ1 = {x, −x}; φ2 = 2{y}, 2{−y}; φ3 = 2{x}, 2{−x}; φ4 = 2{y}, 2{−y}, 2{−x}, 2{x}; φ5 = −y; φ6 = y; φ7 = −y; receiver = {y, −y, −y, y, x, −x, −x, x}. Sensitivity enhanced quadrature detection in the indirect dimension (35–38) is obtained by recording a second data set with φ4 = 2{y}, 2{−y}, 2{x}, 2{−x}; φ5 = φ5 + π; φ6 = φ6 + π; φ7 = φ7 + π; and receiver = receiver + π for each t₁ increment. In addition, phase φ4 is incremented along with the receiver by 180° for each complex t₁ point (39). The delays used are τ_a = 2.25 ms, τ_b = 1/(4|J_NH|) = 2.68 ms, and τ_eq = (2 − 3)/(k_ex) ∼ 5 ms. Gradient strengths G/cm (length in milliseconds) are as follows: g0 = −15(1), g1 = 5(1), g2 = 12(1), g3 = 8(0.3), g4 = 10(0.5), g5 = 0.5(t₁), g6 = 6(0.3), g7 = 25(0.3). A spin-lock element is applied immediately after acquisition at the same power level and for the same duration (T_relax) as used for the experiment measuring |Δν| (SI Fig. 5) so that the heating effects are constant over all measurements.

To extract accurate ΔD_NH values, exchange between TROSY and anti-TROSY components must be minimized during the CPMG relaxation element of Fig. 2 (see SI Text). In the case of a ¹H-¹⁵N spin pair, such exchange results from relaxation of the ¹H spin with external protons that effectively “flip” the spin-state of the ¹H of interest (Fig. 1d, red and blue arrows). Such spin-flips can be minimized effectively through the use of highly deuterated proteins and applications described here have used such deuterated systems. In addition, the small ¹H spin-flip rate has been quantified on a per-residue basis (as described under Data Analysis in SI Text) and subsequently used in fits of TROSY and anti-TROSY relaxation dispersion profiles to account for relaxation from external protons (software available from the authors upon request).

Applications of the Methodology

As a first example that serves to establish the validity of the methodology, we have studied the binding of a 17-residue target peptide from the protein Ark1p to the SH3 domain from Abp1p (24) (K_d = 0.55 ± 0.05 μM; data not shown). In these studies, binding was monitored through the SH3 domain that was ¹⁵N-labeled. Large relaxation dispersion profiles were obtained in measurements performed on protein dissolved in isotropic solution (no alignment media) when a small amount of Ark1p peptide was added ([Ark1p]/[SH3] ∼ 5%). The chemical-shift differences extracted from fits of relaxation dispersion profiles to a simple two-site exchange model,

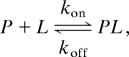produced Δν values that are in excellent agreement with chemical-shift differences between free and fully bound SH3 domain that have been measured directly from separate protein samples (SI Fig. 6). Values of k_on = (6.3 ± 0.7) × 10⁸ M⁻¹·s⁻¹ and k_off = 350 ± 10 s⁻¹ were calculated from the dispersion data recorded at 25°C with the larger than diffusion limited k_on reflecting the large contribution from electrostatics to binding (the Abp1p SH3 domain has a net negative charge of 12 and the Ark1p peptide a net positive charge of 6 at pH 7).

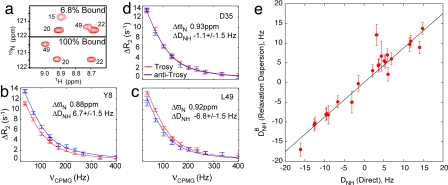
Fig. 3a shows regions of ¹H, ¹⁵N correlation spectra of the Abp1p SH3 domain with 6.8% and 100% bound peptide (25°C). Peak positions in the spectrum of the 6.8% sample are essentially identical to those in spectra of the apo-state with significant differences in comparison to the fully bound spectrum (SI Fig. 7). Correlations from the minor state, corresponding to the bound form in the 6.8% sample, are not observed in spectra because of severe exchange broadening and the low population of the bound conformer. It is therefore not possible to measure dipolar couplings of this state by using standard experiments. The significant change in the charge of the complex relative to that of the free SH3 domain suggests, however, that there will be large changes in molecular alignment for bound and free protein dissolved in a charged, weakly ordering medium, such as the phage particles used for alignment here (SI Fig. 8). Thus, for protein dissolved in ordering media, the exchange reaction will lead to a time-dependent modulation of alignment and hence of bond vector orientations relative to the external magnetic field. Dipolar couplings can therefore be quantified by using the experiments described above. In principle, modulation of dipolar couplings could also occur through structural changes that accompany ligand binding. However, recent studies have shown that such structural changes are minimal for the Abp1p SH3 domain (unpublished data).

Fig. 3.

Measuring ¹H-¹⁵N dipolar couplings of the invisible peptide-bound state of the Abp1p SH3 domain and validation of the methodology. (a) Selected region of ¹H-¹⁵N TROSY-HSQC spectra of Abp1p SH3 with 6.8% and 100% peptide bound, 800 MHz, 25°C. (b–d) Dispersion profiles of selected residues measured at 800 MHz, from which ΔD_NH is obtained (as described in the text). Intrinsic relaxation rates have been subtracted from the dispersion curves. (e) Dipolar couplings of the invisible minor state, corresponding to the Ark1p peptide-bound form of Abp1p SH3, D_NH^B, agree well with dipolar couplings, D_NH, measured directly from a fully bound sample. As couplings from separate samples are compared with small differences in the amounts of phage and hence slight differences in A_a values, the slope of the best-fit correlation is not 1 [(A_a, R) = ((−6.4 ± 0.3) × 10⁻⁴, 0.38 ± 0.07) and ((−7.35 ± 0.05) × 10⁻⁴, 0.36 ± 0.01) calculated from D_NH^B and D_NH, respectively]. Alignment parameters A_a and R are as defined in ref. 18.

Fig. 3 b–d shows TROSY and anti-TROSY relaxation dispersion profiles for select residues from Abp1p SH3 with 6.8% bound peptide, measured on a fractionally aligned sample. In the absence of alignment, TROSY and anti-TROSY dispersions are equivalent to within noise (see below), but differences can manifest for partially oriented samples. Cases where Δϖ (shift differences in parts per million) and ΔD_NH have the same (Tyr-8) and opposite (Leu-49) signs are presented, along with an example where ΔD_NH ∼ 0 for which TROSY and anti-TROSY profiles are similar (Asp-35).

Dispersion profiles were analyzed simultaneously to extract common exchange rates and populations, along with values of Δϖ and ΔD_NH for each residue. To obtain dipolar couplings of the minor, invisible state (bound), D_NH^B, dipolar couplings of the ground state (apo), D_NH^A, were measured directly (on the same sample) by using conventional experiments (25) and subtracted from ΔD_NH. Values of D_NH^B in this case can be verified by a comparison with corresponding D_NH values that are measured directly from spectra of the fully bound form. Fig. 3e shows a correlation plot of such a comparison and it is clear that very good agreement is obtained, verifying the methodology (SI Tables 1 and 2). Of interest, the one significant outlier in the plot is Asp-15, which has a ¹H spin-flip rate that is 3-fold higher than for all other amides. In principle, this outlier could easily be eliminated on the basis of its anomalous relaxation properties, although we have not done so here. As a further verification, we calculated the orientation of alignment tensors determined from the structure of the Ark1p peptide/Abp1p SH3 complex using either (i) D_NH^B values measured by means of relaxation dispersion on the 6.8% bound sample where correlations from the complex are “invisible” or (ii) D_NH values measured directly from spectra of the fully bound state, and each of the corresponding principal axes of the two frames is within 6° (SI Fig. 8 and SI Table 1).

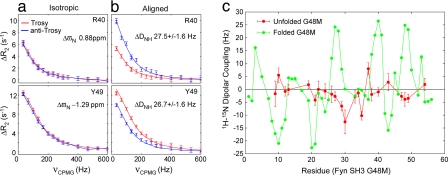
As a second example demonstrating the approach, the folding reaction of the G48M Fyn SH3 domain (9) is considered. Previous relaxation dispersion studies (26) (without alignment) have shown that the folding reaction proceeds from an invisible unfolded state populated at 5% (p_U = 5%) through an on-pathway intermediate populated at 0.7% that is also not observed in spectra. Because p_I is close to an order of magnitude smaller than p_U, the reaction can be approximated as two-state to first-order, as indicated in SI Fig. 9, which shows a good correlation between shifts of the unfolded, excited state extracted from the two-state model and predicted random coil values. In the isotropic phase, TROSY and anti-TROSY dispersion profiles are identical (Fig. 4a) but become very different in the aligned sample (Fig. 4b), which reflects the nonzero values of ΔD_NH. Dipolar couplings of the ground (green, folded) and excited (red, unfolded) states are shown in Fig. 4c (SI Table 3), and as expected the dipolar couplings from the unfolded state are significantly attenuated relative to those from the folded domain because of an increased level of dynamics. Further analysis of the dipolar couplings of the unfolded state in terms of structural preferences of the ensemble must await additional experiments, performed by using alignment media where electrostatic contributions to alignment are significantly reduced over their effects here, simplifying the interpretation of the data (because steric effects only can then be used to predict the alignment properties of the ensemble).

Fig. 4.

Measuring ¹H-¹⁵N dipolar couplings of the excited, unfolded state of the G48M Fyn SH3 domain. (a) TROSY and anti-TROSY ¹⁵N dispersion profiles (800 MHz) are identical when measured in isotropic phase, with clear differences when protein is dissolved in aligning media (b). (c) Comparison of D_NH^B (red) and D_NH^A (green) values of the invisible unfolded state and the folded conformer measured on the same sample by means of relaxation dispersion and direct methods, respectively.

As described in Material and Methods and SI Text, dipolar couplings from residues whose dispersion profiles were fit with reduced χ² > 2 or where Δϖ < 0.2 ppm were removed from Fig. 4c (and Fig. 3e). In practice, when |Δϖ| values are below a certain threshold (0.2 ppm used here), it is not possible to extract accurate values of ΔD_NH because dispersion profiles are small. In principle, nonflat dispersion curves, even for Δϖ ≈ 0 ppm, can be obtained in cases where ΔD_NH ≠ 0; however, in the applications considered presently, the degree of alignment was not sufficient to produce quantifiable dispersion profiles in these cases. The folding example presented here is particularly challenging because many residues have large Δϖ (see SI Table 3) that tend to “mask” ΔD_NH values. SI Fig. 10 shows that the error in extracted ΔD_NH increases rapidly with Δϖ for shift differences >5 ppm. Remarkably, however, it is possible to extract D_NH^B values that are well under 10% of |Δν ± 0.5ΔD_NH|, despite linewidths of peaks from the invisible state that are >100 Hz. This results directly from the fact that dispersion profiles reporting on Δν + 0.5ΔD_NH, Δν, and Δν − 0.5ΔD_NH can be obtained.

In summary, a method is presented for the measurement of dipolar couplings of low populated, transient states that are “invisible” in NMR spectra. The method relies on the fact that modulation of both chemical shifts and dipolar couplings occurs in exchanging systems that are partially aligned. It is thus possible to measure both chemical shifts and bond vector orientations of excited protein states that can be used as a basis for the calculation of structures, expanding along the lines described in ref. 9. In studies of unfolded proteins, the extracted dipolar couplings can be used to test assumptions of structural preferences of the ensemble, as has recently been demonstrated in applications to the nucleocapsid-binding domain of the Sendai virus (27) and α-synuclein (28, 29). It now becomes possible, however, to carry out studies on systems where such unfolded states are not the predominant forms in solution, without increasing their concentration through the addition of denaturants that could perturb structure or lead to aggregation (30). Further applications of interest include studies of ligand binding to occluded sites in receptors where it is clear that entry must occur through structural rearrangements that are only transiently sampled (7) or studies of enzymes where function involves loop rearrangements (10, 11, 31). In the later case, little may be known about the “excited” loop conformations, and dipolar couplings provide a powerful way to probe them. It is becoming increasingly clear that excited states play an important role in biochemical processes; the methodology presented here provides tools for their characterization at a level of detail that has normally been reserved for applications to highly populated conformations.

Materials and Methods

Sample Preparation.

The Abp1p and G48M Fyn SH3 domains, along with the Ark1p peptide, were expressed and purified as described in SI Text. The Abp1p/Ark1p sample was ≈90% U-²H, ≈100% U-¹⁵N-labeled, 1.3 mM in protein, 6.8% bound peptide, 50 mM sodium phosphate, 100 mM NaCl, 1 mM EDTA, 1 mM NaN₃, 90%/10% H₂O/D₂O, pH 7.0. The G48M Fyn SH3 domain sample was ≈98% U-²H, ≈100% U-¹⁵N-labeled, 1 mM in protein, 50 mM sodium phosphate, 1 mM EDTA, 1 mM NaN₃, 90%/10% H₂O/D₂O, pH 7.0. Sample alignment was obtained through the addition of ≈25 mg/ml (Abp1p SH3) and ≈35 mg/ml (G48M Fyn SH3) Pf1 phage (32), purchased from ASLA BIOTECH (residual ²H water splitting of ≈30 Hz), which provided dipolar couplings between −10 and +7 Hz and −22 and +26 Hz for the Abp1p (apo) and Fyn (folded) SH3 domains, respectively.

NMR Spectroscopy and Data Analysis.

A set of constant-time ¹⁵N CPMG relaxation dispersion experiments (TROSY, anti-TROSY, and ¹H CW decoupled) were recorded on fractionally aligned samples (25°C) at a pair of static magnetic field strengths corresponding to ¹H resonance frequencies of 500 and 800 MHz, using spectrometers equipped with room-temperature probe-heads. Experimental details are given in SI Text. Residual dipolar couplings of major state (observable) conformations were measured by using the IPAP approach (25).

Datasets were processed and analyzed with the program NMRPipe (33), and signal intensities were quantified by using the program FuDA (available upon request). Relaxation dispersion data were interpreted by using a two-state exchange model described in SI Text, with all dispersions analyzed simultaneously. Dipolar couplings from residues whose dispersion profiles were fit with reduced χ² > 2 or where Δϖ < 0.2 ppm were removed from Figs. 3e and 4c but are included in SI Tables 2 and 3. Also removed from Fig. 4c are points for which errors in D_NH^B values exceed the range of experimental D_NH^B couplings (±5 Hz; see SI Fig. 10).