Purely stochastic binary decisions in cell signaling models without underlying deterministic bistabilities

Abstract

Detection of different extracellular stimuli leading to functionally distinct outcomes is ubiquitous in cell biology, and is often mediated by differential regulation of positive and negative feedback loops that are a part of the signaling network. In some instances, these cellular responses are stimulated by small numbers of molecules, and so stochastic effects could be important. Therefore, we studied the influence of stochastic fluctuations on a simple signaling model with dueling positive and negative feedback loops. The class of models we have studied is characterized by single deterministic steady states for all parameter values, but the stochastic response is bimodal; a behavior that is distinctly different from models studied in the context of gene regulation. For example, when positive and negative regulation is roughly balanced, a unique deterministic steady state with an intermediate value for the amount of a downstream signaling product is found. However, for small numbers of signaling molecules, stochastic effects result in a bimodal distribution for this quantity, with neither mode corresponding to the deterministic solution; i.e., cells are in “on” or “off” states, not in some intermediate state. For a large number of molecules, the stochastic solution converges to the mean-field result. When fluctuations are important, we find that signal output scales with control parameters “anomalously” compared with mean-field predictions. The necessary and sufficient conditions for the phenomenon we report are quite common. So, our findings are expected to be of broad relevance, and suggest that stochastic effects can enable binary cellular decisions.

The detection of external stimuli by receptors on a cell membrane followed by intracellular signaling, gene transcription, and effector functions is ubiquitous, and necessary for life. The regulatory processes involved in gene transcription are often mediated by small numbers of molecules. This makes stochastic effects important and, in recent years, many interesting consequences of such fluctuations have been elucidated theoretically and observed in experiments (e.g., refs. 1–4). The importance of stochastic effects on enzymatic reactions in the zero order ultrasensitivity regime has also been described (5, 6). Less attention has been devoted to the effects of stochastic fluctuations on cell signaling dynamics. However, many such processes involve small numbers of molecules. One important example is provided by T lymphocytes (T cells), the orchestrators of the adaptive immune response. T cell signaling and activation can be stimulated by as few as three molecules that represent signatures of pathogens (called agonists) (7–12). The small numbers of molecules involved can make stochastic effects important for membrane-proximal signaling in T cells. Here, we study simple and general models inspired by recent descriptions of membrane-proximal signaling in T cells, and find an interesting consequence of stochastic fluctuations. An essential feature of the model, dueling positive and negative feedback loops, is ubiquitous, and so our findings may be of broad relevance in cell biology.

Many examples (particularly models of gene regulation) have been studied wherein a deterministic treatment of the kinetic scheme describing the relevant processes has two stable steady states in a certain parameter regime (1–3, 13, 14). In such systems, stochastic effects can lead to bimodality (e.g., populated “on” and “off” states) in the parameter range where bistability is predicted by the deterministic equations as well as outside this range where there is a single stable steady state (1–3, 13, 14). The latter phenomenon is a consequence of stochastic fluctuations enabling the system to sample parameters (e.g., rate constants) that effectively fall within the range where two deterministically stable fixed points are present. In these examples, the existence of bistability in the deterministic analysis in some parameter range underlies the observation of bimodal behavior in the stochastic treatment.

The model we study exhibits a different feature. The deterministic dynamical equations yield a single steady state in all parameter ranges; i.e., there is no bistability. Yet, stochastic fluctuations result in a bimodal long-time response with neither mode corresponding to the steady state obtained deterministically. Upon increasing the copy numbers of molecules, the stochastic description ultimately converges to the deterministic behavior. Thus, we find a purely stochastically driven instability when none exists in the deterministic treatment in any parameter range. When fluctuations are important, we find that average quantities scale with parameters “anomalously” compared with the corresponding mean-field behavior. Our analyses suggest that the necessary and sufficient conditions for this phenomenon to occur are quite common.

Signaling Model

Our simple (“toy”) model is inspired by ideas proposed recently to describe T cell responses to diverse stimuli (7–9, 15–17). T cell receptor (TCR) molecules expressed on the surface of T cells can bind complexes of peptides (p) bound to MHC proteins on the surface of antigen-presenting cells (APCs). TCR can potentially bind strongly to pMHC molecules where the peptide is derived from a pathogen's proteins (agonists). In contrast, thymic selection ensures that TCR bind weakly to “self” or endogenous pMHC molecules that are also expressed on APCs (18). The binding of TCRs to pMHC molecules can initiate signaling cascades that result in T cell activation and an immune response. T cells are as good a sensory apparatus as any in biology, and can detect as few as three agonists in a sea of tens of thousands of endogenous pMHC molecules, and it has been suggested that this extraordinary sensitivity is mediated by cooperative interactions between self pMHC and agonists (7–10, 19).

Another interesting response of T cells to pMHC molecules is called antagonism (15, 20). Antagonists are pMHC molecules obtained by mutating agonist peptide residues. When present on APC surfaces in sufficient numbers, they can shut down intracellular signaling stimulated in response to agonists. Recent experimental results (15) have suggested that this phenomenon may be mediated by dueling positive and negative feedback loops (Fig. 1). One of the earliest steps in downstream signaling initiated by the binding of the TCR to pMHC molecules is the phosphorylation of cytoplasmic domains of the TCR complex by a kinase called Lck. It has been proposed that Lck also activates its own inhibitor, a phosphatase called Shp (negative feedback). This inhibitory interaction is prevented by a product (ERK) of signaling downstream of phosphorylation of the TCR complex that protects Lck by phosphorylating one of its sites (positive feedback). It has been proposed, and supported by detailed calculations (16, 17), that the positive feedback is dominant when T cells are stimulated by agonists (and synergistic endogenous ligands), and negative feedback shuts down signaling when sufficient numbers of antagonists are present.

Fig. 1.

A schematic representation of dueling positive and negative feedback loops stimulated upon receptor binding to stimulatory or inhibitory ligands. The negative regulator can shut off signaling by inactivating the receptor-associated signaling complex (negative feedback), whereas the positive regulator could prevent this inhibitory interaction and increase or continue production of downstream signaling products (positive feedback).

Although the specific molecular identity of positive and negative regulators involved in T cell signaling is still debated (21), the idea that dueling positive and negative feedback loops play a role in determining whether signaling is shut off (antagonism) or sustained/amplified (agonism) is of general significance to cellular decisions that lead to distinct outcomes. Furthermore, such processes are often mediated by small numbers of molecules. Therefore, we set out to study the effects of stochastic fluctuations on the following simple and general model with dueling positive and negative feedback regulation

Although this model is general, seeing how it relates to T cell signaling makes clear that it is relevant to situations where cells make distinct decisions (e.g., agonism and antagonism in Fig. 1). Reaction 1 mimics the production of the positive regulator ERK (E) upon agonist (A₁) binding to TCR. Thus, it subsumes a large number of steps in the actual signaling cascade into one. Of course, agonists also lead to production of the negative regulator Shp (S), but this is ignored in this general model. Similarly, some production of E by antagonist (A₂) binding to the receptor is ignored, and reaction 2 mimics the production of the negative regulator. Reaction 3 represents positive feedback and mimics protection of Lck from the action of Shp, in that the interaction of E with A₁ protects it (by forming A₁^PROT) from the inhibitory action of S (reaction 5). Protected A₁ species can generate positive regulators E (reaction 4), and both positive and negative regulators can be inactivated (reaction 6).

Results

The mean-field deterministic equations corresponding to the model described by Eqs. 1–6 can be written down following mass action kinetics [supporting information (SI) Text, SI Table 1, and SI Figs. 6–9], and yield the following solution for the steady state:

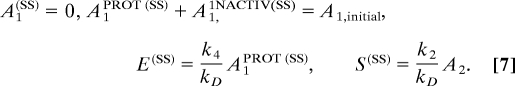At steady state, the number of A₁ molecules equals zero, the number of S molecules is a function of the number of A₂ molecules, the number of E molecules depends on the number of protected A₁ molecules, and all solutions that satisfy the constraint that the sum of the number of A₁^PROT species and A₁^INACT species sum to the initial number of A₁ are allowed. Thus, unique steady states cannot be obtained from Eqs. 7 without knowledge of the initial conditions. Rather, there is a line of possible steady states. Stability analysis shows that all, but one, eigenvalues of the Jacobian matrix are negative. The only nonnegative eigenvalue is zero, and corresponds to sliding along the line of possible steady states, A₁^PROT(SS) + A₁^{1,INACTIV(SS)} = A_1,initial, with corresponding change in the steady-state value of E. Solving the dynamical equations with specific initial conditions and taking the long-time limit obtains a unique point on this fixed line. Thus, the deterministic solutions of the model are a set of unique steady-states for all parameter values.

Although we have studied different parameter ranges for a stochastic description of this model (SI Text), let us first consider situations that are inspired by T cell signaling. Reactions 1, 2, and 4 represent multistep processes (22). Reactions 3 and 5, the dueling feedback loops, are thought to represent one-step phosphorylation or deactivation steps (15). So, we study situations where k₃ and k₅ are much larger than k₁, k₂, and k₄; i.e., both positive and negative feedback loops are strong. Recent studies (9, 17) with detailed models of membrane-proximal signaling in T cells suggests that k₄ could be larger than k₁, but we have taken them to be equal (k₄ > k₁ is considered in the SI Text). Changing the relative values of k₁ and k₂ would simply modify the specific value of the ratio of initial numbers of A₁ and A₂ molecules that would result in a transition from “agonism” to “antagonism.”

Fig. 2 shows results of spatially homogeneous stochastic simulations with discrete number of molecules [using the Gillespie algorithm (23)] of the model represented by Eqs. 1–6. When there are only a few molecules of A₁ and A₂, essentially all of the stochastic trajectories commit to one of two final states: all of the A₁ molecules are converted to the protected species, A₁^PROT, or are annihilated and signaling stops. This bimodality is in striking contrast to the mean-field solution that does not exhibit bistability for any parameter values. The qualitative phenomenon of finding a bimodal stochastic solution when the deterministic solution is unique for all parameter values is preserved as long as the positive and negative feedback loops are sufficiently strong (SI Text).

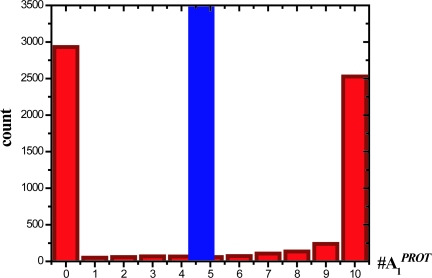
Fig. 2.

Bimodal stochastic solutions distinct from the unique deterministic solution. Histogram showing the bimodal distribution of the protected agonists at steady state (red) for a situation when there are 10 agonist (A₁) and 10 antagonists (A₂). The corresponding single steady state solution of the deterministic ODEs (blue) is also shown. The other parameter values are: k₁ = 1, k₂ = 1, k₃ = 100, k₄ = 1, k₅ = 100, k_D = 1 (all s⁻¹), and statistics were collected over 5,000 trajectories obtained by using the Gillespie algorithm. The result is robust to variations in the parameter values as long as there is strong feedback.

The mechanism underlying this result is as follows. The species A₁ is converted to either A₁^PROT or A₁^INACT. The effective rates of production of these species can be obtained from the deterministic equations. Both rates equal zero initially and at long times, and exhibit a maximum (SI Fig. 9). The initial rise and amplitudes of the maxima depend on the values of the initial number of A₁ and A₂ molecules, and are very different if one of these quantities is much larger than the other. In these circumstances, either agonism or antagonism dominates in the deterministic and stochastic solutions. The more interesting cases are ones where the generation of positive and negative regulations is roughly balanced (Fig. 2) because it could result in a transition from agonism to antagonism. Now, the rates at short times and amplitudes of the maxima for the production of A₁^PROT and A₁^INACT are comparable in the mean-field sense, and the deterministic equations yield a single steady state solution with an intermediate value of A₁^PROT. However, stochastically, one of two reactions 1 and 2 occurs first. There is a stochastic delay, τ, before the other reaction occurs, and for this duration, the reaction propensities are effectively as in cases where A₁ ≫ A₂, or vice versa. For small numbers of A₁ and A₂ molecules, τ can be long. If τ is longer than the intrinsic time scale associated with the feedback reaction corresponding to the reaction that occurred first (e.g., reaction 3 if 1 occurred first), then the small number of A₁ molecules will all be converted to either A₁^PROT or be annihilated, depending upon whether reaction 1 or 2 occurred first. So, the stochastic trajectories partition into two classes (those that end with all A₁ molecules annihilated or protected), and the stochastic solution is bimodal.

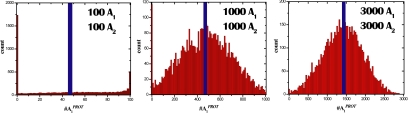
The time delay (τ) becomes smaller as the number of molecules of A₁ and A₂ increases. This observations suggests that, for a sufficiently large number of particles, it will not be longer than the intrinsic time scale associated with the feedback loops and the stochastic solution will not be bimodal. Rather, it will be distributed around the mean-field solution. Fig. 3 shows results of simulations that demonstrate this unequivocally. Thus, for the same parameter values, as the number of molecules decreases past a threshold, the stochastic solution exhibits an instability from one solution to bimodality. This transition from unimodal to bimodal solutions is driven by stochastic effects, and occurs in the absence of any underlying deterministic bistability.

Fig. 3.

A purely stochastically driven transition. Histograms showing the distribution of the protected agonists at steady state (red) and corresponding steady state solution of deterministic ODEs (blue) for different amounts of agonist and antagonist. All other parameters are identical to that in Fig. 2.

The qualitative differences between the stochastic and deterministic descriptions due to the dominance of fluctuation effects suggests that the manner in which the response scales with different control parameters may be different. For example, we expect the steady state amount of A₁^PROT to scale with k₁A₁/k₂A₂ for the stochastic simulations. This is because the probability of conversion to A₁^PROT is essentially equal to the probability that reaction 1 occurs first, which is given by k₁A₁/(k₁A₁ + k₂A₂). Conversely, probability of annihilating all A₁ molecules is equal to k₂A₂/(k₁A₁ + k₂A₂) (equal to probability that reaction 2 occurs first). Both expressions depend only on the combination k₁A₁/k₂A₂. This implies, for example, that the amount of A₁^PROT scales linearly with k₁ (a measure of how effective the agonist is in stimulating signaling). The deterministic solution, on the other hand, is not expected to obey this linear scaling. Indeed, numerical solutions support these expectations (SI Fig. 8).

The complexity of the model described by Eqs. 1–6, however, makes it difficult to explore these differences in scaling behavior precisely. The complexity also prevents us from analyzing the necessary and sufficient conditions for purely stochastic instabilities (results in Figs. 2 and 3) in cell signaling dynamics. Therefore, we formulated a simpler model that enabled exploration of these issues.

This minimal model, which can be solved exactly, includes the following features: irreversibility, branching, and feedback. The model is described in terms of the three coupled reactions shown below:

The deterministic equations corresponding to these reactions can be written down (SI Text) following the mass action kinetics. Let us denote the numbers of x, y,and z species at time t by N_x(t), N_y(t), and N_z(t), respectively. At t = 0, only Z and Y species are present; i.e., N_x (0) = 0, N_y (0) = N, and N_z (0) = M. As for the more complex model, the steady state values of the numbers of each species cannot be determined by setting the right sides of the above rate equations to zero; i.e., only a line of possible steady states can be obtained. Linear stability analysis of the steady state solutions shows that there is a neutral mode (with an eigenvalue 0) corresponding to sliding along the line of possible steady states, and stable modes along the directions δN_x + (k₂N_x^s + k₁)(M − N_x^s)/k₃δN_y and δN_y, respectively, which span the plane of the steady states. It is easy to solve the time dependent equations and take the t → ∞ limit to obtain the unique steady-state solution for given initial conditions. The time-dependent solution to the deterministic equations describing system (8) is:

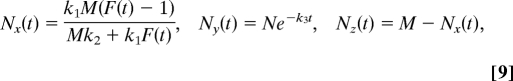where F(t) = exp[(Mk₂ + k₁)N(1 − e^−k3t)/k₃]. At long times (t ≫ k₃⁻¹), the steady state particle numbers are

Given initial conditions, these equations determine a unique steady state, a behavior identical to that exhibited by the model described by Eqs. 1–6. Unlike the more complex model, the deterministic scaling behavior can be determined, and is given by N_x^s(k₁, k₂, k₃, N, M) = Mf(Mk₂k₁⁻¹, Nk₁k₃⁻¹).

The following Master Equation describes the stochastic time evolution of the reactions shown in (8)

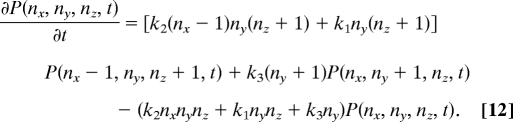P(n_x, n_y, n_z, t) denotes the probability of having n_x, n_y, and n_z particles at time t. The probability distribution at t = 0 is given by P(n_x, n_y, n_z, t = 0) = δ_nx,0δ_ny,Nδ_nz,M. Note that, at steady state (or in the limit, t → ∞), there will be no y species present, and therefore, P(n_x, n_y, n_z, t → ∞) = φ(n_x, n_z)δ_ny,0. However, any form of φ(n_x, n_z) will make the right hand side of Eq. 12 vanish. Therefore, as for the deterministic equations, irreversibility makes it necessary to solve the time-dependent Master equation for a particular initial condition to obtain the steady-state solution.

Using the method of generating functions (24), Eq. 12 can be solved exactly (SI Text) to obtain:

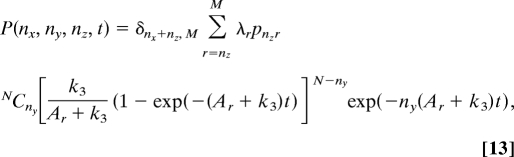where A_r = r((M − r)k₂ + k₁) and p_nzr = ^rC_nz(−1)^n_z Γ(M + k₁/k₂ + 1 − r)Γ(M + k₁/k₂ − n_z)/Γ(M + k₁/k₂ + 1 − n_z − r)Γ(M + k₁/k₂). {λ_r} are determined from the equations

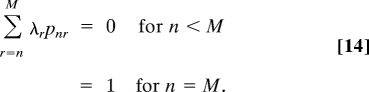At long times (t → ∞), the above probability distribution takes the form,

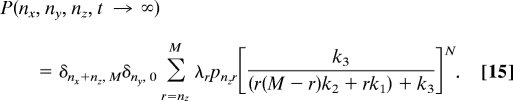Note that this solution to the Master equation indicates the appearance of a spectrum of time scales (indexed by r and n_y), which is presumably related to stochastic delays.

Eq. 15 results in a steady state probability distribution that is bimodal for small numbers of molecules (SI Fig. 11a) when the deterministic solution does not exhibit bistability in any parameter range. In the more complex model that we studied (Eqs. 1–6), mean-field behavior was obtained as the numbers of A₁ and A₂ molecules increased past a threshold value even though their relative numbers were kept constant. The corresponding limit for the minimal model is k₃ → ∞, N → ∞, with the ratio N/k₃ (or the dimensionless, Nk₁/k₃) remaining constant. This is because a large value of N corresponds to a large amount of the source of a positive regulator (A₁ in Eqs. 1–6) and a large value of k₃ corresponds to greater annihilation or a big source (A₂ in Eqs. 1–6) of negative regulation. SI Fig. 11b shows that, like the more complex model, there is a purely stochastic transition as the stochastic solution is unimodal and distributed around the deterministic solution above a threshold value of N and k₃. So, these results establish that the sufficient conditions for the phenomena we report are: irreversibility, branching, and feedback loops. But, are these also necessary conditions?

The possibility of two different outcomes is obviously necessary, and branching is ubiquitous in cell signaling processes that lead to functional decisions. We have also found that removing irreversibility abolishes the phenomenon (data not shown). Ultimately, all reactions are, in principle, reversible. However, in the time scales of interest to signal propagation in cells, many steps are effectively irreversible.

Feedback regulation is also necessary as the bimodal stochastic solution does not exist if k₂ in the minimal model tends to zero (SI Fig. 15). Insight into the kind of feedback regulation that is necessary can be obtained by contrasting our studies of dueling feedback loops in cell signaling to a model for binary drift in population genetics (25, 26). Consider a population of heterozygote individuals with two forms, B₁ and B₂, for a particular allele. In the absence of mutations, the number of each type of allele can change from generation to generation, even in a population of fixed size, due to mating. The effects of binary selection on the numbers of B₁ and B₂ forms can be roughly represented as follows (25, 26):

with k and k′ related to the relative fitness of each phenotype.

The model described by Eq. 16 also contains branching and irreversibility. There is also an effective feedback, but unlike Eqs. 1–6 or 8, there is no separate intrinsic time scale associated with the feedback loops. A special case of this model (with no selection), k = k′, shares some features with the systems we are considering. The deterministic changes in this limit are trivially zero, and any initial condition (along the fixed line of B₁ + B₂ = population size) remains fixed. These deterministic steady states are unique, but the stochastic solutions yield a bimodal distribution. This is because the stochastic trajectories are divided into two classes: ones that terminate when the number of B₁ particles vanishes and those that terminate when the number of B₂ reaches zero.

There is an important difference, however, between the model for binary drift with k = k′ and the class of cell signaling models we have been considering. The stochastic solution of the model represented by Eq. 16 does not converge to the deterministic solution when the number of particles becomes large. The stochastic solution at t → ∞ is always bimodal. The stochastic trajectories cease to evolve when either B₁ or B₂ become zero because only then is the effective rate of conversion between these species equal to zero. The deterministic rates of formation of B₁ and B₂ equal the same constant for all times. Increasing the numbers of molecules does not eliminate this difference between the deterministic and stochastic cases. As the number of particles increases, the stochastically determined time (τ′) required for B₁ or B₂ to equal zero increases, but ultimately it always happens. There is no separate intrinsic time scale that can compete with increasing values of τ′ as the number of particles increases and prevent this from happening (i.e., a bimodal solution). Recall that, for the signaling models that we focused on, the relative values of the stochastic delay, τ, and the separate time scale associated with feedback loops determined the stochastically driven transition when the number of molecules was lowered (Fig. 3 and SI Fig. 11b). The absence of such an interplay prevents a purely stochastic instability in the binary drift model as the number of particles decreases. Correspondingly, if the rate coefficients in the model represented by Eq. 16 were time dependent with an intrinsic time scale, the phenomenon of a purely stochastic instability would be recovered.

The analyses presented above suggest that the necessary and sufficient conditions for a purely stochastic bimodality in the absence of any deterministic bistabilities are: (i) irreversibility, (ii) branching, and (iii) feedback regulation with an associated distinct and fast time scale.

The analytical solution for the probability distribution (Eq. 15) obtained for the minimal model of cell signaling that satisfies these conditions enables us to calculate average properties, such as the average number of molecules of the product, 〈x〉. This allows us to examine whether 〈x〉 scales with parameter values in the same way as N_x determined from the mean-field equations (see above). The average value, 〈x〉, is

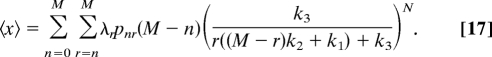So, in general, there is no simple scaling law, such as N_x scaling with Nk₁/k₃, as in the deterministic limit. Does this “anomalous” scaling, originating from the importance of stochastic fluctuations, revert to mean-field scaling behavior in the limit corresponding to a large numbers of particles?

To answer this question, as shown above, we need to consider the value of 〈x〉 in the limit of large values of N, M, and k₃. Consider first the limit of large values of N and k₃ for a fixed value of Nk₁/k₃. Simple algebra yields the value of 〈x〉 in this limit to be

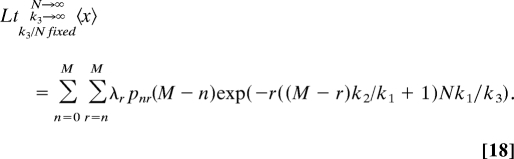So, the deterministic scaling with Nk₁/k₃ (Eq. 10) is recovered in the appropriate limit. Similarly, mean-field scaling is recovered in the limit of large values of N and M (SI Text).

The general solution (Eq. 18) for 〈x〉 does not allow us to explicate the non-mean-field scaling when fluctuations are important. This can be obtained analytically only in special limits. For example, consider the limit of infinitely strong feedback (k₂ → ∞). In this limit, 〈x〉 takes the following form (SI Text)

Fig. 4 shows that 〈x〉 obtained from numerical solutions of the Master equation (Eq. 8) for different values of N and k₃ collapse to one master curve when scaled according to Eq. 19, a scaling that is distinctly different from the mean-field scaling with Nk₁/k₃. We have not been able to determine whether these specific differences in scaling laws between the deterministic and biologically relevant stochastic solutions are universal to all models which satisfy the necessary and sufficient conditions (identified earlier) for a purely stochastic instability.

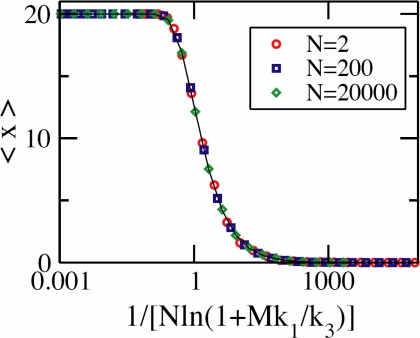
Fig. 4.

Results from the minimal model. Non-mean-field scaling in the limit of large positive feedback (k₂ → ∞): The average values of X species, 〈x〉, at steady state obtained from Gillespie simulations scale with (1/log(1 + Mk₁/k₃)) instead of the mean field scaling variable Nk₁/k₃. The values of the parameter k₂ is 100 s⁻¹ (i.e., a large value). k₁ = 0.0012 s⁻¹ and M = 20 are held fixed as k₃ and N are varied. The solid line is a plot of the scaling function shown in Eq. 19.

Discussion

Dueling positive and negative feedback loops are ubiquitous in biology. In many instances, these processes involve small numbers of the pertinent molecules, and hence stochastic fluctuations can be important. We report a striking result for such systems. The models we have studied correspond to unique deterministic steady states for all parameter values, and do not exhibit bistability. Yet, when there are a small number of molecules, stochastic effects result in a bimodal solution with neither solution corresponding to the mean-field result. Our analyses suggest that the necessary and sufficient conditions for this phenomenon are irreversibility, branching, and the existence of an intrinsic and relatively fast time scale associated with feedback regulation. Our studies show that for specific examples of such systems, near the transition from one phenotype to another (e.g., agonism to antagonism), mean-field scaling does not apply to the stochastic solutions. Whether the specific differences in scaling between mean-field and stochastic solutions that we report are universal for the class of models that exhibit the phenomenon revealed by our studies remains an open question.

There is a key difference between models of gene regulation and cell signaling where bimodality has been observed in stochastic limits under conditions where the deterministic equations yield monostable solutions and our results. In the former examples (double negative feedback, dimer mediated gene regulation, etc., e.g. refs. 1 and 27–32), bistable deterministic solutions exist in some other parameter regime. Stochastic bimodality displayed by binary drift models in population genetics are also different from the phenomena we report in that the stochastic solutions are always bimodal, regardless of the number of particles; i.e., there is no stochastically driven transition from a single solution to bistable solutions.

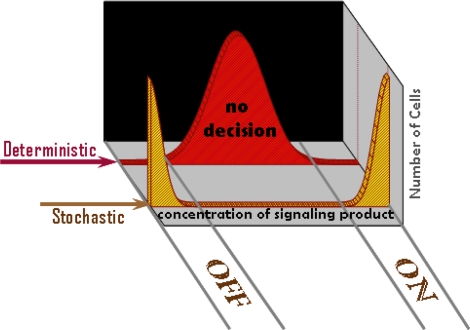
The necessary and sufficient conditions for the phenomenon that we report (branching, irreversibility, and feedback loops with distinct time scales) are quite common in cell biology. Our results suggest that these features, when combined with stochastic fluctuations, can enable cells to make binary decisions, whereas this would not be possible in a deterministic world. For instance, if gene transcription and effector function required greater than a threshold value of a downstream signaling product, in a mean-field world, cells would be unable to make decisions with a distinct functional outcome (Fig. 5). Under the same conditions, stochastic effects would result in cells being either “on” or “off” (Fig. 5), as observed in experimental studies in diverse contexts.

Fig. 5.

Stochastic fluctuations can enable cellular decisions. Schematic representation showing that irreversibility, branching, and dueling feedback loops associated with intrinsic time scales, when combined with stochastic effects, can result in distinct functional decisions for each cell. A deterministic treatment would mask this ability of cells to make decisions.

For example, a recent study of HIV latency by Weinberger et al. (4) showed a “temporary” bimodal cell population in a time window when there is no instability in the set of rate equations used to describe the signaling events. The main difference between this study and the results we have discussed is that, in ref. 4, the observed bimodality disappears at long times. Another example is provided by T cell signaling. It has been proposed that dueling feedback regulation could underlie how antagonists shut off signaling in T cells. Experiments show a bimodal response for a downstream signaling product (Erk), with the proportion of “off” cells increasing as the number of antagonists becomes larger (15, 16). Stochastic simulations of a model of the T cell signaling network are in accord with these experimental observations (SI Text); i.e., bimodal distributions are the norm because of fluctuations, whereas the deterministic equations do not exhibit bistability in any parameter regime. However, we emphasize that a bimodal or “digital” ERK response in T cells could also result from important contributions from other molecular mechanisms (33).

We hope that the possibility of purely stochastic instabilities that lead to distinct cellular decisions will be broadly explored in the context of cell signaling processes by carrying out single cell assays for systems where the necessary and sufficient conditions we have described are naturally present or are engineered.

Abbreviation

TCR

T cell receptor.