The blinking spotlight of attention

Abstract

Increasing evidence suggests that attention can concurrently select multiple locations; yet it is not clear whether this ability relies on continuous allocation of attention to the different targets (a “parallel” strategy) or whether attention switches rapidly between the targets (a periodic “sampling” strategy). Here, we propose a method to distinguish between these two alternatives. The human psychometric function for detection of a single target as a function of its duration can be used to predict the corresponding function for two or more attended targets. Importantly, the predicted curves differ, depending on whether a parallel or sampling strategy is assumed. For a challenging detection task, we found that human performance was best reflected by a sampling model, indicating that multiple items of interest were processed in series at a rate of approximately seven items per second. Surprisingly, the data suggested that attention operated in this periodic regime, even when it was focused on a single target. That is, attention might rely on an intrinsically periodic process.

Selective attention denotes the ability to enhance processing of a particular location or object. In recent years a number of studies have suggested that multiple locations can be concurrently attended (1–6). In most of these cases, however, it is difficult to distinguish a true (i.e., sustained) division of the attentional spotlight, from a strategy in which a single attentional focus would switch rapidly between the different targets. Indeed, both strategies could explain the occurrence of classic “set size effects” (i.e., decreases of performance with increasing number of attended items) either because attention is a limited resource (“parallel” strategy), or because the effective time that attention samples each object decreases when several objects must be attended (“sampling” strategy). With respect to visual search tasks, in which a single target must be detected among a variable number of elements, this debate has divided the community for quite some time, with no accepted conclusion [Sternberg S (1973) in Annual Meeting of the Psychonomics Society in St. Louis, MO, and refs. 8–14]. A similarly unresolved argument has been made regarding multiple-object tracking paradigms (15–18).

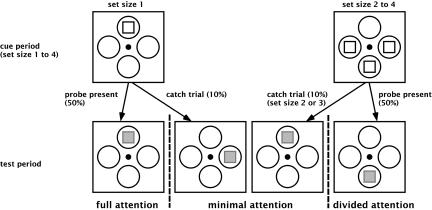
Here, we propose a quantitative strategy for distinguishing between these alternatives: The psychometric function for detection of a single target as a function of its duration can be used to predict the expected psychometric function for multiple targets, and the predicted shape is quite different for parallel and sequential strategies. We can thus determine which strategy best describes the performance of human observers with multiple attended items. The mathematical details of this method are given in supporting information (SI) Appendix, but the underlying idea can also be understood in simple terms. A “probe” event of variable duration must be detected by the observer (Fig. 1). When only a single location is cued, the observer can allocate their attentional resources entirely to this location (“full attention” condition). In other trials, there can be two or more cued locations (“divided attention” condition; note that the term “divided” refers here to a particular experimental instruction, independent of the attentional allocation strategy—parallel or sequential—chosen by the subject). Finally, on catch trials, the probe occurs in an uncued, unexpected location (“minimal attention” condition). Within a “parallel” model, attention is shared across the targets so performance for a given probe duration will lie somewhere between the performance levels obtained with full and with minimal attention at this same duration (Fig. 2A). As the number of cued locations increases, the psychometric function will move closer to the function found for minimal attention (governed by a parameter we call the division cost). For a “sampling” strategy, performance is again a mixture of the full and minimal attention functions but in a manner determined by the location of attention at the onset of the probe and the rate at which it moves from one cued location to the next. Each successive sample, whether directed to the location of the probe or one of the other cued locations, might temporally overlap with the probe for a certain duration, drawing a corresponding contribution from the “full” or the “minimal attention” functions, respectively (see Fig. 2 B and C for examples and SI Appendix for a more detailed description).

Fig. 1.

Experimental design. Four disks filled with high-contrast dynamic random noise were constantly shown to the subjects. At the beginning of each block, a cue display indicated which of the disks were likely to contain the probe for the following trials (set size 1–4). The probe was a contrast decrement of variable duration, occurring with 50% probability in one of the cued elements. At set size 1, “full attention” could be allocated to the probe, whereas at set sizes 2, 3, and 4, attention had to be “divided” between multiple targets. In 10% of trials (including probe-present trials), a catch stimulus (similar to the probe) was shown at an uncued location. By definition, we assume that it received “minimal attention.” (Set size 4 trials had no uncued location and therefore could not serve as catch trials). At the end of each trial, subjects reported whether the probe was presented among the cued locations, and (using a separate key) whether a catch stimulus had been detected at an uncued location. Probe and catch stimulus duration varied independently between 50 and 1,000 ms. The strength of the contrast decrement could either be 50% (“easy” version) or 30% (“difficult” version).

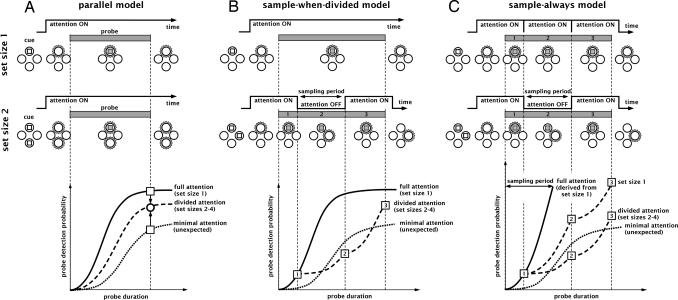
Fig. 2.

Computational principle. The detection probability of a probe event (e.g., brief contrast decrement) increases with its duration. Using the psychometric functions obtained for full attention (when the probe location is known) and minimal attention (when the probe occurs at an unexpected location), one can derive predicted functions for divided attention (when the probe occurs at one of multiple possible target locations). Depending on the strategy assumed for attentional allocation (“parallel,” “sample-when-divided,” or “sample-always”), the predicted functions will differ. We can thus distinguish among these three alternative models of divided attention. (A) Within a parallel model, probe information for divided attention accrues at a rate intermediate between that obtained for full and for minimal attention; performance only depends on performance with full and minimal attention at the same probe duration. (B) Within a sampling model, performance for divided attention (shown here for one example trial with a set size of 2) originates from a series of periods during which information accrues either at the rate of full attention (periods marked 1 and 3 in this example) or at the rate of minimal attention (period 2). Only the onset portion of the full attention psychometric curve, with values below the postulated sampling period, is used to generate these predictions (because attention will not rest at a given location for longer than the postulated sampling period). Note that the illustration is only meant to exemplify what happens on a single hypothetical trial; this explains the accelerating shape of the information accrual function for this illustrative trial. In the general case, because the onset time of each attentional sample on any given trial is unknown, we integrate the depicted calculation over all possible onset times (see SI Appendix); this integration will result in regular nonaccelerating psychometric functions (data not shown). (C) In the “sample-always” model, information accrues in discrete epochs, even when a single location is cued. The “set size 1” psychometric function therefore reflects a collection of such epochs and not the true full attention function. The full attention curve can be recovered from the set size 1 curve, however, by inverting the previously described calculation (see SI Appendix). Performance with divided attention is then derived as before (B) by combining periods of full attention and minimal attention.

We consider two versions of the “sampling” model. According to the “sample-when-divided” version (Fig. 2B), the periodic sampling strategy is used only when more than one item must be attended; for a single attended item, even at long durations, attention will sample the probe for its entire duration. This reflects the classic idea of a switching “spotlight” of attention (19–22). According to the “sample-always” version (Fig. 2C), periodic sampling occurs even when only one item is attended: At long durations the probe is not sampled continuously, but in a succession of epochs whose information is combined (by probability summation) before the decision is made (for convenience, the “duty cycle” of this periodic sampling process was assumed to be 1, i.e., there was no “off” time between successive samples). The psychometric curve at set size 1, in this case, is already the result of a temporal sampling process, and so another full-attention curve must be hypothesized (and ultimately computed, based on the observed performance at set size 1; see SI Appendix). Such systematic sampling could occur, for example, if the interplay between information sampling and information processing stages restricted information transmission to particular moments. Although such a strategy might seem inefficient, the idea is supported by recent findings suggesting that certain forms of motion perception, for a single moving element, could rely on attentional sampling at a more-or-less fixed rate (23, 24). Overall, we thus compared 3 models (parallel, sample-always, sample-when-divided) and attempted to determine which model could best explain human performance in a contrast decrement detection task with multiple potential target locations. Two different contrast decrement strengths were used, resulting in an “easier” and a more “difficult” version of the task. (As we will see later, these two versions entail different attentional requirements, as defined by visual search slopes: efficient search for the easy task, inefficient search for the difficult task.). Each model was given a single free parameter: the sampling period (from 50 ms to 1,000 ms) for the two sampling models, a division cost parameter (from 0 to 1) for the parallel model, reflecting the cost in performance for sharing attention with each additional target. The entire parameter space was explored, and the best parameter value (i.e., the value that generated a prediction closest to the performance of a given human observer) was determined for each model. The model with the lowest prediction error is likely to reflect the attentional allocation strategy used by our observers.

Results

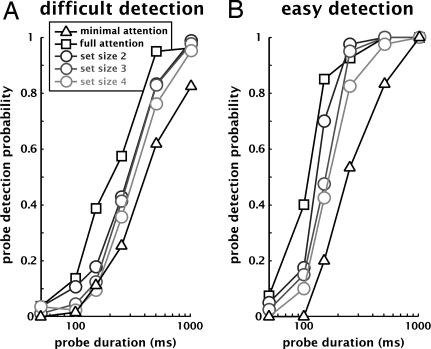
Psychometric functions from one representative subject are shown in Fig. 3. Over the group of eight subjects, a three-way ANOVA (task difficulty × set size × probe duration) confirms that the probability of detecting the probe increases with increasing duration [F (5, 336) = 553.4, P < 0.0001] and that it is also affected by set size [F (3, 336) = 9.9, P < 0.0001]. Importantly, although task difficulty had a main effect on performance [F (1, 336) = 346.5, P < 0.0001] and significantly interacted with probe duration [i.e., affected the slope and/or the threshold of the psychometric functions; F (5, 336) = 36.0, P < 0.0001], it did not reduce the effects of set size [F (3, 336) = 0.2, P = 0.9]. We can thus investigate, both for the difficult and easy versions of the task, the attentional strategy that led to these significant set size effects. The same three-way ANOVA for performance obtained in the “minimal attention” condition (when the probe appeared at one of the uncued locations) again revealed a main effect of probe duration [F (5, 252) = 136.1, P < 0.0001] and of task difficulty [F (1, 252) = 108.5, P < 0.0001], but no main effect of set size [F (2, 252) = 0.5, P = 0.59] and no interaction between set size and task difficulty [F (2, 252) = 1.2, P = 0.31]. This is somewhat expected: Set size determines the division of attentional resources among the cued elements, but should not affect what goes on outside of the focus of attention. Thus, we collapsed the minimal attention data across set sizes (Fig. 3).

Fig. 3.

Psychometric functions for one subject in the difficult (A) and easy (B) versions of the contrast decrement detection task. Probe detection probability increases steadily with probe duration (note the log scale on the x axis). Although the functions are steeper and shifted to the left in the easy version compared with the difficult version, set size (the number of cued elements) significantly affects performance in both cases.

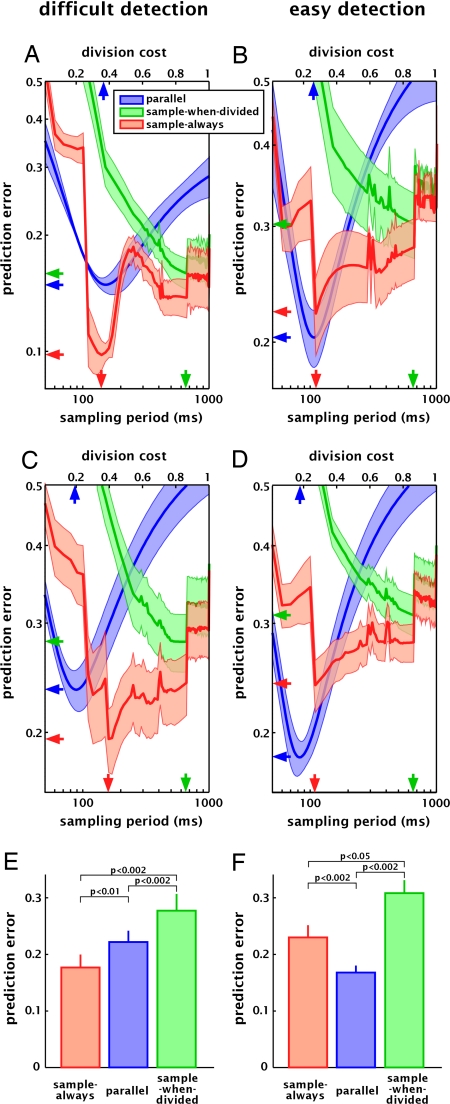
The derivation of optimal parameters for each model is illustrated in Fig. 4 A and C for the “difficult” task, and in Fig. 4 B and D for the “easy” task. From a given subject's psychometric functions with full and minimal attention (Fig. 3), we computed the expected psychometric functions for divided attention (set sizes 2, 3, and 4) within each of the three models (as illustrated in Fig. 2 and detailed in SI Appendix). For each model, we explored the range of possible parameter values (the single free parameter was the sampling period for the sampling models and the cost of each additional attended element for the parallel model), and each time, we computed the prediction error, i.e., the distance between predicted and observed data (Fig. 4 A and B shows these prediction errors for the same subject as in Fig. 3; Fig. 4 C and D shows an average over the group of eight subjects). The “optimal” parameter value was the one yielding the lowest prediction error (vertical arrows in Fig. 4 A–D) when compared with the actual experimental data. The “best” model (i.e., most likely to reflect the subject's strategy) was taken to be the one yielding the smallest prediction error (horizontal arrows in Fig. 4 A–D). The average prediction errors at the optimal parameter value of each model are reported in Fig. 4 E and F.

Fig. 4.

Model prediction errors for one subject (A and B, same subject as in Fig. 3) and averaged across eight subjects (C and D), in the difficult (A and C) and the easy (B and D) versions of the contrast decrement detection task. The prediction error is the r.m.s. distance between observed and predicted data in the divided attention conditions (i.e., set sizes 2, 3, and 4). This error is computed for each possible value of the model parameter (sampling period for the sample-always and the sample-when-divided models, lower horizontal axis; division cost for the “parallel” model, upper horizontal axis). The mean prediction error (±SEM, shaded area) across set sizes is plotted for each model. The optimal model is the one yielding the lowest prediction error (horizontal arrows on the left vertical axis), which in A is the sample-always model and in B is the parallel model. The optimal parameter values for each model are indicated by the vertical arrows. (C) Average prediction errors across eight subjects in the difficult version of the task. The shaded area represents SEM across subjects. The sample-always model was the optimal for all subjects tested, with an optimal “sampling period” of 140 ms on average (range 100–190 ms). (D) Average prediction errors across eight subjects in the easy version of the task. The optimal model in this case is the parallel model, with an optimal “division cost” of 17% on average (range 9–25%). (E and F) Prediction error of each model at its optimal parameter value (average across eight subjects). (E) For a difficult contrast decrement detection task, the model that best reflected human performance was a sampling model, in which periodic sampling occurred even during undivided attention (sample-always model). (F) For an easier version of the same task, the parallel strategy yielded the lowest prediction error. The classic idea of a switching spotlight (sample-when-divided model) did not closely reflect our observers' strategy in either situation.

A two-way ANOVA (model type ×task difficulty) revealed no main effect of task difficulty [F (1, 42) = 0.31. P > 0.5] on prediction accuracy but a significant effect of model type [F (2, 42) = 11.9, P < 0.0001] and a significant interaction [F (2, 42) = 3.23, P < 0.05], showing that the various models' ability to predict experimental data depended on task difficulty (Fig. 4 E and F). The model that best predicted our observed data (determined with post hoc pair-wise t tests, P < 0.05) was the sample-always model when the task involved a challenging contrast decrement detection (with the sampling period ≈140 ms, ranging from 100 to 190 ms across our eight subjects; Fig. 4 A, C, and E), whereas the optimal model was a parallel one for an easy version of the same task (with a performance cost of 17% for each additional item to be attended; Fig. 4 B, D, and F). This distinction was observed for all subjects tested, a result that would be highly unlikely to occur by chance, were these two models assumed to be equivalent (P < 0.00005). The sample-when-divided model performed significantly worse than the other two, both in the easy and in the difficult versions of the task (with an optimal sampling period at 660 and 580 ms, respectively). Note that prediction errors were also computed for the false alarm data (SI Fig. 6): in this case the two-way ANOVA did not yield a significant effect of model type [F (2, 42) = 0.04, P > 0.9] or a significant interaction between model type and task difficulty [F (2, 42) = 0.04, P > 0.9]. Thus, the previous result is unlikely to be due to some tradeoff between correct detections and false alarms.

The better performance of the parallel model in the easy version of the task is unlikely to be due to eye movements or faulty fixation, because gaze cannot be simultaneously divided between multiple locations. However, the better performance of the sample-always model during the difficult task raises the possibility that our observers could have used a gaze-switching strategy. Given our modeling results, this would require that the eyes move approximately seven times per second, even when a single location is attended. Or, it could arise from intersaccade intervals that are randomly, different integer multiples of one seventh of a second, a distribution of eye movement timing that has not been previously reported. Nevertheless, to address this alternate explanation, we had two of our subjects perform the difficult version of the task while their eye movements were monitored (SI Fig. 7). Even though eye movements toward the targets were never observed, both observers displayed the usual pattern of results, with the sample-always model yielding the best prediction (at a sampling period of 160 and 180 ms, respectively), followed by the parallel and the sample-when-divided models.

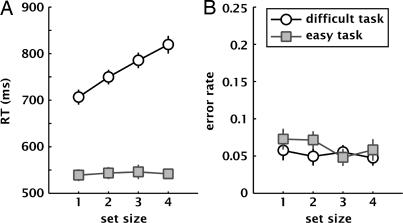
What might be the inherent difference between the easy and difficult versions of our detection task, which makes one a parallel process and the other an apparently sequential one? In a control experiment we presented our stimuli in a situation akin to a “visual search” experiment. We manipulated effective set size on each trial by precueing a random subset of the four elements using central arrows. The probe, when present, was always shown at one of the cued locations and remained until the subject responded by pressing the appropriate button (probe present/absent). We measured the reaction times as a function of effective set size on each trial, both for the difficult and the easy contrast decrement levels (Fig. 5). A two-way ANOVA (set size ×task difficulty) with reaction time as the dependent variable revealed a main effect of set size [F (3, 56) = 5.3, P < 0.005] and a main effect of task difficulty [F (1, 56) = 425.1, P < 10⁻⁶], as well as a significant interaction [F (3, 56) = 4.72, P < 0.01]. No significant main effect or interaction was found with error rate as the dependent variable (P > 0.2). Post hoc tests showed that set size significantly affected reaction time for the difficult task [F (3, 28) = 8.1, P < 0.0005] but not for the easy task [F (3, 28) = 0.05, P > 0.98]. In other words, detecting the stronger contrast decrement relied on a parallel search (slope 1 ms per item), whereas the search was “serial” (slope 38 ms per item) for the fainter contrast decrement. This qualitative difference between the two difficulty levels probably reflects the different strategies used by our observers for allocating attention in the 2 versions of the main experiment.

Fig. 5.

Reaction times (A) and error rates (B) for contrast decrement detection in the control experiment, as a function of set size (number of precued elements), for the two different difficulty levels (n = 8). Whereas error rates are unaffected by task difficulty, reaction times strongly differ depending on the task. The search slopes (average RT increase for each set size increase) are 38 ms per item and 1 ms per item, respectively, for the difficult and easy versions of the task, suggesting that the task difficulty alters the underlying attentional requirements.

Discussion

Our results show that attention might resolve a difficult, attentionally demanding task by periodically sampling information from the different target locations, at a rate of approximately seven elements per second. This strategy is not identical, however, to the classic hypothesis of a “serial spotlight” of attention postulated by two-stage theories of visual processing (19–22): it appears, indeed, that attention also operated in this periodic sampling regime when it was focused on a single target location. Without this property, a classic “serial switching” model was shown to perform poorly at explaining human psychometric functions. This may elucidate why, so far, serial switching models have fared relatively poorly in previous attempts at pitting them against parallel models [e.g., Eckstein (13)].

For an easy version of the contrast decrement detection task (i.e., one that generates flat search slopes and probably requires little attention), a parallel allocation of attentional resources to the different potential targets appeared to be a viable strategy. However, the parallel model mainly dictates the spatial distribution of attention during the trials, and not the temporal strategy: we cannot rule out the idea that periodic samples were also taken during this task if we assume that each sample would comprise information from all targets at once. As a side note, the fact that we obtained distinct results in two different versions of the task rules out the possibility that a systematic artifact in our analysis method could be responsible for the better performance of the sample-always model in the difficult contrast decrement detection task.

Of course, the present conclusions are derived from modeling of psychometric functions, which (like all modeling efforts) necessitates making assumptions about psychological processes. There is still the possibility, therefore, that these assumptions and the corresponding models do not cover the entire spectrum of alternatives and that adding assumptions (or free parameters) to a parallel or a classic “serial switching” model might endow it with better prediction accuracy. For example, recent evidence suggests that independent attentional resources exist for the two visual hemifields (25). It is possible that a hybrid model assuming parallel allocation of attention across hemifields, but periodic sampling of information within each hemifield, might better reflect our observers' performance. This would be an interesting possibility to explore in further model refinements.

If attention, when focused on a single location, samples information periodically like a blinking spotlight, then why have the hundreds of previous studies of attentional mechanisms not revealed this remarkable property? The fact that most experimental paradigms (even those involving electrophysiology) rely on averaging signals across several trials is probably a good place to start looking for an explanation. If the onset of each periodic attentional sample (an internal process) bears no relation to stimulus onset (an external event), such averaging would conceal the effects of periodic attentional sampling to the experimenter. On the other hand, our quantitative method allows us to address, albeit only statistically, the temporal allocation of attention on single trials. Another outstanding possibility could be that our task and experimental conditions are unique for generating this pattern of results. It is true that our conclusions obtained in a task requiring the sustained monitoring of a particular feature (contrast) at multiple static locations may not generalize to studies concerned with transient aspects of attention or to tasks requiring the sustained monitoring of multiple locations independent of featural information (e.g., multiple-object-tracking paradigms). Similarly, we address only spatial aspects of attention, whereas it is well known that some feature-based forms of attention can enhance the processing of a particular feature throughout the entire visual field, i.e., in a nonspatial way (26–28). It would seem, however, that even if the present results were shown to hold only for a very particular form of attention under specific experimental conditions, they would still provide a forceful challenge for current theories of attention, most of which are not equipped to explain our findings—with only a few exceptions (29).

In conclusion, a more profound question beckons: Why should the attentional system adopt the less-than-optimal strategy of not sampling continuously, especially if there is only one location being sampled? Active periodic sampling of the outside environment is a ubiquitous property of sensory systems: saccades in vision, sniffs in olfaction, whisker movements in rat somatosensation, and even echolocation in bats or electrolocation in the electric fish are all examples of explicit cyclic mechanisms for overt perceptual sampling (30). Attention might have evolved from these periodic processes, as a more economical means of covertly sampling endogenous representations—possibly relying on the widespread oscillations that can be observed in most of these systems (31–40). More simply, it could be that the interplay between information sampling and information processing in the visual system requires the sampling stages to transmit information during particular epochs, rather than continuously; or it could be that the process that directs the sampling must also govern other processing stages and has to alternate between these functions. Whatever the ecological reason (if any) ultimately turns out to be, the suggestion that attention operates periodically will have significant implications for future research.

Experimental Methods

We had eight human observers (three females, five males; age range 25–32) who performed two versions of a task (in separate sessions) involving the detection of a contrast decrement. Subjects were seated in a dimly lit room. Four disk stimuli (radius 1.5° of visual angle) were presented on a gray screen at 4° from fixation in the four cardinal directions (Fig. 1). At the beginning of a block of trials, one to four of the disks were cued as potential targets for this block (the number of cued disks will be referred to as “set size”). Subjects were instructed to focus attention on these disks and ignore others. To minimize the effects of trial and stimulus-onset transients, all disks flickered constantly (even during the intervals between trials and between blocks) with spatiotemporal white noise at maximum contrast (pixel size 0.3°, interval between successive frames 10 ms). A trial lasted for 2 s, and was indicated solely by the presence of the fixation cross. With a 50% probability in each trial, one of the cued disks presented a contrast decrement (the probe), whose duration varied from 50 to 1,000 ms. The task of the subjects was to report whether a decrement had occurred or not, by pressing the appropriate key at the end of the trial. The two versions of the task corresponded to different strengths of the contrast decrement: 50% for the easy version, and 30% for the difficult version. A movie rendition of the task can be downloaded at http://www.klab.caltech.edu/∼rufin/blinkingspotlight/movie1.avi. Psychometric functions for probe detection as a function of its duration were determined for each subject and set size (between one and four). Additionally, we also determined subjects' performance outside of the main focus of attention by presenting a number of catch trials (10% probability) in which the contrast decrement was shown in one of the uncued disks. Subjects were instructed to press a separate key if they detected this decrement. Thus, we also determined the psychometric function for performance with minimal attention. This function is critical because it provides a baseline for computing performance in the divided attention conditions (this is true for all three strategies compared; see SI Appendix). Half of the observers initially performed the easy version of the task, and the other half began with the difficult version. Each subject performed at least 1,152 trials (six sessions × four set sizes × 48 trials) for each version of the task. Two of the observers performed the difficult version of the task a second time (for at least 960 trials each) while their eye positions were monitored by using a binocular infrared eye-tracker at a sampling rate of 120 Hz (ISCAN ETL 200; ISCAN).

After the main experiment, each subject completed two sessions (corresponding to the easy and difficult contrast decrement levels) of a control experiment, in which the cue for potential targets was presented centrally (using one to four central arrows) at the beginning of each trial. Cue validity was 100%: The probe (contrast decrement) always appeared on one of the cued elements. The probe, when present, remained until the subject's response (a so-called “response-terminated search” procedure), and reaction times were measured as a function of the effective set size (i.e., how many potential targets had been cued on this trial). Each subject performed at least 256 trials (four blocks of 64 trials) for each version of the task. A movie rendition of this control task can be downloaded at http://www.klab.caltech.edu/∼rufin/blinkingspotlight/movie2.avi.