A Role for the S0 Transmembrane Segment in Voltage-dependent Gating of BK Channels

Abstract

BK (Maxi-K) channel activity is allosterically regulated by a Ca²⁺ sensor, formed primarily by the channel's large cytoplasmic carboxyl tail segment, and a voltage sensor, formed by its transmembrane helices. As with other voltage-gated K channels, voltage sensing in the BK channel is accomplished through interactions of the S1–S4 transmembrane segments with the electric field. However, the BK channel is unique in that it contains an additional amino-terminal transmembrane segment, S0, which is important in the functional interaction between BK channel α and β subunits. In this study, we used perturbation mutagenesis to analyze the role of S0 in channel gating. Single residues in the S0 region of the BK channel were substituted with tryptophan to give a large change in side chain volume; native tryptophans in S0 were substituted with alanine. The effects of the mutations on voltage- and Ca²⁺-dependent gating were quantified using patch-clamp electrophysiology. Three of the S0 mutants (F25W, L26W, and S29W) showed especially large shifts in their conductance–voltage (G-V) relations along the voltage axis compared to wild type. The G-V shifts for these mutants persisted at nominally 0 Ca²⁺, suggesting that these effects cannot arise simply from altered Ca²⁺ sensitivity. The basal open probabilities for these mutants at hyperpolarized voltages (where voltage sensor activation is minimal) were similar to wild type, suggesting that these mutations may primarily perturb voltage sensor function. Further analysis using the dual allosteric model for BK channel gating showed that the major effects of the F25W, L26W, and S29W mutations could be accounted for primarily by decreasing the equilibrium constant for voltage sensor movement. We conclude that S0 may make functional contact with other transmembrane regions of the BK channel to modulate the equilibrium between resting and active states of the channel's voltage sensor.

INTRODUCTION

Large conductance Ca²⁺-activated K⁺ channels (BK or maxi-K channels) are opened by depolarization and raised intracellular Ca²⁺, and the current through these channels regulates cellular excitability across a variety of tissues, including smooth muscle and brain (for review see Latorre, 1994). The BK channel is related to depolarization-activated K⁺ channels (Kv channels), which have a tetrameric structure with each subunit containing six transmembrane regions (Butler et al., 1993; Shen et al., 1994). Kv channel gating is controlled by voltage sensors, which are formed primarily by the first four transmembrane helices of each subunit (S1–S4; Bezanilla, 2000). Likewise, BK gating is controlled by an intrinsic voltage sensor formed by these segments (Cui et al., 1997; Ma et al., 2006).

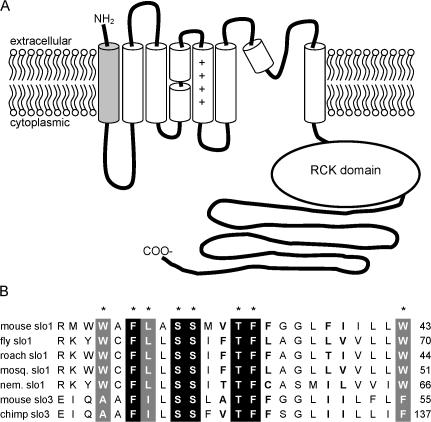
BK channels are unique, however, in that they contain a Ca²⁺ sensor that is formed by the cytoplasmic carboxyl ends of the four channel subunits (Schreiber et al., 1999; Bian et al., 2001; Bao et al., 2002; Bao et al., 2004). Also, BK channels contain an additional transmembrane region, S0, at the amino end of each subunit (Fig. 1) (Wallner et al., 1996; Meera et al., 1997). This segment contains several residues that are highly conserved among BK channel orthologues. This sequence conservation may indicate a role for these side chains in channel structure and function, yet the function of the S0 segment has not yet been studied in detail. It also seems that the S0 region may form an important component of the interacting region between the BK channel and its β subunits (Wallner et al., 1996). Thus it will be important to learn the role of the S0 segment in gating if we are to understand the molecular basis of this interaction.

Figure 1.

The S0 segment and its sequence conservation across BK channel orthologues. (A) Topology of the BK channel subunit; the S0 segment is shaded gray. (B) Alignment of nonidentical slo1 and mammalian slo3 S0 segments. Residues shaded black are 100% identical among all slo1 and slo3 sequences; residues shaded gray are 100% identical among all slo1 sequences. Residues in bold (F34, F38, I39 in mslo1) were the most variable among slo1 sequences. Accession nos.: mouse slo1, NP_034740; fly slo1, Q03720; cockroach slo1, AAN76819; mosquito slo1, AAL40812; C. elegans (nematode) slo1, Q95V25; mouse slo3, AAB99742; chimpanzee slo3, XP_519704.

In this paper, we address the functional role of the S0 segment by using a perturbation mutagenesis strategy (Monks et al., 1999; Hong and Miller, 2000; Li-Smerin et al., 2000). Single residues in the S0 region were substituted with tryptophan and assessed for effects on channel gating in excised patches. We found that three mutations (F25W, L26W, and S29W) resulted in large shifts in the channels conductance–voltage (G-V) relationship compared with wild-type. The mutation effects persisted at nominally 0 Ca²⁺ in these mutants, suggesting that they do not arise solely from a disruption in Ca²⁺-dependent activation. In contrast, channel activity at negative voltages (where voltages sensors are at rest) for these mutants was the same as wild type, suggesting that the mutations may be primarily affecting the voltage activation pathway. Consistent with this idea, the major features of the mutation effects could be accounted for in the context of the dual allosteric model for BK channels (Horrigan and Aldrich, 2002) by decreasing the equilibrium constants for voltage sensor movement. If we assume an α-helical S0 segment, then Phe-25, Leu-26, and Ser-29 would be localized to a contiguous patch on the same face of the helix. Together our results are consistent with several S0 residues forming a tightly focused functional contact with other parts of the BK channel to modulate the equilibrium between resting and active states of the channel's transmembrane voltage-sensing domains.

MATERIALS AND METHODS

Mutagenesis and Expression of Recombinant BK channels

Point mutations were introduced into the mouse BK channel gene (Pallanck and Ganetzky, 1994) in the pcDNA3 expression vector using the QuickChange site-directed mutagenesis kit (Stratagene), and the presence of these single mutations and absence of additional mutations were confirmed by DNA sequencing. Channels were transiently expressed in human embryonic kidney 293 cells (293T; American Type Culture Collection), transfected using Lipofectamine (Invitrogen). Cells were cotransfected with pEGFP (CLONTECH Laboratories, Inc.), and transfected cells were identified by fluorescence microscopy.

Solutions and Electrophysiological Recordings

All experiments were performed with excised inside-out patches from identified transfected cells 1–2 d after transfection. Experiments were done at room temperature (22–24°C). Currents were low-pass filtered at 3–5 kHz and digitized at 20 kHz. Except where noted, solutions bathing both sides of the membrane contained 160 mM KCl and 10 mM HEPES (pH 7.4). For most of the data reported below, the solution at the cytoplasmic face of the patch additionally contained either 2 mM N-(2-hydroxyethyl)-ethylenediamine-triacetic acid (HEDTA), to obtain free [Ca²⁺]'s ranging from 1 to 15 μM, calculated using the program MaxChelator (www.stanford.edu/∼cpatton/maxc.html) for pH 7.4, T = 22°C, and ionic strength = 0.16. For some patches, additional data were obtained at 110 μM free [Ca²⁺], using 2 mM nitrilotriacetic acid (NTA) to buffer the [Ca²⁺], or at nominally 0 Ca²⁺, using 2 mM EGTA with no added Ca²⁺. CaCl₂ was added to these intracellular solutions to bring the free [Ca²⁺] to the indicated levels. The free [Ca²⁺] values reported in this paper were measured from recording solutions using a Ca²⁺-sensitive electrode (Orion), based on a set of standard solutions that contained 160 mM KCl, 10 mM HEPES at pH 7.4, and added CaCl₂ ranging up to 10 mM (in the absence of Ca²⁺ buffers). From these measurements, we estimated the contaminating [Ca²⁺] with no added CaCl₂ to be ∼20 μM, originating mainly from the KCl and HEPES salts.

For recordings in nominally 0 Ca²⁺ _i, the bath solution at the cytoplasmic face of the patch was composed of 50 mM KCl, 10 mM HEPES, and 2 mM EGTA, pH 7.4, with no added Ca²⁺. Under these conditions, we estimate that the free [Ca²⁺] should be no greater than 0.0004 μM (assuming 20 μM Ca²⁺ present as a contaminant), calculated with MaxChelator. This concentration is outside of the range where Ca²⁺ has any significant effect on BK channel gating (Rothberg and Magleby, 2000).

Voltage protocols for each dataset were typically repeated at least five times for each patch, and current traces were averaged online. To minimize voltage errors due to series resistance, we analyzed only recordings in which the maximal current was <4 nA. We estimate that the maximal voltage error contributed by series resistance for these recordings was ∼6 mV. Analyzed data are presented without correction for series resistance.

Data Analysis

We quantified the effects of mutations on gating by comparing parameters obtained from G-V relations after fitting data with a Boltzmann function,

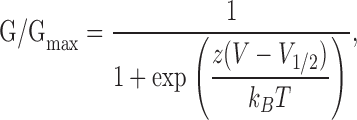where z is the effective gating valence, V_1/2 is the voltage at half-maximal activation, k_B is Boltzmann's constant, and T is temperature. The slope of the G-V relation could be described as s = (k_BT)/z, in units of mV/e-fold increase in relative open probability.

To additionally account for the weakly voltage-dependent gating that occurs with voltage sensors deactivated, data in Fig. 4 were fitted with a modified Boltzmann function:

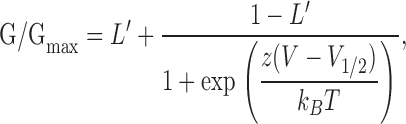(1)

where L′ = L′₀exp(z_LV/k_BT). This provides an estimate of the channel's effective intrinsic gating equilibrium constant at 0 mV, L′₀, at a given [Ca²⁺], along with its effective gating valence, z_L. These additional parameters are constrained by open probability data measured at negative voltages, where voltage sensors are deactivated (Horrigan et al., 1999).

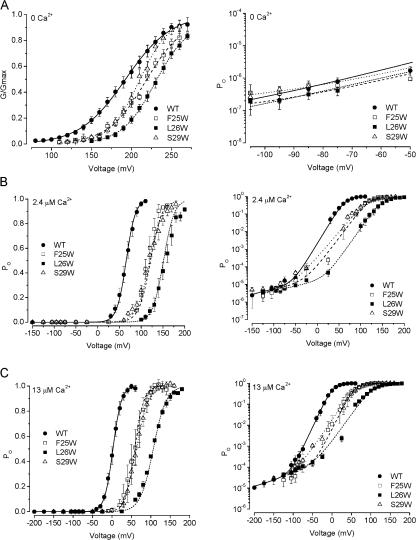
Figure 4.

The shifts in V_1/2 observed with F25W, L26W, and S29W seem to arise from altered voltage sensing. (A) G-V relationships obtained at nominally 0 Ca²⁺ on linear coordinates (left), and P_O measured from wild-type and mutant channels at negative voltages, on semilogarithmic coordinates (right). G-V data from F25W, L26W, and S29W show rightward shifts compared with wild type, suggesting that the Ca²⁺ sensor does not play an obligatory role in these mutation effects. Lines show Boltzmann fits with the parameters: WT V_1/2 = 192 mV, z = 0.97 e₀ (solid line); F25W V_1/2 = 218, z = 1.2 e₀ (dashed line); L26W V_1/2 = 229, z = 1.2 e₀ mV/e-fold change (short dash); S29W V_1/2 = 209, z = 1.4 e₀ (dotted line). P_O data (right) were fitted with Eq. 1, with the Boltzmann parameters given above and the following L₀ values: WT, 1.5 × 10⁻⁷; F25W, 2.10⁻⁷; L26W, 3.3 × 10⁻⁸; S29W, 4.7 × 10⁻⁷ (z_L was fixed at 0.21 e₀ for these fits). (B and C) G-V relationships obtained at 2.4 and 13 μM Ca²⁺, respectively, plotted on linear (left) and semilogarithmic coordinates (right). Limiting open probabilities measured at negative voltages for these two mutants were not different from wild type (see Results), illustrating that the mutation effects are not apparent when voltage sensors are deactivated. Smooth curves show fits with Eq. 1. Parameters for 2.4 μM Ca²⁺ were as follows: WT V_1/2 = 65.6 mV, z = 2.4 e₀, L₀ = 2.3 × 10⁻⁵, z_L = 0.36 e₀; F25W V_1/2 = 122 mV, z = 1.9 e₀, L₀ = 2.3 × 10⁻⁵, z_L = 0.40 e₀; L26W V_1/2 = 151 mV, z = 2.1 e₀, L₀ = 1.5 × 10⁻⁵, z_L = 0.33 e₀; S29W V_1/2 = 119 mV, z = 1.7 e₀, L₀ = 2.7 × 10⁻⁵, z_L = 0.41 e₀. Parameters for 13 μM Ca²⁺ were as follows: WT V_1/2 = 2.46 mV, z = 2.4 e₀, L₀ = 1.7 × 10⁻⁴, z_L = 0.33 e₀; F25W V_1/2 = 60.4 mV, z = 2.6 e₀, L₀ = 3.0 × 10⁻⁴, z_L = 0.40 e₀; L26W V_1/2 = 106 mV, z = 1.5 e₀, L₀ = 2.0 × 10⁻⁴, z_L = 0.33 e₀; S29W V_1/2 = 62.9 mV, z = 1.6 e₀, L₀ = 1.5 × 10⁻⁴, z_L = 0.31 e₀.

For wild-type data and selected mutants, gating was analyzed further by global fitting of G-V and P_O vs. V data obtained at several different [Ca²⁺] with a dual allosteric model (Horrigan and Aldrich, 2002):

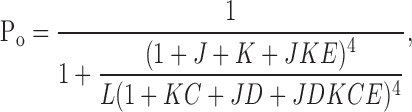(2)

where J = J₀exp(z_JV/k_BT), L = L₀exp(−z_LV/k_BT), and K = [Ca²⁺]/K_D. In these equations, J₀ and z_J correspond to the equilibrium constant for voltage sensor movement at 0 mV and its effective valence, L₀ and z_L correspond to the equilibrium constant for gate movement at 0 mV and its effective valence, K_D is the effective dissociation constant for Ca²⁺, and C, D, and E are the allosteric coupling factors for Ca²⁺ binding and opening, voltage sensor movement and opening, and Ca²⁺ binding and voltage sensor movement, respectively.

Data predicted by the dual allosteric model were calculated from a starting set of kinetic parameters; model predictions were then compared with the experimental data, and kinetic parameters were optimized using an iterative χ² minimization routine, with a modified Simplex search algorithm (Magleby and Weiss, 1990; Rothberg and Magleby, 1998). Automated fitting was combined with manual parameter adjustment in some cases, in order to better account for low open probability data. Model parameters that were not well constrained by experimental data obtained for these studies were fixed at or near values determined in previous studies on BK channels (Horrigan and Aldrich, 2002; Ma et al., 2006; Wang et al., 2006).

RESULTS

In these studies we used perturbation mutagenesis to probe the structure and function of the BK channel S0 segment. We generated and studied channels containing single mutations to tryptophan from residues Ala-24 through Leu-42, and also studied mutations of native tryptophan sidechains Trp-22, Trp-23, and Trp-43 by substituting those residues to alanine. All data were obtained from excised inside-out patches. Of the tryptophan mutants generated for these studies, G36W did not produce current in transfected HEK cells; in this case we instead studied the mutant G36F.

Tryptophan Substitution of S0 Residues at Several Positions Can Produce Shifts in the Voltage-activation of the Channel

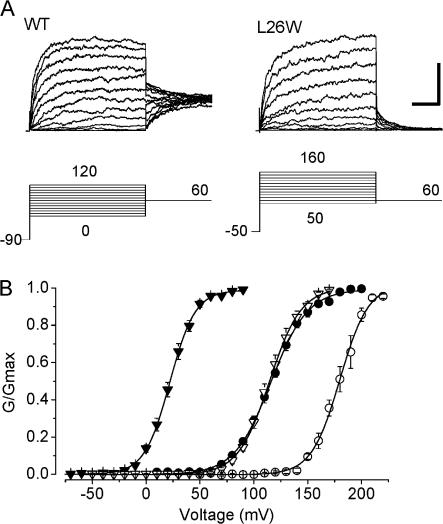
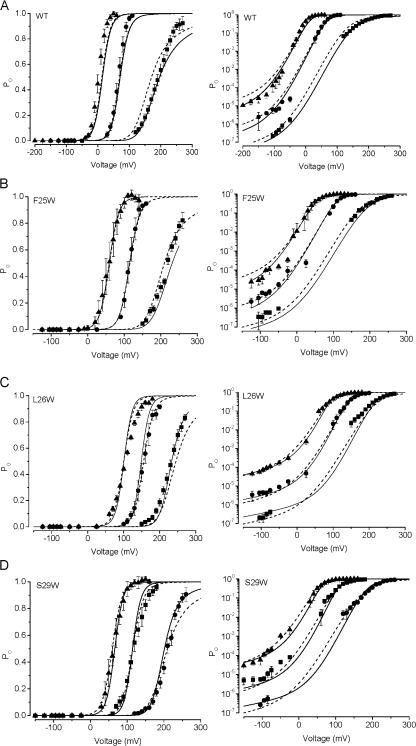
Fig. 2 A shows representative current traces obtained from patches containing wild-type BK channels or the L26W mutant, at 9.9 μM Ca²⁺ _i, illustrating that a single mutation in S0 could produce a large shift in the voltage activation of the channel toward more positive potentials. For L26W, the magnitude of these shifts were greater than +50 mV for [Ca²⁺] ≥ 0.4 μM (ΔV_1/2 = 88 ± 3 mV at 9.9 μM Ca²⁺). Two other mutations in S0 produced relatively large positive G-V shifts, at F25W (ΔV_1/2 = 71 ± 4 mV at 9.9 μM Ca²⁺) and S29W (ΔV_1/2 = 79 ± 7 mV at 9.9 μM Ca²⁺). We also observed shifts in voltage activation toward more negative potentials with some of the S0 mutants, which ranged to −18 ± 3 mV for G35W at 2.4 μM Ca²⁺. Despite the large shifts in V_1/2 that were sometimes observed, all of the mutants in these experiments retained both voltage-dependent and Ca²⁺-dependent gating. Fig. 2 B illustrates that an increase in [Ca²⁺] at the cytoplasmic side of the patch from 0.4 to 9.9 μM produced a leftward shift of 94 mV for wild-type channels, and a leftward shift of 65 mV for L26W channels.

Figure 2.

Mutations in the S0 segment can have large effects on BK channel gating. (A) Representative families of current traces from patches containing WT and L26W channels, at the voltages indicated in the diagrams below each trace. Recordings were obtained with 9.9 μM Ca²⁺ at the cytoplasmic face of each patch. Vertical and horizontal scale bar (at far right) represents 2 nA and 15 ms, respectively. (B) Mean G-V relations for WT (filled symbols) and L26W (open symbols) at 0.4 (circles) and 9.9 μM Ca²⁺ (triangles). Data are fit with a Boltzmann equation (see Materials and methods). Wild-type parameters for the 0.4 and 9.9 μM curves shown here were V_1/2 = 116 mV and 22.0 mV, s = 17, and 12 mV/e-fold change in G/G_max, respectively; L26W parameters for 0.4 μM and 9.9 μM were V_1/2 = 180 mV and 115 mV, s = 13, and 15 mV/e-fold change in G/G_max, respectively.

We recorded currents from each mutant channel along the length of S0 in at least three different [Ca²⁺]_i ranging from 0.4 to 9.9 μM. For individual patches at each [Ca²⁺]_i, we constructed normalized conductance vs. voltage (G-V) relations. These G-V relations were fitted with Boltzmann relations to estimate s and V_1/2, where s is the slope and V_1/2 is the voltage required for half-maximal activation of the channel. For WT channels, the mean V_1/2 values from these experiments at 0.4, 2.4, and 9.9 μM Ca²⁺ were 115 ± 2, 72 ± 2, and 25 ± 2 mV.

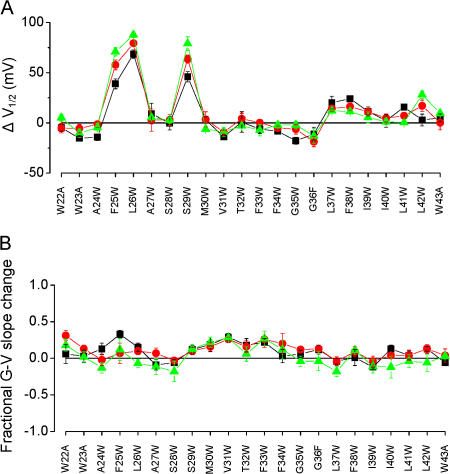
Fig. 3 A summarizes the mean ΔV_1/2 values compared with wild type for each mutant, over a range of [Ca²⁺], and illustrates that the mutation effects on ΔV_1/2 were sensitive mainly to the position of the mutation. For example, one of the largest shifts we observed was with the F25W mutation (see above); this mutation gave a modest increase in side chain volume of only ∼40 Ǻ³. In contrast, the G35W mutation gave a large increase in side chain volume (∼167 Ǻ³), but resulted G-V curves that were nearly indistinguishable from wild type at 9.9 μM Ca²⁺. These results suggest that the magnitude and the direction of these shifts are sensitive primarily to the position of the mutation rather than the size of the volume change.

Figure 3.

Effects of S0 mutations on BK channel voltage activation at 0.4 (black), 2.4 (red), and 9.9 μM Ca²⁺ (green). V_1/2 and slope were determined from Boltzmann fits of G-V relations from individual patches, and ΔV_1/2 = V_{1/2 (mutant)} − V_{1/2 (WT)} and fractional G-V slope change = 1 − (s_mutant/s_WT). (A) Mutations at three key positions produced large shifts in V_1/2. Positive values for ΔV_1/2 (as with F25W, L26W, and S29W) indicated rightward shifts in G-V relations compared with wild type. (B) Fractional changes in the slopes of G-V relations were typically <0.3. Positive values for these indicate slopes that are more steep than wild type. For A and B, each data point represents the mean ± SEM determined from three to nine different G-V curves from each mutant.

Effects of S0 Mutations on the Slopes of G-V Relationships

Unlike the S2, S3, or S4 transmembrane segments, the S0 segment contains no charged residues that could themselves sense the transmembrane voltage. However, mutations in S0 could potentially alter aqueous cavities that might be present near charged residues in the S2, S3, or S4 domains. Changes in these cavities could potentially alter the shape of the electric field surrounding a critical gating charge residue, and thus alter the effective gating charge of the channel (Ma et al., 2006). Alternatively, these mutations could result in a change in the allosteric coupling between voltage sensor movement and channel opening, and such changes might also be observed as a change in the slope of the G-V curves of mutants.

We estimated the slopes of G-V curves for each S0 mutant by fitting with the Boltzmann equation, and quantified mutation effects as the fractional change in G-V slope compared with wild type. Mean slopes for wild-type channels from these experiments at 0.4, 2.4, and 9.9 μM Ca²⁺ were 15.7 ± 1.6, 12.6 ± 0.9, and 11.3 ± 0.8 mV/e-fold change. The results (Fig. 3 B) illustrate that tryptophan mutations in S0 often resulted in slight changes in the slopes of G-V curves. Fractional changes in G-V slope ranged from a 24 ± 6% increase for F25W at 0.4 μM Ca²⁺ (corresponding to an actual mean slope of 12.0 ± 1.0 mV/e-fold change) to slope decreases of 30% for S28W and L37W, both at 9.9 μM Ca²⁺.

We found that the slope changes observed in some of the S0 mutants were not statistically significant compared with slopes of wild-type channels at the same Ca²⁺. This observation in itself may not rule out the possibility that mutations that alter the G-V slope by ∼30% do not alter the effective gating charge of the channel, or other aspects of channel gating. Possible relations between G-V slope and perturbations in the gating mechanism will be addressed below.

Based on these results, the major effects among these S0 mutations appear to be the shifts in mutant channel V_1/2, observed with F25W, L26W, and S29W. Mechanistically, these shifts could result from a change in the equilibria of Ca²⁺ sensor or voltage sensor movement, a change in the coupling between either or both sensors and pore gating, or a direct effect on the channel's basal open–closed equilibrium (Rothberg and Magleby, 1999; Cui and Aldrich, 2000; Rothberg and Magleby, 2000; Horrigan and Aldrich, 2002).

S0 Mutations Appear To Act through Mechanisms Other than a Change in Ca²⁺ Sensitivity

The shifts in V_1/2 observed with several S0 mutants are consistent with a role for the S0 segment in channel gating. To begin to understand the role of S0 in gating, we focused on three mutations that yielded a large effect on channel gating, F25W, L26W, and S29W.

A simple test of whether the mutations are having an obligatory effect on the channel's Ca²⁺ sensing mechanism is to measure channel activity in nominally 0 Ca²⁺. If the shift observed at higher Ca²⁺ is due to a change in Ca²⁺ sensing, then the V_1/2 of these channels at 0 Ca²⁺ should be the same as wild type (i.e., the shift should disappear). We found for F25W, L26W, and S29W that the shifts persisted even at nominally 0 Ca²⁺ (Fig. 4 A), which argues against these mutation effects acting solely through the Ca²⁺ activation mechanism (WT V_1/2 = 194 ± 5.1 mV; F25W V_1/2 = 220 ± 3.1 mV; L26W V_1/2 = 232 ± 3.4 mV; S29W V_1/2 = 211 ± 3.5 mV). We further explore potential mechanistic consequences of altered Ca²⁺ sensitivity in a later section.

Mechanism Underlying the G-V Shifts of F25W, L26W, and S29W

We explored whether the G-V shifts could be due to changes in the basal open–closed (gate) equilibrium in the context of the dual allosteric model of BK channel gating (Horrigan and Aldrich, 2002). This was done by measuring the steady-state activity of single BK channels from wild-type and mutant channels at negative voltages, where voltages sensors should be deactivated (Fig. 4). These recordings represented the activity of many (∼50–300) channels in each patch, measured as NPo. We estimated the number of channels in each patch (N) by first measuring the current amplitude at voltages where all channels were opened, and then dividing this number by the single-channel conductance (Wang et al., 2006). We were then able to estimate open probability at each voltage (per channel) by dividing NPo by N. By fitting these Po values as a function of voltage using Eq. 1, we estimated values for L₀, which is proportional to the basal gate equilibrium (L₀), and z_L, the partial charge associated with gate opening (Fig. 4 B and C; Horrigan and Aldrich, 2002; Ma et al., 2006; Wang et al., 2006). For data obtained at nominally 0 Ca²⁺, this estimate of L₀ can serve as a direct estimate of L₀ (Fig. 4 A).

We further used the mean values estimated for z_L for wild-type and mutant channels at 2.4 μM to estimate values for L₀ at this Ca²⁺ obtained from individual patches, by fitting the Po data obtained at voltages between −85 and −125 mV with an exponential voltage dependence extrapolated to 0 mV.

Our results indicate that L₀ estimated at nominally 0 Ca²⁺ and L₀ (estimated at 2.4 and 13 μM Ca²⁺) could be altered two- to nearly fivefold among the F25W, L26W, or S29W mutant channels (Fig. 4). However, the mean value of L₀ estimated for wild-type channels at 2.4 μM Ca²⁺ (2.4 × 10⁻⁵ ± 1.2 × 10⁻⁵) was not significantly different from the means estimated for the three mutant channels (8.9 × 10⁻⁵ ± 7.9 × 10⁻⁵, F25W; 1.2 × 10⁻⁵ ± 2.9 × 10⁻⁶, L26W; 2.2 × 10⁻⁵ ± 4.8 × 10⁻⁶, S29W). In addition, it will be shown below that, in the context of the dual allosteric model for BK channel gating (Horrigan and Aldrich, 2002), changes in L₀ of this magnitude are, on their own, insufficient to account for the G-V shifts observed with these mutants over the range of [Ca²⁺] we examined. These results suggest that a direct change in gate equilibrium is not likely to be solely responsible for the G-V shifts observed with these three mutations.

A rightward shift in V_1/2 could also be related to either a decrease in the allosteric voltage-coupling factor (D in the dual allosteric model) (Horrigan and Aldrich, 2002), a decrease in the effective gating valence of the voltage sensor (z_J), or a decrease in the voltage sensor equilibrium constant (J₀). A decrease in either D or z_J that would give rise to a large (>25 mV) G-V shift might be apparent in our G-V data as a decrease in the slopes of G-V curves compared with wild type; for a decrease in D, this slope change would be especially apparent at nominally 0 Ca²⁺ (discussed below). We have not observed a statistically significant decrease in G-V slope for any of our S0 mutants, including F25W, L26W, or S29W (Fig. 3 B). For these three mutants, we estimated Boltzmann parameters additionally at nominally 0 Ca²⁺ (Fig. 4 A) and 13 μM Ca²⁺ (Fig. 4 C), and again they were not distinguished from wild type.

To explore the effects of changing these parameters both qualitatively and quantitatively to gain insight toward possible mechanisms underlying the mutation effects in F25W, L26W, and S29W, we used the dual allosteric model for BK channel gating. We first arrived at two similar sets of parameters that described wild-type gating behavior for data obtained at nominally 0, 2.4, and 13 μM Ca²⁺, including low open probability data obtained using single-channel recording (Fig. 4). These wild-type fit parameters were constrained by the G-V data presented in Fig. 5 A, and by parameter values obtained previously for BK channels (Horrigan and Aldrich, 2002; Ma et al., 2006; Wang et al., 2006). Then, using these parameters (presented in Table I, Fit A and Fit B), we changed each parameter individually and compared the predicted G-V data with the experimental data obtained for F25W, L26W, and S29W. Our rationale was that if we could describe the major features of the mutation effects by changing a single parameter in the model, then this would indicate the simplest mechanism that may underlie the mutation effect. It is import to note, however, that this would not necessarily be the only mechanism underlying the mutation effect.

Figure 5.

Description of wild-type and S0 mutant BK channel data with the dual allosteric model. Each dataset is plotted on both linear (left) and semilogarithmic coordinates (right). (A) Wild-type channel activity as a function of voltage at nominally 0 (squares), 2.4 μM (circles), and 13 μM Ca²⁺ (triangles). Smooth curves were generated using the parameters of Fit A (solid line) and Fit B (dashed line), presented in Table I. (B–D) Activity of F25W, L26W, and S29W, respectively, with symbols corresponding to 0, 2.4, and 13 μM Ca²⁺ as in A. Solid and dashed lines were generated with the dual allosteric model using parameters as described in Results.

TABLE I.

Kinetic Parameters Estimated for the Dual Allosteric Model for Wild-type BK Channels

Parameter	Fit A	Fit B
J0	0.05	0.07
zJ (e0)	0.56	0.56
KD (μM)	21.8	21.8
L0	2.0 × 10−7	3.0 × 10−7
zL(e0)	0.21	0.21
C	8	10
D	40	40
E	6	3

Value of z_J was based on estimates presented in Horrigan and Aldrich (2002) and Ma et al. (2006). C and E were not well determined by the current data and were set to the above values to be consistent with estimates of Horrigan and Aldrich (2002), Ma et al. (2006), and Wang et al. (2006).

Fig. 5 illustrates, first, that it is possible to describe the effects of F25W, L26W, and S29W mainly by decreasing J₀, the equilibrium constant for voltage sensor movement. For F25W, it was possible to use the wild-type parameters of Fit A or Fit B with a change only in J₀ to account for the effects of the mutation. In Fig. 5 B, the solid line shows the prediction of the Fit A parameters with J₀ = 0.017, and the dashed line shows the Fit B parameters with J₀ = 0.022; in both cases, the mutant value for J₀ represents an approximately threefold decrease from the wild-type value.

For L26W and S29W, the parameters in Fit A required additional changes to account for the mutation effects, although the parameters for Fit B could describe the data by only changing J₀. The solid line in Fig. 5 C shows the prediction of Fit A parameters for L26W with J₀ = 0.0028 (an ∼18-fold decrease), z_J = 0.65 e₀ (16% increase), and L₀ = 7.5 × 10⁻⁷ (3.8-fold increase); the dashed line, however, shows the prediction of Fit B parameters with J₀ = 0.00825 (an 8.5-fold decrease), and no changes in the other parameters from wild type. In Fig. 5 D, the solid line shows the prediction of Fit A parameters for S29W with J₀ = 0.0074 (an ∼6.8-fold decrease), and z_J = 0.65 e₀ and L₀ = 7.5 × 10⁻⁷ as with L26W. The dashed line shows the prediction of Fit B parameters with the change of only J₀ to 0.022 (a 2.2-fold decrease).

Quantitatively, the G-V shifts observed for F25W, L26W, and S29W at nominally 0 Ca²⁺ are smaller than the shifts observed in the presence of Ca²⁺ (for F25W, 26 mV at 0 Ca²⁺, 58 mV at 2.4 μM Ca²⁺; for L26W, 38 mV at 0 Ca²⁺, 79 mV at 2.4 μM Ca²⁺; for S29W, 17 mV at 0 Ca²⁺, 63 mV at 2.4 μM Ca²⁺). Would this, in principle, demand an effect on Ca²⁺ sensing (in the context of the model)? Interestingly, the smaller shifts observed with 0 Ca²⁺ in these mutants are captured remarkably well, as illustrated in Fig. 5. Although these results do not eliminate the possibility that these mutations may alter Ca²⁺ sensing or Ca²⁺–sensor/gate coupling, they do demonstrate that the size of a G-V shift may increase with increasing Ca²⁺ even with a change only in the voltage sensor equilibrium constant (in the context of the dual allosteric model). The effects of changing model parameters that determine Ca²⁺ sensing is explored in more detail below.

Exploration of Alternative Mechanisms To Describe the G-V Shifts

In the context of the dual allosteric model, it is possible to generate shifts in G-V curves by changing other parameters that define voltage-dependent gating besides J₀, such as L₀, z_J, and D, as well as the parameters K and C, which in part define the Ca²⁺ dependence of gating. We have explored other possible mechanisms in some detail, using different parameter sets in two examples.

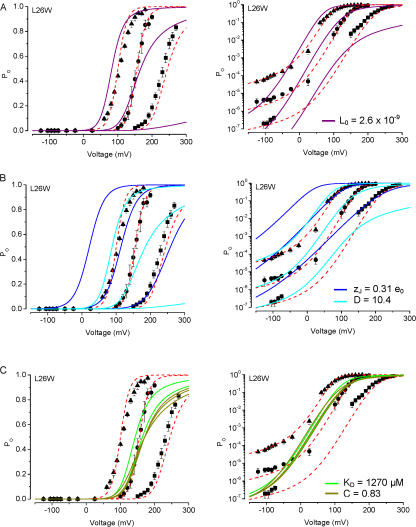
Using L26W, which gave the largest G-V shifts, we explored whether changing any one individual parameter could approximate these mutation effects. In Fig. 6 A, we fitted the G-V curves using the wild-type Fit B parameters, and altering only L₀. This revealed that decreasing L₀ by ∼100-fold (necessary to generate a +80-mV G-V shift compared with WT at 2.4 μM Ca²⁺) could not account either for the observed Po at negative voltages or the G-V relation observed at nominally 0 Ca²⁺ (Fig. 6 A). Similarly, a decrease in D overpredicted the G-V shift observed at nominally 0 Ca²⁺, while a decrease in z_J both overpredicted the G-V shift for 0 Ca²⁺ and underpredicted the G-V shift observed for 13 μM Ca²⁺ for this mutant (Fig. 6 B). Finally, changing only the Ca²⁺ sensor parameters C or K_D by an amount sufficient to produce the large G-V shifts observed with L26W predicted a striking decrease in Ca²⁺ dependence (Fig. 6 C).

Figure 6.

Description of L26W mutant channel data with the dual allosteric model. In each plot, L26W channel activity is shown as a function of voltage with symbols as in Fig. 5. Parameters from the dual allosteric model for WT channel activation (Table I) were changed individually to arrive at the best fit to the mutant data. The graphs illustrate the comparison of models using Fit B parameters with J₀ = 0.00825 (dashed red line) vs.: (A) L₀ = 2.6 × 10⁻⁹ (solid purple); (B) z_J = 0.31 e₀ (solid blue), or D = 10.4 (solid cyan); and (C) K_D = 1270 μM (solid green), or C = 0.83 (solid olive).

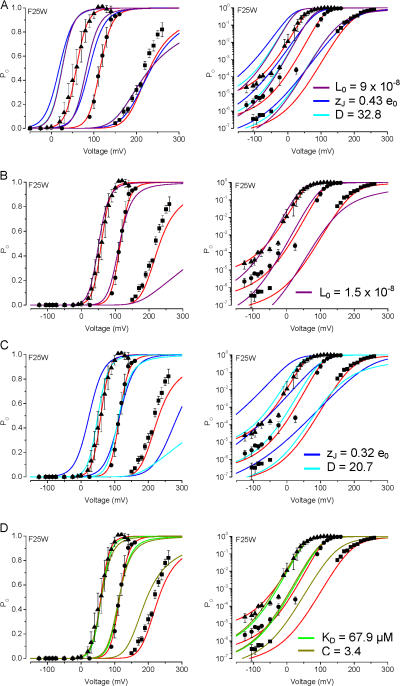
We then explored whether changing any one individual model parameter could approximate these mutation effects, using F25W as an example. The size of the G-V shifts for F25W at each [Ca²⁺] (compared with WT) were similar to those generated by S29W, but smaller than those generated by the L26W mutation.

In Fig. 7 A, we fitted the G-V curve for F25W at nominally 0 Ca²⁺ using the wild-type Fit A parameters, by individually altering either D, z_J, or L₀ (changing C or K would not shift the G-V curve at nominally 0 Ca²⁺). We then used these sets of parameters to predict the G-V curves at 2.4 and 13 μM Ca²⁺. This approach revealed that changes in any of these individual parameters that would produce a similar rightward G-V shift at 0 Ca²⁺ compared with the WT Fit A prediction (to ∼220 mV, and ∼+30 mV shift) would not account for the sizes of G-V shifts observed at higher Ca²⁺. For example, decreases in either D or L₀ underpredicted V_1/2 values at 2.4 μM (V_1/2 = 115 mV by decreasing J₀ vs. 83 mV by decreasing D or L₀) and at 13 μM Ca²⁺ (V_1/2 = 59 mV by decreasing J₀ vs. 26 mV by decreasing D or L₀). Similarly, a decrease in z_J underpredicted the V_1/2 values at 2.4 μM (V_1/2 = 90 mV by decreasing z_J) and at 13 μM Ca²⁺ (V_1/2 = 19 mV by decreasing z_J). In a second approach (Fig. 7, B–D), we fitted the G-V curves for F25W as we did for L26W in Fig. 6, except for F25W we used the wild-type Fit A parameters (and individually changed L₀, z_J, D, K_D, or C). These results illustrate that, consistent with the results in Fig. 6, changing L₀, z_J, or D typically overpredicted the G-V shift observed at nominally 0 Ca²⁺, and in the case of z_J, also underpredicted the G-V shift observed at 13 μM Ca²⁺.

Figure 7.

Description of F25W mutant channel data with the dual allosteric model. In each plot, F25W channel activity is shown as a function of voltage with symbols as in Fig. 5. As with Fig. 6, parameters from the dual allosteric model for WT channel activation (Table I) were changed individually to arrive at the best fit to the mutant data. The graphs illustrate the comparison of models using Fit A parameters with J₀ = 0.017 (solid red curve) vs.: (A) L₀ = 9.0 × 10⁻⁸ (solid purple), z_J = 0.43 e₀ (solid blue), or D = 32.8 (solid cyan); (B) L₀ = 1.5 × 10⁻⁸ (solid purple); (C) z_J = 0.32 e₀ (solid blue), or D = 20.7 (solid cyan); and (D) K_D = 67.9 μM (solid green), or C = 3.4 (solid olive).

It is worth noting that decreases in z_J or D to values that can generate a +50-mV shift in V_1/2 at 2.4 μM Ca²⁺ (using parameters otherwise from Fit A) can result in decreases in G-V slope, estimated by Boltzmann fits. This is illustrated in Fig. 7 C, where the solid red curve (J₀ = 0.017) has a slope of 14 mV/e-fold change, while the solid blue curve (z_J = 0.32 e₀) has a slope of 22 mV/ e-fold change (∼37% decrease compared with changing J₀) and the solid cyan curve (D = 20.7) has a slope of 19 mV/e-fold change (∼25% decrease compared with changing J₀). Also, the sizes of the G-V shifts resulting from decreases in either z_J or D would be Ca²⁺ dependent, with larger rightward shifts occurring with lower [Ca²⁺] (also illustrated in Fig. 7 C). Large reductions in G-V slope were not observed with F25W, L26W, or S29W, and although there was some Ca²⁺ dependence observed with the G-V shifts for these mutants, the larger shifts occurred with higher [Ca²⁺]. These observations suggest that the large rightward G-V shifts observed with these mutations are not likely to arise from decreases in z_J or D alone.

Interestingly, either raising K_D to 68 μM or lowering C to 3.4 predicted mutant V_1/2 values that were close to those predicted by changing J₀ (Fig. 7 D). However, changing these parameters alone predicted V_1/2 values at 0 Ca²⁺ that were identical to those of WT channels, and also underpredicted the observed Po at voltages less than −100 mV. As with any of the model parameters, we cannot entirely rule out a more complicated model in which a change in Ca²⁺ sensitivity contributes to the mutation effects along with changes in voltage sensitivity and/or basal open probability (i.e., L₀).

Together, these results suggest that changing individual parameters other than J₀ cannot generate all of the observed G-V shifts and low Po data as well as changing the parameter J₀ alone. Thus, the simplest model to account for the gating effects of F25W, L26W, and S29W can do so primarily by decreasing J₀.

DISCUSSION

Functional contact between the BK channel's pore-forming α subunit and its auxiliary β1 subunit is critical to the channel's physiological role in the control of electrical excitability in smooth muscle (Brenner et al., 2000; Pluger et al., 2000; Semenov et al., 2006). The conserved S0 segment of BK channels has been of interest because it may participate in recognition and/or functional interaction with the channel's auxiliary β1 subunits (Wallner et al., 1996). While previous experiments have shown that the presence of the segment is critical for channel gating, the nature of its function has not been described (Meera et al., 1997). To learn more about the putative interaction between S0 and the β1 subunit, it is important to understand the functional role of the S0 segment in channel gating.

Function of the S0 Segment

In the present study, we have found that single amino acid changes in the BK channel S0 segment to tryptophan at key positions can produce large changes in channel gating. We went on to analyze the mutation effects systematically, in the context of our current thinking on BK channel gating, to identify a possible functional role of S0. Our results have suggested that the large G-V shifts observed with F25W, L26W, and S29W mutations are consistent with decreases in the voltage sensor equilibrium constant (J₀), such that larger depolarizations are required to fully activate the voltage sensor in these mutants compared with wild-type channels.

Although a decrease in J₀ could account for the major features of these mutations, there are some features of the mutant data that are not captured perfectly by modifying this single parameter (Fig. 5). One must therefore consider the possibility that additional gating parameters (such as L₀ and z_J) are affected slightly, as illustrated in the ability of both Fit A and Fit B to provide reasonably good descriptions of both wild-type and mutant data. In previous studies, BK model parameters have been additionally constrained by including data obtained from gating current experiments, which are technically quite challenging for these channels (Horrigan and Aldrich, 2002; Bao and Cox, 2005). Such experiments may further resolve possible roles of S0 in modulating voltage sensor movement.

If these mutations reveal a functional role for the S0 segment in modulating the equilibrium between the resting and active states of the BK voltage sensor, then this may also be consistent with a possible role for S0 in transducing the actions of the β1 subunit, which include modulation of voltage sensor equilibrium (Bao and Cox, 2005; Wang and Brenner, 2006).

A Possible Structure–Function Relation

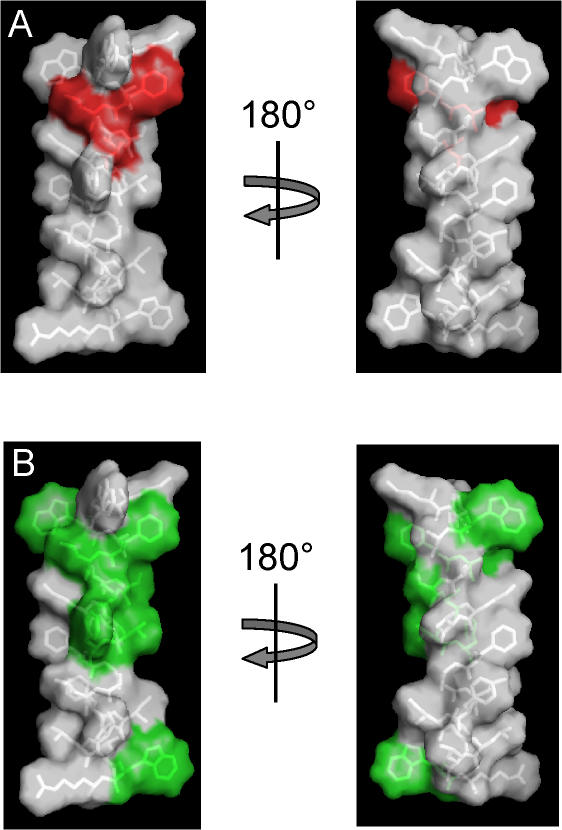
If we assume that the transmembrane S0 segment is helical, as with the other transmembrane domains of Kv channel voltage sensors (Jiang et al., 2003; Lee et al., 2005; Long et al., 2005), then the positions of Phe-25, Leu-26, and Ser-29 would be localized to a contiguous region on the surface of S0. Fig. 8 A illustrates that this surface would be located on one face of the helix, and the disruptive effects of tryptophan substitution at these positions suggests that these residues may approach or contact a portion of the voltage sensor. Phe-25, Leu-26, and Ser-29 are among the S0 residues that are identical among all known slo1 orthologues (Fig. 1; Fig. 8 B), which is consistent with the idea that they are important in BK channel structure and function. In addition, chimeras containing the dslo1 S0 region on an hslo1 background appear to retain the gating properties of wild-type hslo1 (Wallner et al., 1996), consistent with the idea that the identities of these highly conserved residues contribute to determination of the channel's functional properties.

Figure 8.

Sequence that includes the S0 segment modeled as an α helix. Met-21 through Arg-44 were built as a helix using Pymol (Delano Scientific), with side chain rotamers selected to minimize steric clashes within the helix. (A) Side chains Phe-25, Leu-26, and Ser-29, corresponding to the positions of tryptophan mutants that give rise to large G-V shifts, are colored red. These are clustered on one face of the α helix. (B) Sidechains that are identical among slo1 orthologues (Figure 1), colored green. Except for Trp-23, which is one of the native tryptophans that flanks the putative transmembrane segment, all of the highly conserved side chains lie on one face of the helix.

Recently the roles of several charged residues in the BK channel transmembrane domains were analyzed (Ma et al., 2006), and it was found that mutations at several positions in the voltage sensor can result in changes in the equilibrium constant for voltage sensor movement, J₀, while Arg-213 (located in the S4 segment), along with Asp-153 and Arg-167 (both in S2) and Asp-186 (in S3) potentially correspond to voltage-sensing charges that move through some portion of the electric field during voltage activation. Thus the current model of the conformational change underlying BK channel voltage sensor activation involves the combined motion of at least the S2–S4 segments. A region of the S0 segment that includes Phe-25, Leu-26, and Ser-29 may potentially interface with any of these segments, such that tryptophan mutations at this localized region of S0 would increase the energetic requirement for activation.