Definitions of state variables and state space for brain–computer interface

Abstract

The hypothesis is proposed that the central dynamics of the action–perception cycle has five steps: emergence from an existing macroscopic brain state of a pattern that predicts a future goal state; selection of a mesoscopic frame for action control; execution of a limb trajectory by microscopic spike activity; modification of microscopic cortical spike activity by sensory inputs; construction of mesoscopic perceptual patterns; and integration of a new macroscopic brain state. The basis is the circular causality between microscopic entities (neurons) and the mesoscopic and macroscopic entities (populations) self-organized by axosynaptic interactions. Self-organization of neural activity is bidirectional in all cortices. Upwardly the organization of mesoscopic percepts from microscopic spike input predominates in primary sensory areas. Downwardly the organization of spike outputs that direct specific limb movements is by mesoscopic fields constituting plans to achieve predicted goals. The mesoscopic fields in sensory and motor cortices emerge as frames within macroscopic activity. Part 1 describes the action–perception cycle and its derivative reflex arc qualitatively. Part 2 describes the perceptual limb of the arc from microscopic MSA to mesoscopic wave packets, and from these to macroscopic EEG and global ECoG fields that express experience-dependent knowledge in successive states. These macroscopic states are conceived to embed and control mesoscopic frames in premotor and motor cortices that are observed in local ECoG and LFP of frontoparietal areas. The fields sampled by ECoG and LFP are conceived as local patterns of neural activity in which trajectories of multiple spike activities (MSA) emerge that control limb movements. Mesoscopic frames are located by use of the analytic signal from the Hilbert transform after band pass filtering. The state variables in frames are measured to construct feature vectors by which to describe and classify frame patterns. Evidence is cited to justify use of linear analysis. The aim of the review is to enable researchers to conceive and identify goal-oriented states in brain activity for use as commands, in order to relegate the details of execution to adaptive control devices outside the brain.

Appendix 1 The Hilbert Transform

Brain waves are commonly treated as if they were the sum of the outputs of a set of neural oscillators, each of which has a constant frequency and variable amplitude. This treatment is based on the assumption that brain dynamics is linear and time-invariant, which is clearly not the case. The advantage conveyed by this assumption is the ease with which Fourier analysis can be applied to brain waves using the Fast Fourier Transform (FFT) to decompose segments of brain waves into frequency components. The disadvantage is the inability of linear analysis to capture and display the nonlinear state transitions by which brains operate. An alternative linear transform is the Hilbert transform, which when applied to a brain wave recording in effect calculates the rate of change in the amplitude at each time step of the digitized signal. This operation effectively re-expresses an oscillation as a vector that rotates counterclockwise in the complex plane. The amplitude is expressed by the length of the vector, A(t), and the rate of change is expressed by the angular velocity of the rate of rotation of the vector about the origin of the complex plane. The rate of rotation is expressed as a rate of change in phase in degrees/second, radians/second (rad/s), or cycles/second (Hz). The immediate advantage is that the Hilbert transform decomposes a brain wave into an analytic amplitude, A(t), and an analytic phase, φ(t). The change in phase in rad with each time step divided by the digitizing interval in s approximates an instantaneous frequency that can vary, unlike the frequencies that are extracted by Fourier decomposition. The disadvantage is that the Hilbert transform is very sensitive to noise of many kinds; it only works well after band pass filtering of a brain wave. Criteria for optimal band pass filtering have been described elsewhere (Freeman 2004a, b; 2005; 2006).

The application of the Hilbert transform to each intracranial recording from an array of microelectrodes is a multi-step procedure. First, a high pass filter set at ˜400 Hz extracts the MSA, and a low pass filter set at ˜400 Hz extracts the LFP from the same n microelectrode recordings. Second, the low pass data are down-sampled from ˜40,000/s to 200/s and normalized to zero mean for every channel and unit standard deviation (SD) for all channels, trials and data sets to give the normalized LFP. Third, the demeaned, normalized LFP are band pass filtered in the classic empirical ranges: theta (3–7 Hz), alpha (7–12 Hz), beta (12–30 Hz), gamma (30–60 Hz), and high gamma (60–200 Hz), and the n channels in each pass band are segmented to save the data from each trial with ˜3 s preceding and ˜3 s following each CS onset (Fig. 6A). Fourth, the Hilbert transform is applied to get the analytic signal, V_j(t), with a real part (blue curve), the filtered LFP, v_j(t), and an imaginary part (red curve), iu_j(t), the output of the Hilbert transform:

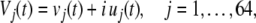1

where the Hilbert transform of v_j(t) in the time segment, t′,

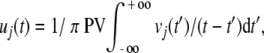2

where PV signifies the Cauchy Principal Value. The imaginary part is also known as the quadrature of the signal, because each cosine component in the recorded signal is transformed to a sine component; taking the derivative by the transform is equivalent to shifting the phase of v(t) by 90° (π/2 rad) to get u(t).

Fifth, the square root of the sum of squares of the real and imaginary parts gives the analytic amplitude, A_j(t), for each channel, j = 1,...,n,

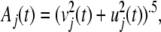3

and the arctangent of the ratio of the imaginary part divided by the real part gives the analytic phase, φ_j(t) (Fig. 6B):

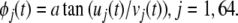4

The mean of the square of amplitude, A² _j(t) over n gives the mean power, A²(t) (Fig. 6D), and the set of n scalar values of A_j(t) divided by A(t) gives the normalized feature vector at each time step, A(t). The feature vector provides a measure of the order parameter of the ensemble of cortical neurons that is under observation. A(t) specifies the normalized spatial pattern formed in the pass band by the signals from the n channels, and it designates a point in n-space that is occupied by the tip of the feature vector as it describes a trajectory through infinite brain state space that is projected into n-space by measurement.

Sixth, the rate of change in the normalized order parameter, D_e(t), is calculated from the analytic power by calculating the Euclidean distance between the tips of the feature vectors in n-space at each successive digitizing step:

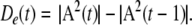5

D_e(t) is a measure of the stability and stationarity of the normalized spatial pattern. Successive points in time specified by A(t) form clusters, whereas epochs of rapid change are manifested by a wide trajectory through n-space. The ratio of the rate of energy dissipation estimated by mean analytic power, A(t), divided by the rate of change in the order parameter, D_e(t), gives a quantity called the “pragmatic information”, H_e(t), which is maximal when the LFP amplitude peaks and when concomitantly the spatial pattern of the LFP is optimally stabilized.

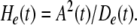6

Seventh, the analytic phase, φ_j(t). is unwrapped by adding π radians at each break point where the arctangent goes to infinity (Fig. 6D), and the analytic frequency, ω_j(t), is estimated by calculating the phase difference between successive digitizing steps in the unwrapped analytic phase, Δφ_j(t), time series and dividing that difference by the duration of the digitizing step, Δt. The mean analytic frequency, ω(t), and its spatial standard deviation, SD_X, are calculated over the n channels at each time step. Typically in neocortical data the values of ω(t) and SD_X are nearly constant for time periods of 60–120 ms indicating stationarity, and they fluctuate over the n channels in brief time periods that demarcate sudden transitions in analytic frequency, power, and spatial pattern. The implication is that areas of neocortex function in near-linear, stationary dynamics most of the waking state, but undergo brief state transitions 3–10 times each second. During the transitions the analytic amplitude, A(t), drops to a low level, and the variances of the analytic frequency, ω(t), given by SD_X(t) increases briefly but dramatically (Fig. 1) in what is known as “phase slip” (Pikovsky et al. 2001). A state transition appears to be required to initiate the formation of a new spatial pattern, A(t), which is the order parameter manifesting a nonconvergent “chaotic” attractor in the landscape of basins of attraction sustained by an area of cortex.