Cooperative folding kinetics of BBL protein and peripheral subunit-binding domain homologues

Abstract

Recent experiments claiming that Naf-BBL protein follows a global downhill folding raised an important controversy as to the folding mechanism of fast-folding proteins. Under the global downhill folding scenario, not only do proteins undergo a gradual folding, but folding events along the continuous folding pathway also could be mapped out from the equilibrium denaturation experiment. Based on the exact calculation using a free energy landscape, relaxation eigenmodes from a master equation, and Monte Carlo simulation of an extended Muñoz–Eaton model that incorporates multiscale-heterogeneous pairwise interactions between amino acids, here we show that the very nature of a two-state cooperative transition such as a bimodal distribution from an exact free energy landscape and biphasic relaxation kinetics manifest in the thermodynamics and folding–unfolding kinetics of BBL and peripheral subunit-binding domain homologues. Our results provide an unequivocal resolution to the fundamental controversy related to the global downhill folding scheme, whose applicability to other proteins should be critically reexamined.

Our understanding of protein folding is primarily based on interpretation of the thermodynamics and kinetics from a simple protein folding model (1–10). The principle of minimal frustration and structural consistency captured by the Gō model allowed us to describe the complicated nature of protein folding at a coarse-grained level (5, 6). Bryngelson et al. (6, 7) posited a phenomenological picture of free energy landscape of a protein-like heteropolymer and classified protein folding into three scenarios depending on whether the free energy landscape is unistable or bistable and also whether a glass transition occurs. Shakhnovich and Gutin (8) presented microscopic statistical-mechanical theories for heteropolymer model, whose consequences provided important insights into the thermodynamics, kinetics, and nature of free energy landscape for protein folding. The conventional view of protein folding assumes a discrete two-state transition between a native state and a denatured ensemble of protein conformations that are separated by a folding barrier (9). The other view termed as one-state (or global) downhill folding asserts that there is a continuous change of protein conformation during folding without distinct free energy barrier (7, 10). The former could be understood as the first order (cooperative) phase transition whereas the latter as the second order (noncooperative) phase transition between a native and a denatured ensemble of protein conformation. An in-depth analysis for possible downhill folding was performed by Abkevich et al. (10) where it was shown that the major determinant for the cooperativity of protein folding is the relative abundance of nonlocal versus local contacts between residues in the native structure of a protein, which also simultaneously compete with the loss of conformational entropy. However, the folding process of two-state proteins may go downhill in the free energy landscape when the folding energy predominates over the loss of the conformational entropy (4), depending upon the conditions of a folding experiment such as their initial locations on the free energy landscape and the heterogeneity of conformational ensemble (7). In the global downhill folding model the folding free energy landscape possesses a global unimodal distribution for all denaturation conditions so that a protein follows a smooth and progressive conformational change, and a continuous folding pathway can be observed simply by an equilibrium denaturation experiment (11, 12).

Muñoz and coworkers (13, 14) presented the experimental observation of a broad thermal denaturation midpoint for Naf-BBL protein, which is a truncated BBL peripheral subunit binding domain (PSBD) from Escherichia coli with a naphthyl-alanine. They not only suggested that Naf-BBL follows the global downhill folding scenario but also claimed that the same scenario holds for other PSBD homologues (13). In contrast, Fersht and coworkers (15, 16) examined the structural, denaturation, and kinetic properties of PSBD homologues from E. coli [unlabeled wild-type BBL, Protein Data Bank (PDB) entry 1W4H], Bacillus stearothermophilus (E3BD F166W, PDB entry 1W4E), and Pyrobaculumaerophilum (POB Y166W L146A, PDB entry 1W4J) (17) and found that 1W4H, 1W4E, and 1W4J follow the typical two-state folding scheme. Whereas Naganathan et al. (18) argued that the experimental data in ref. 15 support the global downhill folding scenario, Fersht and coworkers (16) believe that the conclusion drawn by Muñoz and coworkers was obtained by an incorrect assumption and analysis of the data in refs. 13 and 18. More recently, Sadqi et al. (19) presented an atom-by-atom analysis of NMR data to support the global downhill folding scheme of Naf-BBL (13). However, Ferguson et al. (20) and Zhou and Bai (21) argued back again that the new data presented by Sadqi et al. (19) could well be described by a two- or three-state model. Such an ongoing fundamental controversy (13–16, 18–25) about the folding mechanism for Naf-BBL and PSBD homologues would reshape our concept on protein folding. Faced with these conflicting and ambiguous assertions from experiment, we have attempted to resolve such a controversy by carrying out an exact analysis of thermodynamic and kinetic properties for folding–unfolding of an unlabeled BBL (BBL short, PDB entry 1BBL) with no naphthyl moiety and three PSBD homologues. In addition, a Monte Carlo simulation was used to monitor out-of-equilibrium relaxation kinetics.

Results and Discussion

Thermodynamics of BBL and PSBD.

The aforementioned controversy can be resolved by determining whether the thermodynamic and kinetic properties during folding–unfolding of BBL short and three PSBD homologues exhibit a bimodal or a unimodal pattern. To achieve such a goal one must use a free energy landscape in an exact manner along a proper reaction coordinate. A coarse-grained Muñoz–Eaton (ME) model of a protein folding has been highly useful in explaining folding processes of many proteins (26, 27). However, this original ME model does not distinguish different amino acid types. Furthermore, pairwise interactions between two amino acids within a cut-off distance are treated as attractive interactions in this model. We have extended the original ME model (see Materials and Methods) to a new one that explicitly incorporates both the specificity of amino acid type and the heterogeneity of all pairwise interactions without a cut-off distance into a free energy function. Our model takes into account of both attractive and repulsive pairwise interactions in a more realistic fashion because it uses a hybridized energy function that bridges the gap between the atom-level and residue-level descriptors of protein conformations while retaining the topology of protein structure at a coarse-grained level. Using our extended ME model, which is a multiscale-heterogeneous model capturing the atomic-scale energy function, one can perform an exact analysis for thermodynamic and kinetic properties of proteins and efficiently explore the out-of-equilibrium relaxation kinetics over the entire time scale, including the early folding events and the asymptotic behavior leading to an equilibrium state.

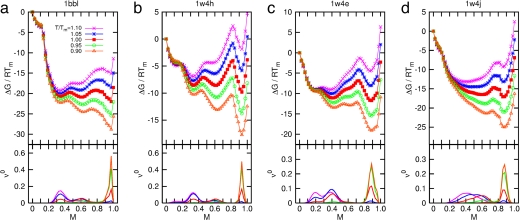
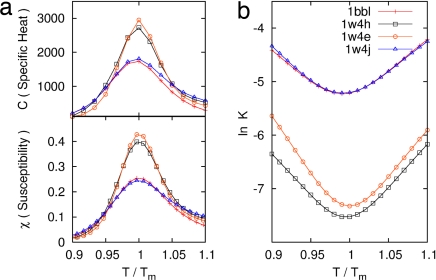
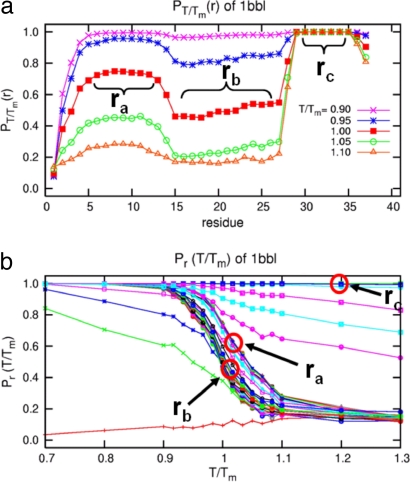
We first optimized the three-dimensional structures of PDB entries 1BBL, 1W4H, 1W4E, and 1W4J by simulated annealing using AMBER 8.0/ff99 (28) with a generalized Born approximation for an implicit consideration of solvent. The strength of pairwise interactions between ith and jth amino acid for j ≥ i + 2 was obtained by summing over all atomic—Coulombic and van der Waals—interaction energies. We then generalized the previously known exact solution (29) of an original ME model to one that contains information on the sequence-specific and heterogeneous pairwise interactions. Fig. 1Upper shows an exact free energy landscape in the unit of RT_m as a function of the fraction M of native residue for 1BBL, 1W4H, 1W4E, and 1W4J, where R is a gas constant and T_m is a folding mid-temperature. Although the free energy landscape of the denatured state is broad and populated with multiple wells having low energy barriers with heights less than or equal to RT_m, a clear free energy barrier on the order of 2∼3 RT_m for 1BBL and 1W4J, and 4∼5 RT_m for 1W4H and 1W4E exists that separates the native from the denatured state. In addition, a discernible discrete jump is identified in the location of the global minimum of free energy as T crosses T_m, which is a signature of the first order phase transition between the native and the denatured ensemble of protein conformation. The invariant position of the native well with temperature indicates that the native state is distinct and constant. When T/T_m ≪ 1 (T/T_m ≫ 1), the pairwise-contact folding energy predominates over the loss of the conformational entropy; thus, the folding barrier diminishes and the folding process goes downhill toward its equilibrium native state in the free energy landscape (the opposite abundance leads the unfolding process downhill) (4, 10). This reconciles with the type 0 scenario of protein folding posited by Bryngelson et al. (7). Because the hydrophobic effect, which plays different roles in affecting the folding behavior of proteins at different temperatures, can cause cold denaturation at low temperatures, the downhill free energy landscape at very low temperature in this model may not be relevant. The exact results for the equilibrium susceptibility χ = [〈M²〉 − 〈M〉²]/T and specific heat C = [〈E²〉 − 〈E〉²]/T² from our Monte Carlo simulation, which are the fluctuation in the fraction of native residue and in the pairwise interaction energy, respectively, are plotted in Fig. 2a as a function of T/T_m. The presence of pronounced peaks in the susceptibility and specific heat around T/T_m = 1 represents a folding–unfolding transition whose associated fluctuations are larger for 1W4E and 1W4H than those of 1BBL and 1W4J. The equilibrium melting curves of the fraction of native conformation P_T/Tm(r) for 1BBL as a function of the location r of residues along a sequence for each temperature T/T_m is presented in Fig. 3a, whereas Fig. 3b plots P_r(T/T_m) as a function of temperature for each residue. Fig. 3a illustrates that while residues r_c on the α-helix at C terminus do not melt for the temperature range studied, P_T/Tm(r) at a given temperature depends on the location and secondary structure of residues. Fig. 3b demonstrates that residues r_b on the loop region unfold cooperatively to the most extent leading to a free energy barrier, which precedes the unfolding of residues r_a on the α-helix at the N terminus. Therefore, a spread in T_m does not necessarily indicate that the free energy landscape is downhill.

Fig. 1.

Exact free energy ΔG in the unit of RT_m (Upper) and equilibrium population ν⁰ (Lower) plotted as a function of M for T/T_m = 0.9∼1.1 for 1BBL (a), 1W4H (b), 1W4E (c), and 1W4J (d) using our extended ME model. The native (denatured) well is located at the global minimum of the free energy landscape for T < T_m (T > T_m). As T crosses T_m, the discrete transition occurs across the free energy barrier of 2∼3 RT_m for 1BBL (a) and 1W4J (d) and 4∼5 RT_m for 1W4H (b) and 1W4E (c), respectively. Because the native state is invariant, the peaks in ν⁰ corresponding to the native state do not move with temperature, whereas the denatured peaks move to lower values of M while maintaining the bimodal distribution. The bimodal nature of eigenvector elements governs the equilibrium population.

Fig. 2.

Equilibrium susceptibility χ, specific heat C, and chevron plot as a function of T/T_m. (a) The peaks around T/T_m for 1W4H and 1W4E are more pronounced than those of 1BBL and 1W4J. (b) The linear folding (unfolding) arm for T < T_m (T > T_m) reflects the existence of a free energy barrier. The sum of folding and unfolding rates at T = T_m is equal to the relaxation rate, signifying the two-state folding behavior.

Fig. 3.

Equilibrium melting curves of each residues for 1BBL. The fraction of native conformation P_T/Tm(r) [P_r(T/T_m)] as a function of r (T/T_m) for each temperature (residue) is presented in a (b). (a) P_T/Tm(r) depends on the location and secondary structure of residues. (b) Residues r_b on the loop region unfold cooperatively to the most extent, which precedes the unfolding of residues r_a on the α-helix at the N terminus. It illustrates that a spread of T_m does not necessarily indicate that the free energy landscape is downhill. (See SI Fig. 6 for other melting curves for 1BBL and 1W4E.)

Chevron Plot and Relaxation Eigenmode.

In simplistic cases the folding of a protein can be modeled (27) by its relaxation kinetics along a one-dimensional free energy landscape such as the one shown in Fig. 1. We have analyzed exactly the time evolution of a conformational probability and its relaxation rate for 1BBL, 1W4H, 1W4E, and 1W4J by using the master equation (30) (see Materials and Methods). Fig. 2b shows a chevron plot as a function of T/T_m. If a protein were to follow a global downhill folding, a chevron plot should show flat dependence on temperature. The facts that a linear folding (unfolding) arm without a rollover behavior for T < T_m (T > T_m) exists and that the sum of folding and unfolding rate at T = T_m is equal to a relaxation rate are important kinetic evidences that 1BBL, 1W4H, 1W4E, and 1W4J fold by a two-state folding mechanism. Fig. 2b also shows that 1BBL and 1W4J fold faster than 1W4H and 1W4E because the free energy barriers for the former are lower than the latter. It is worth noting that the recent kinetic experiment by Fersht et al. (24) for the BBL homologue Ala131Gly and wild-type POB PSBD also showed the similar chevron plot with the steep linear refolding arm, which is the hallmark of cooperative transition.

In an exact analysis (30) of eigenvectors of a relaxation matrix in the master equation, the eigenvector elements of the zero eigenvalue are the equilibrium populations of a protein conformation and their sum is 1.0, whereas eigenvectors of nonzero eigenvalues govern the relaxation mode of a conformational probability toward its equilibrium one. The sum of eigenvector elements for each nonzero eigenvalue is 0.0. The values of eigenvector elements for the zero eigenvalue and the first, second nonzero smallest eigenvalues are plotted in Fig. 1 Lower and supporting information (SI) Fig. 7 in terms of the fraction M of native residue, where one gets an important insight about whether the equilibrium population and the relaxation kinetics toward an equilibrium state are bimodal or unimodal (24). A common feature emerging from these plots is that the distributions of eigenvector elements are bimodal for both the native and denatured state. The location of a distribution maxima along the x axis in Fig. 1 Lower for the native state does not change with temperature, implying that the native states for 1BBL, 1W4H, 1W4E, and 1W4J are invariant (24). The distribution pattern for denatured states is broad and shifted toward lower values of M. SI Fig. 7 Middle shows the longest-relaxation eigenmodes of the population exchange between the native and denatured state during the out-of-equilibrium relaxation toward an equilibrium state for a given temperature. It shows that an increase of native population is always accompanied by a decrease of denatured population and vice versa. SI Fig. 7 Bottom shows in the next eigenmodes of the population exchange that an increase of population in the native and denatured state is compensated for by a decrease of population in the other remaining states and vice versa, which illustrates that a bimodal distribution for the native and denatured states is well separated. Therefore, the exact analysis of relaxation eigenmodes based on our exact free energy landscape vividly reveals a bimodal nature of free energy landscape and of relaxation kinetics for 1BBL, 1W4H, 1W4E, and 1W4J.

Biphasic Relaxation Kinetics.

The out-of-equilibrium Monte Carlo simulations (31) relevant to the temperature-jump experiment (32) were carried out to investigate the relaxation kinetics toward an equilibrium state without resorting to a particular free energy landscape. Using the multiscale-heterogeneous free energy function in our extended ME model, 1,000 independent dynamic trajectories that start from an initial nonequilibrium conformation and end at an equilibrium conformation were generated at a given temperature. A single spin-flip Metropolis algorithm (31) was used in Monte Carlo simulations that were run well beyond the equilibrium time scale at each temperature (see SI Text). Among the particularly important quantities we focused on were an average spin–spin autocorrelation function Y(t + t_w, t_w) = 〈Σ_i=1^NS_i(t_w)·S_i(t + t_w)/N〉 as a similarity measure of a protein conformation at the later time t + t_w with respect to that at the time t and an average pairwise-contact energy E(t). 〈〉 denotes an average over 1,000 different dynamic trajectories, t_w denotes a waiting time after a temperature-jump, and S_i(t) denotes a spin value indicating the nativeness of ith amino acid at time t. The product S_i(t_w)·S_i(t + t_w) is defined to be 1 when the ith spin values at both times are the same, and −1 otherwise. We transformed Y(t + t_w,t_w) by A(t + t_w,t_w) = [1 + Y(t + t_w,t_w)]/2 so that the transformed autocorrelation function is rescaled to change from 0 to 1.

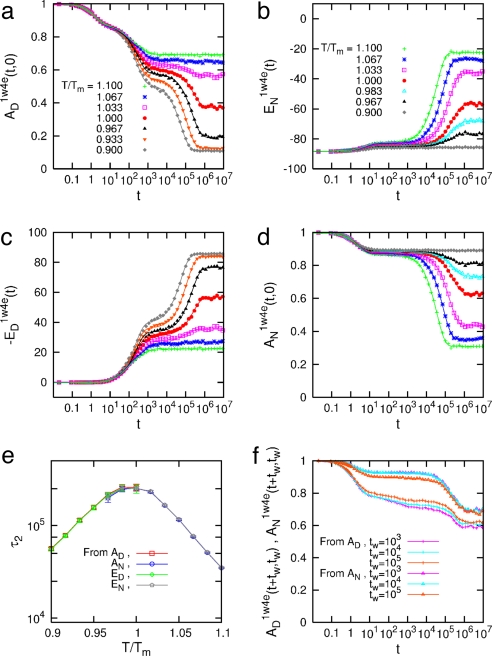
Starting from a fully unfolded (native) state with all spins S_i = 0(1), i = 1, 2, …, N, the time evolution of A_D(t, 0) and E_D(t, 0) [A_N(t, 0) and E_N(t, 0)] over the whole hierarchy of time scales is shown in Fig. 4 a and c (Fig. 4 b and d) for 1W4E and in SI Fig. 8 a and c (SI Fig. 8 b and d) for 1BBL at different quenching temperatures T/T_m = 0.9∼1.1 (see SI Fig. 8). Because 1W4H and 1W4J show a similar behavior to 1W4E and 1BBL, respectively, we only show the results for the latter in Fig. 4 and SI Fig. 8. It was not straightforward to intuitively grasp the physical realization of A_D(t + t_w, t_w); nevertheless, A_D(t, 0) [A_N(t, 0)] turned out to be the fraction of nonnative residue 1 − M(t) [native residue M(t)] at time t, where M(t) = Σ_i=1^NS_i(t)/N. Because the entropic reduction (gain) of a protein conformation in ME model with respect to a fully unfolded (native) state is proportional to M(t) [1 − M(t)], 1 − A_D(t, 0) A_N(t, 0) are directly proportional to the entropy of a protein conformation. The folding funnel picture (7) arises naturally in Fig. 4 a and c and SI Fig. 8 a and c such that the magnitude of pairwise folding energy increases while entropy decreases as the folding proceeds for a given temperature T < T_m, whereas Fig. 4 b and d and SI Fig. 8 b and d show the unfolding funnel. The genuine picture demonstrated in Fig. 4 and SI Fig. 8 is the existence of (i) biphasic relaxation for T ≤ T_m (T ≥ T_m) and (ii) uniphasic relaxation for T far away from T_m. The biphasic relaxation consists of a fast-downhill-relaxation for the re-equilibration of a fully unfolded (native) initial conformation to the denatured (native) conformation in the nearest free energy well, which is followed by a slow relaxation for crossing the free energy barrier to the native (denatured) conformation in the other free energy well (33–35).

Fig. 4.

Out-of-equilibrium relaxation behaviors of 1W4E toward an equilibrium state at T/T_m = 0.9∼1.1. (a–d) Time evolution of an average autocorrelation function A_D^1W4E(t, 0) (a) [A_N^1W4E(t, 0) (d)] and an average pairwise-contact energy A_D^1W4E(t, 0) (c) [A_D^1W4E(t, 0) (b)] starting from a fully unfolded (native) state of 1W4E. The combination of a and c (b and d) shows the folding (unfolding) funnel picture. The solid lines are drawn from the fitted exponential function. (e) The longest relaxation time τ₂ of the biphasic relaxation for T < T_m (T > T_m) follows an Arrhenius relation with T and manifests the existence of a barrier-limited relaxation. The error bars are drawn with three standard deviations. (f) A(t + t_w, t_w ≠ 0) at T = T_m with different waiting times t_w shows biphasic relaxation behavior for large t_w and demonstrates the presence of fast and slow relaxation due to a free energy barrier.

During the biphasic relaxation, two time scales of the fast and slow relaxation for 1W4E and 1BBL are well separated and the slow relaxation for A_D(t, 0) and E_D(t) follows the stretched kinetics (36) of the form e^−(t/τ)β with β = 0.6∼0.8 for T ≅ T_m, where a free energy barrier is highest. Although the heights of low-lying barriers (≤RT_m) in the denatured basin of free energy landscape are not as high as to generate thermodynamically relevant intermediate states, the existence of such low-lying barriers may result in the interconversion between weak kinetic intermediates during the relaxation process of protein conformations and increase the roughness of the free energy landscape. The folding barrier and these low-lying barriers are most pronounced for T ≅ T_m, as is shown in Fig. 1; therefore, the slow relaxation behavior of A_D(t, 0) and E_D(t, 0) could follow the stretched kinetics. What should be clarified here is whether the relaxation modes of A_D(t, 0) and E_D(t) [A_N(t, 0) and E_N(t)] of 1W4E and 1BBL for entire temperature are governed by exponential relaxation, and more importantly whether these relaxations are barrier-limited. A_D(t, 0) is best fitted by a tri-exponential function of the form C₀e^−t/τ0 + C₁e^−t/τ1 + C₂e^−t/τ2, whereas E_D(t) [A_N(t, 0) and E_N(t)] is best fitted by a bi-exponential function of the form C₁e^−t/τ1 + C₂e^−t/τ2 near and below (above) T_m, where τ₀ < τ₁ < τ₂. The relaxation of A_D(t, 0) that occurs in a time scale of τ₀ is the ballistic one that corresponds to the local motion of amino acids and is irrelevant to our discussion. For T far away from T_m, A_D(t, 0) and E_D(t) [A_N(t, 0) and E_N(t)] are best fitted by a single-exponential function C₃e^−t/τ3. τ₁ and τ₃ are temperature-independent because τ₁ corresponds to the downhill motion of an initial configuration to a nearest denatured (native) well of the free energy landscape and τ₃ to the native (denatured) state for T ≪ T_m (T ≫ T_m). On the other hand, the longest-relaxation time τ₂ for each case exhibits a strong temperature dependence and becomes the largest around T = T_m. Fig. 4e for 1W4E and SI Fig. 8e for 1BBL both show an Arrhenius-type relation between τ₂ and T/T_m, which is consistent with the barrier-limited relaxation due to the free energy barrier. If 1BBL and 1W4E were to follow the two-state folding behavior, the presence of a denatured well and a native well on the free energy landscape should be equally pronounced at T = T_m. This ought to result in the strong biphasic relaxation behavior in A(t + t_w, t_w ≠ 0) because heterogeneous initial conformations at t_w could probe the fast and the slow relaxation depending on their initial locations on the free energy landscape (11, 32). Fig. 4f and SI Fig. 8f show A_D^1W4E(t + t_w, t_w), A_N^1W4E(t + t_w, t_w) and A_D^1BBL(t + t_w, t_w), A_N^1BBL(t + t_w, t_w) at T = T_m for t_w = 1,000, 10,000, 100,000, which demonstrates the existence of biphasic relaxation for large t_w due to an apparent free energy barrier.

Average Pathway of Folding and Unfolding.

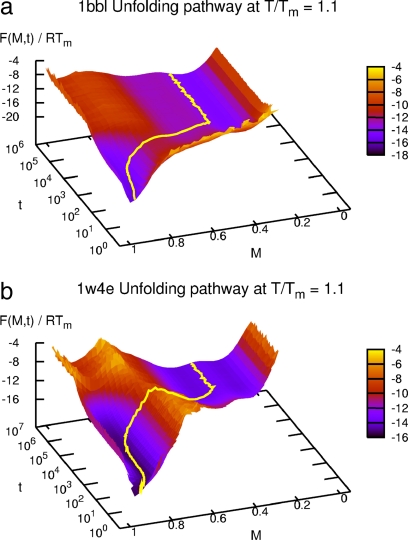
The equilibrium free energy landscape F(M) was obtained via F(M) = −RT ln Z(M) in our Monte Carlo simulation, where Z(M) is the number of protein conformations with M, and was confirmed to be the same as the exact free energy landscape as shown in Fig. 1. We calculated the dynamic free energy-like quantity F(M, t) = −RT ln Z(M, t), where Z(M, t) is the one calculated in the time window t and t + δt, and plotted F(M, t) in Fig. 5 for 1BBL and 1W4E. For t larger than the equilibration time, F(M, t) converges to F(M) for each temperature. This ensures that the dynamic trajectory in our out-of-equilibrium Monte Carlo simulation indeed converges to the correct equilibrium state. Because we knew the average value of M(t) as shown in Fig. 4 and SI Fig. 8, we could envisage the average pathway of folding and unfolding on the surface of F(M, t). Fig. 5a (Fig. 5b) shows the average unfolding pathway of 1BBL (1W4E) at T/T_m = 1.1 starting from the fully native state at t = 0. It first re-equilibrates to a basin of native state, crosses over a unfolding barrier of the height 2∼3 (4∼5) RT_m, and then leads to a basin of denatured state after the equilibration time. (For the folding pathway, see SI Fig. 9.) The average pathway of folding and unfolding shown on the surface of F(M, t) indisputably demonstrates that both 1BBL and 1W4E must undergo a two-state cooperative transition.

Fig. 5.

Average pathway of unfolding as a function of M and t at T/T_m = 1.1 for 1BBL (a) and 1W4E (b). It shows the average unfolding process: re-equilibrating to the native state, attempting to escape from the native well, climbing the unfolding barrier, and relaxing to the denatured state. The averaged value M(t) on the top of a free energy barrier has the heterogeneous contributions mostly from the native and the denatured state.

Why Did the Previous Analysis Not Show the Cooperative Folding?

We revisited Muñoz and coworkers' (13) original numerical calculation based on the free energy function of the form ΔG(T) = n·ΔH + ΔC(T − 373) − T[n·ΔS + ΔC·ln(T/385)] that demonstrated the global downhill folding behavior of 1BBL, where n is the number of native residues and T is the temperature. This function was determined solely by the one-body environmental nature of individual residues for which only the mean enthalpy (ΔH) and the mean entropy (ΔS) per a native residue were taken into account and the change in heat capacity (ΔC) was estimated only from the differences in accessible surface area of an individual residue in each fragment of native structure. Although this function may control the competition between the stabilizing energy and the destabilizing entropy as T changes, it is important to realize that the stabilizing energy there is effectively calculated from the nature of a single residue. Given that the major determinant for cooperative protein folding is nonlocal interresidue interactions especially with a large contact order, a free energy function that does not properly account for nonlocal interresidue interactions is bound to lead to a global downhill folding behavior, to which Muñoz and coworkers (13) fitted their experimental results. Thus, the global downhill folding behavior of 1BBL described numerically by Muñoz and coworkers (13) is not unexpected. When the multiscale-heterogeneous nature of both attractive and repulsive pairwise contacts is not properly taken care of, the same reasoning applies and downplays the crucial role of nonlocal pairwise contacts in competition with the local pairwise contacts and the conformational entropy. The free energy function used by Muñoz and coworkers might describe the overall equilibrium energetics of a native state of Naf-BBL reasonably yet fails to provide an adequate description of the thermodynamics and folding kinetics involving a discrete folding barrier.

Limitations of the Current Model.

Although our extended ME model captures an essential aspect of protein folding in a simple way and is more realistic than the original ME model, there are few shortcomings in our model for describing the full complexity of real proteins in aqueous environments. For example, the effect of desolvation barrier in the pairwise interaction potentials between two residues is not addressed in our model. Chan et al. (37) unraveled that desolvation barriers render protein models with a higher degree of folding cooperativity associated with a higher free energy barrier than their no-desolvation counterparts. When the original ME model (26) was first proposed, single (SSA) or double (DSA) sequence approximation was used. The consequences of such approximations are that the conformational ensemble of the unfolded state is underestimated and the possibility of pairwise contacts of native residues separated by denatured loop is ignored, which may lead to an overestimate of folding cooperativity (4). Deficiencies from using SSA or DSA were removed completely by the exact solution (29) of ME model lately, from which we extended our current model. We also performed additional extensive calculations, employing DSA with allowing pairwise contacts of native residues separated by denatured loop (DSA/L) for which the loop entropy is assigned as in ref. 27. Interestingly enough, the qualitative features of protein folding from using DSA/L remain as cooperative as those from using the exact calculation in this work. Therefore, although the ignorance of the entropy of denatured loops might affect the degree of folding cooperativity, its effect is not large enough to alter the fundamental scheme of protein folding itself into a noncooperative one. Our model is still a Gō-like model so that it does not take into account the nonnative interactions most appropriately and tends to overestimate the folding cooperativity (38). Several works have shown that although the elimination of nonnative interactions enhances folding cooperativity in general, the role of nonnative interactions in protein folding is complicated and will depend on the precise sequence, structure of the native state, and average energy of nonnative contacts (39, 40). The degree of cooperativity could be compromised to some extent, yet the existence or nonexistence of cooperativity itself might not be altered by the ignorance of nonnative interactions. Although the major determinant for the cooperativity of protein folding is the relative abundance of nonlocal versus local pairwise contacts between residues in the native structure of a protein (4, 10), it will be nontrivial and highly challenging to come up with a further realistic model that can fully address the overall effect on the folding cooperativity that is orchestrated by the interplay of pH value, denaturant concentration, and several factors mentioned above.

Conclusion

This article addressed one of the most important issues in protein folding by tackling and resolving the recent controversy on the folding mechanism of fast-folding proteins. We established a rigorous and general framework for the exact and simulational investigation of thermodynamics and kinetics for protein folding and applied it to an unlabeled BBL protein and three PSBD homologues that are target proteins of the intensive debate for a global downhill protein folding. Although the new scenario of global downhill protein folding for BBL protein and three PSBD homologues has been proposed, we demonstrated evidences of two-state cooperative (first order phase) transition for these proteins by using an extended ME model that uses an exact free energy landscape, an exact analysis of relaxation eigenmodes from a master equation, and an out-of-equilibrium relaxation kinetics via kinetic Monte Carlo simulation. Our exact and numerical results are in a qualitative agreement with the recent experimental results (15, 16, 24) and properly address the fundamental controversy related to the global downhill folding not in terms of the statistical dispute but by the fundamental principles of equilibrium thermodynamics and out-of-equilibrium relaxation kinetics. We believe that our work provides a resolution to the long-standing controversy of global downhill protein folding, whose applicability for other proteins needs to be exercised with caution.

Materials and Methods

ME Model.

An effective free energy of a protein conformation is described by ΔG({S_k}) = JΣ_〈i,j〉ε_ij∏_k=i^jS_k − TΣ_k=1^NΔS_conf·S_k, where T is a temperature and N is the number of amino acids in a protein. The conformational state of a protein with N amino acids is represented by the N-spin binary variables {S_k} for amino acids k = 1, 2, …, N. When the dihedral angles (φ_k−1, Ψ_k) of kth amino acid are native (nonnative)-like, S_k takes the value 1 (0). The entropic cost of forming a native amino acid is ΔS_conf < 0 with respect to its nonnative conformation. The pairwise-contact energy between ith and jth amino acid is ε_ij when the distance between two C^αs of ith and jth amino acid is less than a threshold value, e.g., 6.5 Å, in its native structure.

Folding Kinetics by Master Equation.

The time evolution of the conformational probability vector P⃗(t) = (P_l) = (P₀, P₁, P₂, …, P_N) satisfies a master equation dP⃗(t)/dt = −MP⃗(t), where l = 0, 1, 2, …, N − 1, N denotes (N + 1) set of protein conformations each having the same fraction M = l/N of native residue such that 0(N) denotes a fully unfolded (native) state. M = (M_mn) is a relaxation matrix constructed by the transition probability from a state n to m based on the Metropolis algorithm, where M_mn = −1/τ₀ exp(−(ΔG_m − ΔG_n)/RT) if G_m > G_n and −1/τ₀ otherwise, and m, n = 0, 1, 2, …, N − 1, N. Here, ΔG_m and ΔG_n are read from Fig. 1 and τ₀ is a molecular time scale. The diagonal elements of M are set by M_nn = −Σ_m,(m≠n)M_mn such that the sum of column matrix elements is zero and M_mn satisfies the detailed balance condition.