What can one learn from experiments about the elusive transition state?

Abstract

We present the results of an exact analysis of a model energy landscape of a protein to clarify the idea of the transition state and the physical meaning of the φ values determined in protein engineering experiments. We benchmark our findings to various theoretical approaches proposed in the literature for the identification and characterization of the transition state.

Small globular proteins are known to fold rapidly and reversibly under physiological conditions (Anfinsen 1973). This process is highly cooperative in nature and is driven by hydrophobicity. It involves expulsion of the solvent from the interior of the protein’s folded state. The resulting native-state structure has a hydrophobic core that is stabilized by hydrogen-bonds and disulfide bridges. In the simplest case, folding is an all-or-nothing phenomenon in that each individual protein molecule in a solution is either in a folded (N, for native) or denatured (D) state and not in between. This scenario is called a two-state picture (Eyring and Stern 1939; Jackson and Fersht 1991; Otzen et al. 1994; Itzhaki et al. 1995; Fersht 1998; Baldwin and Rose 1999a) if it corresponds to kinetics that is governed predominantly by a single exponential. The two-state picture is anchored in the classic Eyring theory (Eyring and Stern 1939) of chemical reactions, which envisions folding as proceeding along a reaction coordinate so that the free energy changes through three main stages (Fersht 1998; Baldwin and Rose 1999b): D; ‡, the transition state; and N. The transition state corresponds to the highest free-energy barrier and provides a bottleneck for the conversion to the native state.

The phenomenological two-state picture raises many questions when one considers the molecular structure of a protein. For instance, there is a huge number of conformations that the protein may adopt—which of these ought to be classified as ‡, or D? Do the other conformations matter? What is the meaning of the reaction coordinate? Because the transition state must be short-lived and barely populated, how can one find it experimentally or elucidate it theoretically?

One way to deal with the multiplicity of the microscopic conformations is to view the folding phenomenon as being akin to a first-order phase transition (albeit in a finite system) with its kinetic mechanism being similar to nucleation (Abkevich et al. 1994; Fersht 1997). The idea of the transition state morphs then into that of a folding nucleus, which acts as a critically sized droplet of the folded phase. The criticality condition means that the droplet may either shrink (which leads to unfolding) or expand (which leads to folding) with equal probability; that is, the droplet is on the edge between the folded and unfolded basins of attraction. The nucleation interpretation immediately suggests that there could be many different “droplets” that form an ensemble of the transition states (Pande et al. 1998; Pande and Rokhsar 1999a, b). Is this suggestion valid?

The established experimental way to probe the transition state or states is through the techniques of protein engineering (Oxender and Fox 1987; Robson and Garnier 1988; Matouschek et al. 1989, 1990; Jackson and Fersht 1991; Otzen et al. 1994; Itzhaki et al. 1995; Cleland and Craik 1996; Fersht 1998; Carmichael Wallace 1999). The basic idea entails the substitution of amino acids in different positions of a protein with other amino acids and monitoring the resulting changes in the stability of the native state and the kinetics of folding or unfolding. The effects of these substitutions are characterized by means of a set of the folding φvalues (φ_f), which are measures of the changes in the kinetic rates normalized by corresponding changes in the protein stability. In simple situations, the φ_fs take values between 0 and 1. A value that is close to 1 suggests a nearly native-like structure of the site of substitution in the transition state. Therefore, new questions emerge—for instance, how may one identify conformations that are compatible with the measured φ values? Furthermore, how may one interpret nonclassical values that are negative or >1?

The list of such basic and unsolved questions is long and so is the list of different answers that have been offered in the literature. This situation calls for considering a simple model that displays two-state physics and is amenable to exact solution, through which one may resolve the key issues and elucidate the underlying concepts. In this paper, we analyze a model that encapsulates many of the essential features of protein folding kinetics with a nontrivial free-energy landscape. This model is a variant of a system considered by Munoz, Eaton, and their collaborators (Munoz et al. 1997, 1998; Munoz and Eaton 1999). It is Go-like (Abe and Go 1981), and it embodies the topology of the β-hairpin. It was introduced in the context of experimental studies of a corresponding fragment in the protein G (Munoz et al. 1997). Munoz et al. (1997) have considered a peptide of 16 residues with one tryptophan (W43) to investigate the kinetics of β-hairpin formation in a laser-induced temperature jump experiment. Measurements of the tryptophan fluorescence have indicated that the relaxation to equilibrium is governed by a single exponential and corresponds to a single free-energy barrier. The time constant is ~6 μsec, which is about 30 times longer than that found in comparable α-helices. Its equilibrium properties have been further explored theoretically by Flammini et al. (2002) and Bruscolini and Pelizzola (2002). We consider a shorter, 12-amino acid version of the original model; reformulate it in terms of Ising spins, which can take on one of two values, corresponding to the immediate vicinity of the protein being native-like or not; and endow it with single spin flip kinetics—Munoz and Eaton had considered diffusional kinetics instead. The kinetics is formulated in terms of a Master Equation that deals with probabilities and not specific trajectories. We then go on to use the results of our exact solution of the model to understand the nature of the transition state and the significance of φ values.

Results

The model

The native state of the system we study is illustrated in Figure 1 ▶. The system can be described in terms of effective free-energy levels that take into account their underlying microscopic degeneracies through an effective entropy term. The free-energy levels are defined in terms of 11 peptide bonds that are either placed in the native fashion or not. The native placement corresponds to the Ramachandran φ–ψ angles taking on their native-state values. This binary character of the bond placement allows for an Ising-like modeling, and we adopt spin variables S_n, which take values 1 or 0 correspondingly. The free energies per mole can be written as:

Figure 1.

The model β-hairpin system studied in this paper. The stars denote amino acids. The spins S_n correspond to the peptide bonds between the successive amino acids. In nonnative conformations, only parts of the native structure are established. The dotted lines indicate the presence of a hydrogen-bond. The dashed lines correspond to hydrophobic bonds between hydrophobic amino acids.

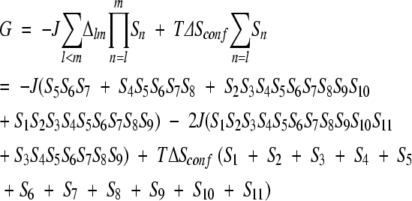(1)

A nonzero value of the product S_lS_{l + 1 …} S_m implies that all peptide bonds between l and m are set in the native fashion, which allows for the establishment of native interactions in the cluster between the bonds l and m. These interactions are either hydrophobic or due to establishment of the hydrogen-bonds, or both. For simplicity, we assume that the strength of the interactions, J, is the same in both cases and equal to 1000 K, whereas the conformational entropy per spin, ΔS_conf, is taken to be 2.14R, where R is the gas constant. In equation 1, T denotes the temperature. Therefore, the stability of the β-hairpin system is controlled by a competition between the gain in the energy of the established contacts and the loss of conformational entropy on setting the conformational angles to their native values.

We choose Δ_lm to be 2 for (l, m) = (1, 11) and (3, 9), 1 for (l, m) = (2, 10), (4, 8), (5, 7), and (1, 9), and 0 otherwise. Note that the placement of the contacts breaks the symmetry between the upper and lower branches of the hairpin. There are several reasons that we consider the simpler 12-residue system. First, the number of conformations is significantly smaller, which facilitates the computational study. Second, the model is simplified by choosing just one interaction parameter. Third, we remove an unnecessary complication of the original model that is related to the fact that two residues at each of the terminal ends of the hairpin are not stabilized by the interactions present in the 16-residue system. In fact, the hairpin conformation is not a free-energy minimum for either the original or the simplified couplings. Let the free energy in conformation i be denoted by G_i. The equilibrium probability to occupy this conformation, P_i, is then given by

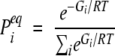(2)

Kinetics: relaxation, folding, and unfolding

The relaxational spin-flip kinetics can be described in terms of the Master Equation (e.g., see Cieplak et al. 1998; Ozkan et al. 2002) for the time-dependent vector of probabilities P with components P_i. By convention, we take i = 1 to correspond to the native state. The Master Equation reads

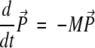(3)

with M_ij for the flip from state j to i equal to 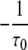if G_i < G_j and 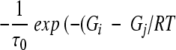otherwise. is the attempt rate, which may generally depend on T. The diagonal elements are set so that the sum of the terms in each column is zero. This choice of the matrix is consistent with the detailed balance condition and the Arrhenius form of the low-T relaxation processes. The time evolution of P can be obtained through an iterative use of the equation P(t + δt) = (1 − δtM)P(t), where δt denotes an infinitesimal time increment. An alternative way to follow the kinetics is by decomposing P into the right-handed eigenvectors and by endowing them with an exponential time dependence of the form exp(−λ _αt), where λ_α is the eigenvalues of the M matrix. One eigenvalue is always zero—it corresponds to the system staying in equilibrium. The smallest nonzero eigenvalue, denoted as k, is the slowest relaxation rate. The inverse of k yields the longest relaxation time. Other eigenvalues correspond to faster processes. The two-state behavior is obtained when there is a substantial separation between the slowest and other rates. Such is, indeed, the case here because our choice of the parameters yields the second longest relaxation time at 300 K to be of order 6% of the longest one. Folding conditions are generated when one disallows all transitions that lead out of the native state—the first column of the M matrix is set equal to zero, and the native state acts as the probability sink. The resulting matrix will be denoted by M_f. On the other hand, the unfolding conditions are generated by making the completely unfolded state a probability sink, and the corresponding column is set equal to zero to obtain the matrix M_u. In these cases, the smallest nonzero eigenvalue corresponds to the slowest folding and unfolding rates, denoted as k_f and k_u, respectively.

The free-energy levels in our model depend on temperature. However, to identify kinetic barriers, it is useful to freeze the levels at their 300 K values and to introduce another fictitious temperature, T′, that can be varied at will. In particular, it can be set to zero to identify characteristic times that diverge in this limit. We find that the eigenvalues (the inverse relaxation times) either tend to zero as T′ approaches zero (there are four such eigenvalues with eigenvectors corresponding to the four local minima) or they tend to integer values of 1, 2, or 3. The other eigenvalues correspond to downhill motion in the free-energy landscape and are determined by the local topology. As T′ increases, there are Arrhenius-like corrections to the T′ = 0 limit and considerable mixing of the levels.

Before we continue with the discussion of our model, we note that a strictly two-level system would be described by the following 2 × 2 matrices:

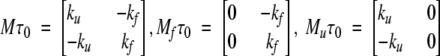(4)

The transition state is implicit k_f and k_u satisfy

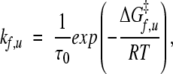(5)

where ΔG_f^‡ = G_‡ − G_D and ΔG_u^‡ = G_‡ − G_N. Each of the M matrices has one zero eigenvalue, and the other eigen-values are k = k_f + k_u, k_f, and k_u for the relaxation, folding, and unfolding situations, respectively, which agrees with the standard expectation (Fersht 1998). The eigenvector corresponding to the nonzero eigenvalue is, in each case, equal to 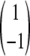. Thus, the observation of Ozkan et al.(2002) that the populations corresponding to the relaxation eigenvector of the lowest nonzero eigenvalue are “rigorously what should be called transition state conformations” is not valid. In the two-level system, the eigenvector contains both the D and the N conformations, albeit with opposite sign. One can show exactly that, quite generally, the sum of the components of the eigenvector is 0 and corresponds to a draining out of the probability of occupancies of conformations with a given sign in the eigenvector accompanied by an associated increase in the probabilities of the remaining conformations.

In the 12-amino acid model, there are 2048 possible conformations. The native state corresponds to all spins being equal to 1 and to the establishment of all eight contacts. The fully unfolded state corresponds to all spins being 0 and no contacts. Of these 2048 conformations, 67 have the property that nonzero values of the spins are contiguous, that is, form a single sequence of ones. Indeed, the 67th conformation is the unfolded state in which all the spins have zero values. In the so-called single sequence approximation (Munoz et al. 1998), one restricts the conformation space to just these 67 states. Figure 2 ▶ shows that the single sequence approximation gives a fairly accurate picture of the thermodynamic quantities. For the parameters chosen, the folding temperature, T_f, is ~300 K, both exactly and in the single sequence approximation, and this is the temperature at which we focus our further studies. At T_f, the probability to occupy the native state is ~1/2, and the specific heat and fluctuations in the fraction of the established native contacts, Q, show a maximum.

Figure 2.

The thermodynamic properties of the system. The solid lines correspond to the single sequence approximation and the dotted lines to the all-state calculation. (Top panel) The equilibrium occupancy of the native state; (middle panel) the specific heat; and (bottom panel) the “contact susceptibility,” that is, the fluctuation in the fraction of the native contacts divided by RT.

The 67 states of the single sequence approximation are shown in Figure 3 ▶ in the form of a triangle. The single circle at the bottom represents the unfolded state (state 67).The bottom row of circles represents states with one nonzero spin. The second row represents states with two contiguous nonzero spins, the third with three, and so on. The top circle represents the single native state (state 1). The kinetic moves from the unfolded state (the bottom state) can connect to any of the single spin states (last but one row), and vice versa. In all other cases, the allowed kinetic moves are only along the diagonal directions on the triangle, as shown by the dotted lines around the 58th state. There are at most four possible moves because the single sequence condition allows for changes occurring exclusively at the interface(s) between the spin ones and the spin zeros.

Figure 3.

A triangular representation of the 67-level system. See text for explanations. The values of the free energies and of the contact numbers shown on the right of the bottom panel refer only to the states along the optimal path and not to all states in each row.

The free-energy landscape: The transition state

The free-energy landscape, of course, depends on the parameters of the model, especially the T. The top panel of Figure 3 ▶ illustrates the principal features of the free-energy landscape at T = 300 K. There are three local minima, denoted by the larger double circles (states 24, 34, and 43), and two local maxima, denoted by the smaller double circles (states 6 and 46). One can ask in which direction, preferentially toward the native or toward the unfolded state, does the flow of the probability occur if only one state is occupied initially. This propensity can be straightforwardly determined by making both the first and last columns of the M matrix equal to 0 and by studying the time evolution of the probabilities. In this way, both the native and unfolded states act as probability sinks. We find that all states at the top of the triangle have a strong preference to flow toward state 1 (i.e., to reach P₁ ≈1 and P₆₇ ≈0), whereas all bottom states produce a flow to state 67. There are six states “on the edge” (5, 16, 25, 33, 40, and 39, shown connected by a line in the figure), which show nearly equal propensities for both directions, and they separate the two regions of behavior. Two of the edge states, 25 and 33, are “confused” the most, and they also have the lowest free energy among the six. Strikingly, none of the edge states is a maximum.

The bottom panel of Figure 3 ▶ illustrates the best paths that allow for the optimal pathway between states 1 and 67, in either direction. They correspond to the states marked by stars within the circles. There are 48 such paths because on several horizontal lines of the figure, there are several states from which to choose. These choices are equienergetical, making the optimal path energetically unique. The corresponding free energies and the numbers of the native contacts formed are shown in the right of the bottom panel. The native state corresponds to the free energy of −938 K. The highest barrier to climb on the best trajectories is 1852 K, and it corresponds to populating two degenerate states: 25 and 33, which are the saddle point states. There are two native contacts that are established in these states: between bonds (or spins) 5–7 and 4–8, that is, S₄ = S₅ = S₆ = S₇ = S₈ = 1. In state 25, S₃ is nonzero, whereas in state 33 it is S₉, which is nonzero. Thus, these two of the edge states are the “transition states” and are shown in the figure as the black circles. The identification of states 25 and 33 as transition states comes also as a result of studies of sensitivities of k_f and k_u to changes in the free-energy values of individual conformations and noting that the influence of such perturbations is largest in the transition states. This large sensitivity is due to the fact that the transition states act as bottlenecks for the folding and unfolding kinetics. When one considers the full 2048-level description, there are 11! = 39,916,800 different directed paths from (00000000000) to (11111111111). Among these, there are 432 optimal trajectories that include the 48 identified in the smaller subset of states—the transition states are the same. In the full set, there are four other conformations having the same energy as the transition states, for example, (10011111000), but the optimal directed paths do not encounter these conformations.

The reaction coordinate for the folding transition consists of a list of conformations that are traveled on a directed optimal trajectory. The free energy plotted against this reaction coordinate is shown in Figure 4 ▶ (bottom panel). It indicates states 25 and 33 as the transition states. This plot is quite distinct from the free energy, G(Q), calculated as a function of the fraction of the native contacts. As seen in the top panel of Figure 4 ▶, G(Q) has a maximum for Q = 1/4, which corresponds to seven states, but only two of them, 25 and 33, are actually the transition states as obtained through the studies of the kinetic connectivities. We note that the choice of Q as a reaction coordinate has been made, for instance, by Munoz et al. (1998)^, Clementi et al. (2000), and Shea et al. (2000). They considered Go and non-Go off-lattice models with strong dihedral angle terms in the potential energy. These models exhibit a double minima structure in the free energy when plotted against energy or the fraction of the native contacts that are established during the time evolution of molecular dynamics simulations. They assumed that states contributing to the maximum separating the two minima (i.e., those that are “half-way” in terms of the number of contacts) form the transition state ensemble.

Figure 4.

(Bottom panel) Variations in the free energy along the optimal paths for four values of the concentration of the denaturant, x. The contact energies are assumed to be J(x) = (1 − x)J. For x = 0, the free-energy landscape is shown in Figure 3 ▶. The reaction coordinate consists of the conformation label(s) shown at the bottom. The states 25 and 33 are the transition states for the three lowest x values shown. For x = 0.5, it is the almost folded state 2 that becomes the transition state. (Top panel) The free energy, G(Q), as a function of the contact number Q. It is obtained by grouping all states into clusters having a given Q and by calculating the average free energy within each cluster with the normalized Boltzmann factors as the statistical weights. The maximum of G(Q) occurs at Q = 1/4 and corresponds to seven conformations with two contacts each.

It should be noted that, in our model, the proper reaction coordinate emerges naturally when arranging the states according to their magnetization, that is, the net spin value, and not Q. The kinetic connectivities relate neighboring values of the magnetizations, which translates into complicated connectivities between states of a given value of Q. This is illustrated in Figure 5 ▶, which shows, in particular, that the transitions link both same and distant values of Q, indicating no simple relation to the transition coordinate.

Figure 5.

The kinetic connectivities in the 67-level system corresponding to the scheme in which the states are arranged according to their Q values. The Q values are indicated on the left side. The connectivities to and within the states with Q = 0 are complicated and are thus not shown. For example, the kinetic moves from state 58 to states 53, 57, 59, and 62, indicated by the dotted lines in Figure 3 ▶, are all between states with Q = 0 even though they correspond to a varying magnetization. Similarly, the moves from state 34 to the two transition states enhance the magnetization but keep Q at the value of 0.25.

It is not straightforward to discern the transition state from the eigenvectors. The smallest nonzero relaxation eigenvalue corresponds to an eigenvector with a mixture of positive and negative components, which add to zero. The transition-state conformations come with a weight of the same sign as the native conformation and with an opposite sign to that of the unfolded conformation. The eigenvectors corresponding to the smallest nonzero eigenvalue for folding and unfolding have just one component of one sign (native and unfolded, respectively), with the transition state being undistinguished and ranked around 40th among the remaining 66 conformations.

Time evolution of the probabilities

Our framework provides a straightforward mechanism for monitoring the temporal evolution of the probabilities of the protein to be in a given conformation and average values of physical quantities in terms of linear combinations of the eigenvectors of the M matrix. The smallest nonzero eigenvalues describe the long time behavior. The combined effect of all eigenvectors, at any time, can be assessed from the full time evolution of P. Figure 6 ▶ shows the evolution of P₁ and P₆₇ in the 67-level system under the conditions of folding, unfolding, and relaxation. The plots for folding and unfolding are not symmetric: the occupation of the unfolded state disappears much more rapidly on folding than of the native state on unfolding. This is because there are many more ways to exit from state 67 compared with just two ways to exit from state 1, leading to much smaller contributions from state 1 to the eigenvectors corresponding to large eigenvalues (or short times).

Figure 6.

Time evolution of the probability to occupy the native (solid line) and unfolded (dashed line) states in the 67-level system. The initial state of the system is the unfolded state in the top panel and the folded state in the bottom two panels.

Figure 7 ▶ shows a similar plot for the transition state 33 and 40, a neighboring conformation. Note the disparity in the scales of the y-axis in Figures 6 ▶ and 7 ▶. In general, there is nothing in the time evolution of the probability of occupancy of the transition state that would distinguish it from any other states (with the exception of 1 and 67). The maximum values reached by P₃₃ and P₂₅ are on the lowest side when compared with other states. Thus, the likelihood that they would be spotted in a computer simulation is very low.

Figure 7.

Same as in Figure 5 ▶ but for the transition state 33 and a nearby state 40.

The Chevron plots

We now focus on the long time evolution, as determined from the smallest eigenvalues. The experimentally measured kinetic rates are usually represented as the so-called Chevron plots (Chan and Dill 1998; Fersht 1998), in which the logarithms of the rates are plotted against the concentration of a denaturant. The couplings used in our model are meant to correspond to physiological conditions. To mimic the effects of a denaturant, we adjust the coupling J in a linear fashion so that J(x) = (1 − x)J, that is, x is assumed to be equal to the fractional change in J compared with its x = 0 value (see Fig. 4 ▶). Figure 8 ▶ shows that the resulting plots of the logarithms of the rates versus x are Chevron-like with some curvature in the branches. The relaxation curve agrees approximately with the condition k = k_f + k_u, which arises in the two-state picture. Furthermore, it is seen that the 67-level data points are well described by a system reduced just to four levels: 1, 25, 33, and 67. Considering the full set of 2048 states affects the folding branch very little, but it shifts the unfolding branch (and thus also the relaxation curve): more states allow for a faster unfolding in analogy to the asymmetry discussed in the context of Figure 6 ▶, because there are more states to go to from the native state. Nevertheless, there is no qualitative distinction between the Chevron plots for the 67- and 2048-level systems other than the location of the x value at which the folding and unfolding curves intersect.

Figure 8.

Logarithms of the folding, unfolding, and relaxation rates in the four-level (asterisks), 67-level (circles), and 2048-level (squares) systems as a function of x in a model in which J is adjusted linearly by x. The prefactor in the four-level system was adjusted by a factor of 4.06 downward to match the data for the 67-level system.

The linear adjustment in the J coupling appears to be a plausible model to study the effective influence of x. Another simple model that can be considered is to introduce the free-energy adjustments that are coupled to Q and are thus cooperative in nature. One way to do it is to take G_i(x) = G_i +|G_i|Qx. The corresponding Chevron plot is shown in Figure 9 ▶. The folding and unfolding branches are seen to be straighter, but the overall character of the x dependence is qualitatively similar to that shown in Figure 8 ▶.

Figure 9.

Logarithms of the folding, unfolding, and relaxation rates in the 67-level system as a function of x in a model in which the free energies of the levels are adjusted in proportion to Q.

The x-dependence of β^‡

We now consider the x-dependence of the slopes in the Chevron plots. We define

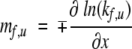(6)

and similarly 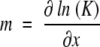where K is the equilibrium constant, which in the two-state model is given by:

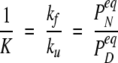(7)

The two-state picture holds if m = m_f + m_u. At T_f, K should be 1, and this is nearly the case if we count not only state 67 but also all of the last but one row states of the triangle of Figure 3 ▶ as belonging to the coarse-grained denatured state. Another quantity of interest is the parameter β^‡, defined as:

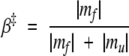(8)

Let us postulate a linear effect of the denaturant’s concentration on the free energies so that G_N(x) = G_N + y_Nx and G_‡(x) = G_‡ + y_‡x, where G_i (i = N, ‡, D) on the right-hand sides of the equations denotes the x = 0 values of the free energy; the denatured state is expected to be unaffected by x. In this case, β^‡ = y_‡/y_N, that is, β^‡ does not depend on x. This expression for β^‡ indicates that this quantity measures the amount of the native-state-like structure contained in the transition state, which, in turn, suggests the common interpretation that it is related to the amount of the buried surface area. There are proteins, however, in which β^‡ shows a linear variation with x. A varying β^‡ would then mean that either the free energy of the transition state varies with x in a way unrelated to the free-energy changes in the native state (e.g., because of the presence of nonnative contacts in the transition state) or that the identity of the transition state varies with x. In the latter case, the adjustments of the free-energy landscape can be captured by a “movie” (Oliveberg et al. 1995; Ternstroem et al. 1999; Oliveberg 2001). In our model, the transition state remains the same, that is, it does not “move” when x changes between −0.25 and 0.25, as shown in Figure 4 ▶, and yet β^‡ varies. The bottom panel of Figure 10 ▶ shows that the dependence is nearly linear. The slopes in the 67- and 2048-level systems are almost the same. It is only in the limit of four states that β^‡ is constant, and equal to 1/4. If all states are included, the Chevron branches acquire curvature (see Fig. 8 ▶), and β^‡ is merely a measure of the curvature generated by the presence of states that are not present in the two-state picture.

Figure 10.

The top panel shows φ values as obtained in the four-level (asterisks), 67-level (circles), and 2048-level (squares) systems. (AA) The location of an “amino acid” where a mutation is implemented. (Bottom panel) β^‡ as a function of denaturant concentration, x, for the three models. The x enters through an adjustment in J caused by the denaturant (see also Figure 4 ▶).

The φ values

To determine the analog of the φ values in our model, at x = 0, we consider a small local adjustment in J at the location of a given amino acid. The adjustment is taken to be of order 5%. The φ values are practically independent of the magnitude of adjustment between 1% and 5%. There are 12 possible locations that are either at a joint between two bonds (two spins) or at the end points of the system. Note that various amino acid locations correspond to different numbers of bonds that are affected. For instance, the ninth amino acid belongs to bonds S₈ and S₉ (see Fig. 1 ▶), which are coupled to four interactions that are affected as a result of a “mutation” on this site. Each adjustment affects the folding and unfolding rates by δk_f and δk_u, respectively, which allows one to calculate

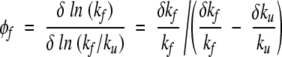(9)

and

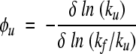(10)

for a mutation at any of the 12 amino acid sites. Note that the folding and unfolding φvalues satisfy the condition φ_f + φ_u = 1.

The two-state picture interprets the φ values in terms of changes in the Gibbs free energy of the folded state and the transition state brought about by the mutation. Specifically, using equation 5,

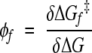(11)

and

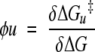(12)

where the symbol δ indicates a change in, say, ΔG = G_N − G_D relative to the respective wild-type value. The two-state picture is obtained when one restricts the conformation space to just four levels: 1, 25, 33, and 67. The set of the corresponding φ_f values is shown in Figure 10 ▶ as asterisks and marked as 4-state. They are equal to 1 at sites 5, 6, 7, and 8 (between bonds S₄ and S₈); equal to 1/3 at site 4; to 1/4 at sites 9; and to 0 at the remaining end sites. This pattern is consistent with the structure of states 25 and 33. When we consider 67 levels, the sites near the turn still have high φ_f values, but they become reduced to ~0.8. At the same time, the values near the end points are enhanced, and only the very end points continue to have strictly vanishing φ values. The pattern of the φ_f values gets a small shift when the full set of 2048 states is considered. It should be noted that the φ values depend on T and on other modifications in the free-energy landscape such as a lowering of one of the free-energy minima.

Discussion

There are several approaches to interpret the transition state in fast-folding proteins in which no intermediates are involved. We have already discussed some of the concepts and results. These are (1) the reaction coordinate is neither Q nor another macroscopic observable but a list of conformations traveled on the optimal trajectories; (2) the transition state/states can be identified by enumerating possible trajectories; (3) the transition states are substates of the edge states that are as likely to fold as to unfold; (4) transition states are not easily determined by the eigenvector of the M matrix corresponding to the longest relaxation time; (5) an x-dependent β^‡ does not indicate a moving transition state.

The free-energy landscape of our model is not endowed with a funnel (Onuchic et al. 1995), and yet it provides for fast folding. Whether the landscape incorporates a funnel or not, one would expect that the transition states are akin to saddle points with very low occupational probabilities. Such states ought to be hard to spot through simulations.

It should be pointed out that studies of the so-called disconnectivity graphs for the polyalanines (Becker and Karplus 1997; Dobson et al. 1998; Levy et al. 2001) also do not yield a funnel-like landscape and suggest instead that the conformational space should be visualized as a broad basin with several pronounced minima at its bottom. The disconnectivity graphs constructed by Wales et al. (2000) for various protein-like systems are endowed with many “transition states.” These, however, are defined as saddle point conformations separating two arbitrary local energy minima. One of these saddle points should correspond to the transition state of Eyring, but all others are not expected to be relevant kinetically.

The issue of multiplicity of folding nuclei

A multiplicity of distinct transition states or critical droplets is also implied by the nucleation-condensation picture of folding (Abkevich et al. 1994; Fersht 1997) and the neoclassical approach of Pande, Rokhsar, and their collaborators (Pande et al. 1998; Pande and Rokhsar 1999a, b). In practice, the droplets were identified as the edge conformations such that time evolution leads to folding and unfolding with equal probabilities. In lattice models, these probabilities are calculated by determining the fate of enumerated short Monte Carlo trajectories that originate from the conformations. Our calculations show that only the lowest free-energy edge states are transition states. Pande and Rokhsar have also studied off-lattice models through all-atom molecular dynamics simulations in unfolding trajectories. In particular, they considered the β-hairpin system of protein G (Pande and Rokhsar 1999b; related studies were done in Dokholyan et al. 2000 and Ding et al. 2002) and identified four characteristic stages—or clusters of conformations—denoted consecutively as F, H, S, and U. They identified conformations (regions of values of the radius of gyrations and of Q), which correspond to the edge states separating F and H and similarly the edge states separating S and U. Both are treated as independent transition states without a comparison of their free energies and without a determination of the edge region between H and S. The edge region between H and S may actually correspond to the highest energy, and if so it would correspond to the true transition state provided the paths that go through the stages F-H-S-U are close to being optimal. The procedure of determining “transition states” for pairs of certain stages may not be always correct, because the problem of the optimal path is global in nature and partitioning it into subtasks may work only as an approximation. We should also point out that their procedure identifies the hydrophobic cluster (in our model, spins 1, 2, 3, 9, 10, and 11) as folding first and the turn region as folding last. This does not agree with either the original interpretation of the experiment (Munoz et al. 1997, 1998) or with the structure of the transition state found in our model. It is interesting to note, however, that an all-atom multicanonical Monte Carlo simulation with implicit solvation effects performed by Dinner et al. (1999) suggests that the folding does, indeed, start at the hydrophobic cluster. Furthermore, the folding rate is found to be dominated by the time scale of interconversion between compact conformations. Although the experiment (Munoz et al. 1997, 1998) dos not exclude this folding scenario, the additional experiments and simulations may yield a more complete understanding of the folding kinetics in the β-hairpin. Our model is not meant to generate a realistic picture of the hairpin but is meant to merely provide an illustration of the concepts.

Transition state through abrupt changes in the structure

The picture of multiple folding nuclei has been also advocated by Klimov and Thirumalai (2001). They also argued that these nuclei should contain nonnative contacts. Our analysis does not allow us to draw any conclusions about the role of the nonnative contacts because they are not addressable in the present model. Their method of identification of the folding nucleus is based on sudden changes in structure in the very last stages of folding, that is, when the time evolution ought to be entirely governed by the eigenvector corresponding to the smallest folding eigenvalue, which has very little weight in the transition state. Note that there are no sudden changes in properly averaged time-dependent observables, as evidenced in our model by Figures 6 ▶ and 7 ▶. In particular, the probabilities to establish contacts are given by curves that are smooth and monotonic. Thus, any abrupt features should be either due to the presence of intermediates (i.e., be outside of the two-state picture) or be due to insufficient averaging. If one trajectory shows an abrupt structural change at one point, there must be other trajectories that would have abruptness at other points so that a many trajectory average is smooth.

A similar criticism applies to the molecular-dynamics-based identification of the transition state (Li and Daggett 1994; Kazmirski et al. 2001). The operational definition of the transition states is given “as the ensemble of structures populated immediately prior to the onset of a large structural change” during unfolding. Note that all sufficiently averaged quantities should be smooth functions of time, as discussed above. Thus, any method based merely on abrupt changes in the structure probably cannot identify the transition state. Furthermore, it should be noted that unfolding simulations typically impose unfolding conditions through an application of a high temperature (above 200°C) and sometimes high pressure. Both of these circumstances are expected to alter the free-energy landscape significantly—possibly beyond any meaningful comparison with the experiment.

The reaction coordinate and eigenvectors

We have already mentioned the attempts to link the transition state to the eigenvalue analysis (Ozkan et al. 2001, 2002) of the Master Equation. They argue that the eigenvector corresponding to the lowest eigenvalue of the relaxational M matrix can be interpreted as providing a reaction coordinate and a selection of the transition state. We find in our model that the relaxational eigenvector is a linear combination of essentially all 67 conformations, and the true transition state is the 12th weakest weight state.

Selection of the transition state based on the φ values

An entirely different way to determine the transition state is generated by a computational exploration of the conformations of a protein followed by an attempt to match them with experimentally determined φ_f values. If the models are off-lattice, then the procedure involves some clustering of conformations. Examples of this approach are in papers by Vendruscolo et al. (2001) and Paci et al. (2003). The assumed connection of a conformation with the φ_f values is through the degree of nativeness, κ_i, of the local structure. This degree is defined by the number of established native contacts that are linked to the mutated amino acid divided by the maximal native number. The calculated values of κ_i are then compared with the experimental values φ_i, which are defined as φ_f at site i. The transition-state conformations are assumed to be those that minimize the distance between κ_i and φ_i. Paci et al. (2003) have found a dynamical way of generating the best conformations of this sort by running a simulation that punishes the departures from the experimental values of φ_i.

It is easy to test this approach in the 67-level model. We determine the κ_i values and compare them with the φ_i obtained through the Master Equation approach. We find that there are seven conformations that have the smallest and identical Euclidean distance of 0.636 from the kinetically derived values. In addition to the two transitions states 25 and 35, these are states 4, 15, 31, 32, and 34 defined as (11111111000), (01111111000), (00011111111), (00011111110), and (00011111000). These seven conformations form a V-shape in the diagram of the states shown in Figure 3 ▶. All of them have the κ values given by (0 0 0 ⅓ 1 1 1 1 ¼ 0 0 0). Our conclusion is that even though the κ-value-based method does succeed in finding the transition states, it also finds many other spurious conformations. We conclude that this approach is not fool-proof if it is not followed by some additional selection of the states. The need for additional criteria for the selection of transition-state conformations was highlighted by Vendruscolo et al. (2001), who used the β Tanford analysis for this purpose.

Nonclassical φ values

We now consider the issue of the nonclassical, that is, negative or >1, values of φ. Ozkan et al. (2001^{, 2002}) argue that the folding pathways have a different character away from the native state, where there is a multiplicity of parallel “routes downhill,” and near the native state, where folding is slow and serial-like. They postulate that the transition state is located near the place where there is a change in the network topology, and it acts as a switch for the flows of probability. They consider a specific model that is assumed to have two main channels for the flow and suggest that mutations may destabilize one, say slow, channel and direct more flow to another channel. This picture allows them to argue that the φ values are measures of the acceleration/deceleration of folding resulting from the mutations. Their model yields nonclassical values of φ.

Consider a folding rate that is a sum of two independent, parallel processes (i.e., of the probability flow through two channels): k_f = k_f1 + k_f2 and similarly k_u = k_u1 + k_u2. We assume that the single channel folding and unfolding rates are described as in equation 5 but with the individual barrier heights ΔG_fi^‡ and ΔG_uγ^‡ (γ= 1, 2). Suppose that a mutation shifts the native-state free energy by g so that

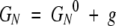(13)

where the superscript 0 indicates the wild-type value. We assume that the mutation does not affect the free energy of the denatured state, G_D = G_D⁰, whereas the individual transition-state free energies get shifted in proportion to g. Thus

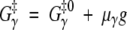(14)

where μ_γ are the coefficients of proportionality. Note that equation 9 can be rewritten as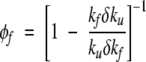

In the two-channel case,

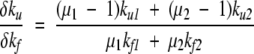(15)

Note that the coefficients μ_γare expected to be <1 and positive, which means that 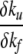is negative and thus φ_f can-not exceed 1. A possibility that nonclassical values of φ would arise is if the coefficients have opposite signs. This could arise naturally when the transition state has nonnative contacts, as noted by Li et al. (2000). In the case of the three-state barnase, the nonnative contacts have been revealed through protein substitution studies (Matouschek et al. 1992; Tissot et al. 1996; Dalby et al. 1998) as arising in a long-lasting intermediate state.

Conclusions

Our benchmarking of various methods to determine the transition state in the exactly solvable model indicates that the most practical method entails using the experimental values of φ combined with kinetic simulations to determine the set of conformations that are both the most compatible with the φ values and are edge states. A further refinement would entail picking conformations with the lowest free energy from this predetermined set. Such a refinement is probably less necessary for a large protein with multiple constraints imposed by the φ values. It is possible that for sufficiently large proteins, compatibility with the kinetic simulations may already select the correct state.

Article published online ahead of print. Article and publication date are at http://www.proteinscience.org/cgi/doi/10.1110/ps.04713804.