Critical nucleation size in the folding of small apparently two-state proteins

Abstract

For apparently two-state proteins, we found that the size (number of folded residues) of a transition state is mostly encoded by the topology, defined by total contact distance (TCD) of the native state, and correlates with its folding rate. This is demonstrated by using a simple procedure to reduce the native structures of the 41 two-state proteins with native TCD as a constraint, and is further supported by analyzing the results of eight proteins from protein engineering studies. These results support the hypothesis that the major rate-limiting process in the folding of small apparently two-state proteins is the search for a critical number of residues with the topology close to that of the native state.

To uncover the principles that govern the protein folding process, recent studies have focused on small single-domain proteins. So far, the folding behavior of more than three dozen small proteins has been investigated. They very generally fold in an apparent two-state manner in the absence of detectable early folding intermediates (Jackson 1998; Krantz et al. 2002). Some of the small proteins have been studied in further detail, including the characterization of the rate-limiting transition states by a protein engineering procedure (Goldenberg 1999) and the detection of hidden intermediates that exist after the rate-limiting step by a native-state hydrogen exchange method (Bai et al. 1995; Englander 2000; Chu et al. 2002). Interestingly, the folding rates of these proteins, despite the fact that they span over six orders of magnitude from microseconds to seconds (Munoz et al. 1997; Chiti et al. 1999), correlate with various simple parameters describing the structural properties of the native state including contact order (CO; Plaxco et al. 1998), long-range order (LRO; Gromiha and Selvaraj 2001), fraction of local contacts (Mirny and Shakhnovich 2001), total contact distance (TCD; Zhou and Zhou 2002), and secondary structure contents (Gong et al. 2003).

The earlier observation of the empirical correlations has spurred the development of several quantitative kinetic theories (Plaxco et al. 1998; Alm and Baker 1999; Debe et al. 1999; Munoz and Eaton 1999; Makarov et al. 2002; Kaya and Chan 2003; Makarov and Plaxco 2003; Weikl and Dill 2003) to predict folding rates. Among the theoretical models, the topomer search model (Makarov et al. 2002) also provides a theoretical basis for the empirical correlation between folding rate and the number of native contacts separated by a long distance in sequence (LRO; Gromiha and Selvaraj 2001). The rate-limiting step in the topomer search model is the search for a topomer with full native-like backbone structure in the unfolded state before the formation of the transition state (Makarov and Plaxco 2003). This requirement, however, makes it difficult to explain the native-state hydrogen exchange results that indicate partially unfolded intermediates exist after the rate-limiting step (Bai et al. 1995; Englander 2000; Chu et al. 2002). Moreover, the model leaves little role for transition states in determining folding rates.

We found that a more unified model could be obtained if the rate-limiting step of folding is the search for the topomers of a critical nucleus with a native-like topology rather than the full native backbone structure. The hypothesis that the rate-limiting step is the search for a critical nucleus with a native-like topology was initially proposed by Sosnick et al. (1996; see Fig. 1 ▶) and formulated quantitatively later by Plaxco et al. (1998) using a simple theoretical model. However, a quantitative relationship between the properties of nuclei and folding rates so far has not been found for real proteins. To seek the evidence for these hypotheses in real proteins, we analyzed the topology, described by a total contact distance (Zhou and Zhou 2002), of the hidden intermediates and the size (number of folded residues in the native conformation) of the transition states of small apparently two-state proteins. We discovered a quantitative correlation between folding rate and topologically determined size of the transition state.

Figure 1.

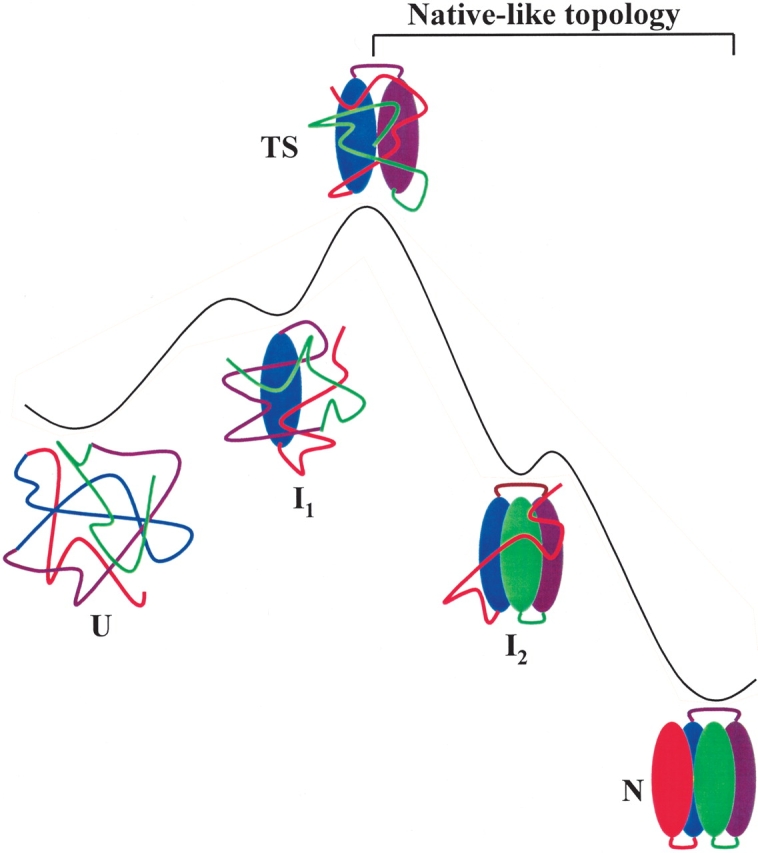
A schematic diagram of a putative folding pathway for an apparent two-state protein and the change of topology along the folding coordinate. In this illustration, the formation of the middle region is the rate-determining step. The two hidden intermediates are not observable in the conventional kinetic folding experiments. I₂ can be identified by native-state hydrogen exchange method (Chu et al. 2002).

Results

Topology of hidden intermediates

If the rate-limiting transition state has a native-like topology, we reasoned that any state between the rate-limiting transition state and the native state should also have native-like topology. To test this, we first investigated the topology of the hidden intermediates of cytochrome c (cyt. c; Bai et al. 1995) and Rd-apocyt b₅₆₂ (Chu et al. 2002) using TCD because the folded regions of these hidden intermediates are well defined. TCD (Zhou and Zhou 2002) is very similar to the contact order proposed earlier by Plaxco et al. (1998) except that the sum of the sequence separations of the contacts is normalized by using the total number of residues rather than using the total number of contacts as in the contact order (Zhou and Zhou 2002):

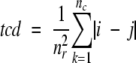(1)

where n_r is the number of residues of a protein, and n_c is the number of nonlocal residue–residue contacts. A nonlocal contact is defined as two residues having heavy atoms within a cutoff distance R_cut and separated by at least a sequence cutoff value l_cut. In this paper, we used R_cut = 6 Å and l_cut = 2. i and j are the residue numbers in the sequence. This renormalization not only has good physical basis (Zhou and Zhou 2002) but also allows very small proteins and short peptides to be included in the correlation between topology and folding rates, whereas the contact order has failed in such cases (see Discussion).

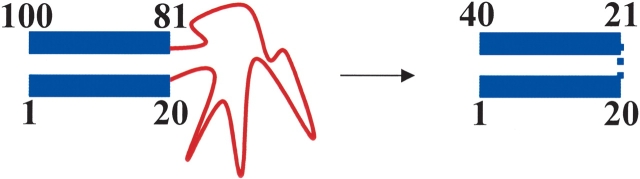
An immediate question related to the calculation of TCD value of a partially unfolded structure is how to model the effect of unfolded loops on the folding rate. Previously, Munoz and Eaton (1999) simply ignored the loop effect in their model for calculating folding rates. Alm and Baker (1999) and Fersht (2000), however, have modeled the loop effect on folding rates using a polymer theory, which correctly predicted the small effect (< fourfold) of short loops (~10 amino acids) on the folding rates (Ladurner and Fersht 1997; Viguera and Serrano 1997). More recent experimental study by Scalley-Kim et al. (2003) has shown that the effect of a very long loop (~100 amino acids) on the folding rate is still small (< fivefold), suggesting that unfolded loops generally have little effect on folding rates. Because the folding rates of small apparently two-state proteins span six orders of magnitude, the loop effects on the folding rate therefore are relatively small. Therefore, we also ignored the loop effect on the folding rates in our analysis. The unfolded regions were substituted with putative linkers without sequence separation (see Fig. 2 ▶ for illustration). The TCD values calculated under this assumption for the hidden intermediates of cyt. c (Bai et al. 1995) and Rd-apocyt b₅₆₂ (Chu et al. 2002) are shown in Table 1. Indeed, the TCD values of the hidden intermediates are very close to the value of native state (81%–102%; see Table 1) despite the fact that they involve the deletion of significant numbers of residues (up to 67 in the case of cyt. c) from the native protein.

Figure 2.

Illustration for calculation of TCD of a partially unfolded structure. The unfolded region was substituted with a putative bond without sequence separation. In this illustration, the C-terminal region following the unfolded loop was renumbered after the loop was substituted with a putative bind. The TCD value was calculated using the structured region with renumbered sequence to obtain |i - j| values in equation 1.

Table 1.

TCDs values of hidden partially unfolded forms (PUF)

Proteins	Unfolded regions	Tcd
Cyt. c (Bai et al. 1995)a		0.84
PUF1a	[70–85]	0.80
PUF2a	[70–85, 36–60]	0.86
PUF3a	[19–85]	0.81
Rd-apocyt b562 (Chu et al. 2002)		0.81
PUF1	[1–22]	0.73
PUF2	[1–22, 95–106]	0.66

^a In these calculations, the effect of heme is not considered.

Correlation between the size of the transition state and the folding rate

The finding that the TCD values of the hidden intermediates are close to those of native states in cyt. c and Rd-apocyt b₅₆₂ led us to use TCD values as constraints to reduce native structure in the search for the size of the transition state assuming that the transition state is the smallest substructure with a TCD value close to the native state. This is done using a computer program. The program deletes a stretch of six contiguous residues that have the least effect on the TCD value in each step. This process may be viewed as unfolding proteins block by block on a pathway that causes the least change of TCD values in each step. However, it should be noted that this process does not necessarily reflect the actual unfolding process. Figure 3A ▶ illustrates the results from four small proteins: cyt. c, Rd-apocyt b₅₆₂, mAcP (Chiti et al. 1999), and TNfn3 (Hamill et al. 2000). These proteins have similar sizes (90–106 residues) but very different native TCD values (0.60–1.26). During the reduction (or unfolding) process, the TCD values of these proteins are unchanged initially, and start to decrease more rapidly and almost monotonically after a significant number of residues were unfolded. This monotonic feature provides a basis for defining and obtaining the size of transition state (see below).

Figure 3.

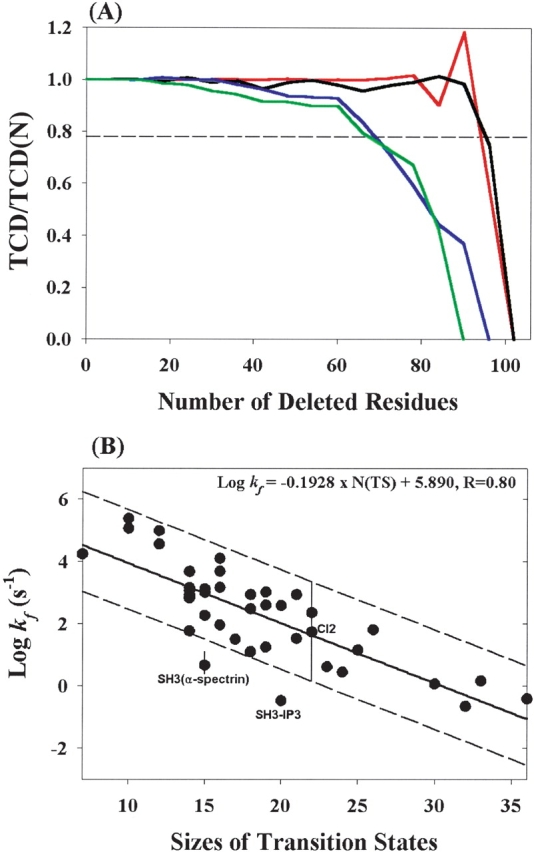
Reduction of the native structures. (A) Plots of TCD/TCD(N) vs. the number of deleted residues for cyt. c (red, TCD(N) =0.84), Rd-apocyt b₅₆₂ (blue, TCD(N) =0.79), mAcP (pink, TCD(N) =1.52), and TNfn3 (green, TCD(N) =1.24). TCD is the corresponding topology of the structure after deletion of a six-residue segment in each step (see Materials and Methods) and TCD(N) is the topology for the native state structure. The dashed line represents 78% of the TCD(N) value. (B) Correlation between folding rates and the sizes of the “transition states” generated using the reduction procedures. The solid line is the result of a linear fitting. The dotted line indicates a ~50-fold deviation from the solid line determined by the maximum range of the folding rates from single mutants of CI2 (Jackson 1998). Note: The molecule (SH3–PI3) in the experiment had additional four residues (WNSS) at the C terminus (Guijarro et al. 1998) of the structure in the PDB file (2PNI) that is used to calculate the TCD value.

We found that the native structures with smaller native TCD values (cyt. c and Rd-apocyt b₅₆₂) can be reduced to very small sizes without significantly affecting the TCD values. In contrast, more “complex” topologies (higher TCD values, mAcP, and TNfn3) are more sensitive to the size reduction. In general, the smaller the TCD value of a native state, the slower the decreasing rate of the TCD value. It is independent of cutting size (1–20) in each step. Thus, these results suggest that there is an intrinsic relationship between the topology of the native state and the size of the substructures. If one reverses the reduction process, that is, in the folding direction, these curves suggest that the same fraction of the topology, relative to the native value, is reached by different sizes (number of residues undeleted) of the substructures for different proteins, independent of the original sizes (total number of amino acids) of the native proteins. These results suggest that there may be a quantitative correlation between the folding rates and the sizes of the substructures with the same fraction of the topology of the native states.

To determine the sizes of these “transition states,” we use the smallest substructures with TCD values above 78% of those of the native states by choosing contiguous six residues as the cutting size (see Materials and Methods). Indeed, there is a significant correlation between the folding rates and the sizes of the reduced structures for the 41 apparently two-state proteins (see Table 2, Fig. 3B ▶). The correlation coefficient is 0.80 (0.85 if excluding SH3–α-spectrin and SH3–IP3; for SH3–IP3, the protein used in the experiment has four more residues [WNSS] at the C terminus than the pdb structure; Guijarro et al. 1998). This correlation coefficient is, in fact, slightly higher than that of the correlation between TCD values of the native state and the folding rates (r =0.76) for this data set. The regression line indicates that the size of the transition state can account for about five orders of magnitude differences in folding rates.

Table 2.

Structural and kinetic parameters for the 41 small apparent two-state proteins

Proteins	PDB code	Size of NS	Size of TS	Log kf	TCD(N)
Villin 14T	2VIKa	126	18	2.95	0.97
Ribosomal protein L9	1DIVb	56	14	2.86	0.88
FKBP12	1FKBa	107	23	0.63	1.30
Ubiquitin	1UBOa	76	16	3.18	1.07
Procarboxipeptidase A2	1PBAa	81	21	2.95	1.08
McrP	2HQIb	72	30	0.08	1.48
U1A	1URNa	96	18	2.49	1.20
HPr	1HDNa	85	25	1.17	1.35
Tendamistat	2AITa	75	26	1.82	1.42
CspA	1MJCa	69	15	2.28	1.14
CspB	1CSPa	67	19	3.03	1.10
Twitchin	1WITb	93	33	0.18	1.48
Titin	1TITb	89	17	1.51	1.26
FN_III	1FNF_10a	94	22	2.37	1.14
FN_III	1FNF_9a	90	36	−0.40	1.30
α-spectrin SH3 domain	1SHGc	57	15	0.61	1.35
Src SH3 domain	1FMK	57	21	1.54	1.28
Sso SH3 domain	1BF4	64	14	3.02	0.88
PI3 SH3 domain	2PNI	86	20	−0.46	1.21
Fyn-SH3 domain	1NYFa	58	16	1.97	1.22
E2P	2PDDb	43	7	4.25	0.75
Im9	1IMQb	86	14	3.17	0.93
ACBP	2ABDa	86	14	2.84	1.04
Monomeric λ-repressor	1LMBa	79	14	3.69	0.75
CD2	1HNGb	98	19	1.26	1.25
N-Ribosomal/Protein L9	1CQU	56	14	2.95	0.91
Cyt. c	1HRCa	104	14	3.08	0.84
Rd-apocyt b562	1M6T	106	16	3.70	0.81
CI2	1COAa	64	22	1.75	1.14
Protein L	2PTLa	62	14	1.78	1.13
Protein G	3GB1	56	20	2.60	1.10
mAcP	1APSa	98	32	−0.64	1.52
TNfn3	1TENa	90	24	0.46	1.24
WW domain	1PIN	34	16	4.11	0.95
Protein A B-domain	1BDC	60	10	5.08	0.71
Engrailed homeodomain	1ENH	54	12	4.57	0.83
Villin head piece	1VII	36	12	4.34	0.67
Barnase	1A2P	108	18	1.11	0.86
Ribosomal protein S6	1RIS	97	19	2.61	1.33
NTL9 (1–39)	1COU_1_39	39	15	3.13	1.51
β-hairpin (41–56)	3GB1	16	10	5.39	0.89

^a From Jackson (1998).

^b From H. Zhou and Zhou (2002).

^c References: β-hairpin (Munoz et al. 1997); 1RIS (Miller et al. 2002); T9 to D65 for src-SH3 domain (Riddle et al. 1999); E15 to F76 for protein I (Kim et al. 2000), 1 to 39 for NTL9 (1–39) (Horng et al. 2003); G1326 to T1415 for 1FNF_9 and Vall416 to T1509 for 1FNF_10 (Plaxco et al. 1997); SH3-PI3 (Guijarro et al. 1998); 1A2P (Chu and Bai 2002); 1CQU (Luisi and Raleigh 2000); 1M6T (Chu et al. 2002); 1PIN (Jager et al. 2001); 1BDC (Myers and Oas 2001); IVII (Wang et al. 2003); 1ENH (Mayor et al. 2003); 3GB1 (McCallister et al. 2000); 1BF4 (Guerois and Serrano 2000); 1SHG (Martinez et al. 1999).

Sizes of the transition states from φ values

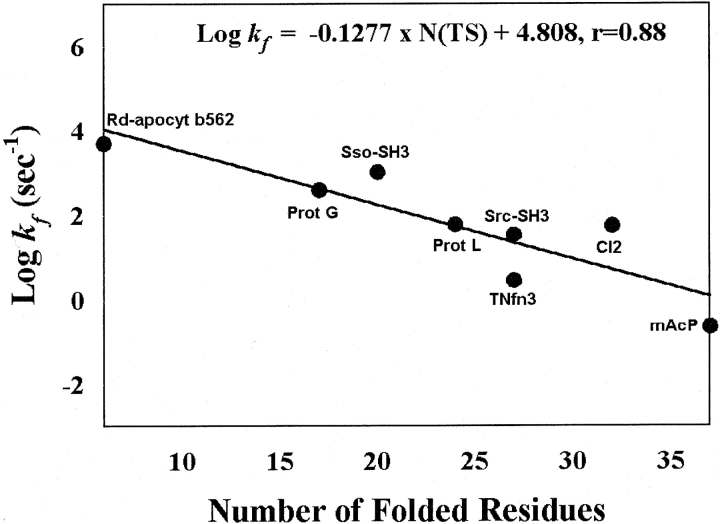
To test the correlation between the sizes of the “transition states” from the reduction procedure and the folding rates independently, we examined the sizes of the transition states characterized by the φ-value analysis from protein engineering studies (Fersht et al. 1992). We modeled transition-state structures of eight extensively studied proteins in a simple binary manner with “folded” and “unfolded” regions by setting a threshold 3 value of 0.35. A residue with φ value larger than 0.35 and its nearest neighbors are considered folded. Otherwise, a residue is considered unfolded (see details in methods). We found that the sizes of the transition states (or number of folded residues in the transition state) indeed correlate with the folding rates (r=0.88 and p =0.004, see Fig. 4 ▶), in agreement with the result from the reduction procedure. We also examined other ways in defining transition structures (see Materials and Methods) and found that this correlation is very robust. This result provides the independent experimental support for the dependence of the folding rate on the size of the transition states obtained from the reduction procedure.

Figure 4.

The correlation between the folding rate and the size of the transition state derived based on the experimental φ values (see Materials and Methods).

The fact that the number of residues with φ > 0.35 in the transition state correlates with the folding rate but not the m_f values (Sosnick et al. 1996), the derivative of the logarithm of the folding rate constants with respect to denaturant concentrations, or transition state placement (Plaxco 1998) suggests that only the residues that make strong interactions in the transition states are important for determining the folding rate. Thus, the size presented in this paper may be considered as an “effective size.” The concept of an “effective size” further rationalizes the above treatment of the residues with missing φ values. Because these residues are on the surface or in the loop regions they unlikely interact strongly with other residues in the transition state. Therefore, they do not contribute to the “effective size” of the transition state.

Discussion

Size and topology of transition states and folding rates

The importance of topology and size of transition state in determining the folding rate of protein folding has been clearly suggested in the earlier studies of protein folding. Sosnick et al. (1996) proposed that the intrinsic rate-limiting step in the folding of a protein is the search for a large nucleus with a native-like topology that could support later downhill folding to the native state (Krantz et al. 2004). Plaxco et al. (1998) used contact order to quantitatively represent the topology of protein structure and found that the contact order of the native structure correlates with folding rate. In the same paper, these authors also proposed a simple model based on the earlier work of Zwanzig (1995) to show that a correlation between a transition state placement and folding rate should exist. This model, however, also implied a correlation between the folding rate and the size of the transition state, although the relationship between transition placement and the folding rate was the focus (Plaxco et al. 1998). However, these predictions so far have not been verified for real proteins. Now, it appears that our discovery of the correlation between the size of the transition state and the folding rate has provided strong evidence for these theoretical hypotheses.

Topomer-search of transition state

In the previous topomer search model (Debe et al. 1999; Makarov et al. 2002), the rate-limiting process involved the search of all contacts in the native structure. Using a Gaussian chain model, Makarov et al. (2002) derived a rate equation:

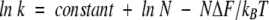(2)

where k is the folding rate, N is number of contacts, ΔF is the mean free-energy gained for contact formation, k_B is the Boltzmann constant, and T is the temperature. It was found that only the number of contacts for those residues with sequence separation larger than 12 were important for determining the folding rates rather than the total number of contacts in the native state. We found that the number of residues in the transition state, N^TS, satisfies equation 2 for both the transition states determined by the reduction procedure (r =0.73 for 41 proteins) and the experimental φ values (r =0.87 for eight proteins). Thus, the topomer search model, if used for searching a transition state with native-like topology, provides a theoretical explanation for the correlation between folding rates and the number of folded residues in the transition state.

Implications of the size of the transition states in the folding mechanism

The discovery of the correlation between the sizes of the transition states (or number of folded residues in the transition states) and folding rates has a number of implications in understanding protein folding. First, it provides a quantitative evidence for a topologically controlled nucleation model for real proteins. The size dependence of folding rates suggests that conformational entropy plays a dominant role in determining the kinetic barrier of folding. On average, the more residues folded in the transition state, the greater the reduction of conformational entropy and the higher the kinetic barrier. Thus, the rate-limiting step appears to involve the search for a group of folded residues that is large enough to have a similar topology as the native state so that it can support further folding in a downhill manner to the native state (see Fig. 1 ▶; Sosnick et al. 1996). Second, the determination of transition-state size by the native TCD value (Fig. 3A ▶) provides a rationale for the observation of hidden intermediates in two-state proteins. A large protein with a simple topology (small TCD value) will have a small transition state, and therefore, leaves a large number of residues to be folded after the formation of the transition state. This creates the condition for a population of multiple hidden intermediates after the rate-limiting transition states. Both cyt. c and Rd-apocyt b₅₆₂ have large native sizes but small TCD values of the native state. Finally, the size dependence might provide a simple explanation to the recent finding that the folding rates of three-state proteins correlate with the size of proteins (Galzitskaya et al. 2003) because these proteins have late transition states whose sizes would be close to those of the native states.

It needs to be pointed out that the above results provide no information on how a protein reaches its nucleation size. The prenucleation event can be dominated by any one of the following processes: diffusion-collision (Karplus and Weaver 1976), a hierarchical process with high energetic folding intermediates (Baldwin and Rose 1999), a hydrophobic collapse-reorganization (Dill 1999), or a combination of them, depending on the energetic interactions in the native structure (Zhou and Karplus 1999).

Energetic interactions in transition states and folding rates

Although the size and topology of the transition state can explain the major difference in the rate of folding for small apparently two-state proteins, the deviation of the folding rate from the regression line in Figure 3B ▶ can be as large as ±50-fold, suggesting that other factors can modulate folding rates. An obvious factor that can affect the folding rate is the energetic interactions among the residues in the transition states. The range of folding rates of the single nondisruptive mutants of CI2 (Jackson 1998) illustrated in Figure 3B ▶ suggests that this factor essentially can fully account for the ±50-fold deviation.

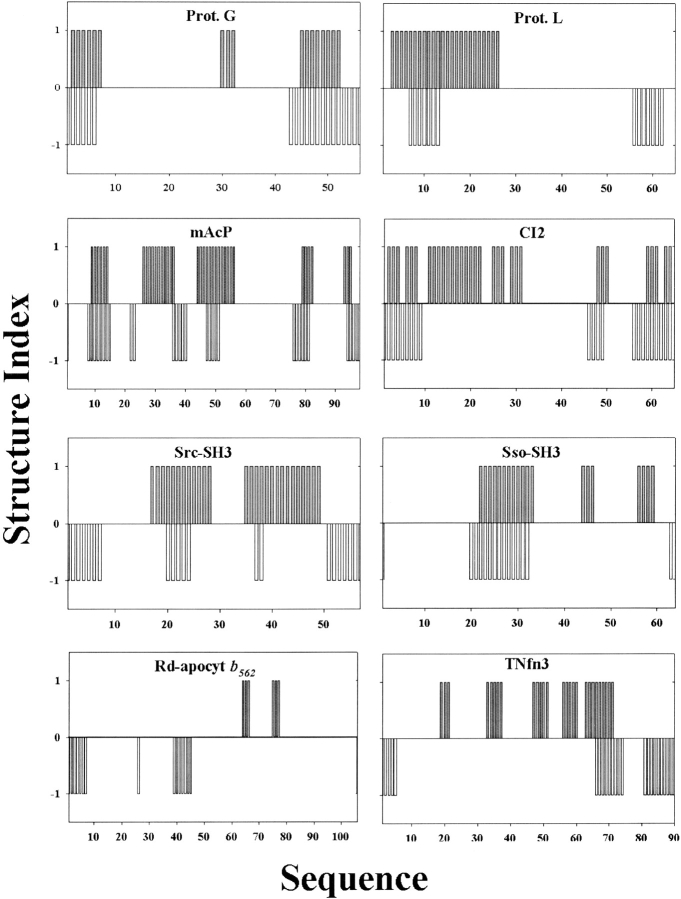
In addition, we found that the reduction procedure did not accurately predict the structure of transition states as specified by the φ values (<0.35) for most of the eight proteins that have been extensively characterized. Figure 5 ▶ shows the comparison between the experimentally determined structure using the φ values and the calculated structure from the reduction procedure for the eight proteins. These results suggest that there might be many native-like partially unfolded structures with similar sizes and topology. The reduction procedure only selected one of them. Indeed, a complete enumeration study shows that there are ~10⁶ of very different substructures with 25 residues that have TCD values between 85% and 90% of the native TCD value of CI2. We speculate that the exact structure of a transition state is also determined by the detailed interactions at the atomic level. For example, the protein G B-domain and its variant NuG1 have similar structures in the native state; however, the structures of their transition states are completely different (Nauli et al. 2001). Although the transition state of the protein G B domain mainly involves the formation of the C-terminal β-hairpin, the transition state of NuG1 involves the formation of the N-terminal β-hairpin. Both the size and the topology of the N- and C-terminal β-hairpins are similar.

Figure 5.

Comparison of the structures of transition states determined from experimental φ values and from the reduction procedure using structure indexes for the eight proteins. A residue or its nearest neighbor with φ > 0.35 is considered structured and given a structure index 1. Otherwise, it is given a structural index 0 to represent that the residue is unfolded in the transition state. Similarly, a residue that is folded in the transition state based on the reduction procedure is given a structure index of −1 (the minus sign is for the purpose of comparison). It is given a structural index of 0 if the residue is unfolded in the transition state.

It is very important to point out that the failure to predict the exact structures of transition states by the reduction procedure does not mean the correlation between the size of transition state derived from the reduction procedure and folding rate is not physically real. The same correlation was also found by the analysis of experimental φ values of transition states as illustrated in Figure 4 ▶. It is likely that the size and topology are more robust properties than the exact structure of transition state. For instance, earlier theoretical models for predicting folding rates and the reduction procedure yield similar results. Munoz and Eaton’s model is able to correlate the energy barrier to the folding rates (r =0.87) but unable to accurately predict the φ values or the structures of transition states (Munoz and Eaton 1999; if the 0.35 threshold value is used to define the folded structure). Similarly, a significant correlation between the calculated energy of transition state and the folding rate has been obtained (r =0.67) from a more sophisticated model of Alm et al. (2002). However, among the 19 proteins studied by Alm et al. (2002), only half of them yield correlation coefficients that are larger than 0.5 between the experimental and predicted φ values. It has negative correlation coefficients for four of the proteins. Because it is still not possible to predict reliably how a single mutation would affect the thermodynamic stability of the native state based on the high-resolution structure, we reasoned that a reliable prediction of φ values that are very much associated with the detailed energetic interactions in both transition states and native states from theoretical model alone would be even more difficult. In particular, it has been shown that nonnative hydrophobic interactions might occur generally in partially unfolded structures including the transition states (Feng et al. 2003). These nonnative interactions so far have been completely ignored in all of the above models, including the reduction procedure.

Other empirical correlation parameters

In addition to TCD values, there are several other empirical parameters that previously were found to correlate with folding rates. For this set of 41 proteins, we find that the folding rates correlate with long-range order (R =0.85) but not contact order for structures of native protein (R =0.35). Mainly contact order failed to account for very small proteins and short peptides such as the WW domain and the β-hairpin. Using lro as a parameter to represent the topology in the reduction procedure, the correlation between the size of the reduced substructure and folding rate is basically reproduced (R =0.71). This result suggests the robustness of the dependence of folding rates on transition-state sizes.

Recently, Gong et al. (2003) also found a correlation between folding rates and a parameter that combines the secondary structure contents and the inverse size of native structures. For the 41 proteins discussed here, the correlation coefficient is 0.79. Using the reduced substructures generated from the reduction procedure, we also found a significant correlation between this parameter and the folding rate (R =0.75). However, in contrast to the native state, the correlation between this term and folding rate for the transition state is mostly contributed by the size dependence (R_size =0.70).

Conclusion

In summary, the results presented here provide a quantitative evidence for the hypothesis that the search for a critical nucleus with the topology close to that of the native protein is the rate-limiting step for small apparently two-state proteins. The size of the transition states, encoded by the topology of the corresponding native state, is the dominant determinant for the five orders of magnitude difference in the folding rates. The detailed energetic interactions at the atomic level appear to be responsible for modulating the folding rate in the range of ±50-fold and for determining the exact structure of the transition state. The results also help to understand why hidden intermediates are observed in some small proteins and the folding rates of larger proteins are correlated with their sizes.

Materials and methods

The size of the “transition state” derived from a reduction procedure

We derived the size of a “transition state” using a reduction procedure with the native TCD value as a constraint. In each step, contiguous six residues in the structure that have the minimum effect on TCD values are deleted. The deletion is continued until the smallest number of folded residues with the closest value above 78% of the native TCD value is found. The 78% cutoff value is chosen because it gives the best correlation between the size of the “transition state” and folding rate (see Results) from the survey of the parameter space for the sizes of deletion from three to nine and the cutoff value of TCD from 50% to 98% of the native TCD value (with a grid size of 1% and 2%, respectively). A block size of five or six produces stronger correlations over a wide space of TCD values than other block sizes. The physical basis for this observation is not entirely clear. It may be connected to the fact that nucleation of an α-helix involves five residues and the formation of the transition state of a β-hairpin involves six residues.

The sizes of transition states derived from experimental φ values

The φ value of a residue is the ratio of the free energy change in the transition state over that of the native state upon a nondisruptive mutation at the corresponding site (Fersht et al. 1992). The experimental φ values of the eight proteins were obtained from published results: mAcP (Chiti et al. 1999; Vendruscolo et al. 2001), SH3-src (Riddle et al. 1999), Protein G (Nauli et al. 2001), Protein L (Kim et al. 2000), CI2 (Itzhaki et al. 1995), TNfn3 (Hamill et al. 2000), SH3-sso (Guerois and Serrano 2000), Rd-apocyt b₅₆₂ (Chu et al. 2002). For mAcP, theoretical values generated after using limited experimental values as constraints (Vendruscolo et al. 2001) were used because the experimental φ values were not measured for some hydrophobic residues that are significantly buried. The highest φ value was taken when there are multiple φ values at the same position. The transition state structures are modeled with the following two rules: (1) missing φ values are treated either as zero or linearly interpolated. The former is based on the fact that most missing φ values are from more flexible surface residues that are unlikely to form strong interactions with other residues in transition states. The latter assume that the neighboring residues are located in a similar native environment. (2) A residue was considered to be folded if it or its nearest neighbor has a φ value (or an interpolated φ value) greater than 0.35. All other residues are considered unfolded. The 0.35 threshold value is chosen to make the sizes of the transition states close to those from the reduction procedure. For this threshold value, the correlation coefficient between the sizes of transition states and folding rates is 0.88 (zero-value approximation) and 0.83 (interpolation approximation), respectively.