Exploring the origins of topological frustration: Design of a minimally frustrated model of fragment B of protein A

Abstract

Topological frustration in an energetically unfrustrated off-lattice model of the helical protein fragment B of protein A from Staphylococcus aureus was investigated. This Gō-type model exhibited thermodynamic and kinetic signatures of a well-designed two-state folder with concurrent collapse and folding transitions and single exponential kinetics at the transition temperature. Topological frustration is determined in the absence of energetic frustration by the distribution of Fersht φ values. Topologically unfrustrated systems present a unimodal distribution sharply peaked at intermediate φ, whereas highly frustrated systems display a bimodal distribution peaked at low and high φ values. The distribution of φ values in protein A was determined both thermodynamically and kinetically. Both methods yielded a unimodal distribution centered at φ = 0.3 with tails extending to low and high φ values, indicating the presence of a small amount of topological frustration. The contacts with high φ values were located in the turn regions between helices I and II and II and III, intimating that these hairpins are in large part required in the transition state. Our results are in good agreement with all-atom simulations of protein A, as well as lattice simulations of a three- letter code 27-mer (which can be compared with a 60-residue helical protein). The relatively broad unimodal distribution of φ values obtained from the all-atom simulations and that from the minimalist model for the same native fold suggest that the structure of the transition state ensemble is determined mostly by the protein topology and not energetic frustration.

Understanding how a protein folds from a random coil to a well-defined three-dimensional structure has remained a puzzling problem for well over 30 years. Two stringent constraints govern the folding of the protein: the kinetic necessity to fold within a biologically reasonable time frame and the thermodynamic requirement of a unique, stable native state (1). In recent years, an approach based on the statistical treatment of the energetics of protein conformations has provided new insight into the protein folding problem. This energy landscape theory contends that a global overview of the protein energy surface is crucial to the understanding of the folding process (2–8).

The energy landscape of a foldable protein lies in between a completely rough and a completely smooth surface, neither of which is observed for a natural protein. Rough energy landscapes are typical of frustrated systems such as random heteropolymers in which many competing interactions are present. In such systems, the energy bias, δE, toward the native state is approximately equal to the roughness, ΔE², of the surface, and hence many low-lying energy traps will be present (9). The perfectly smooth landscape is an idealized case in which the surface exhibits no roughness and the driving force toward the native state becomes the dominant parameter. Although systems with this type of smooth funnel surface (unfrustrated systems) will find their native state, real proteins have no need of such a perfect design—folding needs only to be sufficiently fast and the native fold robust. The energy landscape of a foldable protein can best be described as a funnel riddled with small depressions that can transiently trap the protein in local minima (6, 9–11). The roughness of the folding surface results from the incorrect contacts that are likely to form as the protein samples its wide range of available conformations. The funnel-like shape, which is superimposed onto this roughness, arises from the stabilizing effect of the native contacts. Once a certain portion of the protein has achieved its native structure, the energy of the system will on average decrease, leading to an overall slope of the energy landscape toward the native state. A strong driving force toward the native state is essential to overcome Levinthal’s paradox. This concept of sufficient smoothness in the energy landscape is the Principle of Minimum Frustration (6, 12), and the energy surface of a protein is commonly referred to as a minimally frustrated funnel.

The framework described above focuses mainly on aspects of energetics and frustration arising from the inability of a protein to satisfy all of its mutual interactions. This ignores, in detail, the nature of the folded protein topology and the necessity of the polypeptide chain to achieve a specific three-dimensional conformation for successful folding. The requirement for a complete theory of protein folding to embrace these detailed topological features (13, 14) has been intimated from the analysis of folding free energy landscapes, which used detailed models of protein and solvent (15–17). The objective of this study is to begin a systematic exploration of the influence of the protein final topology on its folding and on measurable properties related to folding such as the φ values of Fersht (18) that reflect the role specific residues play in the transition states for folding.

The sources of frustration in a protein can be broadly categorized as energetic and topological. Energetic frustration is associated with the amino acid sequence in the protein. It occurs when incorrect contacts are formed as the chain folds from a random coil to its native configuration, when the sequence forces mismatched residues to be in contact in the native state or when there is competition between interactions. This type of frustration is minimized by careful natural selection or through protein engineering of the sequence. Proteins optimized for fast folding and robustness will have a reasonably well-designed sequence that will fold with a minimum of incorrect contacts formed in the process (19, 20).

Topological frustration is due to the polymeric nature of the protein and the shape of the native fold (21, 22). It is in part the excluded volume problem that results from the connected nature of the protein. Because the protein chain cannot cross itself, certain regions of configurational space are less likely to be sampled by the protein. Some parts of the chain will not be able to form contacts with other parts of the chain, potentially causing frustration in the folding process. Also, native contacts that are closer in the sequence have a greater likelihood of being formed than those that are further apart. The three-dimensional structure of the protein can also be a source of frustration, as certain topologies (for instance those with very little symmetry) can be more difficult to fold to than others (23, 24). The analogy between symmetric core structures and small clusters for good folding topologies has been suggested by Berry et al. (25, 26).

In the present work, we utilize the following functional definition of topological frustration. In a topologically unfrustrated system, all contacts will be evenly distributed throughout the protein and will be of the same structural importance (same probability of formation). In other words, the structure can start forming from any point along the chain. No one contact or set of contacts has to be formed first, failing which the protein will not fold. As a consequence, the number of native interactions is an optimal coordinate to describe the folding process. The presence of topological frustration is manifest in “inequality” among native interactions, some forming preferentially in folding. As a result, the transition state is no longer homogeneous (as it is for a topologically and energetically unfrustrated system). The participation of each contact (or residue) in the transition state can be inferred from its respective Fersht φ (18) values. The φ values are experimentally determined through the measurement of the folding and unfolding rates for site-directed mutants of the protein compared with the native sequence. From such experiments, a measure of the degree of structure formation in the transition state relative to the folded and unfolded states is obtained (5, 18, 27). The presence of topological frustration in the folding process can be established from the shape of the distribution of the Fersht φ values of the protein (18). We note that a potential consequence of frustration is that the folding process may require additional variables, beyond the native contacts, to fully describe the process of folding. In such cases a few variables may be sufficient—for example, those describing collapse and the number of native contacts—or the process may be very complicated and not well described by a small set of variables.

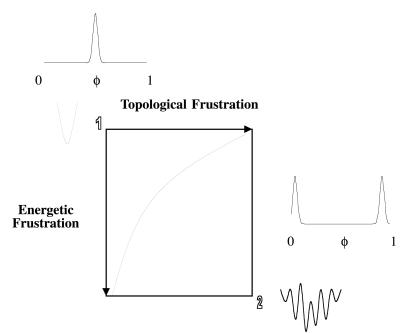
The significance of the φ values will be discussed in detail in the main body of the text. As a brief introduction to motivate our separation of frustration into energetic and topological components, we consider the diagram shown in Fig. 1. The utility of separating the contributions to frustration as we have done are to explore how and where proteins with differing levels of energetic and topological frustration manifest this character in their φ value distributions, and to examine the general features that topology contributes to altering this distribution.

Figure 1.

Folding landscape frustration diagram. The axes denote energetic and topological frustration. In the upper left corner of the figure (point 1), no energetic or topological frustration is present and the folding landscape is a smooth funnel. At the other extreme (point 2), energetic and topological frustration are prevalent and the landscape is very rugged. Proteins will fold on a landscape that lies between these extremes. The degree of energetic and topological frustration will vary with the design of the protein and the choice of the native topology. As frustration increases along either axis the distribution of φ values becomes less ideal and tends to spread out until reaching a limiting bimodal distribution denoting strong pathway dependence of folding.

Materials and Methods

The model we will study is an α-carbon (C_α)-based off-lattice minimalist representation of fragment B of protein A (PA) from Staphylococcus aureus. This small, 46-residue, protein has a simple bundle structure consisting of three helices separated by helix-breaking prolines in the turn regions. It has been extensively studied both experimentally (28, 29) and theoretically through all-atom (15, 30), lattice (31, 32), and off-lattice (33) simulations. Furthermore, its transition state has been thoroughly characterized in the all-atom simulation (15). Experimentally, this protein is known to fold rapidly without forming any detectable intermediates (29).

We have opted to model PA by using an off-lattice representation, as this type of model accurately reproduces the three-dimensional structure of the protein as well as allows us considerable freedom in adjusting the degree of frustration of the model.

To isolate the role of topological frustration in the folding process, we design a model representation for PA which has (to first order) no energetic frustration (Gō-type model). This is achieved by assigning attractive interactions between all residues that are in contact in the native state (favorable contacts) and hard sphere interactions between all others. Any remaining frustration present in our model must now be due to topology. To determine the extent (if any) of the topological frustration, we calculate the distribution of Fersht φ values for our model. Frustration is manifest in the asymmetry or multimodal nature of the φ distribution (see Fig. 1).

Each amino acid residue in our model of PA is represented by a bead (C_α) of 50 atomic mass units. Each bead is connected to adjacent beads by virtual bonds of fixed length r₀ = 3.78 Å. All bonds were kept fixed by using the shake algorithm (34). The bond angles were described by a harmonic potential with force constant k_θ = 20ɛ and an equilibrium bond angle θ₀ = 105°. Dihedral potentials were not used in this model except in the proline turn regions. The general absence of dihedral potentials allows for a model with maximum flexibility. However, weak harmonic dihedral potentials§ (with a force constant of 2.5ɛ and equilibrium dihedral angles taken from the reference protein structure) were imposed in the proline turn regions (residues 12 and 30). This was done for two reasons. The first was to mimic the nature of proline residues, which inherently restrict the backbone conformations. Prolines have the effect of constraining their neighboring residues into specific, fixed positions/orientations. In PA they act as helix-breakers. The second reason is that C_α models cannot distinguish between right and left-handed chirality. Fixing the angles around the prolines solves this problem by making the structure with the correct chirality lower in energy.

An original set of native contacts consisting of residue pairs with helical or longer-range interactions is determined from the reference crystallographic structure as follows. Two residues, i, i + 4, or further apart, for which the side chains (any heavy atom) are less than 4 Å apart and for which the C_α is less than 8 Å apart are considered to form native contacts. Seventy-two native contacts (available on request) were obtained in this manner and used to define the pairs of native (favorable) interactions.

The native interactions were described by the Lennard–Jones potential:

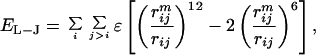1

where r_ij is the distance between the C_α atoms i and j for the pairs of atoms defining native contacts in the reference structure. The well depth ɛ is set at 2 kcal/mol (1 kcal = 4.18 kJ), which yields a folding temperature in the vicinity of 350 K, and the minimum of the potential well is located at the native separation distance, r_ij^m, between the residue pair i, j. The nonnative interactions are described by a hard sphere potential of the form:

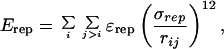2

where ɛ_rep = 2 kcal/mol and the repulsive radius σ_rep = 7.8 Å.

The PA model was incorporated into the molecular dynamics program charmm (35). We started with an all-trans extended chain and progressively cooled the structure in 25-K increments from 700 K to 200 K. This range of temperatures allowed us to probe high-energy extended structures as well as the low-energy compact states. The time was measured in units of τ = (m/ɛ)^1/2r₀. The model was allowed to evolve in a continuum manner following Langevin dynamics. A friction coefficient of 0.2τ and a step size Δτ of 0.0075τ were used. The system was simulated for 2,500,000Δτ at each temperature. Snapshots were saved only every 500Δτ so that each data point can be considered to be independent. The thermodynamic analysis was performed with the weighted histogram analysis method (36).

To explore the kinetics of folding for this model, several hundred independent folding runs, initiated from different high-temperature random coil structures, were performed at the transition temperature for folding determined from the thermodynamic analysis (350 K). The simulations were stopped as soon as the protein reached the native basin (defined in Results and Discussion) and the first passage times were recorded. Typical folding trajectories comprised between 350,000Δτ and 1,000,000Δτ steps of Langevin dynamics for this system. This procedure was applied to the wild-type protein and to a number of mutants.

Results and Discussion

Two-State Thermodynamics and Kinetics of Folding.

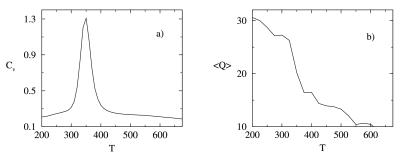
Our model for PA presents the kinetic and thermodynamic signatures of a two-state folder. The collapse and transition temperatures, determined independently from the behavior of the specific heat and of the average number of native contacts 〈Q〉 as a function of temperature (Fig. 2), illustrate this point. The number of native contacts Q was redefined from the average of the low-temperature 200 K structures as all i, i + 4, and greater contacts of less than 8 Å. Folding and collapse are seen to occur concurrently at T_f = T_c = 350 K, indicating that our designed model is a good folder (37, 38). The heat capacity curve is very narrow and sharp, and the average number of native contacts rises quite abruptly at the transition temperature. These are signatures that our system exhibits a clear two-state behavior, and that the transition is first-order-like. We contrast this behavior with the one of a more frustrated (poorly folding) sequence in which the heat capacity curve is broad and the average number of native contacts shows a slow and gradual transition from the nonnative state to the native state (20, 39).

Figure 2.

Temperature dependence of the specific heat (a) and average number of native contacts (b) for the optimized PA model. Together these provide an indication of the first-order-like folding of this model protein.

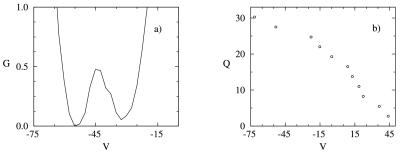
The free energy is plotted as a function of the internal energy, V, in Fig. 3a. Two equal free energy minima corresponding to the native and nonnative basins occur at V = −55 kcal/mol and V = −32 kcal/mol, respectively. These minima are separated by a barrier of 0.6 k_BT_f at V = −43 kcal/mol. For temperatures above the transition temperature, the curve shifts to the high-energy states, whereas for temperatures below the transition temperature, the curve shifts to the low-energy states. This too is a signature of a two-state first-order-like transition. The folding transition in this model is entropically and energetically driven, with the energy and entropy varying almost linearly with Q. The almost complete cancellation of these two terms leads to the small free energy barrier observed in Fig. 3a. This small barrier is a characteristic of well-designed models with pairwise interactions in which the entropic and energetic contributions balance each other out, leading to an apparent downhill (sometimes barrierless) folding at the transition temperature. The lack of (or small) barrier does not contradict the fact that the folding transition is two-state first-order-like. We insist on the “like” in describing the first-order nature of the folding transition because we are dealing with finite system. A well-designed sequence can have a small barrier, yet still be two-state, as evidenced by the sharpness of the transitions observed in the heat capacity and average number of native contacts versus temperature. The distributions of nonnative and native states (data not shown) also show a clear separation in energy at the transition temperature. The difference in energy between the native and the nonnative states (which is related to the energy gap) (39–41) is large (27 k_BT_f), indicating a stable native state and an absence of low-energy misfolded configurations. These last features are signatures of a good folding sequence with a smooth landscape (42). We note that in our model, Q and V are correlated (Fig. 3b), and hence the free energy G as a function of Q has features similar to G as a function of V.

Figure 3.

Thermodynamic functions at the transition temperature. (a) Free energy (G, in kcal/mol) as a function of energy (V in kcal/mol). (b) Number of native contacts, Q, as a function of energy.

The kinetics of the model are also indicative of a two-state folding transition with a single exponential distribution of first passage times. Thus, the combined observations from our thermodynamic and kinetic analyses suggest Q to be a reasonable reaction coordinate for folding in this system.

φ Values and Topological Frustration.

To determine the extent to which our model presents topological frustration, we calculated the φ values of the interhelical native contacts. φ values are obtained through mutagenic studies and serve as a probe of the degree of structure present in the transition state (43). The φ values are defined as the ratio (upon mutation) of the difference in free energies between the transition state and the unfolded state with respect to the difference in free energy between the folded state and the unfolded state (the overall stability). We refer to the φ of a contact i defined in this manner as the thermodynamic φ_thermoⁱ:

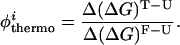3

In the above expression, the superscripts T, U, and F refer to the transition state, the unfolded state, and the folded state ensembles, respectively. The difference in free energy ΔΔG is given by:

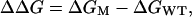4

where the subscripts M and WT refer to the mutant and wild-type proteins, respectively. To lowest order, the thermodynamic φ_thermoⁱ can be viewed as the ratio of the difference in the fraction of native contacts formed in the transition (Q_i^T) and unfolded (Q_i^U) states over the difference in those formed in the folded (Q_i^F) and unfolded states (Q_i^U):

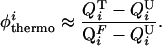5

Experimentally, the free energy difference between the transition state and the unfolded state (ΔG^T-U) is obtained from the folding rate k following Kramer’s expression (18, 44, 45):

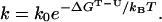6

By assuming that the preexponential factor k₀ does not vary significantly as a result of mutation, we can rewrite the expression for the thermodynamic φ_thermoⁱ in terms of a kinetic φ_kinⁱ:

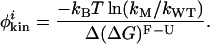7

The φ values in our study were calculated by using both thermodynamic and kinetic connection formulas according to Eqs. 3 and 7. Experimentally, only kinetic φ_kinⁱ can be measured. For a well-designed sequence which folds in a two-state manner, φ_thermoⁱ and φ_kinⁱ are well correlated. As long as the free energy surface is sufficiently smooth with minimal trapping and single-exponential kinetics, the assumptions used to obtain φ_kinⁱ (namely Kramer’s rate and a constant k₀) are reasonable. For such systems, the transition state can be determined thermodynamically from the free energy profiles by using an appropriate reaction coordinate.

As mentioned in the Introduction, the φ values can present two limiting scenarios. If a mutation is performed in a region of the protein that is unstructured in the transition state, Δ(ΔG)^T-U will be equal to zero and hence φ = 0. This mutation will affect the rate of unfolding but not the rate of folding. We consider such a mutated residue (or contact) to be “unimportant” (insofar as the transition state is concerned). If, on the other hand, the mutation is performed in a region that is structured in the transition state of the wild type, Δ(ΔG)^T-U will be equal to Δ(ΔG)^F-U and φ = 1. The rate of folding will now be significantly affected, while the rate of unfolding will remain unchanged. φ values between 0 and 1 indicate either partial structure in the transition state or are representative of an ensemble of conformations, some of which have structure in the region that is mutated, some of which do not.

To explore the importance of specific native interactions in the folding of PA, we perform a mutation by removing a native contact. This type of mutation mimics the double mutations used in experimental studies to determine φ values (43). We have mutated representative contacts lying across helices I–II, II–III, and I–III and calculated the kinetic φ_kinⁱ and thermodynamic φ_thermoⁱ values for each contact. In the thermodynamic calculations, we identified the transition state from the peak in the plot of the free energy as a function of the energy (or equivalently as a function of Q). The unfolded, transition, and folded states of the wild type are defined as those conformations of the polypeptide lying within the following range of energy values: unfolded states, −35 < V; transition states, −46 < V < −38; folded states, V < −48. Equivalent results were obtained when cutoffs based on Q were used. [We recall that the energy and Q are correlated in our model (Fig. 3b), so that the cutoffs based on V or Q give similar results.]

The expression for the free energy difference ΔG^X (where X = U, T, or F) is obtained by averaging over the wild-type ensembles of unfolded, transition, or folded structures:

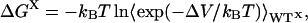8

and hence φ_thermoⁱ is given by:

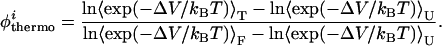9

The energy ΔV between the mutant and wild-type structure is taken to be the energy of the interaction that was removed.

The kinetic φ_kin values were calculated from Eq. 7. Several hundred folding runs were performed for each mutant (as described in Materials and Methods) to obtain the folding rates from the slope of the logarithm of the unfolded population versus the folding time (first passage time). The kinetic evaluation of the φ values is computationally extremely costly, hence when thermodynamically derived φ values can be used it is clearly advantageous.

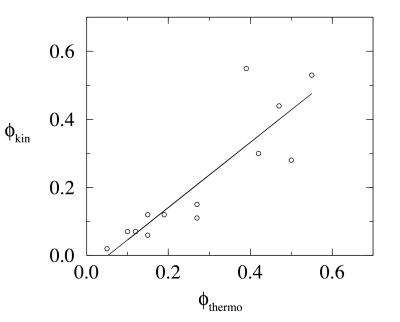
The kinetic and thermodynamic φ values are given in Table 1 and their respective distributions in Fig. 4. The numerical errors in the determination of the φ values are less than 0.02. The φ values obtained by the two methods are in good agreement, with a correlation factor of 0.87 (Fig. 5). Although the exact numbers are not in perfect agreement, the qualitative agreement is excellent. The discrepancies between the kinetic and thermodynamic φ values can in part be attributed to the small size of the free energy barrier (Fig. 3a), which made the unique identification of the transition state difficult. The high and low φ contacts identified by the two methods are the same. This agreement gives encouraging confirmation that the reaction coordinate Q (or equivalently the energy) can be used to satisfactorily locate the transition state from the free energy profiles for minimally frustrated systems. It is important to emphasize that the thermodynamic φ_thermo determined by using a single reaction coordinate is not necessarily a less satisfactory measure of structure in the transition state than is the kinetic φ_kin. The validity of our thermodynamic calculation relies heavily on our ability to identify a suitable reaction coordinate to monitor the folding process. With a correct reaction coordinate in hand, one is able to unambiguously locate the transition state. For well-designed sequences, however, it is not necessary to identify this elusive “true” reaction coordinate. A number of reaction coordinates (such as the number of native contacts) can be used to satisfactorily identify the transition state ensemble of conformations from the free energy profiles.

Table 1.

Kinetic and thermodynamic φ values at the folding transition temperature

Contact pair*	φthermo	φkin
4–37	0.05	0.02
5–23	0.12	0.07
8–19	0.27	0.15
8–37	0.15	0.12
8–41	0.27	0.11
9–19	0.50	0.28
9–20	0.55	0.53
13–44	0.19	0.12
14–44	0.15	0.06
19∼40	0.1	0.07
22–40	0.42	0.30
26–34	0.47	0.44
27∼33	0.39	0.55

^*Helix I (1–10); helix II (16–28); helix III (33–46). 

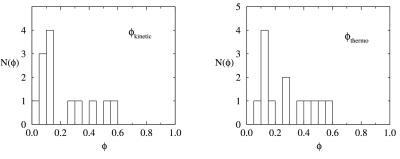
Figure 4.

Distribution of φ values, N(φ), at the transition temperature for thermodynamically and kinetically determined φ values.

Figure 5.

Correlation between thermodynamic and kinetic φ values.

Recent studies have shown that even for moderately good folders the “real” transition state structures form a significant subset of the states identified from the free energy barrier. One can question whether the φs determined thermodynamically in simulations can be compared with the experimentally obtained kinetic φs. On-going investigations in our research groups on protein models with different degrees of frustration (off-lattice simulations by J.-E.S., J.N.O. and C.L.B. and lattice simulations by H. Nymeyer, N. D. Socci, and J.N.O.) show that for proteins with sufficiently reduced frustration, the thermodynamic and kinetic φ values are very similar. The very formulation of the kinetic φ values is, after all, based on the thermodynamic two-state picture. If the free energy cannot be described in terms of a reaction coordinate as a two-well system separated by a transition state barrier, then Kramer’s rate expression no longer holds and the entire foundation of the kinetic φ collapses.

The good agreement between the thermodynamic and the kinetic φ values supports the use of experimental φ values as measures of structure in the transition state. We do not claim that simple reaction coordinates always describe the folding process. It is an adequate description for systems with smooth landscapes. As the landscape becomes more rugged, the thermodynamic φ determined from the free energy surface projected onto a reaction coordinate will no longer be a suitable measure of the degree of structure in the transition state. Analogously, the kinetics will no longer be single exponential and the rate of folding will not obey Kramer’s expression. Consequently, kinetic φ_kin values will be very difficult to interpret in a consistent fashion.

Important and Unimportant Contacts for the Folding Process.

The distribution of φ values (Fig. 4) is unimodal and centered on φ = 0.3, with small tails extending to φ = 0 and φ = 0.55. The distribution of φ values lies in between the two extreme scenarios discussed previously, but resembles more closely the picture of an unfrustrated folder. The φ distribution is not sharply peaked (as in the topologically and energetically unfrustrated case) but rather displays a small spread. We conclude that our model for PA contains a certain amount of intrinsic frustration. This frustration is topological in nature, as we have designed this model without energetic frustration. The extent of the topological frustration is weak, following from the unimodal (rather than bimodal) distribution of φ values. Most contacts are of equal importance in the transition state and only very few lie at the fringe of the φ values. These later contacts (φ near 0 and 1) are of particular interest, as they reveal the nature of the topological frustration in our model and start to provide us with a structural characterization of the transition state ensemble.

The high φ values are located primarily in the turn regions between helices I and II and between helices II and III. This observation suggests that the two hairpins are in large part required in the transition state. The low φ values occur for the long-range contacts between helices I and III, suggesting that these two helices are rarely in contact in the transition state. We compared the φ values of our minimalist model with the contact probabilities in the transition state of the all-atom simulation of Guo and Brooks (15). While such a comparison is not perfect, we expect a reasonable correlation between the contact probabilities in the transition state and the φ values because we are only considering long-range interactions that are not formed in the unfolded state. The high contact probabilities are located in the turn region between helices II and III and between helices I and II, the very regions we determined to be topologically frustrated (high φ values). In particular, Guo and Brooks (15) found that contacts 25–35 and 25–36 (using out numbering scheme) had among the highest probability of forming a contact in the transition state. We identified similar contacts (26–34 and 27–33) as having high φ values. The small contact probabilities occur between helices I and III, which correspond to our low φ region. Because φ values are determined by both topology and energetics, we would expect a lesser agreement between the transition state probabilities (from the all-atom simulations) and the φ values (from the minimalist simulation) for those contacts for which the φ value participation is topologically negligible. The real protein is, however, sufficiently well designed that despite these limitations, the low contact probabilities in the transition state and the low φ values fall in the same regions.

The qualitative features of folding that we have observed in our off-lattice simulation seem to be common to all small, fast-folding α-helical proteins. The general picture of the folding process and of the transition state is in excellent agreement with the all-atom simulation of Guo and Brooks (15) as well as with the 3 letter code 27-mer lattice simulation of Onuchic et al. (4, 5). [The 27-mer lattice model was shown to be equivalent to a 60-residue α-helical protein by using the law of corresponding states (4, 5).] The agreement between the all-atom and off-lattice results for PA is not unexpected. PA is a highly designed sequence as evidenced by its experimentally observed two-state folding behavior. It folds very rapidly to its stable native state, which indicates that energetic frustration is minimal. A model that neglects the energetic frustration but captures the topology of the protein should be an adequate representation of PA. This is the essence of our off-lattice model. Of greater interest is the similarity between our results and those of the lattice model, where the shape of the φ distribution is essentially the same. In both cases, we recover a relatively broad unimodal distribution, with tails extending to low and high values. The transition state ensemble for small fast-folding helical proteins would therefore appear to be determined mostly topologically rather than energetically.

The concepts of energetic and topological frustration introduced and explored in this paper are pertinent to the design of fast-folding, stable proteins. It is important to emphasize that any frustration, whether topological or energetic, is a detriment to the folding process. A successful method for protein design will target the minimization of frustration through amino acid substitutions by iteratively “optimizing” the φ value distributions to be more central and unimodal. While elimination of energetic frustration (e.g., kinetic folding traps) through mutations has been appreciated in the past, minimizing frustration associated with the specific topology to which the protein is folding is less well understood. In principle one can use the same ideas of introducing amino acid substitutions to achieve the “best” φ value distribution for a given folded topology. However, it is clear that all conceivable structures may not be appropriate targets for design. Beyond some critical level of topological frustration it may be impossible to find a good sequence for some topologies. This may be why it is anticipated that only a finite number of fold motifs exist in nature (46). Objectives of our ongoing work are to provide a more quantitative understanding of this relationship.

Also emerging from our studies is the relationship between the extent of frustration in a protein and the nature of the folding reaction coordinates. In a minimally frustrated system, a number of “global coordinates” (such as the number of native contacts) correlate well with the energy and extent of folding, and can be used as suitable folding coordinates. As the system becomes more frustrated, these coordinates begin to deviate from this simple relationship and are no longer adequate to describe the folding mechanism; additional, and often more detailed, coordinates are necessary to describe folding in this situation. When topological frustration plays a dominant role in the folding mechanism, it becomes imperative to consider details of the specific final topology of the protein in developing an optimal set of coordinates to describe the folding mechanism.

Abbreviation

PA

protein A