Can correct protein models be identified?

Abstract

The ability to separate correct models of protein structures from less correct models is of the greatest importance for protein structure prediction methods. Several studies have examined the ability of different types of energy function to detect the native, or native-like, protein structure from a large set of decoys. In contrast to earlier studies, we examine here the ability to detect models that only show limited structural similarity to the native structure. These correct models are defined by the existence of a fragment that shows significant similarity between this model and the native structure. It has been shown that the existence of such fragments is useful for comparing the performance between different fold recognition methods and that this performance correlates well with performance in fold recognition. We have developed ProQ, a neural-network-based method to predict the quality of a protein model that extracts structural features, such as frequency of atom–atom contacts, and predicts the quality of a model, as measured either by LGscore or MaxSub. We show that ProQ performs at least as well as other measures when identifying the native structure and is better at the detection of correct models. This performance is maintained over several different test sets. ProQ can also be combined with the Pcons fold recognition predictor (Pmodeller) to increase its performance, with the main advantage being the elimination of a few high-scoring incorrect models. Pmodeller was successful in CASP5 and results from the latest LiveBench, LiveBench-6, indicating that Pmodeller has a higher specificity than Pcons alone.

The ability to use an algorithm or energy function to distinguish between correct and incorrect protein models is of importance both for the development of protein structure prediction methods and for a better understanding of the physical principles ruling protein folding. Energy functions can be divided into different categories depending on the background principles and what structural features of a model they use. In order for an energy function to be useful in protein structure predictions, it should not only be able to identify the native protein configuration, but also detect to native-like structures, because it often is not possible to generate the native structure without experimental information. Ideally, the energy function should correlate well with a distance measure from the native structure. Exactly how to define what conformations are native-like is not trivial, but several different measures have been developed (for review, see Cristobal et al. 2001).

Many different energy functions for evaluating protein structures have been developed. These focus either on the identification of native, or native-like, protein models from a large set of decoys (Sippl 1990; Park and Levitt 1996; Park et al. 1997; Lazaridis and Karplus 1999; Gatchell et al. 2000; Petrey and Honig 2000; Vendruscolo et al. 2000; Vorobjev and Hermans 2001; Dominy and Brooks 2002; Felts et al. 2002), to guide protein folding simulations (Simons et al. 1999), to detect protein with similar folds in threading studies (Bowie et al. 1991; Godzik et al. 1992; Jones et al. 1992; Sippl and Weitckus 1992; Torda 1997) or are used in other fold recognition methods (Jones 1999a).

The principles of the design of an energy function can be roughly divided into three groups, physical-, knowledge-, and learning-based. In physical energy functions, the goal is to describe the physics of the interaction between atoms as carefully as possible. These functions are often parametrized on much smaller systems than proteins. Here a molecular mechanics force field such as OPLS (Jorgensen et al. 1996), CHARMM (Brooks et al. 1983), or Amber (Weiner et al. 1984) is used. In addition to this, terms that are not included implicitly such as entropy and solvent effects are added. It has recently been shown that using the generalized Born solvation model (Still et al. 1990) as a description of solvent effects, physical energy functions can be used to identify the native conformation (Dominy and Brooks 2002; Felts et al. 2002). Knowledge-based energy functions are calculated from the difference between features of a random protein model and what is observed in a real protein. Most frequently used is the preference of different residues to interact (Jones et al. 1992; Sippl 1993a; Bauer and Beyer 1994; Godzik et al. 1995; Huang et al. 1995; Miyazawa and Jernigan 1996; Park and Levitt 1996; Park et al. 1997; Skolnick et al. 1997; Chao Zhang and Kim 2000; Tobi and Elber 2000; Tobi et al. 2000); the interaction can be either distance-dependent or only dependent on contact. Also, interaction between different atom types has been used (Bryant and Amzel 1987; Colovos and Yeates 1993; Melo and Feytmans 1997 Melo and Feytmans 1998; Samudrala and Moult 1998; Rojnuckarin and Subramaniam 1999; Lu and Skolnick 2001), as have buried and exposed surfaces (Bowie et al. 1991; Jones et al. 1992; Lüthy et al. 1992) and torsion angle potentials (Kocher et al. 1994; Gilis and Rooman 1997 Gilis and Rooman 2001). Finally, learning-based functions can be developed by training an algorithm to distinguish between correct and incorrect models. The training can be done by using methods ranging from advanced machine learning methods to simplified optimization of a few parameters (Chang et al. 2001; Fain et al. 2002; Krieger et al. 2002).

Several studies have examined the possibility of different energy functions to detect the native structure among a set of decoys (Park and Levitt 1996; Park et al. 1997; Dominy and Brooks 2002). These decoys can be generated in several different ways, and the generation of them is often tightly coupled with the development of the energy functions. The first generation of decoys was generated by putting the sequence from a particular protein onto the backbone of another protein. Novotny studied different parameters distinguishing between models built on the native and an incorrect backbone (Novotny et al. 1988). Later, Sippl developed knowledge-based energy functions to identify the native structure among a large set of decoys (Sippl 1990), created by threading the sequence through the backbone of other proteins. The energy function was built from probabilities to detect two residues at a specific distance from each other. This work is the basis of Prosa II (Sippl 1993b), used in this study. Similar knowledge-based energy functions have also been used in programs that allowed gaps in the threading (Godzik et al. 1992; Jones et al. 1992). This creates a much larger set of potential decoys, but also complicates the energy function as it is necessary to include factors for gaps. An alternative method to create a knowledge-based energy function, based on exposed and buried surfaces, was developed by Bowie. This method has been used both in threading studies (Bowie et al. 1991) and for evaluating protein structure correctness (Lüthy et al. 1992), and is now used in Verify3D (Eisenberg et al. 1997).

Alternative to threading, decoys can be created by using lattice models (Park and Levitt 1995 Park and Levitt 1996), and fragment building (Simons et al. 1997). Because these methods do generate a large set of plausible structures, without the existence of a structurally similar protein, these methods can be used ab initio or in new-fold protein structure predictions (Park et al. 1997).

In this study, we have used decoys built from threading or other alignment methods. In contrast to the early threading decoys, we have used a large set of different alignment methods and then generated all-atom models for the best of these. A recent study by Melo et al. (2002) used a similar approach to study different statistical potentials for fold assessment. One other important difference from earlier studies is that we use a more relaxed and in our minds more realistic definition of native-like models. We define “correct” models in a similar way as used in CASP (Moult et al. 2001; Sippl et al. 2001), CAFASP (Fisher et al. 1999), and LiveBench (Bujnicki et al. 2001a,b); that is, by finding similar fragments between the native structure and a model. We use these models to develop ProQ, a neural-network-based method to predict the quality of protein models. We show that ProQ performs on par with earlier methods in distinguishing native structures from a large set of decoys, whereas it performs better when detecting correct models. Furthermore, the method can be combined with the results from the fold recognition method Pcons (Lundström et al. 2001) to increase its specificity. This approach is similar to GenTHREADER (Jones 1999a), which also uses neural networks to examine the quality of the final models to increase the specificity.

Development of ProQ

Our goal in this study was to develop a method that can identify correct models from a large subset of incorrect models. The models were produced using Modeller-6 (Sali and Blundell 1993) with alignments from LiveBench-2 (Bujnicki et al. 2001b). We chose to use a machine-learning based method as it should be able to find more subtle correlations than a purely statistical method. Once we decided to use neural networks, we had to decide what the target function should be for the networks; that is, how we should measure the distance to the native conformation. Finally, we had to decide what features calculated from a protein conformation should be used as input to the neural networks. In the following sections we describe the development of the final versions of ProQ.

How to measure the quality of a protein model

The first choice to make is to decide how to measure the quality of a protein model. A common way to assess the quality of a protein model given the correct structure is to calculate the root mean square deviation (RMSD) after an optimal superposition. However, one problem with RMSD is that it strongly depends on the length of the protein. An RMSD of 3Å for a 30-residue protein is not comparable with a 3 Å value for a protein of 300 residues. A second problem is that a fairly good protein model with one bad region might have a very high RMSD. Several other traditional measures have similar problems. Instead, we wanted to use measures that could detect native-like protein models. Such measures have been developed as a part of benchmarks developed to measure the performance of fold recognition methods, such as CASP (Moult et al. 2001), CAFASP (Fisher et al. 1999), and LiveBench (Bujnicki et al. 2001a).

For the development, we chose to use two different measures, LGscore (Cristobal et al. 2001) and MaxSub (Siew et al. 2000), to evaluate model quality. These two measures are also used in the LiveBench project (Bujnicki et al. 2001a); for a short description, see Materials and Methods. The reason for using two different measures is that no single quality measure is perfect. The main difference between MaxSub and LGscore is their dependence on the length of the target protein. Long target proteins are more likely to get a good LGscore, whereas short targets are more likely to get a good MaxSub score. By using information from two different measures with different length dependence, we hope that this length bias is reduced.

Models were classified into correct and incorrect models based on both LGscore and MaxSub. Correct models should have LGscore > 1.5 and MaxSub > 0.1, whereas incorrect models should have LGscore < 1.5 and MaxSub < 0.1. In this way, borderline cases in which one measure gives a high score while the other gives a low score are ignored. In addition to MaxSub and LGscore, two other measures were also used for evaluation purposes, but not for training: CA3 and Contact (see Materials and Methods).

Neural networks

Once we decided how to measure the quality of a model, we had to decide how to correlate structural information with this measure. We chose to use a neural-network-based approach, as this method easily could be tested on many various types of inputs and outputs. The networks were trained based on different types of input data, summarized in Table 1. Networks were first trained with only atom or residue contact or surface accessibility as input data. After the initial training, the input data showing the highest performance were combined in a stepwise manner to the final neural network model. Measures that showed no significant correlation with the quality of a model were discarded, including measures related to compactness, such as too closely or too loosely packed atoms and the number of nonallowed Φ/Ψ dihedral angles. The last is in agreement with the observations by Melo et al. (2002).

Table 1.

Correlation coefficient and Z-score for different input parameters to the neural networks

Input parameters	Predicting LGscore correlation/Z-score	Predicting MaxSub correlation/Z-score
Atom-3 contacts	0.41/0.9	0.30/0.9
Atom-13 contacts	0.48/1.1	0.32/0.9
Residue-6 contacts	0.43/1.1	0.31/0.9
Residue-20 contacts	0.35/0.8	0.25/0.6
Surface accessibility <25%	0.51/1.4	0.38/1.2
Surface accessibility 25%–50%	0.21/0.4	0.06/0.2
Surface accessibility all	0.53/1.5	0.46/1.3
Atom-13 + Residue-6	0.53/1.4	0.39/1.1
Atom-13 + Residue-6 + Surface all	0.63/2.0	0.50/1.5
Atom-13 + Residue-6 + Surface all + Q3	0.71/2.4	0.58/2.1
Atom-13 + Residue-6 + Surface all + Q3 + Cα	0.74/2.6	0.60/2.2
Atom-13 + Residue-6 + Surface all + Q3 + Cα + fatness	0.75/2.7	0.62/2.4
Atom-13 + Residue-6 + Surface all + Q3 + Cα + fatness + frac	0.76/2.7	0.71/2.6

Atom-3 is the atom contacts between three different atom types, Atom-13 the contacts between 13 different atom types, Residue-6 and Residue-20 the contacts between 6 and 20 different residue types, respectively. Q3 is the fraction of similarity between predicted secondary structure and the secondary structure in the model. C_α is the difference between the all-atom model and the aligned C_α coordinates from the template that were used to build the model, as measured by LGscore and MaxSub for networks predicting LGscore and MaxSub, respectively. frac is the fraction of the protein that is modeled.

Two different sets of neural networks were trained, one to predict LGscore and one to predict MaxSub. In the following, ProQ-LG denotes networks predicting LGscore and ProQ-MX denotes networks predicting MaxSub.

Atom–atom contacts

Physical-based energy functions are almost always built on the potential of atomic interaction energies, but most knowledge-based energy functions do not use this information. However, there are some exceptions to this. Colovos and Yeates (1993) used the distribution of atom–atom contacts in the Errat method, Melo and Feytmans (1997) have developed mean force potentials at the atomic level, and others have used distant-dependent atomic potentials (Samudrala and Moult 1998; Lu and Skolnick 2001).

We chose to represent atom–atom contacts in a similar way as used in Errat; that is, for each contact type the input to the neural networks was its fraction of all contacts. Alternative representation, such as the number of different types of contacts, could also be used. However, most alternative measures are more dependent on the size of the model and therefore more difficult to use in the neural networks. A protein model can contain up to 167 different (non-hydrogen) atom types, but luckily they can be grouped into a smaller number of groups. Two different atom groupings were tried, either using three atom types (carbon, nitrogen, and oxygen; Atom-3) as in Errat, or alternatively 13 different types (Atom-13, Table 2). The contact cutoff between two atoms was optimized to 5 Å for both representations; the exact choice of cutoff was not crucial. Using only atom–atom contacts, a correlation coefficient (CC) with the quality measures of <0.5 and a Z-score of ~1.0 is obtained (Table 1). The Atom-13 grouping showed a slightly higher performance than Atom-3 for both ProQ-LG and ProQ-MX (Table 1), and this was independent of the contact cutoff (data not shown). The more detailed description of the atom–atom contacts should be able to detect more subtle differences, but it is also more sensitive to noise, which could hide important properties and lead to a decrease in performance.

Table 2.

Different atom types used in Atom-13

Atom type	Description
C	Backbone
N	Backbone
O	Backbone
Cα	Backbone
CH3	Methyl group present in Ala, Ile, Leu, Met, Thr, and Val
CH/CH2	Carbon with one or two hydrogens, present in all residues except Gly
C(OO−)	Carbon in carbon acid group in Asp and Glu
=O	Double-bonded oxygen present in the acidic amino acids Asn and Gln
(C)OO−	Oxygens in carbon acid group, Asp and Glu
OH	Hydroxyl in the residues Ser, Thr, Tyr
NH2	Amino group with two hydrogens in Arg, Asn, Gln, His, and Lys
NH	Amino group with one hydrogen in Arg, His, and Trp
S	Sulfur in Cys and Met

By looking at individual atom–atom contacts in the Atom-13 group, it can be seen that methyl–methyl and methyl–hydrocarbon contacts are slightly correlated with model quality (CC = 0.2–0.3). This is a fairly low correlation, but compared with the correlations for all other atom–atom contacts, which have an average of 0.05, it is significantly higher. Because methyl groups are present in most hydrophobic amino acids, this indicates that hydrophobic contacts are an important factor for predicting model quality. Thus, in correct structures the fraction of hydrophobic contacts is likely to be more frequent than other contacts. Another potentially interesting observation is that main-chain nitrogen and hydrocarbon contacts are negatively correlated with model quality; however, the exact meaning of this is unclear to us.

Residue–residue contacts

Residue–residue distances have been used in many statistical energy functions. The information can be represented in several different ways, including binary contact/noncontact information and distance-dependent functions. Furthermore, the sequence separation between two residues can be included. If a crude binary contact function and no distance-dependent separation are included, the most important feature captured by a residue–residue function is hydrophobicity (Cline et al. 2002), but if a more detailed function is used, features such as secondary structure preferences can be captured. Here, we chose to use a binary distribution and not include the distance between residues. One reason to use a simple binary description of contacts is that this avoids problems with too few data examples and dependency of the model size. Another reason is that some of the features, such as secondary structure preference, captured with a more detailed description can be better described using other measures. The final reason is that we tried using multiple cutoffs, but that did not show any improvement.

Two different groupings were tested for the residue contacts, Residue-6 with the representation described in Table 3 and Residue-20 using contacts between all 20 amino acids. As for the atom–atom contacts, the contact cutoffs were optimized for both representations and finally set to 7 Å for both ProQ-LG and ProQ-MX. In contrast to the atom–atom contacts, the representation with the least number of parameters showed the best performance, CC = 0.43/0.35 versus 0.31/0.25 (for ProQ-LG/ProQ-MX; Table 1). This is probably caused by the facts that Residue-6 is less noisy and that certain important properties are displayed more clearly in Residue-6 than in Residue-20. One such property is the contacts between hydrophobic residues discussed above, which are much more clearly displayed in Residue-6 as one single parameter, whereas the same information in Residue-20 is shared among all contacts with other hydrophobic residues (21 different contact types in this case). The performance of residue–residue contacts is similar to the performance obtained by using atom–atom contacts.

Table 3.

Residue groups in Residue-6

Group	Amino acids
1. Positive	Arg, Lys
2. Negative	Asp, Glu
3. Aromatic	Tyr, Trp, Phe, His
4. Polar	Thr, Ser, Gln, Asn
5. Hydrophobic	Cys, Val, Met, leu, Ile, Ala
6. SS-breakers	Pro, Gly

Solvent accessibility surfaces

Solvent accessibility surfaces were described as a classification into one of four different bins, <25%, 25%–50%, 50%–75%, and >75% exposure. Then the fraction of each amino acid type in each group was fed into the network. This measure showed a higher performance than atom and residue contacts (Table 1). The <25% exposure contained most information, and for ProQ-LG it performed almost as well as when using all four groups, CC = 0.51 versus 0.53; the difference in performance for ProQ-MX is slightly higher, with CC = 0.38 versus 0.46.

Combining and additional measures

By combining the best performing atom and residue contacts sets (Atom-13 and Residue-6), a performance comparable to surface accessibility can be achieved (CC = 0.53/0.39 versus 0.53/0.46). However, all three parameter sets do contain non-overlapping information because performance increases to CC = 0.63/0.50 when they are all combined. The Z-scores are also improved from 1.0 to 2.0 and 1.5 for ProQ-LG and ProQ-MX, respectively.

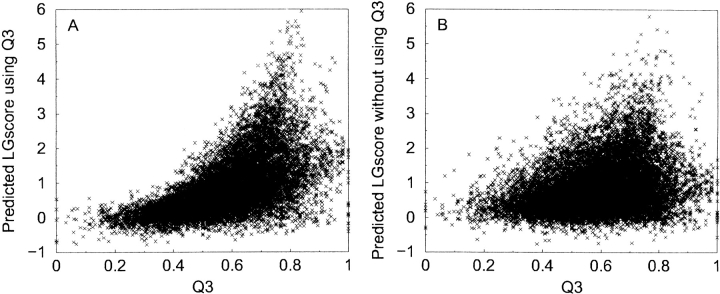
It is well known that only for very good homology models the accuracy in secondary structure assignments is higher than what can be obtained by using the best secondary structure prediction programs, such as PSIPRED (Jones 1999b). Therefore, a measure of similarity between predicted and model secondary structure could correlate with model quality. We have measured the similarity as the fraction of residues that agree in secondary structure classification/predictions (Q3). This information gives a significant increase in performance for both ProQ-LG and ProQ-MX (CC = 0.71/0.58). This is mainly caused by filtering out of incorrect models as networks trained with Q3 tend to predict lower quality to models with low Q3 and higher quality to models in the region Q3 ∈ {0.7, 0.8} (Fig. 1 ▶). This agrees with our intuition as a model with low Q3 is likely to be of low quality and a model in the region {0.7, 0.8} should have about the same Q3 as a native-like model, as the prediction accuracy for secondary structure prediction is ~75%.

Figure 1.

Fraction of similarity between predicted secondary structure and the secondary structure in the model (Q3) plotted against predicted LGscore, for networks trained with Q3 (A) and without Q3 (B). The networks trained with Q3 tend to give low scores to models with low Q3 and higher scores in the region Q3 ∈ {0.7, 0.8}

Because the models we used were produced using homology modeling, another type of information that could be included is a measure on how much the homology modeling procedure disturbs the structure. An incorrect model is quite likely to have large gaps/insertions that add unrealistic constrains to the homology modeling procedure. Therefore, if a simple C_α-model calculated from the template is fairly similar to the all-atom model, the model is more likely to be correct. Including the “distance” between the two models into the network improves the performance for ProQ-LG more than for ProQ-MX (Table 1).

Including information about the globular shape of the protein, as represented by the fatness function, improves the correlation slightly. A large improvement for ProQ-MX is obtained by including information on how large a fraction of the protein is modeled. This number is actually an upper bound for the MaxSub score, as if only 50% of the protein is modeled, the highest possible MaxSub score is 0.5. ProQ-MX not using this information tends to give higher scores to shorter models. The same tendency can also be seen for ProQ-LG but less pronounced.

In general, it is slightly more difficult to predict MaxSub than LGscore, judging from the correlation coefficients and Z-scores in Table 1. However, for the best performing input parameters, even though the correlation is lower for ProQ-MX, both ProQ-LG and ProQ-MX are equally good at separating correct from incorrect models, with a Z-score ~2.6.

Concluding remarks

From the development of ProQ it seems as if no single feature tested here is very good at separating correct and incorrect protein models, whereas the use of a combination of several features can be quite successful, as the increase in Z-score from 1 to 2.7 for ProQ-LG gives evidence. This could be explained by the fact that incorrect protein models might have many good; that is, native-like, features, whereas correct models might have many bad; that is, native-unlike, features. Therefore, a combination of measures is the best way to distinguish between these models.

Results and Discussion

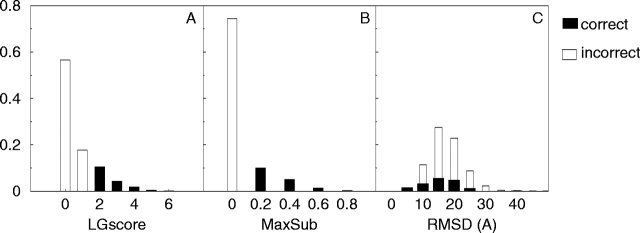
A total of 11,108 protein structure models were created using Modeller-6 (Sali and Blundell 1993) with alignments from LiveBench-2 (Bujnicki et al. 2001b). The quality of these models was assessed by comparing them to the native structure using LGscore (Cristobal et al. 2001) and MaxSub (Siew et al. 2000). Most of the models are of poor quality, with ~75% of all models defined as incorrect, 15% as correct, and 10% as borderline, given the definition in Materials and Methods (Fig. 2 ▶). RMSD is not a suitable measure because the correct and incorrect distributions overlap. This is because many of the correct models are only partly correct, with a few bad regions giving rise to high RMSD. To provide a less-biased comparison, two additional quality measures, CA3 and Contact, were also used. These measures were only used in the evaluation and not in the development of ProQ. The CA3 is a very intuitive measure, and the Contact measure is conceptually very different from LGscore and MaxSub (see Materials and Methods).

Figure 2.

Distribution of LGscore (A), MaxSub (B), and RMSD (C) for the training set (LiveBench-2).

It is important that a predictor of protein quality not only functions well on one set of protein models, but on several sets. Therefore we have also tested ProQ on models from a later version of LiveBench, LiveBench-4. This set is similar in construction (using Modeller) to the LiveBench-2 set, but it is independent and there exist no homologous targets between LiveBench-2 and LiveBench-4. Models from Decoys ‘R’ Us (Samudrala and Levitt 2000) were also used to evaluate the performance and for making comparisons to earlier studies. On all sets the performance of the two ProQ methods (ProQ-LG and ProQ-MX) was compared with three other methods for evaluating the quality of the protein models described in Table 4. In the following, we first discuss the result on the two LiveBench sets, then the performance on the decoy sets.

Table 4.

Description of the methods for evaluating protein model quality that were compared in the benchmark

Method	Description (used measure)
1. ProQ-LG	neural network trained to predict LGscore
2. ProQ-MX	neural network trained to predict MaxSub
3. Errat (Colovos and Yeates 1993)	statistics of interactions between different atom types (Total-Errat)
4. Prosa II (Sipple 1993b)	statistical potential, (zp surf, polyprotein pII3.0.long.ply)
5. Verify3D (Eisenberg et al. 1997)	3D–1D profiles, gives a score for each residue (average score)

LiveBench

First the correlation coefficients between LGscore, MaxSub, CA3, and Contact for the different methods were calculated (Table 5). ProQ-LG and ProQ-MX show the highest correlation with the measures they were trained on. ProQ-LG has the highest correlation on the two independent measures, CA3 and Contact; whereas ProQ-MX does not perform as well as ProQ-LG, but still better than Prosa II, Verify3D, and Errat.

Table 5.

Correlation coefficients for different quality measures

Method	LGscore LB-2/LB-4	MaxSub LB-2/LB4	CA3 LB-2/LB-4	Contact LB-2/LB-4
ProQ-LG	0.76/0.80	0.59/0.69	0.76/0.81	0.73/0.78
ProQ-MX	0.58/0.71	0.71/0.78	0.55/0.70	0.55/0.68
Errat	0.20/0.17	0.15/0.17	0.15/0.11	0.13/0.07
Prosa II	0.50/0.64	0.38/0.63	0.48/0.60	0.44/0.58
Verify3D	0.41/0.55	0.35/0.53	0.40/0.53	0.37/0.51

Quality measures are LGscore, MaxSub, CA3 (the maximum number of C_αs that can be superpositioned under 3Å RMSD) and contact (see Methods) for LiveBench-2 and LiveBench-4.

Besides ProQ, Prosa II shows correlations with LGscore and MaxSub comparable to the networks trained on a single parameter set (CC_LB2 = 0.50/0.38), and the correlations with CA3 and Contact are on a similar level. Verify3D performs only slightly worse than Prosa II, but Errat does not correlate very well with any of the quality measures. Clearly, the performances are consistent over the different quality measures and between the two LiveBench sets. In general, the correlations for the different methods are somewhat higher on LiveBench-4 than on LiveBench-2, most likely because LiveBench-4 has a higher fraction of correct models. However, the differences in performance between the different methods are more or less the same for both sets.

The correlation coefficient takes all points into account, and might be dominated by the many incorrect models in the set; consequently, it does not necessarily contain information about the ability of a method to select good models. To evaluate this, the sum of LGscore and MaxSub for the first-ranked model for each target in the two LiveBench sets was calculated. A similar evaluation scheme was also used in LiveBench-2 (Bujnicki et al. 2001b). According to this scheme, ProQ-LG and ProQ-MX select models of similar quality, and with 10%–30% better quality than Prosa II and Verify3D, depending on the choice of quality measure. Errat selects models that have quality similar to a random pick (data not shown).

The ability to separate correct models from incorrect models and find native structures was measured by Z-scores (see Materials and Methods for definition). Z denotes the Z-score for separating correct from incorrect models, and Z_nat denotes the Z-score for finding native structures. It can be noticed that there is a correlation between Z and Z_nat; that is, methods good at separating correct and incorrect models are also good at finding native structures. Native structures are in general easier to detect than correct models, as all Z_nat-scores are higher than Z-scores for all methods (Table 6). The Z-scores in Table 6 are averages over all structures in the different sets (additional tables with values for individual proteins are available at http://www.sbc.su.se/~bjorn/ProQ/tables/). On the LiveBench sets, the two ProQ methods show the largest separation between correct and incorrect models, with Z-scores equal to 2.7, about two times higher than any of the other methods. Prosa II and Verify3D show a small tendency to give higher scores to correct models than incorrect ones, but the Z-scores are hardly significant (Z ≤ 1.6). Errat does not separate correct and incorrect models at all (Z = 0.3), but is quite good at finding the native structure (Z_nat ≥ 5.0). Errat was originally designed to detect correct and incorrect regions of native protein structures. For the particular task of discriminating correct and incorrect models, Errat might actually be too sensitive; that is, one misplaced residue or loop can generate a low score for an otherwise perfect model.

Table 6.

Z-score and Z-score native for different methods on different test sets

Method	LB-2 Z/Znat	LB-4 Z/Znat	4state_reduced Z/Znat	LMDS Z/Znat	Lattice_ssfit Z/Znat	Structal Z/Znat
ProQ-LG	2.7/5.2	2.7/5.1	2.3/4.4	−0.4/3.9	—/11.7	—/2.4
ProQ-MX	2.6/5.0	2.8/4.6	2.0/3.5	0.0/1.8	—/11.6	—/1.6
Errat	0.3/5.0	0.3/5.7	1.7/2.5	0.2/3.1	—/5.1	—/3.6
Prosa II	1.2/3.5	1.6/3.5	2.0/2.7	0.4/2.5	—/5.6	—/1.7
Verify3D	1.0/2.8	1.1/2.8	1.0/2.6	0.8/1.4	—/4.5	—/1.4

The lattice_ssfit and structal methods contained too few correct models to calculate Z-score.

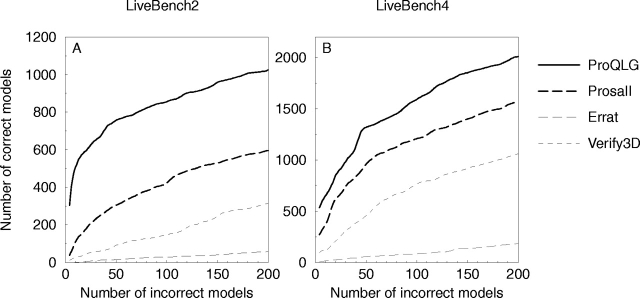
The discrimination of incorrect and correct models was also studied by sorting the models according to the score and plotting the cumulative number of incorrect models versus correct models; this has been done in several earlier studies (Park and Levitt 1996; Park et al. 1997; Lundström et al. 2001). On LiveBench-2, ProQ finds twice as many correct models in the region with <10% incorrect models than the best other method (Prosa II; Fig. 3A ▶). For clarity only ProQ-LG is shown in this figure. On LiveBench-4, ProQ still finds more correct models than all other methods, even though the performance difference is not as pronounced as on LiveBench-2 (Fig. 3B ▶).

Figure 3.

Cumulative plot of incorrect versus correct models for different methods on the LiveBench-2 (A) and LiveBench-4 (B) data sets. The curves were smoothed using averages of seven consecutive points.

Additional decoy sets

The performance of ProQ was also tested on models from Decoys ‘R’ Us (Table 6; Samudrala and Levitt 2000). The quality of the models in the different decoy sets is very different. In principle, the sets can be grouped into three different categories, sets with lower (LMDS and lattice_ssfit), same (4state_reduced), or higher (structal) quality models compared with the LiveBench sets (Table 7). In the structal set, the correlations for ProQ and Prosa II are very similar (CC ≈ 0.70) for all four quality measures, and Verify3D and Errat have correlations of ~0.50. For the 4state_reduced set, the correlations are slightly lower, whereas no method shows any significant correlation in the LMDS and lattice_ssfit sets.

Table 7.

Description of the different decoy sets that were used

Name	No. models	No. proteins	〈length〉	〈LGscore〉	No. correct	No. incorrect
LiveBench-2 (LB-2)	11,108	180	130	0.8	1894	8270
LiveBench-4 (LB-4)	9603	106	158	1.3	3517	5249
4state_reduced	4656	7	64	1.2	1300	1118
LMDS	4336	10	54	0.8	145	2933
lattice_ssfit	16,000	8	72	0.3	2	15,364
structal (hg_structal + ig_structal)	4500	90	214	3.9	4498	0

(No. models) the total number of models in a specific set (for which all methods could calculate a score), (No. proteins) the number of proteins in the set, 〈length〉 the average length of the models, 〈LGscore〉 the average LGscore of the models, (No. correct) and (No. incorrect) the number of models in the set defined as correct and incorrect, respectively.

As for the LiveBench sets, the separation between correct and incorrect models was measured by Z-scores. In the 4state_reduced set, all methods except Verify3D separate incorrect and correct models fairly well (Z ≥ 1.7), but they all fail completely in the LMDS set (Z ≤ 0.8).

This is probably mainly caused by the quality of the models in the sets, as the models in LMDS have lower quality than the models in the 4state_reduced set (Table 7). Furthermore, the number of correct models in LMDS is quite few, and they are mostly dominated by one single target, making the results somewhat biased, and the quality of the model defined as correct is just above the cutoff, making this test set even more difficult. Also, the method by which the sets were generated might influence the result. 4state_reduced is generated using a scoring function, whereas LMDS is generated by an energy minimization in an all-atom force field. The minimization procedure might produce models with less unfavorable regions than the sampling of the rotamer states used in 4state_reduced. Thus, the LMDS is a more difficult set, which also is reflected by the lower Z-scores for all methods.

Finding the native structure in a large set of decoys has been the objective of many different studies. The 4state_reduced set has been used in many of these studies, to evaluate how well knowledge-based potentials (Park and Levitt 1996; Lu and Skolnick 2001) and physical potentials (Dominy and Brooks 2002; Fain et al. 2002; Felts et al. 2002) discriminate native structures. In Dominy and Brooks (2002), they have produced a summary of Z-scores for finding the native structure for many different kinds of potential functions; the average of these Z-scores corresponds to Z_nat in this study. These scores ranges from 2.3 to 3.6 for different potential functions. ProQ-LG is doing slightly better with Z_nat = 4.4, and ProQ-MX performs on par with the best methods in that comparison. The Z_nat for LMDS and lattice_ssfit is comparable with scores obtained in earlier studies (Fain et al. 2002). Also, the number of times the native structure is ranked first by the different methods is comparable with the ranks obtain in earlier studies (Table 8; Petrey and Honig 2000^; Lu and Skolnick 2001). In general, it should be easy to find native structures in a set of models with low quality, and hard in a set of high quality. The first is also observed for three sets of fairly low-quality models (the two LiveBench sets and lattice_ssfit), where almost all methods rank the native structure first for many of the targets (Table 8). However, to our surprise for a set of high quality models, the structal set, both ProQ-LG and Errat rank the native structures first in two out of three cases. Still, except for the structal and the LiveBench sets, all decoy sets contain a fairly low number of targets, making it hard to draw confident conclusions.

Table 8.

Number of times the native structure is ranked first among all models in the different test sets (number of times)/(total number of targets in the set)

Method	LB-2	LB-4	4state_reduced	LMDS	Lattice_ssfit	Structal	Total
ProQ-LG	146/180	91/106	5/7	4/10	8/8	55/90	309/401
ProQ-MX	121/180	71/106	6/7	3/10	7/8	44/90	252/401
Errat	143/180	93/106	1/7	5/10	3/8	61/90	306/401
Prosa II	143/180	93/106	5/7	6/10	8/8	40/90	295/401
Verify3D	142/180	89/106	4/7	2/10	7/8	24/90	268/401

Finally, we want to repeat the interesting observation that Errat shows a very good ability to detect the native structure (Z_nat ≥ 2.5 for all sets), but it is not very useful for detecting native-like structures (Z ≤ 1.7 for all sets).

Combining with Pcons

Pcons (Lundström et al. 2001) is a consensus predictor that selects the best possible model from a set of models created using different fold recognition methods. It basically relies on the idea that if many methods indicate the same model, that model is more likely to be correct. It has been thoroughly benchmarked in the LiveBench project (Bujnicki et al. 2001b), and it clearly outperforms any single server by producing more correct predictions and showing a higher specificity.

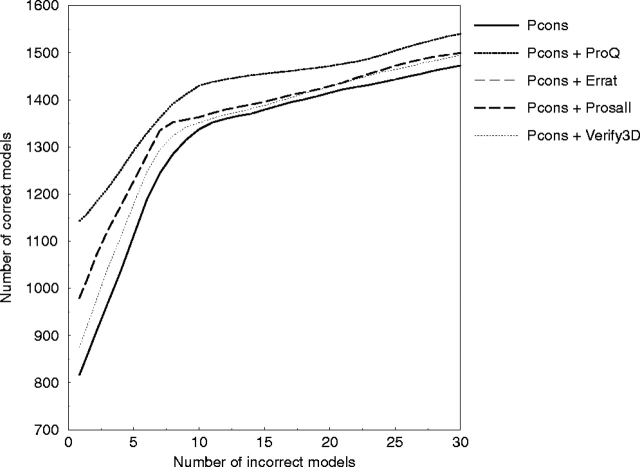
The different methods used in the comparison above were combined with the Pcons score using multiple linear regression to predict LGscore with the same cross-validation sets as before. Pcons combined with ProQ (Pcons + ProQ) gives a slight increase in performance compared with Pcons alone (Fig. 4 ▶). The improvement is only observed in the region with <10% incorrect models; above 10% there is no significant performance gain. Pcons + Prosa gives about half the improvement compared with Pcons + ProQ in this region, whereas all other combinations show no significant improvement.

Figure 4.

Cumulative plot of incorrect versus correct models for different methods combined with Pcons on the LiveBench-2 test set. To make the curves easier to analyze, they were smoothed by using averages.

The combination Pcons and ProQ was successful in CASP5 (B. Wallner, F. Huishang, and A. Elofsson, in prep.) and is now also participating in the LiveBench project as Pmodeller. Results from LiveBench-6 (http://bioinfo.pl/LiveBench/6/) show that all versions of Pmodeller have >10% higher specificity than the corresponding Pcons version alone, as measured by the mean value used in the LiveBench evaluation (Table 9). The mean value is the average over the number of correct predictions when allowing up to 10 false predictions.

Table 9.

Comparison of specificity results between different versions of Pmodeller (Pcons + ProQ) and Pcons from LiveBench-6

Version	Pcons mean	Pmodeller mean
Pcons2	40.2	44.2
Pcons3	43.3	48.5
Pcons4	36.3	43.9

The “mean” column is the average over the number of correct predictions when allowing up to 10 false predictions. The numbers were taken from the LiveBench-6 Web site (http://bioinfo.pl/LiveBench/6/).

Conclusions

The aim of this study was to the evaluate if structural information can be used to separate correct from incorrect models. This was done by training neural networks to predict two different quality measures, LGscore (Cristobal et al. 2001) and MaxSub (Siew et al. 2000), based on different types of training data. The final neural network model, ProQ, was compared with three other methods for structural evaluation as described in Table 4 and also combined with the fold recognition consensus predictor Pcons (Lundström et al. 2001).

We show that ProQ (ProQ-LG and ProQ-MX) performs at least as well as the other measures when it comes to the identification of the native structure and is better for the detection of correct models. This performance is maintained over several different test sets. This is encouraging because finding correct models is more relevant in real structure prediction applications than only finding the native structure. The reason that ProQ is better at detecting correct models is most likely that it was optimized for this particular task, and is thus better than methods designed to find native structures. ProQ also uses a combination of several structural features, which seems to improve the detection of correct models.

ProQ combined with the Pcons consensus fold recognition predictor resulted in a slight performance improvement. The main advantage is that several high-scoring false-positive models could be eliminated, resulting in a higher specificity. A similar result can be seen in GenTHREADER (Jones 1999a), which shows a very good specificity. The combination Pcons and ProQ (Pmodeller) was successful in CASP5 (B. Wallner, F. Huishang, and A. Elofsson, in prep.) and results from the latest LiveBench. LiveBench-6 indicates that Pmodeller has a better performance than Pcons alone.

Because ProQ is better at detecting correct models, it might be useful for evaluating model quality from alignments in the twilight zone (Jaroszewski et al. 2002), where model quality is expected to be significantly lower then the quality for alignments with clear relationships.

Materials and methods

Test and training data

All machine-learning methods start with the creation of a representative data set. We chose to use a data set from LiveBench-2 (Bujnicki et al. 2001b), as this represents models that are possible to be obtained for unknown targets and that show a range of quality differences. LiveBench is continuously measuring the performance of different fold recognition Web servers by submitting the sequence of recently solved proteins structures with no obvious close homolog (10⁻³ BLAST cutoff; Altschul et al. 1997) to a protein in the Protein Data Bank (Westbrook et al. 2002). The LiveBench-2 data set was collected during the period 2000-04-13 to 2000-12-29 and contains protein structure predictions for 199 targets from 11 different servers. Of these, 180 models were used here, as 19 of the final PDB structures did not include all atoms and could therefore not be used in the evaluations. Models from seven of these servers were used: PDB-BLAST (Rychlewski et al. 2000), FFAS (Rychlewski et al. 2000), Sam-T99 (Karplus et al. 1998), mGenTHREADER (Jones 1999a), INBGU (Fischer 2000), FUGUE (Shi et al. 2001), and 3D-PSSM (Kelley et al. 2000). In addition to these, models produced by the structural alignment server Dali (Holm and Sander 1993) were used for training but not for testing. From each server, up to 10 different alignments were produced, and from these alignments all-atom models were built using Modeller-6 (Sali and Blundell 1993). In total, 11,108 protein models were built from LiveBench-2 and used for the development of the neural networks. Of the 11,108 models, 17% were classified as correct and 74% as incorrect, and the final 9% were classified as borderline.

Additional test sets

As an additional independent test, a total of 9603 models were produced using Modeller-6 and alignments from LiveBench-4 (LiveBench-3 was canceled because of a massive data loss) collected during the period 2001-11-07 to 2002-04-25. Models were also downloaded from Decoys ‘R’ Us (Samudrala and Levitt 2000; http://dd.stanford.edu/) and used in the evaluation. The properties of all test sets are summarized in Table 7; the average quality of the models in the sets is quite variable. LiveBench-4 and 4state_reduced contain a reasonable ratio of correct and incorrect models, ranging from 28% to 37% correct models. LMDS and lattice_ssfit have a very low number of correct models (<3%), whereas the structal set only contains correct models. This will have an impact on the usefulness and applicability of the different sets. Below follows a short description of how the different sets from Decoys ‘R’ Us were produced.

The 4state_reduced set was generated by exhaustively enumerating the backbone rotamer states of 10 selected residues in each protein using an off-lattice model with four discrete dihedral angle states per bond. From this data set, compact models that scored low using a variety of scoring functions as well as having a low RMSD were selected (Park and Levitt 1996). All-atom models were built using SEGMOD (Levitt 1992).

The structal set contains globins and immunoglobulins, and was built by comparative modeling using SEGMOD (Samudrala and Levitt 2000), using other globins and immunoglobulins as templates.

The lattice_ssfit set was generated by exhaustively enumerating the conformational space for a sequence on a tetrahedral lattice. The best scoring conformations were selected and fitted to predicted secondary structure using a four-state model for the dihedral angles.

The local minima decoy set (LMDS) was generated from the correct structures by randomly modifying dihedral angles in the loop regions. The generated structures were minimized in torsion space using a modified classic ENCAD force field with united and soft atoms (Levitt et al. 1995), and with terms added to favor compactness and the formation of secondary-structure hydrogen bonding and to disfavor the burial of charged residues and any other formation of hydrogen bonds.

Neural network training

Neural network training was done using fivefold cross-validation, with the restriction that two models with a BLAST (Altschul et al. 1997) hit with an E-value <10⁻³ had to be in the same set, to ensure having no similar models in the training and testing data. However, this was only applied to eight sequences because most of the target sequences were not similar.

For the neural network implementations, Netlab was used, a neural network package for Matlab (Bishop 1995; Nabney and Bishop 1995) using one hidden layer. A linear activation function was chosen as it does not limit the range of output, which is necessary for the prediction of LGscore. The training was carried out using error back-propagation with a sum of squares error function and the scaled conjugate gradient algorithm.

The neural network training should be done with a minimum number of training cycles and hidden nodes to avoid overtraining. The optimal neural network architecture and training cycles were decided by monitoring the test set performance during training and choosing the network with the best performance on the test set (Brunak et al. 1991; Nielsen et al. 1997; Emanuelsson et al. 1999). We know that this is a problem because it involves the test set for optimizing the training length, and the performance might not reflect a true generalization ability. However, practical experience has shown the performance on a new, independent test to be as good as that found on the data set used to stop the training (Brunak et al. 1991). This is also illustrated by the similar performance both on LiveBench-2 (test set) and LiveBench-4 (new test set; Table 5). If two networks performed equally well, the network with the least number of hidden nodes was chosen. Because the training was performed with fivefold cross-validation, five different networks were trained each time. In the final predictor, the output is the average of all five networks.

Training parameters

Each protein model was described by the following structural features: atom and residue contacts, solvent accessibility, similarity between predicted secondary structure and secondary structure in the model, and the overall shape of the model as described by an inertial ellipsoid. These are parameters that can be calculated for any protein structure. If a protein model is built by aligning a query sequence to a known template structure, two additional parameters are used: the model length divided by the query sequence length and the similarity between the aligned C_α coordinates from the template structure, to the C_α coordinates of the all-atom model build from the same alignment as measured by either LGscore or MaxSub.

Other parameters related to compactness, such as too closely or too loosely packed atoms and nonallowed dihedral angles, were also tried but showed no success.

Atom–atom contacts

Different atom types are distributed nonrandomly with respect to each other in proteins. Proteins with low quality have a more randomized distribution of atomic contacts than a protein with high quality, which a neural network could learn to recognize. In protein models from Modeller there exist 167 nonhydrogen atom types; to use contacts between all of these 167 atom types would give a total of 14,028 different types of contacts, which is far too many parameters. To reduce the number of parameters, two different groupings were tried, one with only carbon, nitrogen, and oxygen atom types and one with the 13 different atom types shown in Table 2.

Two atoms were defined to be in contact if the distance between their centers was within 5 Å. The 5 Å cutoff was chosen by trying different cutoffs in the range 3–7 Å. Contacts between atoms from residues adjacent in sequence were ignored. Finally, the number of contacts from each group was normalized by dividing by the total number of contacts.

Residue–residue contacts

Different types of residues have different probability to be in contact with each other, for instance, are hydrophobic residues more likely to be in contact than positive and negative charged residues. To use this information in the neural network training, two different representations of the residues were tried, one using all 20 amino acids and one reduced representation with the six different groups described in Table 3, as used in earlier studies (Mirny and Shakhnovich 1999; Elcock 2001).

Two residues were defined to be in contact if the distance between the C_α atoms or any of the atoms belonging to the side chain of the two residues was within 7 Å and if the residues were separated by more than five residues in sequence. Cutoffs in the range 4–12 Å were tested, and 7 Å showed the best performance. Finally, the number of contacts for each residue group was normalized with the total number of contacts.

Solvent accessibility surfaces

As for the atom and residue contacts, the exposure of different residues to the solvent is also distributed nonrandomly in proteins. For instance, a protein model with many exposed hydrophobic residues is not likely to be of high quality.

Lee and Richards (1971) solvent accessibility surfaces, defined by rolling a probe of the size of a water molecule (1.4 Å radius) around the van der Waals surface of the protein, was calculated using the program Naccess (Hubbard 1996). The relative exposure of the side chains for each residue group was used; that is, to which degree the side chain is exposed. The exposure data were grouped into one of the four groups, <25%, 25%–50%, 50%–75%, and >75% exposed, and finally normalized by the number of residues.

Predicted secondary structure

STRIDE (Frishman and Argos 1995) was used to assign secondary structure to the protein models based on its coordinates. Each residue was assigned to one of the three classes, helix, sheet, or coil. This assignment was compared with the secondary structure prediction by PSIPRED (Jones 1999b) for the same residues. The fraction of similarity between the two assignments was taken as input to the neural network. For the native structure, this value is the same as the Q3 measure used in secondary structure prediction accuracy evaluation.

Fatness

The overall shape of the protein was measured by representing the protein with an ellipsoid with the same center of gravity and moment of inertia as the protein. The shape of the protein is essentially described by the magnitude of the three principle axes of the ellipsoid. The fatness is the ratio of the longest and shortest of these axis as defined in Bowie and Eisenberg (1994).

Model quality measures

In this study we have used LGscore (Cristobal et al. 2001), MaxSub (Siew et al. 2000), CA3, and Contact to measure the quality of a model. LGscore and MaxSub were used both in developing ProQ and for evaluation, whereas CA3 and Contact only were used as a reference in the evaluation.

LGscore and MaxSub detect segments in common between the model and the correct target structure. Based on these segments, a structural comparison score, S_str, is calculated

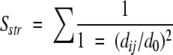(1)

where the sum is taken over all residues in the segments, d_ij is the distance between residue i in the model and j in the correct structure, and d₀ is a distance threshold (normally set to 5 Å). For a perfect model d_ij will be zero and S_str will be equal to the length of the model; for a completely wrong model S_str will be zero.

The difference between LGscore and MaxSub is that LGscore uses a statistical distribution to relate S_str to the probability of finding a higher score by chance (P-value). MaxSub, on the other hand, divides the structural comparison score by the length of the correct target structure. Thus, both measures give a value between 0 and 1, but for two identical structures LGscore is 0 and MaxSub is 1, and vice versa for two unrelated structures. For computational reasons, the negative logarithm of LGscore is used in this study, and unless stated otherwise in the term LGscore refers to this value.

The two other measures, CA3 and Contact, are two other commonly used measures. CA3 is the most intuitive measure; it is just the maximum number of residues that can be superimposed within 3 Å between the model and the native structure. This is similar to the GDT_TS score used in CASP (Moult et al. 2001). The Contact measure is a modified version of the Touch score used in LiveBench (Bujnicki et al. 2001b), and is a measure of the overlap of contact scores, the contact score being defined as:

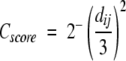(2)

where d_ij is the distance between two residues i and j that are separated by at least five residues. The C_score is calculated between matching residues in the model and the target. For each matching residue, two scores are obtained, one for the model and one for the target. The overlap is defined as the lowest of these two values. The overlap is normalized for each residue, so that the overlap can have values between 0 and 1. The quality of a model is the sum over all normalized overlaps.

Performance measures

Two types of performance measures were used in this study, ordinary correlation coefficient (CC) between predicted and correct values and the Z-scores defined by equations 3 and 4. The Z-scores measure the ability of different methods to separate incorrect models from correct and native structure from all decoy structures. Given a decoy set, the Z-scores are defined as follows:

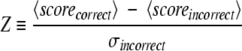(3)

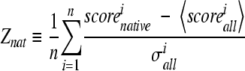(4)

where 〈score_correct〉 and 〈score_incorrect〉, are averages of the scores associated with correct and incorrect, respectively; 〈score_allⁱ〉 is the average score for models of the i-th target, 〈score_nativeⁱ〉 is the score for the i-th native structure, n is the total number of structures in the set, and σ_incorrect and σ_allⁱ are the standard deviations for the models classified as incorrect and for models of the i-th target, respectively.

Z is a unique measure for this study, but Z_nat is the average of the ordinary Z-score calculated in many previous studies. The most appropriate way to define Z_nat would have been to compare it to incorrect structures only, instead of to the whole ensemble of structures. With the present definition, sets with models of high quality will never get a high Z-score; however, as a comparison within the same set, the definition of Z_nat is adequate. The reason for using it is to facilitate comparisons to earlier studies.