A synthetic host-guest system achieves avidin-biotin affinity by overcoming enthalpy–entropy compensation

Abstract

The molecular host cucurbit[7]uril forms an extremely stable inclusion complex with the dicationic ferrocene derivative bis(trimethylammoniomethyl)ferrocene in aqueous solution. The equilibrium association constant for this host-guest pair is 3 × 10¹⁵ M⁻¹ (K_d = 3 × 10⁻¹⁶ M), equivalent to that exhibited by the avidin–biotin pair. Although purely synthetic systems with larger association constants have been reported, the present one is unique because it does not rely on polyvalency. Instead, it achieves its extreme affinity by overcoming the compensatory enthalpy–entropy relationship usually observed in supramolecular complexes. Its disproportionately low entropic cost is traced to extensive host desolvation and to the rigidity of both the host and the guest.

The design and characterization of synthetic, monovalent host–guest molecular recognition pairs still constitutes an open challenge in supramolecular chemistry, and it is of particular interest to inquire into the limits of the affinity that can be achieved with designed systems of low molecular weight. The affinities routinely displayed by protein-ligand systems represent a tantalizing target for supramolecular chemists. Can small receptors reach these affinities, or is there something special about proteins that cannot be matched by small host molecules? Houk's emphasis on the importance of buried surface-area as a determinant of affinity (1) would seem to suggest that low molecular weight hosts cannot rival receptors that are proteins.

The avidin-biotin complex is a clear inspiration, as it is one of the tightest binding biomolecular system, achieving an extraordinarily high affinity of ≈10¹⁵ M⁻¹ through noncovalent interactions (2). The crystal structure of the avidin-biotin complex provides some clues on how to achieve such ultrahigh stability (3). Cooperative, multiple, noncovalent interactions are essential for realizing such strong complexation and, indeed, the binding site of avidin is composed of an array of polar and aromatic residues, all of which cooperatively contribute to optimize biotin recognition and binding. Several aromatic amino acid residues (Trp and Phe) form a rigid “hydrophobic box” around the binding site and a number of polar residues (Thr, Ser, Asn, and Tyr) stabilize the complex through a network of multiple hydrogen bonds. This complex structure induces a large negative (favorable) enthalpy change (ΔH°) resulting from the formation of multiple hydrogen bonds, as well as robust van der Waals contacts inside the “hydrophobic box” (4). At the same time, a large negative (unfavorable) entropy change (ΔS°) is expected due to the severe conformational restriction of the biotin molecule upon complexation with avidin. This effect is, however, cancelled by a large, positive entropy of desolvation, eventually making the overall entropy of complexation nearly zero (4).

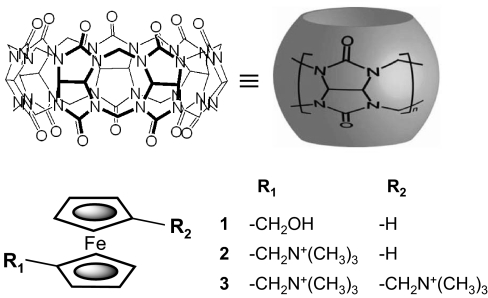
In our quest to design host–guest systems that reach high levels of binding affinity in aqueous media, we took inspiration from Nature and targeted molecular partners with a high degree of size/shape complementarity and chemical functionalities that can develop considerable noncovalent attractive forces between them. The cucurbit[n]uril hosts (CB[n], n = 5–10) (5, 6) include a number of very symmetric molecular containers, readily synthesized by the condensation of glycoluril with formaldehyde in acidic media. We have recently shown (7) that cucurbit[7]uril (CB[7], Fig. 1) forms a very stable complex (K = 3 × 10⁹ M⁻¹) with hydroxymethylferrocene (guest 1). The introduction of a positive charge on the guest, positioned to interact with one of the host's rings of carbonyl oxygens, leads to a sizable increase in the corresponding equilibrium association constant, which reaches K = 3 × 10¹² M⁻¹ for guest 2 (7, 8). We conjectured that it would be possible to further boost the affinity by appropriately positioning a second positive charge that would form similar interactions with the host's other ring of carbonyls.

Fig. 1.

Chemical structures of the host cucurbit[7]uril and ferrocene guests: 1-hydroxymethylferrocene (1), 1-trimethylammoniomethylferrocene (2), and 1,1′-bis(trimethylammoniomethyl)ferrocene (3).

Here we report the success of this strategy, and consequently the first example of a fully synthetic, monovalent host–guest system that matches the affinity of avidin and biotin. The present study thus places synthetic hosts squarely in the same arena as proteins, and leads to a revision of our expectations for what is achievable with low-molecular-weight receptors. Further analysis, both experimental and computational, provides insights into the basic physical chemistry of molecular recognition, and especially the tradeoff between energy and entropy.

Results and Discussion

We designed and synthesized 1,1′-bis(trimethylammoniomethyl)ferrocene (3) as a monovalent guest complementary to the host CB[7], with its round hydrophobic cavity and an electrically negative rim at each of its two portals. The thermodynamics of the binding reaction was investigated by isothermal titration calorimetry (ITC). Preliminary studies indicated an extremely high affinity, precluding the direct determination of the association constant. Instead sequential competition titration experiments were carried out with sets of guest molecules, in which each successive target guest competes for a limited concentration of CB[7] with the prior guest, whose thermodynamic parameters of association with CB[7] have already been measured. The main challenge in designing such experiments is proper selection of a set of reference guests exhibiting gradually increasing affinity, and different reaction enthalpies with CB[7] so that the ITC method can be successfully applied at each step. After multiple ITC experiments we selected the reference guests listed in Table 1.

Table 1.

Complexation thermodynamics for cucurbit[7]uril with 3 (as well as 1 and 2) determined by two independent series of 4-step competition ITC experiments in aqueous solution at T = 298.15 K

Step	Guest	Competitor	K/M−1	ΔH°/kJ mol−1	TΔS°/kJ mol−1
First series of 4-steps competition ITC experiments
1)	L-Phe±	(None)	(1.8 ± 0.2) × 106	−43.4 ± 0.4	−7.7 ± 0.5
2)	1,6-Hexanediamine2+	L-Phe±	(2.1 ± 0.4) × 109	−32.8 ± 0.7	20.4 ± 0.8
3)	Aminomethylcyclohexane1+	1,6-Hexanediamine2+	(1.3 ± 0.4) × 1011	−57.8 ± 1.5	5.6 ± 1.5
4)	3	Aminomethylcyclohexane1+	(3.0 ± 1.0) × 1015	−92 ± 3	−4 ± 4
				(−90 ± 1)*	(−2 ± 2)†
Second series of 4-steps competition ITC experiments
1)	Cyclopentanone	(None)	(4.2 ± 0.3) × 105	−40.2 ± 0.4	−8.1 ± 0.5
2)	Spermine4+	Cyclopentanone	(4.8 ± 0.6) × 108	−27.3 ± 0.7	22.3 ± 0.8
3)	N,N'-Bis(aminoethyl)-1,6-hexane-diamine4+	Spermine4+	(1.7 ± 0.4) × 1011	−36.9 ± 1.5	27.2 ± 1.5
4)	3	N,N'-Bis(aminoethyl)-1,6-hexane-diamine4+	(3.3 ± 1.0) × 1015	−87 ± 3	2 ± 4
				(−90 ± 1)*	(−1 ± 2)†
Complexation thermodynamic parameters for CB[7] with 1 and 2
	1	L-Phe±	(3.2 ± 0.5) × 109	−90 ± 2	−36 ± 2
	2	1,6-Hexanediamine2+	(4.1 ± 1.0) × 1012	−89 ± 2	−17 ± 3
				(−90 ± 1)*	(−18 ± 2)†

*Uncertainties of thermodynamic parameters, e.g. enthalpy, are accumulated and thus increased from one step to the next upon performing multistep competition ITC experiments. To obtain more accurate value with reduced uncertainty, we performed direct determination of the enthalpy in the absence of competitive guest.

^†Entropy change with reduced uncertainty is calculated by using enthalpy obtained by direct determination.

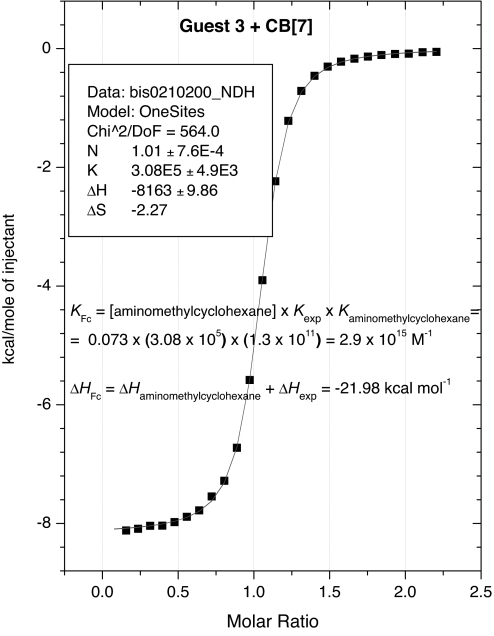
Table 1 lists the measured binding thermodynamics for two sequential studies of the new guest 3; both yield an association constant of 3 × 10¹⁵ M⁻¹, and the values in Table 1 show excellent internal consistency, supporting the validity of the measurements. A typical titration curve obtained in the competition titration ITC experiment is shown in Fig. 2 and more ITC data are included in supporting information (SI) Figs. 5–10. Affinities were also measured for ferrocene guests 1 and 2, but these required only one reference guest, rather than three as in the case of guest 3. These results, also included in Table 1, are consistent with those reported in ref. 7.

Fig. 2.

Competition ITC experiments on complexation of 3 with CB[7] in 73 mM solution of aminomethylcyclohexane HCl used as competitor (Curve fitting was performed by using the Single Set of Identical Sites Model).

Direct ITC measurements of ΔH° at different temperatures allowed us furthermore to determine the heat capacity changes (ΔC_p) for complexation of 1, 2 and 3 with CB[7] as −250 ± 30, −140 ± 30, and −110 ± 30 J mol⁻¹ K⁻¹, respectively (for detailed discussion, see SI Text). The negative sign of ΔC_p is reasonable for the hydrophobic interactions operating upon complexation. In good agreement with the overall area of hydrophobic contacts upon complexation, the absolute ΔC_p values are comparable to those reported for cyclodextrin complexes (10) but much smaller than those for protein–ligand interactions (11).

Strikingly, the enthalpy change for complexation of 3 with CB[7], −90 kJ mol⁻¹, is essentially the same as the enthalpy change for the lower affinity guests 1 and 2, and the entropy change on binding is near zero. That is, addition of the two successive cationic sidearms to the guest has basically no effect on the enthalpy change on binding (ΔH° = −90 kJ mol⁻¹). However, it causes an increase in the entropy change (TΔS°) of 16–18 kJ mol⁻¹, which results in a 1,000-fold increase in the corresponding binding constant. Thus, the enthalpy–entropy compensation effect, which is commonly observed in supramolecular recognition systems (9–10, 12–15), does not seem to operate in this case.

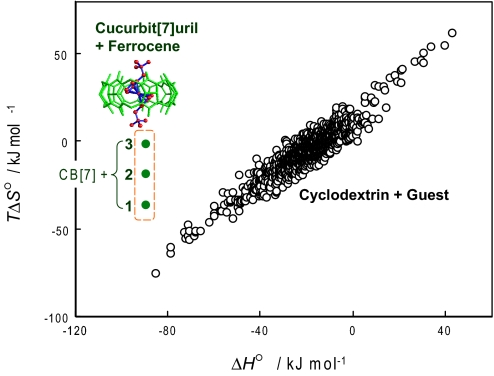
It is of interest to put these results in the context of complexation by cyclodextrins, which are typical cyclic hosts similar in size to the cucurbiturils and likewise possessing a hydrophobic cavity and hydrophilic portals (for detailed discussion, see SI Text). Fig. 3 thus plots changes in entropy and entropy upon binding for a range of cyclodextrin binding reactions (10, 12), along with the corresponding data for CB[7] and guests 1, 2, and 3. The CB[7] series deviates markedly from the cyclodextrin entropy–enthalpy compensation plot.

Fig. 3.

The thermodynamic data obtained for complexation of guests 1, 2, and 3 with CB[7] (green dots), which are significantly deviated from the enthalpy–entropy compensation plot for cyclodextrin-guest complexation (black circles: data adopted from refs. 9 and 10).

We used molecular modeling to gain insight into the deviation of these systems from the usual pattern of enthalpy–entropy compensation. The second-generation Mining Minima algorithm (M2) (14) identifies low-energy conformations of the free host, the free guest, and their complex, and sums the contributions of the minima to obtain the overall configuration integrals of the free and bound species. These integrals permit calculation of the standard free energy of binding. The method uses a force-field description of potential energy and an implicit treatment of the solvent. It has yielded good agreement with experiment in prior studies of aqueous (16, 17) and nonaqueous (14) systems. Of particular relevance here is that the M2 method provides a partitioning of the free energy of binding into two parts: the change in average energy, ΔE, which comprises both the potential energy U, and the solvation free energy W as captured in the implicit solvent model; and the contribution of configurational entropy, −TΔS_config°, which accounts for the loss of mobility of the host and guest on forming the complex. The value of ΔS_config° comprises changes in the rotational, translational, conformational, and vibrational entropy (18), and depends on the standard concentration (1 M). The sum of the change in configurational entropy and the change in solvation entropy, ΔS_solv°, gives the total change in entropy on binding ΔS° as measured for example by ITC (18); hence ΔS_solv° = ΔS° − ΔS_config°.

Tables 2 and 3 summarize the results of M2 calculations for CB[7] with guests 1, 2, and 3. The calculations are consistent with the extremely high measured free energies of binding and reproduce the ranking of the three guests (Table 3). Interestingly, the loss in configurational entropy, which reflects the increased conformational restriction of the host and guest upon complexation, depends only weakly upon the structure of the guest, and is essentially the same for the ultra-high affinity guest 3 as for the lower affinity guest 1 (Table 2). Apparently the main contribution to the penalty comes from the restriction of ferrocenyl core, and it is only marginally affected by the restriction of appended trimethylammonium groups.

Table 2.

Entropic characteristics of complex formation between CB[7] and guests 1, 2, and 3 determined from ITC experiments (TΔS°) and M2 calculations (TΔS_config°), with TΔS_solv = TΔS° − TΔS_config°

Complex	TΔSexp. total°	TΔSconfig°	TΔSsolv
CB[7]·1	−36 ± 2	−75	39
CB[7]·2	−18 ± 2	−63	45
CB[7]·3	−2 ± 2*	−78	76

All quantities are given in kJ mol⁻¹.

*Average of data presented in Table 1.

Table 3.

Energetic characteristics of supramolecular complex formation, computed with M2

Complex	Calculated binding free energy	Energy efficiency	Interfacial efficiency
	ΔG°	ΔG°/ΔE	ΔG°/Δ(area)
CB[7]·1	−32	0.30	0.075
CB[7]·2	−61	0.49	0.12
CB[7]·3	−102	0.57	0.18

Energies are given in kJ mol⁻¹, areas are given in Ų.

The change in solvation entropy on binding, computed by subtracting the computed configurational entropy from the experimentally determined total entropy, is positive in sign, consistent with the idea that binding allows hydrating waters to return to the bulk. Guest 3 is most strongly favored by the gain in solvation entropy, which perfectly balances the large loss in configurational entropy due to loss of mobility of the host and guest. This unique thermodynamic behavior allows almost all of the binding energy to be translated into binding free energy, thus avoiding the large entropic penalty expected on the basis of enthalpy–entropy compensation and producing the extraordinarily high affinity observed for this system. The calculations clearly indicate that the perfect size/shape matching between CB[7] host and guest 3 cannot by itself provide the driving force required to achieve the observed binding constant of ≈10¹⁵: the release of structured water back to the bulk solvent upon binding is an equally important factor.

Prior M2 calculations for other host–guest systems have shown strong, nearly linear compensation of changes in energy E by changes in configurational entropy (14, 16–18). This observation led to the idea of the energy efficiency, ΔG°/ΔE, as a measure of the degree to which a host–guest system overcomes energy-entropy compensation. Values of this quantity for prior systems range from 0.15 to 0.27. The present study reveals strikingly large values of the energy efficiency for CB[7] with the ferrocene guests (Table 3); the value reaches 0.57 for guest 3, indicating that less than half of the energy driving binding is cancelled by losses in configurational entropy, and supporting the concept that guest 3 achieves high affinity by overcoming entropy-enthalpy compensation. This phenomenon is accounted for by the combination of the rigidity and the mutual complementarity of CB[7] and guest 3. More typical host–guest systems lose more entropy relative to the energy they gain. If they are rigid and thus lose little entropy, they do not fit together well and therefore are not strongly favored energetically. If they are flexible and can therefore achieve a good fit and favorable energy, binding comes at a large entropic cost. The present system is rigid yet complementary.

Another measure of host–guest efficiency is the change in free energy achieved for a given size of the host–guest interface, the latter being measured as the change in molecular surface area upon binding. The interfacial efficiency, ΔG°/Δ(area), is of particular interest because it has been argued that a larger interfacial area is the chief reason protein-ligand systems typically achieve higher affinity than host–guest systems (1). The values of this quantity computed for prior host–guest systems (16) range from 0.04 to 0.1 kJ mol⁻¹Å⁻². The present study yields significantly larger values of up to 0.18 for guest 3, indicating that these systems make especially good use of the available interfacial surface area to generate affinity.

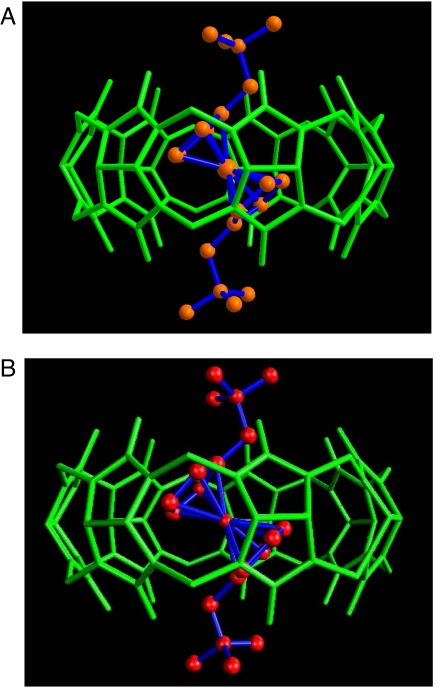
Single crystals of the complex formed between 3 and CB[7] were obtained by slow evaporation of the solvent. The crystal structure of the complex was solved by x-ray diffraction methods and is shown in Fig. 4a. The structure shows the complete inclusion of the ferrocenyl residue in the CB[7] cavity, with its main axis (passing through the centers of both cyclopentadienyl rings) tilted (43.7° and 41.9° for two independent positions) in relation to the main sevenfold symmetry axis of the host. The tilting of the ferrocenyl residue allows the almost ideal positioning of each of the trimethylammonium groups to maximize ion–dipole interactions with the carbonyl rims on each of the host portals. The most stable computed conformation of this complex from the second-generation Mining Minima algorithm (Fig. 4b) matches the crystal structure (Fig. 4a) closely.

Fig. 4.

X-ray crystal structure of CB[7]·3 complex (A) and computed conformation of CB[7]·3 complex from the second-generation Mining Minima algorithm (B).

The tight fit of ferrocene guest 3 inside the CB[7] cavity was also evident in NMR spectroscopic experiments. Although the exchange between the complex and the free guest was slow in the NMR time scale, as anticipated from observations in other highly stable CB[7] complexes (7), spin-lattice relaxation time (T₁) measurements were particularly useful. The much shorter T₁ values observed for the ferrocene core protons of 3 when bound to CB[7] as compared with those of free 3 indicate that the rotational motion of the ferrocene becomes restricted due to the tight fit of the guest upon complexation with CB[7], consistent with the computational result that the entropic penalty comes from the restriction of the ferrocene core.

The reversible, one-electron oxidation of ferrocene guest 3 was investigated by using voltammetric techniques to quantitatively examine the roles of hydrophobicity in the tight binding. Half-wave potentials (E_1/2) of +0.65 V and +0.84 V (versus Ag/AgCl) were obtained respectively in the absence and presence of one equivalent CB[7] (SI Fig. 12). The complexation-induced half-wave potential shift is very pronounced (ΔE_1/2 = 0.19 V), revealing a significant loss in the complex stability by 18 kJ mol⁻¹ in ΔΔG° or by a factor of 1,400 in the K value upon oxidation of the ferrocene center. Such a redox-induced affinity change could be used as a versatile tool for electrochemically and photochemically manipulating various chemical and biological supramolecular systems, which constitutes a unique advantage of the CB[7]-ferrocene system relative to the natural avidin–biotin pair.

It is crucial to understand how such obviously different supramolecular systems as avidin-biotin versus CB[7]·3 complexes can display such similar overall association thermodynamics. As can be seen from the crystal structure of ligand-free avidin, the binding site, which has a shape similar to the biotin molecule, is filled with structured water molecules that form a hydrogen-bonding network, all of which are expelled from the cavity upon complexation with biotin (3). This profound dehydration from the binding site is obviously the major source of the observed positive entropy. However, this positive entropy is offset by the negative effect arising from the conformational fixation of biotin in the binding site, as well as the fixation of the three-dimensional structure of two regions of the avidin polypeptide chain, resulting in an overall entropy close to zero (4). From the entropic point of view, there are similar molecular events occurring in our CB[7]·3 system, where the positive entropy gained by dehydration from the CB portals and cavity as well as the ferrocene guest is cancelled by the negative entropy arising from the severe conformational fixation of the guest inside the cavity. The large negative enthalpy, as great as −90 kJ mol⁻¹, is a major driving force to form an extremely strong complex, as the ferrocene core of the guest core fits very well in size and shape inside the rigid CB[7] cavity, achieving optimal van der Waals contacts. In fact, the guest volume included inside CB[7] is 154 ų, which is approximately equal to 55% of the host cavity volume, in excellent agreement with the optimum cavity filling fraction proposed by Mecozzi and Rebek (19). Interestingly, the crystal structures of avidin (3) and the avidin–biotin complex (3) reveal that the binding site is rather rigid, surrounded by five aromatic residues (Tyr, Phe, and three Trp), and additional rigidity is provided by the anchoring of two Trp side chains to other residues by hydrogen bonds. The large negative enthalpy for the formation of the avidin-biotin complex arises not only from the strong van der Waals contacts, but also from the network of hydrogen bonds provided by the residues around the binding site that are exquisitely prepositioned to assure the precise fit to biotin. Importantly, both the avidin-biotin and CB[7]·3 systems fail to obey enthalpy–entropy compensation, which has been demonstrated to prevail in almost all supramolecular systems (9, 10, 12–15), due to the rigid host cavity and the extensive entropic dehydration effects.

Conclusions

We have described the supramolecular complexation of neutral and cationic ferrocene derivatives by the host CB[7], with an ultrahigh stability similar to that of the avidin-biotin complex. The extremely large affinities of the complexes surveyed here are traceable to a large enthalpic gain, originating from the tight fit of the ferrocene core to the rigid CB cavity, critically assisted by the entropic gain arising from the dehydration of the CB portals, and largely uncompensated by losses in configurational entropy. This pattern contrasts with proteins, which typically gain affinity by thoroughly wrapping their ligands and thus generating high interfacial areas. The latter strategy is not accessible to most host–guest systems because of their small size. Conversely, it seems unlikely that the strategy of the systems studied here, gaining affinity through near-perfect complementarity of rigid molecules, will be accessible to proteins, whose acyclic nature makes it difficult for them to achieve the rigidity of a cyclic, low molecular weight host.

The new high-affinity host–guest pair reported here could serve as an extremely strong but redox-active reversible fastener in self-assembling chemical and biological supramolecular systems. More generally, we believe that the failure to obey the enthalpy–entropy compensation is one of the most promising features of the CB[7]-ferrocene system and may establish a guiding principle to design a structurally diverse range of extremely strong supramolecular complexes in the future.

Materials and Methods

Host Compound.

CB[7] was prepared as described in ref. 20 with some modifications. The residual acid (H₂SO₄) present in the CB[7] sample was eliminated by slow addition of ammonium bicarbonate to the solution of CB[7] until the pH of the solution became neutral. The neutralized CB[7] solution was then evaporated to dryness and the residue was redissolved in a minimum amount of water with sonication and purified by GPC (Superdex 30 column, water, 1 ml/min). Lyophilization of the eluted solution produced ultrapure CB[7].

Guest Compounds 1 - 3.

Guests 1 and 2 (iodide salts) were prepared as reported in ref. 7. Guest 3 (iodide salt) was synthesized from 1,1′-bis(N,N-dimethylaminomethyl)ferrocene with iodomethane, as described in ref. 21.

Isothermal Titration Calorimetry (ITC).

The association constants and thermodynamic parameters for the inclusion complexation of guests 1, 2, and 3 with CB[7] were determined by titration calorimetry with a VP-ITC instrument (MicroCal). An aqueous solution (0.05–0.5 mM) of CB[7] was placed in the sample cell, to which a solution of ferrocene derivative (1–5 mM) was added stepwise in a series of 25–30 injections (10 μl each), and the heat evolved was recorded at 25°C. The heat of dilution was measured by injecting the guest solution into a blank solution containing no host, and the net heat effect was obtained by subtracting this value from the overall heat effect observed. Because the association constants are extremely large, the ITC experiments were performed by using the multistep competition method with a series of competitors shown in Table 1. Typical ITC thermograms are shown in Fig. 3 and SI Figs. 5–10. The data were analyzed and fitted by the Origin program (MicroCal). The complexation enthalpies for the inclusion of guests 2 and 3 with CB[7] were also determined by the direct measurement of the heat effect upon interaction between the guest and the host in pure water at 5, 15, 25, 35, and 45°C in the absence of a competitor, as shown in Supporting Information; the results obtained are well compatible with that obtained by the multistep titration experiments at 25°C. From the slope of the temperature dependence of ΔH° obtained (see SI Fig. 11), we can calculate the ΔC_p values as −250 ± 30, −140 ± 30, and −110 ± 30 J mol⁻¹ K⁻¹ for CB[7]·1, CB[7]·2, and CB[7]·3, respectively.

Cyclic Voltammetry.

The electrochemical experiments were performed in a single-compartment cell fitted with a glassy carbon working electrode (0.071 cm²), a platinum counter electrode and Ag/AgCl reference electrode. The surface of the working electrode was polished with a 0.05-μm alumina/water slurry on a felt surface. The electrolyte solution was purged with purified nitrogen before the measurements and kept under a nitrogen atmosphere throughout the experiments. A Bioanalytical Systems 100B/W electrochemical workstation was used for potentiostatic control and recording of the voltammetric data.

NMR Spectroscopy.

All NMR experiments were performed on a Bruker DRX500 NMR spectrometer operating at the proton Larmor frequency of 500.23 MHz. D₂O signal was used for the field-frequency lock. The spin-lattice relaxation times (T₁) were obtained by using the standard inversion recovery pulse sequence and a delay of 5 T₁ between acquisitions was used.

¹H Spin-Lattice Relaxation Time (T₁) Measurements.

The tight fit of the ferrocene core to the rigid CB cavity was manifested by the changes in spin-lattice relaxation time (T₁). T₁ values for the protons of 3 decreased upon complexation with CB[7]. For example, at 25°C, T₁ values of the protons (a, b, c, and d) are 0.67, 0.90, 3.25, and 4.50 s for free 3, but 0.47, 0.66, 1.86, and 2.68 s for 3 included in CB[7]. In particular, the protons of the cyclopentadienyl (Cp) ring (c and d) show remarkable change in T₁. The T₁ values increased with increasing temperature: at 40°C, for example, T₁ values of the protons (a, b, c, and d) are 1.16, 1.50, 5.77, and 7.42 s for free 3, but 0.56, 0.69, 2.09, and 2.98 s for 3 complexed with CB[7]. The increasing T₁ values with increasing temperature suggest that the correlation times (τ) are in the liquid-like region of the T₁–τ curve, where a shorter T₁ corresponds to higher rigidity. Therefore, the much shorter T₁ values for the ferrocene protons of complexed 3 compared with those of free 3 suggest that the rotational motion of the Cp rings of 3 becomes restricted upon complexation with CB[7], which is ascribed to the fixation of 3 inside the cavity. Furthermore, the T₁ values for the protons of 3 complexed with CB[7] display little dependence upon temperature. The invariance of T₁ with temperature indicates that the correlation time approach the minimum of the τ versus T₁ curve, and therefore that the Cp rings of 3 inside CB[7] are conformationally and rotationally tightly fixed.

X-Ray Crystallography.

Yellow plate-shaped crystals were grown by slow vapor diffusion of acetone into an aqueous solution containing CB[7] and 3. Because the crystals were too small to collect x-ray diffraction data on a conventional diffractometer, the diffraction data were collected with synchrotron radiation (λ = 1.00000 Å) at the Wiggler Beam Line 4A, Pohang Accelerator Laboratory, Pohang, Korea. Data reduction and adsorption correction were performed with the HKL2000 package. The structures were solved by direct methods and refined by full-matrix least squares method with SHELXTL package. All of the nonhydrogen atoms were refined anisotropically, and hydrogen atoms were added to their geometrically ideal positions. x-ray data for [Fc(CH₂N(CH₃)₃)₂]@[C₄₂H₄₂N₂₈O₁₄]2I⁻·12H₂O: C₆₀H₉₈N₃₀O₂₇FeI₂ M = 1963.32, Orthorhombic, Pnma (no. 62), a = 24.476(5) Å, b = 45.296(9) Å, c = 21.060(4) Å, V = 23348(8) ų, Z = 12, T = 93 K, μ(λ = 1.00000 Å) = 2.684 mm⁻¹, d_calc = 1.676 g·cm⁻³, 37,872 reflections measured, 11,779 unique (R_int = 0.0337), R₁ = 0.0915, wR₂ = 0.2545 (I > 2σ(I)), R₁ = 0.1141, wR₂ = 0.2713 (all data), GOF = 1.159.

Computational.

The starting structure of CB[7] was drawn from the crystal structure (7), and its partial atomic charges were calculated with the program Vcharge (22) (VeraChem, Germantown, MD) using VC/2004 parameters. Starting structures of the ferrocene guests (1–3) were prepared with the 2D sketcher module of Quanta (Accelrys, San Diego, CA). Their partial charges were fitted to reproduce electrostatic potentials from quantum calculations performed with GAMESS (23) at the RHF/6–31G* theory level, and the charges of chemically equivalent atoms were averaged. Bonded and Lennard–Jones parameters for all compounds were drawn from CHARMM22 parameter set (Polar hydrogen parameter set for CHARMm, version 22, 1992, Accelrys); the ferrocene carbons bonded to Fe were assigned the C5R atom type but parameters for the FeC bond-stretches and FeCFe angle-bends were assigned based upon the CM atom type. The starting conformations of the complexes were generated by using the docking module in M2 software to fit each guest molecule into the lowest-energy conformation of CB[7] obtained from separate conformational search calculations. The initial conformations of the host, guests, and complexes were furthermore relaxed by energy minimizing them with the conjugate gradient method with a root-mean-square (RMS) gradient tolerance of 0.01 kcal/mol, and then by the Truncated Newton–Raphson method with a RMS gradient tolerance of 0.0001 kcal/mol. Standard free energies of binding were computed with the second generation Mining Minima (M2), using procedures described in ref. 16. New sets of energy minima were sought until the free energy (chemical potential) difference between successive iterations, each including multiple energy minima, had converged to within 0.05 kcal mol⁻¹. A total of 27 energy minima were processed for the complex of CB[7] with 3.