Nonequilibrium Single Molecule Protein Folding in a Coaxial Mixer

Abstract

We have developed a continuous-flow mixing device suitable for monitoring bioconformational reactions at the single-molecule level with a response time of ∼10 ms under single-molecule flow conditions. Its coaxial geometry allows three-dimensional hydrodynamic focusing of sample fluids to diffraction-limited dimensions where diffusional mixing is rapid and efficient. The capillary-based design enables rapid in-lab construction of mixers without the need for expensive lithography-based microfabrication facilities. In-line filtering of sample fluids using granulated silica particles virtually eliminates clogging and extends the lifetime of each device to many months. In this article, to determine both the distance-to-time transfer function and the instrument response function of the device we characterize its fluid flow and mixing properties using both fluorescence cross-correlation spectroscopy velocimetry and finite element fluid dynamics simulations. We then apply the mixer to single molecule FRET protein folding studies of Chymotrypsin Inhibitor protein 2. By transiently populating the unfolded state of Chymotrypsin Inhibitor Protein 2 (CI2) under nonequilibrium in vitro refolding conditions, we spatially and temporally resolve the denaturant-dependent nonspecific collapse of the unfolded state from the barrier-limited folding transition of CI2. Our results are consistent with previous CI2 mixing results that found evidence for a heterogeneous unfolded state consisting of cis- and trans-proline conformers.

INTRODUCTION

The goal of most protein folding experiments is to detect and characterize the various conformational states populated as a protein folds into its native and functional structure. This process can be described as a diffusional conformational search along a multidimensional energy landscape where the states populated correspond to various energy minima and the folding landscape itself depends on the solution conditions used (1,2). Protein folding experiments can be conducted under either equilibrium or nonequilibrium solution conditions and the different conformational states populated can be detected using either ensemble-averaged or single-molecule detection methods (3–5). In general, nonequilibrium in vitro refolding measurements conducted under standardized native solution conditions are preferred because they populate the conformational states most relevant to in vivo folding (6), and single molecule detection methods are desirable because they directly access the full distribution of conformations present within an ensemble and thus allow the direct experimental detection and characterization of conformational subpopulations (7–10). Novel single-molecule fluorescence spectroscopies with high spatial and temporal resolutions continue to extend our ability to resolve protein-folding processes along a variety of reaction coordinates (11). In parallel, microfabrication methods have enabled the construction of continuous-flow microfluidic mixers with ultrafast response times. Such mixers often employ hydrodynamic focusing of the sample stream to submicron dimensions to achieve extremely rapid diffusional mixing (12). Such silicon-etched mixers have found numerous applications in the study of biomolecular folding reactions because of their low sample consumption rate and submillisecond dead times (13–17). Coaxial mixing geometries can further enhance the diffusional mixing process by axisymmetric hydrodynamic focusing of sample fluids into thin cylindrical jets (18). Such ensemble mixers attempt to resolve protein-folding intermediates along the temporal reaction coordinate alone. However, by slowing down the fluid flows in such mixers to 1–10 μm/ms, the residence times of sample molecules within a confocal detection volume becomes sufficient for single molecule detection and single molecule spectroscopies can be used to resolve conformational subpopulations along additional reaction coordinates.

Since their inception, single molecule methods have successfully addressed many outstanding questions in biology by resolving subpopulations of molecular species present within a heterogeneous mixture. Single-molecule (single-pair) fluorescence resonance energy transfer (smFRET) in particular has the subnanometer spatial resolution required to discriminate between different conformational subpopulations of biomolecules present within an ensemble (19,20). In diffusion-based implementations of smFRET, single molecules, which have been labeled with both a donor (D) and an acceptor (A) fluorophore, diffuse across a diffraction-limited confocal volume giving rise to short bursts of fluorescence. During such burst events, the donor is repeatedly excited and can transfer its excitation energy to the acceptor via a distance-dependent Förster mechanism (21,22). For each such burst, the emitted fluorescence intensities in each detection channel (I_D and I_A) are used to calculate the average efficiency of energy transfer (E_FRET) and the average interfluorophore distance (R) for each single-molecule burst event using

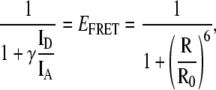(1)

where γ accounts for differences in fluorescence quantum yields and detection efficiencies between the donor and acceptor fluorophores and R_o is the interfluorophore distance at which the efficiency of energy transfer (E_FRET) is 0.5. Binning the burst events along the E_FRET or R axes yields the full distribution of these molecular properties within an ensemble and, for protein folding studies, allows the resolution of folded and unfolded subpopulations which are otherwise averaged out in ensemble measurements. Modeling of the shot-noise contribution to these distributions can also be used to extract additional information (23–25).

Novel single-molecule spectroscopies continue to extend the information content of diffusion-based smFRET studies beyond the traditional E_FRET reaction coordinate. For example, alternating laser excitation (ALEX) allows the molecular sorting of dual-labeled (D-A) species from single-labeled species (D-only and A-only) along a molecular stoichiometry (S) axis (26,27). The use of pulsed laser sources and time-correlated, single-photon counting enables the extraction of fluorescence lifetime and anisotropy information from the various subpopulations detected (28,29). Fluorescence correlation spectroscopy (FCS) or photon antibunching analysis of single molecule burst data can yield the timescales of intramolecular conformational fluctuations within different subpopulations (30–33). Finally, the extension of single-molecule FRET to three fluorophores allows the separation of molecular species along two or more interresidue distance or stoichiometry reaction coordinates, thereby further enhancing our ability to resolve and characterize bioconformational intermediates (34–36).

These various diffusion-based smFRET spectroscopies have traditionally been applied to biological systems under equilibrium solution conditions; however, Lipman et al. (37) recently conducted time-resolved smFRET protein folding studies under nonequilibrium solution conditions using a microfabricated continuous-flow mixer with a dead-time of ∼50 ms. Using the combined resolving power of the E_FRET and folding-time reaction coordinates, the authors were able to resolve the barrier-limited two-state folding transition (τ_1/2 = 150 ms) of cold shock protein from the solvent-induced nonspecific collapse of the unfolded state (τ < 100 μs) and were thus able to directly characterize a signal arising from the unfolded state of cold shock protein under native folding conditions. The ability to isolate and further characterize unfolded states under in vitro refolding solution conditions using additional single-molecule parameters and spectroscopies is likely to yield novel insights into protein-folding mechanisms. However, the majority of small single-domain protein model systems fold faster than the 50-ms dead-time of the device of Lipman et al. In this article, we present a novel coaxial single-molecule mixing device with the temporal resolution required to study such faster protein folding reactions. Here we describe and characterize our novel mixing device and also demonstrate its use to transiently populate, detect, and characterize the unfolded state of Chymotrypsin Inhibitor Protein 2 (CI2) under in vitro refolding conditions.

We first describe the construction of the mixers and the optical setup used for these studies. Computational fluid dynamics simulations that explore details of the mixing reaction are then presented. Next, these simulations are compared with experimental fluid flow data and instrument response functions measured under a variety of flow conditions. Finally, the refolding reaction of CI2 is explored at the single molecule level. The Discussion addresses potential sources of systematic or standard errors. We conclude with some potential future applications for the coaxial single-molecule mixer.

MATERIALS AND METHODS

Mixer construction

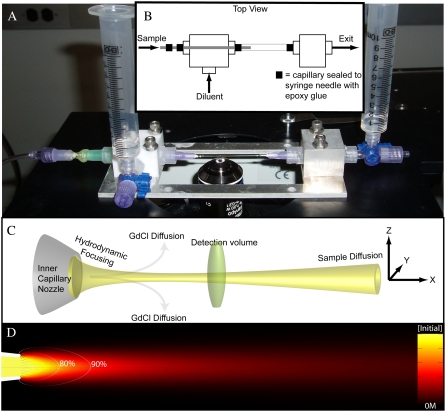
Fig. 1, A–D, show an actual image (A), a schematic (B), an illustration (C), and a simulation (D) of the coaxial mixer. All mixers were constructed using custom-made aluminum baseplates (Laseronics, Torrance, CA), Teflon or aluminum T-junction connector blocks, poly-propylene 1/8-NTP male LEUR-LOCK connectors (Value Plastics, Fort Collins, CO), 10-ml syringes for diluent and exit reservoirs, 300 μm inner diameter (ID)/600 μm outer diameter (OD) square outer capillaries (Vitrocom, Mountain Lakes, NJ), and 250 μm OD round inner capillaries (Vitrocom) pulled to have defined nozzles with 5–10 μm inner diameters using a P-2000 laser pipette puller (Sutter Instruments, Novato, CA). Assembly of the mixers was conducted under a conventional light microscope using epoxy glue to seal both the inner and outer capillaries to opposite sides of the T-junction connector block (see Fig. 1 B). Two LUER needles were carefully glued to the inner capillary to create a macroscopic port for sample solution injection and to protect it from mechanical strain and breaking. Granulated MIN-U-SIL silica particles (US Silica, Berkeley Springs, WV) were reversibly packed into the inner capillary as an in-line filter to minimize clogging and to stabilize the inner capillary flow properties by increasing its back pressure. Flow through the inner capillary was manually driven using a pressurized syringe. Flow through the square outer capillary was gravity-driven using a height differential between the diluent and exit reservoirs. Before all experiments, each mixer was thoroughly rinsed with acetone, methanol, and water to remove all contaminating fluorescent species. All buffers and samples were filtered (<0.2 μm) before use to minimize clogging (bovine serum albumin was not used in any of the buffers because it increases the frequency of clogs via aggregation at the inner capillary nozzle). The mixer was mounted on a high-resolution scanning stage (Mad City Labs, Madison, WI) using a simple clamp. During each experiment, the diluent and exit reservoir fluid heights were manually updated every few minutes to maintain stable flow and velocity profiles.

FIGURE 1.

(A) An image of the single molecule mixer. Diluent and exit fluid levels are both set to the first syringe marking (at 1 ml) so there is no bulk flow in the system (ΔH = 0). (B) A top view schematic illustrating the design and how fluids flow in and out of the mixing region through the two connector blocks. (C) A closeup of the mixing region illustrating hydrodynamic focusing of the sample stream, diffusion of GdCl away from the sample stream, single molecule detection as labeled sample molecules traverse the confocal detection volume, and the diffusion of sample molecules away from the axis of flow (x axis). (D) An x,y cross-section of a simulated flow profile with sample streamlines (solid lines), trigger-point contour lines (open lines), and the normalized protein sample concentration in a 40 × 200-μm field of view.

Optical setup and smFRET-ALEX measurements

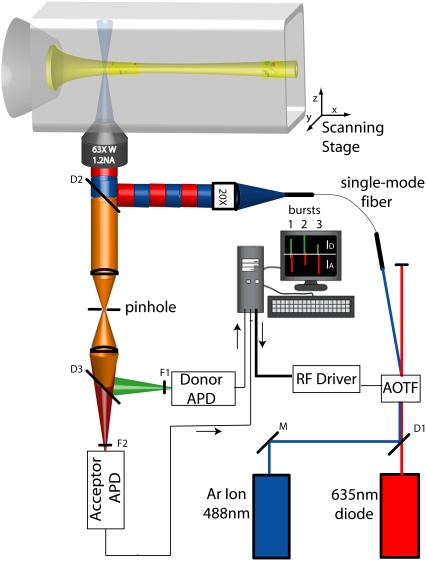
Fig. 2 illustrates the basic elements of the optical setup. The 488-nm line of an argon ion laser (Midwest Laser Products, Frankfort, IL) and a 635-nm diode laser beam (Coherent, Santa Clara, CA) were combined using a 560LP dichroic mirror, D1 (Omega Optical, Brattleboro, VT). The combined beam was then passed through an acousto-optic tunable filter (AOTF) (Neos Technologies, Melbourne, FL) to achieve microsecond acousto-optic modulation of the excitation beam in a manner similar to (yet more cost effective than) the electro-optic modulation (26) or direct-modulation (38) alternating laser excitation (ALEX) systems previously described. ALEX allows the digital sorting and analysis of single molecule fluorescence bursts into D-only, A-only, and DA subpopulations (26). This AOTF-μs ALEX implementation has been described before (39). Briefly, a commercial driver system and a homewritten LabView routine were used to apply different radiofrequencies onto the acousto-optic crystal inducing the deflection and coupling of alternating laser lines (488–635) into an appropriately positioned single-mode fiber (P1-405A-FC-2, Thor Labs, Newton, NJ). The output of this fiber was expanded, collimated, and coupled into the back aperture of a 60× 1.2 NA UPlanApo Olympus water immersion objective on an IX71 inverted confocal microscope (Olympus America, Center Valley, PA) using a double-band excitation dichroic mirror, D2 (488-637DBXP, Omega Optical). The back aperture of the objective was underfilled (β ∼ 3) to obtain the nearly Gaussian point spread function (PSF) required for proper fluorescence cross-correlation spectroscopy (FCCS) fitting (40–42). The continuous-wave excitation powers coupled into the objective for each laser line were 300 μW at 488 nm and 60 μW at 635 nm (after alternation this would yield a total of 180 μW with the 50% duty cycle used). Donor and acceptor fluorescence signals were both focused onto a single 100-μm pinhole to reject out-of-focus light, separated using a 630DRLP emission dichroic mirror, D3 (Omega Optical, Brattleboro, VT), and finally refocused onto two separate avalanche photodiode (APD) detectors (Perkin Elmer Optoelectronics, Fremont, CA). Homewritten LabView routines were used for the acquisition of photon arrival times in the D and A channels. Detected photon streams were analyzed as previously described to obtain single molecule E_FRET-S two-dimensional histograms (27). The recently-described dual-channel burst search algorithm was then applied to all the data sets to quantitatively eliminate the contributions of D-only, A-only, and acceptor photobleaching during a burst to the E_FRET histograms (23).

FIGURE 2.

Microsecond ALEX optical setup using an acousto-optic tunable filter (AOTF). The 488-nm and 635-nm laser lines are combined with a dichroic mirror D1 and coupled into the AOTF. The negative first-order diffractions of the two laser lines are alternatively coupled into a single mode fiber. Light emanating out of the fiber is collimated (by a 20× objective) and coupled to the microscope through dichroic mirror D2. Florescence is collected, focused through a pinhole, and split into donor and acceptor signals before being filtered by emission filters F1 and F2 and refocused onto two avalanche photodiode detectors (APDs). Control of the AOTF RF signal and counting of photons is accomplished using homebuilt LabView data acquisition hardware and software.

Two-dimensional x,y and y,z flow profiles were imaged using a scanning stage (Mad City Labs) with a scanning resolution of 20 nm in x,y and 50 nm in z and a scanning range of 200 μm × 200 μm × 100 μm in the x, y, and z axes respectively. This allowed us to scan an x,y image of the sample stream and then move to defined x positions along the axis of flow to acquire single-molecule or FCCS data streams at each distance. All two-dimensional image acquisition and analysis routines were written in LabView and are described elsewhere (43). Three-dimensional flow profiles were acquired on a Leica-AOBS laser-scanning confocal microscope using commercial software (Leica Microsystems, Bannockburn, IL).

Fluorescence cross-correlation spectroscopy velocimetry

Using the optical setup described above under continuous excitation with ∼200 μW of the 488-nm laser line, the detected photons incident on the D and A APDs were sent to an ALV6010 Multiple Tau Correlator (ALV, Langen, Germany). Cross-correlation functions from ALV's commercial software were exported into and fit in OriginLab 7.5 (OriginLab, Northampton, MA) using an FCCS fitting function which models three-dimensional diffusion and uniform translational flow of the sample molecules (44–46),

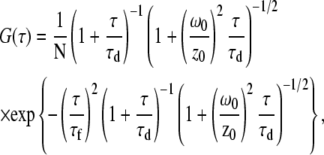(2)

where τ_d is the diffusional residence time of the sample molecules in the observation volume under zero-flow conditions. This value was determined and fixed in the fit by taking a control FCCS measurement of the sample molecules inside a detached segment of the square capillaries used to construct the mixers and under 0 M GdCl solution conditions. The value τ_f is the residence time of the sample molecules in the observation volume in the absence of diffusion (i.e., due solely to translational flow). N is the average number of molecules within the observation volume. The values ω₀ and z₀ are the radial width and height of the confocal point spread function (PSF), which is directly determined by bead-scanning measurements (see below). To calculate the fluid velocity at different spatial positions in our flow profiles we then used the simple relation,

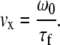(3)

The value ω₀ was determined both by bead-scanning measurements and by an optimized version of the commonly-used FCCS control measurement using rhodamine 6G (R6G). The resulting axial velocity profiles typically consisted of data points at 10 μm intervals starting 5–10 μm from the inner capillary nozzle.

Bead-scanning PSF imaging, multicolor optical alignment, and FCCS ω_o controls

To determine ω₀/z₀ in Eq. 2, ω₀ in Eq. 3, and also to ensure that the PSF has a Gaussian intensity profile which is spatially coincident in both detection channels (a requirement for accurate FCCS velocimetry), 100-nm TetraSpeck fluorescent microspheres with multiple excitation and emission peaks (Invitrogen-Molecular Probes, Eugene, Oregon) were mounted onto GOLDSEAL glass coverslips (Thermo-Fisher, Waltham, MA) using MY133, a polymer-based n = 1.335 (at 589 nm) optical adhesive/mounting medium (My Polymers LTD, Rehovot, Israel). Immobilized beads were scanned through both the 488-nm and the 635-nm excitation volumes while collecting the fluorescence photons in the D and/or A channels at each pixel in the scanned image. Not only does this method of directly imaging the three resultant PSFs yield the required fitting parameters for Eqs. 2 and 3 but it also provides a very sensitive method for aligning the D and A excitation and detection volumes so that all three PSFs overlap with each other. This minimizes the unwanted affects of chromatic or spherical aberrations in the optical system and increases both the FCCS signal and the resolution of the smFRET-ALEX histogram (23). Although bead scanning is the only control which yields the ω₀/z₀ ratio required for fits to Eq. 2, within the range ω₀/z₀ = [0.23–0.37] typical of most experimental PSFs, the extracted fluid velocities remain essentially unaffected by changes in this fitting parameter (data not shown). However, because the bead-scanning PSF measurements described were conducted above GOLDSEAL coverslips rather than within the 300 μm ID 600 μm OD square glass capillaries used to build the mixers, the τ_d of R6G, a molecule of known diffusion coefficient, was also measured within the square glass capillaries. We then converted this τ_d value into a PSF spot width using

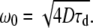(4)

Although the diffusion coefficient of R6G has been reported elsewhere (47), it is sensitive to both the solution viscosity and to various optical parameters. Thus the mean and standard deviation (SD) of the diffusion coefficient of R6G used in Eq. 4 (D_{R6G aq} = 387 ± 26 μm²/s) was determined for this study by taking FCCS measurements of R6G in a standardized buffer (20 mM sodium Borate, pH 7) under optical conditions (i.e., optical alignment, coverslip thickness, objective collar setting, depth of focus, sample index of refraction, etc.) identical to those used for the bead-scanning PSF measurements. The mean and SD of the ω₀ distribution (n = 9) obtained from the bead-scanning PSF measurements together with the mean and SD of the distribution of τ_d values obtained from the R6G FCCS measurements, were then used to determine the mean and SD of the diffusion coefficient according to Eq. 4. Standard error propagation was used in this analysis.

Computational fluid dynamics simulations

All simulations were conducted using the COMSOL Multiphysics 3.2 finite element modeling software package (COMSOL, Stockholm, Sweden). Briefly, a finite element grid of roughly 5000 fluid elements was generated and overlaid on an image-derived model of the mixing region. Then the incompressible axisymmetric steady-state Navier-Stokes equation and the convective diffusion equation were simultaneously solved for both the fluid velocity field, 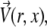and the denaturant concentration, c_Gd (r, z),

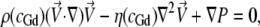(5)

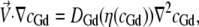(6)

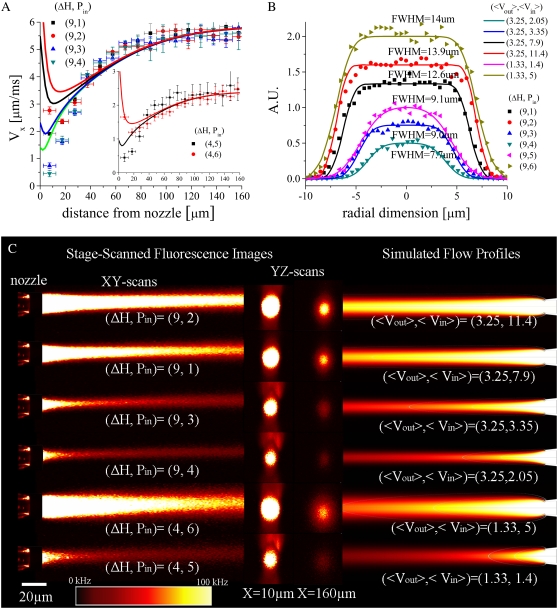
where P is the fluid pressure tensor, the denaturant-dependent fluid density is given by ρ(c_Gd) = 1000 + (0.0257)c_Gd − (2.7e-7)(c_Gd)², the denaturant-dependent fluid viscosity is given by η (c_Gd) = (8.9e-4) + (4.877e-8)c_Gd − (7.031e-12)(c_Gd)² + (2.403e-15)(c_Gd)³, and the denaturant-dependent diffusion coefficient is given by D_Gd(c_Gd) = (1.285e-9) − (2.54e-13)c_Gd + (1.16e-17)(c_Gd)² using SI units for all parameters and mM units for the denaturant concentration. These equations were obtained using a third-order polynomial B-spline fit to previously published data ((48,49) and X. Michalet, unpublished). The protein sample's diffusion coefficient (D_prot = 1.64e-10) was determined using Eq. 4 together with the τ_d value obtained from the zero-flow control measurement described above and the predetermined confocal spot-width (see FCCS ω₀ control above). No-slip boundary conditions were used at all capillary walls; and average fluid velocity boundary conditions for the inner and outer capillary channels, hereafter given by (〈V_out〉, 〈V_in〉), were determined by first adjusting 〈V_out〉 so that the simulated terminal flow velocity far from the inner capillary nozzle agreed with the value from the FCCS velocimetry experiment and then adjusting 〈V_in〉 so that the full width half-maximum (FWHM) of the simulated sample stream at ∼10 μm from the nozzle matched that derived from a transverse y,z confocal scan of each experimental sample stream.

We define the trigger point, x_trig, for folding in our continuous-flow mixer by the contour lines where either an 80 or 90% drop in denaturant concentration has been established (open lines in all simulation images). Because different sample streamlines will cross each of these contour lines at different distances from the inner capillary nozzle, each streamline will have a different x_trig value. Similarly, at a given distance from the inner capillary nozzle, the denaturant concentration varies with radial distance from the axis of flow. Therefore, we report both the average and the standard deviation of the normalized amplitude change in denaturant concentration along streamlines that are within 3 μm from the central axis of flow; this defines our simulated denaturant response function (see solid lines later, in Fig. 5). The dead-time of the mixer, t_dead, is defined as the average time required for sample molecules to travel along different streamlines from the nozzle aperture to their respective trigger points on either the 80% or the 90% x_trig contour line. The uncertainty associated with these t_dead estimates is given by the range of times required for sample molecules to reach their respective trigger points (50).

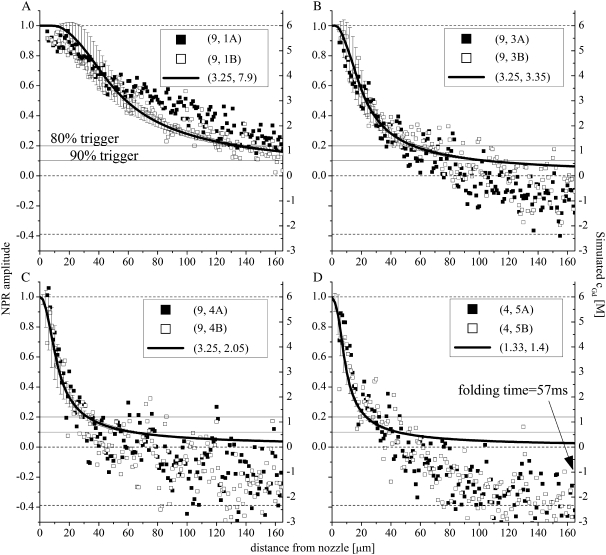
FIGURE 5.

NPR amplitudes (solid and open data points, left axis) versus simulated denaturant concentration/response functions (solid lines and error bars, right axis) for four of the flow conditions shown in Fig. 4. (A) (〈V_out〉, 〈V_in〉) = (3.25, 7.9); (B) (〈V_out〉, 〈V_in〉) = (3.25, 3.35); (C) (〈V_out〉, 〈V_in〉) = (3.25, 2.05); and (D) (〈V_out〉, 〈V_in〉) = (1.33, 1.4). The solid horizontal lines indicate the 80% and 90% trigger-point contour lines. As 〈V_in〉 is increased, the stream widens, the trigger points move to distances further from the nozzle, and the standard deviation of the simulated denaturant concentration present within a 3 μm radius of the axis of flow at a given distance from the nozzle (error bars) increases. The dotted line at the NPR = −0.388 is the nonequilibrium endpoint NPR signal (at a folding time of 57 ms) obtained for the slowest flow conditions (D).

It should be noted here that because dispersive mass transport of sample molecules in both the transverse and axial flow directions cause different sample molecules to diffuse through different parts of the mixing region, each detected single molecule will have a different axial flow velocity history and a different local denaturant concentration history. The response functions shown and the distance-to-time transfer functions used in the data presented below assume nondiffusing sample molecules traveling along the simulated sample streamlines.

Experimental instrument response function measurements

To ensure that all the parameters and equations used in the simulations yield denaturant response functions which match the actual response functions for a given set of flow conditions, the instrument response functions of the mixer were experimentally measured under a variety of flow conditions using the nonspecific denaturant-dependent collapse of Chymotrypsin Inhibitor protein 2 (CI2) as a readout. Under flow conditions too fast for smFRET-ALEX (〈V〉_out ∼5 μm/ms), to monitor this collapse, a time-averaged proximity ratio (〈PR〉) was calculated for each pixel in the imaged flow profile using the equation

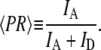(7)

The brackets denote that this is an average over the integration time for each pixel (∼10–100 ms). A comparison between Eq. 2 and Eq. 7 shows that PR = E_FRET when γ = 1 (which is an assumption made for all the E_FRET calculations in this article). Therefore, by generating a 3-μm-wide line profile of 〈PR〉 along the flow axis we can indirectly monitor the ensemble-averaged collapse amplitude as a function of distance/time. In contrast to the single-molecule E_FRET distributions shown below, the 〈PR〉 signal is a time-average of all the molecules that traverse the confocal volume during the integration period and therefore depends on the D-only and A-only signal contributions of the sample. Therefore, for each pixel in the PR image, we report the normalized proximity ratio (NPR) collapse amplitude:

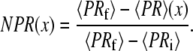(8)

This method of normalization is convenient because it enables a direct comparison of the NPR amplitude to the simulated denaturant concentration response functions. The equilibrium 〈PR〉 signal under 6 M GdCl solution conditions was used for 〈PR_i〉 and the signal expected for the collapsed and unfolded state under 0 M GdCl conditions was used for 〈PR_f〉 (see dotted lines later, in Fig. 5).

Under flow conditions compatible with smFRET, we probed the collapse amplitude directly using the mean E_FRET value of the unfolded state after the D-only and A-only contributions were eliminated using ALEX (26) together with the dual-burst search algorithm (23).

Protein expression, purification, and labeling

The CI2 construct used in these studies was the generous gift of Dr. Marcus Jäger. Its sequence composition has been previously described (51) as was the labeling approach (52) used to introduce the Alexa-488 and Alexa-647 Donor-Acceptor dye pair required for these FRET studies. The diluent used for the refolding measurements was a 20-mM phosphate buffer at pH = 6.5. All measurements were conducted at room temperature which typically varied from 23–26°C.

RESULTS

Mixer characterization

Fig. 1, A and B, show an image and a top-view schematic of the single molecule mixing device. The sample is injected into the inner capillary from the sample injection tube to the left. Fig. 1 C (schematic) and Fig. 1 D (simulation) illustrate the mixing region where after emerging from the inner capillary nozzle (ID ∼ 5–10 μm) the sample is focused by and diffusionally mixed with the diluent within the square outer capillary. The OD of the inner capillary is matched to the ID of the square outer capillary so that the two are coaxial to within ∼25 μm. The flow velocities in the mixers typically range from 1 to 5 μm/ms for single molecule detection. Thus, the dimensionless Reynolds numbers (Re = ρv_xd/η) at the center of the 300 μm ID square outer capillary range from 0.3 to 1.5 indicating laminar flow conditions (53). The dimensionless Péclet number, Pe = v_x/(D/r), is a measure of the ratio of convective to diffusive mass transport (54). For the flow streams found in this study, Pe is in the range of 1–10 for Gd⁺ ions and 2–200 for protein samples depending on the flow conditions. Thus, protein molecules traversing the diffraction-limited PSF do not reenter it and therefore do not give rise to secondary detection events. Furthermore, by confining the trajectories of the sample molecules to the center of the PSF, a significant increase in the resolution of smFRET measurements can be obtained (55,56).

There are a variety of entrance effects which can affect the response time and mixing uniformity of the device to varying degrees under different flow conditions. Inhomogeneous transverse (YZ) velocity profiles (57) and—especially for single molecule mixers—dispersion within the sample stream along the axis of flow (58) can cause different sample molecules to have different distance-to-time transfer functions and can thus affect the temporal-resolution of continuous-flow mixing devices. One creative solution to the inhomogeneous velocity profile issue is to decouple diffusional mixing from the reformation of a uniform velocity profile using a secondary sheath flow around the sample stream (50). However, in all two-dimensional mixing geometries, sample fluids still contact the top and bottom channel surfaces resulting in inhomogeneous velocity profiles along the z axis. This results in decreased focusing near the top and bottom channel walls, and necessitates further geometry optimization to obtain the best response functions (59). In contrast, the sample stream in our coaxial mixer is confined to a narrow region far from any outer capillary walls and is therefore subjected to velocity inhomogeneities and other unwanted effects only in the immediate vicinity of the inner capillary nozzle where the denaturant concentration is still high and the sample remains unfolded. These fluid velocity inhomogeneities should decay over an entry length l = 0.05ρ 〈v_in〉 d²/η ∼ 7 μm under typical single molecule flow speeds (60). Consistent with this prediction, simulations show that under typical single-molecule flow conditions the sample stream attains a uniform transverse velocity profile within ∼10 μm from the nozzle, and that this decay-length scales with 〈V_in〉 (Fig. 3).

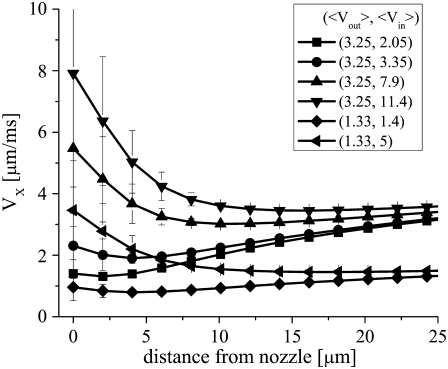
FIGURE 3.

Simulated axial fluid velocity profiles versus distance from the inner capillary nozzle aperture. The error bars are the standard deviation of the distribution of flow velocities present within 5 μm from the axis of flow at each position (i.e., a measure of the transverse inhomogeneity in the system). The simulation parameters (〈V_out〉 and 〈V_in〉 used to obtain each curve are given in the figure legend.

After a uniform transverse velocity profile has been established, there is then a further increase in the axial velocity of the sample fluid with distance from the nozzle, which depends on the amount of momentum transfer between the coflowing diluent and sample streams. This, in turn, depends on a variety of factors including the degree of hydrodynamic focusing present, the exact shape of the inner capillary, and the viscosities and densities of the sample and diluent fluids. The complex nature of the hydrodynamic focusing and momentum transfer processes within this region and their sensitivity to η (c_Gd), ρ (c_Gd), and the shape of the inner capillary nozzle makes the application of phenomenological models difficult if not tenuous (data for such attempts are not shown). Indeed, existing analytical models even fail to accurately predict the entrance length for the reestablishment of a parabolic velocity profile, in the case of two coflowing streams with identical densities and viscosities coming into contact after a well-defined two-dimensional barrier, while numerical solutions have been somewhat more successful (61). Here we rely on numerical simulations and focus on identifying the simulation parameters and equations (i.e., 〈V_in〉, 〈V_out〉, η(c_Gd), ρ (c_Gd), and to a lesser extent, nozzle shape) which yield the best manual fits to our experimental velocity and sample stream FWHM data, and which also allow the extraction of denaturant concentration profiles from such experimental data.

To obtain the required simulation parameters we first scanned an x,y image of the inner capillary nozzle, and from this, defined a model of the nozzle's physical dimensions which was then used in the simulations. The resolution of this model is as good as the resolution of the imaging system used (∼300 nm). The quantity 〈V_out〉 was then adjusted so that the simulated fluid velocity far from the nozzle visually matched the terminal fluid velocity obtained from FCCS velocimetry measurements for each flow condition (see Fig. 4 A). Next, 〈V_in〉 was adjusted so that the simulated FWHM of the sample concentration profile at ∼10 μm from the nozzle matched the imaged FWHM of each scanned fluorescence image of the flow stream (see Fig. 4 B). Fig. 4 A shows some typical experimental FCCS axial velocity profiles and their corresponding simulated profiles. The discrepancies between the experimental and simulated fluid velocities near the nozzle are most likely due to either: 1), nonuniform and transverse fluid flows which are not compatible with the assumptions of Eq. 2; or 2), the zero-flow τ_d control experiment (conducted under 0 M GdCL conditions) yields a τ_d which is too small and which may not be applicable near the nozzle where the protein sample is unfolded and surrounded by a viscous 6 M GdCl solution. Fig. 4 B shows y profiles of the sample stream fluorescence intensities at ∼10 μm from the nozzle together with their corresponding simulated sample concentration profiles. Fig. 4 C shows both x,y and y,z stage-scanned images of the various flow streams together with their corresponding simulated sample concentration profiles. A comparison between the transverse y,z images at 10 μm and 160 μm illustrates the extent of sample diffusion away from the axis of flow within the field of view of our scanner. A comparison between the experimental and simulated data sets illustrates the degree to which our simulations accurately reproduce the fluid mechanics achieved in the mixer under typical experimental conditions.

FIGURE 4.

(A) Experimental (data points) versus simulated (lines) axial fluid velocity profiles. (B) Normalized experimental transverse sample stream fluorescence intensities at x ∼10 μm (data points) versus simulated sample concentration profiles (solid lines). To parameterize the simulations, 〈V_out〉 and 〈V_in〉 were consecutively modified so the terminal fluid velocity and sample stream FWHM near the nozzle, respectively, matched the corresponding experimentally determined values. (C) Stage-scanned confocal x,y and y,z sample fluorescence flow profiles and corresponding simulated sample concentration profiles for six different flow conditions. The dimensions of the images are 40 × 165 μm for the x,y images and 40 × 40 μm for the y,z images.

Fig. 5 shows that the denaturant concentration response functions obtained from simulations parameterized using the protocol outlined above reproduce the experimentally determined NPR response functions determined for each set of flow conditions. The degree of overlap between the experimental data points and the simulated curves for the various flow conditions indicates that the denaturant diffusion coefficient expression used in and the resultant denaturant concentration profiles obtained from the simulations reproduce the experimental response functions expected for a given flow profile. The stability of the measured NPR response functions over 1 h is demonstrated by the reproducibility of the solid and open data points. For example, it is evident from Fig. 5 A that, under very divergent flow conditions, the flow is less stable than under more focused flow conditions (Fig. 5, B–D). The solid horizontal lines in each figure indicate the 80% and 90% trigger points. The marked overshoot of the response amplitudes below 0 for the slower-flowing streams is a consequence of the protein sample beginning to fold within the mixer. From Fig. 5 D we can estimate that, at a folding time of 57 ms (the time required for molecules to flow from the 90% trigger point to the endpoint at 165 μm), the denaturant-dependent collapse phase would account for 1:1.4 or ∼70% of the total signal change.

Supplementary Material, Fig. S1, illustrates the long-term stability of the more focused flow streams over the longer timescales (4–6 h) required for the acquisition of single-molecule datasets. The key to this flow stability is control of both the inner (P_in) and outer (P_out) capillary fluid pressures just before the mixing region. Processes which can thwart efforts to achieve stable flows in microfluidic devices are clogging of narrow channels (see Fig. 5 A) and applied pressure fluctuations (often from mechanically driven pressure sources) in wider channels. Here, we employ granulated silica particles to minimize clogging and short-term instabilities in P_in by simultaneously filtering the sample fluid while reducing the hydrodynamic radius of the inner capillary. In contrast, gravity-driven flow through the relatively wide and therefore inherently less clog-prone diluent stream averts any potential mechanical fluctuations in P_out which might have existed had this flow been mechanically driven.

As discussed both above and also in the literature (55,56), one major advantage of a coaxial mixing geometry for single molecule detection is that sample molecules are guided through the center of the confocal detection volume. This eliminates background fluorescence from out-of-focus sample molecules and also enables the detection of a large majority of sample molecules because each has a smaller probability of being missed by the probe volume as it flows through the device. Fig. 6 shows a series of three-dimensional laser-scanning confocal images of an effectively nondiffusing 70 kDa FITC-dextran sample being focused in one of the mixers. Under such conditions (〈V_out〉 ∼ 3.5 μm/ms and Péclet No. ∼100), sample molecules can be focused to submicron dimensions so that a large majority of the sample molecules are detected and the burst size distributions obtained are significantly narrowed compared to diffusion-based measurements (55,56). The dead times under such flow conditions can be as low as 5 ms; however, smFRET histograms generated under such conditions are dominated by photon shot noise. We therefore performed smFRET measurements under slightly slower flow conditions with dead times of ∼15–20 ms with a 9 μm ID nozzle.

FIGURE 6.

Three-dimensional rendering of laser-scanning confocal images of a 10 nM FITC-dextran (70 kDa) sample being hydrodynamically focused in one of the mixers (nozzle ID ∼9 μm). The optical axis goes into and to the right of the images. These images were passed through a nonlinear image filter (Leica Confor 2 median filter), diminishing low-intensity background signals which would otherwise obscure the sample stream. The flow conditions are given as the height difference between the entry and exit reservoirs (ΔH) and an arbitrary P_in number which has no correlation to the actual pressure applied to the inner capillary.

Single molecule mixing/protein folding

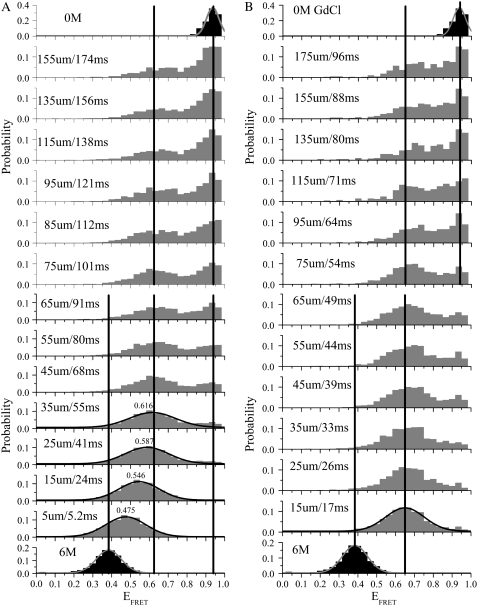
Fig. 7 shows two sets of smFRET histograms taken at different distances/times away from the inner capillary nozzle under two different flow conditions: in Fig. 7 A, (〈V_out〉, 〈V_in〉) = (0.65, 1.2); and in Fig. 7 B, (〈V_out〉, 〈V_in〉) = (1.4, 1.1); units are in [μm/ms]. The equilibrium E_FRET distributions (black) under the initial (6 M GdCl) and final (0 M GdCl) conditions were fitted with Gaussian functions (red curves) yielding means of 〈E_FRET〉 = 0.384 and 〈E_FRET〉 = 0.936, respectively. The diffusion of denaturant molecules away from the sample stream is evidenced by the gradual shift of the collapsed-unfolded state from 〈E_FRET〉 = 0.384 to 〈E_FRET〉 = 0.625 (in Fig. 7 A) or to 〈E_FRET〉 = 0.65 (in Fig. 7 B)—this discrepancy is most likely due to alignment differences between the two runs. The sample stream in Fig. 7 A is wider (i.e., more divergent) than in Fig. 7 B and thus the dead time is larger and the instrument response function is less uniform. For Fig. 7 A, the simulated t_dead values are 30 ± 3 ms and 53 ± 3 ms for the 80% and 90% trigger point contours, respectively. In agreement with these simulation results, the denaturant-dependent peak shift seen in Fig. 7 A is ∼84% complete by the third data point at 25 μm/41 ms. Under the faster and more focused flow conditions used in Fig. 7 B, the trigger-point is reached before the first data point taken at 15 μm/17 ms. However, under these conditions the greater shot noise contribution to the histograms limits the resolution of the various subpopulations present within the nonequilibrium ensemble (23). For example, the unfolded cis-proline fraction of CI2, which constitutes roughly 23% of the total Trp fluorescence folding amplitude (62,63) and which should remain unfolded at the endpoint of our mixing experiment, is better resolved from the folded state under the slower flow conditions with less shot-noise (Fig. 7 A) than under the faster flow conditions with greater shot-noise (Fig. 7 B).

FIGURE 7.

Nonequilibrium single molecule E_FRET histograms of D-A-labeled CI2 collected at different distances/times and under two different single molecule flow conditions. In panel A, the flow is slower (〈V_out〉 = 0.65 μm/ms) and less focused—the resulting dead time is longer (∼53 ms for the 90% trigger point contour) and the dynamic range extends to 174 ms. In panel B, the flow is faster (〈V_out〉 = 1.4 μm/ms) and more focused—the resulting dead time is shorter (∼19 ms) and the dynamic range is reduced to 96 ms. Each histogram has 30 bins. The vertical lines are a guide to the eye and indicate the means of 1), the initial equilibrium (solid histograms) distribution (in 6 M GdCl); 2), the nonequilibrium (shaded histograms) collapsed (〈E_FRET〉 = 0.625–0.65) state; and 3), the endpoint folded state of CI2.

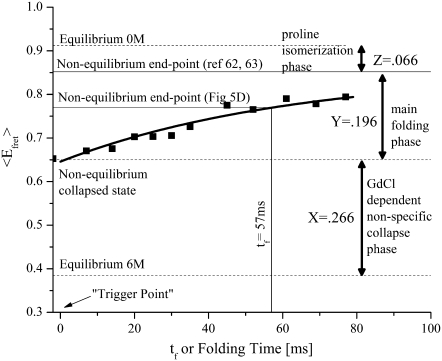
Analysis of the histograms from Fig. 7 B shows that the main folding phase exhibits two-state folding behavior on the millisecond timescale, as directly evidenced by the disappearance of the collapsed unfolded state at 〈E_FRET〉 = 0.65 and the appearance of the folded peak at 〈E_FRET〉 = 0.94. Previously published measurements on wild-type and the G26A mutant of CI2 yielded refolding half-lives of t_1/2 = 12.5 ± 1 ms and 15.4 ± 1 ms, respectively (64). Stop-flow Trp fluorescence kinetic measurements (data not shown) on the unlabeled version of the CI2 construct used in these studies (which has two additional cysteines and a K53R mutation relative to the G26A mutant) yielded a t_1/2 of 35 ± 3 ms (n = 4). Fig. 8 shows ensemble averages of the single molecule histograms shown in Fig. 7 B where the origin for the folding time axis has been defined by the simulated t_dead value for these flow conditions (∼19 ± 2 ms). Fitting this data to a single exponential decay function with an endpoint fixed by the 23% amplitude expected for the cis-proline folding phase (62,63) yields a τ_1/2 of 43 ± 4 ms for the main folding phase. This value is slightly larger than that obtained for the unlabeled protein, indicating that the rather large single-molecule FRET dyes attached to CI2 at labeling positions 1 and 40 might have a relatively small but detectable effect on the folding kinetics of this protein under native conditions.

FIGURE 8.

Ensemble averages of the single molecule histograms in Fig. 7 B are shown as a function of folding time. Single exponential fitting of the data assuming a 23% amplitude for the cis-proline fraction yields a τ_1/2 of 43 ± 4 ms.

Further analysis of the ensemble averaged single molecule data in Fig. 8 shows that, at a folding time of 57 ms, the denaturant-dependent collapse amplitude accounts for ∼0.266/(0.77–0.384) = 69% of the total signal change. This value is within experimental error of the value (70%) obtained in our ensemble mixing analysis (see Fig. 5 D) where we assumed a value for the denaturant-dependent collapse amplitude.

DISCUSSION

There are many potential sources of systematic and standard error in FCS velocimetry. First, FCS theory requires that the PSF of a given experimental system (which is sensitive to all optical components in the excitation and emission light paths) have a three-dimensional Gaussian intensity distribution (40–42,44–46); and for traditional single-spot FCCS (a single excitation volume with two detection volumes) this intensity distribution must be spatially coincident in both detection channels. This latter requirement can be difficult to satisfy for FCCS of dual-labeled FRET samples given that chromatic aberrations persist to significant degrees in most optical systems. Second, the fluid velocity measurement is systematically dependent on the value of ω_o; the accuracy and precision of this measurement is a limiting factor for many FCS-based measurements including FCS velocimetry, and has gained significant attention among FCS users in recent years (65,66). Third, at the flow rates required for single-molecule detection, the fitted value for τ_f is somewhat dependent on the value of τ_d determined and fixed by the zero-flow control experiment. And because our protein molecules fold during the mixing experiment, the value used for τ_d will change with position as the folding ensemble shifts from the unfolded state with one τ_d to the folded state with another τ_d. All these issues together highlight the need for extreme caution when attempting to use single-spot FCCS for fluid velocimetry measurements.

To address the first of these issues we decided to directly image the PSF before each experiment under optical conditions which are similar to those present in the mixer. The ideal control for this purpose would be to embed a point-source fluorescent bead with the correct excitation and emission spectra which match those of the sample molecules into a 1.333 refractive index matrix inside the 300 μm ID square capillary and scan these beads through the PSF at a depth of ∼150 μm from the capillary bottom. For this study, a specially designed polymer adhesive called MY133 was used. Although MY133 optical adhesive has the desired refractive index and is highly efficient in immobilizing beads, it must be air-cured and thus cannot be used to embed beads inside square capillaries. However, we find that for the underfilled optical conditions used in these experiments, if the coverslip thickness setting on the objective is correctly set, imaging 150 μm above either the square capillary glass surface (thickness ∼150 μm) into a 3% agarose matrix or a GOLDSEAL coverslip of thickness ∼140 μm using the MY133 polymer adhesive yields essentially identical PSFs (data not shown); therefore, for all subsequent PSF measurements, we used the MY133 bead-scanning control on GOLDSEAL coverslips to ensure that the PSF in each detection channel is Gaussian. The next immediate question asked was whether the PSFs for both detection channels overlap with each other. This second point, which is often taken for granted in FCCS measurements, derives from the fact that it is possible to have chromatic aberrations or slight optical misalignments which can give rise to artifacts in the FCCS curves due to nonoverlapping detection volumes. To address this issue, we used the multicolor bead scanning tool to generate proximity ratio images (see above) of the PSF, which can be used to align the two detection channels so that they completely overlap in all spatial directions (data not shown). This ensures that chromatic aberrations will not affect our FCCS velocimetry results. Another way to ensure overlapping detection volumes is to perform forward and backward cross-correlations between the donor and acceptor detection channels during velocimetry data acquisition. As we found for all the measurements presented above, if the two cross-correlation curves overlap sufficiently, then there is no offset along the axis of flow between the two detection volumes (data not shown). However, this control must be used with caution because acceptor photobleaching during transit of dual-labeled molecules through the PSF (38) can also induce an offset between the forward and backward cross-correlations under flowing conditions (data not shown).

To determine the beam waist size, ω_0, of the focused beam inside the square glass capillaries, a standard R6G FCCS determination of ω₀ was used. As mentioned above, the determination of an appropriate diffusion coefficient for this control is crucial to the accuracy and validity of FCCS fluid velocimetry. In this work, we extracted the diffusion coefficient of R6G in a 20 mM borate buffer. The value given in Culbertson et al. (47) was slightly larger (by ∼7%) because it was determined in 20 mM Borate with 100 mM Tris. Such a sensitivity to buffer conditions translates into systematic errors in the fluid velocity calculations and thus highlights the need to account for even slight changes in ionic strength to obtain accurate FCCS velocimetry data.

The complication of a steadily varying τ_d for the protein sample along the axis of flow (due to changes in both the radius of gyration of the protein as well as the viscosity of the surrounding solution), was addressed by comparing velocimetry data obtained using a fixed τ_d (zero-flow control under 0 M GdCl conditions) to data obtained from fits in which this variable was not fixed. The results differed slightly at slow flow velocities (<1 μm/ms) and the error bars for the variable τ_d fits were larger. However, since the simulation parameterization algorithm described in Materials and Methods uses FCCS velocimetry data primarily from positions far from the inner capillary nozzle where the proteins are mostly folded and the denaturant has already diffused away from the sample stream, the zero-flow control under 0 M GdCl conditions still provides a reasonable estimate and is suitable for the purposes of this article.

With respect to the simulations presented in this study, one variable which may be a potential source of error is the denaturant diffusion coefficient expression. There are currently no experimental measurements for the diffusion coefficient of guanidinium ions as a function of denaturant concentration. Although the theoretical expression used in this study seems to reproduce the diffusional mixing process fairly well (X. Michalet, unpublished), experimental verification for this expression would be desirable for future fluid dynamics simulations of diffusional mixing processes using guanidinium ions.

CONCLUSION

The coaxial capillary-based continuous-flow mixing device described herein has been shown to be suitable for monitoring bioconformational reactions at the single-molecule level. We have characterized the fluid flow properties within the mixing device using confocal imaging, FCCS velocimetry, and computational fluid dynamics simulations and have shown that the device can transiently populate folding intermediates under native folding conditions. Future applications of the device include the study of other diffusion-initiated chemical reactions at the single molecule level, the physical sorting of biomolecules at the single-molecule level (67,68), and the use of multispot array optics (69,70) or CCD-based imaging methods (71) to obtain multipoint time-trajectory data on nonimmobilized single-molecules under nonequilibrium solution conditions.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.