Large-scale modulation of thermodynamic protein folding barriers linked to electrostatics

Abstract

Protein folding barriers, which range from zero to the tens of RT that result in classical two-state kinetics, are primarily determined by protein size and structural topology [Plaxco KW, Simons KT, Baker D (1998) J Mol Biol 277:985–994]. Here, we investigate the thermodynamic folding barriers of two relatively large proteins of the same size and topology: bovine α-lactalbumin (BLA) and hen-egg-white lysozyme (HEWL). From the analysis of differential scanning calorimetry experiments with the variable-barrier model [Muñoz V, Sanchez-Ruiz JM (2004) Proc Natl Acad Sci USA 101:17646–17651] we obtain a high barrier for HEWL and a marginal folding barrier for BLA. These results demonstrate a remarkable tuning range of at least 30 kJ/mol (i.e., five to six orders of magnitude in population) within a unique protein scaffold. Experimental and theoretical analyses on these proteins indicate that the surprisingly small thermodynamic folding barrier of BLA arises from the stabilization of partially unfolded conformations by electrostatic interactions. Interestingly, there is clear reciprocity between the barrier height and the biological function of the two proteins, suggesting that the marginal barrier of BLA is a product of natural selection. Electrostatic surface interactions thus emerge as a mechanism for the modulation of folding barriers in response to special functional requirements within a given structural fold.

Conventionally, the folding and function of single-domain proteins are described as two-state processes in analogy to elementary chemical reactions. The protein molecule is assumed to reside in either of two states: folded or active and unfolded or inactive, which interconvert by crossing a high free-energy barrier with transition-state-like kinetics. However, proteins can in principle exist in many different conformations or microstates because of their thousands of degrees of freedom. Such inherent complexity is best described by using low-dimensional free-energy surfaces, which are obtained by projecting the solvent-averaged energy as a function of atomic coordinates onto a few order parameters [the energy landscape approach (1)]. A free-energy surface description includes the two-state folding model as a particular scenario, but is more general. In this approach barriers, basins of attraction, and even finer topographical details of the surface (i.e., roughness) emerge from detailed balancing between conformational entropy and the energy from stabilizing interactions (see refs. 2 and 3 for some specific examples). Therefore, surfaces that exhibit marginal barriers or are even completely barrierless appear as interesting alternatives to the two-state folding picture (1). These predictions have been confirmed experimentally in recent years (4–6).

If the folding barriers are comparable to the thermal energy (RT), ensembles of conformations with an intermediate degree of structure become significantly populated and interconvert with diffusive dynamics. This realization opens a realm of possibilities for the experimental study of protein folding reactions and mechanisms (recently reviewed in ref. 7). Moreover, it also has important implications for protein function because the conformational fluctuations associated with marginal folding barriers could be exploited to modulate activity and/or synchronize the action of enzymes in sequential reactions (8). Examples of how this could be achieved have been recently explored for protein binding with the fly-cast model (9, 10) and related analyses (11), as well as for the optimization of allosteric coupling (12).

Another important consequence of shallow free-energy surfaces is that their shape can be resolved in equilibrium experiments sensitive to the energy fluctuations associated with protein conformation, such as differential scanning calorimetry (DSC). Building on this idea, Muñoz and Sanchez-Ruiz have recently developed a phenomenological variable-barrier model for the analysis of DSC data (13). In this analysis, the DSC thermogram is fitted to an idealized (i.e., a Landau quartic polynomial) one-dimensional free-energy surface from which it is possible to estimate the barrier height and the population of conformational ensembles with an intermediate degree of structure (13). Although these folding barriers are intrinsically “thermodynamic,” an excellent correlation has been recently reported between such thermodynamic barriers and the rates of folding for a number of small, single-domain proteins (14).

Here, we are interested in the factors that modulate thermodynamic folding barriers in a general sense and their relationship with protein function. We now know that folding barriers increase with protein size, and that proteins <55 residues are likely to have marginal folding barriers (15). The role of protein structure (or topology) on the determination of folding rates, and thus folding barriers, was originally established by the observation of good correlations between folding rates and empirical structural parameters [i.e., the relative contact order (16)], and then further corroborated by the application of simple statistical mechanical models to the prediction of folding rates (17). However, these factors do not permit the fine modulation of folding barriers that could play a significant role in protein function. Recent work shows that surface electrostatic interactions are important for protein stability to the extent that it can be enhanced significantly by engineering the charge distribution of proteins (18–24). Such a role in protein stabilization, together with the realization that proteins sharing the same structure exhibit very different charge distributions (20, 25), makes electrostatic interactions good candidates for the tuning of folding/unfolding free-energy barriers. Indeed, recent experimental work shows that a few suitably chosen charge-reversal mutations can change the unfolding time by orders of magnitude (22).

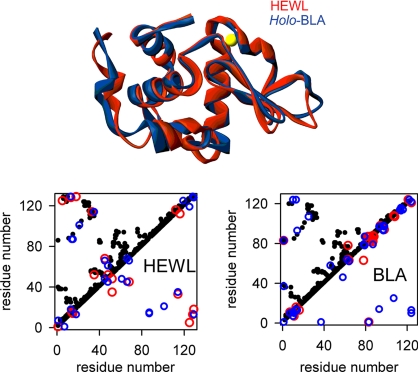
To investigate the effect of electrostatics on thermodynamic folding barriers we use two genetic and structural homologues: the calcium-binding, soluble milk protein α-lactalbumin (BLA, bovine αLa) and hen egg-white lysozyme (HEWL). The two proteins have almost identical size and the same overall tertiary structure (Fig. 1Upper). In principle, BLA and HEWL could be expected to have similar folding free-energy surfaces and thus thermodynamic folding barriers. Their structural contact maps (Fig. 1 Lower, black dots) also highlight a common folding topology. However, mapping the electrostatic interactions between surface residues onto these contact plots reveals very different patterns (Fig. 1 Lower, blue and red dots). Moreover, the folding/unfolding thermodynamic properties of these two proteins, which are both paradigms for traditional protein folding studies (26–28), are distinct. The equilibrium unfolding process of HEWL is effectively approximated to a two-state transition under most conditions (29), whereas the thermal denaturation of BLA has been shown to deviate from two-state (see figures 9 and 10 in ref. 30). Moreover, BLA readily forms molten globule (MG) states under mild denaturing conditions (27).

Fig. 1.

Superposition of the backbone structures of HEWL and holo-BLA (calcium is shown in yellow) (Upper) and residue contact maps (Lower). In the contact maps, each dot represents a pair of β-carbons within 6 Å of each other. Red/blue circles represent destabilizing/stabilizing charge–charge interactions above/below ±1 kJ/mol. These interaction energies were calculated as described in SI Materials and Methods, Electrostatic Calculations).

From the analysis of the DSC thermograms for both proteins we obtain in this work a high thermodynamic barrier for HEWL and a marginal barrier for BLA. We also show a connection between the height of the thermodynamic folding barrier and the electrostatic interactions in HEWL and BLA, which is clearly reflected in the pK values (determined by NMR) for these proteins. Furthermore, calculations based on a simple Ising-like model provide evidence that the charge distribution in BLA seems to be specifically designed to lower the thermodynamic folding barrier of this protein. We finally analyze and discuss in some detail the possible relation between barrier height and biological function.

Thermodynamic Folding Barriers of HEWL and BLA

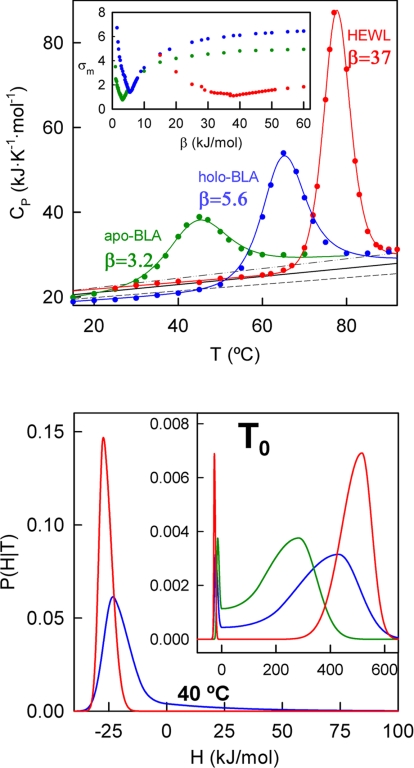
To estimate the thermodynamic folding-unfolding barrier for HEWL and BLA we have performed DSC experiments under solvent conditions that are typical for the in vitro studies with these proteins (30, 31). The thermograms expressed in absolute heat capacity units (Fig. 2Upper) are then analyzed with the phenomenological variable-barrier model (13). This model uses a free-energy functional consisting of a quadratic expression for the dependence of the free energy with the order parameter (i.e., the unfolding enthalpy). The functional describes the one-dimensional free-energy surface corresponding to a given characteristic temperature (T₀) with three parameters: (i) the barrier height, β. For values of β significantly higher than the thermal energy (RT ≈2.5 kJ/mol), the functional shows two minima and predicts two well defined macrostates. Values of β smaller than the thermal energy correspond to the one-state or global downhill scenario (32). (ii) Σα, which corresponds to the difference in enthalpy between the two minima that are observed in the surface when β > 0. (iii) The asymmetry factor, f, which, provided that β is sufficiently large, determines the relative magnitude of the enthalpy fluctuations within the two free-energy wells.

Fig. 2.

Varable-barrier analysis of HEWL and BLA thermal denaturation. (Upper) Experimental DSC profiles for apo-BLA, holo-BLA, and HEWL. The lines are best fits to the variable-barrier model. The barrier heights (β) derived from these best fits are shown alongside the lines in kilojoules per mole. (Inset) Plot of maximum deviation of the fit vs. β. The black lines are theoretical predictions for the native-state heat capacities and the standard uncertainties associated with these predictions (dashed lines). (Lower) Probability distributions of enthalpy microstates derived from the fits (color code is maintained). The probability distributions correspond to their characteristic temperatures and to holo-BLA and HEWL at 40°C.

It is apparent in Fig. 2 that the experimental heat capacity values at low temperatures are close to Freire′s prediction (33) for the heat capacity of the native state. This agreement indicates (13) that an asymmetry factor of f = 0.1 should be appropriate for the analysis. By using the predicted native baseline and fixing f = 0.1 the nonlinear least-squares fitting of the DSC thermogram involves only three fitting parameters (T₀, Σα, and β). Such a small number of fitting parameters may preclude the achievement of “visually perfect” fits, but should lead to a very robust estimate of the thermodynamic barrier height (the main purpose of this exercise).

For HEWL (50 mM acetate buffer, pH 4.5), good fits of the variable-barrier model to the DSC data could only be obtained with values for the barrier height (β) of ≈35 kJ/mol or higher (Fig. 2 Upper). This high barrier implies a well defined two-state-like thermodynamic behavior, as can be clearly observed in the probability density profile (Fig. 2 Lower). However, for the calcium-bound holo-BLA (1 mM CaCl₂, 10 mM phosphate, 5 mM citric acid buffer, pH 5.6) the best fit is obtained with a β value of only 5.6 kJ/mol (Fig. 2 Upper) and higher barriers significantly worsen the quality of the fit (see Fig. 2 Upper Inset). A barrier of 5.6 kJ/mol is apparent in the one-dimensional free-energy surface, but it is comparable to the thermal energy (i.e., ≈2 RT₀) and produces a bimodal probability density in which the two lobes merge in the middle (see plots of probability vs. enthalpy in Fig. 2 Lower). That is, the barrier is small enough to result in a significant population of microstates with an intermediate degree of unfolding under native conditions (i.e., at comparatively low temperatures: 30–50°C; see Fig. 2 Lower) as well as under conditions that favor the unfolded state (see Fig. 2 Lower Inset). We also carried out the same experiments and analysis in the apo form under identical solvent conditions (but replacing CaCl₂ by 1 mM EDTA). This profile shows a lower T_m value (45°C compared with a T_m of 66°C for holo-BLA), and yields a β-value slightly lower than the holo form: 3.2 kJ/mol (≈1.5 RT₀; see Fig. 2).

pK values and Conformational Flexibility

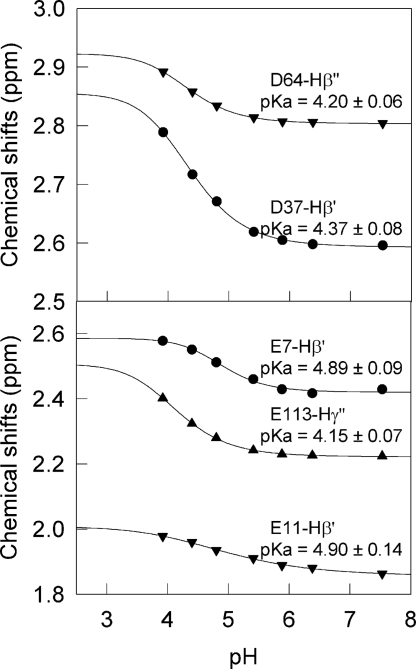
Ionizable groups are extremely sensitive to the electric field in their local environment and pK deviations from typical model compound values reflect the magnitude and sign of the net electrostatic interactions around the titrated group (34). In principle, it should be possible to predict such pK shifts by using the x-ray structure of the protein and an appropriate method to calculate electrostatics (35, 36). However, in conformational ensembles exhibiting large structural fluctuations the electric field would be averaged out and the pK values closer to those observed in unfolded polypeptides. By the same token, electrostatic interactions that preferentially stabilize the ensemble of partially unfolded conformations should result in pK values that move away from the ones expected from the native structure and toward those of model compounds. Hilser and coworkers have shown that local conformational fluctuations are directly connected to the proton binding behavior of native proteins (37). Therefore, a connection between the drastically different thermodynamic folding barriers of HEWL and BLA (see preceding section) and electrostatic interactions should be reflected on the pK values of their ionizable groups. The pK values of carboxylic acid groups in HEWL are already available from the literature (38). To determine the pK values of the carboxylic groups of holo-BLA we have performed a pH titration monitoring the independent ionizable groups by NMR (see Methods). We performed the titration at 40°C over the pH range 3.5–7.5. At pH ≤ 3.5 the spectra lose the wide chemical-shift dispersion characteristic of folded structures, possibly signaling the onset of acid-induced denaturation (see figure 1 in ref. 30). During the experiment we could observe pH-induced changes in the chemical shift of aliphatic protons in response to the titration of their neighboring acidic functional group. Despite the larger inherent uncertainty of the determination of pK values with such limited pH range, residues E7, E11, E25, H32, D37, D46, E49, D63, D64, D83, D84, D87, E113, D116, and the C-terminal carboxyl group of L123 produced semicomplete titration curves in at least one aliphatic proton. The fits of these data to sigmoidal titration curves are of reasonable quality (see representative examples in Fig. 3). The estimated pK values are also shown in Fig. 3.

Fig. 3.

Protonation states for some representative aliphatic protons in aspartate (Upper) and glutamate (Lower) residues of holo-BLA residues as monitored by NMR. Each symbol represents the chemical shift of a resolved residue cross-peak at a given pH. The lines show the best fits to a titration curve.

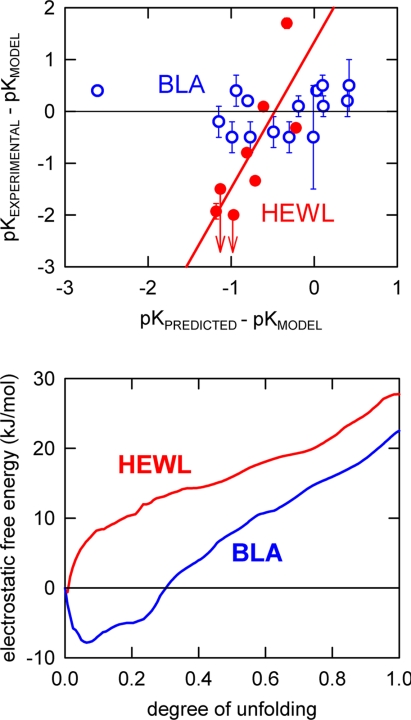
In Fig. 4Upper we plot the experimental pK values for HEWL and holo-BLA versus the pK values predicted from a simple Tanford–Kirkwood (TK) calculation. Both experimental and predicted pK values are plotted as deviations from the characteristic values of the relevant model compound: aspartate or glutamate. Although admittedly oversimplistic, the TK calculation reproduces the main energetic features of the surface charge distribution in proteins and is successful in predicting stabilizing charge-deletion and charge-reversal mutations (20, 39, 40). Furthermore, it has been shown specifically for BLA that the charge–charge interaction energies calculated with the TK method and the finite-difference–Poisson–Boltzmann model are in close agreement (40).

Fig. 4.

Electrostatics and thermodynamic folding barriers. (Upper) Plot of experimental pK values versus TK-predicted pK values for carboxylic acid groups in HEWL and holo-BLA. The values (both experimental and predicted) are referenced to characteristic pK values of 4 for Asp and 4.5 for Glu. Other model pK values (61) produce a similar plot. The points labeled with arrows correspond to pK values reported as ≤2 and ≤2.5. (Lower) Profiles of the calculated TK electrostatic free energy versus degree of unfolding.

The experimental carboxylic pK values for HEWL depart significantly from model-compound values indicating the presence of strong local electrostatic fields, and, furthermore, there is a good correlation (r = 0.91) between the experimental pK values and those calculated with the TK method (Fig. 4 Upper). This suggests that the observed deviations arise from specific electrostatic interactions occurring in the native structure. The slope of the correlation, however, is much larger than one, indicating that the TK calculation reproduces the relative effects, but it underestimates the overall magnitude of the electrostatic interactions.

The experimental pK values for carboxylic acid residues in holo-BLA show a completely different pattern. In this case the experimental pK values are all very similar to the model compounds values (points clustering around the zero line in Fig. 4 Upper), thus indicating a weak electrostatic field around the carboxylic groups. Interestingly, the TK calculation predicts large shifts in the pK values of holo-BLA. In fact these predicted shifts are similar in magnitude to the predicted shifts for HEWL (see Fig. 4 Upper). Accordingly, the correlation between experimental and predicted values produces an almost horizontal line demonstrating that the net electrostatic interactions in holo-BLA are similar to those of unstructured polypeptides and much weaker than expected from the native three-dimensional structure. These results are consistent with the thermodynamic folding free-energy barriers for BLA and HEWL. For BLA the conformational excursions characteristic of marginal folding barriers would involve the ionizable residues in the protein resulting in an averaged-out electrostatic field and small shifts in pK values. In contrast, the large thermodynamic folding barrier of HEWL almost eliminates the sampling of partially folded conformations so that the net electrostatic field in solution is similar to the one calculated from the unique three-dimensional structure.

Calculations of Electrostatic Contributions in Folding Ensembles

In the two previous sections we have shown a connection between the folding barrier height and the net strength of the electrostatic interactions for HEWL and BLA. However, an important question is whether the electrostatic effect is what modulates the folding barrier. Electrostatic interactions are in fact one of the most distinctive features between these two proteins of almost identical size and structure, and with 38% sequence identity. Many of the differences in sequence involve ionizable residues, resulting in a much larger number of charges for BLA (42 vs. 32 for HEWL). Differences in charge distribution between the two proteins become readily apparent by plotting the electrostatic interactions calculated with the TK method on the structural contact map (see Fig. 1 Lower).

To investigate the effect of the charge distribution of each protein on its folding free-energy surface we used a simple Ising-like statistical mechanical model to generate all possible partially folded conformations that have one or two stretches of native conformation, such as …uuuuNNNNNuuuuu… or …uuuNNuuuNNNuuu… [the double-sequence approximation (41)]. In this case such calculation results in ≈10⁷ conformations per protein. We then calculate the electrostatic free energy for each conformation by adding the pairwise TK interaction energies for all pairs of charges that are found in native stretches on the given conformation. Fig. 4 Lower shows the results of this calculation projected onto a single order parameter: the number of residues in unfolded conformation, which is shown here normalized to the total number of protein residues. For HEWL the resulting one-dimensional electrostatic free-energy profile shows a minimum corresponding to the fully native structure (zero degree of unfolding). However, for BLA the profile has a double-dip minimum that is located in partially unfolded positions (0.1 and 0.2). Therefore, whereas the electrostatic interactions in HEWL primarily stabilize the fully native structure, those of BLA stabilize partially unfolded conformations. A similar (albeit at a lower scale) phenomenon has been previously identified as the source for different folding transition states in the structurally homologous proteins L and G (42).

In other words, BLA charge distribution seems to be specifically designed to lower the thermodynamic folding barrier of this protein from the high value expected from its size and topology down to the limit of marginal folding barriers. Although this calculation is undoubtedly oversimplified, the qualitative result should be robust. In fact, the calculation should be regarded as a lower limit of the true electrostatic effect: the results shown in Fig. 4 Lower use TK electrostatic energies scaled by a factor of 2, whereas the comparison between experimental and predicted pK values in HEWL suggests a larger underestimation for this method (i.e., a factor of 2.8; see Fig. 4 Upper).

Implications of a Marginal Folding Barrier in BLA

Folding over a marginal folding free-energy barrier readily explains the peculiar conformational features of BLA in solution.

Griko, Freire, and Privalov pointed out 13 years ago that the extent of residual structure in the denatured state of BLA is “exceptionally high” (30). This conclusion has since then been supported by additional evidence obtained in bovine and other forms of BLA (27, 43–46). Interestingly, a recent theoretical analysis of the observable properties of folding over marginal barriers indicates that the height of the barrier and the position of the unfolded minimum in the folding free-energy surface are directly connected (47). In particular, when the folding barriers become comparable to the thermal energy the unfolded minimum is expected to move closer to the native state increasing its degree of residual structure. In light of this theoretical result, the highly structured denatured state of BLA is simply a manifestation of the marginal thermodynamic folding barrier of BLA that we estimate from DSC experiments.

Recent NMR studies indicate that BLA has a flexible structure in solution even in its calcium-bound holo form (43). This protein has been shown to bind the surfactant SDS at micromolar concentrations, a result that can hardly be explained without invoking significant structural flexibility (43). Moreover, a certain degree of conformational flexibility seems to be required for BLA function as a substrate specifier for galactosyltransferase (48–50). Obviously, conformational flexibility and dynamics in native conditions can be directly explained with the presence of a marginal folding barrier for BLA.

Under the solvent conditions used in our DSC experiments (pH 5.6, high salt), both holo and apo forms of BLA fold into a defined three-dimensional structure. However, the less stable apo-BLA forms a MG by decreasing the salt concentration, not only in acidic, but also in neutral conditions (27, 29). MG states are compact and have secondary structure content, but lack a defined three-dimensional structure. The intrinsically disorganized MG state further unfolds in a continuous fashion, which implies the absence of a significant free-energy barrier. In fact, MG states could be analogous to partially unfolded globally downhill, or one-state, folding proteins, as it has been recently shown for the small protein BBL near its denaturation midpoint (6). The partial destabilization of proteins with marginal thermodynamic folding barriers could trim the already minimal barrier, resulting in a free-energy surface with a single minimum located halfway along the reaction coordinate (e.g., MG-like). The barrier of a few kilojoules per mole and the low stability of apo-BLA are consistent with this possibility, whereas the stability boost provided by calcium binding could be sufficient to block the onset of MG-like states in holo-BLA. Furthermore, the formation of the MG state in apo-BLA on lowering the ionic strength reinforces the role played by electrostatics on the modulation of the folding barrier. It would be quite interesting to determine whether the same principles apply to other MG-forming proteins.

Conclusions

We have shown here that two structurally homologous proteins can have drastically different thermodynamic folding barriers, ranging from the marginal barrier of BLA to the high barrier resulting in two-state-like thermodynamics of HEWL. This is a remarkable result, showing a tunability range for these systems of >30 kJ/mol, equivalent to five to six orders of magnitude in population, which seems to occur by the engineering of electrostatic interactions on the protein surface. Such a tunability range of a single-protein scaffold is only slightly narrower than the whole range of experimentally available protein folding rates (14). Our results highlight that whereas size and topology are primary factors in determining folding barriers, there is room for large barrier modulation by specific protein energetics, like electrostatic interactions. Such interplay between various energetic factors in determining folding barriers has also been focus of recent theoretical studies (51). In any event, we should emphasize that our results with HEWL and BLA correspond to populations of partly folded structural ensembles and thus are strictly thermodynamic. Although there seems to be a direct relationship between thermodynamic barriers and folding rates in small single-domain proteins (15), this should not be a universal property. Such agreement implies topographically simple, smooth-folding free-energy surfaces. More complex proteins with structural subdomains and disulfide bonds should have corrugated landscapes with several folding paths and possibly kinetic traps (2, 3). Under such a scenario, which is the one that applies to both HEWL (52) and BLA (53), folding kinetics is dominated by escape from local traps rather than by the underlying thermodynamics (1).

One interesting implication of this work is the possibility of tuning folding barriers in vitro by the engineering of electrostatic interactions. In recent years, computational procedures to design surface charge distributions toward enhancement of protein stability have been developed and tested (18–24). Our results in HEWL and BLA suggest that these same methods might be extensible to the engineering of folding barriers.

Finally, an important question that emerges from this work is: why are the thermodynamic folding barriers for these homologous proteins so different? A possibility is that these drastically different conformational behaviors have been naturally selected in response to specific biological requirements. Indeed, a look at the biological function for the two proteins supports this idea. HEWL is a bactericide that needs to work in extremely harsh extracellular conditions. A high thermodynamic folding barrier will greatly increase the half-life of HEWL in its active form (54), thus producing a more efficient bactericide. In addition to being a secreted milk protein, BLA has an intracellular function as substrate-specifier for galactosyltransferase, and it also binds reversibly to membranes by adopting a MG-like conformation (43, 55). Binding of BLA increases membrane permeability (56), an effect that might be related to the apoptotic activity toward cancer cells exhibited by the HAMLET variant of human α-lactalbumin (57). The electrostatically modulated marginal thermodynamic barrier of BLA provides an explanation to its readiness to partially unfold into a MG-like state on interfacial contact with the negatively charged membrane surface. Furthermore, it explains the structural changes observed in membrane-bound BLA in response to differences in the overall charge, lipid mix, and/or fluidity of the host membrane (46, 56, 58). From the apparent reciprocity between biological function and special folding properties we conclude that BLA is an example of a marginal folding barrier selected by natural evolution.

Methods

See supporting information (SI) Materials and Methods for a detailed description.

DSC experiments, calculation of absolute heat capacities, and variable-barrier analyses were carried out as described (13, 59, 60). Electrostatic calculations based on the Tanford–Kirkwood model were carried out as we have previously described in detail (19, 39). Chemical shift versus pH profiles for carboxylic acid residues in holo-BLA were determined from the analysis of TOCSY spectra.