3D visualization software to analyze topological outcomes of topoisomerase reactions

Abstract

The action of various DNA topoisomerases frequently results in characteristic changes in DNA topology. Important information for understanding mechanistic details of action of these topoisomerases can be provided by investigating the knot types resulting from topoisomerase action on circular DNA forming a particular knot type. Depending on the topological bias of a given topoisomerase reaction, one observes different subsets of knotted products. To establish the character of topological bias, one needs to be aware of all possible topological outcomes of intersegmental passages occurring within a given knot type. However, it is not trivial to systematically enumerate topological outcomes of strand passage from a given knot type. We present here a 3D visualization software (TopoICE-X in KnotPlot) that incorporates topological analysis methods in order to visualize, for example, knots that can be obtained from a given knot by one intersegmental passage. The software has several other options for the topological analysis of mechanisms of action of various topoisomerases.

INTRODUCTION

DNA knotting is common in living cells and is easily observed in such systems like bacterial plasmids (1), replication bubbles of bacterial chromosomes (2) or tightly packed DNA in phage capsids (3). DNA topoisomerases enable passages of DNA segments through each other and hence can knot and unknot circular DNA (4–6). Topoisomerases are responsible for unknotting, unlinking and maintaining the proper supercoiling of DNA during processes such as replication, transcription and recombination (7,8). There are many specialized topoisomerases that cut and reseal one or two strands of DNA (type I and II, respectively). When the transient cut is made in one segment of DNA by a topoisomerase, the enzyme transfers another segment of the same or other DNA molecule through the cut. In the case of type II topoisomerases, double-stranded DNA passes through the transient double-stranded break. After the transfer the transient break is resealed. Passages between double-stranded segments from the same circular DNA molecule can lead to knotting or unknotting. Passages between segments from different circular DNA molecules can lead to catenation or decatenation. Type I DNA topoisomerases can also create double-stranded DNA knots when acting on nicked circular DNA. When acting on single-stranded circular DNA, type I topoisomerases can form single-stranded DNA knots and catenanes. Topoisomerase-mediated knotting and catenation reactions have been studied both in vivo and in vitro (2,9–12).

In vitro experiments have shown that some type II topoisomerases can keep the steady-state level of DNA knotting lower than the thermodynamic equilibrium expected for a system where intersegmental passages within long circular DNA molecules occur at random (13). A great effort has been devoted to elucidate the mechanism by which some DNA topoisomerases belonging to type II (Topo II) are able to maintain a low level of DNA knotting in vitro (14–19). Separate studies revealed that some Topo IIs show a relaxation preference for crossings of a certain chirality as this protects unknotted negatively supercoiled DNA from being a substrate of energy consuming Topo II action (8,20).

To understand mechanistic details of topoisomerase action and of observed topological biases, it is necessary to characterize the preferred reaction pathways by which a given knot type is converted into the unknot. It is not only important to determine which pathways are used but also which are not used. Since topological analysis may be complex, we present here the TopoICE-X software that offers a user friendly interface to help in studies aimed at understanding and modeling the mechanism of action of different topoisomerases. TopoICE-X is part of the software package KnotPlot for visualizing and manipulating knots in three dimensions.

Knot notation

The crossing number of a knot is the smallest number of crossings needed to draw the knot. Tables of knots up to 10 crossings are in most knot theory books (21,22) and are also available on the web (for example, the Knot Atlas, katlas.math.toronto.edu/wiki/and KnotInfo, www.indiana.edu/~knotinfo/).

Knots are frequently referred to by their placement in these tables. For example, 5.1 refers to the first five crossing knot in the Rolfsen table (21), while 5.2 corresponds to the second five crossing knot in this table. For chiral knots, this table only lists one of the enantioforms out of the left- and right-handed versions of a given knot. Some knots belong to the class of knots called rational. Knots that belong to this class can be represented using rational numbers. The notation N(a/b) refers to the rational knot corresponding to the fraction a/b. This notation is not unique. For example, N(5/2), N(5/3), N(5/7) all refer to the same rational knot, 4.1. For more information on rational knots, please see ref. (23–26). Note, however, that knowledge of rational knots is not needed for using the presented program since the user can refer to pictures of knots instead of notation. TopoICE-X implements the mathematical approach described in ref. (27,28). A related program, TopoICE-R, models recombinase action (29).

RESULTS

TopoICE-X (Topological Interactive Construction Engine-Crossing change) is a 3D visualization and manipulation program within KnotPlot (30) that can be used to test various models of topoisomerase action on knots belonging to the rational family of knots. All prime knots with less than eight crossings are rational. Hence, this family of knots includes the majority of knots observed in biological experiments. KnotPlot can be freely downloaded from http://knotplot.com/download. TopoICE-X can be used to:

1. Determine if it is possible to convert one rational knot into another rational knot via one crossing change and visualize possible conversions.

2. Generate a graph showing all shortest reaction pathways between a given pair of rational knots when restricted to rational knots up through 13 crossings.

3. Generate a list of all rational knots up through 13 crossings that can be obtained from a given rational knot via one crossing change.

One intersegmental passage connectivity between two different knots

To understand the distribution of knots in a given topoisomerase knotting experiment, it is important to know which of these knots can arise as a result of a single catalytic event and which may require several catalytic events for their formation. Examples 1 and 2 illustrate how TopoICE-X is used to determine if it is possible to convert a given knot type into another one by a single crossing change. Other examples can be found in the TopoICE-X manual that is provided as Supplementary data.

In ref. (2), the knots 6.2 and 3.1 were observed to form in replication intermediates. It was proposed that 6.2 knots could be formed by one passage from 3.1 knots. We can check whether this proposal is correct and how this passage could occur. We will address this point in Example 1. In ref. (31), formation of 5.1 knots from unknots was observed to be stimulated by the presence of condensin and MucB proteins. It was proposed that this happens in two steps, where first a trefoil knot is formed and this is converted in the second passage to a 5.1 knot. This will be checked in Example 2.

Example 1: Is it possible to convert 3.1 = into 6.2 = via a single crossing change?

The user can enter these knots into TopoICE-X by either clicking on an image of the knot or entering its notation (see TopoICE-X manual for more instructions). If the user clicks on ‘Find solutions’, solution #1 of 1 appears in the KnotPlot window (Figure 1A). In this case, only one solution is found. See the TopoICE-X manual for examples where more there is more than one solution.

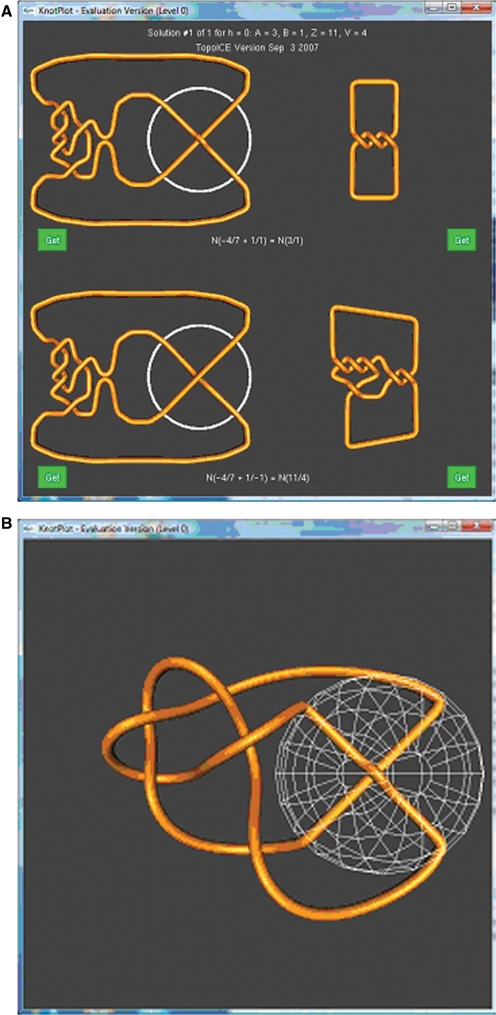
Figure 1.

(A) The substrate (top) and product (bottom) knots are each shown in two different configurations. The configurations on the right are standard minimal crossing representations of the substrate knot (top right) and product knot (bottom right). The representations on the left are shown in such a way such that the one crossing on which topoisomerase acts has been separated from the other crossings. A circle has been drawn around this crossing. The topoisomerase action is modeled by changing the overcrossing segment to an undercrossing segment (and vice versa), via intersegmental passage. (B) The top left knot after the DNA conformation not bound by topoisomerase has been simplified. White mesh sphere represents the topoisomerase.

The notation and mathematics of rational tangles is used to draw these diagrams (28). For this reason, the resulting diagrams can be complex. To obtain simpler 3D configurations, click on one of the green ‘Get’ buttons closest to the knot diagram for simplification. For example, clicking on the upper left ‘Get’ button will select just the upper left diagram in the above KnotPlot window. This will also take one to the TopoICE dynamics control panel, where portions of the knot can be relaxed to obtain better 3D diagrams. One can choose to relax the configuration outside the sphere that encloses the region of topoisomerase-mediated intersegmental passage (while keeping the segments within the sphere fixed), or the configuration inside the sphere (while keeping the segments outside the sphere fixed), or the entire knot. Relaxing the outside results in the configuration shown in Figure 1B.

Example 2: Is it possible to convert the unknot 0.1 = N(1/1) = into the knot 5.1 = N(5/1) = ?

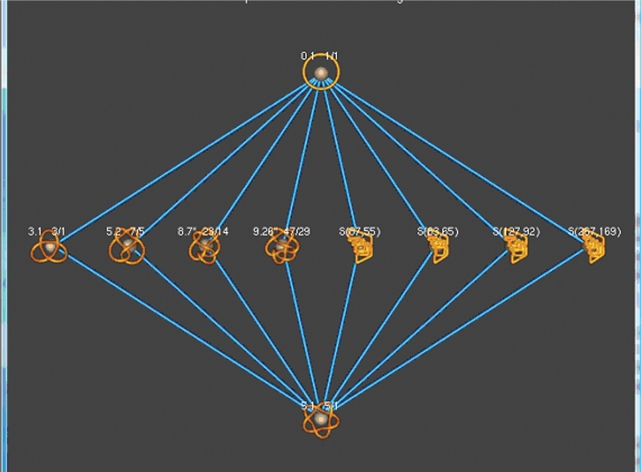
In this case, when the user inputs these knots into TopoICE-X, the words ‘It is not possible to convert N(1/1) into N(5/1) via a single crossing change’ appears in the KnotPlot window. Hence, the knot N(5/1) cannot result from a single topoisomerase action starting from N(1/1). To see shortest reaction pathways between this pair of knots, click on ‘find path between N(1/1) and N(5/1)’. This will create a graph showing all possible shortest pathways between the rational knot 5.1 and unknot, where an intersegmental passage results in a rational knot with less than 14 crossings (Figure 2). Clicking on an edge connecting a pair of knots will show the conversion (similar to Figure 1A). From this graph, we can see that two intersegmental passages are needed to transform the unknot into the knot 5.1.

Figure 2.

All possible topoisomerase-mediated reaction pathways from the unknot to 5.1 involving rational knots with less than 14 crossings.

Note, that since only two intersegmental passages are required to convert the unknot to the knot 5.1, we are mathematically guaranteed that there are no shorter pathways even if a pathway involves nonrational knots. Suppose, however, that TopoICE-X determines that three or more intersegmental passages are required to convert one knot into another knot when the pathway involves only rational knots. In this case, a shorter pathway could be possible if we did not restrict our pathways to rational knots. See the TopoICE-X manual for more details.

A knot and its neighbors

When the size of knotted DNA molecules is small, a topoisomerase will usually decrease their complexity. However, when the DNA circle is long, the probability of knot formation increases (32), and the action of a topoisomerase on a given knot type may result in the formation of many different knots including more complex ones than the starting one. For example, topoisomerase I acting on unknotted nicked circular DNA of 5.4 kb was capable of forming multiple kinds of knots including complex ones (9). If the conditions of the reaction with a topoisomerase are set in such a way that only one round of the reaction is permitted (33–35), one may observe the formation of many knots that can be obtained by just one intersegmental passage from a given starting knot. Knots that can be interconverted into each other by one intersegmental passage are neighbors in the knot space (27,36,37). By seeing which neighbors are formed preferentially and which are absent, one would gain important information for modeling the mechanism of action of a given topoisomerase. To establish preference or absence of certain neighbors, it is important to know what the expected neighbors are when intersegmental passage happens without any topological bias. Example 3 shows how to apply TopoICE-X to find all possible rational knots with crossing number lower than 14 that are neighbors of a knot of interest (knot 5.2 in this case).

Example 3: Find all possible rational knots with less than 14 crossings that can be obtained from the knot 5.2 = N(7/5) = via one round of topoisomerase action.

To find knots that can be obtained from knot 5.2 via one round of topoisomerase action, the user can enter this knot and then click on ‘Find Now’. This will find all rational knots up through 13 crossings that can be obtained from the rational knot N(A/B) = N(7/5) = 5.2 by one intersegmental passage. They will be displayed by crossing number with the smallest crossing number knots listed first (Figure 3).

Figure 3.

A portion of the table showing rational knots with less than 14 crossings that may be obtained from the knot 5.2 via one round of topoisomerase action.

From this table, we can see that the first three simplest knots that can result from the knot 5.2 by one topoisomerase crossing change are the knots 0.1, 3.1, 5.1. The user can click on any knot to see the conversion. For example, the conversion between knots 5.2 and 5.1 is shown in Figure 4. Determining this conversion without the aid of TopoICE-X would be difficult.

Figure 4.

Converting the knot 5.2 to 5.1 via one crossing change.

When human topoisomerase IIα acts on the knot 5.2, one observes a significant amount of unknots accompanied by five crossing knots but not 3.1 knots (38). The five crossing knots are most likely unreacted 5.2 knots, but one cannot mathematically rule out 5.1 knots. The absence of 3.1 knots implies that topoisomerase has a strong topological bias that results in a preferred pathway of knot relaxation. Models have been proposed to explain this bias by investigating the topology of the conversion from 5.2 to the unknot (19).

CONCLUSIONS

The types of knots created by topoisomerase have given insight in a number of situations. In addition to using knotting reactions to study topoisomerases, knotting by topoisomerases has been used by a variety of laboratories to analyze various protein–DNA complexes (31,39–43). Topoisomerase when acting on protein-bound DNA will produce a different spectrum of knots than when it acts on naked DNA. The conformation of the protein-bound DNA will affect the types of knots produced. This technique, called difference topology, has been used in some cases to show a protein-bound DNA conformation is chiral. Potential protein-bound DNA conformations have also been proposed based on the types of knotted products. Knots created via topoisomerase action have also been used to study biological processes such as DNA replication (2,44). In addition, knotting reactions have been applied to RNA. Escherichia coli DNA topo III, a type I topoisomerase, has been shown to knot synthetically created circular ssRNA (45).

Analysis of such experiments will be greatly simplified by the use of TopoICE-X. As discussed in Example 1, given a pair of rational knots, one can first determine if a conversion between these knots via one intersegmental strand passage is mathematically possible. If it is possible, one can analyze the topological conformations to determine if the conversion is biologically likely and if so, to determine topological models of the reaction. As discussed in Example 2, if the conversion is not possible, then TopoICE-X can be used to find all shortest pathways between the given pair of knots involving rational knots with less than 14 crossings. As discussed in Example 3, one can also find all rational knots of distance 1 from a given knot. This should be particularly helpful when comparing models for the DNA conformation acted upon by a topoisomerase; one can compare the topological conformations (as in Figure 1) of the DNA products that occurred in the experiment to those that are mathematically possible, but did not occur.

Although substrate DNA is normally unknotted, knotted substrates are sometimes employed such as in Example 3. Large quantities of certain knot types can be created in vitro and in vivo (46–49). TopoICE-X can be used to analyze a large number of potential knotted substrates to determine the best knot type to check a given hypothesis. TopoICE will be especially helpful when the knot types of the products are not fully identified. The RecA coating method (10) can be used to identify the knot types of the products via electron microscopy. However, it is currently difficult and time-consuming to use this method to obtain sufficient amounts for statistical analysis. Gel electrophoresis is a simpler method for partially identifying knots (50). A knot ladder can be used to determine the crossing number and sometimes even the knot type (46,51), although distinguishing between mirror images is more difficult (52). Combining gel electrophoresis data with TopoICE-X analysis of a given topoisomerase-mediated reaction may significantly reduce the possible knot types associated to a given DNA band in a gel.

Currently, TopoICE-X can only be used to analyze rational knots. Most knots observed in biological experiments are rational. The exceptions which have been identified are composites of rational knots. This is not unexpected as all knots with less than eight crossings are either rational or a composite of two rational knots. In most in vitro experiments, the majority of knots are small crossing knots. Knot complexity usually increases with the size of the DNA plasmid. For example in ref. (11), the majority of knots produced via T4 topoisomerase acting on supercoiled DNA using a 3.8-kb plasmid were of small crossing number, while knots with up to 18 or more crossings were produced using a 6.4-kb plasmid. One likely source of nonrational DNA knots is DNA extracted from tailless mutants of phage P4 (49). About 95% of the 10-kb DNA were knotted. While those knots with less than eight crossings must be either rational or composites of rational knots, the knot type of higher crossing knots could not be determined. In fact, it was not possible to determine the maximum crossing number of these knots.

TopoICE-X should be of interest to all researchers in DNA topology who study topological consequences of the action of various DNA topoisomerases. For more information about this software, please see the TopoICE-X manual in Supplementary Material and that is also available at http://knotplot.com/download.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.