The Protein Folding Problem

Abstract

The “protein folding problem” consists of three closely related puzzles: (a) What is the folding code? (b) What is the folding mechanism? (c) Can we predict the native structure of a protein from its amino acid sequence? Once regarded as a grand challenge, protein folding has seen great progress in recent years. Now, foldable proteins and nonbiological polymers are being designed routinely and moving toward successful applications. The structures of small proteins are now often well predicted by computer methods. And, there is now a testable explanation for how a protein can fold so quickly: A protein solves its large global optimization problem as a series of smaller local optimization problems, growing and assembling the native structure from peptide fragments, local structures first.

INTRODUCTION

The protein folding problem is the question of how a protein’s amino acid sequence dictates its three-dimensional atomic structure. The notion of a folding “problem” first emerged around 1960, with the appearance of the first atomic-resolution protein structures. Some form of internal crystalline regularity was previously expected (117), and α-helices had been anticipated by Linus Pauling and colleagues (180, 181), but the first protein structures—of the globins—had helices that were packed together in unexpected irregular ways. Since then, the protein folding problem has come to be regarded as three different problems: (a) the folding code: the thermodynamic question of what balance of interatomic forces dictates the structure of the protein, for a given amino acid sequence; (b) protein structure prediction: the computational problem of how to predict a protein’s native structure from its amino acid sequence; and (c) the folding process: the kinetics question of what routes or pathways some proteins use to fold so quickly. We focus here only on soluble proteins and not on fibrous or membrane proteins.

THE FOLDING CODE: WHAT BALANCE OF FORCES ENCODES NATIVE STRUCTURES?

Anfinsen’s Thermodynamic Hypothesis

A major milestone in protein science was the thermodynamic hypothesis of Christian Anfinsen and colleagues (3, 92). From his now-famous experiments on ribonuclease, Anfinsen postulated that the native structure of a protein is the thermodynamically stable structure; it depends only on the amino acid sequence and on the conditions of solution, and not on the kinetic folding route. It became widely appreciated that the native structure does not depend on whether the protein was synthesized biologically on a ribosome or with the help of chaperone molecules, or if, instead, the protein was simply refolded as an isolated molecule in a test tube. [There are rare exceptions, however, such as insulin, α-lytic protease (203), and the serpins (227), in which the biologically active form is kinetically trapped.] Two powerful conclusions followed from Anfinsen’s work. First, it enabled the large research enterprise of in vitro protein folding that has come to understand native structures by experiments inside test tubes rather than inside cells. Second, the Anfinsen principle implies a sort of division of labor: Evolution can act to change an amino acid sequence, but the folding equilibrium and kinetics of a given sequence are then matters of physical chemistry.

One Dominant Driving Force or Many Small Ones?

Prior to the mid-1980s, the protein folding code was seen a sum of many different small interactions—such as hydrogen bonds, ion pairs, van der Waals attractions, and water-mediated hydrophobic interactions. A key idea was that the primary sequence encoded secondary structures, which then encoded tertiary structures (4). However, through statistical mechanical modeling, a different view emerged in the 1980s, namely, that there is a dominant component to the folding code, that it is the hydrophobic interaction, that the folding code is distributed both locally and nonlocally in the sequence, and that a protein’s secondary structure is as much a consequence of the tertiary structure as a cause of it (48, 49).

Because native proteins are only 5–10 kcal/mol more stable than their denatured states, it is clear that no type of intermolecular force can be neglected in folding and structure prediction (238). Although it remains challenging to separate in a clean and rigorous way some types of interactions from others, here are some of the main observations. Folding is not likely to be dominated by electrostatic interactions among charged side chains because most proteins have relatively few charged residues; they are concentrated in high-dielectric regions on the protein surface. Protein stabilities tend to be independent of pH (near neutral) and salt concentration, and charge mutations typically lead to small effects on structure and stability. Hydrogen-bonding interactions are important, because essentially all possible hydrogen-bonding interactions are generally satisfied in native structures. Hydrogen bonds among backbone amide and carbonyl groups are key components of all secondary structures, and studies of mutations in different solvents estimate their strengths to be around 1–4 kcal/mol (21, 72) or stronger (5, 46). Similarly, tight packing in proteins implies that van der Waals interactions are important (28).

However, the question of the folding code is whether there is a dominant factor that explains why any two proteins, for example, lysozyme and ribonuclease, have different native structures. This code must be written in the side chains, not in the backbone hydrogen bonding, because it is through the side chains that one protein differs from another. There is considerable evidence that hydrophobic interactions must play a major role in protein folding. (a) Proteins have hydrophobic cores, implying nonpolar amino acids are driven to be sequestered from water. (b) Model compound studies show 1–2 kcal/mol for transferring a hydrophobic side chain from water into oil-like media (234), and there are many of them. (c) Proteins are readily denatured in nonpolar solvents. (d) Sequences that are jumbled and retain only their correct hydrophobic and polar patterning fold to their expected native states (39, 98, 112, 118), in the absence of efforts to design packing, charges, or hydrogen bonding. Hydrophobic and polar patterning also appears to be a key to encoding of amyloid-like fibril structures (236).

What stabilizes secondary structures? Before any protein structure was known, Linus Pauling and colleagues (180, 181) inferred from hydrogen-bonding models that proteins might have α-helices. However, secondary structures are seldom stable on their own in solution. Although different amino acids have different energetic propensities to be in secondary structures (6, 41, 55, 100), there are also many “chameleon” sequences in natural proteins, which are peptide segments that can assume either helical or β conformations depending on their tertiary context (158, 162). Studies of lattice models (25, 29, 51) and tube models (11, 12, 159) have shown that secondary structures in proteins are substantially stabilized by the chain compactness, an indirect consequence of the hydrophobic force to collapse (Figure 1). Like airport security lines, helical and sheet configurations are the only regular ways to pack a linear chain (of people or monomers) into a tight space.

Figure 1.

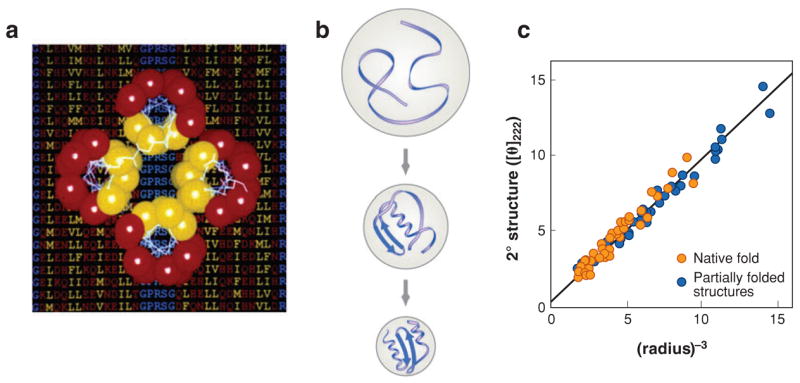
(a) Binary code. Experiments show that a primarily binary hydrophobic-polar code is sufficient to fold helix-bundle proteins (112). Reprinted from Reference 112 with permission from AAAS.

(b) Compactness stabilizes secondary structure, in proteins, from lattice models. (c) Experiments supporting panel b, showing that compactness correlates with secondary structure content in nonnative states of many different proteins (218). Reprinted from Reference 218 with permission.

Designing New Proteins and Nonbiological Foldamers

Although our knowledge of the forces of folding remains incomplete, it has not hindered the emergence of successful practical protein design. Novel proteins are now designed as variants of existing proteins (43, 94, 99, 145, 173, 243), or from broadened alphabets of nonnatural amino acids (226), or de novo (129) (Figure 2). Moreover, folding codes are used to design new polymeric materials called foldamers (76, 86, 120). Folded helix bundles have now been designed using nonbiological backbones (134). Foldamers are finding applications in biomedicine as antimicrobials (179, 185), lung surfactant replacements (235), cytomegalovirus inhibitors (62), and siRNA delivery agents (217). Hence, questions of deep principle are no longer bottlenecks to designing foldable polymers for practical applications and new materials.

Figure 2.

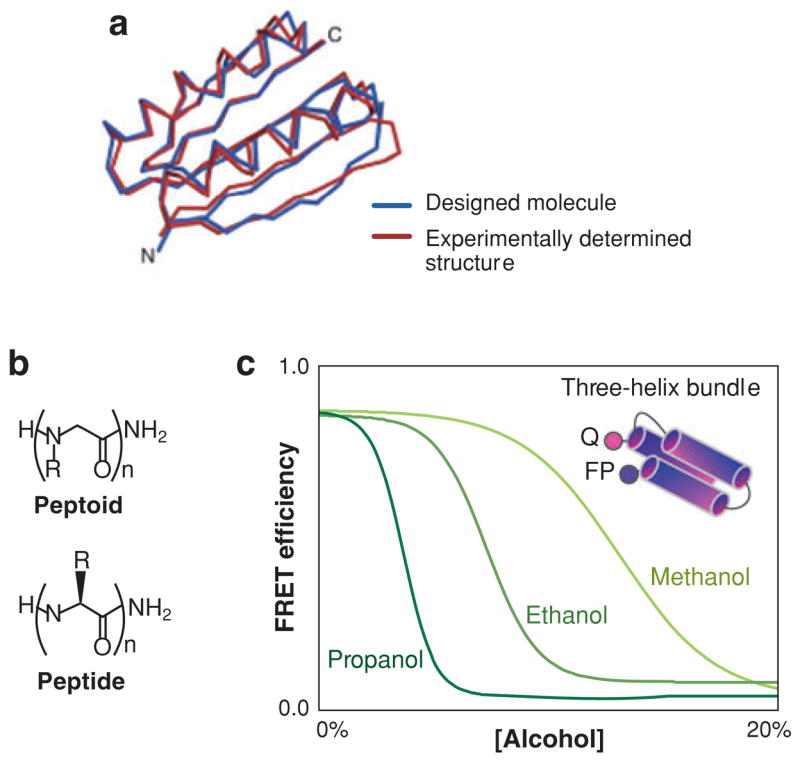
(a) A novel protein fold, called Top7, designed by Kuhlman et al. (129). Designed molecule (blue) and the experimental structure determined subsequently (red). From Reference 129; reprinted with permission from AAAS. (b) Three-helix bundle foldamers have been made using nonbiological backbones (peptoids, i.e., N-substituted glycines).

(c) Their denaturation by alcohols indicates they have hydrophobic cores characteristic of a folded molecule (134).

COMPUTATIONAL PROTEIN STRUCTURE PREDICTION IS INCREASINGLY SUCCESSFUL

A major goal of computational biology has been to predict a protein’s three-dimensional native structure from its amino acid sequence. This could help to (a) accelerate drug discovery by replacing slow, expensive structural biology experiments with faster, cheaper computer simulations, and (b) annotate protein function from genome sequences (9). With the rapid growth of experimentally determined structures available in the Protein Databank (PDB), protein structure prediction has become as much a problem of inference and machine learning as it is of protein physics.

Among the earliest uses of protein databases to infer protein structures were secondary structure prediction algorithms (33, 34, 190). In the mid-1980s, several groups began using the methods of computational physics—atomic force fields plus Monte Carlo sampling—to compute the structures of the Metenkephalin, a five-residue peptide (95, 141). The early 1990s saw significant strides in using databases and homology detection algorithms to assemble structures from homologous sequences (192) and to recognize folds by threading unknown sequences onto three-dimensional structures from a database (111). A key advance was the exploitation of evolutionary relationships among sequences through the development of robust sequence alignment methods (32, 64, 224).

CASP: A Community-Wide Experiment

In 1994, John Moult invented CASP (Critical Assessment of Techniques for Protein Structure Prediction) (165), a biennial, community-wide blind test to predict the unknown structures of proteins. Organizers identify proteins likely to be solved or whose structures have not yet been released, and predictors have roughly 3–5 weeks to predict their native structures. CASP has grown from 35 predictor groups and 24 target sequences in CASP1 in 1994 to over 200 groups and 100+ targets in CASP7 in 2006.

Over the seven CASPs, two trends are clear (164, 219). First, although much remains to be done, there has been substantial improvement in protein structure prediction. Web servers and software packages often predict the native structure of small, single-domain proteins to within about 2–6 Å of their experimental structures (8, 17, 242). In addition, fast-homology methods are computing approximate folds for whole genomes (182, 214). Figure 3 shows a quantitative assessment of performance at the first five CASP meetings. The most significant gains have occurred in the alignments of targets to homologs, the detection of evolutionarily distant homologs, and the generation of reasonable models for difficult targets that do not have templates (new folds). Since CASP5, predictions have also benefited from the use of metaservers, which solicit and establish consensus among predictions from multiple algorithms. Second, while most methods rely on both physics and bioinformatics, the most successful methods currently draw heavily from knowledge contained in native structural databases. Bioinformatics methods have benefited from the growth in size of the PDB (9, 219).

Figure 3.

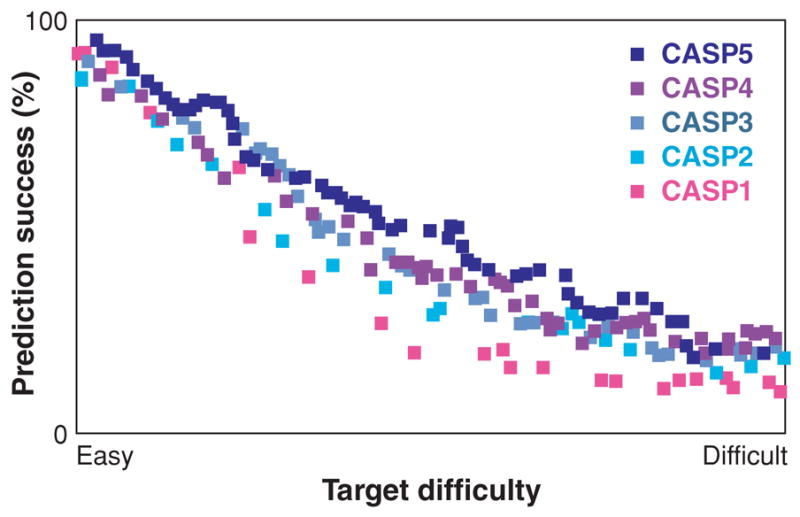
Progress in protein structure prediction in CASP1–5 (219). The y-axis contains the GDT TS score, the percentage of model residues that can be superimposed on the true native structure, averaged over four resolutions from 1 to 8 Å (100% is perfect). The x-axis is the ranked target difficulty, measured by sequence and structural similarities to proteins in the PDB at the time of the respective CASP. This shows that protein structure prediction on easy targets is quite good and is improving for targets of intermediate difficulty. Reprinted from Reference 219 with permission.

The following challenges remain (8, 164, 219): (a) to refine homology models beyond those of the best template structures; (b) to reduce errors to routinely better than 3 Å, particularly for proteins that are large, have significant β content, are new folds, or have low homology; (c) to handle large multidomain or domain-swapped proteins; (d) to address membrane proteins; and (e) to predict protein-protein interactions. Structural genomics is likely to help here (87, 222). In any case, the current successes in computer-based predictions of native protein structures are far beyond what was expected thirty years ago, when structure prediction seemed impossible.

ARE THERE MECHANISMS OF PROTEIN FOLDING?

In 1968, Cyrus Levinthal first noted the puzzle that even though they have vast conformational spaces, proteins can search and converge quickly to native states, sometimes in microseconds. How do proteins find their native states so quickly? It was postulated that if we understood the physical mechanism of protein folding, it could lead to fast computer algorithms to predict native structures from their amino acid sequences. In its description of the 125 most important unsolved problems in science, Science magazine framed the problem this way: “Can we predict how proteins will fold? Out of a near infinitude of possible ways to fold, a protein picks one in just tens of microseconds. The same task takes 30 years of computer time” (1).

The following questions of principle have driven the field: How can all the denatured molecules in a beaker find the same native structure, starting from different conformations? What conformations are not searched? Is folding hierarchical (10, 119)? Which comes first: secondary or tertiary structure (80, 239)? Does the protein collapse to compact structures before structure formation, or before the rate-limiting step (RLS), or are they concurrent (7, 89, 101, 195, 205, 213)? Are there folding nuclei (58, 152)?

Several models have emerged. In the diffusion-collision model, microdomain structures form first and then diffuse and collide to form larger structures (115, 116). The nucleation-condensation mechanism (70) proposes that a diffuse transition state ensemble (TSE) with some secondary structure nucleates tertiary contacts. Some proteins, such as helical bundles, appear to follow a hierarchical diffusion-collision model (155, 169) in which secondary structure forms and assembles in a hierarchical order. In hierarchic condensation (139), the chain searches for compact, contiguous structured units, which are then assembled into the folded state. Or, proteins may fold via the stepwise assembly of structural subunits called foldons (22, 126), or they may search for topomers, which are largely unfolded states that have native-like topologies (45, 150). These models are not mutually exclusive.

There Have Been Big Advances in Experimental and Theoretical Methods

The search for folding mechanisms has driven major advances in experimental protein science. These include fast laser temperature-jump methods (22); mutational methods that give quantities called φ-values (71, 84, 106) [now also used for ion-channel kinetics and other rate processes (42)] or ψ-values (204), which can identify those residues most important for folding speed; hydrogen exchange methods that give monomer-level information about folding events (125, 149); and the extensive exploration of protein model systems, including cytochrome c, CI2, barnase, apomyoglobin, the src, α-spectrin, and fyn SH3 domains, proteins L and G, WW domains, trpzip, and trp cage (154). In addition, peptide model experimental test systems provide insights into the fast early-folding events (14, 109, 124). Furthermore, single-molecule methods are beginning to explore the conformational heterogeneity of folding (23, 133, 166, 194).

There have been corresponding advances in theory and computation. Computer-based molecular minimization methods were first applied to protein structures in the 1960s (18, 79, 171), followed by molecular dynamics (140, 155), improved force fields (40) (reviewed in Reference 114), weighted sampling and multi-temperature methods (130, 210), highly parallelized codes for supercomputers (2, 57), and distributed grid computing methods such as Folding@home (198, 241). Models having less atomic detail also emerged to address questions more global and less detailed in nature about protein conformational spaces: (a) The Go model (82), which was intended to see if a computer could find the native structure if native guiding constraints were imposed, is now widely used to study folding kinetics of proteins having known native structures (37, 38, 113, 197, 225). (b) More physical models, typically based on polymer-like lattices, are used to study the static and dynamic properties of conformational spaces (19, 50). (c) Master-equation approaches can explore dynamics in heterogeneous systems (26, 36, 77, 138, 161, 176, 231, 232). Below, we describe some of what has been learned from these studies.

The PSB Plot: Folding Speed Correlates with the Localness of Contacts in the Native Structure

One of the few universal features of protein folding kinetics was first observed by Plaxco, Simons, and Baker (PSB), namely, that the folding speed of a protein is correlated with a topological property of its native structure (88, 184). As shown in Figure 4, Plaxco et al. found that the folding rates of two-state proteins—now known to vary more than 8 orders of magnitude—correlate with the average degree to which native contacts are local within the chain sequence: Fast-folders usually have mostly local structure, such as helices and tight turns. Slow-folders usually have more nonlocal structure, such as β-sheets (184), although there are exceptions (237). Folding rates have been subsequently found to correlate well with other native topological parameters such as the protein’s effective chain length (chain length minus the number of amino acids in helices) (107), secondary structure length (104), sequence-distant contacts per residue (90), the fraction of contacts that are sequence distant (163), the total contact distance (245), and intrinsic propensities, for example, of α-helices (131). And, there are now also methods that predict the folding rate from the sequence (91, 186). It follows that a protein typically forms smaller loops and turns faster than it forms larger loops and turns, consistent with the so-called zipping and assembly (ZA) mechanism, described below, which postulates that search speed is governed by the effective loop sizes [the effective contact order (ECO) (53, 73)] that the chain must search at any step.

Figure 4.

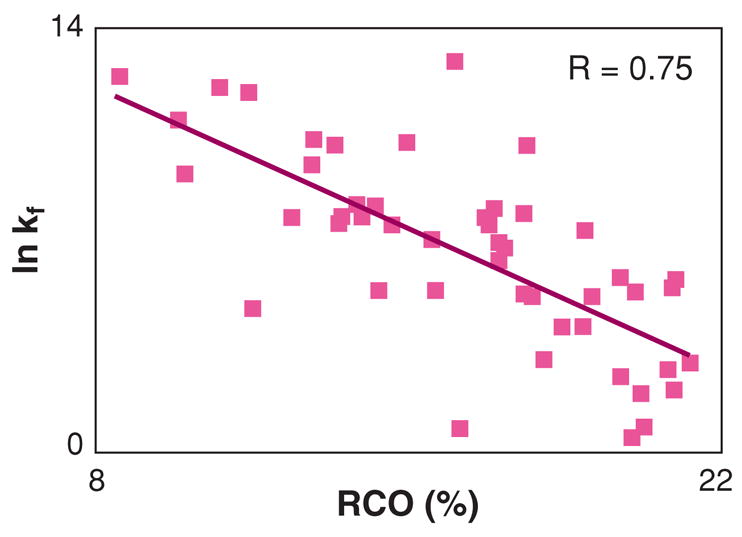
Folding rate versus relative contact order (a measure of localness of contacts in the native structure) for the 48 two-state proteins given in Reference 91, showing that proteins with the most local contacts fold faster than proteins with more nonlocal contacts.

Proteins Fold on Funnel-Shaped Energy Landscapes

Why has folding been regarded as so challenging? The issue is the astronomical number of conformations a protein must search to find its native state. Models arose in the 1980s to study the nature of the conformational space (19, 47), i.e., the shape of the energy landscape, which is the mathematical function F(φ, ϕ, X) that describes the intramolecular-plus-solvation free energy of a given protein as a function of the microscopic degrees of freedom. A central goal has been to quantify the statistical mechanical partition function, a key component of which is the density of states (DOS), i.e., the number of conformations at each energy level. In simple cases, the logarithm of the DOS is the conformational entropy. Such entropies have not been determinable through all-atom modeling, because that would require astronomical amounts of computational sampling (although replica-exchange methods can now do this for very small peptides). Hence understanding a protein’s DOS and its entropies has required simplified models, such as mean-field polymer and lattice treatments (51), spin-glass theories (19, 47), or exact enumerations in minimalist models (132).

A key conclusion is that proteins have funnel-shaped energy landscapes, i.e., many high-energy states and few low-energy states (19, 49, 50, 52, 138). What do we learn from the funnel idea? Funnels have both qualitative and quantitative uses. First, cartoonizations of funnels (Figure 5) provide a useful shorthand language for communicating the statistical mechanical properties and folding kinetics of proteins. Figure 5 illustrates fast folding (simple funnel), kinetic trapping (moats or wells), and slow random searching (golf course). These pictures show a key distinction between protein folding and simple classical chemical reactions. A simple chemical reaction proceeds from its reactant A to its product B, through a pathway, i.e., a sequence of individual structures. A protein cannot do this because its reactant, the denatured state, is not a single microscopic structure. Folding is a transition from disorder to order, not from one structure to another. Simple one-dimensional reaction path diagrams do not capture this tremendous reduction in conformational degeneracy.

Figure 5.

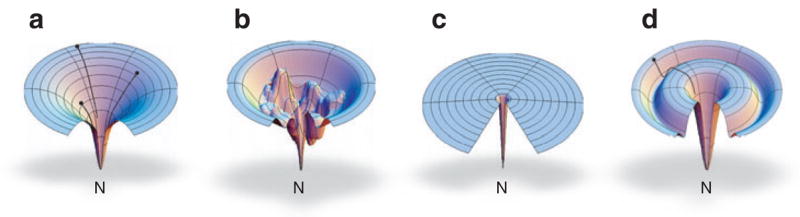
One type of energy landscape cartoon: the free energy F(φ, ϕ, κ) of the bond degrees of freedom. These pictures give a sort of simplified schematic diagram, useful for illustrating a protein’s partition function and density of states. (a) A smooth energy landscape for a fast folder, (b) a rugged energy landscape with kinetic traps, (c) a golf course energy landscape in which folding is dominated by diffusional conformational search, and (d) a moat landscape, where folding must pass through an obligatory intermediate.

A funnel describes a protein’s conformational heterogeneity

Conformational heterogeneity has been found in the few experiments that have been designed to look for it (16, 143, 157, 206, 209, 244). For example, using time-resolved FRET with four different intramolecular distances, Sridevi et al. (206) found in Barstar that (a) that the chain entropy increases as structures become less stable, (b) that there are multiple folding routes, and (c) that different routes dominate under different folding conditions. Moreover, changing the denaturant can change the dominant pathway, implying heterogeneous kinetics (143). Figure 6 shows the funnel landscape that has been determined by extensive mutational analysis of the seven ankyrin sequence repeats of the Notch ankyrin repeat domain (16, 157, 209).

Figure 6.

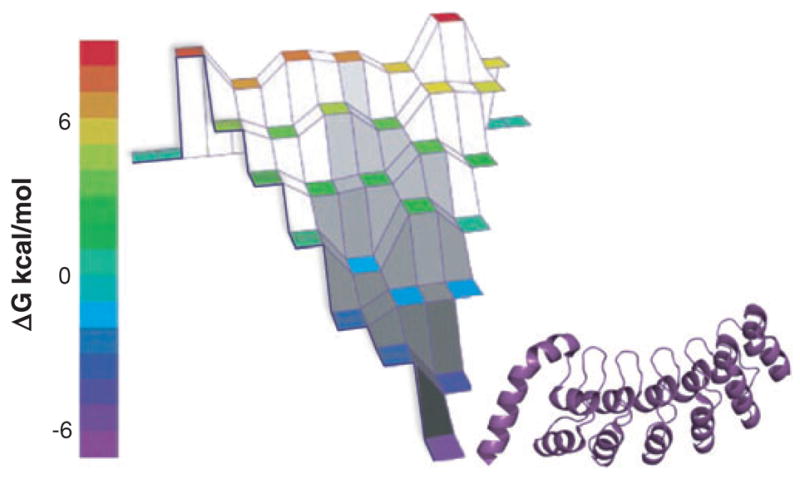
The experimentally determined energy landscape of the seven ankyrin repeats of the Notch receptor (16, 157, 209). The energy landscape is constructed by measuring the stabilities of folded fragments for a series of overlapping modular repeats. Each horizontal tier presents the partially folded fragments with the same number of repeats. Reprinted from Reference 157 with permission.

A funnel describes a protein’s chain entropy

The funnel idea first arose to explain denaturation, the balance between the chain entropy and the forces of folding (48). Proteins denature at high temperatures because there are many states of high energy and fewer states of low energy, that is, the landscape is funneled. For cold unfolding, the shape of the funnel changes with temperature because of free-energy changes of the aqueous solvent. When you can accurately compute a protein’s DOS, you can predict the protein’s free energy of folding and its denaturation and cooperativity properties. Figure 7 shows an example in which the DOS (set onto its side to illustrate the funnel) was found by extensive lattice enumeration for F13W*, a three-helix bundle, with predictions compared to experiments (146).

Figure 7.

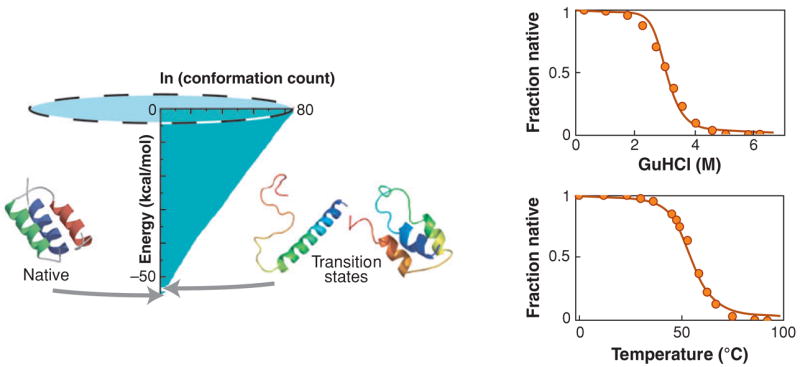
(Left) The density of states (DOS) cartoonized as an energy landscape for the three-helix bundle protein F13W*: DOS (x-axis) versus the energy (y-axis). (Right) Denaturation predictions versus experiments (146). The peak free energy (here, where the DOS is minimum), typically taken to be the transition state, is energetically very close to native.

Funnels provide a microscopic framework for folding kinetics

Folding kinetics is traditionally described by simple mass action models, such as D →I →N (on-path intermediate I between the denatured state D and native state N) or X →D →N (off-path intermediate X), where the symbol I or X represents macrostates that are invoked for the purpose of curve-fitting experimental kinetics data. In contrast, funnel models or master-equation models aim to explain the kinetics in terms of underlying physical forces. They aim to predict the microstate composition of those macrostates, for example. The states in master-equation models differ from those in mass-action models insofar as the former are more numerous, more microscopic, are defined by structural or energetic criteria, and are arranged kinetically to reflect the underlying funnel-like organization of the dynamical flows.

For example, Figure 8b shows a master-equation model for the folding of SH3, illustrating the apparently paradoxical result that folding can be serial and parallel at the same time. The protein has multiple routes available. However, one of the dominant series pathways is U →B →BD →BDE →BCDE →N. BD is the TSE because it is the dynamically least populated state. B precedes BD diagrammatically in series in this pathway. Yet, the probability bucket labeled B does not first fill up and then empty into BD; rather the levels in both buckets, B and BD, rise and fall together and hence are dynamically in parallel. Such series and parallel steps are also seen in computer simulations of CI2 (189), for example. Sometimes a chain contact A forms before another contact B in nearly all the simulation trajectories (series-like). But another contact C may form before B in some trajectories and after B in others (parallel-like). Some folding is sequential, as in Fyn SH3 (123), cytochrome (66), T4 lysozyme (24), and Im7 (74), and some folding is parallel, as in cytochrome C (83) and HEW lyzosyme (151).

Figure 8.

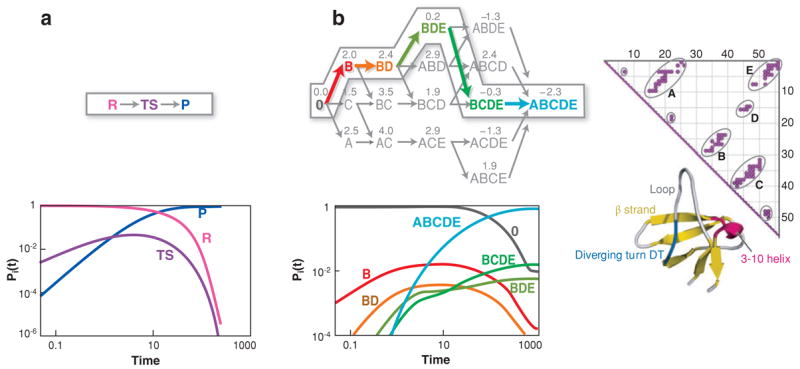
(a) A simple single-pathway system. R, reactant; TS, transition state; P, product. (b) Pathway diagram of SH3 folding from a master-equation model. The native protein has five contact clusters: A = RT loop; B = β₂β₃; C = β₃β₄; D = RT loop-β₄; and E = β₁β₅. Combined letters, such as BD, mean that multiple contact clusters have formed. Funneling occurs toward the right, because the symbols on the left indicate large ensembles, whereas the symbols on the right are smaller ensembles. The numbers indicate free energies relative to the denatured state. The arrows between the states are colored to indicate transition times between states. The slowest steps are in red; the fastest steps in green. BD is the transition state ensemble because it is the highest free energy along the dominant route. While B and BD would seem to be obligatorily in series, the time evolutions of these states show that they actually rise and fall in parallel (232).

Or, consider the traditional idea that a reaction’s RLS coincides with the point of the highest free energy, ΔG^‡, along the reaction coordinate. As a matter of principle, the RLS need not necessarily coincide with the free-energy barrier. There is evidence that they may not coincide for some protein folding processes (13, 15, 27). What’s the distinction? To find the RLS, you need a dynamical model. You would find the eigenvector corresponding to the slowest eigenvalue (in two-state kinetics). Microscopic master-equation modeling typically finds that this eigenvector only identifies the process U →N, with no finer pinpointing of any special structures along the way. In contrast, ΔG^‡ is a thermodynamic quantity—the maximum free energy along the fastest route, which usually does correspond to some specific ensemble of structures. Below, we describe why these matters of principle are important.

How do we convert folding experiments into insights about molecular behavior?

To interpret data, we must use models. φ-value experiments aim to identify RLSs in folding. But how we understand the molecular events causing a given φ-value depends on whether we interpret it by funnels or pathways. A φ-value measures how a folding rate changes when a protein is mutated (42, 67, 71, 105, 144, 153, 154, 176, 178, 193) (see Reference 231 and references 1–24 therein). φ equals the change in the logarithm of the folding rate caused by the mutation, divided by the change in the logarithm of the folding equilibrium constant. If we then seek a structural interpretation of φ, we need a model. Using the Bronsted-Hammond pathway model of chemical reactions, φ is often assumed to indicate the position of the TSE along the folding reaction coordinate: φ = 0 means the mutation site is denatured in the TSE; φ = 1 means the mutation site is native in the TSE. In this pathway view, φ can never lie outside the range from 0 to 1; in the funnel view, φ is not physically restricted to this range. For example, φ < 0 or φ > 1 has been predicted for mutations that stabilize a helix but that destabilize the bundle’s tertiary structure (231). Unfortunately, experiments are not yet definitive. While some φ-values are indeed observed to be negative or greater than 1 (44, 85, 176, 193), those values might be experimental artifacts (193). Other challenges in interpreting φ have also been noted (65, 188). To resolve the ambiguities in interpreting φ, we need to deepen our understanding beyond the single-reaction-coordinate idea.

How do we convert computer simulations into insights about molecular behavior?

Similarly, insights about folding events are often sought from computer modeling. It is much easier to calculate structural or energetic quantities than kinetic quantities. For example, some modeling efforts compute φ-values by assuming some particular structure for the TSE (78, 233) or some particular reaction coordinate, such as the RMSD to native structure, radius of gyration, number of hydrogen bonds, or number of native contacts (196). Alternatively, a quantity called pfold (56), which defines a separatrix (a sort of continental divide between folded and unfolded states), is sometimes computed. Although pfold predicts well the RLSs for simple landscapes (147), it can give less insight into protein landscapes having multiple barriers or other complexity (30). To go beyond classical assumptions, there has been an extensive and growing effort to use master-equation approaches (13, 26, 31, 36, 60, 61, 77, 110, 161, 172, 176, 201, 202, 208, 211, 212, 231, 232) to explore underlying assumptions about reaction coordinates, pathways, transition states, and RLSs.

Funnel models can explain some non-canonical behaviors in ultrafast folding

More than a dozen proteins fold in microseconds (128). Some fold in hundreds of nanoseconds (127, 237). Is there a state of protein folding that is so fast that there is no free-energy barrier at all (156)? This has sometimes been called downhill folding (93, 122, 128, 187). There is currently an intensive search for downhill folders—and much controversy about whether or not such folding has yet been observed, mainly in BBL, a 40-residue helical protein. That controversy hinges on questions of experimental analysis (68, 69, 75, 103, 168, 170, 191): establishing proper baselines and ionization states to find denaturation temperatures and to determine whether the equilibrium is two-state, for example, which would imply a barrier between D and N.

Remarkably, all known ultrafast-folders have anti-Arrhenius thermal kinetics. That is, heating those proteins at high temperatures slows down folding, the opposite of what is expected from traditional activation barriers. Here too, any molecular interpretation requires a model, and the common expectation is based on the classical Arrhenius/Eyring pathway model. Is the Arrhenius model sufficient for funnels involving many fast processes? Ultrafast folding kinetics has recently been explored in various models (59, 77, 122, 148, 167). One funnel model (77) explains that the reason why increasing the temperature leads to slower folding is because of thermal unfolding of the denatured chain, leading to a larger conformational space that must be searched for the chain to find route to native downhill. It predicts that the ultimate speed limit to protein folding, at temperatures that will disappear all other barriers, is the conformational search through the denatured basin. Near the speed limit of protein folding, the heterogeneity and searching that are intrinsic to funnels can be an important component of the folding physics. That model also explains that helical proteins fold faster than β-sheets, on average, because helices have more parallel microscopic folding routes (because a helix can nucleate at many different points along the chain).

The Zipping and Assembly Hypothesis for the Folding Routes

Protein folding is a stochastic process: One protein molecule in a beaker follows a different microscopic trajectory than another molecule because of thermal fluctuations. Hence, protein folding is often studied using Monte Carlo or molecular dynamics sampling. However, computations seeking the native state using purely physical models are prohibitively expensive, because this is a challenging needle-in-a-haystack global optimization problem (96, 132, 216). Since the beginnings of experimental folding kinetics, there has been the view that the Levinthal paradox—of how a protein searches its conformational space so quickly—might be explained by a folding mechanism, i.e., by some higher-level description (beyond the statement that it is stochastic) that clarifies how the protein decides which structures to form and avoids searching vast stretches of the conformational space in the first place.

Zipping and assembly (ZA) is a hypothesis for a general folding mechanism. On fast timescales, small fragments of the chain can search their conformations more completely than larger fragments can (53, 73). There are certain problems of global optimization—including the ZA mechanism of protein folding and the Cocke-Kasami-Younger method for parsing sentences (54, 102)—in which the globally optimal solution (native structure, in this case) can almost always be found (although not guaranteed) by a divide-and-conquer strategy, a fast process of cobbling together smaller locally optimal decisions. Accordingly, in the earliest time steps after folding is initiated (picoseconds to nanoseconds), each of the different peptide fragments of the chain searches for small local metastable structures, such as helical turns, β-turns, or small loops. Each peptide segment searches its own conformations, at the same time that other segments are searching. Not stable on their own, a few of those local structures are sufficiently metastable to survive to the next longer timescale, where they grow (or zip) into increasingly larger and more stable structures. On still longer timescales, pairs or groups of these substructures can assemble into structures that are still larger and more native-like, and metastability gives way to stability (97, 102, 103, 199, 215, 223, 228–230, 232).

The ZA mechanism shares much in common with other mechanisms, such as diffusion-collision, hierarchical, and foldon models. The last two mechanisms, however, are descriptors of experiments. They do not prescribe how to compute a protein’s folding route from its amino acid sequence. In contrast, the ZA mechanism is such a microscopic recipe, starting from the amino acid sequence and specifying a time series of ensembles of conformations the chain searches at each stage of folding. ZA is a funnel process: There are many parallel microscopic routes at the beginning, and fewer and more sequential routes at the end. The ZA mechanism provides a plausible answer to Levinthal’s paradox of what vast stretches of conformational space the protein never bothers to search. For any compact native polymer structure, there are always routes to the native state that take only small-conformational-entropy-loss steps. ZA otherwise explores very little of conformational space. These few routes constitute the dominant folding processes in the ZA mechanism. One test of this mechanism is the prediction of the change of folding routes (229), measured by the change in φ-value distributions (143), upon circular permutation of the chain. Proteins can be circularly permuted if the chain termini are adjacent to each other in the wild-type native structure. In such cases, the ends are covalently linked and the chain is broken elsewhere. This alters the native topology (contact map) dramatically, and sometimes the folding routes, but does not appear to substantially change the native structure (20, 142, 143, 160, 221).

PHYSICS-BASED MODELING OF FOLDING AND STRUCTURE PREDICTION

Computer simulations of purely physics-based models are becoming useful for structure prediction and for studying folding routes. Here the metric of success is not purely performance in native structure prediction; it is to gain a deeper understanding of the forces and dynamics that govern protein properties. When purely physical methods are successful, it will allow us to go beyond bioinformatics to (a) predict conformational changes, such as induced fit, important for computational drug discovery; (b) understand protein mechanisms of action, motions, folding processes, enzymatic catalysis, and other situations that require more than just the static native structure; (c) understand how proteins respond to solvents, pH, salts, denaturants, and other factors; and (d) design synthetic proteins having noncanonical amino acids or foldameric polymers with nonbiological backbones.

A key issue has been whether semiempirical atomic physical force fields are good enough to fold up a protein in a computer. Physics-based methods are currently limited by large computational requirements owing to the formidable conformational search problem and, to a lesser extent, by weaknesses in force fields. Nevertheless, there have been notable successes in the past decade enabled by the development of large supercomputer resources and distributed computing systems. The first milestone was a supercomputer simulation by Duan and Kollman in 1998 of the folding of the 36-residue villin headpiece in explicit solvent, for nearly a microsecond of computed time, reaching a collapsed state 4.5 Å from the NMR structure (57). Another milestone was the development by Pande and colleagues of Folding@home, a distributed grid computing system running on the screensavers of volunteer computers worldwide. Pande and colleagues (241) have studied the folding kinetics of villin. High-resolution structures of villin have recently been reached by Pande and colleagues (110) and Duan and colleagues (136, 137). In addition, three groups have folded the 20-residue Trp-cage peptide to ~1 Å: Simmerling et al. (200), the IBM Blue Gene group of Pitera and Swope (183), and Duan and colleagues (35). Recently, Lei & Duan (135) folded the albumin-binding domain, a 47-residue, three-helix bundle, to 2.0 Å. Physics-based approaches are also folding small helices and β-hairpin peptides of up to ~20 residues that have stable secondary structures (63, 81, 108, 240, 246; M.S. Shell, R. Ritterson & K.A. Dill, unpublished data). Physical potential models have also been sampled using non-Boltzmann stochastic and deterministic optimization strategies (121, 174, 207, 220).

Here are some of the key conclusions. First, a powerful way to sample conformations and obtain proper Boltzmann averages is replica exchange molecular dynamics (REMD) (210). Second, although force fields are good, they need improvements in backbone torsional energies to address the balance between helical and extended conformations (81, 108, 240), and in implicit solvation, which dramatically reduces the expense relative to explicit water simulations but which frequently overstabilizes ion-pairing interactions, in turn destabilizing native structures (63, 246).

Can modern force fields with Boltzmann sampling predict larger native structures? Recent work indicates that, when combined with a conformational search technique based on the ZA folding mechanism, purely physics-based methods can arrive at structures close to the native state for chains up to ~100 monomers (177; M.S. Shell, S.B. Ozkan, V.A. Voelz, G.H.A. Wu & K.A. Dill, unpublished data). The approach, called ZAM (zipping and assembly method), uses replica exchange and the AMBER96 force field and works by (a) breaking the full protein chain into small fragments (initially 8-mers), which are simulated separately using REMD; (b) then growing or zipping the fragments having metastable structures by adding a few new residues or assembling two such fragments together, with further REMD and iterations; and (c) locking in place any stable residue-residue contacts with a harmonic spring, enforcing emerging putative physical folding routes, without the need to sample huge numbers of degrees of freedom at a time.

ZAM was tested through the folding of eight of nine small proteins from the PDB to within 2.5 Å, using a 70-processor cluster over 6 months (177), giving good agreement with the φ-values known for four of them. Figure 9 shows the ZAM folding process for one of these proteins, and Figure 10 shows the predicted versus experimental structures for all nine. In a more stringent test, ZAM was applied in CASP7 to the folding of six small proteins from 76 to 112 residues (M.S. Shell, S.B. Ozkan, V.A. Voelz, G.H.A. Wu & K.A. Dill, unpublished data). Of the four proteins attempted in CASP7 that were not domain-swapped, ZAM predicted roughly correct tertiary structures, segments of more than 40 residues with an average RMSD of 5.9 angstroms, and secondary structures with 73% accuracy. From these studies it has been concluded that ZA routes can identify limited-sampling routes to the native state from unfolded states, directed by all-atom force fields, and that the AMBER96 plus a generalized Born implicit solvent model is a reasonable scoring function. Fragments that adopt incorrect secondary structures early in the simulations are frequently corrected in later-stage folding because the emerging tertiary structure of the protein often will not tolerate them.

Figure 9.

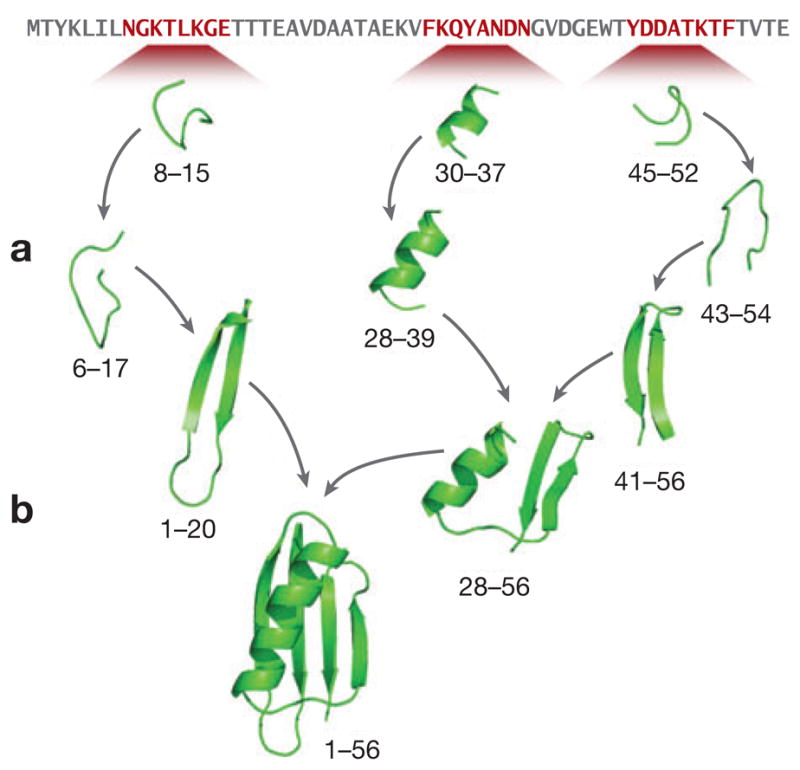
The folding routes found in the ZAM conformational search process for protein G, from the work described in Reference 177. The chain is first parsed into many short, overlapping fragments. After sampling by replica exchange molecular dynamics, stable hydrophobic contacts are identified and restrained. Fragments are then either (a) grown or zipped though iterations of adding new residues, sampling, and contact detection, or (b) assembled together pairwise using rigid body alignment followed by further sampling until a completed structure is reached.

Figure 10.

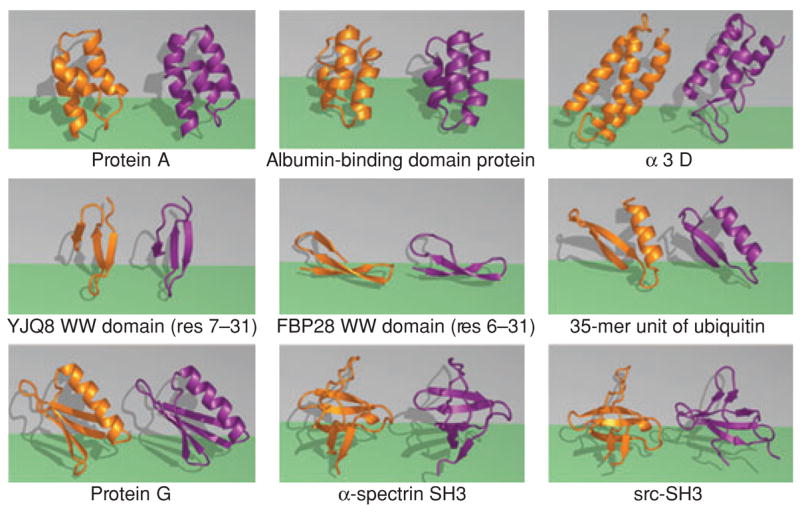
Ribbon diagrams of the predicted protein structures using the ZAM search algorithm (purple) versus experimental PDB structures (orange). The backbone C-RMSDs with respect to PDB structures are protein A (1.9 Å), albumin domain binding protein (2.4 Å), alpha-3D [2.85 Å (excluding loop residues) or 4.6 Å], FBP26 WW domain (2.2 Å), YJQ8 WW domain (2.0 Å), 1–35 residue fragment of Ubiquitin (2.0 Å), protein G (1.6 Å), and -spectrin SH3 (2.2 Å). ZAM fails to find the src-SH3 structure: Shown is a conformation that is 6 Å from the experimental structure. The problem in this case appears to be overstabilization of nonnative ion pairs in the GB/SA implicit solvation model.

SUMMARY

The protein folding problem has seen enormous advances over the last fifty years. New experimental techniques have arisen, including hydrogen exchange, φ-value methods that probe mutational effects on folding rates, single-molecule methods that can explore heterogeneity of folding and energy landscapes, and fast temperature-jump methods. New theoretical and computational approaches have emerged, including methods of bioinformatics, multiple-sequence alignments, structure-prediction Web servers, physics-based force fields of good accuracy, physical models of energy landscapes, fast methods of conformational sampling and searching, master-equation methods to explore the physical mechanisms of folding, parallel and distributed grid-based computing, and the CASP community-wide event for protein structure prediction.

Protein folding no longer appears to be the insurmountable grand challenge that it once appeared to be. Current knowledge of folding codes is sufficient to guide the successful designs of new proteins and foldameric materials. For the once seemingly intractable Levinthal puzzle, there is now a viable hypothesis: A protein can fold quickly and solve its big global optimization puzzle by piecewise solutions of smaller component puzzles. Other matters of principle are now yielding to theory and physics-based modeling. And current computer algorithms are now predicting native structures of small proteins remarkably accurately, promising growing value in drug discovery and proteomics.

SUMMARY POINTS

1. The protein folding code is mainly embodied in side chain solvation interactions. Novel protein folds and nonbiological foldamers are now being successfully designed and are moving toward practical applications.

2. Thanks to CASP, the growing PDB, and fast-homology and sequence alignment methods, computer methods now can often predict correct native structures of small proteins.

3. The protein folding problem has both driven—and benefited from—big advances in experimental and theoretical/computational methods.

4. Proteins fold on funnel-shaped energy landscapes, which describe the conformational heterogeneity among the nonnative states. This heterogeneity is key to the entropy that opposes folding and thus to folding equilibria. This heterogeneity is also important for understanding folding kinetics at the level of the individual chain processes.

5. A protein can fold quickly to its native structure by ZA, making independent local decisions first and then combining those substructures. In this way, a protein can avoid searching most of its conformational space. ZA appears to be a useful search method for computational modeling.