Population intervention models in causal inference

Summary

We propose a new causal parameter, which is a natural extension of existing approaches to causal inference such as marginal structural models. Modelling approaches are proposed for the difference between a treatment-specific counterfactual population distribution and the actual population distribution of an outcome in the target population of interest. Relevant parameters describe the effect of a hypothetical intervention on such a population and therefore we refer to these models as population intervention models. We focus on intervention models estimating the effect of an intervention in terms of a difference and ratio of means, called risk difference and relative risk if the outcome is binary. We provide a class of inverse-probability-of-treatment-weighted and doubly-robust estimators of the causal parameters in these models. The finite-sample performance of these new estimators is explored in a simulation study.

1. Introduction

Robins (2000) proposed estimators for a new class of models that relate the distribution of counterfactuals in a population to the universal application of, or exposure to, a treatment or a risk factor. For example, Robins proposed estimators for parameters such as E(Y_a | V ), which is interpreted as the mean of the outcome of interest in the target population when every subject receives the same treatment, or exposure, a, among strata defined by a subset of the baseline covariates, V , such as gender. Several estimators have been proposed for this parameter, including the likelihood-based G-computation estimator, and those based on an estimating equation approach, namely the inverse-probability-of-treatment-weighted estimator and the doubly-robust extension (van der Laan & Robins, 2002). Given a specific model, such as E(Y_a | V ) = m(a, V | β) = β₀ + β₁a + β₂V + β₃aV , these estimators require respectively an estimator of the conditional distribution of the outcome given the treatment and confounders, an estimator of the treatment assignment distribution, or both. Here, we discuss similar approaches to a new class of regression models that are particularly relevant to population-based studies of risk factors. We term these models population intervention models.

The estimating equation approach provides a convenient mathematical method for deriving a class of estimators for a wide variety of causal inference problems. However, before applying the machinery (van der Laan & Robins, 2002), one must first define the parameter of interest. We suggest that E(Y_a | V ) is often not the parameter of interest in observational studies of risk factors. For instance, marginal structural models compare the prevalence of disease in a population in which everyone smokes three packs of cigarettes against the prevalence in the same population in which everyone smokes two packs and so on. Of more public health interest might be a model which relates the prevalence of disease in the current target population, with its distribution of smokers, to a population where no one smokes; that is, a more compelling regression might be one that returns estimates of the impact of intervention in a population, relative to the current distribution of a risk factor, such as E(Y_a) – E(Y ) or E(Y_a)/E(Y ), where a is a target level of the risk factor. Epidemiologists might recognize this parameter as something akin to attributable risk. In this paper, we will propose a new class of estimators for parameters comparing the distribution of an outcome in the current target population relative to that in the same population when all individuals have uniform treatment/exposure.

2. Data, model and parameters of interest

To define our model, we use the causal inference framework originally proposed by Rubin (Rubin, 1978) treating causal inference as a missing-data problem. Consider a study in which we observe, chronologically ordered, on each randomly sampled subject baseline covariates W ,a treatment/exposure variable A and a final outcome Y . The observed data structure O = (W, A, Y ) represents a random variable with a certain population distribution P₀ , and the sample O₁,..., O_n represents n independent and identically distributed observations of O. We are concerned with estimation and testing of the effect of an intervention, A = a, on the distribution of Y relative to the actual population distribution of Y , possibly within strata defined by a subset of baseline covariates V ⊂ W .

In order to formulate such a parameter of interest and corresponding model we will use the counterfactual framework in which the observed data structure O is viewed as a missing-data structure on a collection of treatment-specific data structures, the so-called counterfactuals. First, we assume that each subject has a set of associated treatment-specific outcomes (Y_a : a ∈ A), so that X = {(Y_a : a ∈ A), W} represents a full data random variable with a population distribution F_X0 Here A denotes the set of possible treatments. Secondly, one assumes that the observed data, O = (W, A, Y = Y_A), correspond to observing the A-specific component of the collection of treatment-specific data structures X ={X_a ≡ (Y_a, W ) : a ∈ a} corresponding to the treatment A the subject actually received; that is, treatment assignment serves as a censoring variable. Here A is short-hand for a vector of censoring indicators, where the 0’s and a single 1 correspond to unobserved counterfactuals, X_a, a ≠ A, and the observed counterfactual, X_A, respectively. This assumption was originally introduced by Rubin (1986) as the stable-unit-treatment-value assumption and has also been referred to as the consistency assumption. Since O is a missing-data structure on the full data structure X with missingness variable A, the distribution of O is a function of the distribution F_X0 of X and the conditional distribution g₀ of treatment A,given X; that is $O\sim P_{F_{X0},g_0}$, where g₀(a | X) ≡ pr(A = a | X) is referred to as the treatment mechanism. In order to have an identifiable causal parameter we will also rely on the so-called randomization assumption on g₀:

$$g_0(a\mid X)=g_0(a\mid W),$$

or, equivalently, A is conditionally independent of X, given W . Within Rubin's framework, this assumption is known as strong ignorability; it is also often referred to as the assumption of no unmeasured confounding. Under these assumptions, the density of the observed data structure with respect to an appropriate dominating measure factorizes as follows:

$$p_0\left(O\right)=f_W\left(W\right)f_{Y\mid A,W}(Y\mid A,W)g_0(A\mid W).$$

If g₀(a | W ) > 0, F_W almost everywhere, then it also follows that the first two factors of the observed data density identify the counterfactual distribution of (Y_a, W ):

$$p_{Y_a,W}(y,w)\equiv f_{Y\mid A,W}(y\mid A=a,w)f_W\left(w\right),$$ (1)

where (1) was named the G-computation formula by Robins (2000).

This counterfactual framework allows us to define our parameter of interest as some difference between the conditional distribution F_Ya | V and the population distribution F_Y V , where this difference can be parameterized in several ways. Formally, our parameter of interest is

$${\psi }_0(a,V)=\Psi (F_{X0},g_0)(a,V)\equiv \Phi (F_{Y_a\mid V},F_{Y\mid V}),$$

for some known functional Φ. In words, ψ₀ measures the effect of setting A = a for everybody in our population on the distribution of Y , within stratum V = v. A Φ-specific intervention model is now defined as a model on this parameter ψ₀:

$${\psi }_0(a,V)=m(a,V\mid {\beta }_0),$$

for some Euclidean parameterization β → m(a, V | β). The following sections present estimators for two classes of parameters, namely the additive risk and relative risk:

$$\begin{array}{cc}\hfill {\psi }_{0,\mathrm{AR}}(a,V)& =E(Y_a\mid V)-E(Y\mid V)=m(a,V\mid {\beta }_0),\hfill \\ \hfill {\psi }_{0,\mathrm{RR}}(a,V)& =\frac{E(Y_a\mid V)}{E(Y\mid V)}=m(a,V\mid {\beta }_0).\hfill \end{array}$$ (2)

Note that the structural nested mean models of Robins (1989, 1994) provide parameters that compare the mean of an outcome, within strata of A and W , under the ‘natural’ population distribution of treatment versus that under an intervention when A = 0 for all subjects, that is, E(Y | A, W ) – E(Y₀ | A, W ). Thus, the parameters discussed here capture a different effect, specifically not conditioning on A. Also, as discussed in the Appendix of van der Laan et al. (2007), one can also derive the marginal or stratified causal parameters of interest from these structural nested mean models.

3. Estimating additive risk for a single target intervention

This section presents estimators for the case of only one target intervention of interest, a*. For instance, if A measures cigarette smoking, we would only be interested in the intervention a* = 0. We describe a direct estimating equation approach for the additive risk that enjoys the very attractive property of being consistent even when the model for E(Y | V) is misspecified. Note that, if m(V | β) = E(Y_a^* | V) – E(Y | V), then E(Y_a^* | V) = m(V | β) + E(Y | V) and thus, treating E(Y | V) as known, we can use the estimating functions already provided by Robins & Rotnitzky (1992) for models E(Y_a^* | V) = m(V | β) + E(Y | V). For instance, the inverseprobability-of-censoring-weighted estimating function for E(Y_a^* | V) is

$$\begin{array}{cc}\hfill D_{h,\mathrm{IPCW}}(0\mid g,\eta ,\beta )& =\frac{h\left(V\right)I(A=a^{\ast })}{g(a^{\ast }\mid W)}\{Y-E(Y_{a^{\ast }}\mid V)\}\hfill \\ \hfill & =\frac{h\left(V\right)I(A=a^{\ast })}{g(a^{\ast }\mid W)}\{Y-\eta \left(V\right)-m(V\mid \beta )\},\hfill \end{array}$$ (3)

where η(V ) ≡ E(Y | V ) and h(V ) is some arbitrary function of V . The estimator, defined as the solution of the estimating equation $0={\sum }_{i=1}^n{D}_{h,\mathrm{IPCW}}(0_i\mid g_n,{\eta }_n,\beta )$, is consistent if g_n(A | W ) consistently estimates g₀(A | W ) and η_n(V ) consistently estimates η₀(V ), where the subscript, 0, always refers to the true parameter. The doubly-robust estimating function extension to this estimator is given by

$$\begin{array}{cc}\hfill & D_{h,\mathrm{DR}}(0\mid g,\eta ,Q,\beta )=\frac{h\left(V\right)I(A=a^{\ast })}{g(a^{\ast }\mid W)}\{Y-\eta \left(V\right)-m(V\mid \beta )\}\hfill \\ \hfill & -\frac{I(A=a^{\ast })-g(a^{\ast }\mid W)}{g(a^{\ast }\mid W)}h\left(V\right)\{Q(W,A)-\eta \left(V\right)-m(V\mid \beta )\}\hfill \end{array}$$ (4)

(van der Laan & Robins, 2002, p. 35), where Q(A, W ) ≡ E(Y | A, W ). The doubly-robust estimator, defined as the solution of the estimating equation $0={\sum }_{i=1}^n{D}_{h,\mathrm{DR}}(0_i\mid g_n,{\eta }_n,Q_n,\beta )$, is consistent if η_n(V ) consistently estimates η₀(V ) and either Q_n(W , A) consistently estimates Q₀(A, W ) or g_n(A | W ) consistently estimates g₀(A | W ).

Both of these estimators thus rely on consistent estimation of η(V ), which can be problematic if V is high-dimensional and nonparametric estimation is infeasible. However, a small modification to both the D_h,IPCW and D_h,DR estimating functions yields consistent estimators even when η(V ) is misspecified. To be specific, we propose estimators based on the following estimating functions, now indexed by h and η₁:

$$D_{h,{\eta }_1,\mathrm{IPCW}}(0\mid g,\beta )=D_{h,\mathrm{IPCW}}(0\mid g,{\eta }_1,\beta )+C_h(O\mid {\eta }_1,\beta )$$ (5)

$$D_{h,{\eta }_1,\mathrm{DR}}(0\mid g,Q,\beta )=D_{h,\mathrm{DR}}(0\mid g,{\eta }_1,Q,\beta )+C_h(O\mid {\eta }_1,\beta ),$$ (6)

where C_h(O | η₁, β) = –Yh(V ) + E{h(V )η₁(V )} and η₁ represents an index of the estimating function with the optimal choice being η₀ = E(Y | V ). In the estimating equation η₁ can now be replaced by an estimator of η₀, which is not necessarily consistent, and C_h can be obtained by finding the expected values of the original estimating functions D_h,η1, _ipcw(0 | g,β) and D_h,η1, _DR(0 | g, Q,β), assuming that all parameters other than η are known. It turns out that the resulting ‘leftover’ part can be easily estimated nonparametrically by C_h(O | η_n,β), where η_n is an estimator converging to η₁.

4. Estimating intervention effects over all possible interventions

4.1. Background

In this section, we propose estimating functions for more general models that simultaneously capture the effect of a number of different interventions, corresponding to all the different values that the treatment variable A can assume. We focus on models for the additive risk difference and the relative risk, see (2), for which we present inverse-weighting-based estimating functions as well as their doubly-robust extensions. Since we now observe one counterfactual outcome of interest for each observation, the former will be referred to as inverse-probability-of-treatment-weighted rather than inverse-probability-of-censoring-weighted estimating functions.

The estimators based on these estimating functions are consistent if the user can supply a consistent estimator of the treatment mechanism g₀(A | W ). In order to deal with the curse of dimensionality, it will generally be necessary to assume a model G within which one can then obtain a maximum likelihood estimator,

$$g_n\equiv \arg \underset{g\in \mathcal{G}}{\max }\prod _{i=1}^{n}g(A_i\mid W_i),$$

or versions of this involving regularization and/or model selection. Our proposed doubly-robust estimators are consistent if g₀(A | W ) or E(Y | A, W ) is estimated consistently; E(Y | A, W ) can be estimated using straightforward regression methods.

Note that the models discussed in this section can also be applied if one is interested in a single target intervention a*. By borrowing information from other interventions to estimate the effect at the intervention of interest, the resulting estimators can achieve a smaller variance than those described in § 3. However, they are likely to suffer from greater bias if the model is incorrectly specified.

4.2. Estimation and inference

In each of the models we will apply the following general strategy for deriving a class of estimating functions, using as an illustrative example the additive risk intervention model. Our general strategy corresponds to the estimating function methodology presented in van der Laan & Robins (2002); estimating functions are implied by the so-called orthogonal complement of the nuisance tangent space, which is equivalent to the class of all influence curves of regular asymptotically linear estimators. Such estimating functions are orthogonal in the L²(P) Hilbert space to all scores implied by fluctuations of the nuisance parameters. Such estimating functions always have first-order robustness with respect to specifying a variation-independent nuisance parameter; in many settings, these estimating functions remain unbiased even under complete misspecification of nuisance parameters. This has important practical consequences, such as in testing a null hypothesis about the additive risk, since the validity of such a test is not affected by bias in the model for η(V ).

Stage 1

The population parameter η₀, which is used for comparison by the intervention model, implies a marginal structural model for the conditional distribution of Y_a, given V . For example, for a given η₀(V ), the additive risk intervention model implies the marginal structural model E(Y_a | V ) = η₀(V ) + m(a, V | β₀).

Stage 2

Given η₀, this marginal structural model implies a class of inverse-probability-of-treatment-weighted and doubly-robust estimating functions as established in previous literature. For example, the class of doubly-robust estimating functions for E(Y_a | V ) = η₀(V ) + m(a, V | β₀), with η₀ treated as known, is given by

$$\begin{array}{cc}\hfill D_{h_1}(O\mid g,Q,{\eta }_0,\beta )& \equiv \frac{h_1(A,V)}{g(A\mid W)}\{Y-{\eta }_0\left(V\right)-m(A,V\mid \beta )\}\hfill \\ \hfill & -\frac{h_1(A,V)}{g(A\mid W)}\{Q(A,W)-{\eta }_0\left(V\right)-m(A,V\mid \beta )\}\hfill \\ \hfill & +\sum _{a\in \mathcal{A}}{h}_1(a,V)\{Q(a,W)-{\eta }_0\left(V\right)-m(a,V\mid \beta )\},\hfill \end{array}$$ (7)

where the index h₁ can be an arbitrary function of A and V . Note that this estimating function depends on the unknown nuisance parameters g₀(A | W ) and Q₀(A, W ). The first term of this estimating function represents the inverse-probability-of-treatment-weighted estimating function, and the last two terms are its projection on to the nuisance tangent space T_RA = [φ(A, W ) : E{φ(A, W ) | W }= 0] of the treatment mechanism only assuming the randomization assumption. This estimating function is doubly-robust with respect to misspecification of g₀ and Q₀ in the sense that, if max_a{h₁(a, V)/g₁(a | W)} < ∞, F_W0 almost everywhere, and either g₁ = g₀ or Q₁ = Q₀, then

$$E_0{D}_{h_1}(O\mid g_1,Q_1,{\eta }_0,{\beta }_0)=0.$$

Stage 3

To make the estimator robust to misspecification of η, determine the influence curve of the estimator β_n, solving 0 = ∑_iD_h1(O_i | g₀, Q₀,η_n,β) for an appropriate estimator η_n of η₀ under a nonparametric model for η₀. We treat this class of influence curves, ignoring standardizing constants and matrices, as a new class of estimating functions. This results in a corrected class of estimating functions given by

$$D_{h_1}(O\mid g,Q,\eta ,{\beta }_0)+C_{h_1}(O\mid \eta ,{\beta }_0).$$

The latter term actually corresponds to the influence curve of the estimator E₀D_h1(O | g₀, Q₀, η_n, β₀) of the parameter E₀ D_h1(O | g₀, Q₀, η₀,β₀), with the parameters other than η₀ treated as known. The influence curve is defined with regard to a regular, asymptotically linear estimator, μ_n, of parameter μ₀ as follows: ${\mu }_n-{\mu }_0=n^{-1}{\sum }_{i=1}^n{\mathrm{IC}}_i\left(O_i\right)+op\left(n^{-1∕2}\right)$In the additive risk intervention model,

$$C_{h_1}(O\mid \eta ,\beta )=-\sum _{a\in \mathcal{A}}{h}_1(a,V)Y+E\left\{\sum _{a\in \mathcal{A}}{h}_1(a,V)\eta \left(V\right)\right\},$$

where this class of influence curves is indexed by h₁, with β treated as known, and η is the only unknown parameter.

Stage 4

Finally, in each of our three intervention models, the corrected estimating functions remain unbiased if η is misspecified. This allows us to treat η as another index in the class of estimating functions, which results in the final class of proposed estimating functions indexed by functions h₁, h₂:

$$D_{h_1,h_2}(O\mid g,Q,\beta )\equiv D_{h_1}(O\mid g,Q,h_2,\beta )+C_{h_1}(O\mid h_2,\beta ).$$

The members of our class of estimating functions {D_{h1, h2} : h₁, h₂ are doubly-robust against misspecification of its two nuisance parameters, g₀ and Q₀, in the following sense: if max_a h₁(a, V )/g₁(a | W ) < ∞, F_W0 almost everywhere, and either g₁ = g₀ or Q₁ = Q₀, then

$$E_0{D}_{h_1,h_2}(O\mid g_1,Q_1,{\beta }_0)=0.$$

For each of our models we propose a particular choice (h₁, h₂) depending on the true data-generating distribution, which can easily be estimated. Misspecification of this choice does not affect the unbiasedness of the estimating function, but only results in using a different, suboptimal, unbiased estimating function. As a consequence, a different choice from the optimal h₁ and h₂ does not affect the consistency and asymptotic linearity (van der Laan & Robins, 2002) of the resulting estimator of β₀.

4.3. Class of estimating functions for additive risk intervention models

For a given η₀(V ), the additive risk intervention model implies the marginal structural model E(Y_a | V ) = η₀(V + m(a, V | β₀). Our general strategy now results in the following class of estimating functions for β₀, indexed by arbitrary functions h₁(A, V) and h₂(V) and depending on two nuisance parameters g₀(A | W) and Q₀(A, W):

$$\begin{array}{cc}\hfill D_{h_1,h_2}(O\mid g,Q,\beta )& \equiv \frac{h_1(A,V)}{g(A\mid W)}\{Y-h_2\left(V\right)-m(A,V\mid \beta )\}\hfill \\ \hfill & -\frac{h_1(A,V)}{g(A\mid W)}\{Q(A,W)-h_2\left(V\right)-m(A,V\mid \beta )\}\hfill \\ \hfill & +\sum _{a\in \mathcal{A}}{h}_1(a,V)\{Q(a,W)-h_2\left(V\right)-m(a,V\mid \beta )\}\hfill \\ \hfill & -\sum _{a\in \mathcal{A}}{h}_1(a,V)Y+E\left\{\sum _{a\in \mathcal{A}}{h}_1(a,V)h_2\left(V\right)\right\}.\hfill \end{array}$$ (8)

Our proposed choice for (h₁, h₂)is given by

$$\begin{array}{cc}\hfill h_1(A,V)& \equiv \frac{\partial }{\partial \beta }m(A,V\mid \beta )g_0(A\mid V),\hfill \\ \hfill h_2\left(V\right)& \equiv E(Y\mid V).\hfill \end{array}$$ (9)

The optimal choice for (h₁, h₂) remains to be investigated. Our goal was to propose choices that are sensible and relatively simple. The natural choice for h₂ is E(Y | V ). The choice of h₁ is motivated by the discussion in Chapter 6 of van der Laan & Robins (2002), with g₀(A | V ) added as a stabilizing factor that can ameliorate the impact of very small estimated treatment probabilities g_n(A | W), as also suggested in Robins et al. (2000). A more general discussion of the choice of h in the context of nonparametric models of causal effects can be found in Neugebaur & van der Laan (2006). Finally, to simplify the notation, the dependence of the estimating function on the unknown mean, in the last term, is not reflected in our notation.

4·4. Class of estimating functions for relative risk intervention models

For a given η₀(V), the intervention relative risk model implies the marginal structural model E(Y_a | V) = η₀(V)m(A, V | β₀). Our general strategy now results in the following class of estimating functions for β0, indexed by arbitrary functions h₁(A, V) and h₂(V) and depending on two nuisance parameters g₀(A | W) and Q₀(A, W):

$$\begin{array}{cc}\hfill D_{h_1,h_2}(O\mid g,Q,\beta )& \equiv \frac{h_1(A,V)}{g(A\mid W)}\{Y-h_2\left(V\right)m(A,V\mid \beta )\}\hfill \\ \hfill & -\frac{h_1(A,V)}{g(A\mid W)}\{Q(A,W)-h_2\left(V\right)m(A,V\mid \beta )\}\hfill \\ \hfill & +\sum _{a\in \mathcal{A}}{h}_1(a,V)\{Q(a,W)-h_2\left(V\right)m(a,V\mid \beta )\}\hfill \\ \hfill & -\sum _{a\in \mathcal{A}}{h}_1(a,V)m(a,V\mid \beta )Y+E\left\{\sum _{a\in \mathcal{A}}{h}_1(a,V)m(a,V\mid \beta )h_2\left(V\right)\right\}.\hfill \end{array}$$

Our proposed choices for (h₁, h₂), similar to those discussed for the additive risk model, are given by

$$\begin{array}{cc}\hfill h_1^{\ast }(A,V)& \equiv h_2^{\ast }\left(V\right)\frac{d}{d\beta }m(A,V\mid \beta )g_0(A\mid V)\hfill \\ \hfill h_2^{\ast }\left(V\right)& \equiv E(Y\mid V).\hfill \end{array}$$

4.5 General mean intervention models

We now consider a general mean intervention model corresponding to a general choice of Φ{E(Y_a | V ), E(Y | V )}= m(a, V | β). Given η₀(V ), this model implies a marginal structural model E(Y_a | V ) = f{η₀(V ), m(a, V | β)} for some bivariate real-valued function f . Our general strategy now results in the following class of estimating functions for β₀:

$$\begin{array}{cc}\hfill D_{h_1}(O\mid g,Q,\eta ,\beta )& \equiv \frac{h_1(A,V)}{g(A\mid W)}[Y-f\{\eta \left(V\right),m(A,V\mid \beta )\}]\hfill \\ \hfill & -\frac{h_1(A,V)}{g(A\mid W)}[Q(A,W)-f\{\eta \left(V\right),m(A,V\mid \beta )\}]\hfill \\ \hfill & +\sum _{a\in \mathcal{A}}{h}_1(a,V)[Q(a,W)-f\{\eta \left(V\right),m(a,V\mid \beta )\}]\hfill \\ \hfill & -\sum _{a\in \mathcal{A}}{h}_1(a,V)f^{10}\{\eta \left(V\right),m(a,V\mid \beta )\}Y\hfill \\ \hfill & +E\left[\sum _{a\in \mathcal{A}}{h}_1(a,V)f^{10}\{\eta \left(V\right),m(a,V\mid \beta )\}\eta \left(V\right)\right],\hfill \end{array}$$

where f¹⁰(x, y) ≡ ∂f(x, y)/∂x.

It follows that E₀D_h1(O | g₀, Q₀, η₁, β₀) only equals zero at a misspecified η₁ if x → f(x, y) is linear, which holds precisely for the additive and relative risk models, but fails to hold for most other functions of interest. For example, if one models the log odds in the binary outcome case, then this class of estimating functions does rely on consistent estimation of the nuisance parameter η₀(V ), beyond consistent estimation of either g₀(A | W )or Q₀(A, W ).

4.6. Estimation and asymptotic inference

Given estimators h_1n, h_2n, g_n and Q_n of h₁, h₂, g₀ and Q₀, the estimator β_n for the additive and relative risk models is defined as the solution of the estimating equation

$$0=\sum _{i=1}^n{D}_{h_{1n},h_{2n}}(O_i\mid g_n,Q_n,\beta ).$$

One can use the Newton–Raphson algorithm for solving this estimating equation, and, if one has a good initial estimator available, then β_n will be asymptotically equivalent to the one-step estimator as obtained in the first step of the Newton–Raphson algorithm:

$${\beta }_n^1={\beta }_n^0-c_n^{-1}\frac{1}{n}\sum _{i=1}^n{D}_{h_{1n},h_{2n}}(O_i\mid g_n,Q_n,{\beta }_n^0),$$

where

$$c_n=\frac{\partial }{\partial {\beta }_n^0}\frac{1}{n}\sum _{i=1}^n{D}_{h_{1n},h_{2n}}(O_i\mid g_n,Q_n,{\beta }_n^0).$$

Statistical inference for β₀ can now be based on β_n ∼ N(β₀, ∑_n), where

$${\Sigma }_n=\frac{1}{n}\sum _{i=1}^n\mathrm{EIC}\left(O_i\right)\mathrm{EIC}{\left(O_i\right)}^{⊺}$$

and EIC(O) is an estimator of the influence curve IC(O | P₀) of our estimator. The Appendix contains a derivation of the influence curve when g_n consistently estimates g₀. In general, we recommend using the bootstrap to estimate the distribution of n^−1/2(β_n – β₀).

5. Simulation study

To examine the finite-sample properties of our estimators, simulation studies were conducted to evaluate the performance of estimators of models of the additive risk. In the notation introduced in § 2, the data consist of independent and identically distributed realizations of O = (W = (V, Z), A, Y ). Interest lies in estimating the projection of the risk difference E(Y | V ) – E(Y_a | V ) on to the working model m(a, V | β) = β₀ + β₁a + β₂V + β₃(V – 3)₊ + β₄aV + β₅a(V – 3)₊, where (V – 3)₊ is a linear spline term. This model was chosen because we wanted to examine the performance under situations in which the model for the additive risk does and does not closely approximate the true additive risk as a function of V . Our model above accomplishes this if, when a = 0, the model closely approximates the true function, whereas, for a = 1, the model is clearly misspecified; see Figs 1 and 2. A linear model was used to estimate the additive risk, which does not lead to difficulties in estimation given that our estimating approach does not require this model to constrain the risk difference to the interval (−1, 1) and, in this case, the true additive risks are well away from these bounds. If one expects more significant additive risks and/or has V that are unbounded, then other forms of m could be chosen to avoid estimating additive risks outside (−1, 1).

Fig. 1.

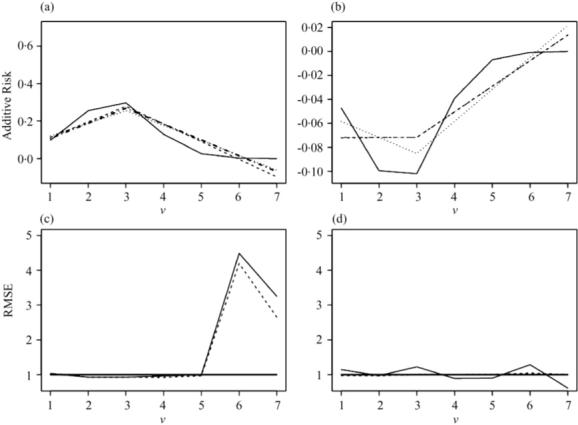
Simulation study. Performance of additive risk estimators with n = 100. The estimators and true values for each V = v for (a) a = 0, (b) a = 1, for the truth, solid line, iptw, dashed line, dr1, dashed-dotted line, and dr2, dotted line. The relative mean-squared error, rmse, relative to the iptw for (c) a = 0 and (d) a = 1 for the DR1, dashed line, and DR2, solid line, with the solid thick black line at rmse for reference.

Fig. 2.

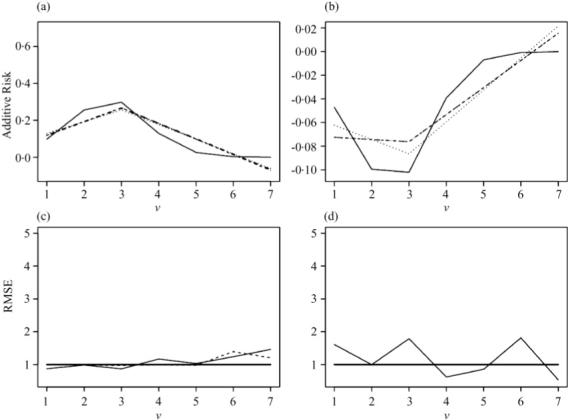
Simulation study. Performance of additive risk estimators with n = 1000. The estimators and true values for each V = v for (a) a = 0, (b) a = 1, for the truth, solid line, iptw, dashed line, DR1, dashed-dotted line, and DR2, dotted line. The relative mean-squared error, rmse, relative to the iptw for (c) a = 0 and (d) a = 1 for the DR1, dashed line, and DR2, solid line, with the solid thick black line at RMSE= 1 for reference.

The data were generated as follows. Both V and Z were distributed uniformly over the integers 1−7. Both Y and A are binary, following the conditional distributions

$$\begin{array}{c}\hfill \mathrm{logit}\left\{\mathrm{pr}(A=1\mid W)\right\}=Z-V+0.5ZV\hfill \\ \hfill \mathrm{logit}\left\{\mathrm{pr}(Y=1\mid W,A)\right\}=-2+Z+2V^2+0.5A+0.25A{V}^2.\hfill \end{array}$$

The performance of three estimators is examined: an inverse-probability-of-treatment-weighted estimator, refered to as IPTW, without the correction factor, C_h1(O | η₀, β₀), which is derived from the estimating function given by the first term of (7); a doubly-robust estimator, referred to as DR1, that is defined by the estimating function (4) and also does not use the correction factor; and another doubly-robust estimator, referred to as DR2, that is defined by the estimating function (8), which has the correction factor that should make the estimator robust to misspecification of η. For all these estimators, we use h₁(A, V ) = ∂m(A, V | β)/∂β = (1, A, V, (V – 3)₃ , AV, A(V – 3)₊). The functions g(A | W and η(V) are estimated through logistic regression, with the model for α(A | W) correctly specified as logit{g(1 | W, α)}= α₀ + α₁Z + α₂V + α₃ ZV , but the model for η(V ) misspecified as logit{η(V | γ)} = γ₀ + γ₁V; the true model is a more complicated, approximately quadratic form. The estimator h_{2, n}(V ) = η_n(V ) obtained from this model is then used for h₂(V ). One would thus expect the estimators IPTW and DR1of β to be biased, because of an inconsistent estimator of η(V ), whereas the estimator DR2 should be less biased. The nuisance parameter Q(A, W ), required by the estimators DR1 and DR2, is estimated through the correctly specified logistic regression model logit{Q(A, W | θ)}= θ₀ + θ₁Z + θ₂V² + θ₃A + θAV². The term E{∑_a∈Ah₁(a, V)h₂(V)} required by the estimator DR2 is estimated through the five-dimensional, to fit the dimension of β, vector of averages,

$$\widehat{E}\left\{\sum _{a\in \mathcal{A}}{h}_1(a,V)h_{2,n}\left(V\right)\right\}=\frac{1}{n}\sum _{i=1}^n\left\{\sum _{a\in \mathcal{A}}{h}_1(a,V_i)h_{2,n}\left(V_i\right)\right\}.$$

Finally, we use a numerical optimization routine to find the minimum of the norm of the estimating equations with respect to β:

$${\beta }_n=\arg \underset{\beta }{\min }\Vert \sum _{i=1}^n{D}_{h_1,h_{2,n}}(O_1\mid g_n,Q_n,\beta )\Vert .$$

We compare the three estimators to the true values of E(Y | V) – E(Y_a | V) for a = 0, 1 and V = 1,..., 7, using sample sizes of n = 1000. Figure 1 compares the mean estimates, over the 1000 simulations, for the three estimators to the true values at the two values of the intervention, a = 0and a = 1, separately in Figs 1(a) and (b), respectively. In addition, the overall relative performance, both variance and bias, is displayed as the relative mean-squared error, relative to the estimator IPTW, as RMSE1 and RMSE2 for the estimators DR1 and DR2, respectively, see Figs 1(c) and (d). The same simulation is repeated for a sample size of 1000; see Fig. 2.

The results suggest that, although the model for the additive risk does not contain the truth, it does a reasonable job of approximating the trend of E(Y | V ) – E(Y_a | V ) as a function of V for a = 0; see Fig. 1(a). However, for a = 1 the model is clearly biased; see Fig. 1(b). The gain in relative efficiency is apparent for a = 0 for both of the doubly-robust estimators relative to the estimator IPTW and this gain all comes from reduction in variance. In this particular case, the bias reduction resulting from the correction factor, for misspecification of η(V ), is small relative to the bias of the underlying additive risk model, Fig. 1(c). The biases for all three estimators are relatively large if a = 1 and there is no gain over the simpler estimator IPTW; see Fig. 1(d).

The story is somewhat different for larger sample sizes. The variance now is very small relative to the bias so that all differences in performance are based on differences in bias. Thus, even those estimators with, DR2, and without the correction factor for misspecification of η(V ), IPTW and DR1, have similar performance at a = 0; see Figs 2(a) and (c). For a = 1, now the two approaches without the correction factor again have identical performance, but the DR2 model now bends, see Fig. 2(b), to reduce the bias overall. However, given the limits of the estimating model for the parameter of interest, i.e. additive risk, reducing bias for some V increases it at others; the relative mean-squared error dips below 1 at V 4, 5 and 7 as shown in Fig. 2(d). Finally, if one repeats these simulations with η(V ) correctly specified, DR1 and DR2 behave nearly identically, implying that there is no further bias-reduction advantage in the estimator DR2 when the estimator of η(V ) is consistent and both estimators have similar variances.

The results suggest that the safest estimator is DR2, as it had both the benefits of lower bias and lower variance, where the relative contributions of these two sources of error change as a function of sample size.

6. Discussion

For some risk factors, one is interested in a single intervention corresponding to a particular level of the risk factor. In the case of smoking, for instance, we would only be interested in an intervention that eliminates the exposure completely; it would make little sense to estimate the disease distribution in a counterfactual population in which every subject smokes three cigarettes a day as that would require one to compel many people to start smoking. In other applications, such as air pollution studies, however, it does make sense to examine the intervention effect for interventions corresponding to different target levels. For such cases, we recommend the use of models of the form m(a, V | β) = E(Y_a – Y | V ).

Although not presented here, the intervention-models approach can easily be extended to time-dependent treatments, where the data structure includes both treatments A(j) and confounders L( j) measured at times j = 1,..., p, and a final outcome Y . In this case, the counterfactuals of interest, Y_ā, are indexed by an entire treatment history, ā = (a(0), a(1),..., a(j)). As outlined above, if η₀(V ) is known or can be estimated nonparametrically, we can use the existing estimating equations developed for estimating the mean of E(Y_ā | V ). Using the doubly-robust estimating functions presented by van der Laan & Robins (2002) for marginal structural models for time-dependent treatments, we can simply plug in η₀(V ) + m(ā, V | β) for E(Y_ā | V ), where m(ā, V | β) = E(Y_ā | V). In a manner analogous to the approach outlined in this article, these estimating equations can also be altered for robustness against misspecification of η(V).

Appendix

Estimating the influence curve for asymptotic inference

Our estimator β_n for the general mean intervention models will be consistent if either g_n is consistent for g₀ or Q_n is consistent for Q₀. Regarding statistical inference, we assume that g_n consistently estimates g₀. It is then straightforward to show that, under regularity conditions, β_n is asymptotically linear with influence curve

$$\begin{array}{cc}\hfill \mathrm{IC}(O_i\mid P_0)=& -c_0^{-1}\{D_{h_1,h_2}(O\mid g_0,Q_1,{\beta }_0)+{\mathrm{IC}}_{\mathrm{nuis}}(O\mid P_0)\}\hfill \\ \hfill & -c_0^{-1}\left[\sum _a{h}_1(a,V)h_2\left(V\right)-E\left\{\sum _a{h}_1(a,V)h_2\left(V\right)\right\}\right],\hfill \end{array}$$

where ic_nuis is the influence curve of Γ(G_n) as an estimator of

$$\begin{array}{cc}\hfill \Gamma \left(G\right)& \equiv P_{F_{X0},G}\frac{h_1(A,V)}{g_0(A\mid W)}\{Q_1(A,W)-Y\},\hfill \\ \hfill c_0& \equiv \frac{d}{d{\beta }_0}{E}_0{D}_{h_1,h_2}(O\mid g_0,Q_1,{\beta }_0).\hfill \end{array}$$

In the special case in which h₂ = h*₂, it can be shown that

$${\mathrm{IC}}_{\mathrm{nuis}}=-\Pi (D_{h_1}(\cdot \mid Q_1,g_0,{\eta }_0,{\beta }_0)\mid T_2\left(P_0\right)\},$$

where D_h1(O | Q₁, g₀,η₀,β₀) is the doubly-robust estimating function for the standard marginal structural model corresponding to the intervention model with η₀ being known; see (7) for its definition in the additive risk intervention model. Also, T₂(P₀) ⊂{φ(A, W ) : E(φ(A, W) | W) = 0} is the tangent space of the model $\mathcal{G}$ for g₀ at p₀, and Π{· | T₂(P₀) is the projection operator on to this subspace T₂(P₀) within the Hilbert space $L_0^2\left(P_0\right)$.

In general, it seems to be a reasonable approach to use ic(O | P₀) with this particular choice of ic_nuis in this influence curve decreases the variance of the influence curve, since it subtracts a T₂(P₀) component of D_h1(O | Q₁, g₀, η₀, β₀). As a consequence, a typically conservative influence curve is given by

$$\begin{array}{c}\hfill \mathrm{IC}(O_i\mid P_0)=-c_0^{-1}[D_{h_1,h_2}(O\mid g_0,Q_1,{\beta }_0)+\sum _a{h}_1(a,V)h_2\left(V\right)-\phantom{]}\hfill \\ \hfill E\phantom{[}\left\{\sum _a{h}_1(a,V)h_2\left(V\right)\right\}],\hfill \end{array}$$

which corresponds to the influence curve one would obtain if one uses g_n = g₀ as if g₀ were known.

Statistical inference for β₀ can now be based on β_n ∼ N(β₀, ∑_n), where

$${\Sigma }_n=\frac{1}{n}\sum _{i=1}^n\mathrm{EIC}\left(O_i\right)\mathrm{EIC}{\left(O_i\right)}^{\mathrm{T}}$$

and eic(O) is the estimate of the influence curve ic(O | P₀) obtained by plugging in our estimates of g₀, Q₀, h*₁, h*₂ and β₀. As mentioned in § 4, one can avoid deriving the influence curve of the estimator by using the bootstrap to estimate the distribution of n^1−/2(β_n – β₀).