Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 2008 Aug 15;105(34):12242–12247. doi: 10.1073/pnas.0805858105

Evaluating and optimizing computational protein design force fields using fixed composition-based negative design

Oscar Alvizo *, Stephen L Mayo †,‡
PMCID: PMC2516967  PMID: 18708527

Abstract

An accurate force field is essential to computational protein design and protein fold prediction studies. Proper force field tuning is problematic, however, due in part to the incomplete modeling of the unfolded state. Here, we evaluate and optimize a protein design force field by constraining the amino acid composition of the designed sequences to that of a well behaved model protein. According to the random energy model, unfolded state energies are dependent only on amino acid composition and not the specific arrangement of amino acids. Therefore, energy discrepancies between computational predictions and experimental results, for sequences of identical composition, can be directly attributed to flaws in the force field's ability to properly account for folded state sequence energies. This aspect of fixed composition design allows for force field optimization by focusing solely on the interactions in the folded state. Several rounds of fixed composition optimization of the 56-residue β1 domain of protein G yielded force field parameters with significantly greater predictive power: Optimized sequences exhibited higher wild-type sequence identity in critical regions of the structure, and the wild-type sequence showed an improved Z-score. Experimental studies revealed a designed 24-fold mutant to be stably folded with a melting temperature similar to that of the wild-type protein. Sequence designs using engrailed homeodomain as a scaffold produced similar results, suggesting the tuned force field parameters were not specific to protein G.

Keywords: fixed amino acid composition, force field optimization, random energy model

A major aim of computational protein design (CPD) is to design amino acid sequences that adopt a desired tertiary structure. This requires a CPD procedure yielding sequence scores that accurately reflect experimentally determined stabilities. Because experimental energies are determined with respect to an unfolded state, a CPD force field should accurately model interactions in both the folded and unfolded states. However, modeling the unfolded state in a useful way has proven difficult. As a result, most CPD force fields omit the specific effects of sequence changes on the unfolded state and optimize interactions only in the folded state (1). This disregard of the unfolded state is partly to blame for discrepancies between computationally derived and experimentally determined protein stabilities and for the difficulty of developing a properly tuned CPD force field (2, 3).

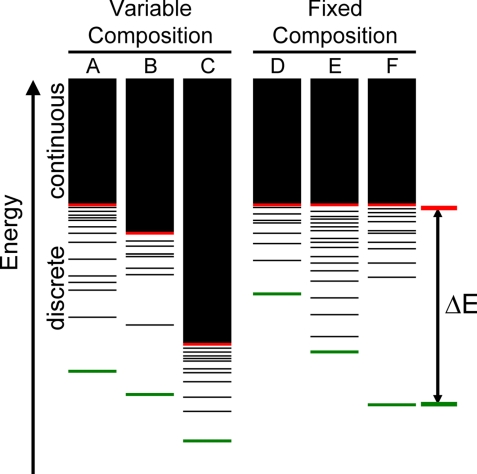
Separating the tuning of a CPD force field into its two logical components, the unfolded and folded states, could ultimately lead to force fields with significantly improved predictive power. The work presented here demonstrates a procedure for achieving this separation by invoking the random energy model (REM) (4) to minimize the influence of the unfolded state in determining sequence designs. In this way, force field evaluation and tuning can be focused on the more tractable folded state. REM was initially developed for spin glass models and later adapted for proteins (5–8). REM asserts that the energy spectrum for any specific amino acid sequence is divided into continuous and discrete regions (Fig. 1). The conformational energies in the discrete region rely on best-fit contacts, making them sequence specific. The continuous region, however, represents conformations that are accessible only at higher temperatures where the rapid interconversion between conformations leads to a distribution of conformational energies that depends solely on the amino acid composition. Consequently, all sequences with identical amino acid composition are expected to have identical continuous region distributions and, thus, identical unfolded state energies (Fig. 1 D, E, and F) (9). As a result, the free energies of folding of fixed composition sequences are directly correlated to their folded state energies. The same cannot be said when comparing sequences with varied composition (Fig. 1 A, B, and C). In this case, the continuous region varies between sequences and the free energy of folding cannot be directly compared without explicit consideration of the unfolded state. A sequence can potentially have the best energy in the folded state and fail to have the most favorable free energy of folding (Fig. 1C).

Fig. 1.

Fig. 1.

Open in a new tab

Conformational energy spectra for six sequences. Each spectrum is divided into a continuous and a discrete region. The continuous region is depicted as a solid black bar above the red marker. The lowest energy conformation for each of the sequences is shown in green. ΔE is defined as the energy difference between the lowest energy conformation and the energy at the transition between the continuous and discrete regions. Energy spectra A, B, and C represent sequences with different amino acid compositions obtained from standard, nonfixed composition designs. Energy spectra D, E, and F represent sequences with identical amino acid composition.

Here, we exploit the fixed composition concept by limiting designs to sequences with fixed amino acid composition (10, 11). By doing so, we can eliminate unfolded state contributions and focus on evaluating and optimizing the force field for the folded state. If the unfolded states for fixed sequence designs are inconsequential, any discrepancies between experimental and computational stabilities can be attributed to the force field's inability to predict the impact of sequence variation on the folded state.

Application of a fixed composition method imposes a large negative design constraint on the system (10, 11). The importance of negative design for protein sequence selection was revealed with hydrophobic/polar lattice model simulations (12, 13). Early studies on lattice models demonstrated that to recover sequences that specifically folded to the target structure, polar monomers had to be explicitly considered at surface positions even though they did not impart favorable energy to the system (12). The alternative led to sequences dominated by solvent-exposed hydrophobic monomers. Incorporation of an explicit negative design constraint on amino acid sequence selection was demonstrated by Dahiyat and Mayo (14), who went on to show that CPD could be successfully applied to complete protein domains (15). In that and related work, either a pseudobinary pattern or an explicit binary pattern of polar and nonpolar amino acids was used to impose fold specificity (15, 16). Alternative negative design approaches include the use of amino acid reference energies to control amino acid composition (17–19). Many studies have shown that amino acid composition is closely tied to the structural class of the folded protein (20, 21).

In addition to normalizing unfolded state energies, fixed composition design directly considers the fold specificity of sequences (i.e., the ability of an amino acid sequence to adopt a single or limited number of structures). REM theory indicates that as ΔE increases, the accessible conformations for a sequence exponentially decrease (7). Because the unfolded state energies are identical for amino acid sequences with the same composition, finding sequence arrangements that optimize the energy of the folded state is equivalent to maximizing ΔE (Fig. 1 D, E, and F). Optimized sequences with large favorable scores on the target fold are thus expected to exhibit an energy spectrum in which achieving an alternative conformation with lower energy is improbable.

Explicitly fixing the amino acid composition for a design has the inherent problem of requiring knowledge of the composition before the design calculation is started. For the work presented here, the wild-type sequence of the 56-residue β1 domain of streptococcal protein G (Gβ1) is used. Because Gβ1 has a high thermal stability, with a melting temperature (Tm) of 88°C, its wild-type amino acid sequence is expected to be near optimal (given the constraint of maintaining the wild-type amino acid composition). Consequently, the CPD force field can be evaluated and optimized based on its ability to recover the wild-type sequence before laborious experimental testing of designed sequences. More specifically, the use of a wild-type sequence bias energy can be used in a stepwise fashion to force recovery of the wild-type sequence and to identify problematic force field components. The computed Z-score of the wild-type sequence and the experimental testing of unbiased designs can then be used to assess the overall quality of the CPD force fields.

Results and Discussion

The Initial Force Field: Identifying Inaccuracies.

Standard force field parameters and potential functions (14, 15, 22–24) were used for our initial fixed composition designs because they have been previously tested and successfully applied to a wide range of protein design problems. The initial force field included terms for van der Waals interactions, hydrogen bond formation, and electrostatic interactions. Solvation was modeled by using a solvent-accessible surface area-based term that encourages hydrophobic burial and polar exposure. Side-chain flexibility was taken into account by using expanded versions of the backbone-dependent rotamer library of Dunbrack and Karplus (25).

Successful application of the initial force field required imposing some type of binary pattern, either explicitly or by restricting buried positions to nonpolar amino acids and exposed positions to polar amino acids (15, 16, 26). In our fixed composition designs, however, we removed these restrictions and, within the fixed composition limits, allowed all amino acids at all positions. Without any binary pattern or regional restrictions, we expected the resulting fixed composition sequences to reveal previously hidden inaccuracies in the standard force field, and to allow us to identify aspects that could be improved.

Fixed composition designs were first performed on Gβ1 by using the initial (standard) force field. All non-Gly positions (a total of 51 positions) were included in the design, and the amino acid composition was fixed to that of the wild-type protein. A wild-type sequence bias was imposed and incrementally increased until the wild-type sequence was recovered. Fig. 2A shows the top-ranked sequences obtained from each calculation. At lower sequence biases, the computed sequences exhibited poor recovery of the wild-type amino acids, revealing substantial inaccuracies in the initial force field. The unbiased design (sbias0.0) had 16% identity with the wild-type sequence, an increase of only 5% over random fixed composition sequences (Table 1). Only 2 out of 10 designed core positions were computed to take on wild-type amino acids, and even lower percentages of boundary and surface positions were recovered (8% and 17%, respectively).

Fig. 2.

Fig. 2.

Open in a new tab

Computed sequences for Gβ1 fixed composition designs. Designed core, boundary, and surface positions are shown in red, green, and blue, respectively. The wild-type sequence is shown, followed by the sequences computed at increasing sequence bias values (kcal/mol per position). Dots represent wild-type amino acids. (A) Sequences obtained by using the initial force field. (B) Sequences obtained by using the tuned force field.

Table 1.

Percent wild-type sequence identity before and after force field optimization

Computed sequences Percent sequence identity*
Total Core Boundary Surface
Gβ1, initial force field
    sbias0.0 16 20 8 17
    sbias2.0 55 70 33 59
    sbias4.0 84 80 67 93
    sbias5.0 92 90 92 93
    sbias6.0 100 100 100 100
Gβ1, tuned force field
    sbias0.0 53 100 50 38
    sbias0.5 76 100 50 86
    sbias1.0 92 100 83 97
    sbias1.5 96 100 92 97
    sbias2.0 100 100 100 100
ENH, initial force field
    sbias0.0 22 20 9 28
    sbias2.0 46 30 27 59
    sbias4.0 66 60 55 72
    sbias6.0 96 90 91 100
    sbias8.0 96 90 91 100
    sbias9.0 100 100 100 100
ENH, tuned force field
    sbias0.0 42 80 45 28
    sbias0.5 64 80 55 62
    sbias1.0 86 90 82 86
    sbias1.5 90 90 91 90
    sbias2.0 94 90 100 93
    sbias2.5 100 100 100 100
Open in a new tab

*Wild-type sequence identity was determined by using only the positions in the design. Values are rounded to the nearest integer. Wild-type sequence identities for random fixed composition sequences for Gβ1 were calculated to be 11%, 8%, 11%, and 12% for total, core, boundary, and surface positions, respectively.

The inaccuracies in the initial force field were further highlighted by the poor quality of the sequences computed using strong sequence bias energies (as high as 5 kcal/mol per position). All of the computed sequences contained charged and/or polar amino acids at core positions (Fig. 2A). The sequence recovered at a sequence bias of 5 kcal/mol replaced a core Leu with a Glu. In a small protein with a well packed hydrophobic core, it is unlikely that substituting nonpolar amino acids with charged residues would result in a more stable variant (27). Exploratory modifications to the force field suggested that changing to a solvent exclusion-based solvation model would result in improved prediction of core residues (28). This model emphasizes polar desolvation, which results in larger penalties for burial of polar atoms; consequently, charged or polar amino acids in hydrophobic environments are strongly disfavored.

Further inspection of the computed sequences revealed a bias toward sequence arrangements that benefit from the strong hydrogen bond potential contained in the initial force field. Certain core positions were computed to take on polar side chains, partly because they were able to form strong interresidue hydrogen bonds. For example, core position 20 mutated from Ala to Gln to form two hydrogen bonds with surface residues. The predicted Gln side chain assumes a strained conformation to satisfy the interactions. Similarly, Thr at core position 30 is predicted to form a hydrogen bond with the α-helical backbone. Due to Thr's polar character and low α-helical propensity (29), this mutation is likely to be destabilizing. We anticipated that lowering the explicit benefit for hydrogen bond formation would reduce this unwanted preference for polar side chains in the core.

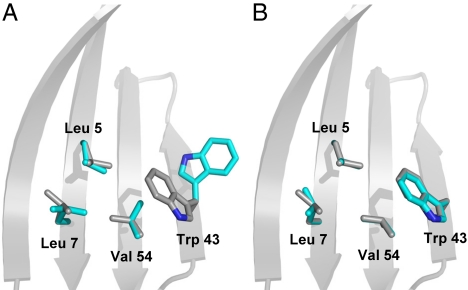
The discrete nature of rotamer libraries also appears to be problematic, in that a suitable conformation for the wild-type amino acid may not be available for certain positions. For example, the absence of a rotamer with χ angles similar to those seen in the crystal structure for core Leu-7 resulted in spurious predictions. The poor choice of rotamer configuration at position 7 propagates throughout the core and results in the expulsion of Trp-43 in all of the computed sequences obtained with the initial force field (Fig. 3A). The use of a larger, more representative rotamer library should mitigate this type of problem, as it is more likely to contain conformations comparable with the structural and chemical constraints of the design target.

Fig. 3.

Fig. 3.

Open in a new tab

Predicted and wild-type crystal structure conformations for four Gβ1 design positions. (A) Conformations obtained by using a standard rotamer library. (B) Conformations obtained by using a conformer library. Predicted conformations are shown in cyan; wild-type crystal structure conformations are depicted in gray.

Three of the computed sequences obtained with the initial force field were selected for further study. Sequences obtained at a sequence bias of 0.0, 2.0, and 5.0 kcal/mol per position (sbias0.0, sbias2.0, and sbias5.0) were chosen for experimental characterization. Not surprisingly, circular dichroism (CD) spectra showed that the proteins with the largest differences from wild type (sbias0.0 and sbias2.0) were unfolded (data not shown). Sbias5.0 (92% overall sequence identity with Gβ1), with a Tm of 64.1°C, was folded but significantly destabilized compared to Gβ1.

Tuning the Force Field.

Multiple rounds of optimization were required to obtain a force field that yielded viable sequences. In an effort to hinder the selection of charged or polar residues in the core, we first changed the model used to calculate atomic solvation: The surface area-based model was replaced by a solvent exclusion-based model (28). In addition, the explicit benefit for hydrogen bond formation was decreased (well depth reduced from 8 to 4 kcal/mol) and completely eliminated for interresidue interactions involving surface positions. To increase the chances of recovering native-like conformations, we replaced the rotamer library with a larger conformer library (30, 31). Because the reduction in the explicit benefit for hydrogen bond formation also affects the benefit for salt-bridge formation between charged amino acids, we compensated by reducing the distance dependent dielectric constant from 40r to 20r. Further details on the modifications are described in Materials and Methods.

The sequences computed with the tuned force field are shown in Fig. 2B. Unlike the sequences obtained with the initial parameters, the tuned-parameter sequences exhibited no obvious irregularities that discouraged further evaluation. All core positions at all bias levels (including sbias0.0) achieved wild-type amino acid identities, ensuring that the core is well packed and hydrophobic (Table 1 and Fig. 2B). In addition, use of a conformer library resulted in core side chain conformations that overlaid nicely with those seen in the wild-type crystal structure, even though the Gβ1 structure was not included in the set of structures used to generate the conformer library (Fig. 3B).

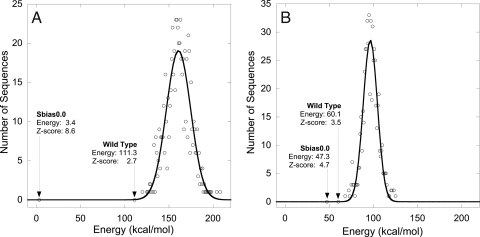
Additional results are illustrated in Table 1. The total wild-type recovery of the unbiased sequence (sbias0.0) increased from 16% to 53%. Wild-type sequence recovery was 100% for core, 50% for boundary, and 38% for surface positions, representing 5-fold, 6-fold, and 2-fold improvements, respectively, compared to the initial sibas0.0 design. The sequence bias required to recover the wild-type sequence decreased from 6.0 to 2.0 kcal/mol/position. More importantly, the Z-score for the wild-type sequence increased from 2.7 for the initial force field to 3.5 for the tuned force field (Fig. 4), consistent with expectations of force field improvement (32–35). A clearer picture of the improvement is seen by comparing the wild-type sequence with sequences obtained using no sequence bias. Initial parameters yielded a Z-score of 8.6 for the computed unbiased sequence (sbias0.0), a difference of 5.9 compared to the 2.7 value obtained for the wild-type sequence (Fig. 4A). The fact that a sequence resulting in an unfolded protein had such a large Z-score relative to that calculated for the wild-type sequence is further evidence of the poor predictive power of the initial force field in the absence of any sequence patterning. In contrast, the tuned force field parameters produced a Z-score for the unbiased sequence (sbias0.0) of 4.7, a difference of only 1.2 relative to the wild-type sequence (Fig. 4B).

Fig. 4.

Fig. 4.

Open in a new tab

Energies and Z-scores for wild-type and unbiased sequences (sbias0.0) computed in Gβ1 fixed composition designs. (A) Initial force field parameters. (B) Tuned force field parameters. The energy distributions were obtained by evaluating the energy of 1,000 random sequences with the wild type's amino acid composition. The energy scores omit contributions from the van der Waals potential function.

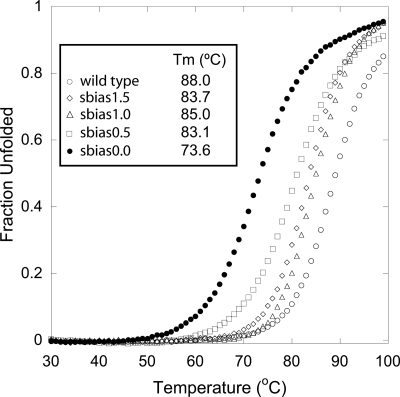
Definitive validation of the tuned force field was provided by experimental analysis of the computed sequences. Proteins corresponding to sbias0.0, sbias0.5, sbias1.0, and sbias1.5 were all shown to be folded by CD [supporting information (SI) Fig. S1], and sbias0.0, with only 53% overall sequence identity to Gβ1, was shown to be folded by 1D NMR (Fig. S2). Temperature denaturation experiments revealed all of the designed proteins to be highly thermostable with Tms of 74, 83, 85, and 84°C for sbias0.0, sbias0.5, sbias1.0, and sbias1.5, respectively (Fig. 5). In contrast to the unbiased sequence obtained with the initial parameters, the unbiased sequence obtained with the tuned parameters resulted in a protein that was stably folded and well behaved.

Fig. 5.

Fig. 5.

Open in a new tab

Temperature denaturation of Gβ1 mutants obtained with the tuned force field parameters. From left to right, the data show sbias0.0 (filled circles), sbias0.5 (open squares), sbias1.5 (open diamonds), sbias1.0 (open triangles), and the wild-type sequence (open circles).

Transferability of Tuned Force Field: Engrailed Homeodomain.

To test the transferability of the tuned force field parameters, we carried out fixed composition designs on a 51-aa fragment of the Engrailed homeodomain from Drosophila melanogaster (ENH). ENH is a small globular protein with no sequence or structure similarity to Gβ1 (36).

Table 1 shows sequence statistics from fixed composition designs on ENH. The wild-type sequence was recovered at a sequence bias of 2.5 kcal/mol per position. The unbiased design (sbias0.0) resulted in a sequence with 42% wild-type identity, with the core recovering 80% of the wild-type amino acids (Fig. S3). Using the tuned force field parameters, the Z-score difference for the unbiased design versus wild type was only 1.7 (4.6 − 2.9). This is in contrast to a Z-score difference of 5.5 (8.0 − 2.5) when using the initial parameters.

The tuned force field computed reasonable sequences for ENH, with improved Z-scores when compared to the initial force field. These results support the idea that the modifications to the force field are not specific for the Gβ1 scaffold. However, to best eliminate bias toward a particular scaffold, the force field optimization procedure would ideally be carried out simultaneously on multiple scaffolds.

Conclusions

Fixed composition design proved to be an effective way to tune the positive design parameters in our CPD force field. By limiting the designs to sequences with identical amino acid composition, we were able to attribute inconsistencies between computational and experimental results to the force field's inability to accurately model the folded state. A direct comparison between computational and experimental results was possible because the unfolded state energy is presumed to be equal for all sequences.

Iterative use of fixed composition design allowed for a set of force field parameters to be identified that resulted in the prediction of folded and well behaved sequences. The implementation of this procedure is straightforward and generalizable to any protein design force field, provided a sequence for the selected scaffold is shown to be near optimal for its folded structure. To limit unintentional bias toward the target scaffold, the fixed composition optimization procedure should be carried out on multiple scaffolds.

Materials and Methods

Fixed Composition Scaffolds.

Coordinates for the backbone structure of Gβ1 and ENH were obtained from the Protein Data Bank entry 1PGA and 1ENH, respectively. Any strain or steric clashes in the structure were removed by performing 50 steps of energy minimization (37). Residue classification into core, boundary, and surface groups was performed as described previously (15). All 51 non-Gly positions were included in the design, and within fixed composition restraints, all amino acids found in the wild-type Gβ1 sequence were allowed at all designed positions.

Fixed Composition Force Fields.

The initial force field used standard potential functions and parameters including scaled van der Waals, hydrogen bonding, electrostatic, and surface area-based solvation terms, as described previously (14, 15, 22–24). Expanded versions of Dunbrack and Karplus' 1995 backbone-dependent rotamer library were used (25). Aromatic residues were expanded 1 SD about their χ1 and χ2 values, and hydrophobic residues were expanded 1 SD about their χ1 values; polar residues were not expanded.

The tuned force field used a solvent exclusion-based solvation potential (28). All published solvation parameters were used with the exception of polar burial, which was decreased by 40% (28). The benefit for side chain–side chain hydrogen bond formation was decreased by 50% for core and boundary residues. Hydrogen bond energies were decreased by an additional 75% if they occurred between immediate neighbors (n + 1 and n − 1 positions). Hydrogen bonds at surface positions received a benefit from the electrostatic potential, but not from the hydrogen bond potential. The distance-dependent dielectric constant was reduced from 40r to 20r.

The tuned force field used a larger backbone-dependent conformer library (30) instead of a rotamer library. The conformer library was constructed by using Cartesian coordinates taken directly from high-resolution crystal structures as described by Lassila et al. (31). For constructing the conformer library, a P value for nonpolar amino acids was set to 0.3; a P value of 0.6 was used for Asp, Glu, Asn, and Gln; and representative conformers for Arg and Lys were obtained with a P of 0.8.

Fixed Composition Sequence Optimization.

Before sequence optimization, an energy matrix containing all one-body and two-body interactions was created. The one-body term for each rotamer was modified to reflect a specified sequence bias energy. Each rotamer that differed in identity from the wild-type amino acid at a particular position received a penalty. The resulting sequence was thus penalized for each residue that differed from the wild-type sequence. All calculations were first carried out in the absence of a sequence bias. The bias energy was then incrementally increased by 1.0 or 0.5 kcal/mol per position, with all other parameter kept fixed, until the wild-type sequence was recovered.

Monte Carlo simulated annealing was used for the fixed composition Gβ1 designs. The fixed composition restraint was imposed in a Monte Carlo algorithm called FMONTE. The FMONTE algorithm randomly picks four positions and arbitrarily switches the amino acids at two, three, or all four of the positions. A random rotamer is chosen at each of the switched positions, and the sequence energies are compared. All calculations were carried out for 1,000 annealing cycles at 1,000,000 steps per cycle, and the temperature was cycled from 4,000 K to 150 K. Fixed composition designs on ENH were performed using a fixed composition version of the FASTER algorithm (38), as it is a more effective search algorithm.

Protein Expression and Purification.

Plasmids coding for mutant proteins were created by site-directed mutagenesis of the wild-type gene in pET-11a or ordered from Blue Heron Biotechnology. Electroporation was used to transform plasmids into BL21 (DE3) cells. Cells were allowed to express protein for 3 h after induction with IPTG, then harvested and lysed by sonication. Cell extracts were spun down and precipitated by addition of 50% acetonitrile. The soluble protein was separated from the precipitate by centrifugation and purified by HPLC. Pure proteins were analyzed by either trypsin digest or by collision-induced dissociation mass spectrometry to verify designed amino acid sequences.

Experimental Characterization.

CD studies were performed using an Aviv 62A DS spectropolarimeter with a thermoelectric cell holder. Samples were prepared in 50 mM sodium phosphate buffer at pH 5.5. Wavelength scans and temperature denaturations were carried out in cuvettes with a 0.1-cm path length at a concentration of 50 μM (300 μl). Three wavelength scans were performed at 25°C for each sample and averaged. Data were collected from 200 nm to 250 nm at 1-nm intervals and averaged for 1 sec. Temperature denaturations were carried out from 0°C to 99°C, sampling every 1°C. Samples were equilibrated for 90 sec before data were collected (averaging time 30 sec). 1D 1H NMR spectra were collected on a Varian Unityplus 600-MHz spectrometer at 25°C. Samples were prepared in 50 mM sodium phosphate buffer pH 5.5 using 9:1 H2O/2H2O.

Supplementary Material

Supporting Information
supp_105_34_12242__index.html (645B, html)

Acknowledgments.

We thank Marie Ary for help with the manuscript, Scott Ross and Karin Crowhurst for their assistance with NMR, and Ben Allen for preparation of the conformer library. This work was supported by the Ralph M. Parsons Foundation, the Howard Hughes Medical Institute, and the National Institutes of Health.

Footnotes

The authors declare no conflict of interest.

This article contains supporting information online at www.pnas.org/cgi/content/full/0805858105/DCSupplemental.

References

  • 1.Gordon DB, Marshall SA, Mayo SL. Energy functions for protein design. Curr Opin Struct Biol. 1999;9:509–513. doi: 10.1016/s0959-440x(99)80072-4. [DOI] [PubMed] [Google Scholar]
  • 2.Dill KA, Shortle D. Denatured states of proteins. Annu Rev Biochem. 1991;60:795–825. doi: 10.1146/annurev.bi.60.070191.004051. [DOI] [PubMed] [Google Scholar]
  • 3.Lazar GA, Desjarlais JR, Handel TM. De novo design of the hydrophobic core of ubiquitin. Protein Sci. 1997;6:1167–1178. doi: 10.1002/pro.5560060605. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Derrida B. Random-energy model: Limit of a family of disordered models. Phys Rev Lett. 1980;45:79–82. [Google Scholar]
  • 5.Bryngelson JD, Wolynes PG. Spin glasses and the statistical mechanics of protein folding. Proc Natl Acad Sci USA. 1987;84:7524–7528. doi: 10.1073/pnas.84.21.7524. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Shakhnovich EI, Gutin AM. Formation of unique structure in polypeptide chains. Theoretical investigation with the aid of a replica approach. Biophys Chem. 1989;34:187–199. doi: 10.1016/0301-4622(89)80058-4. [DOI] [PubMed] [Google Scholar]
  • 7.Shakhnovich EI, Gutin AM. A new approach to the design of stable proteins. Protein Eng. 1993;6:793–800. doi: 10.1093/protein/6.8.793. [DOI] [PubMed] [Google Scholar]
  • 8.Pande VS, Grosberg AY, Tanaka T. Statistical mechanics of simple models of protein folding and design. Biophys J. 1997;73:3192–3210. doi: 10.1016/S0006-3495(97)78345-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Shakhnovich EI, Gutin AM. Engineering of stable and fast-folding sequences of model proteins. Proc Natl Acad Sci USA. 1993;90:7195–7199. doi: 10.1073/pnas.90.15.7195. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Koehl P, Levitt M. De novo protein design. I. In search of stability and specificity. J Mol Biol. 1999;293:1161–1181. doi: 10.1006/jmbi.1999.3211. [DOI] [PubMed] [Google Scholar]
  • 11.Koehl P, Levitt M. De novo protein design. II. Plasticity in sequence space. J Mol Biol. 1999;293:1183–1193. doi: 10.1006/jmbi.1999.3212. [DOI] [PubMed] [Google Scholar]
  • 12.Yue K, Dill KA. Inverse protein folding problem: Designing polymer sequences. Proc Natl Acad Sci USA. 1992;89:4163–4167. doi: 10.1073/pnas.89.9.4163. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Yue K, et al. A test of lattice protein folding algorithms. Proc Natl Acad Sci USA. 1995;92:325–329. doi: 10.1073/pnas.92.1.325. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Dahiyat BI, Mayo SL. Probing the role of packing specificity in protein design. Proc Natl Acad Sci USA. 1997;94:10172–10177. doi: 10.1073/pnas.94.19.10172. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Dahiyat BI, Mayo SL. De novo protein design: Fully automated sequence selection. Science. 1997;278:82–87. doi: 10.1126/science.278.5335.82. [DOI] [PubMed] [Google Scholar]
  • 16.Marshall SA, Mayo SL. Achieving stability and conformational specificity in designed proteins via binary patterning. J Mol Biol. 2001;305:619–631. doi: 10.1006/jmbi.2000.4319. [DOI] [PubMed] [Google Scholar]
  • 17.Kuhlman B, Baker D. Native protein sequences are close to optimal for their structures. Proc Natl Acad Sci USA. 2000;97:10383–10388. doi: 10.1073/pnas.97.19.10383. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Raha K, Wollacott AM, Italia MJ, Desjarlais JR. Prediction of amino acid sequence from structure. Protein Sci. 2000;9:1106–1109. doi: 10.1110/ps.9.6.1106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Wernisch L, Hery S, Wodak SJ. Automatic protein design with all atom force-fields by exact and heuristic optimization. J Mol Biol. 2000;301:713–736. doi: 10.1006/jmbi.2000.3984. [DOI] [PubMed] [Google Scholar]
  • 20.Chou KC, Zhang CT. Prediction of protein structural classes. Crit Rev Biochem Mol Biol. 1995;30:275–349. doi: 10.3109/10409239509083488. [DOI] [PubMed] [Google Scholar]
  • 21.Zhang TL, Ding YS, Chou KC. Prediction protein structural classes with pseudo-amino acid composition: Approximate entropy and hydrophobicity pattern. J Theor Biol. 2008;250:186–193. doi: 10.1016/j.jtbi.2007.09.014. [DOI] [PubMed] [Google Scholar]
  • 22.Dahiyat BI, Mayo SL. Protein design automation. Protein Sci. 1996;5:895–903. doi: 10.1002/pro.5560050511. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Dahiyat BI, Gordon DB, Mayo SL. Automated design of the surface positions of protein helices. Protein Sci. 1997;6:1333–1337. doi: 10.1002/pro.5560060622. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Street AG, Mayo SL. Pairwise calculation of protein solvent-accessible surface areas. Fold Des. 1998;3:253–258. doi: 10.1016/S1359-0278(98)00036-4. [DOI] [PubMed] [Google Scholar]
  • 25.Dunbrack RL, Jr., Karplus M. Backbone-dependent rotamer library for proteins. Application to side-chain prediction. J Mol Biol. 1993;230:543–574. doi: 10.1006/jmbi.1993.1170. [DOI] [PubMed] [Google Scholar]
  • 26.Malakauskas SM, Mayo SL. Design, structure and stability of a hyperthermophilic protein variant. Nat Struct Biol. 1998;5:470–475. doi: 10.1038/nsb0698-470. [DOI] [PubMed] [Google Scholar]
  • 27.Meyer SC, Huerta C, Ghosh I. Single-site mutations in a hyperthermophilic variant of the β1 domain of protein G result in self-assembled oligomers. Biochemistry. 2005;44:2360–2368. doi: 10.1021/bi048197l. [DOI] [PubMed] [Google Scholar]
  • 28.Lazaridis T, Karplus M. Effective energy function for proteins in solution. Proteins. 1999;35:133–152. doi: 10.1002/(sici)1097-0134(19990501)35:2<133::aid-prot1>3.0.co;2-n. [DOI] [PubMed] [Google Scholar]
  • 29.Chou PY, Fasman GD. Conformational parameters for amino acids in helical, beta-sheet, and random coil regions calculated from proteins. Biochemistry. 1974;13:211–222. doi: 10.1021/bi00699a001. [DOI] [PubMed] [Google Scholar]
  • 30.Shetty RP, De Bakker PI, DePristo MA, Blundell TL. Advantages of fine-grained side chain conformer libraries. Protein Eng. 2003;16:963–969. doi: 10.1093/protein/gzg143. [DOI] [PubMed] [Google Scholar]
  • 31.Lassila JK, Privett HK, Allen BD, Mayo SL. Combinatorial methods for small-molecule placement in computational enzyme design. Proc Natl Acad Sci USA. 2006;103:16710–16715. doi: 10.1073/pnas.0607691103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Bowie JU, Luthy R, Eisenberg D. A method to identify protein sequences that fold into a known three-dimensional structure. Science. 1991;253:164–170. doi: 10.1126/science.1853201. [DOI] [PubMed] [Google Scholar]
  • 33.Chiu TL, Goldstein RA. Optimizing potentials for the inverse protein folding problem. Protein Eng. 1998;11:749–752. doi: 10.1093/protein/11.9.749. [DOI] [PubMed] [Google Scholar]
  • 34.Chiu TL, Goldstein RA. Optimizing energy potentials for success in protein tertiary structure prediction. Fold Des. 1998;3:223–228. doi: 10.1016/S1359-0278(98)00030-3. [DOI] [PubMed] [Google Scholar]
  • 35.Street AG, Datta D, Gordon DB, Mayo SL. Designing protein β-sheet surfaces by Z-score optimization. Phys Rev Lett. 2000;84:5010–5013. doi: 10.1103/PhysRevLett.84.5010. [DOI] [PubMed] [Google Scholar]
  • 36.Clarke ND, Kissinger CR, Desjarlais J, Gilliland GL, Pabo CO. Structural studies of the engrailed homeodomain. Protein Sci. 1994;3:1779–1787. doi: 10.1002/pro.5560031018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 37.Mayo SL, Olafson BD, Goddard WA., III DREIDING: A generic force field for molecular simulations. J Phys Chem. 1990;94:8897–8909. [Google Scholar]
  • 38.Hom GK, Mayo SL. A search algorithm for fixed-composition protein design. J Comput Chem. 2006;27:375–378. doi: 10.1002/jcc.20346. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information
supp_105_34_12242__index.html (645B, html)
0805858105_0805858105SI.pdf (444.7KB, pdf)

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES