Rational design of new binding specificity by simultaneous mutagenesis of calmodulin and a target peptide

Abstract

Calcium-saturated calmodulin (CaM) binds and influences the activity of a varied collection of target proteins in most cells. This promiscuity underlies CaM's role as a shared participant in calcium-dependent signal transduction pathways, but imposes a handicap on popular CaM-based calcium biosensors, which display an undesired tendency to cross-react with cellular proteins. Designed CaM/target pairs that retain high affinity for one another, but lack affinity for wild-type CaM and its natural interaction partners, would therefore be useful as sensor components, and possibly also as elements of “synthetic” cellular signaling networks. Here we have adopted a rational approach to creating suitably modified CaM/target complexes by using computational design methods to guide parallel site-directed mutagenesis of both binding partners. A hierarchical design procedure was applied to suggest a small number of complementary mutations on CaM and on a peptide ligand derived from skeletal muscle light chain kinase (M13). Experimental analysis showed that the procedure was successful in identifying CaM and M13 mutants with novel specificity for one another. Importantly, the designed complexes retained affinity comparable to the wild-type CaM/M13 complex. These results represent a step toward the creation of CaM and M13 derivatives with specificity fully orthogonal to the wild-type proteins, and show that qualitatively accurate predictions may be obtained from computational methods applied simultaneously to two proteins involved in multiple linked binding equilibria.

Calmodulin (CaM) forms high affinity complexes with an astonishing array of proteins involved in signaling and regulatory events. Interactions between CaM and CaM targets are essential to healthy cellular physiology in all eukaryotes, and have been extensively studied using structural, biochemical, and genetic methods. (1) Most calcium-dependent CaM interactions require insertion of short amino acid sequences from the target proteins into a hydrophobic cleft located between CaM's amino- and carboxy-terminal EF hand motif pairs (Figure 1A). (2, 3) Calcium-loaded CaM binds to isolated target sequences with affinity comparable to its complexes with the intact proteins, and with dissociation constants often in the nanomolar range. With few exceptions, CaM ligands tend to be highly basic, presenting lysine and arginine residues that form salt-bridge networks with negatively-charged and polar amino-acid side chains bordering the binding cleft on CaM (Figure 1B). In addition, many CaM targets appear to be anchored by a key pair of bulky groups spaced apart by 2.5 or 3.5 helical turns. (4) Deletion or mutation of these anchor residues dramatically reduces CaM-binding affinity. (5, 6)

Figure 1. Sequence and structure of CaM-binding peptides.

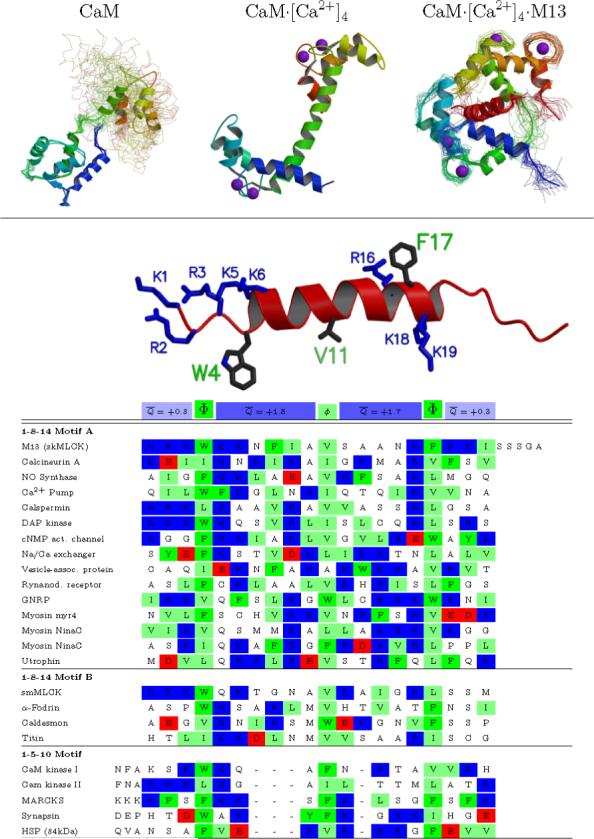
(A) CaM: The solution structure of CaM in the absence of Ca2+ shows relatively well structured N- and C-terminal domains but free motion between the domains. CaM·[Ca2+]₄: The crystal structure of CaM in the presence of calcium shows a different structure for each domain, and a single well-defined helical connection between them (although this region is flexible in solution). CaM·[Ca2+]₄·M13: The solution structure of peptide-bound CaM shows a domain structure similar to CaM·[Ca2+]₄, but a very different relation between them —the linking helix bends to enclose the helical peptide between the two domains. (B) An alignment of a representative set of mammalian CaM-binding peptides shows a general motif, but no clear consensus sequence. Two larger hydrophobic residues are spaced 2.5 or 3.5 helical turns apart, and anchor the peptide into each domain of CaM. An additional smaller hydrophobic group located one or two turns from the first is also conserved. There is no further conservation at any given position, but all the peptides are basic (+1 to +8 net charge). This net charge is fairly evenly distributed, with an average of roughly +1.5e located in each of the regions between the hydrophobic anchors, and an average of roughly +0.5e on the three residues on either side of the of the core helical region. Sequences taken from Rhoads and Friedberg. (4) Structural figure generated with molscript (60) and raster3d. (61)

Considerable interest in CaM/peptide interactions has revolved around potential applications in biotechnology. CaM-affinity chromatography (7) is a commercially available basis for purification of bacterially expressed proteins tagged with CaM-binding epitopes, and CaM-binding molecules have also been used analogously to antibodies in protein-detection and cell-sorting assays. (8, 9) More recently, CaM has been fused to derivatives of green fluorescent protein (GFP) and used to actuate a series of unimolecular and bimolecular calcium indicators for optical imaging. (10-14) These sensors have the advantages that they may be genetically encoded, that they are tuned to physiological calcium fluxes, and that they may be targeted to sub-cellular compartments with appropriate localization signals. An experimental calcium sensor for magnetic resonance imaging (MRI) has also been constructed by conjugating CaM and CaM targets to magnetic nanoparticles. (15) However, an important drawback of most CaM-based molecular tools is their susceptibility to unwanted interactions with cellular CaM and CaM targets; this interference explains, for instance, why CaM-affinity purification cannot be applied to proteins overexpressed in eukaryotic cells (which contain many natural CaM targets), (16) and why CaM-based sensors function inefficiently in cellular environments with high levels of endogenous CaM. (17, 18)

The ability to understand and control determinants of binding specificity at the CaM/target interface is important both for biotechnological applications and for appreciation of how CaM transduces metabolic signals via multiple protein interaction networks. Many studies have probed the contributions of both the charged and hydrophobic anchor residues to CaM binding affinity, (5, 6, 19-22) but relatively few have sought to manipulate specificity through purposeful mutagenesis of one or both binding partners. A step in this direction was taken by Mayo and colleagues, (23, 24) and involved the integration of computational and experimental methods to bias CaM specificity toward one of its many target peptides. In their modeling efforts, these authors neglected “negative selection” of CaM variants with high affinity for undesired targets, focusing solely on stabilization of the desired complex. More recently, Palmer et al. (17) constructed charge mutants of CaM and one of its targets to produce a GFP-based sensor resistant to binding by wild-type CaM. This work involved manipulation of both sides of the CaM/peptide interface, but resulted in approximately 10^5-fold reduction in overall binding affinity, with respect to the wild-type complex. These studies leave unresolved questions as to whether significant alteration of CaM binding specificity (i.e. recognition of new peptides) is actually consistent with high-affinity complex formation, and whether novel specificity can be designed by consideration of the molecular structure.

A central challenge in creating CaM mutants specific for unnatural peptide targets is that CaM and peptide residues must be simultaneously varied to produce effective combinations at the interaction surface. Two solutions to the problem are: (1) to generate large libraries of CaM and target sequences and select for tight binding pairs with low affinity for the wild-type proteins; or (2) to use structural and energetic considerations to design and test specific mutant proteins with the desired properties. Computationally guided approaches have been shown to be very powerful methods for the design of proteins (25-32) and their binding interfaces. (33-35) Here we have chosen to pursue such an approach, in large part because of the wealth of structural and biochemical data on CaM complexes available on which to base predictions; we focused in particular on the well-studied CaM complex with M13, a peptide derived from skeletal muscle light chain kinase. (36) The calculations we applied were designed to sample an extensive space of possible CaM- and M13-derived sequences and conformations as effectively as possible, and to select promising mutants by explicitly incorporating the balance between wild-type and mutant binding equilibria (four possible interactions) that give rise to specificity. Our results are significant in that they led to a set of high affinity variant CaM/M13 pairs with modified anchor residues and partial resistance to wild-type proteins, and because they constitute a test case for design methods that might be extended to treat other multi-protein systems involving binding and competition.

Methods

Structure preparation

All calculations were based on the minimized average from the NMR structure determination of Calmodulin (CaM) bound to the M13 peptide from rabbit skeletal muscle myosin light chain kinase (Protein Data Bank (37) ID 2BBM). (38) Hydrogen atoms attached to carbons were removed for consistency with the param19 parameter set used in the calculations. The positions of hydrogen atoms attached to hetero-atoms were re-optimized using the hbuild facility (39) of the charmm computer program. (40)

Protein design methodology

Sequences compatible with a low energy complex structure were selected using a discrete structural search of side chain conformers using the Dead End Elimination and A^* algorithms (DEE/A^*). (41-46) The Dunbrack and Karplus rotamer library (47) was used, augmented by rotamers at ± 10° of χ₁ and χ₂ for each rotamer. Hydroxyl groups on Ser, Thr and Tyr were sampled at ± 60° and 180°. As each design site was chosen to be a relatively independent group, only those positions directly considered in the sequence redesign were allowed conformational flexibility. This approach may limit the results obtained, but provides a bias towards maintaining the structure of the complex near that of the native structure.

A hierarchical approach was used to ensure diversity of sequence and structural variability. A “sequence-mer” energetic description was used in the initial DEE/A^* search, yielding all sequences for which the computed stability of the complex was within 30 kcal/mol of the global minimum. Each of these sequences was expanded to give the ten lowest energy structural states. Only one of any set of near-neighbor structures (rotamer states differing only by the enhanced sampling of χ₁ and χ₂) was allowed in this group of ten.

Energies for the initial search were calculated using the charmm computer program with the param19 polar-hydrogen, molecular-mechanics force field. (40) A distance-dependant dielectric constant of 4r was used for electrostatic interactions. All energies were calculated relative to isolated model compounds of the variable side chains (minimum energy isolated side chain). Locally written software was used for the search.

Energies of the structures obtained by the above search were refined with solvation effects treated using a continuum electrostatic model to replace the 4r Coulombic term. Each of the complexes was rigidly separated, and the electrostatic component of the solvation energy in both the bound and unbound states was computed using a finite-difference Poisson– Boltzmann (FDPB) approach, as implemented in a locally-modified version of the program delphi. (48-51) Calculations were performed with the param19 parameters using a two-stage focusing procedure (the molecule occupying first 23% then 92% of the grid) on a 129 × 129 × 129 grid. The hydrophobic contribution to the solvation free energy was estimated by a term proportional to the solvent accessible surface area, using a factor of 5 cal/mol/Ų. The solvation energies of the isolated model compound reference states were also computed. The difference between the energy of any given structure (including both molecular mechanics and FDPB energetic contributions) and the sum of the appropriate reference compound energies is the computed stability of that structure. The difference between the lowest energy complex structure and the lowest energy separated proteins (including all contributions) is the computed binding free energy. The rigid body approximation is clearly an imperfect representation of binding in this system; CaM is known to undergo a major conformational change, and the relatively short M13 peptide is likely unstructured in solution. The binding reaction considered here may be viewed as the second step in a two-step process: the components first adopt the structures observed in the complex and then rigidly bind (this is a thermodynamic separation, not necessarily a mechanistic one). The neglect of energetic differences in the structural rearrangement step is a recognized deficiency in the model; accurate evaluation of these contributions is a major challenge, particularly considering that neither CaM nor M13 adopt a single well-defined structure in the unbound state.

Protein and peptide preparation

Wild-type and mutant CaM expression vectors were derived from a gene for Xenopus laevis CaM (generous gift of Atsushi Miyawaki, RIKEN Brain Science Institute, Wako City, Japan). The CaM gene was inserted into a standard IPTG-inducible expression vector (Invitrogen, Carlsbad, CA), modified to include an N-terminal hexahistidine tag and free cysteine residue (for labeling in parallel experiments), and introduced into E. coli BL21 DE3. Expressed proteins were purified from 1 L cultures by Ni-NTA affinity chromatography (Qiagen, Valencia, CA), followed by gel filtration chromatography using an FPLC instrument (GE Healthcare, Piscataway, NJ). Once purified, proteins were assayed by gel electrophoresis, stored at 4 °C with 1 mM dithiothreitol in phosphate buffered saline (PBS) solution, and used for titration measurements within two days. Protein concentrations were quantified using optical densities (OD) at 280 nm. Extinction coefficients for each CaM mutant were determined by titration with known quantities of fluorescent CaM-binding probe peptide. Mass spectrometry (MS) measurements were used to verify the integrity of all expressed proteins.

Wild-type and variant M13 peptides were synthesized by solid-phase methods and purified by high performance liquid chromatography over a C18 reversed phase column (Grace Vydac, Columbia, MD). Identity of purified peptides was confirmed by MS. Peptide concentrations were determined by OD at 280, 214 (M13 W4F), or 335 nm (probe peptide), using extinction coefficients determined by amino acid analysis of measured peptide solutions. Peptides were stored for up to one month at 4 °C in PBS. The sequence of wild-type M13 peptide was: K(biotin)GGKRRWKKNFIAVSAANRFKKISSSGAL, where K(biotin) denotes a lysine-conjugated biotin label required for experiments in another study. The sequence of the probe peptide used for competition experiments was: KRRWKKNFIAVSAANRFK-dansyl; the carboxy-terminal dansyl moiety gave rise to the fluorescence changes observed in binding measurements.

Measurement of binding titration curves

For each mutant CaM, a titration curve was obtained to determine the protein's affinity for a highly fluorescent M13-derived probe peptide. A fixed amount of probe was diluted to 0.5 μM in a 500 μL volume of PBS also containing 400 μM CaCl₂. To this solution, in a 1 mL fluorescence cuvette, aliquots of CaM were added (also from a solution containing 400 μM CaCl₂ in PBS). The resulting curves, showing an increase in fluorescence as all of the probe became bound to CaM, were used to determine CaM/probe dissociation constants. Once the probe binding affinity had been measured for each CaM variant, the affinities for wild-type and mutant peptides were determined by titration in competition with excess probe. Aliquots of each M13 variant were added to an initial volume of 500 μL, containing 0.1 μM CaM (wild-type or mutant), 10 μM probe, and 400 μM CaCl₂. As more M13 was added, the fluorescence decreased from a high plateau back towards a lower baseline value, as bound and highly fluorescent probe peptide was displaced by M13. These curves were used to determine dissociation constants between each measured pair of CaM and M13 variants. All fluorescence measurements were performed at room temperature (∼20 °C) on a Cary Eclipse fluorimeter (Varian, Walnut Creek, CA), using excitation and emission wavelengths of 335 and 441 nm, respectively, and slit widths of 5 nm.

Titration data analysis

Titration data were analyzed using the program Kaleidagraph (Synergy Software, Reading, PA). For probe vs. CaM titration experiments, fluorescence data were corrected for dilution and converted into plots of ΔF vs. ΔF/[CaM], where ΔF denotes the observed fluorescence change and [CaM] denotes the concentration of unbound CaM. Data for CaM to probe ratios of 1.0 to 3.0 was used to define the CaM/probe dissociation constant (K_P), according to the following equation:

$$\Delta F=\Delta F_{\max }-K_{\mathrm{P}}\frac{\Delta F}{\left[\mathrm{CaM}\right]}$$ (1)

where ΔF_max is the maximum observed change in fluorescence. Dissociation constants for M13 variants (K_M) were determined by competition with probe peptide for binding to CaM. Data for M13 to probe ratios of 0.02 to 1.0 were converted and fit to the following linear equation:

$$\Delta F=\Delta F_{\max }-K_{\mathrm{M}}\left(\frac{\Delta F}{\left[\mathrm{M}13\right]}\right)\left(\frac{\left[\mathrm{P}\right]}{K_{\mathrm{P}}}-1\right)$$ (2)

where [M13] and [P] denote the concentrations of uncomplexed M13 and probe, respectively. Binding free energies were computed from the dissociation constant using the relation ΔG = +RT ln K_M, using a temperature of 298 K (the positive value is taken to give free energies of association); a more negative ΔG indicates a more stable complex. Derivation of the competition binding equation above required the assumption that all CaM is bound either by probe peptide or by M13; this simplification is justified because of the high peptide to CaM ratio used in the experiments and the relatively high binding affinities observed in all cases. All measurements of binding affinity were obtained by averaging data from two or three independent titration curves, using only curves for which a correlation coefficient of 0.85 or above was obtained in the linear least-squares fitting step. Errors in K_P denote standard errors of the mean for the multiple measurements, and errors in K_M values were calculated by combining the corresponding observed standard errors with propagated uncertainties in K_P.

Results

Introduction of sequence variability at target zones

Designed specificity generating modifications on CaM and M13 were selected using a hierarchical computational procedure that filtered the most promising candidates in stepwise fashion out of a large initial collection of possible sequences (Figure 2). In the first step of this procedure, several structural “target zones” were manually chosen based on visual analysis of the CaM/M13 complex structure. (38) Residues in each of the zones were then computationally varied to a select set of amino acids. Basic residues on M13 defined several of the target zones, because of the numerous hydrogen-bonded salt bridges and longer-range electrostatic interactions these residues make with acidic groups on CaM. Charge reversal (or polar substitution) at these positions was introduced computationally by allowing substitution of each M13 lysine or arginine with D, E, N, or Q and by allowing complementary positions on CaM to vary among K, R, N, or Q. In all cases, the wild-type residue was also allowed. Residues K1, R3 and K18 on M13 were found not to make any close interactions, and were therefore excluded from consideration. A second group of target zones was defined by the hydrophobic side chains (W4, V11, and F17) that help anchor M13 into complementary binding pockets on CaM. Aromatic residues in the natural M13 sequence were allowed to vary between W, F, and Y, and aliphatic residues were allowed to vary among V, L, I, S, and T. Tyrosine, serine and threonine were also included in order to account for possible hydrogen bond formation. For the central valine anchor, W, F, and Y were allowed in addition to the aliphatic residues, and to accommodate these larger side chains, alanine was an allowed alternative at the corresponding variable CaM positions.

Figure 2. Hierarchical design protocol.

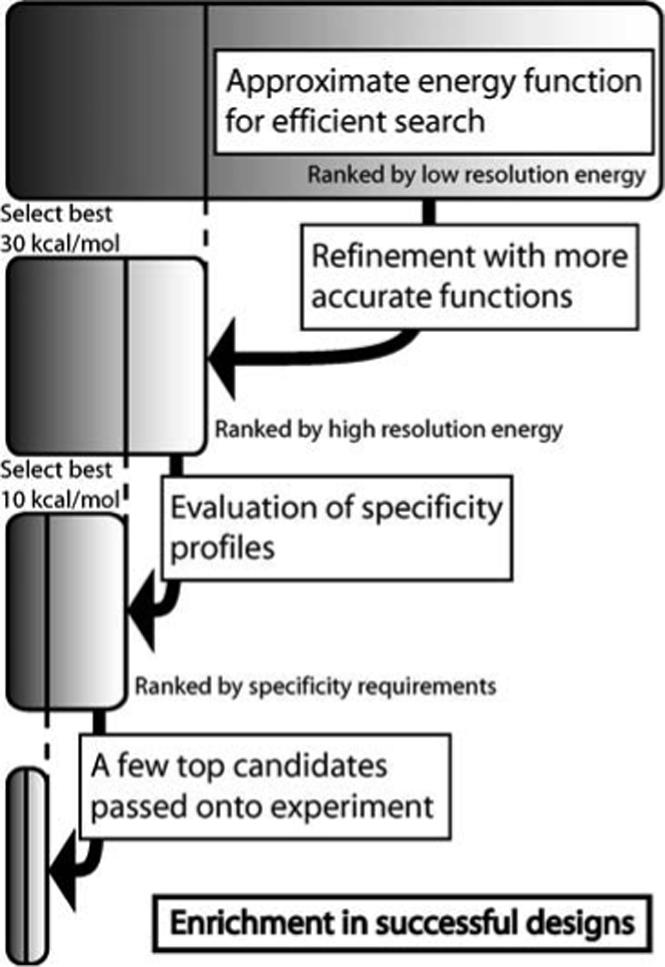
(1) The search of the largest space is done with an approximate energy function which obeys all the constraints of the discrete search algorithms DEE and A^*. (2) The top results from the approximate search are re-evaluated with a more accurate energy function which may include term that are more expensive or that are incompatible with the search algorithms used in the first step. (3) The best candidates are subjected to more detailed evaluations, including estimation of additional properties such as specificity of binding. (4) Only the top selections from the final evaluation are passed on for experimental evaluation.

Computational sequence selection

4901 distinct CaM/M13 mutant pairs (denoted generically as CaM'/M13') were considered in the initial search, computationally generated by substituting M13 basic and anchor residues, along with their interaction partners on CaM, as described above (the additional 979 CaM/M13' and CaM'/M13 pairs were also considered). A discrete set of side-chain conformations (rotamers) was used to account for structural variability; the total number of structural states considered was 2.4 × 10¹³. In the first step of the analysis, all low energy conformational states for each design site were identified by a discrete search of side-chain rotamer states, using the Dead-end Elminination (DEE) and A^* algorithms. (41-46) These models included the ten lowest energy conformations of all sequences with a total minimum energy (evaluated using the charmm/param19 force field) (40) within 30 kcal/mol of the global minimum. These energies were computed using a distance-dependant dielectric constant to approximate solvent screening, which was computationally efficient but limited in its treatment of solvent–side-chain interactions. The survivors from the initial search (3678 sequences, 36780 structural states) were therefore re-evaluated using a more accurate, but relatively time-consuming, Poisson–Boltzmann/Surface Area (PBSA) treatment of solvation. (48-51) The solvation energies of each complex structure (and of the isolated side-chain models used as a reference state) were computed and combined with in vacuo energies computed with the molecular-mechanics (MM) force field. (40) This yielded a new energetically ranked list of all low energy sequences, with each sequence represented by up to ten low energy structures. Analysis of correlations between the pair-wise electrostatic model used in the initial search and the MM/PBSA model used for energetic refinement suggest that the 30 kcal/mol cutoff used in the first search allows all sequences within roughly 10 kcal/mol of the MM/PBSA global minimum to be fully sampled (data not shown). At this stage, all variants with a computed stability more than 10 kcal/mol above the global free energy minimum were eliminated from further consideration.

Estimation of affinity and specificity

The procedure outlined above provided the low energy conformations of all sequences compatible with the complex structure (4378 structural states). But while a stable complex structure was a necessary characteristic of the desired mutant complexes, it did not in itself guarantee the changes in specificity we were trying to achieve. A further step in the analysis was therefore implemented to select CaM'/M13' pairs with favorable free energies of complex formation, and with specificity orthogonal to wild-type CaM/M13—only variant pairs with these properties would remain intact in an environment where mutant and wild-type CaM and M13 all compete for interactions with one another. To predict binding and specificity effects, energetic parameters associated with complex formation were computed. First, for each structural complex selected above, CaM and M13 were rigidly separated, and the energy of each isolated molecule was evaluated using the MM/PBSA method. The energetic difference between the lowest energy complex structure and the lowest energy isolated structures provided an estimate of the binding free energy (ΔG^bind) for each pair of CaM and M13 sequences. For each pair of variant sequences, four additional values were computed by comparing ΔG^bind for wild-type CaM/M13, variant CaM'/M13', and the two undesired “decoy” complexes, CaM'/M13 and CaM/M13' (again, primes denote mutant protein forms). The “relative affinity” (ΔΔG^bind) was estimated by taking the difference in binding free energy between the variant pair (CaM'/M13') and that of the wild-type pair (CaM/M13):

$$\Delta \Delta G^{bind}=\Delta G_{Ca{M}^{\prime }∕M{13}^{\prime }}^{bind}-\Delta G_{CaM∕M13}^{bind}$$ (3)

The “worst-case specificity” (Sp^max) was taken to be the affinity of each CaM'/M13' complex relative to the best-binding decoy (CaM'–M13 or CaM–M13'):

$$S{p}^{\max }=\Delta G_{Ca{M}^{\prime }∕M{13}^{\prime }}^{bind}-\min (\Delta G_{Ca{M}^{\prime }∕M13}^{bind},\Delta G_{CaM∕M{13}^{\prime }}^{bind})$$ (4)

The “best-case specificity” (Sp^min) was the affinity relative to the worst-binding decoy:

$$S{p}^{\min }=\Delta G_{Ca{M}^{\prime }∕M{13}^{\prime }}^{bind}-\max (\Delta G_{Ca{M}^{\prime }∕M13}^{bind},\Delta G_{CaM∕M{13}^{\prime }}^{bind})$$ (5)

Finally, the “average specificity” (Sp^avg) was defined as the energy associated with the partition equilibrium between desired complexes (CaM/M13 and CaM'/M13') and decoy complexes:

$$S{p}^{avg}=[(\Delta G_{CaM∕M13}^{bind}+\Delta G_{Ca{M}^{\prime }∕M{13}^{\prime }}^{bind})-(\Delta G_{Ca{M}^{\prime }∕M13}^{bind}+\Delta G_{CaM∕M{13}^{\prime }}^{bind})]$$ (6)

An ideal design candidate would have a relative affinity near zero (or negative), a negative worst-case specificity, and a negative Sp^avg, and would therefore remain as an intact complex in equilibrium with wild-type CaM/M13 and dissociated proteins.

Of the 543 variant CaM'/M13' sequences that satisfied the absolute stability constraint (total stability within 10 kcal/mol of the global minimum), 349 had ΔΔG^bind at most 3.0 kcal/mol greater than wild-type CaM/M13, consistent with high affinity complex formation. Of these, only 103 also had particularly promising calculated specificity, with Sp^max less than −1.0 kcal/mol; 95 of these variants involved position 19 of the M13 peptide and the remaining 8 involved M13 position 4. Table 2 summarizes the top results for each design site; three energetic measures (ΔG^bind, Sp^min and Sp^max) are listed for the CaM'/M13' variant ranked highest by each of these measures. In some cases, the same variant is ranked highest by all measures, while in other cases distinct choices are preferred based on which measure is chosen. Mutations of the M13 basic residues at positions 2, 5, 6, and 16 all produced destabilization of CaM'/M13' complexes by at least 2 kcal/mol relative to wild-type. Several variants with substitutions at M13 residue 16 nevertheless showed desired specificity profiles (negative Sp^max), but variants modified near M13 positions 2, 5, and 6 did not. At the remaining positions considered (M13 residues 4, 11, 17, and 19), CaM'/M13' pairs with predicted affinity comparable to or better than wild-type were identified. At each of these mutation zones, CaM'/M13' variants with some specificity relative to both CaM'/M13 and CaM/M13' (Sp^max < 0) were found, but variants at positions 11 and 17 were also predicted to display positive Sp^avg, indicating a tendency to disrupt wild-type complexes through binding competition.

Table 2.

Top candidates from single site design^a

	Best ΔΔGbind			Best Spmax			Best Spmin
Site	ΔΔGbind	Spmax	Spmin	ΔΔGbind	Spmax	Spmin	ΔΔGbind	Spmax	Spmin
2	+3.1	+1.5	+1.4	+3.1	+1.5	+1.4	+4.4	+2.8	+0.7
4	+0.1	+0.7	−1.9	+0.4	−1.8	−1.9	+8.2	+6.3	−2.6
5	+6.0	+1.8	−3.7	+8.1	+1.2	−1.4	+7.1	+2.9	−6.0
6	+4.0	+1.5	−1.9	+7.9	−0.1	−0.7	+5.8	+3.4	−2.8
11	−2.2	−0.5	−1.7	−2.2	−0.5	−1.7	−1.0	+0.7	−1.7
16	+1.9	+1.7	−0.9	+4.9	−3.0	−3.1	+3.5	−2.7	−4.3
17	−8.3	−0.6	−7.5	−2.0	−0.8	−1.2	−5.3	+2.4	−8.3
19	−2.2	XX	XX	−2.2	XX	XX	−2.2	XX	XX

^aStable complexes obtained from searching the sequence variants at each site were evaluated for affinity relative to WT (ΔΔGbind), affinity relative to the best binding decoy (Sp^max), and affinity relative to the worst binding decoy (Sp^min). Each value is displayed for the top candidate sequence for each measure. “XX” values indicate that the decoy complex was not found in the search procedure; for rankings on these values, the highest affinity mutant of the set was selected. All values in kcal/mol.

At M13 residues W4 and K19 (and their interaction partners on CaM), variants were found that were computed to satisfy all the design goals: a relative affinity for the desired variant complex near or better than wild-type, specificity of the desired variant with respect to both decoys, and specificity of the wild-type complex compared with the decoys. At M13 position 4, the specificities of these variants and the wild-type complex were computed to be about 2 kcal/mol, with the affinity of the designed CaM'/M13' computed to be within 0.5 kcal/mol of wild type. At position 19, variants were found with affinities as much as 2 kcal/mol better than wild type, and for which the decoy binding was strongly disfavored; these decoys were so destabilized in terms of absolute ΔG that they were eliminated at the initial phase of the computational search. We therefore performed individual calculations (using the same structural and energetic models) of the preferred conformations and binding energetics of all the variants chosen for experimental testing.

Steric interference at M13 position 4

At the M13 position 4 hydrophobic anchor site, the computational search procedure suggested only two variants of M13 and four variants of CaM; all pairs had similar computed effects. M13 W4 was changed either to phenylalanine or to tyrosine; to complement this, CaM F92 was substituted by tryptophan, in combination with one of the mutations I125L, I125V or I105V, or with the double mutation I105V/II25L. W92F/I125L was chosen as a representative CaM', and both M13' possibilities were considered further. To address the effect of the aliphatic variations, a CaM' with a single W92F mutation was also considered. Calculated structures for the designed complexes of these mutants are shown in Figure 3. Mimimum energy structures and computed affinities (relative to wild type) are shown for both cognate (CaM'/M13') and decoy combinations. The cognate complexes preserve the same number of heavy atoms as the wild type, and are able to pack in a similar manner — the larger tryptophan replacing F92 on CaM packs into a space left unoccupied by the replacement of M13 W4 by a smaller F or Y. As a result, the computed binding energies of the wild type and the CaM'/M13' designed complexes are within 0.5 kcal/mol of one another. The corresponding lowest energy decoy complexes fall into two structural classes: Wild-type CaM matched with M13 W4F and W4Y gives an under-packed pocket; the reduced van der Waals contact leads to a computed destabilization of about 2 kcal/mol for these complexes. By contrast, the CaM F92W mutation in combination with the natural M13 peptide leads to an over-packed interface. While the conformation of M13 W4 seen in the NMR ensemble would clash quite strongly with a W at CaM position 92, an alternate conformation that does not severely clash is also sampled in the calculations. Still, a small overlap between this W4 orientation and L125 leads to a computed destablilization of 2 kcal/mol in the F92W/I125L variant. By contrast, in the F92W variant (without the additional I125L mutation), additional van der Waals interactions lead to a computed enhancement of binding free energy by a similar amount.

Figure 3. Steric interference at M13 site 4.

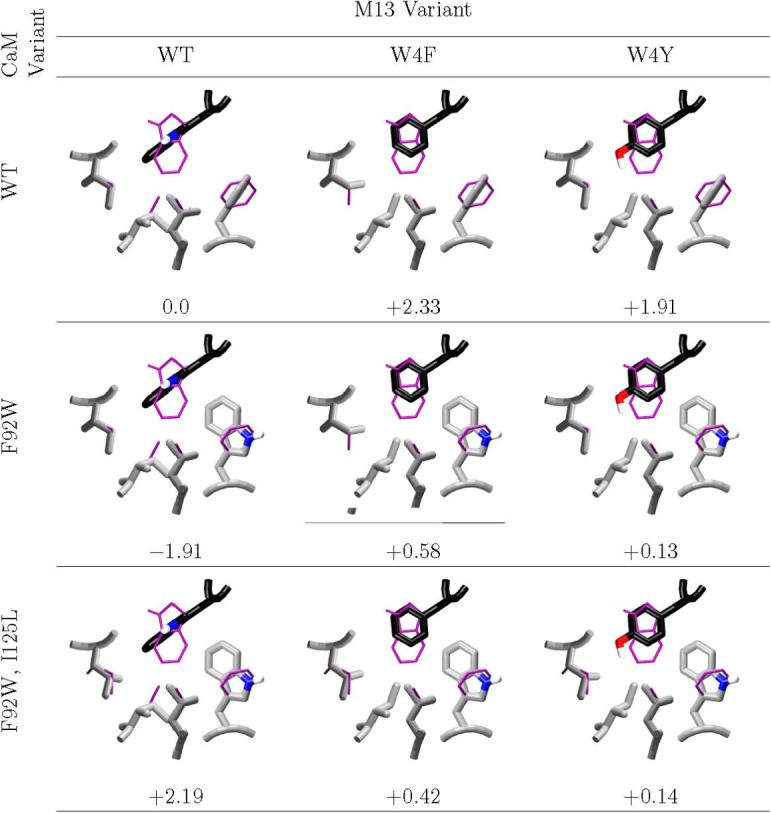
The computed minimum energy complex structures of design candidates and decoys at M13 position 4 are shown, along with the computed binding affinity, relative to wild-type. The desired complexes all have computed affinities within roughly 0.5 kcal/mol of wild-type; all but one decoy are computed to be destabilized by about 2.0 kcal/mol. In all cases, the wild-type NMR average structure is shown in thin purple. Carbons of M13 are colored black, and carbons of CaM are colored light grey. Structural figure generated with vmd (62) and raster3d. (61)

Charge reversal at M13 position 19

The computational selection identified a single charge reversal substitution of M13, K19 to glutamate, in combination with nearly one hundred possible complementary variants of CaM. Three representative CaM' choices were selected: S81R/E83K/E87R contains three positive charges, and represents the most severe variation from natural CaM; S81R/E83N/E87H represents a more modest variation, with only a fixed single positive charge, an acid to amide substitution, and a single titratable histidine; S81R/E83H/E87H represents a third alternative, with two titratable histidines and a single fixed positive charge. Figure 4 details the minimum energy structures and computed affinities of all relevant complexes. All of the substituted side chains at this site are relatively exposed to solvent, and the NMR ensemble shows that a great deal of flexibility may be permitted here. The computed minimum energy structure of the wild type places K19 to make a bridging interaction between both glutamates; this configuration is among those present in the NMR ensemble, and in all of the variant CaM'/M13' complexes the minimum energy structure includes a similar network of interactions. In all of these predicted structures, the M13 mutant residue E19 forms a salt bridge with the CaM mutant residue R81; additional hydrogen bonds are made to one of the side chains replacing CaM residues E83 and E87, but not to both. Among the variant complexes, the most highly charged variant (with all three CaM positions replaced with basic residues) is computed to bind 2.0 kcal/mol tighter than wild type, and the two less charged variations (with N or H at two of the positions) are both computed to bind with roughly 1 kcal/mol lower affinity than wild type. By contrast, the decoy complexes are all computed to be destabilized. Wild-type CaM matched with M13' K19E places the new acidic side chain in close proximity to two other negatively charged groups. The optimal structure places these groups as far apart as possible, but still incurs a computed repulsion of nearly 10 kcal/mol. The natural M13 behaves very similarly when paired with the most highly charged CaM' variant (S81R/E83K/E87R) — a 10 kcal/mol penalty is computed even when the side chains are as widely separated as possible. The less-charged CaM'/M13 decoy complexes show a different set of interactions, but although they are better able to achieve separation of repulsive charges, they still experience a computed destabilization of 2−3 kcal/mol relative to wild-type CaM/M13, and of 1.0−1.5 kcal/mol relative to the CaM'/M13' complexes.

Figure 4. Charge reversal at M13 site 19.

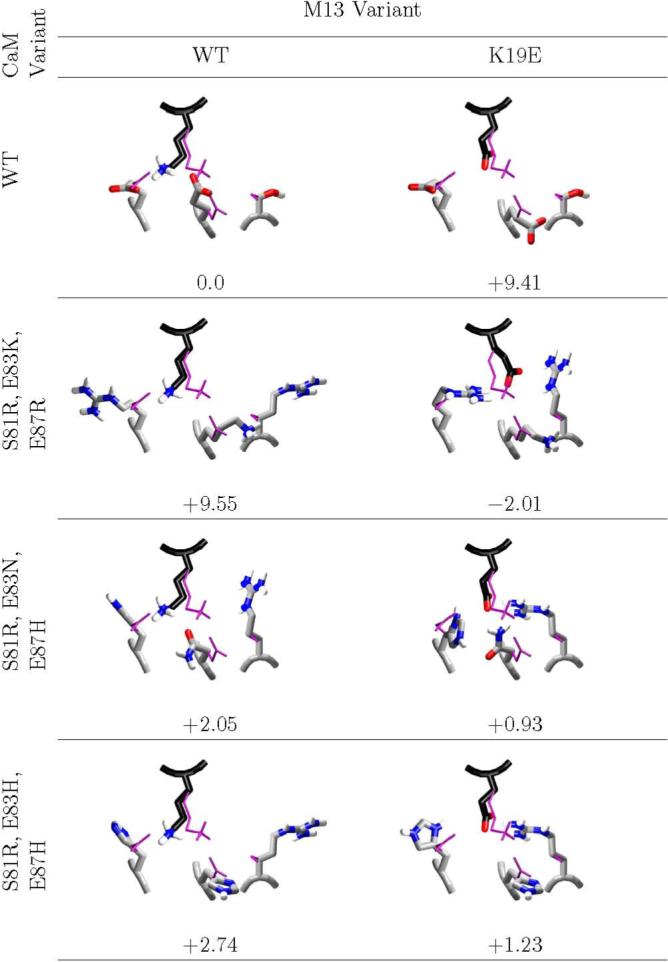
The computed minimum energy complex structures of design candidates and decoys at M13 position 19 are shown, along with the computed binding affinity, relative to wild-type. The desired complexes have computed affinities ranging from 2.0 kcal/mol more stable than wild-type to 1.2 kcal/mol destablized; all decoys are computed to be destabilized by greater than 2.0 kcal/mol. In all cases, the wild-type NMR average structure is shown in thin purple. Carbons of M13 are colored black, and carbons of CaM are colored light grey. Structural figure generated with vmd (62) and raster3d. (61)

Experimental measurement of affinities

The wild-type M13 peptide and variants W4F, W4Y, and K19E were synthesized in order to determine the true effects of our computationally selected mutations on CaM-binding specificity. The complementary CaM mutants (F92W and F92W/I125L for M13 W4 mutants; S81R/E83K/E87R, S81R/E83H/E87H, and S81R/E83N/E87H for M13 K19E) were all produced by standard molecular biology and protein chemistry techniques, and we determined binding affinities by fluorescence titration. Because CaM and the W4 mutants of M13 do not exhibit an intrinsic fluorescence signal useful for this purpose, we synthesized a short fluorescently-labeled peptide (M13 residues 1−18, followed by a C-terminal dansyl group) to use as a probe for occupancy of the CaM peptide-binding groove. Addition of CaM to the probe peptide in the presence of calcium produced a roughly ten-fold increase in total fluorescence (Figure 5A), presumably due to burial of the dansyl group in the complex and protection from quenching by solvent. CaM/probe dissociation constants were determined by monitoring dansyl fluorescence intensity as each CaM variant was titrated into a solution of probe. The probe peptide bound to wild-type CaM and variants with K_d's in a range from 1−100 nM (Table 3). Because binding of M13 variants to the CaM mutants was expected to be one to three orders of magnitude stronger than probe binding, CaM/M13 dissociation constants were measured by titration in the presence of roughly 100-fold excess of competing probe. Fluorescence curves (Figure 5B) showed a decrease in intensity as M13 was added to pre-formed CaM/probe complexes, forcing release of the probe peptide and quenching of the dansyl fluorescence. Data from these curves were converted to linear plots (Figure 5C) and used to determine K_d's for the CaM and M13 combinations discussed in the theoretical section above.

Figure 5. Determination of CaM/M13 binding constants.

(A) CaM/M13 binding constants were determined by titration in the presence of competing excess of a dansylated CaM-binding probe peptide. The probe exhibits low fluorescence in the absence of CaM (gray curve) or in the presence of wild-type CaM and 1 mM EDTA (dotted curve). In the presence of CaM and 100 μM CaCl₂, however, the total probe fluorescence rises dramatically (solid curve) and shifts slightly toward lower wavelengths. (B) Fluorescence decreases progressively as competing M13 peptide is added to a solution of 10 μM probe peptide, 0.1 μM CaM, and 400 μM CaCl₂. Normalized fluorescence is shown as a function of the ratio of M13 to probe concentrations, for titrations involving the CaM mutant F92W. Data are shown for addition of wild-type M13 (filled circles), M13 W4F (open triangles), and M13 W4Y (open squares). Curves are plotted as visual aids only. (C) Data from competition experiments as in (B) were transformed into plots of ΔF/ΔF_max vs. Θ, where ΔF_max and ΔF are the maximum fluorescence change, and the observed fluorescence change for each data point, respectively. Θ is a function of free M13 and probe concentrations, and is defined as (ΔF ΔF_max )([P] K_P −1) [M13], with the probe concentration given by [P], and the dissociation constant for probe binding to CaM given by K_P. Plots here were converted from data shown in panel B, and use the same symbols to refer to three M13 variants; slopes of the linear fits shown are equal to the dissociation constants for complexes of CaM with M13.

Table 3.

Experimental binding affinities^a

	M13 variant
CaM variant	Probe	WT	W4F	W4Y	K19E
WT	21 ± 10	0.19 ± 0.09	1.5 ± 0.7	2.6 ± 1.3	1.4 ± 0.06
F92W	6.3 ± 2.9	0.019 ± 0.009	0.84 ± 0.44	1.1 ± 0.5	—
F92W, I125L	5.2 ± 0.9	0.085 ± 0.062	0.54 ± 0.27	0.68 ± 0.16	—
S81R, E83K, E87K	46 ± 14	0.90 ± 0.27	—	—	1.1 ± 0.3
S81R, E83N, E87H	35 ± 20	0.61 ± 0.35	—	—	1.1 ± 0.6
S81R, E83H, E87H	44 ± 12	0.39 ± 0.17	—	—	1.6 ± 0.5

^a“—” indicates undetermined values. All values in nM.

Binding affinities for CaM and M13 variants are summarized in Table 3. The measured binding affinity between wild-type CaM and wild-type M13 (K_d of 0.19 ± 0.09 nM) was comparable to values in the literature; differences among the reported measurements may reflect small variations in experimental conditions or in the sequences of the peptides and proteins. Wild-type CaM bound less tightly to each M13 mutant than to wild-type M13 (t-test p < 0.05 for all pair-wise K_d comparisons), showing that the mutants chosen successfully interfered with this interaction, by the equivalent of 1−2 kcal/mol. CaM mutants also tended to display highest affinity for wild-type M13. In contrast, some M13 variants preferred binding to specific CaM mutants, rather than to wild-type CaM: both the wild-type M13 and probe peptide (containing M13 residues 1−18) showed significantly higher average affinity for F92W-containing mutants of CaM than for the other CaM species (t-test p < 0.05 for between-group comparisons). On a pair-wise basis, wild-type M13 and M13 mutants W4F and W4Y also seemed to prefer CaM F92W and F92W/I125L to wild-type CaM by factors of 2−10, although the individual margins were not significant at the p < 0.05 level. The affinity of F92W for wild-type M13 (K_d of 0.019 ± 0.009) was the highest measured in this study. Collectively, these results strongly suggest that the CaM F92W mutation increases the affinity of M13 variants with aromatic anchors at the 4 position. On the other hand, binding of M13 to the CaM S81/E83/E87 mutants was weakened by factors of 2−5 with respect to wild-type CaM/M13, while the affinity of M13 K19E for these CaM mutants was approximately equal to that for wild-type CaM.

Experimental specificity parameters

ΔΔG^bind and specificity parameters were computed for each CaM'/M13' pair and are listed in Table 4. Free energy parameters corresponding to statistically significant differences between individual K_d measurements are asterisked (two-sample means test p < 0.05; not relevant for Sp^avg), and other data points indicate trends in energy and specificity. All of the CaM'/M13' pairs have positive ΔΔG^bind, reflecting the fact that they are apparently destabilized with respect to wild-type CaM/M13. All of the CaM'/M13' complexes also have positive Sp^max, indicating that in spite of the design goals, at least one decoy complex (CaM'/M13 or CaM/M13') was measured to be more stable than the complex of mutant CaM and M13; the more stable decoy was invariably the complex of mutant CaM with the wild-type M13 (CaM'/M13). Most of the designed mutant complexes were somewhat more stable than the corresponding CaM/M13' decoys, accounting for negative Sp^min values of 0−1 kcal/mol, and indicating that they would remain intact even in the presence of excess wild-type CaM. This binding affinity difference was most pronounced for the complex between M13 W4F and CaM F92W/I125L, which appeared to be more stable than the W4F complex with wild-type CaM by roughly a factor of four. M13 mutants W4F and W4Y showed the greatest preference for their cognate mutant CaMs, reinforcing the notion that satisfying tight hydrophobic packing at the anchor positions is critical in determining binding energy.

Table 4.

Specificity profiles^a

Variant			Energetic measures
CaM′	M13′	ΔΔGbind	SpCaM′/M13	SpCaM/M13′	Spavg
F92W	W4F	+0.8	+2.2	−0.3	+1.0
F92W	W4Y	+1.0	+2.4*	−0.5	+0.8
F92W, I125L	W4F	+0.6	+1.1	−0.6	−0.1
F92W, I125L	W4Y	+0.7	+1.2*	−0.8	−0.3
S81R, E83K, E87R	K19E	+0.9	+0.3	−0.1	−0.8
S81R, E83N, E87H	K19E	+1.2*	+0.8	+0.1	−0.3
S81R, E83H, E87H	K19E	+1.0*	+0.1	−0.2	−1.1

^aValues in kcal/mol.

^*indicates data points with significance of p < 0.05 using the two-sample means test.

Although the hydrophobic anchor M13 mutants showed the greatest preference for complementary complex formation compared with some of the decoy complexes, the charge reversal M13 K19E seems to result in the most favorable Sp^avg. Sp^avg values reflect the potential for a mixture of CaM and M13 variants to partition into CaM/M13 and CaM'/M13' complexes as opposed to the decoys. The negative Sp^avg values displayed by M13 K19E and CaM S81/E83/E87 mutant pairs are due to the fact these complexes and their corresponding decoy complexes have significantly less favorable binding energy than the wild-type CaM/M13 complex; an equilibrium that minimizes total free energy will therefore result in CaM/M13 and CaM'/M13' formation. Because some of the decoy complexes containing the M13 W4 mutants are by comparison quite stable, these M13 mutants are not expected to partition as readily into complementary mixtures with CaM F92W and F92W/I125L. M13 W4Y and W4F variants therefore display correspondingly higher Sp^avg values.

Discussion

The rational design or modification of proteins and protein binding interfaces remains a challenging problem. Here we have used a computational procedure to select a small number of candidate variants of both CaM and the M13 peptide, with a goal of engineering tight binding complexes with novel specificity. The computationally selected mutant pairs all retain high affinity, indicating a fundamental success of the procedure. However, while partial specificity was achieved, the designed variants did not satisify all of the goals, suggesting deficiencies in the current state-of-the-art in treating problems of specificity.

Significance of observed specificity changes

Perfect products of the computational design procedure would have been mutant M13' and CaM' proteins with high affinity for one another but little affinity for the corresponding wild-type proteins — such mutants could be said to have binding specificity “fully orthogonal” to the endogenous species. The experimental measurements indicate that although we have been successful at retaining high affinity and at modifying the specificity of CaM and M13, the new specificity is not yet orthogonal. In particular, while some of the M13 mutants seemed to prefer cognate mutant CaM's, all of the mutant CaM's still bound better to wild-type M13; these findings were reflected in the specificity parameters we analyzed, in the form of sometimes negative values of Sp^min and uniformly positive values of Sp^max. Another parameter, Sp^avg, denoted the free energy difference associated with the transition from cognate CaM/M13 and CaM'/M13'complexes to the two decoy complexes. Five out of seven of our mutant pairs showed favorable values of Sp^avg. These values were not highly correlated with either Sp^max or Sp^min; although Sp^avg is a function of Sp^max and Sp^min, it represents a distinct energetic quanitity.

Which of the possible measurements of CaM'/M13' stability or specificity is most important in practical terms depends on how the mutants are to be are utilized, and on the relative concentrations of wild-type and mutant proteins in the environment. Consider the case where mutant CaM' and M13' are used to construct a biosensor: CaM is known to be an abundant protein in most cells; concentrations on the order of 10 μM have been reported in some cell types, (52-54) but individual target concentrations are likely to be lower. If CaM, but not the other targets, is in excess to the CaM/M13-based biosensor, the difference in stability between CaM'/M13' and CaM/M13' may be most important in determining whether the biosensor works without interference in the cell. Of the M13 mutants we identified, W4F and W4Y are likely to be best in this sense, since they show apparent preference for CaM F92W mutants compared with wild-type CaM. Although total CaM concentrations are in fact high, it has also been argued that CaM is actually a limiting factor in some cellular contexts. (55, 56) This suggests that most CaM is found in complexes with various targets, and that the concentration of free CaM may be orders of magnitude lower than the total amount of CaM in the cell. In an environment where this is true, a CaM/M13-based sensor might function optimally if its Sp^avg is favorable—that is, if sensor components CaM' and M13' tend to partition into complexes together, when placed in equilibrium with roughly balanced competitor CaM and M13. Of the mutants we analyzed, the designed complexes between M13 K19E and CaM mutants at the S81/E83/E87 positions had the most negative Sp^avg values. The complex between M13 K19E and S81R/E83H/E87H was the most robust, showing a statistically significant decrease in stability of 1.0 kcal/mol with respect the wild-type complex, but almost indistinguishable affinity from its decoy complexes; these properties gave this variant the most favorable Sp^avg we observed, −1.1 kcal/mol.

A different specificity criterion might take precedence in the case where mutant CaM is used to purify recombinant M13-tagged proteins from eukaryotic cells: (7) Here it would be most important that variant CaM proteins are specific only for the mutant M13 tags, and not for endogenous CaM targets that might bind with high affinity to wild-type CaM. Of the CaM mutants we identified and tested, none would be ideal for this application — all mutant CaM's still had highest affinity for wild-type M13. Eukaryotic cellular environments contain CaM targets with a range of binding affinities for calcium-saturated CaM roughly from 0.1 to 100 nM. (57) Because CaM-affinity purification would typically take place in the presence of a large excess of CaM (attached to a solid support), many of these targets would be expected to bind either to wild-type CaM or our mutants. The ideal CaM mutant for purification applications would display K_d's well over 1 μM for endogenous CaM targets, but in the nanomolar to micromolar range for mutant M13-tagged proteins of interest.

Binding affinity of mutant proteins

High affinity complex formation between mutant CaM and M13 is a shared requirement for molecular purification tools and some CaM-based biosensors; (10, 13, 15) in this respect the designs identified in this study were successful, although further work will be required to identify CaM'/M13' mutant pairs that show low enough affinity for wild-type partners to be useful for some applications. Compared with other studies in which M13 or both CaM and M13 proteins were modified, our changes resulted in modest CaM/M13 complex affinity changes. Two stability-related observations were especially notable: First, although we found a decrease in stability by roughly 1 kcal/mol when charge was reversed at the K19 site on M13, complementary introduction of extra positive charge on the CaM interface with this residue did not result in further destabilization. This finding seems natural, given the symmetry of charge-charge interactions in proteins; but an earlier study in which charged residues were exchanged between CaM and M13 resulted in complexes that were destabilized by many orders of magnitude in K_d with respect to the wild-type pair. (17) Second, we discovered a mutation on CaM that seemed to increase CaM's affinity for wild-type M13 and W4 variants. M13 mutants with enhanced affinity for wild-type CaM have been identified in a number of previous studies, but affinity-enhancing CaM mutations have been less widely discussed. CaM/M13 stability improvement due to the CaM F92W mutation was predicted by the calculations and measured experimentally, and may be due to increased van der Waals contact surface between the mutant CaM and its target peptide.

The role of steric and electrostatic interactions in specificity

By design, the variants fell into two general classes: charge-reversal and steric re-patterning mutants. The steric re-patterning mutations were computed to give modest variations in affinity, which was borne out experimentally. The only qualitative misprediction in this case involved the affinity of the CaM variant F92W,I125L for wild-type M13. The calculations suggested that the single F92W mutant would bind more tightly than wild type while the addition of I125L would significantly reduce affinity. Experimentally the loss of affinity relative to the single mutant was found to be much smaller; discrete conformational sampling and a lack of relaxation in the calculations provides a likely explanation.

The charge-reversal mutants were calculationally evaluated as much stronger determinants of specificity, but this specificity was not realized experimentally. This region is quite exposed to solvent, and thus is likely rather flexible. In particular, the M13 peptide backbone may be able to move to separate unfavorable charges more than was accounted for calculationally. Entropic costs involved in making favorable interactions at an exposed site also could play a role in the diffuculty of making accurate assessments at this point, as might in accuracies in the solvation model used. Of the several positions considered for charge-reversal variations in the initial design, three are located between the two hydrophobic positions, and thus are significantly buried in the bound-state. The remaining two positions considered (including the K19 position that was selected for experimental evaluation) are located at more solvent exposed regions on either side of the sequence bounded by the hydrophobic anchors. If variations could be designed at the more buried positions, they may be less succeptible to these problems. However, all the mutations at these locations were computed to significantly destabilize the complex. While is it possible reasonable mutations to these sites may be found by allowing for finer conformational sampling during the search, the challenge of finding a well-packed geometry that is also capable of making favorable electrostatic interactions (a necessity for the mutant/mutant complex to bind with high affinity) is a significant one.

These results provide a number of important lessons. Firstly, steric re-patterning at a binding interface can modulate specificity of interaction in a modest manner. The possibility of electrostatic interactions in determining specificity is obvious, but pure packing effects should not be neglected. Secondly, successful design of specificity requires accurate assessment of both favorable and unfavorable interactions. This is a general problem facing methods involving negative design — current protein-design methodologies make approximations that can easily produce false negatives (favorable states that are computed to be unfavorable) — as has been recognized in studies of homo/heterodimer formation both by Havranek and Harbury, (58) and by Sauer and coworkers. (59) While these issues may be addressed at a buried site by inclusion of a small degree of local relaxation, the problems are aggravated in particular circumstances: surface exposure (leading to increased sidechain flexibility), interactions of charged groups (necessitating accurate solvation treatments), and regions of poorly constrained secondary structure (allowing significant backbone flexibility). All of these are considerations at the charge-reversal site considered here.

Comparison between computed and experimental measurements

Calculationally, each designed pair of CaM/M13 mutants captured the full spectrum of desired properties; clearly there were discrepancies between the computational results and the measured free energies. These differences are likely to have arisen from three factors: limited accuracy of the energy calculations (especially solvent-related terms), limited sampling of side-chain conformations, and the possibility of backbone reorganization in the mutant complexes with respect to the wild-type CaM/M13 NMR structure. The first of these problems is well-known. A special difficulty in determining solvent effects on bimolecular binding energy (as opposed to protein stability) is that it is essential to consider solvation energy in both the complexed and the uncomplexed states. The MM/PBSA approach we used to attempt this was more rigorous than many models, but still stopped short of a molecular-level description of solvent. Although an explicit consideration of the solvent might have improved the accuracy of our calculations, it would have been extremely demanding computationally, and thus impractical to apply to a wide space of potential protein designs; an additional limitationis the relative lack of information about the structure and dynamics of the uncomplexed proteins.

Computational requirements also prevented us from modeling the full conformational flexibility of side chains in our design procedure — nstead we limited our search space to preferred side-chain rotamers. Finer sampling would have increased the search space exponentially, and would have been impractical at early stages in the computational selection. A possible improvement to our method might involve loosening these requirements at late stages in the design process; this would help relieve steric clashes that caused us to overestimate some of the CaM/M13 complex free energies, and may have led to errors in our calculation of specificity parameters. The most confounding source of inaccuracy in structure-aided protein design problems is the potential for larger scale or backbone-related conformational rearrangements. These shifts are largely unpredictable because they may involve many small changes throughout the molecules. An indication of the extent to which such rearrangements have occured in the CaM/M13 system may be obtained by considering the additivity of structurally separated mutations on the total free energy of the complex. Future work will probe this by combining mutations near the M13 W4 and K19 sites, which are separated by roughly 20 Å in the CaM/M13 complex structure. If no significant rearrangements have occured in response to the mutations, we would expect to find approximate additivity of effects at both sites. If broad conformational rearrangements are taking place, the identification of CaM and M13 mutants with further specificity enhancement may require the greater level of trial and error associated with screening-based protein design methods.

Table 1.

Targeted sites for design^a

M13 variable residues
K R R W K K N F I A V S A A N R F K K I S S S G A L
+ + + + +
		CaM contact residues
M13 Site		Variable	Nearby Unvaried
+	2	E127	M124
	4	F92 I100 L105 I125	M109 M124 A128 V136 M144 M145
+	5	E11	M145
+	6	E14	L18
	11	L39 V91 L112	A88 F92
+	16	E84	M71 M72
	17	I27 V55 I63	L32 M36 M51 I52 M71
+	19	S81 E83 E87	E84

^aSeveral individual M13 positions were varied in combination with the closest contacting residues on CaM: + indicates an M13 basic residue; indicates a hydrophobic anchor point. All CaM residues with any side-chain heavy atom within 6.0 Å of any M13 side-chain heavy atom in the group are listed.

Abbreviations

CaM

calmodulin

GFP

green fluorescent protein

DEE

dead end elimination

FDPB

finite-difference Poisson–Boltzmann

MM

molecular mechanics

PBSA

Poisson–Boltzmann surface area