Drug interactions modulate the potential for evolution of resistance

Abstract

Antimicrobial treatments increasingly rely on multidrug combinations, in part because of the emergence and spread of antibiotic resistance. The continued effectiveness of combination treatments depends crucially on the frequency with which multidrug resistance arises. Yet, it is unknown how this propensity for resistance depends on cross-resistance and on epistatic interactions—ranging from synergy to antagonism—between the drugs. Here, we analyzed how interactions between pairs of drugs affect the spontaneous emergence of resistance in the medically important pathogen Staphylococcus aureus. Resistance is selected for within a window of drug concentrations high enough to inhibit wild-type growth but low enough for some resistant mutants to grow. Introducing an experimental method for high-throughput colony imaging, we counted resistant colonies arising across a two-dimensional matrix of drug concentrations for each of three drug pairs. Our data show that these different drug combinations have significantly different impacts on the size of the window of drug concentrations where resistance is selected for. We framed these results in a mathematical model in which the frequencies of resistance to single drugs, cross-resistance, and epistasis combine to determine the propensity for multidrug resistance. The theory suggests that drug pairs which interact synergistically, preferred for their immediate efficacy, may in fact favor the future evolution of resistance. This framework reveals the central role of drug epistasis in the evolution of resistance and points to new strategies for combating the emergence of drug-resistant bacteria.

The widespread use of antibiotics pits clinical need against the reality of evolution (1–3). The clinical goal is to kill as many pathogenic bacteria as possible, or inhibit their growth to allow the immune system to gain the upper hand; but a drug that kills or inhibits the growth of susceptible pathogens confers a dramatic selective advantage to resistant lineages, eventually making the drug ineffective. Although major advances have been made in describing the impact of single drugs on bacterial resistance (3), it is still unclear how drugs in combination affect the evolution of resistance. Combinations of drugs may inhibit bacterial growth in complex ways, deviating from the neutral situation expected when the drugs do not interact (4–6). Compared with this null situation, drug combinations that interact to increase each other's effects are termed “synergistic”; drugs whose combined effect is smaller than expected are termed “antagonistic” (4–7, 39) (Fig. 1D). We have previously shown that these epistatic drug interactions profoundly affect the selective advantage of a single horizontally transferred resistance allele (8). Here, we focus on the more complex scenario of the evolution of multidrug resistance by spontaneously occurring mutations.

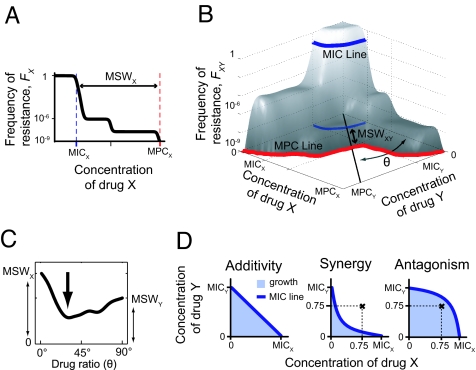
Fig. 1.

Schematic illustration of the MIC and MPC, and their extensions to multidrug environments. (A) Selection for resistance occurs primarily within the mutant selection window (MSW)—drug concentrations ranging from the MIC (dashed blue) inhibiting wild-type growth to the MPC (dashed red) above which the frequency of resistance (F_X) drops to nondetectable values. (B) In drug combinations, these notions extend to the MIC line (blue) and the MPC line (red). Resistance frequency [F_XY(C_X, C_Y), gray surface] is a function of the two-drug dosage and depends on the frequencies of resistance to the individual drugs, cross-resistance, and epistatic interactions. “Effective drugs,” obtained by combining X and Y at fixed proportions, are geometrically represented by lines extending from the origin (thick black line at angle θ), from which their MSW is defined (double-headed arrow). (C) The MSW of these effective drugs is plotted against the ratio of the drug combination (represented by θ); the smallest of these windows characterizes the drug combination's potential to limit the emergence of resistance. (D) The shape of the MIC line of two drugs defines their epistatic interactions: a linear line signifies no epistasis (Left), deviation below linearity signifies synergy (Center), deviation above linearity signifies antagonism (Right). The drug concentration marked by allows wild-type growth in the antagonistic case (therefore, F_XY = 1) but not in the synergistic case (F_XY ≪ 1). In both cases, frequencies of resistance to the individual drugs alone are the same (F_X = 1, F_Y = 1), illustrating that F_XY is not in general equal to F_XF_Y but rather depends critically on epistatic interactions.

In many infectious and noninfectious diseases, including HIV (9), tuberculosis (10), malaria (11, 12), and cancer (13), high rates of mutation confer resistance to individual drugs. Combination therapies are therefore used to increase the killing of single-drug-resistant strains or mutants. Unfortunately, multidrug resistance still arises: multiple mutations conferring resistance may accumulate, or a single mutation may confer resistance to several drugs (cross-resistance). We address here the frequency of such spontaneous resistant mutations in Staphylococcus aureus, one of the most worrisome multidrug-resistant bacteria (14). Although a major mode of resistance in S. aureus is horizontal gene transfer, resistance acquired vertically by spontaneous mutations is another concern and combination therapies aimed at preventing their emergence are frequently used (15, 16). The approach we develop using S. aureus as a model system is general in scope and can be applied to pathogens such as Mycobacterium tuberculosis, where resistance acquired during treatment by spontaneous mutations is critical.

Antibiotics impose a strong selection pressure on bacterial populations (17, 18): susceptible cells do not grow, and resistant cells already present in the population are selectively enriched. A commonly used measure of the potential to evolve resistance by spontaneous mutations is the size of the mutant selection window (MSW)—the range of drug concentrations where resistance is selectively enriched (19, 20). The MSW ranges from the minimum inhibitory concentration (MIC) that inhibits wild-type growth, to the mutant prevention concentration (MPC) where even very rare mutants are unlikely to grow (Fig. 1A). The frequency of resistance and the MSW of several clinically important individual drugs have been well characterized (21–26), and evidence suggests that the MSW of drug combinations can be smaller than the MSW of any of their individual drug constituents (27). Yet, a general relationship between the frequencies of cells resistant to combinations of drugs and the frequencies of resistance to each drug alone has not been established, and the effect of drug–drug interactions (epistasis and cross-resistance) on this relationship is not known.

We use both experimental and theoretical tools to explore how interactions between antibiotics impact the landscape on which selection can act. We develop a high-throughput system to measure frequencies of resistant S. aureus mutants over a matrix of concentrations of pairwise drug combinations, and apply this tool to three different types of drug pairs. Motivated by the diversity of results observed, we develop a quantitative theoretical model that makes clear the central role of drug epistasis and the impact of cross-resistance on the potential for evolution of resistance in multidrug environments. This model yields direct predictions for the impact of drug synergy on the emergence of resistance.

Results

Extending the MPC to Antibiotic Combinations Necessitates Consideration of Drug Epistasis.

Resistant mutants may appear spontaneously because of replication errors at frequencies typically lower than 1 in 10⁶ cells. The frequency of those mutants and the drug window within which they survive characterize the potential of the population to evolve resistance and is represented by the curve F_X(C_X)—the frequency of mutants that resist concentration C_X of drug X (Fig. 1A). This curve typically presents plateaus with sharp drops, indicating the existence of subpopulations of resistant cells. The drug concentration at which the frequency drops to nondetectable levels is the MPC, defined here as F_X < 10⁻⁹ (see Materials and Methods). The mutant selection window (MSW) of a drug extends from the MIC to the MPC. To allow comparison between different antibiotics, we normalize drug concentrations to their respective MICs (note, though, that the absolute values of the MPCs in μg/ml are also of direct clinical importance due to drug toxicity). The size of the MSW is then (MPC − MIC)/MIC (for instance, if the MIC is 1 μg/ml and MPC = 100 μg/ml, MSW ≅ 100).

By analogy with resistance to a single drug, we introduce the surface F_XY(C_X, C_Y), the frequency of cells that can grow in an environment containing a combination of the two drugs X and Y at the concentrations C_X and C_Y (Fig. 1B). As in the single-drug case, F_XY is likely to exhibit plateaus: the first drop in frequency occurs as wild-type growth is inhibited, and defines the MIC line. The MPC line bounds the region where resistant mutants are unlikely to occur (F_XY < 10⁻⁹). The drugs can be combined in different proportions to effectively produce new “single” drugs, represented geometrically by linear lines extending from the origin in the drug concentrations plane (Fig. 1B, black line at angle θ corresponding to the drug ratio). These effective drugs have their own MSW, according to the geometric points of intersection with the MIC and MPC line. The smallest MSW obtained over all of the combinations of X and Y characterizes the potential of the drug pair X–Y for limiting the evolution of resistance (Fig. 1C, arrow).

The simplest approach in the absence of information on how the drugs interact would assume the frequency of resistance to the drug combination to be the product of the frequencies of resistance to each of the individual drugs, F_XY(C_X, C_Y) = F_X(C_X)F_Y(C_Y) (12, 28). It is known that this expectation breaks down in the presence of mutations that confer resistance to X and Y simultaneously (cross-resistance), but we highlight here that F_XY may also significantly depend on epistatic interactions between drugs. The effect of drug combinations on growth inhibition can deviate from the null situation expected by Loewe additivity (Fig. 1D Left) (5), defining synergistic or antagonistic epistasis [Fig. 1D and supporting information (SI) Fig. S1]. Consider, for example, an environment containing 0.75 MIC of drug X and of 0.75 MIC of Y (Fig. 1D, ). In the antagonistic case, the wild type is able to grow and therefore the frequency of resistance is effectively 1 [F_XY(0.75, 0.75) = 1]. In contrast, if the drugs interact synergistically, the wild type cannot grow and therefore F_XY(0.75, 0.75) ≪ 1. The frequency of resistance to each drug alone is the same in both cases [F_X(0.75) = F_Y(0.75) = 1], but epistatic interactions dramatically affect resistance to the combination. This simple example illustrates that even in the absence of cross-resistance, the frequency of cells resistant to the combination is not trivially the product of the frequencies of cells resistant to each of the single drugs.

Experiments Show That Multidrug Resistance Varies Dramatically Between Drug Combinations.

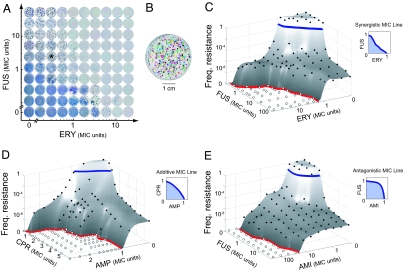
To explore how resistance to combinations of drugs depends on resistance to each drug alone and interactions between the drugs (epistasis and cross-resistance), we designed an experimental setup to systematically measure the frequencies of resistance to more than a hundred different concentrations of a given pair of drugs (see Materials and Methods and Fig. 2). We sampled the resistance surfaces of three drug pairs: fusidic acid–erythromycin (FUS-ERY), ciprofloxacin–ampicillin (CPR-AMP), and fusidic acid–amikacin (FUS-AMI). The drugs were chosen for their clinical relevance, diversity of mechanisms of action, and potential to evolve spontaneous resistance. The assayed drug pairs cover the range of epistatic interactions: the MIC lines, measured independently in liquid media on clonal wild-type populations, show synergy between FUS and ERY (epistasis parameter ε = −0.1; see Materials and Methods), antagonism between FUS and AMI (ε = 0.3), and no epistasis between CPR and AMP (ε = 0.06) (Fig. 2 C–E Insets). We measured resistance to each drug pair at 11 × 11 combined concentrations. Agar plates containing the relevant concentrations of drugs were prepared, inoculated with S. aureus at a range of inoculum sizes (from 10^1.5 to 10⁹ cells per plate), and placed on scanners taking time-lapse high-resolution pictures every hour for 5 days (Fig. 2A). The images obtained were analyzed by an automated image-processing platform designed to count visible colonies on each plate (Fig. 2B).

Fig. 2.

Measurement of resistance frequencies to pairwise drug combinations. (A) Frequencies of resistance of S. aureus to each of 11 × 11 concentrations of a drug pair measured by counting colonies arising on agar plates (see Materials and Methods). Example colony images are shown for the pair of antibiotics ERY-FUS at the final time point (5-day incubation) for the most concentrated cell inoculum (10⁹ cells per well). (B) Individual colonies detected by a custom image-processing platform—here, in false colors, on the plate labeled by an asterisk in A. (C–E) Measured frequencies of resistance (filled circles, or open circles if no resistant colonies appeared) plotted against the two-drug concentrations for FUS-ERY, CPR-AMP, and FUS-AMI. A standard polynomial interpolation surface is shown together with the points (gray surface). The MIC lines, measured independently in liquid media, define the nature of the epistatic interactions between the drugs (blue line, Insets). The MPC lines (red) represent the regions of drug concentrations above which no mutants appear.

Our results show qualitatively different patterns of resistance to the three pairwise drug combinations. The frequency of cells resistant to combinations of FUS and AMI is comparable with that of cells resistant to AMI alone (Fig. 2E). By contrast, the frequency of cells resistant to combinations of CPR and AMP is significantly smaller than the frequencies of resistance to the same concentration of CPR alone, or AMP alone (Fig. 2D). The same is observed for FUS-ERY (Fig. 2C). Furthermore, mixing together FUS and ERY leads to effective drugs whose MSWs can be up to one order of magnitude smaller than the MSW of FUS or ERY alone (Fig. 4 Insets). Thus, combinations of FUS and ERY can be found that significantly narrow the drug regime that selects for resistance. This effect is not observed for FUS-AMI or CPR-AMP. We find that the multiplicative model (i.e., F_XY = F_XF_Y) is unable to capture such diverse behaviors (Fig. S2), underscoring the need for a predictive model of resistance frequencies inclusive of epistasis and cross-resistance.

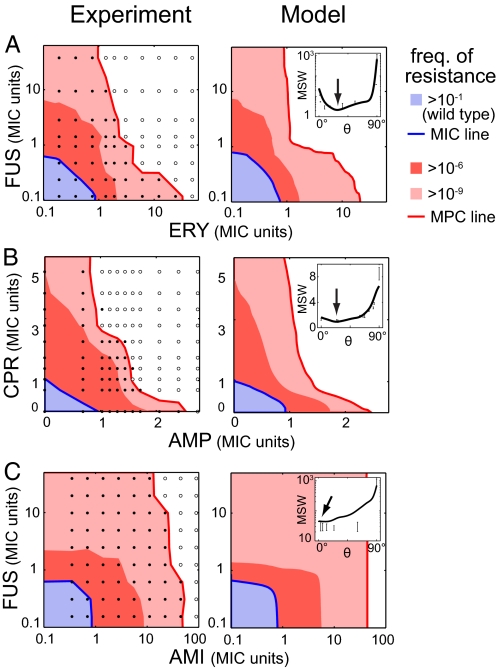
Fig. 4.

Good agreement between experimental measures and theoretical predictions. Shown are comparisons of experimental (Left) and theoretical (Right) frequencies of resistance for FUS-ERY (A), CPR-AMP (B), and FUS-AMI (C) (blue, dark red, and light red as indicated). Theoretical surfaces for each drug pair were computed based on measured frequencies of resistance to each individual drug, measured epistasis between the drugs (MIC line of the wild type), and fitted cross-resistance (see Materials and Methods). Although the behaviors of the three pairs of drugs in terms of epistasis and cross-resistance are very different, the model accounts remarkably well for the frequencies of resistance and MPC lines (red). (Insets) MSW of “effective drugs” obtained by mixing the two drugs at different proportions; experimental points are plotted with their conservative error bars, and the lines correspond to the model prediction. FUS and ERY can be combined to significantly reduce the MSW compared with that of FUS or ERY alone, whereas this is not possible for combinations of CPR and AMP, or FUS and AMI (arrows).

Resistance Frequencies to Individual Drugs, Cross-Resistance, and Epistasis Determine the Frequency of Resistance to Multidrug Combinations.

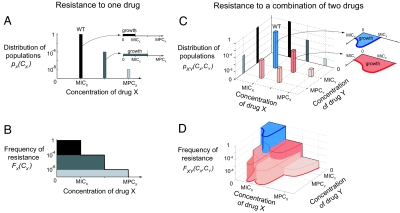
The frequency of resistance F_X to a single antibiotic X derives from the makeup of the bacterial population at the time the antibiotic is introduced. We define p_X(x), the probabilistic density of cells whose MIC of drug X is exactly x (Fig. 3A): it derives from the frequency of resistance as p_X(x) = −dF_X(x)/dx. Because the frequency of resistance to C_X of X is, by definition, the frequency of cells whose MIC is greater than C_X (Fig. 3B), we have

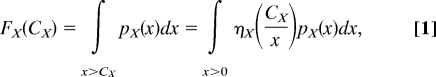where η_X(z) = 1 if z < 1 and is 0 otherwise. In this equation, η_X characterizes the growth of one individual cell: for simplicity we consider only step functions, but η_X could also be smooth and account for natural variations in the response of isogenic cells.

Fig. 3.

A mathematical model for multidrug resistance that incorporates resistance to the individual drugs, epistatic interactions, and cross-resistance. We demonstrate the model by considering a same hypothetical bacterial population subjected to a single drug X (A and B) or to two drugs X and Y combined (C and D). (A) The population is composed of wild-type (WT) and mutant cells that differ in their MICs of drug X. The positions and heights of the bars represent the MIC and the frequency of the corresponding subpopulation. (Inset) Each subpopulation can grow at any drug concentration below its own MIC. (B) The frequency of resistance to any given concentration C_X is the sum of the frequency of the phenotypes that resist concentrations greater than C_X. (C) The same population also analyzed with respect to another drug Y—the bacterial cells' MICs of X and MICs of Y define different subpopulations. Here, the population is made up of five phenotypes represented by 3D bars (blue, wild type; shades of red, mutants) positioned at their MICs of drugs X and MICs of drug Y. The height of each bar represents the frequency of the corresponding subpopulation. Note the projections of these bars onto the x–z plane (gray flat bars) are the three subpopulations obtained in A; similarly, the projections onto the y–z plane are the two subpopulations which differ by their MIC of Y. (Inset) The regions of drug space where each phenotype can grow (e.g., one of the mutants, red) are approximated by scaling the wild-type growth region (blue), which characterizes epistasis. (D) The frequency of resistance at any given concentration (C_X, C_Y) is the sum of the frequencies of the phenotypes whose growth region contains the point (C_X, C_Y). The MPC line (red) is the line above which no mutant can grow.

In the case of two drugs X and Y, the growth region of a bacterial cell is a function of the two-drug concentration, and is delimited by its MIC line [η(C_X, C_Y) = 1 if the cell can grow in (C_X, C_Y), zero otherwise]. Earlier work (8) has shown that growth regions of wild type (η_XY) and resistant mutants (η) tend to have a common shape, which characterizes the epistatic interactions between the drugs. We therefore approximate the region of growth of mutant cells in the population by a linear scaling of the wild type's growth region (Fig. 3C Inset; blue, wild type; red, a mutant). This approximation cannot be tested directly within our experimental data, but the fit of the resulting model to measured resistance frequencies supports its validity. The growth region of a bacterial cell whose MIC of drug X is x and whose MIC of Y is y is approximated by η(C_X, C_Y) = η_XY(C_X/x, C_Y/y).

Next, by analogy to the single drug case, p_XY(x, y) is the density of cells in the population whose MIC of drug X alone is x and whose MIC of drug Y alone is y (Fig. 3C)—note that it does not contain information on the ability of cells to grow in combinations of these drugs, which is carried by η_XY. With these definitions, the frequency of resistance to a given combination (C_XY,C_Y) of drugs X and Y is given by (Fig. 3D)

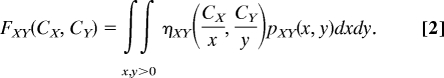Unlike the MIC line (η_XY), which is experimentally measured in liquid media, the density of population p_XY cannot easily be measured. We have built a simple model where p_XY depends only on p_X and p_Y (measured as the derivatives of F_X and F_Y), and on cross-resistance between the drugs. When cross-resistance is absent, mutations conferring resistance to X or Y are independent: the density of population is p_XY^Indep(x, y) ≡ p_X(x)p_Y(y). Conversely, the mechanisms of resistance could be extremely correlated, as would be the case if the “two” drugs were in fact the same: this corresponds to a density p_XY^Correl that depends only on p_X and p_Y (mathematically defined as the density that maximizes the correlation between resistance to X and Y under the constraints p_X(x) = ∫_y>0 p_XY(x, y)dy and p_Y(y) = ∫_x>0 p_XY(x, y)dx; see SI Text.). In general, some mutations confer resistance to only one of the drugs, and others confer resistance to both drugs at once: we model p_XY as a linear combination between the two extreme cases, p_XY = ξp_XY^Correl + (1 − ξ)p_XY^Indep. The parameter ξ reflects cross-resistance, absent when ξ = 0 and maximal when ξ = 1.

This constitutes a model that quantifies exactly how drug epistasis, cross-resistance between drugs, and single-drug resistance determine the frequency of cells resistant to any combination of the drugs X and Y. The densities p_X and p_Y are estimated by the derivatives of the measured frequencies of resistance to the individual drugs F_X, F_Y (Eq. 1). They enable the construction of p_XY^Indep and p_XY^Correl, which, tuned by the cross-resistance ξ, produce p_XY. The MIC line of the wild-type is a direct measurement of η_XY. Finally, p_XY and η_XY predict the frequency of resistance F_XY to any combined concentration of the drugs X and Y (Eq. 2).

The Theoretical Model Captures the Experimental Results.

We next compared the predictions of this model with our experimental results. Frequencies of resistance to the single drugs alone (F_X, F_Y) were measured together with the whole surface. The MIC line of each drug pair (η_XY) was directly measured in liquid media. Cross-resistance (ξ) is the only free parameter and was estimated for each drug pair by a least-squares fitting of predicted to experimental frequencies of resistance. The drug pair FUS-AMI shows strong cross-resistance (ξ = 0.3), whereas the drug pairs CPR-AMP and FUS-ERY show almost no cross-resistance (ξ < 10⁻²). Our experimental results on resistance to combinations of drugs are well captured by the model (Fig. 4). This framework successfully accounts for very different behaviors in terms of epistatic interactions and cross-resistance.

Theory Predicts That Synergistic Epistasis Favors Resistance.

We use this framework to weigh the impact of drug interactions on the evolution of resistance. Cross-resistance increases the MSW of drug combinations; with increased cross-resistance, mutants resistant to both drugs individually occur at frequencies high enough to appear in the population and contribute to the MSW of drug combinations (Fig. S3). The impact of epistasis, however, is less obvious. We present here the simplest model exhibiting the mechanisms by which epistasis affects the potential to evolve resistance to a combinations of drugs. For simplicity, we assume no cross-resistance; the combined impact of cross-resistance and epistasis is presented in Fig. S3.

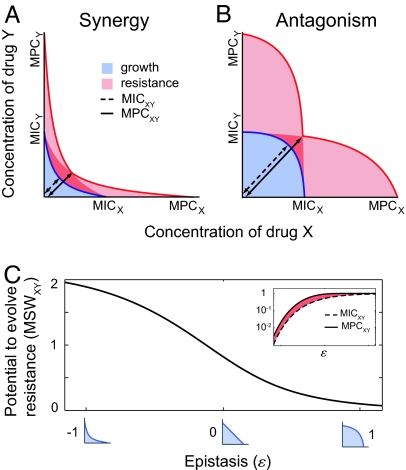
We consider the case where only two mutations exist, one conferring resistance to drug X, the other to drug Y; small mutation frequencies preclude the appearance of double mutants, and the MSWs for drug X and for drug Y have the same size M. Only epistasis between the drugs X and Y varies, and is quantified by the real number ε, which parameterizes the MIC line as x^10ε + y^10ε = 1. Absence of epistatic interactions is represented by ε = 0, while antagonism and synergy correspond to ε > 0 and ε < 0, respectively. Fig. 5 A and B shows the frequencies of resistance to combinations of X and Y for synergistic or antagonistic epistasis. In both cases, 1:1 (θ = 45°) is the ratio of X and Y for which the effective drug has the smallest MSW, defining MSW_XY. Analytical expressions for the corresponding MIC_XY (dashed line) and MPC_XY (solid line) of this “best” effective drug are geometrically derived and a closed form of the smallest MSW, MSW_XY ≡ (MPC_XY − MIC_XY)/MIC_XY, is obtained:

Although the MSW of the combination increases with the MSW of the single drugs, it decreases as the drugs become less synergistic (Fig. 5C). In other words, the more antagonistic the epistasis, the smaller the potential to evolve resistance to the drug combination. This signifies that antagonistic drug combinations can be more efficient than synergistic combinations at reducing the range of drug concentrations that select for resistance. Although the MPC_XY and the MIC_XY of the “best” effective drug both increase in absolute value with the degree of epistasis, the MPC_XY increases at a slower pace than the MIC_XY: relative to the MIC_XY, the value of the MPC_XY decreases (Fig. 5C Inset). Therefore, as epistasis goes from synergy to antagonism, the MSW of the combination shrinks and eventually vanishes when the drugs completely buffer or even suppress one another (Fig. S4).

Fig. 5.

Synergy is predicted to be less efficient than antagonism at reducing the potential for evolving resistance. We consider for simplicity a bacterial population containing only three subpopulations: the wild type, a mutant population resistant only to drug X, and a mutant population resistant only to drug Y (no double mutants or cross-resistance). (A and B) The frequency of resistance to combinations of X and Y strongly depends on their epistatic interactions (synergy in A, and antagonism in B). The MSW of the drug pair is defined by the smallest MSW of the “effective” drugs obtained by mixing X and Y at constant proportions. Here, in each case, the effective drug that possesses the smallest MSW is obtained for the proportion 1X:1Y (black lines with arrows). The MPC of that effective drug (solid line) is smaller relative to the MIC (dashed line) when the drug pair is antagonistic: the MSW of the combination is smaller for antagonistic than for synergistic epistasis. (C) The size of the MSW decreases as epistasis changes from synergy to antagonism. (Inset) This reduction in the size of the MSW (red) is a result of the MPC of the “best” effective drug (solid line) growing more slowly than its MIC (dashed line). As the epistatic interactions vary from synergy to antagonism, the MSW shrinks and eventually vanishes.

Discussion

Current clinical practice emphasizes the use of multidrug treatments primarily to increase the spectrum of activity (29–33), to increase efficacy (34), and, in some pathogens, to decrease the likelihood of the emergence of resistance (29). Clinicians generally prefer synergistic drug pairs when prescribing combination treatments to broaden the spectrum but usually do not consider the effect of drug epistasis on resistance (29). Our results imply that synergistic drug pairs may favor the evolution of resistance. In contrast, largely overlooked antagonistic drug combinations may suppress the emergence of resistance. This study, designed to explore the mostly uncharted territory of resistance to combinations of drugs, comprises drug pairs with different epistasis, different degrees of cross-resistance, and different frequencies of resistance to single drugs. Our theoretical prediction above can be validated experimentally by comparing pairs of drugs with different epistasis but with similar degree of cross-resistance, and similar single-drug MSW. Future screens focusing on finding such pairs could be designed in light of this model.

We focused on the frequency of spontaneous mutations conferring resistance in multidrug environments and emphasized the drug window selective for resistance. We note that this measure of propensity for evolution of resistance does not include other factors that may affect the emergence and spread of drug-resistant pathogens, such as variation in the drug concentration, natural variability in the response of isogenic cells, or the pharmacodynamics of the particular antibiotics (35). The dynamics of antibiotic treatment can lead to rounds of selection and adaptation: resistance may be acquired during the course of treatment. Temporal variations in drug dosage and nongenetic phenotypic tolerance may substantially increase the likelihood of emergence and rate of evolution of resistance. For instance, persister cells may remain dormant long enough for the antibiotic to decay, enabling adaptation and subsequent selection (36, 40). Furthermore, in natural and clinical settings, resistance acquired through horizontal transfer may play a major role in the evolution of resistance. Examining the impact of drug–drug interactions on these factors central to the development of drug resistance is a promising avenue for future research.

In conclusion, we present an experimental–theoretical framework that offers a quantitative, unified understanding of how resistance to individual drugs, cross-resistance, and epistatic interactions affect the propensity for resistance in multidrug combinations. Importantly, our results suggest that antagonistic combinations may narrow the range of drug concentrations where resistant is selected for. In contrast, synergistic drug combinations, typically preferred in clinical settings, may in fact favor the evolution of resistance even though they increase killing efficiency. Our results indicate that drug interactions could be central to a tradeoff between immediate efficacy and the future prevention of resistance.

Materials and Methods

Bacteria and Antibiotics.

We used a streptomycin-resistant S. aureus strain Newman NCTC 8178 (37). Growth media was liquid or agar Luria broth (LB) supplemented, as indicated, with one or two of five different antibiotics (see Table S1). A single colony (starting from a single cell) was inoculated in LB liquid and grown overnight: frozen aliquots of this culture were kept at −80°C. All experiments were initiated from a freshly thawed aliquot from this single batch.

MIC Line.

The MIC line of a drug pair was measured by a standard overnight growth assay in liquid media, inoculating ≈10³ wild-type cells in each of 96 wells (Costar plate; 150 μl per well) forming a 12 × 8 gradient of drug concentration (dilutions of 2/3 to 9/10). The MIC line was defined as the line separating regions of growth and no growth (practically, the contour line of optical density 0.1). The shape of the MIC line was used to define the function η for each specific drug pair (Fig. 2 C–E Insets). The sign of the epistatic interactions was determined by fitting η with the function x^10ε + y^10ε = 1; synergy, additivity and antagonism correspond respectively to negative, null, and positive values of ε.

Frequency of Resistance.

We measured the frequency of resistance with a resolution spanning nine orders of magnitude, across an 11 × 11 grid of drug concentrations. For each two-drug concentration we used one six-well plate (Becton Dickinson Multiwell), and poured 7 ml of agar supplemented with the same concentration of drugs in all six wells (e.g., Fig. S5). After agar solidification, each of the six wells was inoculated with a different number of bacterial cells (approximately 10^1.5, 10³, 10^4.5, 10⁶, 10^7.5, and 10⁹). The plates were then incubated on scanners (see below) in a controlled environmental room at 30°C and 70% relative humidity for 5 days, a duration optimized for the detection of resistant colonies by our custom software (Fig. S6: effect of the incubation time). The frequency of resistance to a given concentration of the drug pair was defined as the total number of mutants in all wells of the relevant drug concentrations with countable colonies (typically, <500 cfu per well) divided by the total number of cells plated on these specific wells. The MPC (respectively MPC line) bounds the drug concentrations where at least one growing colony was observed. This corresponds here to frequencies of resistance greater than 10⁻⁹, while the standard definition of the MPC is usually F_X > 10⁻¹⁰ (20, 38): our measurements of the MSW may differ from those obtained by the standard method. The use of frozen cell aliquots prepared from the same single culture eliminates much of the Luria–Delbrück fluctuations. Some additional fluctuations due to the last 100-fold amplification step are still present (Fig. S7).

Scanner and Imaging Platform.

We built an array of 30 office scanners (Epson Perfection 3170/3490) controlled by one computer. Five plates were placed in each scanner. The scanners were programmed to take time-lapse pictures of the plates at 600 dpi every hour for 5 days. We built an image-analysis platform in MATLAB (MathWorks) to count the number of colonies arising in each plate. The platform detects single colonies larger than one-tenth of a millimeter and tracks their growth by using a custom contour-detection algorithm based on contrast gradients (Fig. 2B).