How DNA coiling enhances target localization by proteins

Abstract

Many genetic processes depend on proteins interacting with specific sequences on DNA. Despite the large excess of nonspecific DNA in the cell, proteins can locate their targets rapidly. After initial nonspecific binding, they are believed to find the target site by 1D diffusion (“sliding”) interspersed by 3D dissociation/reassociation, a process usually referred to as facilitated diffusion. The 3D events combine short intrasegmental “hops” along the DNA contour, intersegmental “jumps” between nearby DNA segments, and longer volume “excursions.” The impact of DNA conformation on the search pathway is, however, still unknown. Here, we show direct evidence that DNA coiling influences the specific association rate of EcoRV restriction enzymes. Using optical tweezers together with a fast buffer exchange system, we obtained association times of EcoRV on single DNA molecules as a function of DNA extension, separating intersegmental jumping from other search pathways. Depending on salt concentration, targeting rates almost double when the DNA conformation is changed from fully extended to a coiled configuration. Quantitative analysis by an extended facilitated diffusion model reveals that only a fraction of enzymes are ready to bind to DNA. Generalizing our results to the crowded environment of the cell we predict a major impact of intersegmental jumps on target localization speed on DNA.

An essential feature in biological processes on DNA is the ability of proteins to quickly locate specific DNA sequences in a vast surplus of nonspecific DNA (1, 2). A protein's search for the target site is thought to be accelerated by facilitated diffusion along nonspecific DNA (3–6). Recent work has yielded considerable insight in the possible search strategies of site-specific proteins (7–15). Assisted by DNA looping some proteins can, for instance, intermittently bind to two DNA segments simultaneously. This way they can directly move from one to another chemically remote segment (16). This intersegmental transfer accelerates target finding on DNA because it assumes a constantly changing random configuration (11). Here, we demonstrate and quantify a similar mechanism, intersegmental jumping, for proteins with only one DNA-binding site.

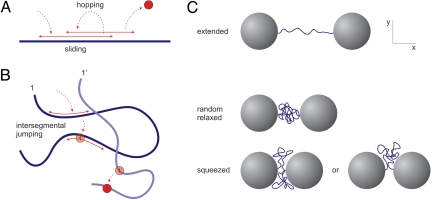
Little experimental work on facilitated diffusion is available. To date, most studies have been investigating DNA cleavage by restriction enzymes in bulk assays, measuring association times as a function of DNA length, or monitoring processivity on DNA constructs with two sites (7, 17–21). Although in these biochemical assays valuable information can be obtained, association rates of proteins to specific sites are difficult to measure, and the underlying kinetics of the target search mechanism are often obscured. Furthermore, it remains experimentally challenging to distinguish 1D and 3D search pathways. In previous single-molecule assays only pure 1D protein search has been addressed (21–24). Here, we present single-molecule measurements of DNA cleavage by EcoRV on individual plasmid-size molecules (6,538 bp; one EcoRV site) having different degrees of conformational freedom. By tuning the DNA extension, the conformation of the DNA can be changed from a relaxed random configuration to an extended polymer. This procedure enables us to selectively “switch off” 3D intersegmental jumping, while leaving sliding, intrasegmental hopping, and long volume excursions intact. By acquiring specific association rates of EcoRV for these DNA conformations at different salt conditions, we can thus determine the relative impact of 3D intersegmental jumps (illustrated in Fig. 1 A and B) on the search process.

Fig. 1.

Protein search pathways and experimental approach. (A) Facilitated diffusion model with sliding and hopping resulting in probing of already visited sites (oversampling) on straight DNA. (B) On coiled DNA the enzyme can be captured by a segment it has not yet visited, leading to an intersegmental jump and reduction of oversampling. Because of random polymer fluctuations a protein performing an intersegmental jump at instant 1 will, upon unbinding at instant 1′ have moved far away from the original segment, accelerating the search process. (C) Experimental approach. Single DNA molecules are held between two beads in optical tweezers. EcoRV cleavage rates are measured at different DNA extensions. The conformational freedom of the DNA at these extensions can be divided into three regimes: (entropically) stretched DNA (Top), globular DNA (relaxed coil) (Middle), and a DNA coil that is squeezed between the beads. (Bottom)

Results and Discussion

Experimental Approach.

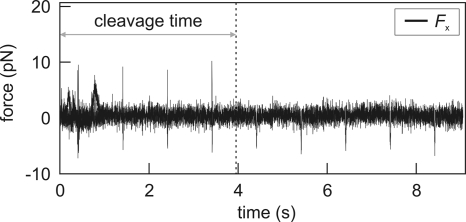
To determine the bimolecular association rate k_on to a recognition site on linear DNA, for different polymer conformations, individual DNA molecules were tethered between two optically trapped beads in a multichannel flow chamber as described (25, 26). The degree of DNA coiling was set by changing the distance between the two beads (Fig. 1C). After the buffer flow was stopped DNA constructs were quickly (≈0.5 s) transported into enzyme solution. The DNA molecule was briefly (<20 ms) stretched to a force of 5–10 pN every second, to check whether it was cut [supporting information (SI) Movie S1]. The transient stretching resulted in spikes in the force trace that disappeared when the DNA had been cleaved in the preceding second (Fig. 2). The cleavage time was defined as the time between moving the construct into the enzyme solution and scission of both DNA strands.

Fig. 2.

Typical data trace of a cleavage event. Displayed is the force on the DNA in the direction along the stretched molecule. Every second, the DNA is rapidly stretched to ≈5–10 pN, resulting in sharp positive force spikes (negative spikes are caused by the fast movement of the beads and do not represent a real force on the DNA). Disappearance of these spikes implies that the DNA molecule has been cleaved in the preceding second. The best estimate for this event is exactly halfway between the last spike and the next stretching attempt. We thus define the reaction time as the time between transportation of the DNA construct into the enzyme-containing flow channel (t = 0 in the graph) and last upward spike plus 0.5 s. The statistical error that is introduced in the measured cleavage time (≈0.5 s) averages out for the large number of data points.

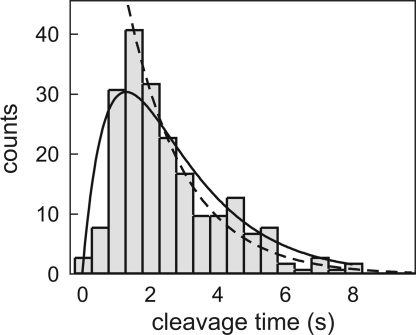
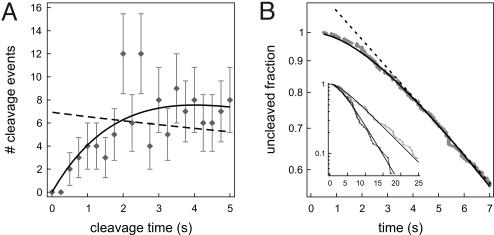
As we are interested in the influence of DNA configuration on the association rate, the complete cleavage reaction (comprising association, induced fit, DNA hydrolysis, and product release) should be limited by diffusion of the protein to the specific site. We have previously demonstrated that the induced-fit process at low DNA tension is very fast and that product release from the plasmid, in bulk experiments normally the slowest step (27, 28), is not rate-limiting in our optical tweezers experiments (25). This result leaves the actual strand cleavage reaction, the hydrolysis of two phosphodiester bonds in the DNA backbone, as a possible rate-limiting step. This latter rate was determined by measuring cleavage times of pCco5 DNA molecules in a stretched configuration at saturating enzyme conditions (500 nM) (Fig. 3). The rate of strand cleavage was found to be 0.60 s⁻¹. Consequently, the average time needed for the cleavage of both strands is 2.5 s. To satisfy the diffusion-limited requirement mentioned above, and to avoid fluctuations in enzyme concentration caused by adsorption onto the walls and tubing of the flow chamber, we used 1 nM EcoRV in all experiments (see Materials and Methods).

Fig. 3.

Determination of DNA hydrolysis rate, obtained with 500 nM EcoRV in reaction buffer with 100 mM NaCl. Because in the optical tweezers experiments only the cleavage of the second strand is observed, the distribution of cleavage times shows a lag phase. The single exponential fit (dashed line) gives a strand cleavage rate k₁ of 0.60 ± 0.03 s⁻¹ for the second strand. Because of degeneracy, cleavage of the first strand should in principle be twice as fast. As a result, the rate of hydrolysis for both DNA strands is 0.40 ± 0.03 s⁻¹. The average time required for DNA cleavage is the inverse, 2.5 ± 0.2 s. The full distribution can also directly be fitted with such a two-step process (k₁[exp(−k₁t) − exp(−2k₁t)]). Doing so (solid line) yields a strand cleavage rate k₁ of 0.54 ± 0.03 s⁻¹, comparable to the rate found above.

Rate Acceleration on Coiled DNA.

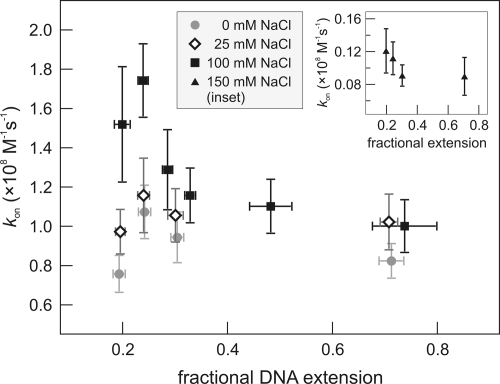
Specific association rates k_on were computed from 385 individual cleavage reactions (see Materials and Methods). Variation of the DNA configuration includes three regimes (see Fig. 1C): (i) extended DNA, where jumping to different DNA segments cannot take place (≈1 pN tension, ≈85% extended); (ii) a DNA configuration that is close to a relaxed coil (fractional extension a between 0.2 and 0.3; and (iii) smaller fractional extensions, where the beads interfere with the coil and the DNA is slightly squeezed out of the narrow gap. Fig. 4 shows the association rates acquired for different DNA conformations. Strikingly, at 100 mM NaCl the specific association rate on DNA held in an extended configuration is almost twice as slow as on coiled DNA. We define R as the ratio between the maximal association rate and the rate found on stretched DNA. The fastest association is measured at a = 0.24 (R = 1.7 ± 0.3). At smaller extensions, a decrease in the rate occurs. Why would the search rate acceleration peak at a fractional extension of 0.24? A relaxed pCco5 DNA molecule (6,538 bp) with free ends would form a coil with a mean square end-to-end distance 〈R_e²〉 ≈ 2Ll_p ≈ (0.49 μm)² (29), corresponding to a = 0.22. The maximal association rate is thus found at the extension where DNA is closest to its free random configuration. We attribute the rate difference with stretched DNA to the disappearance of intersegmental jumping in stretched DNA (Fig. 1 A and B). At a ≤ 0.2, the presence of the two large beads causes a deformation of the DNA coil. In addition to possible obstruction of enzyme access routes, on average the local density of DNA segments around the specific site l_DNA will be lower than for the relaxed coil, resulting in the observed decrease in association rate. The second-order association rate constants deduced from the single-molecule cleavage events, 1.8 ± 0.2 × 10⁸ M⁻¹·s⁻¹ in the coiled configuration is in close agreement with values found earlier in bulk experiments in similar buffers: 1.2–2.2 × 10⁸ M⁻¹·s⁻¹ (30–33).

Fig. 4.

EcoRV association rates to the single recognition site on linear DNA molecules as a function of DNA extension. In 100 mM NaCl the association rate is found to be maximal around a fractional extension a ≈0.22, and decreases rapidly for increasing extensions, reducing almost a factor of two as the DNA is stretched. This effect is attributed to loss of intersegmental jumping in the search process of EcoRV. At low fractional extensions the DNA coil is deformed by the beads, resulting in a lowered local density of DNA segments around the recognition site. At lower salt conditions (0 and 25 mM) this effect disappears. (Inset) Association rates in 150 mM NaCl are ≈10-fold lower for all DNA extensions. Each data point consists of a minimum of 30 measurements.

Salt Dependence of Association Rate.

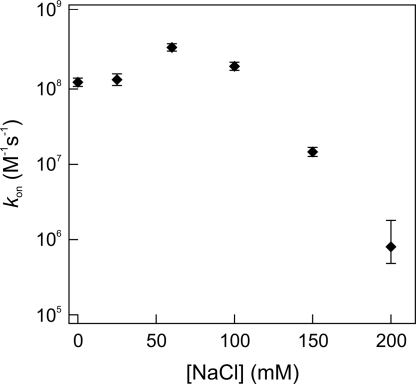
Nonspecific protein–DNA interactions are largely of electrostatic nature and therefore depend on salt concentration (34). Changes in buffer conditions could thus induce a shift in the relative contributions of 1D and 3D pathways in the search process. To examine this effect, we repeated the cleavage measurements on relaxed and extended DNA in buffers with different NaCl concentrations (Fig. 4). At 0 and 25 mM NaCl we observed almost invariable association rates for all DNA extensions, indicating a lowered probability of protein jumping. We found an optimal salt concentration for target finding at 60 mM, consistent with previous biochemical assays (18, 19). Apparently, at this salt concentration the effective sliding length l_sl^eff (the average length of correlated motion along the contour of the DNA, including both hopping and sliding) is maximal. However, we could not probe the difference between the stretched and coiled DNA configuration at 60 mM NaCl. At that concentration the EcoRV association rate approaches the rate of phosphodiester hydrolysis (0.4 s⁻¹), causing the reaction to be rate-limited by this process instead of by diffusion. Using a lower EcoRV concentration could diminish this problem, but as mentioned before we detected fluctuations in the actual amount of enzymes present in the flow chamber if we decreased the EcoRV concentration <1 nM. In reaction buffers containing 150 and 200 mM NaCl, target site location rates were dramatically lowered for all DNA configurations, probably attributable to the reduced affinity of EcoRV for both specific and nonspecific DNA in these buffers (35) (Figs. 4 Inset and 5). Here, the sliding length became so small that the enzyme effectively performed a 3D random walk and facilitation by nonspecific binding was absent.

Fig. 5.

EcoRV association rates measured on coiled DNA as a function of salt concentration, showing an optimum at ≈60 mM NaCl. (At this particular concentration, DNA hydrolysis becomes the rate-limiting step.) For NaCl concentrations >100 mM, the association rate of EcoRV to the specific site decreases exponentially.

Theoretical Modeling of Intersegmental Jumping.

To quantitatively explain the enzyme's acceleration of target site association, we consider EcoRV's search for the specific cleavage site as a combination of (i) sliding diffusion along the DNA with diffusivity D_1d, until dissociation to the bulk (with rate k_off^ns) and (ii) 3D diffusion with diffusivity D_3d where an enzyme eventually (re)binds nonspecifically to a DNA segment (with rate per length k_on^ns). Eventually, the target is found with rate k_on.

Below we describe two limiting cases. If 3D diffusion were much faster than nonspecific binding, i.e., D_3d ≫ k_on^ns (k_on^ns has units of inverse concentration per length per time, i.e., length squared per time like D_3d), an enzyme would perform a long diffusive volume excursion in the bulk before rebinding to the DNA, losing its correlation to the previous dissociation site. The search rate would then be k_on = 2 k_on^nsl_sl, with sliding length l_sl = (D_1d/ k_off^ns)^1/2 (11): typically only proteins binding nonspecifically within a distance l_sl from the target will actually find it. In this case the global conformation of the DNA would not influence the search dynamics, in contrast to what we observed for EcoRV.

Conversely, if D_3d ≪ k_on^ns an enzyme just dissociated from the DNA is likely to rebind immediately. k_on will then be smaller than 2 k_on^nsl_sl, as the enzyme will often slide along previously visited DNA segments, an inefficient oversampling (Fig. 1A). The effective sliding length l_sl^eff = [k_on^ns/(2πD_3d)]^1/2l_sl (36) is a measure of the distance, including intrasegmental (microscopic) hops, that the protein explores before effectively leaving a DNA segment. Experiments suggest that l_sl^eff for EcoRV can be as large as hundreds of base pairs (18, 20). Analysis by Zhou et al. (13) of these experimental data gives the maximal value of the ratio K′_ns = D_1dk_on^ns/(D_3d k_off^ns) as 5.2 × 10³ M⁻¹·bp⁻¹. In terms of effective sliding this corresponds to $l_{\text{sl}}^{\text{eff}}=\sqrt{{K^{\prime }}_{\text{ns}}/(2\pi )}=193\text{bp}$ (using 1 bp = 0.34 nm). However, for such a l_sl^eff one would expect a search rate ≈D_3dl_sl^eff of order 10¹⁰ M⁻¹·s⁻¹, much faster than k_on ≈10⁸ M⁻¹·s⁻¹ found experimentally. More precisely, using l_sl^eff = 193 bp one can use the expression for k_on on infinitely long stretched DNA as discussed in ref. 36 to arrive at an expected k_on ≈2 × 10¹⁰ M⁻¹·s⁻¹ (a result that is essentially independent of the detailed choice of D_1d, k_off^ns, etc.). To explain the a priori unexpectedly low experimental rate we follow an observation by Erskine et al. (30): based on x-ray crystallography data, EcoRV may switch between an open state allowing for DNA binding, and a closed one that does not. The actual rate constant becomes k_on = x_actk_on^act, x_act being the fraction of open (and therefore active) EcoRV and k_on^act its association rate constant. Assuming that k_on ≈1.5 · 10⁸ M⁻¹·s⁻¹ for stretched DNA when l_sl^eff = 193 bp and k_on^act ≈2 × 10¹⁰ M⁻¹·s⁻¹ this gives x_act ≈0.75%. Physiologically, the advantage of this open/closed isomerization could be to provide the cell with a reservoir of EcoRV uniformly distributed in the cytoplasm, instead of being bound nonspecifically to the cell's own DNA. Foreign DNA entering the cell would then immediately be surrounded by a higher concentration of EcoRV that, after switching to the open state, could readily attack the foreign DNA.

So why does coiled DNA enable faster target search than stretched DNA? An enzyme that would otherwise rebind quickly to the segment it just visited can instead be captured by another segment, that is nearby (in 3D space) because of DNA looping (Fig. 1B). This conversion from an intrasegmental hop to an intersegmental jump reduces oversampling, because in chemical distance along the DNA the dissociation and rebinding points are remote. Given an escape time from a segment of typical order of 1 s (30), and with the estimate of 2 ms for the polymer configuration relaxation time (see Materials and Methods), one sees that the polymer configuration will change in between intersegmental jumps, such that successive intersegmental jumps are likely to occur at a point that also in 3D space is remote from the original segment. These considerations are quantified in SI Appendix, in which the work of Berg and Ehrenberg (36), where the DNA was treated as a straight cylinder, is generalized to the coiled configuration by including also foreign segments around the target site as randomly placed straight cylinders. This procedure allows us to estimate the probability of intrasegmental hops of different lengths being converted into intersegmental jumps, and how this affects the search rate k_on. In Table 1 we list values for the relative acceleration R caused by coiling resulting from this theoretical modeling. The fitting parameters were chosen such that consistency is achieved simultaneously with both DNA extension and [NaCl] variation and with previously published values. The value of R is found to rise above unity when l_sl^eff is comparable with or larger than the typical distance l_DNA^−1/2 between DNA segments, where l_DNA is the average density (length per volume) of foreign DNA segments around the specific target site. We interpret the high value of R at 100 mM NaCl in terms of an increased l_DNA because of a mutual attraction of DNA segments at these salt conditions. Such attraction was predicted by Lee et al. (37) from molecular dynamics simulations. Moreover, Qui et al. (38) experimentally demonstrated that such attraction exists between 25-bp DNA pieces above Mg²⁺ concentrations of 16 and 10 mM in cases with, respectively, no monovalent salt and 20 mM NaCl present. In our experiments with 5 mM Mg²⁺ we expected the onset of DNA attraction to occur between 20 and 100 mM NaCl. Table 1 reflects this expected increase of DNA density.

Table 1.

Fitting parameters and the corresponding theoretical value of R (see SI Appendix) compared with the measurements

[NaCl], mM	konstraight, (M·s)−1	lsleff, bp	$1/\sqrt{I_{\text{DNA}}}$, bp	Rtheory	Rmeasured
0	0.8 × 108	97	518	1.11	1.3
25	1.0 × 108	123	485	1.15	1.1
100	1.0 × 108	122	120	1.63	1.7
150	0.09 × 108	9.1	80	1.10	1.3

The measured on rates for extended DNA, k_on^straight, are used as input for the theory to obtain the values of l_sl^eff assuming that the estimate x_act = 0.75% holds for all [NaCl].

Previously, a 3-fold preference of cleaving supercoiled plasmids over relaxed plasmids was observed (17), in qualitative agreement with our results: whereas the density of DNA segments in supercoiled DNA is larger than in a relaxed coil, the density of DNA in the coiled state is larger than when it is held straight. Hence, the amount of reassociations to nearby DNA segments decreases from many to a few in the supercoiling experiment and from a few to zero in our experiment. Combining both studies thus demonstrates already a 6-fold enhancement of the searching rate of restriction enzymes caused by intrasegmental jumping. Considering that in the cell the density of DNA is even higher (because of crowding, condensing agents, and DNA-organizing proteins), we can conclude that in vivo the jumping pathway is an essential tool for efficiently targeting specific sites on DNA.

Materials and Methods

Experiments.

EcoRV was recovered from ammonium sulfate precipitates as described (26). For the DNA cleavage experiments pCco5 plasmid (6.5 kbp in length) was linearized by SpeI digestion (25). The linear DNA contains a single recognition site located almost in the middle. The degree of DNA coiling was controlled by changing the distance between the two attached beads.

A detailed description of the experimental setup is given in ref. 26. Because of nonmixing laminar buffer flow (39), assembled DNA constructs can be transported into a channel containing 1 nM EcoRV with an estimated timing error of 0.5 s. Before each experiment session a 10 mM Tris·HCl buffer (pH 7.5) containing 1 mg/ml BSA was flowed through the chamber for ≈30 min to coat the walls of the chamber and tubing to prevent sticking of EcoRV enzymes. The enzyme reaction buffer contained 10 mM Tris·HCl (pH 7.5), 5 mM MgCl₂, 1 mM DTT, 100 μg/ml BSA, and a variable NaCl concentration. During the cleavage time measurements the buffer flow was stopped to allow undisturbed spatial fluctuations in the DNA molecule held at a certain extension. This configuration was only transiently abandoned to a stretched conformation once per second to check for DNA cleavage. The stretching was done by rapid translation of one of the optical traps, controlled by an acousto-optic deflector (Movie S1). Before the recording of each data point, the flow was switched on for a minimum of 2 min (at ≈100 μm/s) to re-equilibrate the enzyme concentration and ensure sharp borders between different flow channels. The various fractional extensions explored were alternated sequentially during experiments to rule out possible influence of small variations in enzyme and/or salt concentrations on longer timescales.

Determination of Specific Association Rates.

Specific association rates at the different DNA conformations were calculated from the average measured time required for cleavage on >30 DNA molecules at each DNA conformation for each NaCl concentration. For a one-step Poissonian process, the average of measured cleavage times equals the time constant of an exponential fit to the time-binned histogram. However, the cleavage of an individual DNA molecule in our experiments is effectively a multistep process, comprising both association to the specific site and DNA hydrolysis of both strands. At the used EcoRV concentration of 1 nM the association step is mostly rate-limiting (except at 60 mM NaCl). Yet, a histogram computed from the total of 385 events at 100 mM NaCl (shown in Fig. 6) still shows a lag phase for small cleavage times (with rate 0.4 s⁻¹), owing to DNA hydrolysis (both strands), followed by an exponential drop-off. Consequently, by computing the rate simply from the averages of measured cleavage times, one would underestimate the actual association rate. We therefore corrected for DNA hydrolysis by subtracting the average hydrolysis time (2.5 s; see Fig. 3) from the statistical average of the measured cleavage time. The association rate is the inverse of this number (see SI Appendix for details).

Fig. 6.

The effect of hydrolysis on the measured cleavage rates, performed on data taken in 100 mM NaCl. For increased statistics data from all DNA conformations are combined here. (A) The first part of the distribution of cleavage times (0.25-s time bins) shows a lag phase caused by the presence of DNA hydrolysis as a second step in the reaction. The dashed line is the single-exponential fit (to the full distribution), and the solid curve is the fit for a two-step process. The hydrolysis rate (for the cleavage of both DNA strands) obtained by the fit is 0.4 ± 0.1 s⁻¹, in accordance with the direct measurements of this parameter (Fig. 3). (B) Probability distribution of cleavage time, constructed from the same data as in A. Also in this representation a two-step process (solid line) describes the data more accurately than a single exponential (dashed line), signifying the presence of DNA hydrolysis (again with a rate of 0.4 ± 0.1 s⁻¹). (Inset) Probability distributions for data subsets with the smallest (black) and largest (gray) fractional extensions. Although this method may provide an “easy way out” for fitting both hydrolysis and association rate, the uncertainties of the fits are ill-defined, as the individual data points in this cumulative representation are not independent.

Relaxation Time of DNA Fluctuations.

The DNA between the beads undergoes constant thermal fluctuations. The transient stretching cycles could in principle lead to an enhanced mixing of DNA conformational states if the duration of the stretch is shorter than the relaxation time τ_R of the coiled polymer. The latter can be calculated by using the Rouse model (40, 41):

With a persistence length l_p = 50 nm, DNA diameter d = 2 nm, contour length L = 2.2 μm, η as the viscosity of the buffer (≈10⁻³ Pa·s), and k_BT as the thermal energy, we obtain τ_R ≈ 2 ms. Compared with the stretching duration (<20 ms) this is fast enough to exclude any enhanced mixing.

EcoRV Concentration.

We determined the average hydrolysis time for the cleavage of both strands to be 2.5 s (Fig. 3). To make association rate-limiting, a minimum cleavage time of ≈10 s or more is required. With a specific association rate on plasmids of ≈10⁸ M⁻¹·s⁻¹ (30), this requires an enzyme concentration ≤1 nM. Because at low [EcoRV] the specific association rate is proportional to the enzyme concentration, it is crucial that the number of enzymes in the flow chamber is constant in all measurements. To test which protein concentration still yields reliable results we performed cleaving experiments with progressively lower proteins concentrations. For each concentration we determined the average cleaving times for independent sets of trial experiments (i.e., a new protein dilution used in a cleaned or new flow chamber). These tests showed that for EcoRV concentrations <0.7 nM the average cleavage times differed by up to ≈50% between data sets, presumably caused by proteins sticking to and detaching from the walls of the chamber and tubing. At concentrations ≥1 nM such effects were never observed. Therefore, 1 nM EcoRV was used in the experiments.