Dynamical relaying can yield zero time lag neuronal synchrony despite long conduction delays

Abstract

Multielectrode recordings have revealed zero time lag synchronization among remote cerebral cortical areas. However, the axonal conduction delays among such distant regions can amount to several tens of milliseconds. It is still unclear which mechanism is giving rise to isochronous discharge of widely distributed neurons, despite such latencies. Here, we investigate the synchronization properties of a simple network motif and found that, even in the presence of large axonal conduction delays, distant neuronal populations self-organize into lag-free oscillations. According to our results, cortico–cortical association fibers and certain cortico–thalamo–cortical loops represent ideal circuits to circumvent the phase shifts and time lags associated with conduction delays.

Cells in the visual cortex of mammals tend to fire simultaneously when activated by related features of a visual stimulus (1–4). This observation provided some of the early evidence that the nervous system may use an internal temporal code to process information. Since then, multicell electrophysiological studies have revealed the synchronous discharge of neurons distributed in different structures of the cerebral cortex, hippocampal formation, and thalamus (5, 6). Its biological significance derives from the observation that such precise and coordinated spike timing correlates with perception and behavioral performance (7–10). Remarkably, synchrony of neuronal activity is not limited to short-range interactions within a cortical patch. Interareal synchronization across cortical regions including interhemispheric areas has been observed in several tasks (7, 9, 11–14). The topological specificity and temporal unfolding of the synchrony reported in such studies are in agreement with its assumed role of subserving the effective “coupling” of the neuronal dynamics of the respective regions (9, 15).

Beyond its functional relevance, the zero time lag synchrony among such distant neuronal ensembles must be established by mechanisms that are able to compensate for the delays involved in the neuronal communication. Latencies in conducting nerve impulses down axonal processes can amount to delays of several tens of milliseconds between the generation of a spike in a presynaptic cell and the elicitation of a postsynaptic potential (16). The question is how, despite such temporal delays, the reciprocal interactions between two brain regions can lead to the associated neural populations to fire in unison.

Direct cortico–cortical fibers are major pathways of transareal communication and thus one principal substrate for the establishment of long-range synchrony. For instance, severing the corpus callosum was observed to disrupt the interhemispheric synchrony among homotopic cortical areas 17 in the cat (17). However, it is not clear whether direct excitatory cortico–cortical connections alone can mediate the zero phase synchronization of reciprocally coupled neurons for long transmission delays (18, 19). Several mechanisms have been pointed out as partially responsible for the enhancement of such synchrony. Inhibitory synapses and gap junctions have been proposed to stabilize the synchronous firing of cells under some specific conditions and for a limited range of delays (20, 21). In the case of the hippocampus, a canonical circuit of excitatory and inhibitory neurons have been shown to reproduce successfully the experimental findings of long-range synchrony among hippocampal neurons (5, 22, 23). Synaptic plasticity mechanisms have also been shown to stabilize synchronous γ oscillations between distant cortical areas by reinforcing the connections the delay of which matches the period of the oscillatory activity (24).

Nevertheless, significant long-range synchronization is observed across different species with different brain sizes and at different stages of the developmental growth of brain structures. This requires that any generic mechanism for generating zero time lag long-distance cortical synchrony maintains its functionality for a wide range of axonal lengths. Although it is possible that developmental mechanisms compensate for the resulting delay variations (25), it is still difficult to explain all of the phenomenology of long-distance synchronization without a mechanism that inherently allows for zero lag synchronization for a broad range of conduction delays and cell types.

In this paper, we investigate a simple network motif (26) that naturally accounts for the zero lag synchrony among two arbitrarily separated neuronal populations. We want to stress the separation of processes generating local rhythms or oscillations in a brain structure from the mechanisms responsible for their mutual synchronization. The model that we present below provides a proof of principle for a synchronizing mechanism among remote neuronal resources despite long axonal delays. The basic idea is that when two neuronal populations relay their activities to a third mediating population, the redistribution of the dynamics performed by this unit leads to a robust and self-organized zero lag synchrony among the outer populations (27, 28). Even if no particular brain structure or physiological condition is intended to be faithfully reproduced, this type of connectivity pattern is characteristic for the reciprocal interaction of different cortical areas and the associative thalamic nuclei, such as the pulvinar (29, 30), and as we shall show below it can give rise to isochronous dynamics in remote cortical populations. To demonstrate this effect, we conducted extensive simulations with networks of Hodgkin–Huxley (HH) neurons and integrate and fire (IAF) models to characterize the influence of long conduction delays in the synchronizing properties of this network module.

Results

Zero Time Lag Synchronization of Individual Neurons as a Self-Organization Process.

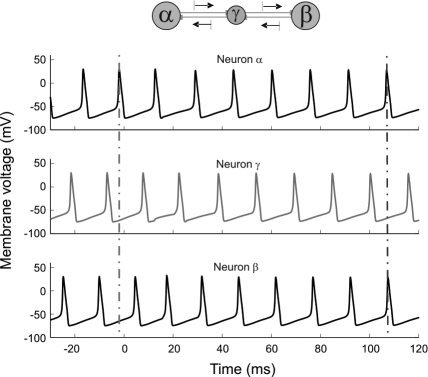
We started by studying the spiking dynamics of a circuit composed of 3 HH cells with reciprocal delayed synaptic connections (for a schematic representation of the network architecture, see Fig. 1Top). To inspect the role of such connectivity in synchronizing distant neurons we considered a configuration in which the isolated neurons had already an intrinsic spiking dynamics and observed how the synaptic activity modified the timing of their action potentials. By adding intracellular constant current stimulation (10 μA/cm²), each isolated neuron developed a tonic firing mode with a natural period of 14.7 ms. The initial phase of the oscillations of each cell was randomly chosen to exclude trivial coherent effects. Finally, all axonal conduction delays were set to a considerably long value of 8 ms. Fig. 1 shows the evolution of the membrane potentials under such conditions when excitatory synaptic coupling among the cells is activated [see supporting information (SI) Materials and Methods for further details].

Fig. 1.

Time series of the membrane voltage of 3 coupled HH cells N_α-N_β-N_γ. At time t = 0 the excitatory synapses were activated. Conduction delay τ = 8 ms. Vertical lines help the eye to compare the spike synchrony before and after the interaction takes place.

Before the coupling is switched on, the 3 cells fire out of phase as indicated by the left vertical guide to the eye in Fig. 1. However, once the interaction between the 3 neurons becomes effective at t = 0, a self-organized process, in which the outer neurons synchronize their spikes at zero lag even in the presence of long conduction delays, is observed. Notice that no external agent or influence is responsible for the setting of the synchronous state, but this is entirely negotiated by the network itself.

This mechanism of synchronization rests on the ability of an excitatory postsynaptic potential (EPSP) to modify the firing latencies of a postsynaptic neuron in a consistent manner. It further relies on the symmetric relay that the central neuron provides for the indirect communication between the outer neurons. The key idea is that this network motif allows for the outer neurons to exert an influence on each other via the intermediate relay cell. Thus, the reciprocal connections from the relay cell assure that the same influence that is propagating from one extreme end of the network to the other is also fed back into the neuron that originated the perturbation promoting the synchronous state. It must be noticed, however, that a pair of identical EPSPs elicited simultaneously on the outer neurons does not have in general an identical effect on both neurons. Actually, the effect of a postsynaptic potential on a neuron strongly depends on the internal state of the receiving cell, and more specifically on the phase of its spiking cycle at which the PSP is arriving (31–33). Because the neurons are in general at different phases of their oscillatory cycles, the effects of the EPSPs (magnitude and direction of the induced phase shifts) are different for the 3 cells. Nevertheless, the accumulation of such corrections to the interspike intervals of the outer neurons is such that after receiving a few EPSPs they compensate the initial phase difference, and both cells end up discharging isochronously, representing a stable state (see SI Materials and Methods). Our simulations also show that a millisecond-precise locking of spikes can be achieved already after the exchange of only a few spikes in the network.

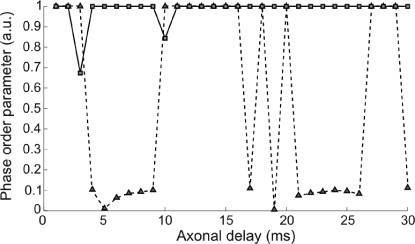
A key issue of the synchronization properties exhibited by such network architecture is whether the zero lag correlation can be maintained for different axonal lengths or whether it is specific to a narrow range of axonal delays. Fig. 2 displays the quality of the zero lag synchronization between 2 HH neurons as a function of the conduction delays. Two scenarios were studied: one in which the neurons were directly coupled via excitatory synapses (dashed line) and a second one in which the 2 neurons interacted through a relay cell also in an excitatory manner (solid line). The synchronization index is given by the order parameter defined in the SI Materials and Methods. A value of 1 (zero) of this index indicates perfect synchrony (uncorrelation) at zero lag. A quick comparison already reveals that whereas the direct excitatory coupling exhibits large regions of axonal conduction delays where the zero lag synchrony is not achieved, the relay-mediated interaction leads to zero time lag synchrony in 28 of the 30 delay values explored (1–30) ms. Only for τ ≈ 3 ms and τ ≈ 10 ms, the 3 cells entered into a chaotic firing mode in which the neurons neither oscillated with a stable frequency nor exhibited a consistent relative lag between their respective spike trains. See also Fig. S1 for a description of the phase relations among the 3 neurons as a function of the axonal delay.

Fig. 2.

Dependence of zero time lag synchronization as a function of the axonal delay between neighbor cells for a scheme of 2 coupled neurons (dashed line) and 3 coupled neurons (solid line). In the case of the 3 interacting cells, only the synchrony between the outer neurons is plotted here.

Robust zero lag synchrony among the outer neurons was also observed when the synaptic interaction between the cells was inhibitory instead of excitatory. Different synaptic rise and decay times within the typical range of fast AMPA- and GABA_A-mediated transmission were tested with results identical to those reported above. These results indicate that the network motif of 2 neurons relaying their activities through a 3rd neuron leads to a robust zero lag synchrony almost independently of the delay times and sign of the synaptic interactions. We also conducted simulations to test the robustness of this type of synchrony with respect to the nature of the relay cell. The results indicate that when a relay cell was operating in a parameter regime different from the outer ones (such as different firing rate or conductances), the zero lag synchrony among them was not disturbed. Remarkably, even in the case where the relay cell was operating in a subthreshold regime, and thus only spiking because of the excitatory input from any of the outer neurons, the process of self-organization toward the zero lag synchrony was observed. It is worth mentioning that in all cases such firing synchronization is achieved through small shifts in the spiking latencies that left the mean frequency of discharges (rate) almost unchanged (the largest variations observed were smaller than a 9% relative change).

Dynamical Relaying-Based Synchronization Is Robust to Broad Distributions of Axonal Delays.

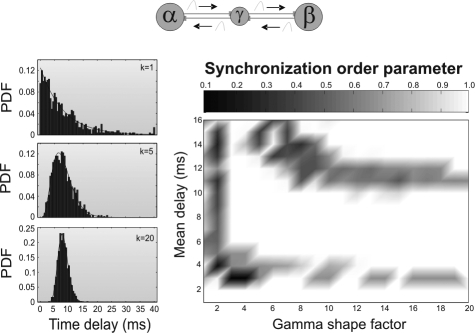
The axons that form cortico–cortical or thalamo–cortical fibers differ in diameter, myelin thickness, and internodal distance. The variability from 1 axon to another of these characteristics affects the speed of propagation of action potentials and eventually translates into the existence of a whole range of latencies in the neuronal communication between separate brain areas. Thus, conduction times along fibers are more suitably considered as a spectrum rather than a single latency value (16, 34). To tackle this issue we modeled the dispersion of axonal latencies by assuming that individual temporal delays of the arrivals of action potentials (i.e., latency times) follow a γ distribution (see Eq. S13 in the SI Materials and Methods). This mimicked the variability among the different axons connecting 2 pools of neurons. Because data about axonal distributions of conduction velocities in long-range fibers is limited (16, 34), and there is probably not a unique prototypical form of such distributions we decided to explore a whole family of γ distributions with different shapes. Fig. 3Left illustrates different γ distributions of axonal delays for 3 different shape factors.

Fig. 3.

Effects of broad distributions of axonal delays on synchrony. (Left) γ distribution of delays with different shape factors (k = 1, 5, and 20) and the same mean (τ = 8 ms). (Right) Synchronization index at zero lag of the outer neurons as a function of the shape factor and mean of the distribution of delays.

Our numerical simulations indicate that for a large region of mean delays (between 3 and 10 ms), the outer neurons synchronize independently of the shape of the distribution. These results can be observed in Fig. 3 Right, where we plot the zero lag synchronization index of the outer neurons of the network motif as a function of the shape of the γ distribution of axonal delays and its mean value. Only distributions with unrealistic small shape factor (i.e., exponentially decaying distributions) prevent synchrony irrespective of the average delay of the synaptic connections. For more realistic distributions, there is an extensive region of axonal delays that gives rise to the zero lag synchrony among the outer neurons. As in the case of single latencies, we found a drop in the synchronization quality for distributions with a mean value of approximately τ ≈10–12 ms, where chaotic firing is observed. The isochronous spiking coherence is in general recovered for larger mean delay values.

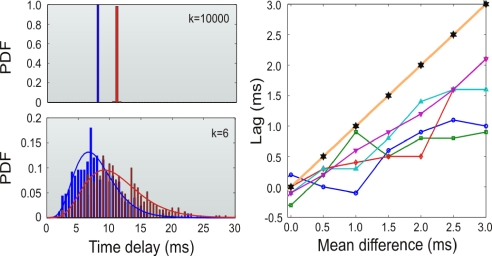
Up until now, we have considered similar distributions of axonal delays in each of the 2 branches connecting the relay neuron to the outer units. This holds when the relay cell occupies a location that is approximately equidistant from the outer elements. Nevertheless, we also investigated the situation in which the axonal delays of each of the 2 pathways of the network motif are described by dissimilar distributions. In those cases, we have found that if the distributions of delays for each branch of the module have different mean values then a nonzero phase lag appears between the dynamics of the outer neurons. This effect is illustrated in Fig. 4. For δ distributions of delays (which is equivalent to the single latency case) the lag amounts to the delay difference that is still much smaller than the sum of the delays accumulated to communicate both neurons. When studying the effect of broader distributions of delays, we observed that outer cells tend to fire with a lag even smaller than the difference in the mean values of the distributions. Thus, broad distributions of delays allow distant neurons to fire at almost zero lag even when the mean delay values of the branches differed in several milliseconds.

Fig. 4.

Effects of dissimilar distributions of axonal delays on the lag of synchronization. (Left) different γ distributions of delays used for the 2 dissimilar branches of the network module. (Upper) Distributions with shape factor k = 10,000 (quasi-δ) and means of 8 and 11 ms. (Lower) Distributions with shape factor k = 6 and means of 8 and 11 ms. (Right) Lag between the discharges of the outer neurons as a function of the difference in the mean of the distributions of delays for the 2 branches. Shape factors k = 6 (squares), k = 8 (circles), k = 10 (diamonds), k = 12 (upright triangles), k = 14 (inverted triangles), and k = 10,000 (stars) were tested.

Populations of Distant Neurons Can Also Exhibit Zero Lag Synchrony via Dynamical Relaying.

A further key step in demonstrating the feasibility of synchronizing widely separated neurons via dynamical relaying is the extension of the previous results to the level of neuronal populations, the scale at which neuronal microcircuits develop their function (35). Far from being independent, the dynamical response of any neuron is massively affected by the activity of the local network of cells or functional unit into which it is embedded and by the long-range afferents originating in distant populations. It is also important to consider the random-like influences usually referred to as background noise, a term that collects a variety of processes from spontaneous release of neurotransmitters to fluctuations of unspecific inputs (36, 37). In such a scenario, we explored whether long-range fibers supporting dynamical relaying, and thus indirectly connecting pools of neurons, are suitable to act as the driving force promoting remote interpopulation synchrony in the presence of local interactions and noise sources.

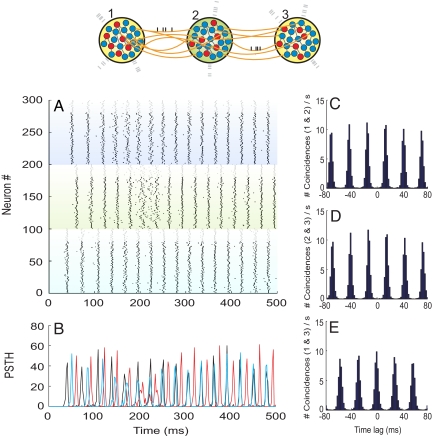
To check whether zero lag-correlated firing is thus induced among neurons in different populations, we built 3 large networks of sparsely connected excitatory and inhibitory IAF neurons (see Materials and Methods and SI Materials and Methods). We interconnected the 3 populations following the topology of the network motif under study, i.e., the mutual relaying of activities of 2 external populations onto an intermediate pool of relay neurons.

We first initialized all 3 networks without the long-range interpopulation connections. Only the recurrent local connections and the Poissonian external background were active and thus responsible for any dynamics in the stand-alone networks. Consequently, each population initially exhibited spiking of their neurons in an incoherent and unsynchronized fashion with respect to neurons belonging to any of the other populations. Once the long-range synapses were activated, we observed that the firing of the neurons organized toward the collective synchrony of the outer populations. Fig. 5 illustrates the typical raster plot, firing histogram, and cross-correlograms of neurons among the 3 interconnected networks for a conduction delay of 12 ms. Similar results were observed when we explored other axonal delays in the range of 2–20 ms. The mean period of the coupled oscillatory activity (≈32 ms) was found to be close to the local rhythm of the isolated networks (≈34 ms), and therefore the coupling had little effect on the frequency of oscillation. A different situation might appear when the populations are tuned so that no prominent oscillatory activity emerges in the isolated networks before they are functionally coupled. In that case, we found from our model that the reciprocal coupling among the networks can act as a generator of oscillations and zero lag synchrony. In the latter case, however, we found a periodicity strongly influenced by the conduction delay times.

Fig. 5.

Dynamics of 3 large-scale networks interacting through dynamical relaying. (A) Raster plot of 300 neurons randomly selected among the 3 populations (neurons 1–100 are from population 1, 101–200 from population 2, and 201–300 from population 3). The top 20 neurons of each subpopulation (plotted in gray) are inhibitory, and the rest are excitatory (black). (B) Firing histogram of each subpopulation of 100 randomly selected neurons (black, red, and blue colors code for populations 1, 2, and 3, respectively). (C) Averaged cross-correlogram between neurons of populations 1 and 2. (D) Averaged cross-correlogram between neurons of populations 2 and 3. (E) Averaged cross-correlogram between neurons of populations 1 and 3. At t = 100 ms, the external interpopulation synapses become active. Bin sizes for the histogram and correlograms are set to 2 ms. Interpopulation axonal delays are set to 12 ms.

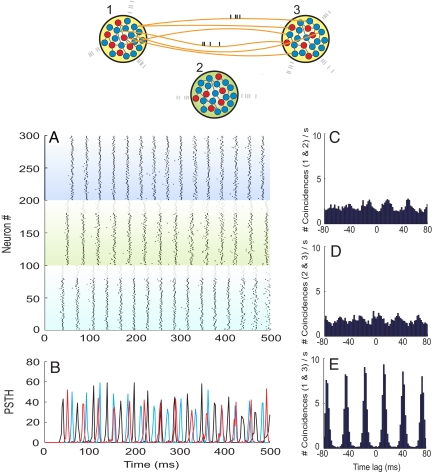
To determine the role of the relay cells (population 2) in shaping the synchronization among cells belonging to the remote neuronal networks (populations 1 and 3), we designed the following control experiment. We investigated the neuronal dynamics obtained under exactly the same conditions as in the former approach with the only variation that this time the 2 outer networks interacted directly. The results are summarized in Fig. 6. The sole change of the topology of the connections meant that networks 1 and 3, even if engaged in oscillations with similar characteristics as before, no longer synchronized their spikes at zero lag.

Fig. 6.

Dynamics of 2 large-scale networks interacting directly. Population 2 is disconnected from other populations. Structure of the panels and parameters are otherwise as in Fig. 5.

Discussion

In the previous paragraphs we introduced a network topology that enhances the zero lag synchronization of distant populations of neurons. Specifically, we showed that 2 populations of cells can become synchronized with zero phase lag if coupled reciprocally to a third population. Synchrony is maintained even when the fibers connecting the networks accumulate axonal delays of several tens of milliseconds. This suggests that such topology may contribute to the large-scale synchronization phenomena reported in a number of experiments during the last 2 decades (10, 15).

In this context, R. Llinás and other authors have suggested the reciprocal coupling of cortical areas with the thalamus as a mechanism to support distributed cortical processing and the emergence of consciousness (38–40). Edward G. Jones and other authors have explicitly proposed the dispersed cortical projections of matrix cells in the dorsal thalamic nuclei together with the layer V corticothalamic projection as the appropriate circuitry to extend thalamocortical activity and to form a substrate for synchronization of widespread ensembles of cortical and thalamic cells (29, 30). The resemblance of such circuitry with the topology studied here is evident once the identification of the associative nuclei of the thalamus as our relay population for cortical activity is performed. However, the principal message of our results is not the identification of the physiological structures potentially responsible for long-range cortical synchrony but to show that the long latencies associated with cortico–thalamo–cortical loops are compatible with synchronization across large distances. Coherent oscillations between remote cortical populations can of course be generated also by reciprocally coupling these areas to other cortical areas or other subcortical structures. In fact, the aggregation of several of such motifs around a putative hub (forming a star-like network with the center unit playing the role of the relay element) also favors satellite nodes to spike in zero lag synchrony (41).

The most important requirement for zero phase lag synchronization is that the relay population of cells occupies a temporally equidistant location from the pools of neurons to be synchronized. It is significant to point out that recent studies have identified a constant temporal latency between thalamic nuclei and almost any area in the mammalian neocortex (42). Thus, in this scheme, thalamic nuclei occupy a central position for the mediation of zero phase solutions.

In general, it is quite probable that a variety of mechanisms are responsible for bringing synchrony at different levels (distinguishing for example, among local and long-distance synchrony) and different cerebral structures. The fact that each thalamus projects almost exclusively ipsilaterally (the massa intermedia is clearly inadequate for supporting the required interthalamic communication) is already an indication that the callosal commissure should play a prominent role in facilitating interhemispheric coherence. Lesion studies have since long confirmed this view (17). However, within a single hemisphere the disruption of intracortical connectivity by a deep coronal cut through the suprasylvian gyrus was observed not to disturb the synchrony of spindle oscillations across regions of cortex located at both sides of the lesion (6). This finding suggests that subcortical, and in particular cortico–thalamic interactions, could be responsible for maintaining both the long-range cortical and thalamic coherence found in such a regime. It is likely that subcortical loops with widespread connectivity such as the associative or nonspecific cortico–thalamo–cortical circuits could run in parallel as an alternative pathway for the large-scale integration of cortical activity within a single hemisphere (30, 35, 40, 43). As we have shown here, with such connectivity pattern even large axonal conduction delays represent no detriment to the observation of zero time lag synchronization. It is also important to remark that connectivity studies in primate cortex have identified the pattern of connections studied here as the most frequently repeated motif at the level of cortico–cortical connections in the visual cortex (44–46). The functional relevance of this topology of cortical network is unclear but according to our results is ideally suited to sustain coherent activity.

In summary, the network motif highlighted here has the property of naturally inducing zero lag synchrony among the firing of 2 separated neuronal populations. The associative thalamic nuclei have the cortex as their main input and output sources and seem to represent active relay centers of cortical activity with properties well suitable for enhancing cortical coherence (30). From the experimental side, the relatively well-controlled conditions of brain slice experiments, allowing for the identification of synaptically coupled neurons and cell type, might be a first step for testing whether the topology investigated here provides a significant substrate for coherent spiking activity. Another important issue is how the dynamic selection of the areas that engage and disengage into synchrony is achieved. It has been hypothesized that a dynamically changing coherent activity pattern may ride on top of the anatomical structure to provide flexible neuronal communication pathways (47). Based on the properties formerly reviewed, subcortical structures such as some thalamic nuclei might be promising candidates to play a role in regulating such coherence and contribute to the large-scale cortical communication.

Materials and Methods

Two neuronal models were numerically simulated to test the synchronization properties of the neuronal circuits investigated here.

In the most simplified version of the neuronal motif we focused on the dynamics of 2 single-compartment neurons that interact with each other via reciprocal synaptic connections with an intermediate third neuron of the same type (see Fig. 1 Top). The dynamics of the membrane potential of each neuron was modeled by the classical HH equations (48) plus the inclusion of appropriate delayed synaptic currents that mimic the chemical interaction between nerve cells.

The second class of models we have considered consists of 3 large balanced populations of IAF neurons (49). Fig. 5 Upper is a sketch of the connectivity. Each network consisted of 4,175 IAF neurons of which 80% were excitatory. The internal synaptic connectivity was chosen to be random, i.e., each neuron synapsed with 10% of randomly selected neurons within the same population, such that the total number of synapses in each network amounted to ≈1,700,000 contacts. In additional to model background noise, each neuron was subjected to the influence of an external train of spikes with a Poissonian profile. The interpopulation synaptic links were arranged such that each neuron in any population receives input from 0.25% of the excitatory neurons in the neighboring population. Note that the interpopulation links remained small in number compared with the local coupling that allows to consider the system as 3 weakly interacting networks of neurons rather than a single homogeneous network. Intrapopulation axonal delays were set to 1.5 ms, whereas the fibers connecting different populations were assumed to involve much longer latencies to mimic the long-range character of such links.

Parameters, evolution equations, simulation schemes, and data analysis for these 2 models are detailed in the SI Materials and Methods.