SOME STEP-DOWN PROCEDURES CONTROLLING THE FALSE DISCOVERY RATE UNDER DEPENDENCE

Abstract

Benjamini and Hochberg (1995) proposed the false discovery rate (FDR) as an alternative to the familywise error rate (FWER) in multiple testing problems. Since then, researchers have been increasingly interested in developing methodologies for controlling the FDR under different model assumptions. In a later paper, Benjamini and Yekutieli (2001) developed a conservative step-up procedure controlling the FDR without relying on the assumption that the test statistics are independent.

In this paper, we develop a new step-down procedure aiming to control the FDR. It incorporates dependence information as in the FWER controlling step-down procedure given by Westfall and Young (1993). This new procedure has three versions: lFDR, eFDR and hFDR. Using simulations of independent and dependent data, we observe that the lFDR is too optimistic for controlling the FDR; the hFDR is very conservative; and the eFDR a) seems to control the FDR for the hypotheses of interest, and b) suggests the number of false null hypotheses. The most conservative procedure, hFDR, is proved to control the FDR for finite samples under the subset pivotality condition and under the assumption that joint distribution of statistics from true nulls is independent of the joint distribution of statistics from false nulls.

1. Introduction

The problems associated with multiple hypothesis testing have become greater with the advent of massively parallel experimental assays, especially microarrays. A naive approach of rejecting the hypotheses whose p-values are no greater than 0.05 will lead to 500 false positives on average for a microarray experiment that measures 10,000 genes. Therefore some form of error rate to control false positives is required. Traditionally, this error rate was represented by the familywise error rate (FWER), which is defined as the probability of erroneously rejecting at least one null hypothesis. Benjamini and Hochberg (1995) proposed the false discovery rate (FDR) as an alternative to the FWER. The FDR is defined to be the expected proportion of erroneously rejected null hypotheses among all rejected ones. The FDR can identify more putatively significant hypotheses than the FWER, and meaning of the FDR can be intuitively explained. Hence researchers are increasingly using the new error rate FDR, especially in exploratory analyses. If interest is in finding as many false null hypotheses as possible among thousands of tests, this new error measure seems more appropriate than the FWER. The FWER is probably more stringent than what most researchers want in the exploratory phase, as it permits no more than a single null hypothesis being erroneously rejected.

A particular problem in microarray data analysis is identifying differentially expressed genes among thousands of them. Dudoit et al. (2002) and Westfall, Zaykin and Young (2001) used the maxT step-down approach to control the FWER. Ge, Dudoit and Speed (2003) introduced a fast algorithm implementing the minP step-down adjustment controlling the FWER. In another direction, Tusher, Tibshirani and Chu (2001), Efron et al. (2001), and Storey (2002) adopted the FDR approach in microarray experiments. This paper is mostly about a new algorithm to compute the FDR. Although we focus on microarray applications, as with the maxT and minP step-down adjustment in the previous paper Ge, Dudoit and Speed (2003), the new algorithm can be applied to other similar multiple testing situations as well.

Section 2 reviews the basic notions of multiple testing, and the concept of the FDR. Section 3 introduces some related work on procedures controlling the FDR. Section 4 presents three versions of our new step-down procedure aiming to control the FDR, gives some theoretical properties for the most conservative version (hFDR), and presents the resampling algorithm. Section 5 describes simulation results on the three versions of the new procedure introduced in Section 4. The microarray applications are in Section 6 and, finally Section 7 summarizes our findings and open questions.

2. Multiple testing and false discovery rates

Assume that there are m pre-specified null hypotheses {H₁, …, H_m} to be tested. Given observed data X = x, a statistic t_i is used for testing hypothesis H_i, and p_i is the corresponding p-value (a.k.a raw p-value, marginal p-value or unadjusted p-value). In the microarray setup, the observed data x is an m × n matrix of gene expression levels for m genes and n RNA samples from treated and control groups, while t_i might be a two-sample Welch t-statistic computed from the expression levels of gene i. The null hypothesis H_i is that gene i is non-differentially expressed between the treated group and the control group. The biological question is how to find as many differentially expressed genes (false null hypotheses) as possible without having too many false positives. A false positive occurs when an unaffected gene is claimed to be differentially expressed (falsely rejecting a null hypothesis). In this paper, we adopt the notation that the observed values are denoted by lower case letters, t_i, p_i for example, and the corresponding random variables are denoted by upper case letters, T_i, P_i for example. For the sake of convenience, we always assume a two-sided test, i.e., p_i = P (|T_i|≥|t_i| | H_i). Let the set of true null hypotheses be M₀, the set of false null hypotheses be M₁, and the full set be M = M₀ ∪ M₁. Let m₀ = |M₀| and m₁ = |M₁|, where |·| denotes the cardinality of a set. Given a rejection procedure, let V denote the number of erroneously rejected null hypotheses and R the total number of rejected ones. Then R–V is the number of correctly rejected hypotheses, denoted by S. The values of V, R and S are determined by the particular rejection procedure and the significance level α, say 0.05. Table 1 shows possible outcomes of a rejection procedure.

Table 1.

Summary table for multiple testing problems

	Set	Number of decisions
		reject	accept	total
true null	M0	false positives: V	correct decisions: m0–V	m0
false null	M1	correct decisions: S	false negatives: m1–S	m1
total	M	R	m–R	m

For any set K = {i₁, …, i_k} ⊆ M, let H_K denote the partial joint null hypothesis associated with the set K. H_M is called the complete null as every null hypothesis is true. Traditionally, the familywise error rate (FWER) has been widely used. The FWER is defined as the probability of erroneously rejecting at least one null hypothesis, i.e., P(V > 0). Since the above probability is computed under the restriction H_M0, using the notations from Westfall and Young (1993), we have

$$\text{FWER}=P(V>0\mid H_{M_0}).$$

Westfall and Young (1993) gives a comprehensive introduction to this subject while focusing on a resampling-based adjusted p-values approach. Let Q be the false discovery proportion (Korn et al. (2004)): the proportion of erroneously rejected null hypotheses among all rejected ones,

$$Q=V/R,$$ (1)

where the ratio is defined to be zero when the denominator is zero. The false discovery rate (FDR) is defined to be the expectation of Q,

$$\text{FDR}=E(Q\mid H_{M_0})=E(V/R\mid H_{M_0}).$$

There are three kinds of FDR control.

• Weak control: control of the FDR under the complete null H_M, i.e., for any α ∈ (0, 1),

$$E(Q\mid H_M)\le \alpha .$$

• Under H_M, we have Q = I(V > 0), where I(·) is the indicator function, so weak control of the FDR is equivalent to weak control of the FWER.

• Exact control: control of the FDR for the true null set M₀, i.e., for any α ∈ (0, 1),

$$E(Q\mid H_{M_0})\le \alpha .$$

• The definition is applicable only when the true null set M₀ is known.

• Strong control: control of the FDR for all possible M₀ ⊆ M, i.e., for any α ∈ (0, 1),

$$\underset{M_0\subseteq M}{max}E(Q\mid H_{M_0})\le \alpha .$$

In practice, we do not know the true null set M₀, and weak control is not satisfactory. It is important to have a strong control. In fact, the majority of existing FDR procedures offer strong control. The first known procedure with proof of strong control of the FDR was provided by Benjamini and Hochberg (1995).

The BH Procedure

Let the indices of the ordered p-values be d₁, …, d_m such that p_d1 ≤ · · · ≤ p_dm. The {d_i} are determined by the observed data X = x. Fix α ∈ (0, 1). Define i^* = max{i: p_di ≤ c_i}, where c_i = αi/m. Then reject H_d1, …, H_di^* if i^* exists; otherwise reject no hypotheses.

The BH procedure is a step-up procedure because it begins with the largest p-value p_dm to see if H_dm can be accepted with the critical value c_m, and then p_dm−1, until p_di^* which can not be accepted any more as p_di^* ≤ c_i^*. Benjamini and Hochberg (1995) proved that their procedure provides strong control of the FDR when the p-values from the true null hypotheses M₀ are independent. The ideas of the BH procedure appeared much earlier in seminal papers by Eklund (1961–1963) as mentioned in Seeger (1968), and later were rediscovered independently in Simes (1986). Eklund (1961–1963) even motivated the procedure by the definition of “proportion of false significances”, which is equivalent to the Q of equation (1). Seeger (1968) and Simes (1986) also gave the proof that this procedure controls the FWER in the weak sense. Similar ideas for controlling the FDR also appeared in Soríc (1989). However, Benjamini and Hochberg’s proof of strong control of the FDR has accelerated the usage of the BH procedure and the FDR concept.

3. Some related previous works

Since the first groundbreaking paper on the FDR by Benjamini and Hochberg (1995), different procedures have been proposed to offer strong control of the FDR under different conditions. A later work by Benjamini and Yekutieli (2001) relaxed the independence assumption to certain dependence structures, namely, when the underlying statistics are positive regression dependent on a subset of the true null hypotheses M₀ (PRDS). There are other works which modify the critical values c_i to produce a more powerful procedure, i.e., to reject more hypotheses while still offering strong control of the FDR at the same significance level α. For example, Kwong, Holland and Cheung (2002) used the same critical values c_i = αi/m, for i = 1, …, m − 1, but with a different definition of c_m. Their c_m is always no less than the c_m defined in the BH procedure, and so their procedure is at least as powerful as the BH. Benjamini and Liu (1999) (hereafter called BL) derived a different set of critical values c_i for a step-down procedure when the underlying test statistics are independent.

The BL Procedure

Fix α ∈ (0, 1). Let i^* be the largest i such that p_d1 ≤ c₁, …, p_di ≤ c_i, where c_i = 1 − [1 − min (1, αm/(m − i + 1))]^1/(m−i+1). Then reject H_d1, …, H_di^* if i^* exists; otherwise reject no hypotheses.

Sarkar (2002) strengthened the Benjamini and Yekutieli (2001) results for the BH procedure in a much more general step-wise framework. He also relaxed the assumption of the BL procedure, from independence to a weak dependence condition: Sarkar assumed that the underlying test statistics exhibit the multi-variate total positivity of order 2 (MTP₂) under any alternatives, and that the test statistics are exchangeable when the null hypotheses are true. There are other works which modify the BH procedure by multiplying the p-values with an estimate of π₀ = m₀/m (Benjamini and Hochberg (2000); Storey (2002); Storey and Tibshirani (2001)).

Most of the papers mentioned above deliver strong control of the FDR under the assumption that the test statistics are independent, or under the assumption that the expectation of some statistics of the dependent data can be bounded by that of independent data, as in the PRDS or in the MTP₂ cases. Hence, these works are able to generalize the results from independence to a weak dependence situation. However, there still seems to be a need to develop a procedure that can be applied to less independent data. For example, Troendle (2000) derived different step-up and step-down procedures for multivariate normal data. Yekutieli and Benjamini (1999) used a resampling procedure to compute FDR adjusted p-values under dependence. In their paper, they proposed FDR adjusted p-values, which are similar in concept to the FWER adjusted p-values in Westfall and Young (1993).

Given a particular rejection procedure, the FDR adjusted p-value for a hypothesis is the smallest level at which H_i is rejected while controlling the FDR. i.e.,

$${\stackrel{\sim }{p}}_i=inf\{\alpha \mid H_i\text{is}\text{rejected}\text{at}\text{FDR}=\alpha \}.$$

The FDR adjusted p-values are determined by a particular rejection procedure. For example, with the BH procedure, the adjusted p-values are

$${\stackrel{\sim }{p}}_{d_i}=\underset{k=i,\dots ,m}{min}\{min(p_{d_k}·m/k,1)\}.$$

On the other hand, if a procedure can assign adjusted p-values, then for any given α ∈ (0, 1) we reject all hypotheses whose adjusted p-values are no greater than α. Yekutieli and Benjamini (1999) proposed a resampling-based FDR local estimator (see equations 9 and 10 of their paper):

$$\widehat{Q}(p)=E\{\frac{R^{\ast }(p)}{R^{\ast }(p)+\widehat{s}(p)}\}.$$ (2)

Here the expectation of equation (2) is computed by resampling under the complete null H_M, and R^*(p) is a random variable defined as #{i ∈ M: p_i ≤ p}, while ŝ(p) is an estimate of the data dependent number s(p) = #{i ∈ M₁: p_i ≤ p}. The s(p) is generally unobservable, as we do not have any information on M₁. Yekutieli and Benjamini (1999) used (2) to propose a rejection procedure aiming at strong control of the FDR.

Benjamini and Yekutieli (2001) (hereafter called BY) provided a conservative procedure by dividing each c_i of the BH procedure by a constant ${\sum }_{l=1}^{m}1/l$.

The BY Procedure

Fix α ∈ (0, 1). Define i^* = max{i: p_di ≤ c_i}, where $c_i=\alpha i/(m{\sum }_{l=1}^{m}1/l)$, then reject H_d1, …, H_di^* if i^* exists; otherwise reject no hypotheses.

Benjamini and Yekutieli (2001) proved that this procedure controls the FDR in the strong sense without relying on the independence assumption. However, this procedure has limited use due to the extreme conservativeness by dividing by ${\sum }_{l=1}^{m}1/l$ approximately ln(m).

Additional works studying the theoretical properties of the FDR include Finner and Roters (2001, 2002); Genovese and Wasserman (2002); Sarkar (2002). Another important direction of the research on the FDR is to control the false discovery proportion (FDP), the random variable Q, rather than its expectation, the FDR (Genovese and Wasserman (2004); Korn et al. (2004); Meinshausen (2006); Romano and Shaikh (2006); van der Laan, Dudoit and Pollard (2004)). Our work differs from this line of research in that we focus on the control of the expectation (the FDR). In the next section, we propose a new step-down procedure, which provides strong control of the FDR for dependent data.

4. A new step-down procedure to control the FDR

4.1. Motivation

In order to develop a step-down procedure providing control of the FDR for generally dependent data, we first review an elegant step-down procedure proposed by Westfall and Young (1993) based on the sequential rejection principle (pages 72–73 in their book).

For any α ∈ (0, 1), consider the following.

1. If P(min(p_d1, …, P_dm) ≤ p_d1 | H_M) ≤ α, then reject H_d1 and continue; otherwise accept all hypotheses and stop.

⋮

i. If P(min(p_d1, …, P_dm) ≤ p_di | H_M ) ≤ α, then reject H_di and continue; otherwise accept H_di, …, H_dm and stop.

⋮

m. If P(P_dm ≤ p_dm| H_M ) ≤ α, then reject H_dm; otherwise accept H_dm.

This sequential rejection principle mimics researchers’ verification procedures in practice. When people are faced with thousands of hypotheses, they will check the hypothesis with the smallest p-value to see if it is really a false null hypothesis. After a number of steps, say at step i, it might be reasonable to estimate the FWER using the null hypotheses H_di, …, H_dm, since they have not been tested yet. The sequential rejection principle can also be written in the form of adjusted p-values. We define the minP step-down adjustment:

$${\check{p}}_{d_i}=P(min(P_{d_i},P_{d_{i+1}},\dots ,P_{d_m})\le p_{d_i}\mid H_{d_i},\dots ,H_{d_m}).$$ (3)

and enforce the step-down monotonicity by assigning

$${\stackrel{\sim }{p}}_{d_i}=\underset{k=1,\dots ,i}{max}{\check{p}}_{d_k}.$$

This procedure is intuitively appealing. More importantly, Westfall and Young (1993) proved that the minP adjustments give strong control of the FWER under the subset pivotality property.

Subset pivotality: for all subsets K ⊆ M, the joint distributions of the sub-vector (P_i, i ∈ K) are identical under the restrictions H_K and H_M, i.e.,

$$\mathcal{L}(P_i,i\in K)\mid H_K\stackrel{d}{=}\mathcal{L}(P_i,i\in K)\mid H_M.$$

Let

$$R_i=\#\{k\in \{d_i,d_{i+1},\dots ,d_m\}:P_k\le p_{d_i}\}.$$

The i-th step of the minP step-down procedure computes P(R_i > 0 | H_di, …, H_dm). This is essentially the FWER obtained by rejecting all untested hypotheses (H_di, …, H_dm) whose p-values are no greater than p_di. In other words, the minP step-down procedure has two stages. The first stage is to define a rejection rule at step i by using the same critical value p_di to reject hypotheses H_di, …, H_dm; the FWER adjusted p-value p̃_di can then be computed by assuming that the hypotheses H_dm, …, H_dm are true. For any level α, the second stage is to reject all hypotheses whose adjusted p-values p̃ _di are no greater than α.

The sequential rejection principle can be applied to compute the FDR as with the minP step-down adjustment by a two-stage consideration. During the first stage, at step i, we define R_i = #{k ∈ {d_i, d_i+1, …, d_m}: P_k ≤ p_di}. The critical issue is to compute the FDR related to this rejection procedure at step i. As with the minP step-down procedure at (3), at step i we can “naively” estimate the FDR under the assumption that the previous i − 1 null hypotheses are false. We emphasize the “naively”, as there might be a small proportion of the first i hypotheses that are true nulls.

According to the definition of FDR = E(V/R), where 0/0 is defined to be zero, we can define the FDR adjusted p-values at step i to be

$${\check{p}}_{d_i}=E\{R_i/(R_i+i-1)\mid H_{d_i},\dots H_{d_m}\},$$ (4)

and enforce the monotonicity p̃_di = max_{k=1, …, i} p̌_dk. In (4), 0/0 is defined to be zero. This equation has some similarities to (2), which was used in the resampling procedure of Yekutieli and Benjamini (1999). Our procedure is different from theirs in two respects: (2) uses the same estimate s̄ of s to compute every FDR adjusted p-value, while (4) has a different s̄ = i − 1 at each step i; (2) always computes the FDR under the complete null H_M, while we compute the FDR under different nulls H_K, where K = {d_i, …, d_m} for a particular step i. The aim of our new procedure is to provide strong control of the FDR under dependence just as the minP procedure provided strong control of the FWER (Westfall and Young (1993)).

It turns out that this procedure is too optimistic. In Section 5, our simulation results clearly show that it does not provide strong control of the FDR for the hypotheses with large FDR adjusted p-values. The reason is that, at step i of the first stage, the only rejected hypotheses are those whose p-values are no greater than p_di. However, at the second stage, we are very likely to reject a hypothesis whose p-value is much greater than p_di at a later step j (> i). Therefore, the original definition is too optimistic. Denote the original definition of R_i by $R_i^l$,

$$R_i^l=\#\{k\in \{d_i,\dots ,d_m\}:P_k\le p_{d_i}\}.$$ (5)

We can define R_i more reasonably without using the same critical value p_di for all P_di, …, P_dm. One way is to adapt the critical values according to the ranked p-values. For k = 1, …, m − i + 1, let $P_{(k)}^i$ be the k-th smallest of the random variable p-values P_di, …, P_dm, and let $p_{(k)}^i=p_{d_{i+k-1}}$ be the k-th smallest of the observed p-values p_di, …, p_dm. The critical values $p_{(1)}^i,\dots ,p_{(m-i+1)}^i$ can be used to compute the number of rejected hypotheses by a step-down procedure:

$$R_i^e={max}_{k=1,\dots ,m-i+1}\{k:P_{(1)}^i\le p_{(1)}^i,\dots ,P_{(k)}^i\le p_{(k)}^i\}$$ (6)

The rejection procedure at step i to compute $R_i^e$ is similar to the BH, BY, and BL procedures in Section 3. These procedures use constant critical values c₁, …, c_m, which depend solely on the significance level α. By contrast, our critical values $p_{(1)}^i,\dots ,p_{(m-i+1)}^i$ depend on the data and the step index i as well: our critical values are more data-driven. In the simulation results of Section 5, the FDR seems to be controlled for the hypotheses of interest: the m₁ hypotheses with the smallest p-values, where m₁ can be suggested from the FDR curve.

We can use a more conservative strategy to compute R_i. At step i of the first stage, if we find $P_{(1)}^i\le p_{(1)}^i$, then we stop. We naively think that we will reject hypothesis H_di and all of the later hypotheses (H_di+1, …, H_dm), i.e., we put R_i = m − i + 1. In summary, a conservative definition of R_i can be given by

$$R_i^h=(m-i+1)·I(\underset{k=i,\dots ,m}{min}{P}_{d_k}\le p_{d_i})$$ (7)

4.2. A step-down procedure

We now present a formal definition of the new step-down procedure in Section 4.1.

1. For each test statistic t_i, compute the p-value p_i = P (|T_i| ≤ |t_i| | H_i).

2. Order the p-values such that p_d1 ≤ ··· ≤ p_dm.

3. For i = 1, …, m, compute the FDR adjusted p-values as

   $${\check{p}}_{d_i}=E\{R_i/(R_i+i-1)\mid H_M\},$$ (8)

   Where R_i can be computed in any one of the three versions $R_i^l,R_i^e,R_i^h$ from equations (5), (6) and (7), respectively.

4. Enforce monotonicity of the adjusted p-values, i.e., p̃_di = max_{k=1, …,i} p̌_dk.

The step-down procedure for the three versions of R_i are called, respectively, lFDR (the lower adjusted), eFDR (the empirical adjusted), and hFDR (the higher adjusted).

Note that under the subset pivotality condition, (4) is equivalent to (8). This is very useful as we can compute all the FDR adjusted p-values under H_M instead of under different H_K, where K = {d_i, …, d_m} depends on step i. If we know the joint null distribution of (P₁, …, P_m) from model assumptions, then we can compute the expectation analytically. In the situations where we are not willing to make assumptions about the null joint distribution, the subset pivotality condition allows the expectation in (4) to be computed by simulating the complete null distribution under H_M by bootstrap or permutation resampling.

4.3. Finite sample results

Proposition 1

For any of the three versions of R_i, the step-down procedure in Section 4.2 controls both the FWER and the FDR in the weak sense.

By noting that the adjusted p-value p̃₁ in the first step is computed in the same way as that in equation (3) of the minP procedure, we have the proof.

Theorem 2

Consider the step-down procedure in Section 4.2 using the definition of $R_i^h$ in (7). For any α ∈ (0, 1), if we reject all hypotheses whose FDR adjusted p-values are no greater than a, and if we assume that subset pivotality holds and that the joint distribution of P_M0 = {P_i, i ∈ M₀} is independent of the joint distribution of P_M1 = {P_i, i ∈ M₁}, then FDR ≤ α.

Corollary 3

Assume that P_M0 and P_M1 are independent, and that P₁, …, P_m satisfy the generalized Šidák inequality,

$$P(P_1\ge p_1,\dots ,P_m\ge p_m)\ge \prod _{i=1}^{m}P(P_i\ge p_i).$$ (9)

Then the BL procedure provides strong control of the FDR under the subset pivotality condition.

Lemma 4

Let X₁, ···, X_B be B samples of random variable X and let X̄ be the sample average. If P(0 ≤ X ≤ 1) = 1, then V ar(X̄) ≤ 1/(4B).

The proofs of Theorem 2, Corollary 3 and Lemma 4 are given in the Appendix.

Remarks

1. Proposition 1 and Theorem 2 also hold when the FDR adjusted p-values are computed based on the test statistics rather than on the p-values. A resampling procedure based on the test statistics is described in Algorithm 1. The independence assumption between P_M0 and P_M1 is replaced by the independence between T_M0 and T_M1. Note that this independence assumption is the same as in Yekutieli and Benjamini (1999), and does not make the further assumption that all null test statistics are independent.

2. For the problem of identifying differentially expressed genes considered in this paper, if the m × n matrix x is normally distributed, specifically, the first n₁ and remaining n₂ columns of x are independently distributed as N (μ₁, Σ₁) and N(μ₂, Σ₂) respectively, where μ₁ and μ₂ are vectors of size m, Σ₁ and Σ₂ are m × m matrices, then the subset pivotality property is satisfied.

   Here is the proof. Let T_i be the statistic for gene i, e.g. the two-sample t-statistic. For any subset K = {i₁,···, i_k}, let its complement set be {j₁,···, j_m−k}. The joint distribution of (T_i1, ···, T_ik) only depends on i₁, ···, i_k components of the vectors μ₁ and μ₂ and the corresponding submatrices of Σ₁ and Σ₂. This joint distribution does not depend on how (H_j1, H_j2, ···, H_jm−k) is specified. This proves subset pivotality for the test statistics. The subset pivotality also holds for the p-values, which are constructed from these test statistics. However, the subset pivotality property fails if we are testing the correlation coefficient between two genes; interested readers are referred to Example 2.2 on Page 43 of Westfall and Young (1993).

3. Sarkar (2002) generalized the results of the BL procedure in another direction. He assumed that the underlying test statistics are MTP₂, and that the test statistics are exchangeable under the null hypotheses. The MTP₂ property is similar to the PRDS condition or the generalized Sidàk inequality, which implies that weakly dependent test statistics behave like independent ones. However, the exchangeability assumption of Sarkar (2002) is not required in our generalization, and our proof is much simpler than that of Sarkar (2002).

4. We assume that the expectation in (8) can be computed without error. When the expectation is computed by B resamplings, using the fact that the random variable R_i/(R_i + i − 1) falls on the interval [0,1], Lemma 4 implies that the estimate for p̌_di in (8) has a standard error no greater than $\sqrt{1/(4B)}$. This quantity $\sqrt{1/(4B)}$ is therefore the maximum standard error of the estimate for the FDR adjusted p-values p̃_di in Step 4 of Section 4.2. Since B=10,000 in most computations of this paper, the standard error is at most 0.005.

Algorithm 1.

Resampling algorithm for computing FDR adjusted p values by using the test statistics only

Compute the test statistic ti, i = 1, · · ·, m on the observed data matrix x and, without loss of generality, label them |t1| ≥··· ≥ |tm|. For the b-th step, b = 1, …, B, proceed as follows. Compute the resampled data matrix xb, for example by randomly permuting the columns of matrix x. Compute the test statistic ti,b for hypothesis Hi, i = 1, ···, m on the data matrix xb. For each i = 1, …, m, mimic the step-down procedure: for j = 1, …, m − i + 1, let $t_{(j)}^{i,b}$ be the j-th largest member of {ti,b, …, tm,b} in absolute value; define Ri,b to be the unique integer k such that $$\mid t_{(1)}^{i,b}\mid \ge \mid t_i\mid ,\dots ,\mid t_{(k)}^{i,b}\mid \ge \mid t_{i+k-1}\mid \text{and}\mid t_{(k+1)}^{i,b}\mid <\mid t_{i+k}\mid .$$ Compute f1,b = I(R1,b > 0) and, for i = 2, …, m, compute fi,b = Ri,b/(Ri,b+i− 1). Steps 1–4 are carried out B times and the adjusted p-values are estimated by ${\check{p}}_i={\sum }_{b=1}^B{f}_{i,b}/B$, with monotonicity enforced by setting $${\stackrel{\sim }{p}}_1\leftarrow {\check{p}}_1,{\stackrel{\sim }{p}}_i\leftarrow max({\stackrel{\sim }{p}}_{i-1},{\check{p}}_i)\text{for}i=2,\dots m.$$

4.4. Resampling algorithms

In this section, we use resamplings to compute (8) so that we can obtain the FDR adjusted p-values. In general, there are two strategies for resampling the observed data x (an m × n matrix) to get the resampled data matrix x^b: permuting the columns of matrix x, and bootstrapping the column vectors. The application of these resampling strategies is in Westfall and Young (1993); more bootstrap methods can be seen in Davison and Hinkley (1997); Efron and Tibshirani (1993). In the simulation study and applications results of this paper, we focus on comparing two groups, and x^b is obtained by permuting the columns of the matrix x to assign the group labels.

The complete algorithm for the empirical procedure $(R_i^e)$ is described in Algorithm S1 in the supporting material. For other versions of R_i, the algorithm is similar and so will be omitted. If the p-values have to be computed by further resampling, then we have the same problem as in the double permutation algorithm of the minP procedure of Ge et al. (2003). In this situation, we can also have an analogous algorithm to Box 4 of Ge et al. (2003). Here, however, we cannot use the strategy in that paper to reduce the space, i.e., we need to compute the whole matrices T and P described in that paper. The details of this algorithm are omitted here.

Another approach is to compute FDR adjusted p-values based on the test statistics only. As we saw with the maxT procedure for controlling the FWER in Ge et al. (2003), the advantages and disadvantages of the maxT procedure compared with the minP procedure are also relevant to FDR adjusted p-values. The FDR adjusted p-values computed from the test statistics are described in Algorithm 1, and this algorithm will be used in the remaining of this paper.

5. Simulation results

5.1. Data generation strategy

For all figures in this section, there are 1000 genes with 8 controls and 8 treatments. We first simulate 1000×16 errors ε_i,j, i = 1, …, 1000, j = 1, …, 16, where the ε_i,j are block independent; specifically in our simulations the ε_i,j are independently and identically distributed as N(0,1), except that cor(ε_10i+k,j, ε_10i+l,j) = ρ for i = 0, …, 99, k ≠ l ∈ {1, · · ·, 10}, j = 1, …, 16. Lastly, we add δ to the treated group, so

$$X_{i,j}={\epsilon }_{i,j}+\delta \text{if}i=1,\dots ,m_1,j=9,\dots ,16;X_{i,j}={\epsilon }_{i,j}\text{otherwise}.$$

Note that the multiple testing problem for this simulation is to find the differentially expressed genes based on one observed data matrix X = x. The data matrix can be parametrized by (m₁, δ,ρ). For each gene i, we compute a two-sample Welch t-statistic t_i. Algorithm 1 is applied with the resampled data x^b generated by randomly permuting the columns of matrix x (B = 10,000). When we apply Algorithm 1, we do not assume that the data have normal distributions, and we do not know anything about the values of (m₁, δ,ρ) in the process that generates x.

5.2. Properties of different FDR procedures

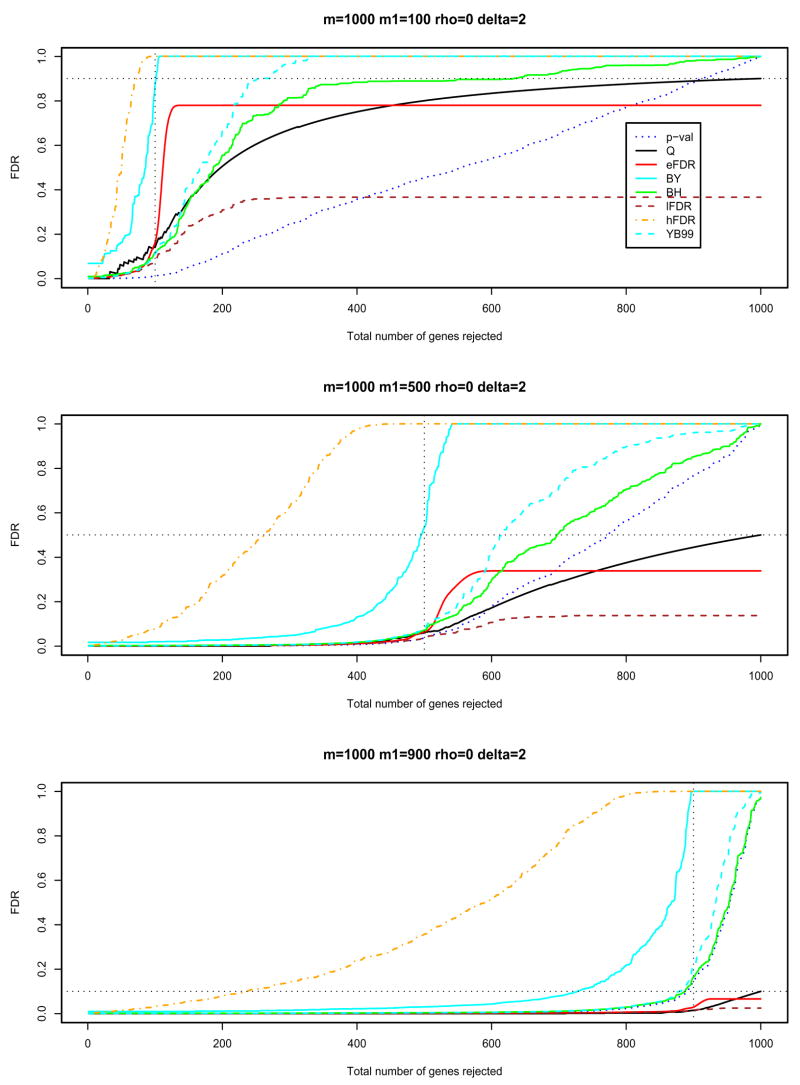
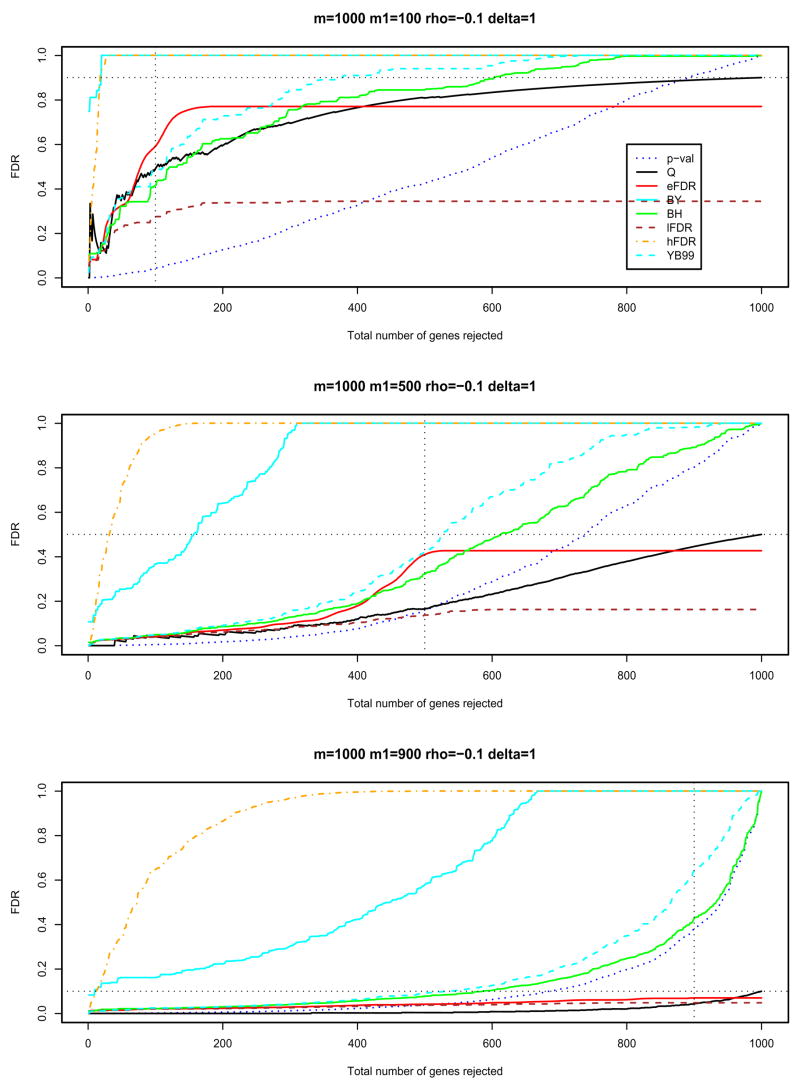
In Figures 1 and 2, and Figures S1 and S2 in the supporting material, the BH procedure, the BY procedure and the FDR procedures with $R_i^e,R_i^l$, and $R_i^h$ in Algorithm 1 (labelled as BH, BY, eFDR, lFDR and hFDR in these figures) have been applied to different simulated data. The raw p-values required for the BH and BY procedures are computed by B = 10, 000 permutations. We also plotted p-val, Q and YB99 for comparisons, where p-val is the raw p-value, Q is the random variable for the false discovery proportion (V/R) and YB99 is the resampling-based FDR upper limit, at (10) of Yekutieli and Benjamini (1999). The y-axis plots the FDR adjusted p-values for each procedure when the top 1, 2, ··· genes are rejected.

Figure 1. Different FDR procedures.

The independent case: ρ = 0 and δ = 2; the dotted vertical line is x = m₁; the dotted horizontal line is y = m₀/m, the overall proportion of false null hypotheses. Different panels are for different values of m₁ (100, 500, 900).

Figure 2.

The negatively dependent case ρ = −0.1 and δ = 1: different FDR procedures and different values of m₁ (100, 500, 900).

In these figures, for the lFDR procedure, the FDR adjusted p-values fall far below the false discovery proportion Q, so the lFDR procedure is too optimistic for FDR control. On the other hand, the BY and hFDR procedures are too conservative; they pay a huge price for allowing a dependence structure. The hFDR procedure has the advantage of giving smaller FDR adjusted p-values for the most extreme genes, while the BY procedure may reject more null hypotheses when target level α is much higher, say 0.5, or 1. Such levels are of limited use as researchers are more interested in smaller target levels, say 0.05 or 0.1. For example, in the middle panel of Figure 1 (m₁ = 500, δ = 2, ρ= 0), at level 0.05, the hFDR procedure rejects 14 hypotheses, while the smallest FDR adjusted p-value for the BY procedure is 0.24. In contrast, at the 0.5 level, the hFDR procedure rejects only 267 hypotheses, whereas the BY procedure rejects 474 hypotheses.

The sample mean difference between the treatments and controls in Figure 1 (δ = 2) is greater than that in Figure S1 in the supporting material (δ = 1). In general, the larger the sample mean difference between the treatments and controls, the more powerful the procedure is to separate differentially expressed genes from non-differentially expressed ones. It is more interesting to look at our eFDR procedure, whose curve reaches its highest value around m₁ and then goes to a plateau. This displays a nice property of the eFDR procedure: it suggests an approximate value of m₁, the number of differentially expressed genes. If we reject fewer than m₁ genes, the adjusted p-value for the eFDR is higher than Q, i.e., the eFDR procedure provides strong control of the FDR. This feature is also displayed in the negatively dependent data in Figure 2 (and positively dependent data in Figure S2 in the supporting material).

The BH, BY and YB99 procedures may be too conservative for large m₁/m since they do not use any estimate of m₀ (see the middle and lower panels of Figures 1, 2, S1 and S2). This extreme conservativeness will not be a major concern in practice where m₁/m tends to be small.

Benjamini and Yekutieli (2001) proved that the BH procedure controls the FDR in the strong sense when the PRDS condition is satisfied. It might be interesting to construct negatively dependent data as a counterexample for the BH procedure, but we do not have one so far. The BH procedure seems to work very well for the negatively dependent data of Figure 2. By noticing that the absolute values of the Student t-statistics are always positively dependent, we use one-sided tests to achieve more negative dependence, and the BH procedure still works well (data not shown). The BH procedure also works for other data generation strategies, such as using a finite mixture model for the errors ε_i,j. The reason we could not find a counterexample for the BH is probably that the simulated data are still not strongly negatively dependent. For the data within each block of size 10, the statistics cannot be strongly negatively dependent, as the negative correlation coefficient cannot be less than −1/9, otherwise the constructed matrix violates the property that the correlation coefficient matrix must be non-negative definite. Therefore 1000 genes are more or less independent. One may want to increase the number of blocks and decrease the size of each block to have a stronger negative correlation. However, with increasing numbers of blocks, the overall dependence decreases. We have simulated the data with block size two and correlation coefficient ρ = −0.7, and the result is very similar to Figure 2.

Note that Figures 1, 2, S1 and S2 consider only one sample of the data X = x. The FDR can be estimated by computing the average of the Q for 1000 samples of X when we reject the genes whose FDR adjusted p-values are no greater than α. Due to computational complexity, we only consider m = 200 and m₁ = 50 with block size two. As we consider a smaller block size, we can decrease the value of ρ from −0.1 to − 0.7. The results are shown in Tables 2 and 3 for independent data and in Tables 4 and 5 for dependent data. Again the eFDR procedure performs better than the BH procedure for smaller values of α. The BH procedure, on the other hand, is better for large values of α.

Table 2.

The FDR (sample average of Q) at the target level α when using 1000 samples of X with m = 200, m₁ = 50, δ = 1, ρ= 0.

α	0.01	0.05	0.1	0.2	0.5
eFDR	0.0017	0.028	0.079	0.15	0.30
BH	0	0.0081	0.069	0.17	0.38

Table 3.

The average number of genes rejected at the target level α when using 1000 samples of X with m = 200, m₁ = 50, δ = 1, ρ= 0.

α	0.01	0.05	0.1	0.2	0.5
eFDR	0.29	1.8	5.2	14	42
BH	0	0.40	5.3	17	54

Table 4.

The FDR (sample average of Q) at the target level α when using 1000 samples of X with m = 200, m₁ = 50, δ = 1, ρ = −0.7.

α	0.01	0.05	0.1	0.2	0.5
eFDR	0	0.035	0.066	0.13	0.32
BH	0	0.0068	0.060	0.14	0.38

Table 5.

The average number of genes rejected at the corresponding target level α when using 1000 samples of X with m = 200, m₁ = 50, δ = 1, ρ = −0.7.

α	0.01	0.05	0.1	0.2	0.5
eFDR	0.30	2.0	5.1	15	49
BH	0	0.37	5.1	17	55

6. Microarray applications

Apo AI knock-out experiment

The Apo AI experiment (Callow et al., (2000)) was carried out as part of a study of lipid metabolism and atherosclerosis susceptibility in mice. The apolipoprotein AI (Apo AI) is a gene known to play a pivotal role in HDL metabolism, and mice with the Apo AI gene knocked out have very low HDL cholesterol levels. The goal of the experiment was to identify genes with altered expression in the livers of these knock-out mice compared to inbred control mice. The treatment group consisted of eight mice with the Apo AI gene knocked out and the control group consisted of eight wild-type C57Bl/6 mice. For the 16 microarray slides, the target cDNA was from the liver mRNA of the 16 mice. The reference cDNA came from the pooled control mice liver mRNA. Among the 6,356 cDNA probes, about 200 genes were related to lipid metabolism. In the end, we obtained a 6,356 × 16 matrix with 8 columns from the controls and 8 columns from the treatments. Differentially expressed genes between the treatments and controls are identified by two-sample Welch t-statistics.

Leukemia study

One goal of Golub et al. (1999) was to identify genes that are differentially expressed in patients with two types of leukemias: acute lymphoblastic leukemia (ALL, class 1) and acute myeloid leukemia (AML, class 2). Gene expression levels were measured using Affymetrix high-density oligonucleotide arrays containing m = 6,817 human genes. The learning set comprises n = 38 samples, 27 ALL cases and 11 AML cases (data available at http://www.genome.wi.mit.edu/MPR). Following Golub et al. (personal communication, Pablo Tamayo), three preprocessing steps were applied to the normalized matrix of intensity values available on the website: (i) thresholding with a floor of 100 and a ceiling of 16,000; (ii) filtering with exclusion of genes with max/min ≤ 5 or (max − min) ≤ 500, where max and min refer respectively to the maximum and minimum intensities for a particular gene across mRNA samples; (iii) base 10 logarithmic transformation. Boxplots of the expression levels for each of the 38 samples revealed the need to standardize the expression levels within arrays before combining data across samples. The data were then summarized by a 3,051× 38 matrix X = (x_ij), where x_ij denotes the expression level for gene i in mRNA sample j. Differentially expressed genes in ALL and AML patients were identified by computing two-sample Welch t-statistics.

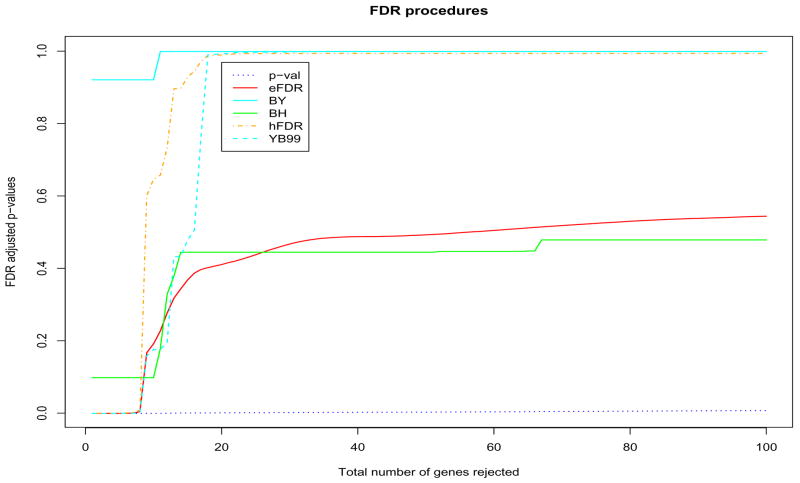
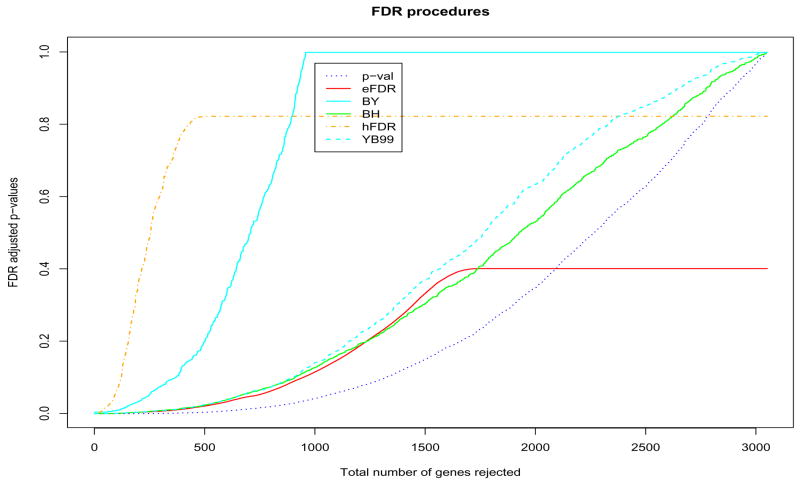
For the two datasets, we applied the BH, BY, eFDR, hFDR and YB99 procedures described in this paper to control the FDR. All of these resamplings were done by permuting the columns of the data matrix. Figure 3 gives the results for the Apo AI knock-out data. The x-axis is always the rank of p-values and y-axis is the FDR adjusted p-values. Note that the rank of different adjusted p-values is always the same as the rank of the raw p-values apart from the t-based procedures (eFDR, hFDR). In that case, the adjusted p-values have the same ranks as the two-sample Welch t-statistics. Similarly, Figure 4 gives the results of applying these procedures to the Leukemia dataset.

Figure 3. Apo AI.

Plot of FDR adjusted p-values when the top 1, 2, … genes are rejected. We only plot the total number of genes rejected up to 100 among 6,356 genes. The adjusted p-values were estimated using all B = 16!/(8! × 8!) = 12,870 permutations.

Figure 4. Leukemia.

Plot of FDR adjusted p-values when the top 1, 2, …, genes among 3,051 ones are rejected. The adjusted p-values were estimated using B = 10,000 random permutations.

7. Discussion

In this paper, we introduce a new step-down procedure aiming to control the FDR. This procedure uses the sequential rejection principle of the Westfall and Young minP step-down procedure to compute the FDR adjusted p-values. It automatically incorporates dependence information into the computation. We have essentially introduced three FDR procedures. The first, lFDR, is too optimistic for controlling the FDR from the simulated data. The second, hFDR, is shown to control the false discovery rate under the subset pivotality condition and under the assumption that joint distribution of statistics from true nulls is independent of the joint distribution of statistics from false nulls. From Remark 2 of Section 4.3, under some parametric formulation of the data, if each test statistic is generated within one gene, the subset pivotality property can be satisfied. As with the Westfall and Young minP step-down procedure, this procedure fails if the subset pivotality condition is not satisfied, for example testing the correlation coefficient between two genes. The hFDR procedure also extends the BL procedure from an independence condition to a generalized Šidák inequality condition, see (9). The third, and most useful procedure, eFDR, is recommended in practice. The theoretical properties of the eFDR, whether finite sample or asymptotic, are left to future research. The validity of the eFDR procedure is currently suggested by our simulation results and can be extended to a large number of hypotheses (Figure S3 in the supporting material shows the simulation for m = 10, 000). One nice feature of the eFDR procedure is that it suggests the number of the false null hypotheses and the FDR adjusted p-value simultaneously. The FDR plot, see Figure 3 or 4, is also useful for diagnostic purposes.

Supplementary Material

Supp. 8. Supporting material.

Figures S1, S2 and S3, and Algorithm S1.

Appendix. The proof of Theorem 2 and Corollary 3 and Lemma 4

Proof of Theorem 2

Denote the α level critical value of min_i∈K P_i | H_M by c_α,K, i.e.,

$$P\{\underset{i\in K}{min}{P}_i\le c_{\alpha ,K}\mid H_M\}=\alpha .$$ (10)

For given α at step i, when using the higher bound $R_i^h$ to compute the FDR adjusted p-values, the hypothesis H_di is rejected if and only if P_di ≤ c_{αi, M\{d1,…,di−1}}. Here α_i = αm/(m −i + 1). Let Λ = (λ₁, …, λ_m1) be a permutation of M₁. For i = 0, …, m₁, let

$$B_{i,\mathrm{\Lambda }}=\{P_{{\lambda }_1}\le c_{{\alpha }_1,M},\dots ,P_{{\lambda }_i}\le c_{{\alpha }_i,M\backslash \{{\lambda }_1,\dots ,{\lambda }_{i-1}\}},P_{{\lambda }_{i+1}}>c_{{\alpha }_{i+1},M\backslash \{{\lambda }_1,\dots ,{\lambda }_i\}}\text{and}{P}_{{\lambda }_1}\le \cdots \le P_{{\lambda }_{m_1}}\}.$$

The events {B_i,Λ: i, Λ} are a mutually exclusive decomposition of the whole sample space, and soΣ_i,Λ P(B_{i, Λ}) = 1. In set B_{i, Λ}, the random p-values P_λ1, …, P_λi are not necessarily the i smallest ones among the random p-values from the set M. However, for given α and Λ, the critical value c_{αk,M\{λ1,…, λk−1}} is an increasing function of k, which implies that we can reject at least the i false null hypotheses H_λ1, …, H_λi, so

$$V/R\le V/(V+i)\le (m-i)/m.$$ (11)

When x ∈ B_{i, Λ}, if we have also erroneously rejected at least one null hypothesis by using the higher bound $R_i^h$ for computing the FDR adjusted p-values, then the fact that c_{αk, M\{λ1,…,λk−1}} is an increasing function of k and that P_λi+1 > c_{αi+1,M\{λ1,…, λi}} implies

$$P_{(1),M_0}\le c_{{\alpha }_{i+1},M\backslash \{{\lambda }_1,\dots ,{\lambda }_i\}},$$ (12)

Here P_(j),K denotes the j-th smallest member of {P_i, i ∈ K}. As {λ₁, …, λ_i} is contained by M₁, the set M\{λ₁, …, λ_i} contains M₀. Using the definition of c_α,K in (10), we have c_{αi+1,M\{λ1,…, λi}} ≤ c_αi+1,M0. Combining this with (12) gives

$$P_{(1),M_0}\le c_{{\alpha }_{i+1},M_0}.$$ (13)

Therefore

$$\begin{array}{l}\text{FDR}=\sum _{i,\mathrm{\Lambda }}E\{V/R·I(B_{i,\mathrm{\Lambda }})\}\\ =\sum _{i,\mathrm{\Lambda }}E\{V/R·I(B_{i,\mathrm{\Lambda }})·I(P_{(1),M_0}\text{is}\text{rejected})\}\\ \le \sum _{i,\mathrm{\Lambda }}(m-i)/m·P(B_{i,\mathrm{\Lambda }}\cap \{P_{(1),M_0}\text{is}\text{rejected}\})(\text{Apply}(11))\\ \le \sum _{i,\mathrm{\Lambda }}(m-i)/m·P(B_{i,\mathrm{\Lambda }}\cap \{P_{(1),M_0}\le c_{{\alpha }_{i+1},M_0}\})(\text{Apply}(13))\\ =\sum _{i,\mathrm{\Lambda }}(m-i)/m·P(B_{i,\mathrm{\Lambda }})·P(P_{(1),M_0}\le c_{{\alpha }_{i+1},M_0})\end{array}$$ (14)

$$\begin{array}{l}=\sum _{i,\mathrm{\Lambda }}(m-i)/m·P(B_{i,\mathrm{\Lambda }})·\alpha m/(m-i)\\ =\sum _{i,\mathrm{\Lambda }}P(B_{i,\mathrm{\Lambda }})·\alpha \\ =\alpha \end{array}$$ (15)

At (14), we use the assumption that P_M0 and P_M1 are independent. At (15), by subset pivotality,

$$\begin{array}{l}P(P_{(1),M_0}\le c_{{\alpha }_{i+1},M_0})=P(P_{(1),M_0}\le c_{{\alpha }_{i+1},M_0}\mid H_{M_0})\\ =P(P_{(1),M_0}\le c_{{\alpha }_{i+1},M_0}\mid H_M)\\ ={\alpha }_{i+1}\\ =\alpha m/(m-i)\end{array}$$

Proof of Corollary 3

Combining (7) and (4), we have

$$\begin{array}{l}{\check{p}}_{d_i}=E\{R_i^h/(R_i^h+i-1)\}\\ =P(\underset{k=i,\dots ,m}{min}{P}_{d_k}\le p_{d_i})·(m-i+1)/m\\ \le [1-{(1-p_{d_i})}^{m-i+1}]·(m-i+1)/m(\text{Apply}(9)).\end{array}$$

Therefore, if p_di ≤ 1 − [1 − min(1, αm/(m − i + 1))]^1/(m−i+1), then [1 − (1 − p_di)^m−i+1] · (m −i + 1)/m ≤ α, and so p̌ _di ≤ α. Thus the BL procedure is more conservative than the step-down procedure in Section 4.2, which was shown to give strong control according to Theorem 2. Therefore the BL procedure also controls the FDR in the strong sense.

Proof of Lemma 4

Let μ = E(X). Construct a random variable Y = I(X ≥ μ) and write p = E(Y). We have Var(X) + (μ − p)² = E(X − p)² ≤ E(Y −p)² + (μ − p)², hence Var(X) ≤ Var(Y) = p(1 − p) ≤ 1/4. Therefore Var(X̄) = Var(X)/B ≤ 1/(4B).