Summary
When antiretroviral therapy (ART) is administered for long periods to HIV-1–infected patients, most achieve viral loads that are “undetectable” by standard assay methods (ie, HIV-1 RNA <50 copies/mL). Despite sustaining viral loads lower than the level of detection, a number of patients experience unexplained episodes of transient viremia or viral “blips.” We propose that transient activation of the immune system by infectious agents may explain these episodes of viremia. Using 2 different mathematical models, one in which blips arise because of target cell activation and subsequent infection and another in which latent cell activation generates blips, we establish a nonlinear (power law) relationship between blip amplitude and viral load (under ART) that suggest blips should be of lower amplitude, and thus harder to detect, as increasingly potent therapy is used. This effect can be more profound than is predicted by simply lowering the baseline viral load from which blips originate. Finally, we suggest that sporadic immune activation may elevate the level of chronically infected cells and replenish viral reservoirs, including the latent cell reservoir, providing a mechanism for recurrent viral blips and low levels of viremia under ART.
Keywords: HIV, latent reservoir, transient viremia, viral blips
Strict adherence to a regimen of antiretroviral therapy (ART) suppresses the viral loads of most chronically infected HIV patients lower than the level of detection by standard assay. A number of otherwise well-suppressed patients experience unexplained transient bursts of viral replication, or “viral blips,” while on therapy, however.1–3 Studies of HIV-infected children suggest that plasma virus during transient episodes in these patients originates from activation and expansion of latently infected cells (archival virus) and from ongoing viral replication, including the appearance and selection of new drug-resistant strains.4 Other explanations for the phenomenon of blips include random fluctuations around a mean viral load less than 50 copies/mL or statistical assay variation;5 rises in target cell availability attributable to vaccination 6–8 or coinfections by opportunistic organisms, which then increase viral replication;9 and transient noncompliance with therapy.
Prior work on untreated chronically infected HIV patients documents the increases in viral load associated with vaccination10–13 and with opportunistic or concurrent infection.14–17 McLean and Nowak18 proposed models of enhanced HIV replication attributable to immune stimulation by means of opportunistic infection and showed how the positive feedback between enhanced HIV replication and incomplete immune control of pathogens attributable to HIV immunosuppression can lead to immune failure and full-blown AIDS in untreated patients. Others have studied residual replication and the generation of blips in HIV-infected patients on ART19–21 and suggested that exposure to antigen may result in transient bursts of viral replication.
Modeling data from a cohort of chronically infected HIV patients on monotherapy, we showed that vaccination with a common recall antigen can increase target cell availability, in turn, leading to increased viral replication and replenishment of long-lived infected cells.7 We further showed that transient concurrent infection can act in a similar manner and serve as a stimulus for transient viral replication, even in well-suppressed patients under treatment with ART.9 Our modeling work also suggested that a consequence of these episodes of transient replication is replenishment of long-lived infected cells, which serve as a possible reservoir for future viral replication.9 This article further explores the hypothesis that viral blips result from transient intercurrent infections in HIV-infected patients under ART, focusing on drug sanctuaries and the latently infected cellular reservoir as sources of viremia.
ORIGIN OF BLIPS: TRANSIENT VIREMIA OR “RANDOM VARIATION”
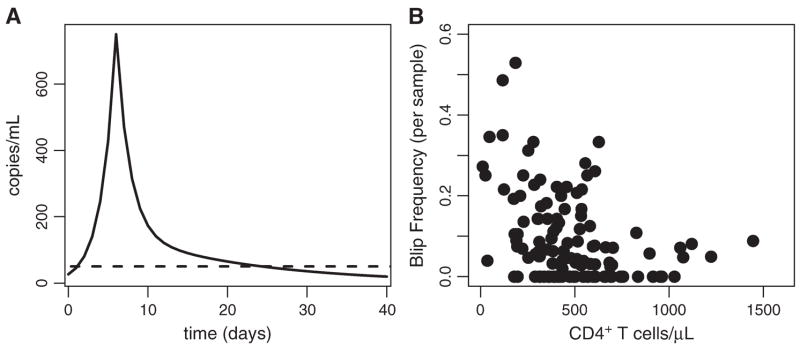
Di Mascio et al,3,22 studying 123 patients treated with ART for between 5 months and 5.3 years (mean = 2.6 years), found that the mean amplitude of the viral transients observed in this cohort was 158 ± 132 HIV RNA copies/mL, with the distribution skewed toward low-amplitude blips. In addition, Di Mascio et al3,22 suggest that a viral blip is not an isolated event (ie, does not comprise just 1 measurement) but a transient and extended episode of detectable viremia (HIV-1 RNA >50 copies/mL) with a duration of roughly 3 weeks. This finding was based on patients with a positive viral load being called to return to the clinic for follow-up viral load measurements. Such follow-up measurements tended to be greater than the threshold of 50 copies/mL more frequently than expected by chance, with durations for up to 3 weeks.3,22 They further showed that the amplitude distribution of these viral transients is consistent with random sampling of a series of events in which viral load typically rises sharply, followed by slower 2-phase decay.3 A cartoon example of such an “extended blip” is shown in Figure 1A. The frequency of viral blips in this study cohort was inversely correlated with CD4+ T-cell count at baseline, before initiation of drug therapy, as shown in Figure 1B.3,23 The observation that blip frequency is inversely correlated with steady-state CD4+ T-cell count suggests that patient-specific factors, such as susceptibility to infection, which increases at low CD4+ T-cell counts, may play a role in transient viral replication.
FIGURE 1.
Extended viral blip shape and correlation with CD4+ T-cell count at the onset of therapy. A, Hypothetic blip with rapid rise and 2-phase exponential decay. B, Viral blip frequency (probability of blip occurrence) per sample versus CD4+ count at start of therapy. Adapted from J Virol. 2003;77; 12165–12172 (Figs. 4B, C).
A second study by Nettles and colleagues5 of a smaller cohort (10 patients), conducted over a shorter period (approximately 6 months) but with an extensive sampling regimen, reported episodes of viremia with a mean duration of less than 3 days and a mean amplitude of approximately 79 copies/mL. No correlation between blip occurrence and illness, vaccination, or measured drug concentrations was found. The authors conclude that these much smaller and shorter duration blips represent random biological variation around mean HIV levels less than 50 copies per mL rather than clinically significant episodes of viremia. In essence, these blips may be attributable to assay variation in patients suppressed to less than 50 copies/mL. Unlike the studies by Di Mascio et al,3,23 there was no correlation between the occurrence of this type of transient viremia and low CD4+ T-cell count. Furthermore, the blips were of lower amplitude (median = 7 9 copies/mL, range: 51–201 copies/mL) than in the studies by Di Mascio et al.3,23 This suggests that the phenomenon observed by Nettles et al5 may indeed be different than that documented by Di Mascio et al,3,23 where susceptibility to infection may have played a role in the generation of higher amplitude blips.
Here, we consider the natural outcome of elevated susceptibility to infection in the form of immune activation by means of opportunistic or other infectious agents and the resulting effects on long-lived cellular reservoirs for HIV. We first discuss in general terms the models presented here, the first of which posits a drug sanctuary so that low-level viral replication continues in the presence of ART and establishes a relatively constant or steady-state level of viremia less than 50 RNA copies/mL. Transient intercurrent illness activates CD4+ T cells, which then support higher levels of viral replication, thus generating a blip. The second model also includes a steady-state level of viremia less than 50 copies/mL but postulates a latently infected cell reservoir that produces viral transients when activated by means of opportunistic infection. Further technical discussion of the models is confined to the Appendix. The results from both models suggest a strong relationship between viral load under ART and blip amplitude. We finally discuss the implications of these results in light of drug resistance, treatment failure, and reservoir replenishment and persistence.
MODELING VIRAL TRANSIENTS
Our models are a generalization of the HIV infection models developed by Perelson et al,24,25 reviewed by Perelson26 and Di Mascio et al,27 and later extended to include stimulation of T-cell proliferation by a growing pathogen.9 We include target (CD4+) T cells, which, once activated by pathogen, are easily infected by HIV. Although most infected cells are short-lived, a small proportion is assumed to be chronically infected. Chronically infected cells are assumed to have lower mortality and to produce virus at a slower rate than short-lived infected cells. Finally, virus is produced by short-lived and chronically infected cells and is cleared from the body at a constant rate per viral particle. A second version of the model includes latently infected cells. In both versions, in the presence of potent but <100% effective ART, viral loads become undetectable and settle down to a steady state less than 50 HIV-1 RNA copies/mL. From measurements of plasma viremia obtained by means of supersensitive assays with lower limits of a few HIV-1 RNA copies/mL, it seems clear that in many patients on suppressive therapies, viral loads stabilize or decay so slowly that the decay is indistinguishable from steady state.28
Recent immunological data suggest that T cells proliferate on brief exposure to pathogen, entering a programmed cascade of divisions that culminates in mature effector cells, which then can clear the pathogen.29–31 Our models include such a programmed response of CD8+ T cells to the presence of antigen. We adapt a model of DeBoer and Perelson32 and DeBoer et al33 that distinguishes the rate of the first division from subsequent divisions to model CD8+ T-cell activation, clonal expansion, and differentiation into effector cells. The effector cells clear the pathogen, but not before the CD4+ T cells, which are targets of HIV infection, also expand because of the presence of antigen. Once activated, target cells are subject to HIV infection at an increased rate. HIV infection of CD4+ T cells is reduced under ART, such that producing sufficient viral replication to be observable as a blip may be difficult. In the following models, we explore 2 potential mechanisms for producing blips in the presence of ART.
Activation of Target Cells
Intercurrent infection can activate target cells. An explanation for transient viremia in the presence of ART is to assume that different cell types, or cell populations, may have varying drug sensitivities, perhaps attributable to nonuniform expression of cell surface P-glycoproteins that may reduce intracellular drug concentration by pumping drug out of the cell.34,35 There is also direct evidence of heterogeneity in intracellular drug concentrations from in vitro studies.34,36,37 We model, as described in the Appendix (section on effector CD8+ cell activation and proliferation), heterogeneity in target cells by allowing 2 cocirculating populations of target cells, one with reduced drug penetration, and hence reduced drug efficacy. Both populations become activated by intercurrent infection and clonally expand. When each of the target cell types becomes infected, short-lived productively infected cells and longer lived chronically infected cells are produced (Fig. 2). Simulations of a similar model have been shown to produce episodes of transient viremia in the presence of opportunistic infection.9
FIGURE 2.
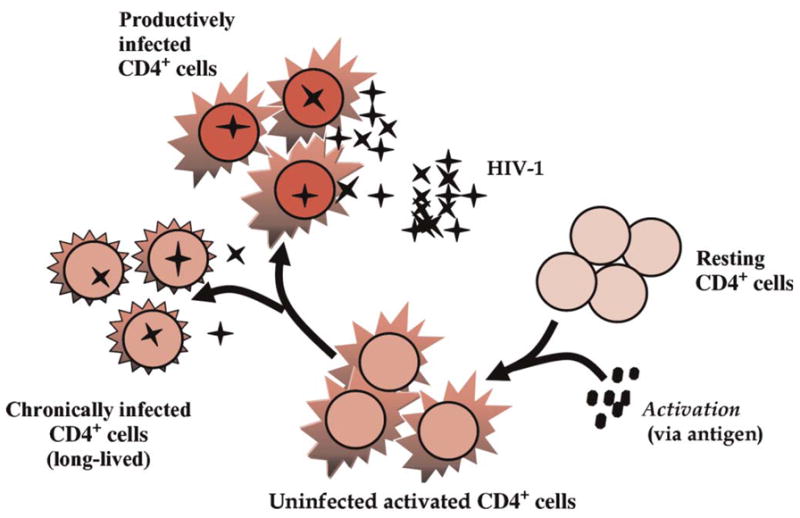
Cartoon illustrating the target cell activation model. In this model, antigen activates a fraction of CD4+ T cells and leads to HIV production from short-lived productively infected cells and longer lived chronically infected cells. This model, described more fully in the Appendix (section on target cell activation), also features 2 cocirculating target cell pools, one of which plays the role of a drug sanctuary with reduced drug penetration (not shown in figure).
Activation of Latently Infected Cells
A second proposed mechanism for episodes of transient viremia under ART involves the activation of latently infected cells by concurrent infection. Our model, as described in the Appendix (section on latent cell activation and replenishment), assumes that latently infected cells are CD4+ T-memory cells; on antigen stimulation, they proliferate and convert into productively infected cells (Fig. 3). The model explicitly includes the activation and proliferation of latently infected antigen-specific memory cells and the replenishment of this pool by reversion to memory after the concurrent infection is cleared. The model also includes separate antigen-specific CD8+ T cells that proliferate in a programmed manner on activation by antigen, with CD8+ effector cells being the mediator of pathogen clearance. Note that to maintain relative simplicity in the model and to simplify the calculation of steady states for the infected cells, we do not include chronically infected cells in this model. The long-lived cells in this model are latently infected cells, which arise from a small fraction of target cell infections and as a fraction of antigen-activated latently infected cells reverts to memory.
FIGURE 3.
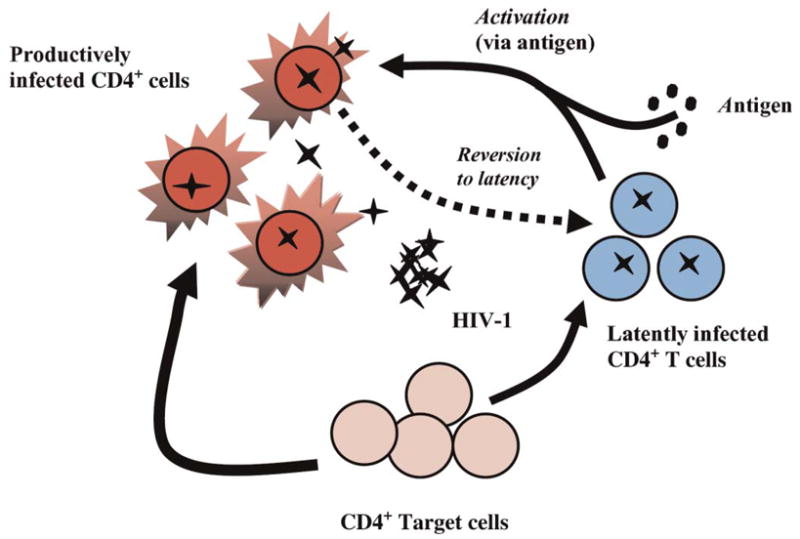
Cartoon illustrating the latent cell activation model. In this model, a small number of latently infected cells (1%) are assumed to be antigen specific and can be activated into productive infection on exposure to antigen. In addition, infection of target cells results in the generation of productively infected cells and a small number of latently infected cells.
Simulations
Both models were solved numerically and analyzed using the R programming language (version 1.9) and run on Windows XP and Linux platforms, using the odesolve package.
RESULTS
Target Cell Activation: Viral Transients From a Drug “Sanctuary”
The model incorporating cell populations with different drug penetrance produces viral transients that scale with steady-state (under ART) viral load: lower viral loads produce relatively smaller amplitude transients under any assumed size of the cellular drug sanctuary (ie, the cell population with reduced drug penetrance). Different low steady-state viral loads may be produced from a sanctuary pool of given size by varying the drug efficacy (combined efficacy of reverse transcriptase inhibitors [RTs] and protease inhibitors [PIs]) in cells of that pool. Simulations at extremely low ART-induced steady-state viral loads often do not produce an observable blip (ie, a burst of replication greater than the assay limit of 50 HIV-1 R NA copies/mL), whereas higher steady-state viral loads can result in blip occurrences, depending on sanctuary pool size. Larger sanctuaries produce more blips and with higher relative amplitudes at a given steady state. Figure 4 shows the variation of blip amplitude and duration with steady-state (under ART) viral load, assuming 3 different sizes of sanctuary cell populations. For the small and intermediate sanctuary sizes and parameters given in Table 1, patients suppressed to <7 copies/mL do not exhibit blips that rise to greater than the assay threshold of 50 HIV-1 RNA copies/mL. Note that viral transients arise only from viral replication in the sanctuary pool, because for the sake of simplicity, we assumed that this is the sole compartment with <100% drug efficacy.
FIGURE 4.
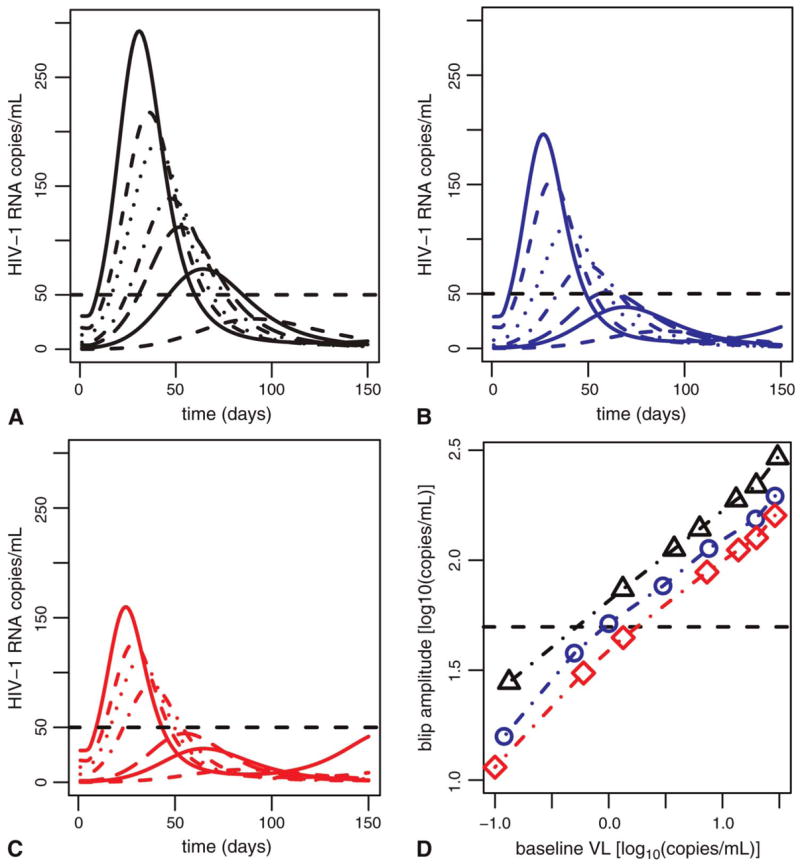
Blip amplitude scales with steady-state viral load (VL) and secondary target pool (drug sanctuary) size. The first 3 panels show results for sanctuaries with a mean size of 1% of target cells in (A), 0.5% in (B), and 0.004% in (C). Different line styles in each frame show blips arising from steady-state viral loads of approximately 30, 20, 10, 7, 3, 1, and 0.1 (HIV-1 RNA copies/mL). To obtain these steady states, we have assumed drug efficacies in the sanctuary population ranging between 0.63 and 0.69 (A), 0.30 and 0.45 (B), and 0.0 and 0.27 in (C) and that λ2 = 99 cells/mL/d (A), λ2 = 57 cells/mL/d (B), and λ2 = 43 cells/mL/d (C). Dashed line shows the assay limit of 50 HIV-1 RNA copies/mL. D, Scaling of peak blip amplitude with target cell pool size and steady-state viral load under treatment. Sanctuary size of 1% (black line), sanctuary size of 0.5% (blue line), and sanctuary size of 0.004% (red line).
TABLE 1.
Model Parameters
| Parameter | Description | Value | Reference |
|---|---|---|---|
| a | Maximum T-cell proliferation rate | 0.09 (d−1) | 9 |
| aL | Latent (memory) cell activation | 0.01 (d−1) | 54 |
| Amax | Pathogen carrying capacity | 108 (cells/mL/d) | 9 |
| αL | Fraction latently infected | 0.001 | 40 |
| c | Virion clearance rate | 23 (d−1) | 55 |
| d0 | Death rate, quiescent cells | 0.01 (d−1) | 54 |
| d | Death rate, division classes | 0.1 (d−1) | 9 |
| dLA | Death rate, antigen specific | 0.325 (d−1) | 56 |
| dE | Death rate, effector cells | 0.325 (d−1) | 56 |
| dT | Death rate, nonspecific | 0.01 (d−1) | 54 |
| δ′ | Density-dependent mortality | 0.7863 d−1 (mL·cell−1)ω | 57 |
| μ′ | Density-dependent mortality | 0.07863 d−1 (mL·cell−1)ω | 57 |
| εRT | Drug efficacy | 0 < εRT < 1 | Appendix |
| εPI | Drug efficacy | 0 < εPI < 1 | Appendix |
| f | Reduction in drug efficacy | 0 < f ≤ 1 | |
| γ | Pathogen clearance rate | 10−3 (d−1) | 9 |
| k1 | Infectivity, primary pool | 8 × 10−7 (mL/d−1) | 57 |
| k2 | Infectivity, secondary pool | 1 × 10−4 (mL/d−1) | 57 |
| K4, K8 | Antigen half-saturation | 1000 | 9 |
| λ1 | Primary T-cell source | 104 (cells/mL/d−1) | 57 |
| λ2 | Secondary T-cell source | 99, 57, 43 (cells/mL/d−1) | |
| N0 | Initial quiescent population | 500 cells/mL | 9 |
| p0 | Initial proliferation rate | 1 ( d −1) | 54 |
| p | Proliferation rate, classes 1, .., k | 2.92 (d−1) | 54 |
| ω | See Appendix | 0.01 | 57 |
| q1, q2 | Viral production rates | 70, 0.28 (d−1) | 57, 58 |
| r0 | Maximum pathogen growth rate | 2 ( d −1) | 9 |
| ρ | Rate of reversion to memory | 0.01 (d−1) | 54 |
The final panel in Figure 4 shows the relationship between peak blip amplitude and steady-state viral load for different sizes of the drug sanctuary. Notice that the relationship is linear on a log-log plot; that is, the relation is as follows:
| (1) |
or
| (2) |
with β ≈ 0.45 and where VL denotes ART-induced preblip steady-state plasma viral load and λ2 is a parameter determining the size of the drug sanctuary. λ is the slope of the lines in Figure 4D, and log10 (λ2) is the approximate Y-intercept. This type of relation is called a power law relation, because blip amplitude is proportional to viral load raised to the power β. Note that this implies that blip amplitude does not scale in a simple manner with viral load. For example, if the steady-state viral load under ART is 3 0 copies/mL, as shown in Figure 4A, the blip amplitude is 280 copies/mL. If the viral load is 3 copies/mL, the blip amplitude is 100 copies/mL. Thus, decreasing the viral load by 27 copies/mL (from 30 to 3 copies/mL) does not simply reduce the blip amplitude by 27 copies/mL. Rather, the blip amplitude is predicted to fall by 180 copies/mL because of this power law relation. Hence, decreasing viral load by increasing the potency of therapy is predicted to give a decrease in blip amplitude that is greater than that simply attributable to lowering the baseline from which the blip originates. Because β < 1, however, the fold reduction in blip amplitude is less than the corresponding reduction in steady-state viral load (ie, in the example cited previously, a 10-fold reduction in plasma viral load only leads to a 2.8-fold reduction in blip amplitude).
Effects of Latent Cell Activation: Transient Viremia From the Latently Infected Pool
In this model, we assume that a steady state under ART is reached with an undetectable viral load (HIV-1 RNA <50 copies/mL) and a latent cell frequency between approximately 0.1 and 1.0 replication-competent latently infected cells per 106 CD4+ T cells.38,39 Of these, only a fraction of latently infected cells are specific for any given antigen. In mice, the fraction of splenic CD4+ T-cell memory cells specific to lymphocytic choriomeningitis virus epitopes ranges from 0.015 at 45 days after exposure to 0.002 at 850 days after exposure.40 We thus assume that 1% of the latent cell pool is activated in the simulations shown in Figure 5. After stimulation of these latently infected memory cells by pathogen during concurrent infection, they undergo a short burst of proliferation and activation into productive infection. At the end of the antigen-mediated response, a small fraction of the stimulated cells enter memory as resting latently infected cells. In this model, we observe viral load transients greater than the level of detection even when steady-state viral loads under therapy are as low as 5 HIV-1 RNA copies/mL (see Fig. 5A). Blip amplitudes scale with the size of the latent pool (see Fig. 5B) and with steady-state viral load (see Fig. 5C, open symbols).
FIGURE 5.
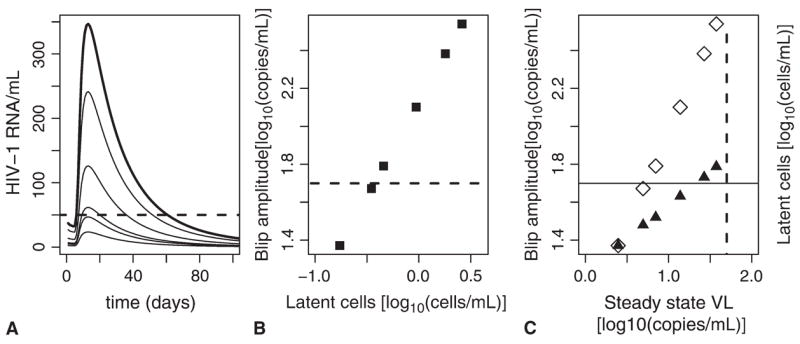
A, Viral transients assuming steady-state (under ART) viral loads (VL) of 37.5, 26.8, 13.8, 7.01, 4.94, and 2.48 RNA copies/mL corresponding to latently infected cell levels of 2.6, 1.8, 0.94, 0.46, 0.35, and 0.17 per 106 CD4+ T cells, respectively. Dashed line is limit of detection (50 copies/mL). B, Power law relation between the size of the latent pool and peak blip amplitude. C, Power law relation between steady-state viral load under ART and blip amplitude, (open diamonds). Power law relation between steady-state viral load and size of latent pool (solid triangles); dashed vertical line is the limit of detection (50 copies/mL).
Again the relationship between blip amplitude and viral load is linear on a log-log plot, and the empirical relation found here is as follows:
| (3) |
where βL11 and VL denote the preblip steady-state plasma viral load, because the relationship between viral load and blip amplitude is approximately linear. Thus, a 10-fold change in preblip plasma viral load leads to a roughly 10-fold change in blip amplitude. Finally, the predicted size of the latent pool is proportional to the steady-state viral load (see Fig. 5C, solid symbols):
| (4) |
where βL2 = 1, V L denotes the preblip steady-state plasma viral load, and “latent cells” denote their preblip steady-state level.
The same type of linear log-log relation between viral load and the size of the latent reservoir was observed in untreated patients, albeit with much higher viral loads ( see Fig. 1). 41
Effects on Long-Lived Infected Cells: Reservoir Replenishment and Stability
Of concern for HIV-infected patients experiencing recurrent episodes of transient viremia are the potential effects on long-lived chronically infected cells or latently infected cells that may serve as viral reservoirs. Productively infected cells are short lived and track changes in viral load during an episode of transient viremia (compare Figs. 6A, B). Effects on chronically infected cells are more lingering. Up to 100 days after an episode, this pool is still elevated to greater than steady state (see Fig. 6B). Recurrent transient episodes of viremia, which occur frequently in some patients, 3 could thus keep long-lived productively infected cells continuously elevated to greater than the steady-state values they would otherwise attain under therapy, and thereby contribute to plasma viral load. A similar phenomenon occurs with latently infected cells; if these pools are activated during a transient episode of viremia, perhaps as part of a memory response to recurrent infection, viral replication could serve to replenish and temporarily expand these reservoirs and repeated activation might keep them replenished indefinitely (see Figs. 6C, D).
FIGURE 6.
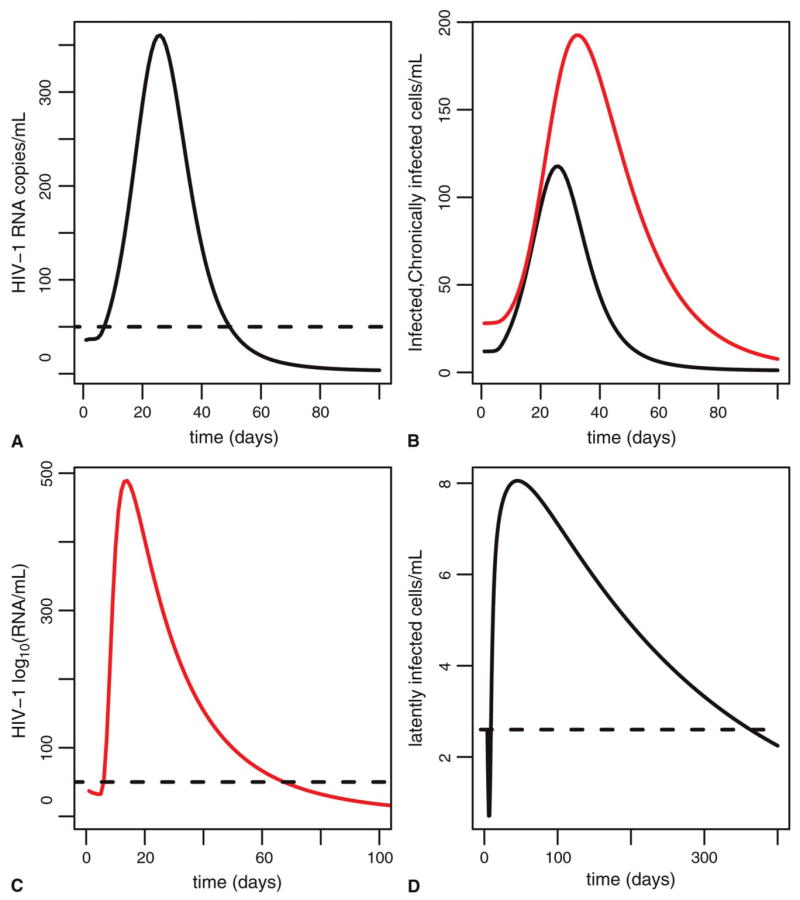
Effects of a transient episode of viremia on infected cells. A, Viral load (target cell activation model); dashed line is limit of detection. B, Effects of a transient episode of viremia on long-lived chronically infected (dashed) and short-lived productively infected cell (solid line) pools. Units are cells/mL. Parameters are as in Table 1. C, Viral load (latent cell model); dashed line is limit of detection. D, Corresponding effects on latently infected pool; dashed line is size of pool before transient episode.
DISCUSSION
Transient Viremia and Drug Resistance
Transient episodes of plasma HIV viremia (50–400 copies/mL) during ART are frequent,2,3,42,43 associated with heightened viral replication,2 and correlated with the emergence of drug-resistant viral variants in some studies.1,44 If transient episodes of viremia result from ongoing viral replication, sufficiently potent ART should suppress them. Although current therapies drive plasma viral loads to “undetectable levels” (ie, less than 50 RNA copies/mL), there is ample evidence to suggest that viral replication continues, including expression of viral messenger RNA (mRNA) in peripheral blood mononuclear cells (PBMCs),45 further viral sequence evolution,46 and extremely low but measurable levels of viral RNA. 28,47,48 This strongly suggests that viral replication continues during treatment in many patients. The underlying causes of continued replication may be different in different patients, but replication is likely facilitated by differential drug penetration in different cellular pools or anatomic sites and variations in drug concentrations attributable to pharmacokinetic effects or incomplete compliance with drug regimens. Our work suggests that high drug efficacy is critical in reducing or eliminating the occurrence of viral transients. As plasma viral loads are suppressed to lower than some threshold (7 copies/mL for the parameters in our models), episodes of transient viremia occur but do not rise to greater than the level of detection by standard assay (50 copies/mL). The implication of this finding is that drug regimens should be optimized to maintain viral loads as low as possible and not merely at levels less than 50 HIV-1 RNA copies/mL.
Transient Viremia, the Latent Reservoir, and Reservoir Replenishment
Long-term studies suggest that latently infected cells are a highly stable reservoir for HIV-1, with an average half-life of up to 44 months in patients on ART with undetectable levels of plasma HIV-1 virus.38,49 In individual patients, the rate of decay of the reservoir is inversely correlated with the extent of residual viral replication under ART.50 Furthermore, patients who experience transient episodes of viremia have slower latent cell decay rates,50 suggesting that transient episodes of viremia may replenish the latent reservoir.
The size of the latent pool in untreated patients is correlated with residual replication and viral load (under ART). Recent work by Havlir et al51 shows a strong association between pretreatment and on-ART HIV DNA levels (latently infected cells) and residual viremia under ART. Work by Blankson et al41 shows a strong relation between plasma viral load (at time of diagnosis) and the size of the latently infected pool in acutely HIV-infected patients. Our work shows a similar relation but with steady-state viral load under ART rather than pretreatment viral load (see Fig. 5D). Although early studies suggested that the latent pool was quiescent, recent work by Chun et al52 has demonstrated the persistence of replication-competent virus in CD4+ cells in aviremic patients under continuous therapy for up to 9.1 years. Furthermore, when placed in overnight culture, the activated CD4+ T cells produced infectious virions, suggesting that these cells could spread infection and help to maintain the latently infected pool. Phylogenetic analysis showed that stimulation of resting latently infected cells produced virus that was found in activated cells. This type of “cross-infection” between resting and activated cells allows continual replenishment of the latent reservoir and consequent “resetting” of its half-life. Our work suggests that occasional intercurrent infections, which generate transient viremia by means of target cell activation or activation of latently infected memory cells, may play a role in this resetting.
In this article, we demonstrate that episodes of transient viremia in otherwise well-suppressed chronically infected HIV patients under drug therapy may be triggered by intercurrent infections that cause a rise in activated T cells, and thus transient bursts of CD4+ T-cell infection and resultant viremia. Such a model can explain the observation of viral blips in ART-treated HIV-infected patients who otherwise have undetectable viral loads. In addition, we have shown that latently infected cells may produce transient episodes of viremia when these resting cells are stimulated into proliferation by antigen and, further, that this pool may be replenished by low-level replication under ART and by reversion to memory of a small portion of the activated cells.
Blip amplitude is found to scale with plasma viral load in our models, exhibiting a linear log-log relation which differs primarily in slope between the target cell activation and latent cell models. Finally, drug efficacy is found to have a dramatic effect on blip amplitude, and thus on the probability of a clinically observable blip occurring. When viral load can be suppressed to lower than a threshold, approximately 7 HIV-1 RNA copies/mL for the parameters used in our models, blips are not observed.
Acknowledgments
The authors thank R. Ribeiro for helpful comments on the manuscript. Portions of this work were performed under the auspices of the US Department of Energy under contract W-7405-ENG-36 and supported by National Institutes of Health grants AI28433 and RR06555 (A. S. Perelson).
APPENDIX
Target Cell Activation
Our model for target cell activation posits 2 cocirculating cell pools with heterogeneous drug penetrance (T1 and T2). Target cells are assumed to have passive sources (λ1 and λ2; see Table 1). These sources, λ1 for the primary pool and λ2 for the secondary drug-resistant pool, are used to set the steady-state target cell population sizes. Furthermore, the target cell populations may have different infection rate constants, k1 and k2.
The model assumes differential drug efficacy in the cocirculating target cell populations: in one population (T1), the combined drug efficacy is ε, which reflects the effects of protease inhibitors (PIs) and reverse transcriptase inhibitors (RTs), and in the second population (T2), drug efficacy is f ε, where efficacy has been reduced by a factor, f, <1. The model includes 2 separate chronically infected cell pools, and derived from infected non–antigen-specific T-cell pools, and . The inclusion of the chronically infected pool is motivated by the suggested 2-phase decay profile of a viral transient3 and by the initial 2-phase decay of viral load in chronically infected HIV patients during combination therapy.25 Combined drug therapy by means of RTs and PIs reduces the number of infections and results in the production of noninfectious virus VNI, respectively; total virus is thus the sum of infectious virus, VI, and noninfectious virus, VNI. Infectious and noninfectious virus is cleared at a constant rate, c, per virion.
Finally, we assume that the magnitude of the immune response against infected cells, and thus their death rate, is an increasing function of infected cell density (see section on density-dependent cell mortality; see Table 1). To the model for programmed proliferation of CD8+ cells under antigenic stimulation (see section on latent cell activation and replenishment), we add the following equations to model the HIV-1 infection of 2 cocirculating target cell types with differential drug penetration:
| A1 (a) |
| A1 (b) |
| A1 (c) |
| A1 (d) |
| A1 (e) |
| A1 (f) |
| A1 (g) |
| A1 (h) |
where the viral load shown in plots is V =VI + VNI. The CD4+ target cells are activated by antigen A according to
| (A2) |
where a is a maximum proliferation rate of activated CD4+ T cells and K4 is a constant governing the level of antigen at which half this maximum activation is reached. Because the model includes density-dependent cell death, we decouple viral production rates from cell death rates and assume virus is produced at constant rates, q1 and q2, from short-lived and chronically infected cells, respectively. Further simulations, sensitivity testing, and discussion of this model can be found in the article by Jones and Perelson.9
Effector CD8+ Cell Activation and Proliferation
We include in our model a programmed response of CD8+ T cells to the presence of antigen. On exposure to antigen, quiescent CD8+ T cells undergo a burst of proliferation, entering a programmed cascade of divisions that culminates in the production of mature activated effector cells.28
| A3 (a) |
| A3 (b) |
| A3 (c) |
| A3 (d) |
| A3 (e) |
Here, A is a growing antigen that stimulates an immune response. For simplicity, we henceforth call A a “pathogen.” The parameter r0 is the pathogen growth rate; γ is the clearance rate constant for the pathogen; p0 and p are constant proliferation rates; N0 is the initial quiescent CD8+ T-cell pool; and Ni, i ≥ 1 is the number of CD8+ cells that have completed i divisions.
Experiments suggest that when quiescent cells are stimulated into proliferation, initial cellular division takes longer than subsequent divisions53 and that the time to first division depends on features of the antigen stimulation. We thus assume that the rate of the first CD8+ T-cell division depends on antigen according to the following equation:
| (A4) |
where K8 represents the critical antigen level required to stimulate a CD8+ response (see Table 1). Here, n is a parameter, frequently called the Hill coefficient, that determines the steepness of the response when A is near the “threshold” K8.
As the CD8+ T cells proliferate, they also differentiate into effectors, E. Here, we assume that cells become effectors after 4 divisions and stop proliferating after 8 divisions .28 Proliferative non effector phases (eg, division classes N0, N1, ..., N3) undergo mortality at a rate of d < dE, the death rate for activated effector cells.
Latent Cell Activation and Replenishment
Latently infected cells, L, are assumed to be continuously replenished by low-level viral replication under ART. In addition, antigen can activate these cells into proliferation and viral production with a small portion of these activated cells reverting to memory. In this model, we add the following, including latent cells and infection under PIs and RTs, to Equation 3 (a–e):
| A5 (a) |
| A5 (b) |
| A5 (c) |
| A5 (d) |
| A5 (e) |
| A5 (f) |
| A5 (g) |
where p0(A) is as defined by a function analogous to that in Equation 4 but with K8 now referring to the antigen level needed to stimulate a latently infected cell. Here, L0 is the resting latently infected memory cell pool, which arises from a small fraction, αL, of target cell infections and as activated latent cells revert to resting at rate p. A fraction of the resting latently infected memory cells, L0, that are antigen specific are activated by antigen A into proliferation, where Li denotes a cell that has divided i times. As discussed in the main text, we assume that 1% is activated by encounter with antigen. Activated cells, Li, i > 1, transition into productively infected cells, T*, at rate aL, proliferate at rate p, and die at rate dLA per cell.
We again invoke density-dependent mortality of productively infected cells (see section on density-dependent cell mortality). Drug therapy reduces the number of infections and results in some infections producing noninfectious virus, VNI; total virus, V, is thus the sum of infectious virus, VI, and noninfectious virus, VNI. Infectious and noninfectious virus is cleared at a constant rate, c, per viral particle before concurrent infection with a pathogen, p0(A) = p0(0) = 0, and the system is assumed to be in a steady state with a small fraction, αL, of HIV infections of target cells leading to the generation of latently infected cells, L0. Although steady state may seem unrealistic, because the latent pool would then never fully decay, only a small imbalance in the creation and destruction of latently infected cells would account for the 44-month half-life observed by Finzi et al38 and Siliciano et al.49 Including this small decay would not affect our results, which consider time scales of a few months.
Density-Dependent Cell Mortality
We introduce density-dependent infected cell mortality into both models as a means of mimicking the effects of a cell-mediated immune response and as a means of producing robust low steady-state viral loads.9,57
When infected cells are subject to density-dependent mortality, the magnitude of the immune response against HIV-infected cells (and thus their death rate) is an increasing function of infected cell density.9,57 Holte et al59 suggested that density-dependent mortality can be modeled by a power law, that is, by replacing constant mortality terms with functions that depend on the total number of productively infected cells raised to a power of ω.
Thus, we assume that the death rate of productively infected cells is as follows:
| (A6) |
and that the death rate of for chronically infected cells (C1, C2) is as follows:
| (A7) |
Here, ω < 1 and are the total number of HIV-infected cells, which represents the stimulus for a cell-mediated response to HIV infection.
References
- 1.Cohen Stuart JWT, Wensing AMJ, Kovacs C, et al. Transient relapses (blips) of plasma HIV RNA levels during HAART are associated with drug resistance. J Acquir Immune Defic Syndr. 2001;28:105–113. doi: 10.1097/00042560-200110010-00001. [DOI] [PubMed] [Google Scholar]
- 2.Havlir DV, Bassett R, Levitan D, et al. Prevalence and predictive value of intermittent viremia with combination HIV therapy. JAMA. 2001;286:171–179. doi: 10.1001/jama.286.2.171. [DOI] [PubMed] [Google Scholar]
- 3.Di Mascio M, Markowitz M, Louie M, et al. Viral blip dynamics during highly active antiretroviral therapy. J Virol. 2003;77:12165–12172. doi: 10.1128/JVI.77.22.12165-12172.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Tobin NH, Learn GH, Holte SE, et al. Evidence that low-level viremias during effective highly active antiretroviral therapy result from two processes: expression of archival virus and replication of virus. J Virol. 2005;79:9625–9634. doi: 10.1128/JVI.79.15.9625-9634.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Nettles RE, Kieffer TL, Kwon P, et al. Intermittent HIV-1 viremia (blips) and drug resistance in patients receiving HAART. JAMA. 2005;293:817–829. doi: 10.1001/jama.293.7.817. [DOI] [PubMed] [Google Scholar]
- 6.Gunthard HF, Wong JK, Spina CA, et al. Effect of influenza vaccination on viral replication and immune response on persons infected with human immunodeficiency virus receiving potent antiretroviral therapy. J Infect Dis. 2000;181:47–62. doi: 10.1086/315260. [DOI] [PubMed] [Google Scholar]
- 7.Jones LE, Perelson AS. Modeling the effects of vaccination on chronically infected HIV-positive patients. J Acquir Immune Defic Syndr. 2002;31:369–377. doi: 10.1097/00126334-200212010-00001. [DOI] [PubMed] [Google Scholar]
- 8.Kolber MA, Gabr AH, De La RA, et al. Genotypic analysis of plasma HIV-1 RNA after influenza vaccination of patients with previously undetectable viral loads. AIDS. 2002;16:537–542. doi: 10.1097/00002030-200203080-00004. [DOI] [PubMed] [Google Scholar]
- 9.Jones LE, Perelson AS. Opportunistic infection as a cause of transient viremia in chronically infected HIV patients under treatment with HAART. Bull Math Biol. 2005;67:1227–1251. doi: 10.1016/j.bulm.2005.01.006. [DOI] [PubMed] [Google Scholar]
- 10.O’Brien WA, Grovit-Ferbas K, Namazi A, et al. Human immuno deficiency virus type 1 replication can be increased in the peripheral blood of seropositive patients after influenza vaccination. Blood. 1995;86:1082–1089. [PubMed] [Google Scholar]
- 11.Staprans SI, Hamilton B, Follansbee S, et al. Activation of virus replication after vaccination of HIV-1 infected individuals. J Exp Med. 1995;182:1727–1737. doi: 10.1084/jem.182.6.1727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Brichacek B, Swindells S, Janoff EN, et al. Increased plasma human immunodeficiency virus type 1 burden following antigenic challenge with pneumococcal vaccine. J Infect Dis. 1996;174:1191–1199. doi: 10.1093/infdis/174.6.1191. [DOI] [PubMed] [Google Scholar]
- 13.Stanley SK, Ostrowski MA, Justement JS, et al. Effect of immunization with a common recall antigen on viral expression in patients infected with human immunodeficiency virus type 1. N Engl J Med. 1996;334:1222–1230. doi: 10.1056/NEJM199605093341903. [DOI] [PubMed] [Google Scholar]
- 14.Donovan RM, Bush CE, Markowitz NP, et al. Changes in virus load markers during AIDS-associated opportunistic diseases in human-immunodeficiency virus-infected persons. J Infect Dis. 1996;174:401–403. doi: 10.1093/infdis/174.2.401. [DOI] [PubMed] [Google Scholar]
- 15.Goletti D, Weissman D, Jackson RW, et al. Effect of Mycobacterium tuberculosis on HIV replication. J Immunol. 1996;157:1271–1278. [PubMed] [Google Scholar]
- 16.Mole L, Ripich S, Margolis D, et al. The impact of active herpes simplex virus infection on human immunodeficiency virus load. J Infect Dis. 1997;176:766–770. doi: 10.1086/517297. [DOI] [PubMed] [Google Scholar]
- 17.Bentwich Z, Maartens G, Torten D, et al. Concurrent infections and HIV pathogenesis. AIDS. 2000;14:2071–2081. doi: 10.1097/00002030-200009290-00002. [DOI] [PubMed] [Google Scholar]
- 18.McLean AR, Nowak MA. Models of interactions between HIV and other pathogens. J Theor Biol. 1992;155:69–102. doi: 10.1016/s0022-5193(05)80549-1. [DOI] [PubMed] [Google Scholar]
- 19.Ferguson NM, deWolf F, Ghani AC, et al. Antigen-driven CD4+ T-cell and HIV-1 dynamics: residual viral replication under highly active antiretroviral therapy. Proc Natl Acad Sci USA. 1999;96:15167–15172. doi: 10.1073/pnas.96.26.15167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Fraser C, Ferguson NM, de Wolf F, et al. The role of antigenic stimulation and cytotoxic T cell activity in regulating long-term immunopatho-genesis of HIV: mechanisms and clinical implications. Proc R Soc Lond B Biol Sci. 2001;268:2085–2095. doi: 10.1098/rspb.2001.1777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Fraser C, Ferguson NM, Anderson RM. Quantification of intrinsic residual viral replication in treated HIV-infected patients. Proc Natl Acad Sci USA. 2001;98:15167–15172. doi: 10.1073/pnas.261283598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Di Mascio M, Percus JK, Percus OE, et al. Duration of an intermittent episode of viremia. Bull Math Biol. 2005;67:885–900. doi: 10.1016/j.bulm.2004.11.003. [DOI] [PubMed] [Google Scholar]
- 23.Di Mascio M, Markowitz M, Louie M, et al. Dynamics of intermittent viremia during highly active antiretroviral therapy in patients who initiate therapy during chronic versus acute and early human immunodeficiency virus type 1 infection. J Virol. 2004;78:10566–10573. doi: 10.1128/JVI.78.19.10566-10573.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Perelson AS, Neumann AU, Markowitz M, et al. HIV-1 dynamics in vivo: virion clearance rate, infected cell lifespan, and viral generation time. Science. 1996;271:1582–1586. doi: 10.1126/science.271.5255.1582. [DOI] [PubMed] [Google Scholar]
- 25.Perelson AS, Essunger P, Cao Y, et al. Decay characteristics of HIV-1 infected compartments during combination therapy. Nature. 1997;271:1582–1586. doi: 10.1038/387188a0. [DOI] [PubMed] [Google Scholar]
- 26.Perelson AS. Modelling viral and immune system dynamics. Nat Rev Immunol. 2002;2:28–36. doi: 10.1038/nri700. [DOI] [PubMed] [Google Scholar]
- 27.Di Mascio M, Ribeiro RM, Markowitz M, et al. Modeling the long-term control of viremia in HIV-1 infected patients treated with antiretroviral therapy. Math Biosci. 2004;188:47–62. doi: 10.1016/j.mbs.2003.08.003. [DOI] [PubMed] [Google Scholar]
- 28.Di Mascio M, Dornadula G, Zhang H, et al. In a subset of patients on highly active antiretroviral therapy plasma HIV-1 RNA can decay from 50 copies/ml to <5 copies/ml with a half-life of six months. J Virol. 2003;77:2271–2275. doi: 10.1128/JVI.77.3.2271-2275.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kaech SM, Ahmed R. Memory CD8+ T cell differentiation: initial antigen encounter triggers a developmental program in naive cells. Nat Immunol. 2001;2:415–422. doi: 10.1038/87720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Van Stipdonk MJ, Lemmons EE, Schoenberger SP. Naive CTLs require a single brief period of antigenic stimulation for clonal expansion and differentiation. Nat Immunol. 2001;21:29–70. doi: 10.1038/87730. [DOI] [PubMed] [Google Scholar]
- 31.Wong P, Pamer EG. Antigen-independent CD8 T cell proliferation. J Immunol. 2001;166:5864–5869. doi: 10.4049/jimmunol.166.10.5864. [DOI] [PubMed] [Google Scholar]
- 32.De Boer RJ, Perelson AS. Estimating division and death rates from CFSE data. J Comp Appl Math. 2005;184:140–164. doi: 10.1007/s11538-006-9094-8. [DOI] [PubMed] [Google Scholar]
- 33.De Boer RJ, Ganusov VV, Milutinovic D, et al. Estimating lymphocyte division and death rates from CFSE data. Bull Math Biol. 2006;68:1011–1031. doi: 10.1007/s11538-006-9094-8. [DOI] [PubMed] [Google Scholar]
- 34.Kim RB, Fromm MF, Wandel C, et al. The drug transporter P-glycoprotein limits oral absorption and brain entry of HIV-1 protease inhibitors. J Clin Invest. 1998;101:289–294. doi: 10.1172/JCI1269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Meaden ER, Hoggard PG, Newton P, et al. P-glycoprotein and MRP1 expression and reduced ritonavir and saquinavir accumulation in HIV-infected individuals. J Antimicrob Chemother. 2002;50:583–588. doi: 10.1093/jac/dkf161. [DOI] [PubMed] [Google Scholar]
- 36.Perno C, Newcombe FM, Davis D, et al. Relative potency of pro-tease inhibitors in monocytes/macrophages acutely and chronically infected with human immunodeficiency virus. J Infect Dis. 1998;178:413–422. doi: 10.1086/515642. [DOI] [PubMed] [Google Scholar]
- 37.Puddu P, Fais S, Luciani F, et al. Interferon-γ up-regulates expression and activity of P-glycoprotein in human peripheral blood monocyte-derived macrophages. Lab Invest. 1999;79:1299–1309. [PubMed] [Google Scholar]
- 38.Finzi D, Hermankova M, Pierson T, et al. Identification of a reservoir for HIV-1 in patients on highly active antiretroviral therapy. Science. 1997;278:1295–1300. doi: 10.1126/science.278.5341.1295. [DOI] [PubMed] [Google Scholar]
- 39.Finzi D, Blankson J, Siliciano JD, et al. Latent infection of CD4+ T-cells provides a mechanism for lifelong persistence of HIV-1, even in patients on effective combination therapy. Nat Med. 1999;5:512–517. doi: 10.1038/8394. [DOI] [PubMed] [Google Scholar]
- 40.Homann D, Teyton L, Oldstone MBA. Differential regulation of antiviral immunity results in stable CD8+ and declining CD4+ memory. Nat Med. 2001;7:913–919. doi: 10.1038/90950. [DOI] [PubMed] [Google Scholar]
- 41.Blankson JN, Finzi D, Pierson TC, et al. Biphasic decay of latently infected CD4+ cells in acute human immunodeficiency virus type I infection. J Infect Dis. 2000;182:1636–1642. doi: 10.1086/317615. [DOI] [PubMed] [Google Scholar]
- 42.Moore AL, Youle M, Lipman M, et al. Raised viral load in patients with viral suppression on highly active antiretroviral therapy: transient increase or treatment failure? AIDS. 2002;16:615–618. doi: 10.1097/00002030-200203080-00013. [DOI] [PubMed] [Google Scholar]
- 43.Sklar PA, Ward DJ, Baker RK, et al. Prevalence and clinical correlates of HIV viremia (‘blips’) in patients with previous suppression below the limits of quantification. AIDS. 2002;16:2035–2041. doi: 10.1097/00002030-200210180-00008. [DOI] [PubMed] [Google Scholar]
- 44.Grueb G, Cozzi-Lepri A, Ledergerber B, et al. Intermittent and sustained low level HIV viral rebound in patients receiving potent antiretroviral therapy. AIDS. 2002;16:1967–1969. doi: 10.1097/00002030-200209270-00017. [DOI] [PubMed] [Google Scholar]
- 45.Furtado MR, Callaway DS, Phair JP, et al. Persistence of HIV-1 transcription in peripheral blood mononuclear cells in patients receiving potent antiretroviral therapy. N Engl J Med. 1999;340:1614–1622. doi: 10.1056/NEJM199905273402102. [DOI] [PubMed] [Google Scholar]
- 46.Zhang L, Ramratnam B, Tenner-Racz K, et al. Quantifying residual HIV-1 replication in persons receiving combination antiretroviral therapy. N Engl J Med. 1999;340:1605–1613. doi: 10.1056/NEJM199905273402101. [DOI] [PubMed] [Google Scholar]
- 47.Dornadula G, Zhang H, Van Uitert B, et al. Residual HIV-1 RNA in blood plasma of patients taking suppressive highly active antiretroviral therapy. JAMA. 1999;282:1627–1632. doi: 10.1001/jama.282.17.1627. [DOI] [PubMed] [Google Scholar]
- 48.Palmer S, Wiegand AP, Maldarelli F, et al. New real-time reverse transcriptase-initiated PCR assay with single-copy sensitivity for human immunodeficiency virus type 1 RNA in plasma. J Clin Microbiol. 2003;41:4531–4536. doi: 10.1128/JCM.41.10.4531-4536.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Siliciano JD, Kajdas J, Finzi D, et al. Long term follow-up studies confirm the stability of the latent reservoir for HIV-1 in resting CD4+ cells. Nat Med. 2003;9:727–728. doi: 10.1038/nm880. [DOI] [PubMed] [Google Scholar]
- 50.Ramratnam B, Mittler JE, Zhang L, et al. The decay of the latent reservoir of replication competent HIV-1 is inversely correlated with the extent of residual viral replication during prolonged anti-retroviral therapy. Nat Med. 2000;6:82–85. doi: 10.1038/71577. [DOI] [PubMed] [Google Scholar]
- 51.Havlir DV, Strain MC, Clerici M, et al. Productive infection maintains a dynamic steady state of residual viremia in human immunodeficiency virus type-1 infected patients treated with suppressive antiretroviral therapy for five years. J Virol. 2003;77:11212–11219. doi: 10.1128/JVI.77.20.11212-11219.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Chun T-W, Nickle DC, Justement JS, et al. HIV-infected individuals receiving effective antiretroviral therapy for extended periods of time continuously replenish their viral reservoir. J Clin Invest. 2005;115:3250–3255. doi: 10.1172/JCI26197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Gett AV, Hodgkin PD. A cellular calculus for signal integration by T cells. Nat Immunol. 2000;1:239–244. doi: 10.1038/79782. [DOI] [PubMed] [Google Scholar]
- 54.De Boer RJ, Oprea M, Antia R, et al. Recruitment times, proliferation, and apoptosis rates during the CD8+ T cell response to LCMV. J Virol. 2001;75:10663–10669. doi: 10.1128/JVI.75.22.10663-10669.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Ramratnam B, Bonhoeffer S, Binley J, et al. Rapid production and clearance of HIV-1 and hepatitis C virus assessed by large volume plasma apheresis. Lancet. 1999;354:1782–1785. doi: 10.1016/S0140-6736(99)02035-8. [DOI] [PubMed] [Google Scholar]
- 56.De Boer RJ, Homann D, Perelson AS. Different dynamics of CD4+ and CD8+ T cell responses during and after acute lymphocytic choriome-ningitis virus infection. J Immunol. 2003;171:3928–3935. doi: 10.4049/jimmunol.171.8.3928. [DOI] [PubMed] [Google Scholar]
- 57.Callaway DS, Perelson AS. HIV-1 infection and low steady state viral loads. Bull Math Biol. 2002;64:29–64. doi: 10.1006/bulm.2001.0266. [DOI] [PubMed] [Google Scholar]
- 58.Zhang ZQ, Wietgrefe SW, Li Q, et al. Roles of substrate activity and infection of resting and activated CD4+ T cells in transmission and acute simian immunodeficiency virus infection. Proc Natl Acad Sci USA. 2004;101:5640–5645. doi: 10.1073/pnas.0308425101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Holte SA, Melvin AJ, Mullins JI, et al. Density-dependent decay in HIV-1 dynamics. J Acquir Immune Defic Syndr. 2006;41:266–276. doi: 10.1097/01.qai.0000199233.69457.e4. [DOI] [PubMed] [Google Scholar]