Mechanism of KCl Enhancement in Detection of Nonionic Polymers by Nanopore Sensors

Abstract

The mechanisms of KCl-induced enhancement in identification of individual molecules of poly(ethylene glycol) using solitary α-hemolysin nanoscale pores are described. The interaction of single molecules with the nanopore causes changes in the ionic current flowing through the pore. We show that the on-rate constant of the process is several hundred times larger and that the off-rate is several hundred times smaller in 4 M KCl than in 1 M KCl. These shifts dramatically improve detection and make single molecule identification feasible. KCl also changes the solubility of poly(ethylene glycol) by the same order of magnitude as it changes the rate constants. In addition, the polymer-nanopore interaction is determined to be a strong non-monotonic function of voltage, indicating that the flexible, nonionic poly(ethylene glycol) acts as a charged molecule. Therefore, salting-out and Coulombic interactions are responsible for the KCl-induced enhancement. These results will advance the development of devices with sensor elements based on single nanopores.

INTRODUCTION

Recent studies have demonstrated that single, nanometer-scale pores, including the ion channels formed by Staphylococcus aureus α-hemolysin (αHL), can be used to detect and quantify specific monovalent ions (1,2), divalent metal cations (3,4), small organic molecules (5–7) nucleic acids (8,9), proteins (10,11), and polymers (12–17). Because these pores are so small, their interaction with an analyte can alter the ionic current that would otherwise flow freely. Analytes apparently change the electrostatic potential profile inside the pore or simply block the ion-conduction pathway.

Binding of analytes to nanopores is random and reversible, and it causes characteristic fluctuations in the ionic current. For this reason, single nanopores inserted in thin membranes have recently been referred to as stochastic sensors (18). Studies (1,2,5,7,19–21) have shown that the frequency of these fluctuations reveals the kinetic rate constants for the analyte-pore interaction. As a result, the concept of a molecular Coulter counter was developed (22).

If an analyte associates with a nanopore for periods longer than the measurement bandwidth, discrete states of ionic current blockade can be directly observed. The degree to which pore conductance is blocked is often characteristic of the analyte (5–7,19,23). Moreover, studies (9,14,17,23,24) have demonstrated that different polymers can cause complex but characteristic blockade patterns. In a manner similar to infrared-ultraviolet-visible (IR-UV-VIS) spectra and mass spectrometry, these patterns provide a fingerprint of polymers that thread through the nanopore (17).

Despite the proof of concept for the use of single nanopores in sensor applications, recent theoretical studies necessitate a better understanding of how polymers interact with nanoscopic pores (25–28). Previous studies (14,17) demonstrated that high-resolution recording of poly(ethylene glycol) (PEG)-αHL nanopore interactions is achievable in 4 M KCl. The goal of this study was to discover the underlying mechanism(s) of the stochastic sensing enhancement observed at high KCl concentrations. Our key finding is that molecules of PEG in aqueous salt solutions act as charged molecules. The salting-out effect, the Coulombic interaction of PEG with the αHL nanopore, and the decrease in PEG chain flexibility with increasing KCl concentrations are responsible for the observed enhancement.

MATERIALS AND METHODS

Bilayer lipid membranes of 40 pF capacitance were formed by the lipid monolayer apposition technique, using 1,2-diphytanoyl-sn-glycero-3-phosphocholine (Avanti Polar Lipids, Alabaster, AL) at 25 ± 1°C, as described previously (29). The membrane-bathing aqueous solution contained 1 M to 4 M KCl in 5 mM Tris-citric acid buffer (pH 7.5). PEG was used as a representative of neutral polymers, because it is used widely in both scientific studies and technological applications. PEGs of various molecular weights (Fluka, Seelze, Germany) and monodisperse PEG 1294 (Polypure, Oslo, Norway) were added from the trans side of the membrane. αHL (Calbiochem, Madison, WI) was added from the cis side of the membrane in a concentration sufficient to form unitary protein nanopore in planar lipid membranes. If not mentioned specially, the applied potential was 40 mV. A positive current is defined by cation flow from trans to cis.

Experiments were carried out using an Axopatch 200B amplifier (Axon Instruments, Foster City, CA) in voltage clamp mode. Membrane potential was maintained using silver/silver chloride (Ag/AgCl) electrodes in 3 M KCl 2% agarose bridges assembled within standard 200 μL pipette tips. Currents were filtered by a low-pass eight-pole Butterworth filter (model 9002; Frequency Devices, Haverhill, MA) at 15 kHz and directly saved into the computer memory with a sampling frequency of 50 to 100 kHz. In experiments, we used dilute polymer solutions in which nonideality effects (30) and polymer-polymer repulsion that could increase PEG partitioning into the protein nanopore (31) are virtually nonexistent. The greatest PEG concentration used in bilayer experiments was 4 mM for PEG 3000 (1.2%, w/w), which is well below the overlap concentration for this PEG molecule (∼13%) (30), and solubility in 4 M KCl (see Results and Discussion). The obtained dependencies were qualitatively similar for all PEG molecules examined (PEG 600, 1000, 1500, 2000, 3000, and 4000); however, only the data for PEG 1500 and 2000 are presented in this study.

The limit of PEG solubility was estimated by the modified cloud-point method (32). In brief, small amounts of PEG (usually between 2 and 40 mg) were added to 10 mL glass vials. Then, small volumes (300–500 μL) of KCl solution were added stepwise at room temperature (25 ± 1°C). After each addition, vials were closed using screw caps with Teflon seals, carefully shaken to achieve full PEG solubility, and placed in a boiling water bath (∼100°C) for 10 to 30 min. Cloud formation was determined visually. Polymer molarities were calculated on a mass percent basis. The mean value of the PEG concentration between two neighboring solutions (one of which still showed — and the other of which no longer showed — a phase split) in each experiment, represented the PEG solubility under those conditions. The difference in concentration between those neighboring solutions determined the inaccuracy of the experimental results. To determine the cloud point more accurately, the experiment was repeated several times with a mixture already close to the phase boundary. Smaller increments of KCl solution were then added to narrow the inaccuracy to < 1%.

Parameters of the molecular signature (mean duration and amplitude of the blockage), transition rate, and kinetic constants of the PEG-nanopore interaction were obtained essentially as described in the works by Krasilnikov et al. (14) and Movileanu et al. (16).

RESULTS AND DISCUSSION

Appearance

Voltage clamping was used to examine the interaction of individual PEG molecules with solitary protein nanopores. The ionic current through the αHL nanopore bathed by a polymer-free solution is quiescent (8,12,31,33,34). Addition of PEG to the subphase causes well-defined current blockades (Fig. 1 A) of which the frequency, amplitude, and duration increase with KCl concentration. Compared to 1 M KCl, the aforementioned blockade parameters are strongly dependent on polymer molecular weight in the presence of 4 M KCl and become useful in the identification of the polymer (14,17). When polydisperse PEG molecules are used in the presence of 4 M KCl, analysis of blockade events reveals the distinct PEG populations. They are clearly observed in the two-dimensional distribution of the events (residence time versus normalized residual conductance) (Fig. 1 B). The obtained resolution (better than the repeat unit) makes it possible to detect and quantify each PEG population in the sample in real time, using software developed in our laboratory.

FIGURE 1.

Influence of polydisperse PEG 1500 (0.4 mM) on the single αHL pore current. (A) This typical trace of the ion current through the αHL pore exhibits stepwise transitions between completely open and partially blocked states that are caused by the entrance of a single PEG molecule into the pore lumen. Time averaging is 0.01 ms. Transmembrane voltage was maintained at 40 mV. The solution contains 4 M KCl. The horizontal dashed lines delimit the location of the blockages. (B) Two-dimensional visualization of the residence time/normalized residual conductance density distribution (two-dimensional contour plot) of > 18,000 events like those presented in A. Each colored “island” represents an individual monodisperse PEG with a number of repeat units shown in the figure. Colored bars denote the number of events at a given residual conductance and residence time. The difference between each of the successive colors is ∼10 events/(Log ms × pA). Such a representation is suitable to build a database for the identification and characterization of a single molecule based on the analysis of an individual blockade event. The ambit of the residual conductance-residence time distribution for monodisperse PEG 1294 is show in the red ellipse.

On-rate constant

To determine the on-rate constant, k_on, defined as 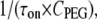data were first collected on the time intervals between the end of one blockade event and the onset of the next to establish the characteristic time τ_on. We observed that the k_on value for all used PEGs increased in a hyperlinear manner with KCl concentration. For PEG 2000, k_on is several hundred times greater in 4 M KCl than in 1 M KCl, and 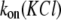dependence is fitted well with a power function (Fig. 2 A).

FIGURE 2.

Dependence of the kinetic parameters of the PEG 2000-αHL pore interaction (A, C, and D) and PEG solubility (B) on KCl concentration. (A) The dependence of the on-rate constant of PEG capture by the αHL pore. The solid line is drawn according to the equation with an adjustable multiplier to fit the k_on data. (B) Solubility of PEG 2000 in different KCl solutions at 100°C and at different temperatures (inset). The line is drawn according to the equation 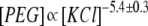with an adjustable multiplier to fit the data. (Inset) Arrhenius plot of PEG solubility in 4 M KCl. The solid line is the first-order regression fit of the data. Temperature coefficient Q₁₀ is 3.3 ± 0.3. Each point represents the mean (±SD) of three to eight independent experiments. (C) Influence of KCl concentration on the transition rate obtained in the presence of PEG. The line is drawn according to the equation 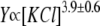with an adjustable multiplier to fit the data. (Inset) The concentration of PEG as a function of the transition rate at different KCl concentrations. The lines are the first-order regression fits of the data. (D) The dependence of the average off-rate constant of the PEG-αHL pore interaction. The line is drawn according to the equation 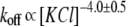with an adjustable multiplier to fit the k_off data. For A, C, and D, each point represents the mean (± SD) of at least three single protein nanopores reconstituted in separate experiments with > 9000 events as in Fig. 1 A. Dashed lines show 95% confidence limits.

The salting-out effect may be one of several reasons for the established enhancement in the on-rate constant. To explore this possibility, the solubility of PEGs at different KCl concentrations was investigated. Studies (35,36) have shown that PEGs have an unusual property in water: they exhibit an upper temperature limit of solubility, which is better known as a cloud point. There also are reports (35,37) that increased salt concentration can lower the precipitation temperature of PEG molecules. However, the limiting PEG concentration, beyond which insolubility and formation of two phases occurs in high KCl concentrations, is unknown, and so we examined it in this study. Our results show that the solubility of PEG (at 100°C) actually decreases with increasing KCl concentration in a sublinear manner (Fig. 2 B). It is fitted well with a power function in which the magnitude of the exponent has a value similar to that of the dependence (Fig. 2 A).

Therefore, it seemed reasonable that the salting-out phenomenon, surmised in a molecular dynamics simulation study (37), might be involved in the observed 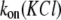dependence. However, the level of PEG solubility in 4 M KCl, even at 100°C, remains high (∼1 mM for PEG 2000). Moreover, PEG solubility increases remarkably at lower temperatures (Fig. 2 B, inset), so that the predicted PEG concentration (at 25°C) becomes preposterously high (∼9.2 M or 18.4 kg/L, for PEG 2000). These results affirm that, at the highest PEG concentration used in this study (4 mM), all PEGs are completely dissolved. Thus, other mechanisms may also be responsible for the strong hyperlinear 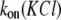dependence.

To clarify these mechanisms, the on-rate constant for different PEG molecules, 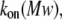was analyzed at different KCl concentrations. The value of k_on decreased with increasing PEG molecular weight (Fig. 3). However, the magnitude of the decrease was dependent on KCl concentration — it was considerably more flat at 4 M than at 1 M KCl. To describe the established 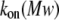dependence, we have used the formalism that was developed by Douglas and Garboczi (38) and successfully used in our previous study (14). This formalism assumes that the dependence of both the on-rate constant and the diffusion coefficient, D(Mw), on PEG molecular weight can be written as 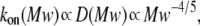indicating that the on-rate constant is diffusion limited. The experimental data for the solution containing 4 M KCl (Fig. 3 A) obey this simple function and can be fitted satisfactorily. At 1 M KCl (Fig. 3 B), the dependence is much more a function of polymer mass than at 4 M KCl (Fig. 3 A) and could not be ascribed to a decrease in the diffusion coefficient. Hence, in the presence of the lower KCl concentrations, diffusion is not the only determinant for the on-rate constant of PEG capture by the αHL pore. It appears that the role of entropy part of PEG-αHL pore interaction increases with decreasing salt concentration and becomes dominant at low salt concentrations (34,39), which allows pore sizing by polymer partitioning (15,40,41).

FIGURE 3.

The average on-rate of polymer capture by αHL pores as a function of polymer mass at 4 M (A) and 1 M KCl (B). The solid line is drawn according to the equation in the work by Douglas and Garboczi (38), 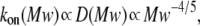with an adjustable multiplier to fit the data for the smallest PEG molecule. Note the 50-fold difference in scales. Each point represents the mean (± SD) of at least three single protein nanopores reconstituted in separate experiments with > 9000 events as in Fig. 1 A.

The 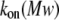dependence established at 1 M KCl is qualitatively similar to that presented in a previous study by Movileanu and colleagues (16). However, there is considerable quantitative difference — the obtained k_on values for each PEG are ∼5× smaller than demonstrated previously (16). The transmembrane voltages, 40 mV and 100 mV, comprise the only methodological difference between this study and that by Movileanu and colleagues (16). This observation suggests that PEG entry into an αHL pore could be voltage dependent. Additional experiments performed at different voltages (±200 mV) confirmed this hypothesis (Fig. 4). k_on is dependent on voltage in a nonlinear manner. The difference in the k_on value measured at different voltages could reach 2 to 3 orders of magnitude. This behavior demonstrates that PEG senses the transmembrane voltage even in solution, probably when it is in the access regions of the pore. The decrease in k_on observed at a high positive voltage probably results from PEG depletion in the region. To our knowledge, this phenomenon has not been noted before. The data resemble the known effect of charged analyte depletion near the opening of nanoscopic pores (42–44). The effect is specific for diffusion-limited transport and confirms our conclusion that PEG entrance into the pore is diffusion limited. The depletion is observed at low concentrations of charged analytes and relatively high transmembrane voltage, which are conditions similar to those in our experiments with PEG molecules. Thus, the neutral polymer PEG appears to be charged, and the Coulombic interaction between PEG and the αHL pore (which is decorated with fixed charges) may occur. This finding is consistent with the observation (45,46) that PEGs can form complexes with cations. The latter could also be responsible for the observed dependence and for the divergence between 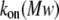values obtained both previously (16) and in this study. The phenomenon is very important and worthy of further investigation.

FIGURE 4.

Voltage dependence and energy of PEG 1500-αHL pore interaction. The average on-rate (A), off-rate (B), and PEG-αHL pore complex formation (C) constant as a function of transmembrane voltage at different KCl concentrations. The minimal values of k_off are at 40 ± 10 mV. The data presented in A and B were used to build the dependence shown in C. (D) The energy of PEG-αHL pore interaction measured at 40 mV as a function of KCl concentration. Values were estimated from the equilibrium formation constant (solid line) and from the formalism outlined in the work by Muthukumar (27) (dashed line). k_on, k_off, and τ_off essential for calculations were obtained at 40 mV in three to five independent experiments (± SD) with > 9000 events as in Fig. 1 A in each point.

Transition rate

As a consequence of the 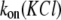dependence (Fig. 2 A), the transition rate, defined by Movileanu and colleagues (16) as 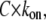is dozens of times larger at 4 M KCl than at 1 M KCl. Examples of such dependencies established for PEG 2000 are shown in Fig. 2 C. Accordingly, the high KC1 concentrations shift the background equivalent concentration of all PEGs used in this study. At an event frequency of 1 Hz, then, the background equivalent PEG concentration comprises: 120.0, 9.0, 2.0, and 0.8 μM (PEG2 000) and 20.0, 2.5, 1.4, and 0.5 μM (PEG 1500) at 1 M, 2 M, 3 M, and 4 M KCl, respectively (Fig. 2 C, inset). For all PEGs reported in this study and in related, previous studies (14,16), the transition rate is directly proportional to polymer concentration with a slope of ∼1 (0.97 ± 0.06). This finding suggests that the partitioning of PEG into the αHL pore can be described by a first-order reaction between the pore and polymer and that only one polymer molecule is responsible for a single blockade event. Similar conclusions have been drawn for the partitioning of polynucleotides into a single αHL pore (47).

Residence time

All the aforementioned data demonstrate that the association rate constant, k_on, is a function of both the KCl concentration and voltage. To comprehend the mechanism of the influence of KCl concentration on PEG-αHL pore interactions, understanding the behavior of the dissociation rate constant k_off at the same conditions is essential. This study shows that both factors have a considerable influence on k_off (Figs. 2 D and 4 B). It is interesting to note that the magnitude of the exponent value for 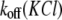dependence closely resembles those of (Fig. 2 A) and (Fig. 2 B) dependencies. Such similarity reinforces the hypothesis about the important role of salting out on the observed phenomenon. The dependence of the off-rate constant, k_off, on voltage (Fig. 4 B) strengthens the involvement of the Coulombic interactions between PEG molecules and the αHL pore. As a result, the constant of the PEG-αHL pore complex formation, K_f, is also voltage dependent (Fig. 4 C).

Energy of interaction

Two approaches were used to estimate the energy of PEG-αHL pore interactions. First, the equilibrium formation constant, K_f, was used, where the energy (in kT -units) is determined as The constant was calculated by using the association k_on and dissociation k_off rate constants obtained at different KCl concentrations like those shown in Fig. 2, A and D. As a result, the maximal values of the free energy of confinement (observed at 40 mV) were established as 0.27 ± 0.03, 0.19 ± 0.02, 0.13 ± 0.02, and 0.03 ± 0.01 kT /PEG repeat unit in the presence of 4 M, 3 M, 2 M, and 1 M KCl, respectively (Fig. 4 D, solid diamonds).

The value 0.27 kT established for 4 M KCl is close to the value that was recently estimated (14) using the assumption specified by Muthukumar (27), whereby the residence time for PEG inside the pore, τ_off, is proportional to depth of an attractive potential well, that, in turn, is proportional to the number of repeat units in the PEG chain, N, as follows: This formalism results in a weak KCl dependence (Fig. 4 D, open diamonds).

In contrast, the approach based on the equilibrium formation constant indicates a strong KCl dependence. The latter is consistent with earlier data (34) showing measurable increases in PEG-αHL pore interaction with KCl concentration augmented from 0.1 M to 1 M. The absence of any adjustable parameters is another advantage of this direct approach. The established strong dependence of the energy of the PEG-αHL pore interaction on KCl concentration could result from both the decrease in a repulsive interaction between PEG and its image charge (induced in low-dielectric surroundings such as the membrane and protein pore wall) (48–50) and the simultaneous increase in van der Waals interactions. Such a suggestion seems logical for two reasons. First, PEG molecules are charged. Second, it has previously been demonstrated (51) that the increase in KCl concentration in the bathing solution decreases the long-range action of the charges even though they are inside of the nanopore. The decrease in PEG chain flexibility, observed in the presence of inorganic cations (37), should slow the PEG creeping through the αHL pore, also increasing its residence time and the energy of PEG-αHL pore interactions.

CONCLUSIONS

Our previous data (14,17) and the results of this study clearly demonstrate that increased salt concentration improves the sensitivity of stochastic sensing with protein pores, such as the αHL pore. The increase in salt concentration decreases the lowest detectable concentration of analytes and considerably refines analyte identification. It is achieved thanks to changes in both (on- and off-) rate constants of the analyte-nanopore interaction. This study shows that the change in the on-rate constant with salt correlates with the change in solubility of the analytes. In other words, the constant could increase, decrease, non-monotonously behave, or remain the same with salt concentration. This finding opens the possibility that the effect of salt on the on-rate constant of novel analytes for the nanopore sensor can be predicted. The salt dependence of off-rate constant seems to be uniform (decreasing with salt) (52) for charged and noncharged molecules.

Our study illuminates the ability of neutral analyte molecules to form complexes with ions and to change solubility depending on the salt concentration. Both effects have significant influence on the stochastic sensing of analytes. Specifically, we our study resulted in two findings:

1. Molecules of PEG are charged in high KCl solutions, leading to nonlinear voltage dependence in rate constants; and

2. There is a striking similarity in the magnitude of power dependencies of both PEG solubility and the rate constants of PEG-αHL pore interactions in KCl.

The enhancement in stochastic sensing with KCl involves two factors: 1), qualitative changes in PEG polymer partitioning that provide two parameters: the residence time and the blockade amplitude; and 2), a significant increase in the on-rate of PEG capture and the free energy of PEG interaction with the αHL pore. These factors permit single molecule identification and involve a salting-out effect, Coulombic interactions, and, probably, a change in the chain flexibility of the polymer.

Findings such as those of this study can help in understanding the physics of molecular interactions in confined spaces. It is hoped that our results will advance the development of devices with sensor elements based on single nanopores, including those made in polymer matrices or carbon nanotubes, and will stimulate experimental and theoretical studies.