Robust omniphobic surfaces

Abstract

Superhydrophobic surfaces display water contact angles greater than 150° in conjunction with low contact angle hysteresis. Microscopic pockets of air trapped beneath the water droplets placed on these surfaces lead to a composite solid-liquid-air interface in thermodynamic equilibrium. Previous experimental and theoretical studies suggest that it may not be possible to form similar fully-equilibrated, composite interfaces with drops of liquids, such as alkanes or alcohols, that possess significantly lower surface tension than water (γ_lv = 72.1 mN/m). In this work we develop surfaces possessing re-entrant texture that can support strongly metastable composite solid-liquid-air interfaces, even with very low surface tension liquids such as pentane (γ_lv = 15.7 mN/m). Furthermore, we propose four design parameters that predict the measured contact angles for a liquid droplet on a textured surface, as well as the robustness of the composite interface, based on the properties of the solid surface and the contacting liquid. These design parameters allow us to produce two different families of re-entrant surfaces— randomly-deposited electrospun fiber mats and precisely fabricated microhoodoo surfaces—that can each support a robust composite interface with essentially any liquid. These omniphobic surfaces display contact angles greater than 150° and low contact angle hysteresis with both polar and nonpolar liquids possessing a wide range of surface tensions.

Superhydrophobic surfaces display water contact angles greater than 150° and low contact angle hysteresis. Their many attractive properties have generated extensive commercial and academic interest (1–7). The highest contact angles reported with water on smooth, low energy surfaces, such as Teflon, are in the range of 120° (8, 9), and it has been shown through extensive theoretical analysis and experimentation that a rough surface texture is necessary for the development of superhydrophobicity (1, 5, 7).

The addition of a liquid droplet to a textured surface leads to either a fully wetted Wenzel state (10) or a Cassie-Baxter state that supports a composite solid-liquid-air interface (11). In the former case, the apparent contact angle θ* of a droplet placed on the surface is given by cosθ* = rcosθ, where the surface roughness r is defined as the actual surface area divided by the projected surface area and θ is the equilibrium contact angle, defined as the contact angle on a smooth surface possessing identical surface chemistry as the textured surface. The large contact area between the liquid and solid in the Wenzel state leads to high contact angle hysteresis (CAH), defined as the difference between measured values of the advancing and receding contact angles. Liquid drops, thus, do not readily roll off the textured surface (12, 13). By contrast, a composite interface facilitates both nonwetting (high apparent contact angles, θ* > 90°), as well as easy droplet roll-off (low CAH), because of the small total contact area between the liquid drop and the solid substrate (6, 12, 14, 15). In this case, the apparent contact angle is given by the Cassie-Baxter relationship cosθ* = r_φφ_s cosθ + φ_s − 1 (16, 17), where r_φ is the roughness of the wetted area and φ_s is the area fraction of the liquid-air interface occluded by the surface texture, as shown in supporting information (SI) Appendix. It should be noted that the magnitudes of both r_φ and φ_s are functions of the substrate topography and the equilibrium contact angle. The question that arises is, “Which of these states is naturally realized by any given surface, and how can one design textures that promote the formation of a composite interface for a given liquid?” The answer is determined by considering the overall free energy of the system comprising the liquid droplet, the surrounding vapor, and the textured solid surface (13, 16, 18, 19). The critical value of the equilibrium contact angle (θ_c) beyond which the composite interface leads to a lower overall free energy, in comparison to the fully wetted interface, can be determined by equating the Wenzel and Cassie-Baxter relations. This simple analysis (see SI Appendix) predicts cosθ_c < 0 or equivalently θ_c > 90° (1, 20, 21). Hence, it may be anticipated from thermodynamic considerations that development of a composite interface and highly nonwetting surfaces with low contact angle hysteresis (θ* ≫ 90°) requires θ >θ_c > 90°. Such arguments highlight the difficulty of developing surfaces that repel liquids with relatively low surface tension (for example alkanes, such as decane or octane), primarily because there are no reports of natural or artificial surfaces with sufficiently low surface energy to enable equilibrium contact angles of θ > 90° with these liquids (9, 21–24). Indeed, despite a plethora of superhydrophobic surfaces, there are no natural examples (see Fig. 1 A and B), and few synthetic embodiments, of superoleophobic surfaces that display apparent contact angles of θ* > 150° and low hysteresis with low surface tension liquids, such as alkanes (21, 22, 25). As a consequence, it is commonplace to observe that low surface-tension liquids, such as gasoline, easily spread on any surface.

Fig. 1.

Critical role of re-entrant texture. (A and B) Droplets of water (colored with methylene blue) and rapeseed oil (colored with oil red O) on a duck feather. (C and D) Schematic diagrams illustrating possible liquid-vapor interfaces on two different surfaces having the same solid surface energy and the same equilibrium contact angle (θ), but different geometric angles (ψ). (E) An SEM micrograph of an electrospun surface containing 44.4 wt% fluorodecyl POSS and possessing the beads-on-strings morphology. The inset shows the molecular structure of fluorodecyl POSS molecules. The alkyl chains (R_f) have the molecular formula −CH₂CH₂(CF₂)₇CF₃. (F) An SEM micrograph of a microhoodoo surface (with W = 10 μm, D = 20 μm and H = 7 μm). The samples are viewed from an oblique angle of 30°.

In our recent work (21), we used re-entrant surface curvature to develop metastable (6, 21, 26, 27) composite solid-liquid-air interfaces that are consistent with the Cassie-Baxter description, and which correspond to a well-defined local minimum in the free energy, even though the fully wetted Wenzel state corresponds to the global minimum in free energy. This approach leads to nonwetting textured surfaces with a given liquid, even though the same contacting liquid easily wets smooth surfaces made from the same material. Such surprising liquid repellency is related to the trapping of air underneath the liquid droplet, and can be understood by studying the Cassie-Baxter relation (11), which enables θ* ≫ 90° as r_φφ_s → 0, even if θ < 90°. Here we extend our earlier work by developing four dimensionless design parameters that describe the robustness of a composite interface and the observed apparent contact angle on a textured surface, given the various thermophysical and geometric properties that parameterize the system. By systematically varying the various chemical and topological surface features, as guided by the design parameters, we develop families of surfaces that are omniphobic; that is, they can form robust composite interfaces and display apparent contact angles greater than 150° and low hysteresis, even with liquids possessing significantly lower surface tension (γ_lv), such as methanol (γ_lv = 22.7 mN/m), octane (γ_lv = 21.6 mN/m), and pentane (γ_lv = 15.1 mN/m).

To illustrate our approach qualitatively, consider the two schematic diagrams shown in Fig. 1 C and D, which depict putative solid-liquid-vapor interfaces for a liquid with θ ∼ 75° on two different textured surfaces having the same solid surface energy (γ_sv). In these figures, ψ is the local geometric angle of the texture. When θ < ψ, as in Fig. 1C, the net traction on the liquid-vapor interface is downward, promoting the imbibition of the liquid into the solid texture, leading to a fully-wetted interface. However, if θ > ψ, as shown in Fig. 1D, the net force is directed upward. In this case the liquid-vapor interface recedes to the top of the pillars, creating a composite solid-liquid-air interface (27). Thus, either of these surfaces allows for the possibility of forming a composite interface provided θ ≥ ψ (14, 18, 21), while any liquid for which θ <ψ will immediately yield a fully wetted interface. Because of this design constraint (θ ≥ ψ), many superhydrophobic surfaces described in the literature, such as arrays of pillars, spikes, or wrinkles, for which ψ ≥ 90°, are unable to support a composite interface with low surface-tension liquids. Surfaces possessing re-entrant texture (ψ < 90°) (18, 21, 25–28) facilitate extremely high apparent contact angles, even if θ < 90°, and are therefore necessary for developing superoleophobic surfaces.

Results and Discussion

Based on the above understanding, we fabricated two different families of structures, shown in Fig. 1 E and F, that both possess re-entrant curvature (21); that is, the surface topography cannot be described by a simple univalued function z = h(x,y) and a vector projected normal to the x-y plane intersects the texture more than once (also see SI Appendix). Fig. 1E shows an example of electrospun fibers (29–32) formed from a blend of a hydrophilic polymer (polymethyl methacrylate or PMMA) and fluoroPOSS molecules (21, 33), a new class of polyhedral oligomeric silsesquioxane (POSS) molecules in which the silsesquioxane cage is surrounded by fluorinated alkyl groups. A number of different molecules with various fluoroalkyl groups surrounding the silicon-oxygen cage have been developed (33), and we use 1H,1H,2H,2H-Heptadecafluorodecyl or fluorodecyl POSS (see inset of Fig. 1E) exclusively in this study. The high concentration of perfluorinated carbons in the alkyl chains leads to extremely low surface energies for these molecules (9, 21, 33). Fig. 1E also shows the so-called “beads-on-strings” morphology (34) of the fiber mat, which gives rise to multiple scales of re-entrant texture in the surface topography and large porosity within the mat.

The structures shown in Fig. 1F were fabricated on flat Si wafers using SiO₂ deposition, followed by a two step etching process (see Methods) comprising reactive ion etching of SiO₂ and subsequent isotropic etching of Si using vapor-phase XeF₂. This results in under-cut silicon pillars, capped with a layer of SiO₂, 300 nm in height. These structures are referred to as “microhoodoos.” The geometry and process of creation of these structures are similar to geological features called hoodoos that are created by erosion.

In contrast to the structures in Figs. 1 C and D, both the electrospun fiber mats and the microhoodoos exhibit continuously varying values of the local geometry angle ψ, ranging from ψ_max = 180° to ψ_min = 0° along the curvature of these structures. Based on our earlier consideration of structures shown in Fig. 1 C and D, these structures should be capable of supporting a composite interface with any liquid for which θ > 0°. Detailed calculations (see SI Appendix) of the Gibbs free-energy landscape for water and hexadecane penetrating the electrospun fiber mats and the microhoodoo arrays clearly reveal the metastable nature of the composite interface obtained for hexadecane on these surfaces. For both the electrospun and microhoodoo surfaces, it is possible to realize apparent contact angles θ* ≫ 90° with hexadecane, even though in each case θ < 90°.

Design Parameters for a Robust Composite Interface.

We first define a suitable design parameter, D* (the feature spacing ratio) to correlate the measured apparent contact angles with the surface texture parameters. For any given equilibrium contact angle θ, the apparent contact angles on the electrospun fiber surface are controlled by the feature spacing ratio D* = (R+D)/R. In terms of the spacing ratio, the Cassie-Baxter relationship (11) may be rewritten as cosθ* = −1 + $\frac{1}{D*}$[sinθ + (π − θ)cosθ]. Thus, higher D* values lead to an increase in the magnitude of apparent contact angles θ*.

We next seek to correlate the robustness of a composite interface to the various surface and liquid properties. We cognated earlier that a surface possessing re-entrant curvature with ψ_min < 90° can lead to a composite interface with any liquid possessing an equilibrium contact angle θ ≥ ψ_min. However, in practice, a composite interface for a particular liquid may not be realizable if the activation energy required to transition irreversibly from the metastable composite interface to the fully wetted interface is not sufficiently large.

The utility of free-energy calculations (16, 42) in estimating the breakthrough pressure required to transition from the composite to a fully wetted interface is in fact rather limited. This is because the analysis typically assumes a locally flat liquid-vapor interface, an assumption that is invalid for liquids under externally applied pressure. In these cases, considerable local sagging (35) and distortion of the liquid-vapor interface occurs and the actual failure of the composite regime typically originates from the sagging of the liquid-vapor interface, rather than from overcoming the activation energy required to transition between the metastable and global equilibrium states. In addition, the assumption of a locally flat solid-vapor interface in the Gibbs free-energy approach leads to predictions of infinite breakthrough pressures if a surface's local geometric angle ψ_min ≤ 0°, owing to a singularity at ψ = 0° (see SI Appendix).

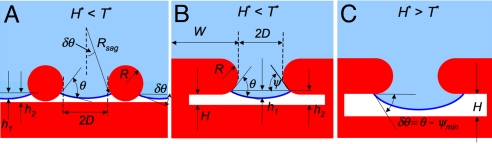
To provide more realistic predictions of the breakthrough pressure, we have developed two design parameters, the robustness height (H*) and the robustness angle (T*). Both robustness parameters quantify the sagging of the liquid-vapor interface as a consequence of the pressure difference across the interface, which could arise from numerous sources, including the application of external pressure, impact of a liquid droplet released from a height, or because of the Laplace pressure within a droplet (35, 36). The first parameter H* provides a dimensionless measure of the pressure (P_H) required to force the sagging height, h₁, for the liquid-vapor interface to reach the maximum pore depth, h₂ (see Fig. 2 A and B). In evaluating H*, we compare P_H to a reference pressure P_ref = 2γ_lv/ℓ_cap, where ℓ_cap = $\sqrt{{\gamma }_{lv}/\rho g}$ is the capillary length of the fluid, ρ is the liquid density, and g is the acceleration due to gravity. P_ref is close to the minimum pressure difference across the composite solid-liquid-air interface for millimetric sized droplets or larger puddles on extremely nonwetting, textured surfaces (see SI Appendix for more details). For a nonwoven mat of electrospun fibers, H* then takes the form (see SI Appendix for derivation details):

Fig. 2.

Design parameters for a robust composite interface. (A) A schematic illustration of the electrospun surface, highlighting the expected liquid-vapor interface with a liquid having an equilibrium contact angle θ < 90°. The important surface texture parameters R, D, h₁, and h₂ are also shown. R_sag is the radius of curvature of the sagging composite interface. The electrospun surface typically possesses lower values of the robustness parameter H* in comparison to the parameter T*. (B) A schematic illustration of the microhoodoo surface with a small pore-depth (h₂). The important surface-texture parameters, R, D, H, and W, shown in the figure, can be varied independently. Such a microhoodoo surface typically possesses lower values of H* in comparison to T*. (C) A schematic illustration of the microhoodoo surface with a larger pore-depth (h₂) developed by increasing the microhoodoo height (H). Such a microhoodoo surface typically possesses lower values of T* in comparison to H*.

The capillary length ℓ_cap appears in Eq. 1 because of our choice of the scaling pressure P_ref : a characteristic pressure whose magnitude is determined by a balance between the surface forces and the body forces arising from gravity that act on the fluid interface (see SI Appendix). In certain cases, gravity can cause significant sagging of the liquid-air interface, even for millimetric sized droplets supported on micrometer sized solid protrusions. For example, using the previous calculations of Quéré and Reyssat (36), it can be shown that the sagging of the liquid-vapor interface for millimetric sized droplets, caused solely by gravity, scales as h₁ ∼ (2D)²/ℓ_cap. For our microhoodoo surfaces (for which 2D varies between 10 and 60 μm), assuming ℓ_cap = 1.5 mm, this yields h₁ ∼ 0.07 to 2.4 μm. Thus, for the most sparsely spaced microhoodoos, the sagging caused by gravity (h₁) can be of the same order as the maximum pore depth (h₂ = 3–7 μm). Other choices of the reference pressure P_ref could also be made (e.g., for studies of impacting droplets or evaporating droplets); this would change the numerical magnitude of H* but not its physical dependence on the geometric parameters characterizing the composite interface.

High values of the robustness height H* indicate the formation of a robust composite interface; however, a composite interface on a surface with H* ≫ 1 can still transition to a fully wetted interface because of a shift in the local contact angle caused by sagging of the liquid-vapor interface (Fig. 2C). On any rough surface, the liquid-vapor interface locally makes an angle θ with the solid substrate (see Fig. 2 A and B). As the applied pressure increases, the liquid-vapor interface becomes more severely distorted, and the magnitude of the distortion can be parameterized by the sagging angle δθ. This distortion causes the liquid-vapor interface to advance downward to a lower value of ψ = θ − δθ. Eventually, the local vapor-liquid interface reaches the bottom of the re-entrant structure (ψ = ψ_min), as shown schematically in Fig. 2C. Any additional increase in pressure cannot be supported by changes in the local geometric angle and the fluid penetrates into the solid texture, leading to a fully wetted interface. Thus, the composite interface transitions to the fully wetted interface when the sagging angle δθ = θ − ψ_min. Based on these ideas, we can evaluate the robustness pressure (P_θ) required to force a sagging angle of δθ = θ − ψ_min. For the electrospun fibers, the robustness angle T* takes the form (see SI Appendix):

Note that for both the electrospun and the microhoodoo surfaces, the available re-entrant curvature leads to ψ_min = 0°, which enables large values of (θ − ψ_min). Geometries with ψ_min < 0° (see SI Appendix) can potentially lead to even higher values of T*.

SI Appendix, Table S1 provides the form of the robustness parameters, H* and T*, for the microhoodoos and the various electrospun surfaces developed in this work. The design parameter T* is a dimensionless measure of the robustness angle, while H* is a dimensionless measure of the robustness height. A composite interface transitions irreversibly to a fully wetted interface through a combination of the two mechanisms discussed above, as any external pressure causes a simultaneous increase in both the sagging height h₁ and the sagging angle δθ (see Fig. 2 and SI Appendix). Thus, more generally, we anticipate the robustness of any composite interface will be proportional to a composite robustness factor A* of the form 1/A* ≈ 1/H* + 1/T* (see SI Appendix for derivation).

Increasing the magnitude of the robustness parameters (H* and T*) increases the magnitude of the robustness factor A*. Large values of this robustness factor (A*≫ 1) imply a robust composite interface, with a high energy barrier between the metastable composite interface and a globally equilibrated wetted interface. On the other hand, values of A* < 1 imply that the composite interface cannot maintain its stability against small pressure differentials across the liquid-vapor interface (see SI Appendix for more details).

To achieve both high apparent-contact angles and a robust composite interface, we seek to maximize the two design parameters D* and A* simultaneously. However, for the electrospun fibers, the two design factors are strongly coupled and inspection of Eqs. 1 and 2 confirms that increasing the value of D* = (R+D)/R (by increasing D or reducing R) for the electrospun fibers will lead to a decrease in the value of either H* or T*, thereby leading to lower values of A*.

For the microhoodoo geometry, on the other hand, the feature spacing-ratio takes the form of D* = ((W + D)/W)². The horizontal features (D and W) for the microhoodoo geometry (see Fig. 2B) are defined by dry etching, while the vertical features (R and H) are defined through isotropic etching. Thus, for this geometry, the design factor D* and robustness factor A* are only weakly coupled (see SI Appendix, Table S1), thereby enabling the hoodoo surface to attain both high apparent contact angles (high D*) and a highly robust composite interface (high A*), at the same time.

Engineering Omniphobic Surfaces.

Many natural surfaces, such as various plant leaves and bird feathers, inherently possess re-entrant surface texture, which enables them to support a composite interface with water and thereby exhibit superhydrophobicity. Herminghaus (26) first pointed out that the surface constituents of a number of superhydrophobic plant leaves, such as the common smoke tree (Cotinus coggygria) and wild cabbage (Brassica oleracea), are hydrophilic. Indeed, recent research has shown that even the wax covering the surface of the lotus leaf is slightly hydrophilic (37).

Even though the re-entrant texture on the lotus leaf's surface leads to large values of the robustness factor with water (A* ∼ 22 using D ∼ 5 μm, W ∼ 2.5 μm and ψ_min ∼ 60°), the corresponding values of the robustness parameters with organic liquids can be extremely small because of the low values of θ. As a consequence, hydrophobic lotus leaves and duck feathers (see Fig. 1B), are readily wet by low surface tension oils, such as rapeseed oil (γ_lv = 35.7 mN/m).

To enable the formation of a robust composite interface on these surfaces with various low surface tension liquids, it is desirable to increase the magnitude of A* through a simultaneous increase in magnitude of both the robustness parameters H* and T*. From Eqs. 1 and 2 it is clear that such an increase can be induced most readily by increasing the value of the equilibrium contact angle (θ).

A simple procedure that allows us to significantly lower the surface energy (and increase θ) of preformed surfaces possessing re-entrant curvature, without significantly affecting their surface texture, is dip-coating (see Methods). An example of an oleophobic surface resulting from this simple procedure is illustrated in Fig. 3A, which shows droplets of rapeseed oil on a duck feather that has been dip-coated in a solution of fluorodecyl POSS molecules (yielding θ* = 145° and A* = 4.3). The dip-coating process also enables the lotus leaf to display apparent contact angles greater than 140° with rapeseed oil (see SI Appendix). However, both the dip-coated lotus leaf (Fig. 3B) and duck feather are readily wetted by a lower surface-tension liquid, such as octane (γ_lv = 21.7 mN/m), because of the low values of A* = 0 and A* = 1.8, respectively. Because fluorodecyl POSS is one of the lowest surface energy molecules available (21), it does not appear possible to further increase the values of the robustness parameters, without modifying the inherent substrate morphology.

Fig. 3.

Imbuing oleophobicity to natural surfaces. (A) Droplets of rapeseed oil (γ_lv = 35.7 mN/m), colored with oil red O, on a duck feather dip-coated in a solution of fluorodecyl POSS. (B) Droplets of octane (γ_lv = 21.7 mN/m) on a lotus leaf dip-coated in a solution of fluorodecyl POSS. (C) Droplets of water (γ_lv = 72.1mN/m), methylene iodide (γ_lv = 50.1 mN/m), methanol (γ_lv = 22.7 mN/m), and octane (γ_lv = 21.7 mN/m) on a lotus leaf surface covered with electrospun fibers (beads-on-strings morphology) of PMMA + 44 wt% fluorodecyl POSS. A reflective surface is visible underneath all droplets, indicating the presence of microscopic pockets of air and the formation of a composite interface (21).

To provide stronger oil-repellency to these surfaces, a re-entrant textured coating that enables higher values of the robustness factor A* with almost any liquid is required. As an example of this approach, Fig. 3C shows droplets of various liquids on a lotus leaf surface coated with electrospun fibers. The beads-on-strings morphology and the high fluorodecyl POSS content provide the needed texture and low surface energy to enable the simultaneous enhancement of both the design parameters D* and A*, as discussed in the following section. Fig. 3C also shows that the electrospun coating displays extremely high contact angles with all liquids tested. We suggest the term “omniphobic” to define such surfaces that can support a composite interface with essentially all known liquids.

Optimizing the Design of Electrospun Surfaces.

By changing the mass fraction of fluorodecyl POSS molecules blended with PMMA, it is possible to systematically vary the surface energy of the blends between γ_sv = 10.2 − 34.2 mN/m (see SI Appendix for γ_sv measurements of all PMMA−fluorodecyl POSS blends). This variation in surface energy leads to a corresponding variation of the equilibrium contact angle, and thus affects both the robustness parameters H* and T* (and thereby A*).

Another approach for modifying the various design parameters is the alteration of the surface texture of the electrospun fabrics. Variations in the concentration of the PMMA plus fluorodecyl POSS solution from which electrospinning is performed produce different fabric morphologies (32), as shown in Fig. 4. A beads-only structure (see Fig. 4A) forms at low solute concentration, the beads-on-strings structure (see Fig. 4B) forms at moderate solute concentration, and the fibers-only structure (see Fig. 4C) forms at high solute concentration (see Methods). Because all three surfaces have the same fluorodecyl POSS concentration, they are expected to have similar surface energies. The advancing and receding contact angles for hexadecane on the beads-only surface are θ*_adv = 156° and θ*_rec = 150° (A* = 9 and D* = 13). Droplets of hexadecane roll off the surface at a tilt angle of about 5°. We are not aware of other superoleophobic surfaces that display such remarkably low hysteresis against a low surface tension oil like hexadecane. In comparison, the contact angles for hexadecane on the beads-on-strings surface are θ*_adv = 153°, θ*_rec = 141° (A* = 40 and D* = 9), while for the fibers-only surface they are θ*_adv = 153°, θ*_rec = 134° (A* = 18 and D* = 7).

Fig. 4.

Controlling the morphology of electrospun surfaces. (A–C) SEM micrographs of the various electrospun fabric textures for the PMMA + fluorodecyl POSS − 44wt% blend, produced by varying the concentration of the electrospinning solution. The insets show droplets (droplet volume V ∼ 2 μl) of hexadecane (γ_lv = 27.5 mN/m; θ = 80°) on each electrospun surface.

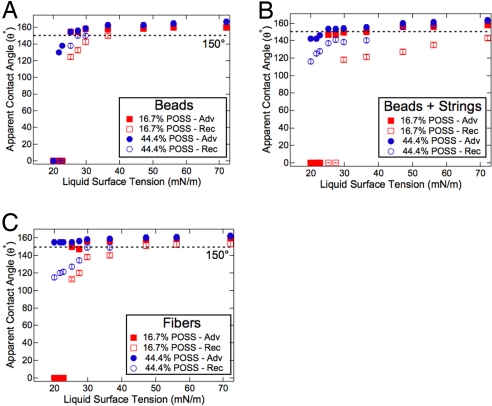
In Fig. 5 we show the apparent contact angles as a function of the liquid surface tension for all three electrospun surfaces. For each surface morphology, two different fluorodecyl POSS concentrations (corresponding to values of γ_sv = 14.0 and 11.1 mN/m) were tested. The various electrospun surfaces exhibit omniphobicity by supporting a composite interface and displaying high apparent-contact angles with liquids possessing a wide range of surface tensions. Furthermore, the contact angle hysteresis decreases and the apparent contact angles increase for all surfaces at higher concentrations of fluorodecyl POSS.

Fig. 5.

Omniphobicity of electrospun fabrics. The apparent advancing (filled symbols) and receding (hollow symbols) contact angles as a function of liquid surface tension for the beads-only, beads-on-strings, and fibers-only electrospun surfaces, respectively. The surfaces contain either 16.7 wt% or 44.4 wt% fluorodecyl POSS.

For the electrospun surfaces, there is a tradeoff between textures that display low hysteresis or high robustness, because the design parameters D* and A* are strongly coupled, as previously noted. In Fig. 5A we show that the beads-only morphology displays the lowest hysteresis with various liquids, as a consequence of the high D* values. However, the surface is not able to support a composite interface with any liquid possessing a surface tension below γ_lv ∼ 21 mN/m. In comparison, both the beads-on-strings and fibers-only surfaces containing 44.4 wt% POSS are able to support a composite interface, even with heptane (γ_lv ∼ 20.1 mN/m). Nevertheless, for both surfaces we observe significant contact angle hysteresis with low surface-tension liquids. Typically, the hysteresis obtained on the beads-on-strings surface was slightly smaller than on the fibers-only surface.

The Microhoodoo Geometry.

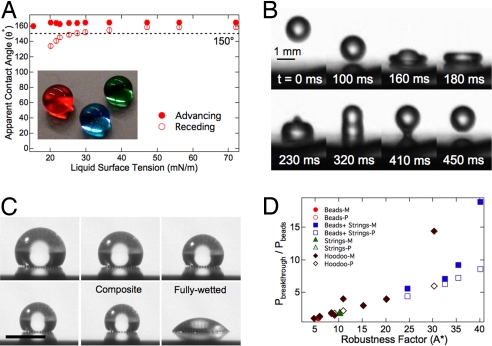
As described earlier, the structural parameters for the microhoodoo geometry— that is, the spacing (D), height (H), radius (R), and width (W) (see Fig. 2B)—can be controlled independently through photo-lithography. Here, we use the design parameters D* and A* to engineer omniphobic hoodoo surfaces that repel a wide range of liquids, possessing surface tensions between γ_lv = 15.1 mN/m (pentane) and γ_lv = 72.1 mN/m (water). Fig. 6A shows the apparent contact angle for a number of different liquids on SiO₂ microhoodoos with φ_s = 0.25, D = 10 μm, H = 7 μm, R = 0.15 μm, and W = 10 μm. After lithographic fabrication, the hoodoos were silanized through a vapor phase reaction with 1H,1H,2H,2H-perfluorodecyltrichlorosilane (see Methods) to lower their surface energy and correspondingly increase the magnitude of the design parameter A*. As an alternative to silanization, the hoodoo samples can also be dip-coated in a solution of fluorodecyl POSS to obtain similar results. These observations of exceptionally high contact angles with relatively low surface-tension liquids are a consequence of the high values of robustness factor A* for the silanized hoodoos (A* = 26 with pentane, the lowest surface tension alkane available in liquid form at atmospheric pressure).

An example of the extreme non-wettability and low contact angle hysteresis obtained on the silanized microhoodoo surfaces, even with relatively low surface-tension liquids, is shown in Fig. 6B. This series of images (see Movie S1) illustrates that a falling droplet of hexadecane (γ_lv = 27.5 mN/m) does not penetrate the silanized microhoodoo surface (same texture as in Fig. 6A, D* = 4 and A* = 38). Instead, the droplet rebounds off this surface, even though the corresponding equilibrium contact angle on a smooth, silanized wafer is θ ∼ 75°. The detailed dynamics of droplet rebound have been studied extensively for the case of a high surface-tension liquid like water (with θ > 90°) on superhydrophobic surfaces (38). However, such dynamic droplet repellency has not previously been demonstrated with low surface-tension liquids like hexadecane, for which the equilibrium contact angle θ < 90°.

Fig. 6.

Omniphobicity of microhoodoo arrays. (A) The apparent advancing and receding contact angles on a silanized microhoodoo surface. The inset shows droplets of heptane (red), methanol (green), and water (blue) on the microhoodoo surface. (B) A series of images obtained using a high-speed digital video camera that illustrates the bouncing of a droplet of hexadecane on a silanized microhoodoo surface. (C) A series of images (obtained over a period of 5 min), showing the evaporation of a droplet of methanol under ambient conditions, on a microhoodoo surface. (Scale bar, 1 mm). (D) A master curve showing the measured (filled symbols; denoted −M in the legend) breakthrough pressures for a number of microhoodoo and electrospun surfaces with various alkanes and alcohols, scaled with the breakthrough pressure of octane on the electrospun beads-only surface containing 44.4 wt% POSS, as a function of the robustness factor A*. Our predictions (hollow symbols; denoted −P in the legend) for the breakthrough pressures are also shown.

To provide a direct measure of the robustness of a composite interface on the microhoodoo surface, we evaluate the breakthrough pressure required to induce the transition from the Cassie-Baxter state to a fully wetted Wenzel state (5). For this measurement, a liquid droplet is placed on the silanized microhoodoo array and allowed to evaporate under ambient conditions. As the droplet evaporates, its radius decreases, and for droplets with radii significantly smaller than the capillary length of the liquid, the local pressure at the composite interface is given by the Young-Laplace relation, P(t) = 2γ_lv/R_drop(t).Fig. 6C exhibits a series of still images (see Movie S2) of a droplet of methanol (γ_lv = 22.5 mN/m, ℓ_cap = 1.7 mm, θ = 60°) evaporating on a microhoodoo surface with φ_s = 0.11, D = 20 μm, H = 7 μm, R = 0.15 μm, and W = 10 μm. The radius of the droplet, recorded just before it transitions to the fully wetted state, is used to compute the breakthrough pressure.

SI Appendix, Table S2 provides the breakthrough pressures with octane, as well as the values of the corresponding design parameters (D*, T*, H*, and A*) for each of the microhoodoo surfaces we synthesized. Certain microhoodoo surfaces can support a composite interface, with droplets having a radius as low as 30 μm, corresponding to a breakthrough pressure of ∼ 1,400 Pa. This result represents the upper limit of our measurement capability because of the fact that at this point the octane droplet is sitting on only two individual hoodoos, with W = 10 μm and D = 5 μm. Thus, the actual breakthrough pressures for these surfaces are expected to be even higher. This value of the breakthrough pressure corresponds to the pressure (ρgh) exerted by a column of ≈200 mm of octane, and illustrates the high robustness of the composite interface supported by the microhoodoos. Even higher breakthrough pressures can be achieved at the same values of D* (or apparent contact angles) with the microhoodoo geometry by simultaneously shrinking the hoodoo width (W) and spacing (D). In comparison, for the electrospun surfaces, a column of octane of height ∼ 20 to 50 mm provides sufficient pressure difference to breakthrough the composite interface.

In Fig. 6D, we plot the breakthrough pressures as a function of the robustness factor A* for a number of microhoodoo and electrospun surfaces with various alkanes and alcohols. The measurements are scaled with the measured breakthrough pressure of octane on the electrospun beads-only surface containing 44.4 wt% POSS (P_beads = 60 Pa). The predictions for the breakthrough pressure for each surface are calculated as P_breakthrough = A* × P_ref. All of the breakthrough-pressure data for the various surfaces approximately collapses onto a single curve. This observation that the breakthrough pressure varies directly with the robustness factor A* demonstrates the utility of the robustness parameters in the design and ranking of the performance of various nonwetting surfaces.

Conclusion

We have demonstrated that it is possible to engineer textured surfaces that repel a range of polar and nonpolar liquids, through appropriate combination of re-entrant curvature and suitable alteration of the solid surface energy. The presence of re-entrant surface texture can lead to a local minimum in the free-energy landscape and allow for the establishment of a metastable Cassie-Baxter state, even with relatively low surface-tension liquids. However, in practice, a surface possessing re-entrant texture may not support the desired composite interface if the breakthrough pressure required to induce the transition to the fully wetted interface is very small. Evaluating the magnitude of two design parameters, H* and T*, with a particular contacting liquid enables an a priori estimation of the robustness of a composite interface, thereby aiding the rational design of the solid surface texture that imbues maximum stability (highest breakthrough pressure) to the composite interface. Simultaneous enhancement of the two design parameters D* and A*, through the independent control of the surface chemical and topological features, allows us to engineer a range of omniphobic surfaces that display extremely high apparent contact angles and support a robust composite interface with all liquids tested. In principle, these design parameters can also be applied to study surfaces possessing multiple scales of roughness (26, 39–41). Even though the development of an exact form of each individual design parameter for such surfaces might prove challenging, it is clear that the presence of multiple scales of roughness enables the simultaneous enhancement of the spacing ratio D* and both the robustness factors H* and T*. This helps rationalize why surfaces, such as the lotus leaf, can display both high apparent contact angles and an extremely robust composite interface with relatively high surface-tension liquids, like water.

Methods

Electrospinning.

Both the polymer and fluoroPOSS were dissolved in a common solvent Asahiklin AK-225 (Asahi Glass Co.). The solution concentrations for producing the beads-only, beads-on-strings, and fibers-only surfaces were 2 wt%, 5 wt%, and 7.5 wt%, respectively. The various solutions were then electrospun using a custom-built apparatus as described previously (30), with the flow rate, plate-to-plate distance, and voltage set to 0.04 ml/min, 25 cm, and 20 kV, respectively.

Microhoodoo Fabrication.

Four-inch test grade p-type silicon wafers were purchased from Wafernet, Inc. A 300-nm thick silicon dioxide thin film was first deposited on piranha-cleaned silicon wafer, by PECVD. Cap geometries were defined via standard photolithography using OCG825 as the photoresist. Cap patterns were then transferred onto silicon dioxide using CF₃ plasma reactive ion etching (RIE). Etch depth was set to 400 nm to expose the bare silicon surface. The caps were then released in a manner designed to result in severe re-entrance using vapor-phase XeF₂ isotropic etching. The cap thickness (2R) was kept at ∼ 300 nm.

Microhoodoo Silanization.

The silane treatment was carried out by a chemical vapor deposition of 1H,1H,2H,2H-perfluorodecyltrichlorosilane. Samples were placed in an oven together with the silane and heated at 140 °C for 30 min.

Dip Coating.

The samples were immersed in a solution of 3 wt% fluorodecyl POSS in Asahiklin − AK225. The samples remained in solution for 5 min, after which they were removed and dried in an oven at 60 °C for 30 min.