The processing of feature discontinuities for different cue types in primary visual cortex

Abstract

This study examines whether neurons in the primary visual cortex (V1) of the cat (also referred to as area 17) are sensitive to boundaries that are delineated by a difference in features other than luminance contrast. Most research on this issue has concentrated on the responses to texture borders (e.g. ‘illusory contours’) and has found neurons that are sensitive to such borders in V2 and to a lesser extent in V1. Here neurons in cat area 17 (V1) were exposed to borders that were oblique to the orientation preference of the neuron and that were created by differences in phase, orientation or direction of motion of two drifting sinewave gratings. Nearby phase borders evoked increased firing in 15 out of 98 neurons, orientation borders in 18 out of 98, and direction borders in 15 out of 70 neurons recorded in area 17 (V1) of anesthetized cats. The firing rates of these neurons were enhanced when a feature border was presented close to their receptive field, partly independent of the cue involved. Control experiments with a contrast border showed that the enhanced firing was due to a release of suppression rather than facilitation. A conceptual model is presented that can describe the data and uncovers a peculiarity of the phase domain compared to the orientation and direction domain. The model unifies the knowledge gained here about orientation-specific center-surround interactions, contextual effects, and end-stopping. The data and model suggest that these phenomena are part of a single mechanism that enables the brain to detect feature discontinuities across a range of features.

1. Introduction

Objects in natural images are most commonly segregated from their surroundings by luminance borders. However, borders defined by characteristics other than luminance may also serve to define boundaries. For example, an abrupt change of phase, orientation or direction of movement of a texture in an image is also perceived as a border. Humans, monkeys, and cats are easily able to detect texture borders (Wilkinson, 1986; Lamme, 1995), so it is not surprising to find interactions between center and surround regions of receptive fields that seem required for the detection of such feature discontinuities in neurons in the primary visual cortex (Nelson & Frost, 1978; Knierim & Van Essen, 1992; Sillito et al., 1995; Levitt & Lund, 1997; Sengpiel et al., 1997; Kastner et al., 1997; Li et al., 2000, Walker et al., 2000).

These center-surround interactions, in primary visual cortex (V1), are thought to form a first stage in the process of detecting feature discontinuity. In their model of the neurons they discovered in primate V2 that detect ‘illusory contours’, von der Heydt and Peterhans (1989) proposed that the ‘end-stopped’ neurons in V1 form the first stage of processing by detecting the ends of texture line segments. Similarly, Sillito et al. (1995) proposed that the contextual effects they found in monkey V1 represent an early stage in the detection of borders created by orientation discontinuities. On the other hand, neurons in V2 have been found that signal the orientation for different kinds of texture borders regardless of the cue type (Leventhal et al., 1998; von der Heydt et al., 2000; Marcar et al., 2000; Song and Baker, 2007).

However, so far it is not clear to what degree V1 is involved in detecting texture. One possibility is that neurons in V2 combine all possible cue differences (i.e. separate phase, orientation and direction discontinuity detectors) arising from their feedforward inputs from V1 while simultaneously detecting the orientation of the texture border. Another possibility is that part of the cue-invariance is already achieved in V1 for example by means of intra-cortical interactions that result in discontinuity detecting neurons, which leaves V2 neurons mainly with the task of combining the outputs of these V1 detector cells in order to calculate the orientation of the texture border.

This study was motivated by the idea that the latter circuit construction might be more efficient, because it reduces the required complex convergence of feedforward inputs from V1 to V2 and takes advantage of intra-cortical connections in V1. The hypothesis was that V1 contains neurons that are not only the pre-processing stage for illusory contours (i.e. abutting line gratings), but for any kind of border defined by a feature discontinuity. In other words, can cells in V1 detect local changes in features independently of the specific cues that determine a feature border?

The ‘feature border stimuli’ used in this study of cat V1 consisted of two abutting patches of drifting gratings, one of which was presented at the optimal orientation, direction, and spatial and temporal frequency for the neuron and the other, separated by an oblique illusory border, was at the same temporal frequency and contrast, but differed in either orientation, direction of motion, or phase of the grating. To test at what distance to the receptive field the contextual effects operate, the position of the border was moved relative to the receptive field. Other studies have investigated the effects of border stimuli on the responses of neurons in V1 of anesthetized or awake animals in a similar setup (Lamme et al., 1999; Nothdurft et al., 2000; Rossi et al., 2001). The novelty of this present approach lies in recording responses to different kinds of feature borders in the same neuron to see if single neurons in V1 are sensitive to a range of different feature boundaries. The results show that about 20% of all cells tested are sensitive to the presence of the feature border. The comparison to responses to a contrast border stimulus indicates that the enhanced spike discharge seen in these cells is most likely due to a release of suppression. Significantly, this release of suppression was seen for borders created by all the different features.

2. Results

Data were obtained from 98 neurons in area 17 (V1) of 10 cats. The illusory borders presented as stimuli were defined by feature discontinuities, not luminance. These feature discontinuities in phase, orientation, and direction of motion created what are collectively referred to here as ‘feature borders’ (see Fig. 1).

Figure 1. Stimulus setup.

The black rectangles depict the minimal response field of the neuron. The control grating (1st row) was a drifting sinusoidal grating of preferred orientation and spatial and temporal frequency. The stimulus size was 15 - 20 degrees of visual angle in width and height. For the border stimuli the orientation of the border was always 45 degrees from the preferred orientation of the neuron. The position of the stimuli was shifted relative to the receptive field along the axis orthogonal to the orientation of the border (x-axis in figure). The arrows depict the drifting of the sinusoidal gratings.

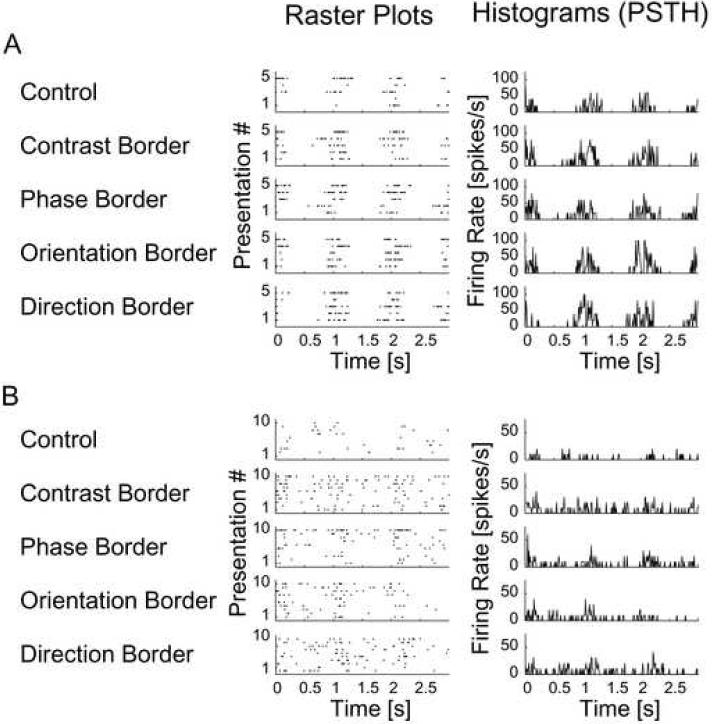
When single neurons were presented with these stimuli, two broad groups of responses were seen. One group of neurons showed enhanced firing rates, while the other group showed only decreased responses compared to the control response measured with a large-scale grating without a feature border. Fig. 2 shows the responses of two cells that were sensitive to feature borders. Fig. 2A shows the responses of a simple (S) cell and Fig. 2B shows the responses of a complex (C) cell. When feature borders were presented close to their receptive fields, the responses of these two neurons were stronger than when presented with the control grating, which lacked a border. In Fig. 2A, the contrast border, which presents a zero contrast to part of the surround, elicited a stronger response than the control. However, the stimuli for the phase, orientation and direction borders also have a contrast stimulus in the surround, yet the response is enhanced almost as strong as that of the contrast border. A similar pattern is seen for the complex cell in Fig 2B, the only difference being that the response is static rather than phasic in time, a defining feature for the definition of complex cells.

Figure 2. Increased responses of an S-cell (A) and a C-cell (B) to border stimuli compared to the control stimulus.

Raster plots show spike events for 5 and 10 presentations of the same stimulus respectively. Each presentation consisted of 3 cycles of the drifting sinusoidal grating. The PSTHs show the mean firing rates over presentations within each 10 ms bin. In this figure, data is shown for only one identical position for the feature borders (−2 degrees of visual angle (dva) for the S-cell, which had a minimal response field length of 0.5 dva and width of 0.9 dva; −1.2 dva for the C-cell, which had a minimal response field length of 1.1 dva and width of 0.9 dva). It can be seen that the responses to the border stimuli (rows 2 - 5) are stronger than to the control grating (first row) for both the S-cell and the C-cell.

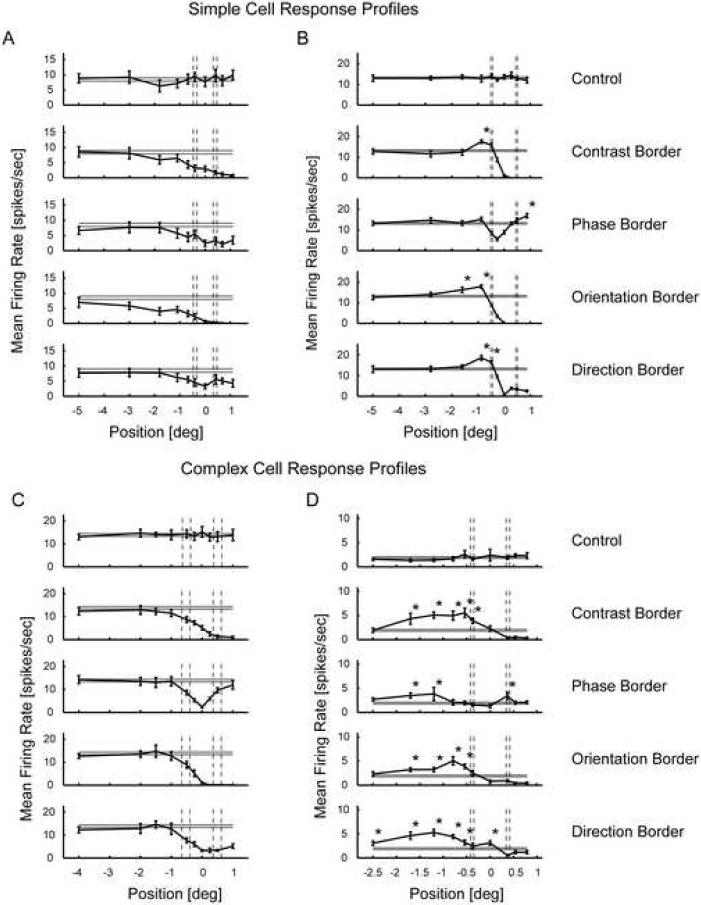
To determine the spatial extent of the border influences, the responses to the different types of feature borders presented at varying positions relative to the receptive field were recorded. This provided a response profile for each neuron, which showed how the firing was modulated over positions for the different border types. Such response profiles are shown in Figs. 3A and C for two other example neurons that did not show the feature border sensitivity, together, for comparison, with the profiles for two neurons that did (Fig 3 B and D). Fig. 3A shows the response of a neuron classified as a simple cell with two subfields. This neuron's response to the border stimuli was in accord with that expected from a receptive field that acts mainly linearly, e.g. like a Gabor filter with an activity threshold. It decreases as the optimal grating is moved away from the receptive field. The firing rate starts decreasing below the control firing rate before it reaches the minimal response field border, depicted with dashed vertical lines, because this particular cell has a high threshold and therefore exhibits length summation outside of the minimal response field. The minimal response field is measured by moving a bar into the receptive field. When a cell has a high threshold the cell gets activated only when the bar is moved far into the field and therefore the minimal response field appears smaller than the receptive field measured by increasing the length of the stimulus (see for example Henry et al., 1978). For the phase border the response would increase back to control level if more ‘positive’ positions had been measured, as seen for example in panel C. Note that there was no significantly enhanced firing rate compared to the control stimulus presentation (two-tailed t-test, α = 0.05, see 4.4 Data Analysis for more details). This is in marked contrast to the simple cell illustrated in Fig. 3B, where there is clearly a different profile of spatial sensitivity. The firing is enhanced when the border is at a particular distance from the receptive field, and even though the position at which this occurs is different for the phase border than for the other three borders, the occurrence of the enhancement per se is independent of border type. What is noteworthy is that enhanced firing occurs also with the contrast border, where the feature border is created by the intersection of the grating and a uniform grey field. A complex cell (Fig. 3C) shows a Gabor-filter type pattern of response, whereas the complex cell shown in Fig. 3D, shows the enhanced response relative to control for all the border stimuli, including the contrast border.

Figure 3. Response profiles of two simple (A and B) and two complex cells (C and D).

Profiles show the mean and standard errors of responses of example neurons to the control and the border stimuli at varying positions. The dashed vertical lines show the approximate extent of the ‘minimal response field’. Panel A shows the response profile of a simple cell that corresponds to the profile expected for a Gabor filter. Panel B shows the response profile of another simple cell with significantly increased firing rates at certain positions of the border stimuli (two-tailed t-test, α = 0.05, see 4.4 Data Analysis for more details). Significant measurements above control level are labeled with an asterisk. Panel C shows a response profile of a complex cell without any responses above control level. Panel D shows the response profile of a complex cell with significantly increased firing rates at several positions for all border stimuli.

The ‘dip’ in response for the phase border prominently seen in panel B and C around position zero can be explained by the antagonistic behavior of subfields: when the phase border splits the receptive field in half, one side excites the neuron while the other side inhibits it at any time in the cycle. The same explanation holds for the complex cell, if the receptive field can be approximated by any sum of simple receptive fields (see Model Results for more explanation).

Twenty-six out of 84 (31%) of the neurons showed a significantly enhanced firing rate for the contrast border, 15 out of 98 (15%) for the phase border, 18 out of 98 (18%) for the orientation border, and 15 out of 70 (21%) for the direction border (two-tailed t-test, α = 0.05, see 4.4 Data Analysis for more details). The peak of the firing rate was up to 50 times higher than in the control case for the contrast border and up to 20 times higher for the other border stimuli. Quantitatively (see below), the effect was consistently larger for the contrast border stimulus than for the other feature borders. Since the mean luminance in the contrast border stimulus could not have exerted any facilitation (it does not increase neuronal activity sustainably), we interpret the enhanced firing rate as release from suppression induced by the grating in part of the surround. This interpretation motivates our further analysis and is discussed more fully below.

Strength of Enhancement of Firing

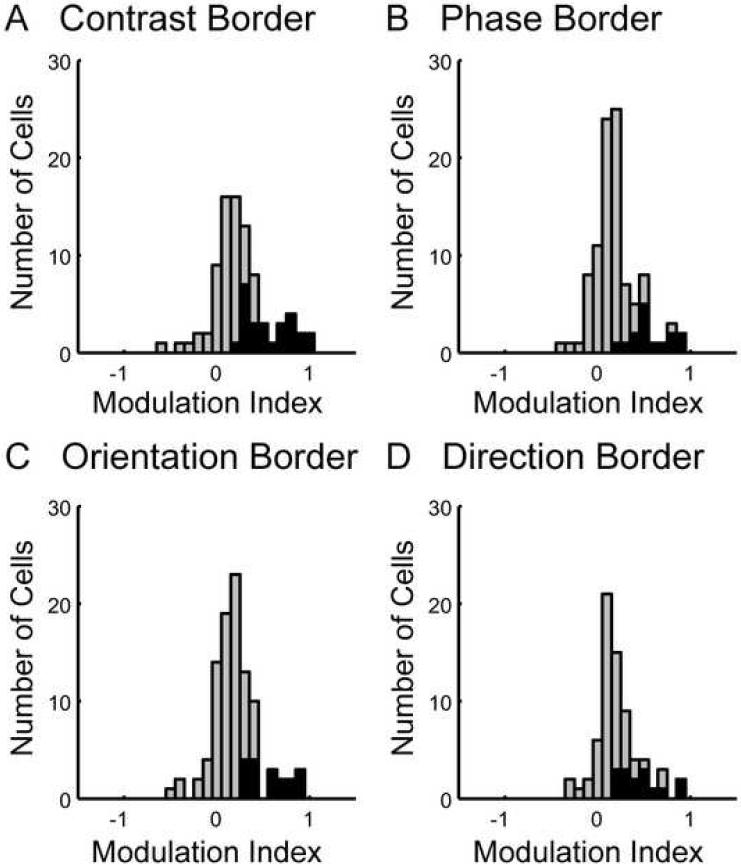
The strength of the firing enhancement was quantified with a modulation index, which was defined as the difference between the maximal response over positions and the control firing rate, divided by the maximal firing rate (see 4.4. Data analysis). The maximal response firing was assessed for each border type independently and might therefore be measured at different positions of the border. The form of this index is motivated by the interpretation that the enhanced firing rate is due to a release of surround suppression. A value of 1 means no response to the full-field control grating, or presumably 100% suppression in the control case, and zero means no difference between control and feature border responses or presumably no suppression and therefore no release of suppression with the feature border stimuli. Negative values are not expected (because the maximum response should be at least as large as the control rate) but can occur due to variability of responses. Fig. 4 shows histograms of the modulation indexes obtained for each border stimulus. All the modulation indexes for cells with significantly enhanced firing rates were between 0.15 and 1. The neurons with modulation index close to 1 showed virtually no response in the presence of a uniform grating, but did respond when a feature border was presented close to the receptive field.

Figure 4. Histograms of modulation indexes.

The histograms show modulation indexes (see 4.4 Data Analysis for definition) of all neurons for the contrast border (panel A), phase border (panel B), orientation border (panel C) and direction border (panel D). Modulation indexes of neurons with significantly enhanced firing rates (see 4.4. Data Analysis or figure 3 for details about the significance test) for at least one position of the corresponding border stimulus are drawn in black, all others in grey.

Comparison across Border Stimuli

A key question was whether neurons are able to signal the local discontinuities across the range of feature borders. In other words, do the modulations of responses to the different border stimuli occur in separate subpopulations, or do the various feature borders tend to evoke the same response in the same neurons? A chi-square analysis of the 4D contingency table of combinations of significant effects elicited by the four different border stimuli showed that there are indeed strong interactions between those effects. The number of neurons showing all four effects (6/70) was significantly higher than what would have been expected if they were mutually independent. Because the proportion of cells showing a significant effect for each border type was between 0.15 and 0.31, the expected proportion of cells showing all effects given that the effects are independent is the multiplication of those four proportion which equals 0.0026. The expected number of cells is therefore 0.2 neurons out of 70 and to find 6 out 70 is a highly significant result: the probability that the four effects are mutually independent of each other is smaller than 10⁻⁶. Additionally, testing the 2D contingency tables for each pair of effects showed that each pair is non-independent: the expected number of cells showing two of the effects was around 5, whereas the observed occurrence was at least twice as big (p < 0.001, chi-square analysis). This shows that all four effects tend to occur in the same subpopulation of neurons and suggests that these neurons show a high degree of cue-invariance of the modulation index.

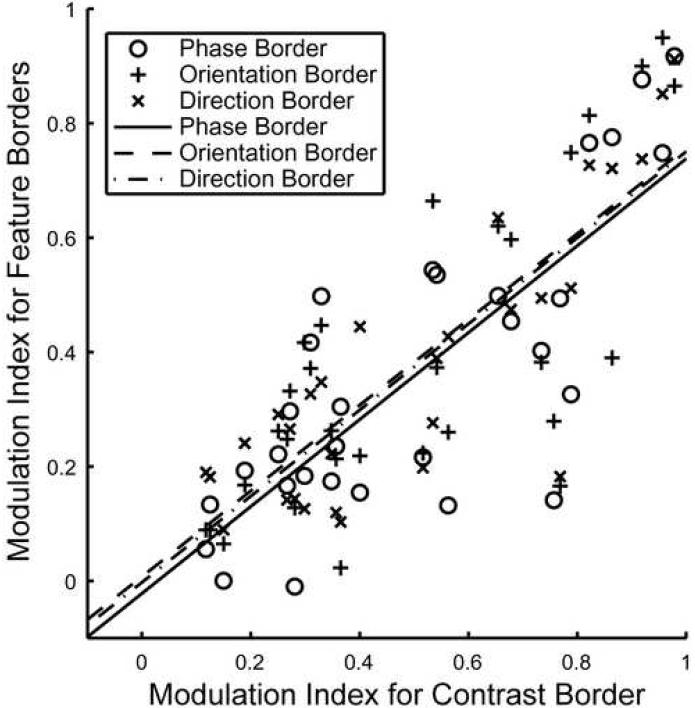
Further quantitative support for the idea of a subgroup of neurons that can detect feature borders independent of the cue is shown in Fig. 5, which shows the modulation indexes for the three feature borders (phase, orientation, and direction) plotted against the modulation indexes for the contrast border for all neurons that showed at least one significant effect (N = 30). There was a high correlation between the different modulation indexes across neurons. To make sure that these correlations are not due to measurement errors of the control response that was used to compute all modulation indexes, the control trials were randomly divided into four equal parts and for each different kind of border stimulus, a non-overlapping one-quarter was used. Using these subsets makes the indexes for the different modulation indexes entirely independent measurements and therefore any correlation among them, across cells, reflects physiology. We quote average correlation coefficients resulting from repeating this random subdivision 1000 times. Between the phase border and the contrast border, the resulting Pearson product-moment correlation coefficient was 0.72. For the orientation border it was 0.69 and for the direction border 0.77. All of these correlation coefficients were highly significant (p < 10⁻⁴, t test). The slopes of the least square straight line fits were 0.76, 0.75, and 0.75 for the phase, orientation, and direction border versus the contrast border. These regression lines were not significantly different from one another (p = 0.70, F-test on the pooled regression, see 4.4. for details), suggesting that the modulation indexes were independent of cue for phase, orientation, and direction borders, i.e. one could not tell which of the three border types was shown to a neuron by measuring the modulation index for that feature border. The common regression for pooled border stimuli had a slope of 0.75 and the intercept was at -0.01. This shows quantitatively that the effect was largest for the contrast border stimulus and hence that the effects were most probably due to a release of suppression and not facilitation. One can infer from the slope that the feature border stimuli released around 75% of the suppression that was released in response to the contrast border.

Figure 5. Comparison of modulation indexes.

Marks show the modulation indexes for the contrast border versus the modulation index for the feature borders (○ for phase border, + for orientation border, * for direction border) for all neurons (N = 30) that showed at least one significant effect (see 4.4. Data Analysis or figure 3 for details about the significance test). Lines represent the least square straight-line fits (slope = 0.76 for phase border, solid line; 0.75 for orientation border, dashed line; 0.75 for direction border, dashed-dotted line).

The modulation indexes for the phase, orientation and direction border were also highly correlated. The correlation between the modulation indexes for the phase border and the orientation border was 0.71, for the phase border and direction border 0.73, and for the orientation and direction border 0.73. This high correlation between all effects is an indication that they could well be due to the same mechanism. All possible combinations of modulation indexes between the phase, orientation and direction borders were fitted with least square line fits. All these regression lines were not significantly different from 1 (a = 0.05, corrected for multiple comparisons), again confirming the common pattern of response to the feature borders created by phase, orientation and direction.

The positions at which the maximal firing rate occurred for the different stimuli were not significantly different for the different border stimuli across the 30 neurons that showed significant effects (ANOVA test). There was also no significant correlation of peak position across border type. So even though the enhancement peaks at different positions for different border stimuli in certain cells (for example Fig. 3D) and at the same position for most border stimuli in other cells (for example the neuron in Fig. 3B), no statement can be made about the significance of either of these examples.

End-Stopping

The effects described above are related to the phenomenon of ‘end-stopping’. For example, the effect of the contrast border stimulus is to release the neurons from suppression by not activating one ‘end-zone’ of the receptive field. To examine this relationship, 71 neurons were additionally tested with bars of varying lengths. The bars were centered on the receptive field so possible asymmetries in the strength of the end-zone inhibition were not detected.

The degree of end-stopping was assessed with a modulation index analogous to that used for the border stimuli. The response to the optimal length corresponded to the maximal firing rate for the border stimuli, and the response to the longest bar shown corresponded to the control. The modulation index for the end-stopping protocol was therefore the difference between the response to a bar of optimal length and the response to a longer bar divided by the response to the optimal length, directly measuring the amount of suppression in the end-zones of the receptive field. Significant end-stopping was found in 18 (25.4%) neurons of the 71 neurons tested (two-tailed t-test, α = 0.05).

A contingency table analysis showed that border effects and end-stopping do not occur independently: 12 of 51 neurons tested for all feature borders and end-stopping showed both effects, while one would expect only 7 by chance. Of 16 neurons that were end-stopped, 12 (75%) also showed a border effect. This co-occurrence of end-stopping and border effect was significant (p < 0.01, chi-square analysis).

This relationship is also confirmed by an analysis of the modulation indexes for end-stopping in neurons that show a border effect versus neurons that do not. The distributions are significantly different from each other (Wilcoxon rank sum test, p = 0.05). The median modulation index of end-stopping is 0.12 for neurons showing no significant border effect and 0.41 for neurons showing a significant border effect.

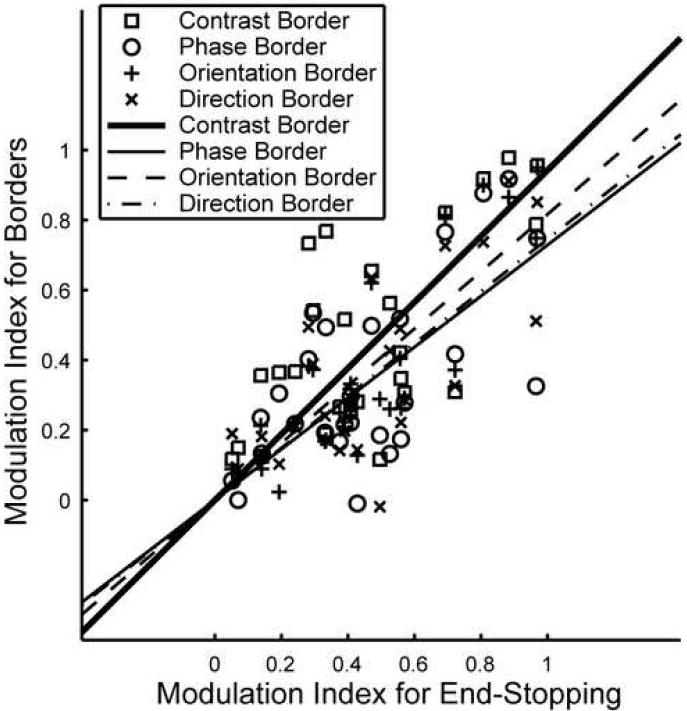
Fig. 6 shows the modulation indexes for the border stimuli plotted against the modulation index for end-stopping for all neurons that showed at least one significant effect (N = 27). The correlation between the modulation indexes for contrast border and end-stopping was 0.67. For the phase border the correlation was 0.84, for the orientation border 0.83, and for the direction border 0.85. All these correlations were highly significant (p < 0.0001, t-test). This shows that the effects of the border stimuli are highly related to the strength of suppression produced by end-stopping. The slopes of the regression lines were 0.94 for the contrast border, 0.73 for the phase border, 0.82 for the orientation border, and 0.75 for the direction border. This means that the effect is smaller for the border stimuli than for end-stopping

Figure 6. Comparison of end-stopping and border effects.

Marks show the modulation indexes for end-stopping versus the modulation index for the border stimuli (□ for contrast border, ○ for phase border, + for orientation border, * for direction border) for all neurons (N = 27) that showed at least one significant effect. Lines represent the least square straight-line fits (slope 0.94 for contrast border, thick solid line; 0.73 for phase border, solid line; 0.82 for orientation border, dashed line; 0.75 for direction border, dashed-dotted line).

Histological Data and Cell Classification

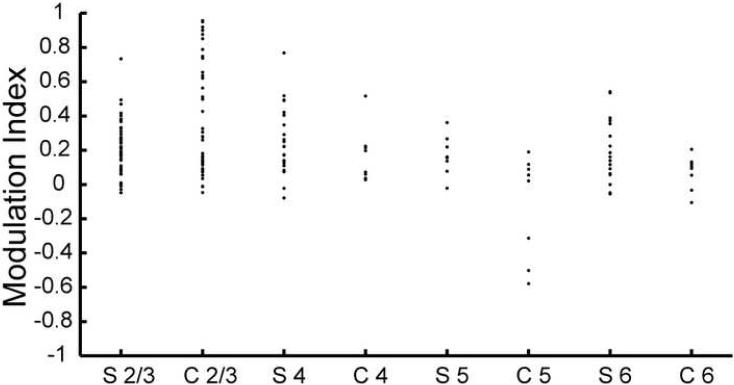
The laminar position of 42 cells was determined using individual pontamine sky blue labeling of the recording site. All recorded neurons were in the medial bank or on the crown of the gyrus in area 17. Of the cells with identified laminar locations, 24 were classified as simple cells (S-cells) and 18 as complex cells (C-cells). A three-way unbalanced ANOVA for cell type, layer, and type of border stimulus, comparing the modulation indexes across these three factors, showed that there was no dependency on the border type, but there was a dependency on the layer, and there was an interaction between cell type and layer (p < 0.05). As a result, the differences in modulation for all combinations of layers and cell types were tested. The non-parametric Kruskal-Wallis test was significant (p < 0.05), and a non-parametric multiple comparison according to Dunn showed that the modulation indexes were significantly larger in layer 2/3 simple cells, layer 2/3 complex cells, and layer 4 simple cells than in layer 5 complex cells. Fig. 7 shows the population of modulation indexes for each combination of cell type and layer. The median modulation index (after pooling all border types together) for layer 2/3 simple cells was 0.21, for the layer 2/3 complex cells it was 0.17, for the layer 4 simple cells 0.22, and for the layer 5 complex cells 0.04, whereas the overall median was 0.17. In accordance with the ANOVA test, a direct comparison of simple and complex cells did not reveal any significant difference of modulation strength between the cell types (Wilcoxon rank sum test, p = 0.05). The median modulation index was 0.19 for simple cells and 0.13 for complex cells.

Figure 7. Strength of suppression in different cell types and layers.

The modulation indexes (averaged over border stimulus type) of all neurons with known laminar position (N = 42) grouped into combinations of cell type and layer. ‘C’ stands for complex cells, ‘S’ for simple cells, ‘2/3’, ‘4’, ‘5’ and ‘6’ for layers.

Gabor Filter Model

Skottun (1994) previously suggested that linear filter theory could explain the responses to illusory stimuli. Because such stimuli have energy in the Fourier-spectrum around the orientation of the feature borders, the border stimuli used in this study could also lead to such effects. Additionally, if the orientation tuning and or spatial frequency tuning of the neuron was not estimated precisely enough, there possibly is even more Fourier energy in the range of the receptive field filter. In order to exclude the possibility that the apparent contextual effects observed in this study could be explained by linear filtering, a model was used based on single Gabor filters (see 4.5. Modeling) and their responses to the border stimuli was explored. The results can be briefly described: although enhanced firing rates do occur in certain situations with the Gabor filter model, it fails to explain the relationships between the modulation indexes for different border stimuli. Although for the orientation border, some cases of modulation indexes correspond to the experimentally observed relationship to the modulation index for the contrast border, the model predicted that for the phase and direction border the strength of the enhancement is always larger compared to the contrast border than observed experimentally. This is due to the fact that the energy in the Fourier-spectrum along the orientation of the border is bigger for the phase and the direction border than for the contrast border. These results indicate that a model of a single Gabor filter cannot explain the experimental observations even if one anticipates imprecision in measurement of the receptive field's spatial dimensions and tuning properties, due to hand-plotting or other technical hurdles.

Conceptual Model of Surround Suppression

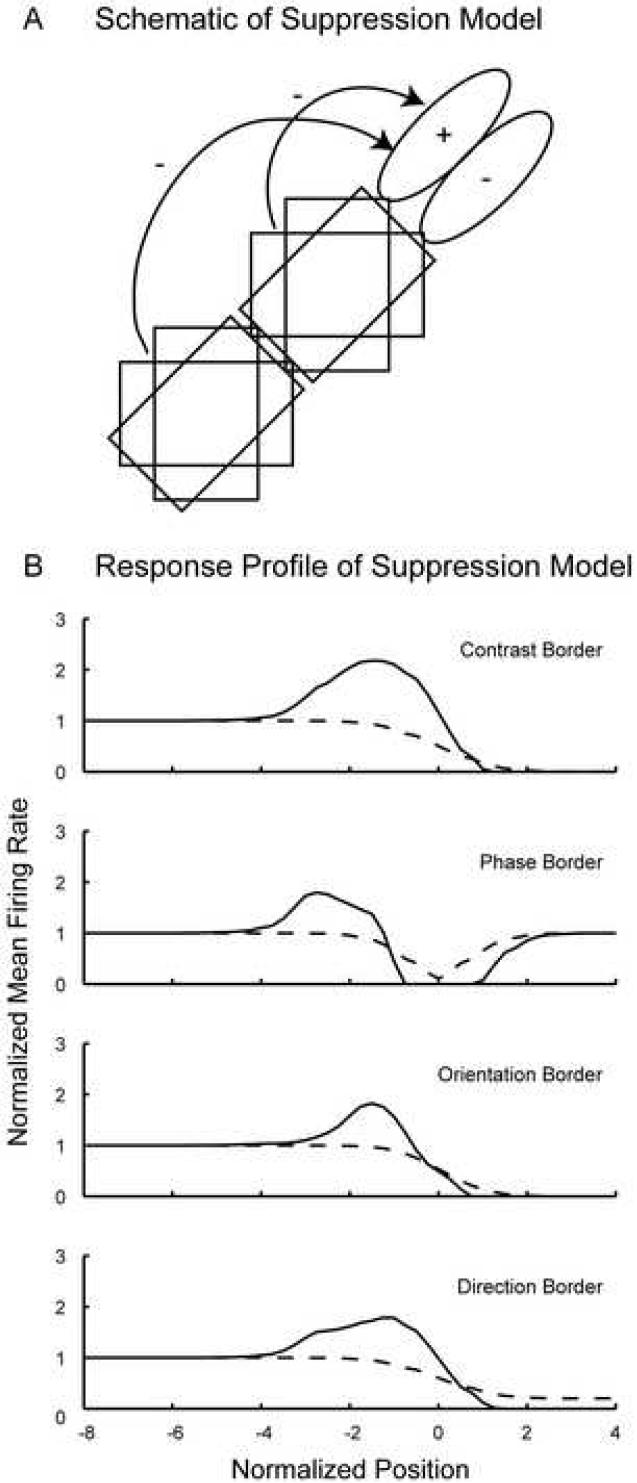
Since the Gabor filter model could not explain the experimental findings, a more elaborate version of the model was developed that could qualitatively explain the response profiles of neurons to the border stimuli, including the relative strengths of the responses to the different border stimuli. The basic model chosen was similar to one previously suggested for end-stopping, i.e. inhibition comes from the neurons with receptive fields neighboring the receptive field of the target neuron (Hubel & Wiesel, 1965). The question is about the form and arrangement of the receptive fields of the inhibitory neurons. To simplify the conceptual model, all receptive fields were modeled as Gabor filters. The target neuron was suppressed by one or more neurons with receptive fields at other positions in visual space. The model was extended from one to several neurons and tested various sets of parameters for the suppressive neurons until a configuration was found that could describe the experimental data. The model was developed systematically by adding one neuron or symmetrical groups of neurons in order to find the basic elements required. Fig. 8 shows the simplest conceptual model that could account for the experimental data. In this case, the target neuron was inhibited by 12 cortical neurons as shown in Fig. 8A. The corresponding response profile shown in Fig. 8B displays enhanced firing rates close to the border stimuli when the surround is turned on (solid line), but not when the surround is turned off (dashed line). Because the analysis of the experimental results in this paper is based on the comparison of responses to that to the control grating stimulus, the model responses were normalized to the control response. The response value is therefore 1 when the optimal grating is on top of the receptive field (most negative positions). When the surround is turned on, part of the surround suppression is released when the contrast, orientation, or direction border moves such that part of the non-optimal grating is impinging on the receptive field. For the phase border, some suppression is released when the phase border lies on top of the suppressive receptive fields in the surround as will be discussed in more detail later. The strength of the surround suppression was adjusted such that the relative strength of the effects of the different kinds of borders corresponds to the experimental observation shown in Fig. 5: The modulation index was biggest for the contrast border (0.54), and similar for the phase border (0.44), the orientation border (0.45) and the direction border (0.45). However, the specific weights used computing the suppression in this model are physiologically meaningless, as the true number of suppressive cells in the surround and the distribution of their receptive fields is unknown. This adjustment was done in order to show that in principle the relative strengths of the effects can be achieved, which is not possible with the Gabor filter model.

Figure 8. Suppression model.

Panel A shows a schematic of the suppression model. The target neuron modeled as a Gabor filter is suppressed by six pairs of Gabor filters, representing suppressing neurons in the surround. Each pair consists of two Gabor filters with opposing phase preference. A group of three pairs has receptive fields at two different distances to the target neuron's receptive field. Each group consists of one pair with the same orientation preference as the target neuron and two pairs preferring oblique orientations (see 4.5. Modeling for more details). The solid line plot in panel B shows the normalized response profile of the model target neuron to border stimuli, whereas the dashed line is the response of the target neuron without the surround turned on.

Interestingly, each suppressive neuron had to have a counter-part with opposite phase selectivity. Although, intuitively, it seems as if the suppression would have to be phase selective in order to explain the effect with the phase border, the effect of the phase border would be too strong relative to the contrast border effect. The reason is that the suppressive neurons themselves are inhibited when the phase border is on top of their receptive fields. This ‘dip’ in the response can for example be seen in Fig. 3C, for a complex cell without surround suppression. This inhibition is readily explained by a Gabor filter response (or a sum of such filters for a complex cell) and is due to the antagonistic behavior of subfields: when an on- and an off-field are activated on one side of the phase border, they are at the same time inhibited on the other side of the border, because of the phase shift of half a cycle. In Fig. 8 the same ‘dip’ can be seen for the Gabor filter model without the surround turned on (dashed line). The suppressive neurons experience this ‘dip’ of their response when the phase border is on top of their own receptive field, therefore releasing the target neuron from suppression when the phase border is close to its receptive field.

The population of suppressive neurons was best implemented by neurons with similar preferred orientations and similar direction selectivity. If the tuning was exactly identical to the target neuron, the effect was too strong for the orientation and direction border compared to the contrast border. The suppressing neurons had to be at two different distances to the target receptive field. If not, the effect of the phase border was too large. This is because the response of a suppressing neuron is itself suppressed below spontaneous firing when a phase border is located in its receptive field.

In the suppression model shown in Fig. 8 the suppressive neurons are located in the end zones. However, the same qualitative result was obtained when the suppressive neurons were placed in the side zone or at oblique positions or all around the classical receptive field (data not shown). Because the strength of release of suppression in this study was measured to be just as strong in complex cells as in simple cells, the model was also extended to a complex cell model. Each receptive field was modeled by the sum of the squared outputs of two phase-shifted (90 degrees) but otherwise identical Gabor filters (‘energy model’, Pollen & Ronner, 1983). Even though such complex cells are not phase selective, they are inhibited by a phase border on top of their receptive fields just like simple cells because each component of the sum is inhibited due to antagonistic behavior. Therefore, the suppression model for complex cells provides the same qualitative response profile as the one for simple cells (data not shown). In fact, the suppressive neurons don't even have to be matched in cell type to the suppressed target neuron. The model would give the same result for a complex cell being suppressed by simple cells in the surround or vice versa.

3. Discussion

The main finding of this study is that there are neurons in cat primary visual cortex that show contextual influences that are able to signal the presence of a nearby feature border independent of the cue. Of all neurons recorded in area 17 (V1), 15 - 31% of neurons increased their firing rates when a border stimulus was presented compared to a control stimulus without a perceptual border. This modulation of response is cue-invariant for phase, orientation, and direction borders. The neurons showing this response pattern tend to be ‘end-stopped’ neurons whose responses are suppressed when the end-zones of the receptive field are stimulated. A possible explanation why end-stopped cells respond with enhanced firing rates to feature borders is that the surround is feature-selective in its suppression. This results in more surround suppression when no feature discontinuity is present.

3.1. Comparison with previous results

Other reports in cat area 17 on similar contextual effects reported 56 - 77% of neurons to show an effect (Nelson & Frost, 1978; Sengpiel et al., 1997; Walker et al., 2000; Akasaki et al., 2002). One reason for the smaller fraction of surround sensitive neurons seen in the present study could well be that in most other studies center-surround stimuli were used, which could release suppression from all around the receptive field. In contrast, this study used border stimuli, which only release suppression from part of the surround. The stimuli were not intended to elicit the largest effect possible but rather to test cue-invariance of averaged responses with a simple setup and to test if border stimuli could elicit reliable effects.

Others have studied the cue-invariance of orientation tuning with texture borders, finding neurons in V2 which signal the orientation of texture borders independent of cue type (Leventhal et al., 1998; von der Heydt et al., 2000; Marcar et al., 2000; Song and Baker, 2007). It is important to note that the present study did not test this kind of cue-invariance of orientation tuning, but instead, the possible cue-invariance of a contextual effect which signals feature discontinuities.

Several previous studies proposed a link between surround suppression, contextual effects, and ‘end-stopping’ (DeAngelis et al., 1994; Sengpiel et al., 1998). This report is the first one to quantify end-stopping and a contextual effect in the same neurons. A clear correlation between the two phenomena is evident from the data presented here. The present results indicate that end-stopped neurons cannot only signal line endings (von der Heydt & Peterhans, 1989) but can also act as cue-invariant detectors of feature borders. The strength of the putative release of suppression is weaker for the feature borders than the release of suppression due to end-stopping. This is to be expected because the border stimuli could only release suppression in the end-zones on one side whereas a small bar can release suppression in end-zones on both sides. However, if the end-zone inhibition is symmetric, then the effect for the border stimuli is rather high, as the expected slope should then be only 0.5, but is in fact higher than 0.75.

These results support the view that contextual effects in V1 neurons can act as orientation discontinuity detectors as suggested by Sillito et al. (1995), but in contrast to their findings, here the most probable underlying mechanism is a release of suppression only, and no facilitatory effects were seen. The difference could well be due to the completely different type of stimuli used in the experiments. Whereas Sillito used stimuli composed of a circular ‘center’ and an annulus as the ‘surround’, we used border stimuli. In the work described here the presence of facilitation versus release of suppression is inferred from comparing the responses to feature border stimuli to the responses to the contrast border. If facilitation was present, one would expect the responses to the feature borders to be larger than the responses to the contrast border, because for the contrast border no facilitation from the non-optimal part of the stimulus is possible, as a uniform field does not drive any visual neurons sustainably. It is still possible however, that different mechanisms are responsible for the enhanced firing rate with the different border types and that for the contrast border there is a release of suppression while for the feature borders (phase, orientation and direction) facilitation is involved. It is not clear however, how facilitation should be occurring for the phase border.

Surprisingly, the contextual effects reported here are as strong for the phase border as for the other domains. Other reports have claimed not to find an effect in the phase domain or only a weak one (DeAngelis et al., 1994; Sillito et al., 1995; Levitt & Lund, 1997). On the other hand, the current findings are in line with the study of Akasaki et al. (2002) who reported effects in the phase domain as well. Also a recent paper by Xu et al. (2005) reported a clear dependence of the suppressive surround on the relative phase.

Song and Baker (2006) studied the mechanisms underlying the responses of neurons in cat area 18 to abutting gratings that were phase-shifted. They showed there was a non-linear phase-invariant component that was evoked by the illusory contour. This is consistent with the result here that the responses cannot be explained by linear filtering only.

3.2. Receptive field extent and nonlinearities

In broad terms, a main finding of this study is that V1 neurons are strongly nonlinear - a finding that is evident from many other studies (see Shapley (1994) for review). One consequence of this nonlinearity is that the “receptive field” is not necessarily well-defined, since the response of a neuron to an extended stimulus need not be the sum of its responses to spatially-localized components. To acknowledge this caveat, we decided not to put any emphasis on quantitative mapping of the receptive field or a detailed analysis of center-surround interactions (e.g., Walker et al. 1999, 2000); rather, we probe the system with a perceptively meaningful stimulus and investigate its effect on the output.

While we acknowledge that the method of hand-plotting used here is not as precise as other methods of plotting the receptive fields (Walker et al. 2000), we wish to emphasize that our results and conclusions here do not depend on a high precision in this matter. In particular, in our experiments and models, the border stimuli are placed at multiple spatial positions, relative to the putative center, and the interpretations of these studies do not depend on knowing the exact position of the center. Similarly, to ensure that our conclusions about the Gabor filter model are robust with respect to imprecision in determining the spatial tuning of the neuron, we presented stimuli with a wide range of orientation and/or spatial frequency mismatches.

3.3. A possible mechanism and perceptual relevance

It is quite possible that the enhanced firing rate of a population of neurons close to a feature border shown in this study is read out by neurons in V2. These neurons in V2 could extract information about the global orientation of the feature border. In this scenario the V2 neurons signal the orientation of a feature border independent of cue, as reported by others, but here the cue-invariance is proposed to have already been provided by the afferent V1 neurons. Of course this hierarchical view is simplified, as there is contradicting evidence regarding the issue of whether texture borders and in particular ‘illusory contours’ are first detected in V1 or in V2 (Grosof et al., 1993; Sheth et al., 1996; von der Heydt & Peterhans, 1989; Ramsden et al., 2001; Song and Baker, 2007). The present study does not add to this particular discussion, as it did not investigate the responses to feature borders per se, but instead quantified the modulations of the responses to a large-sized luminance grating of preferred orientation, due to a feature border close to the receptive field.

The position at which the enhancement of firing rate occurs varies between different border stimuli for the V1 neurons measured here, but this difference is not significant. It is possible that V2 cells are still able to process feature borders in a cue-invariant way based on relatively noisy output from V1 cells concerning the exact position of the feature border.

Interestingly, the enhancement of firing rate due to the contrast border stimulus is larger than those elicited by the phase, orientation, and direction borders. The contrast discontinuity stimulates the neurons slightly more effectively than the other feature discontinuities. If the neurons in V1 that detect feature discontinuities are indeed the input stage for neurons in V2 that signal the orientation of cue-invariant feature borders, contrast induced borders should also stimulate the V2 neurons more vigorously than the other feature borders tested here. Furthermore, the contrast border should be more effective at the highest level of visual processing, i.e. salient in perception, a hypothesis that would be interesting to test psychophysically.

Unlike studies in which the stimuli were center-surround, here the stimuli contained one straight border, created by aligned feature discontinuities. Knierim and Van Essen (1992) suggested that center-surround effects could represent orientation discontinuities. On the other hand, Levitt and Lund (1997) proposed that contextual effects could be due to a complex gain control mechanism that regulates cortical responsiveness, and these effects may have nothing to do with the processing of feature discontinuities. As shown in this study, the effects are also strong with feature border stimuli, and therefore it is more likely that such contextual modulations are actually involved in the processing of feature discontinuities.

3.4. Characterization of neurons

The histological analysis revealed that mainly layer 2/3 complex cells and simple cells, and layer 4 simple cells showed border effects. The strong effects found in layer 2/3 are similar to the findings of Jones et al. (2000) and Akasaki et al. (2002). The contextual effects seen in layer 2/3 are not surprising if one assumes they are mediated by horizontal connections and it has already been reported that extensive arborizations were found in the superficial layer (see Douglas and Martin (2004) for review).

The effects were just as strong in layer 4 simple cells. Almost one third of measurements in neurons found in layer 4 were significant (9/32 of which 8 were simple cells). Layer 4 is known to be the major thalamic input layer (see Gilbert and Wiesel (1983) or Douglas and Martin (2004) for review). Nevertheless, end-stopped cells are found in layer 4 simple cells (Gilbert, 1977; Henry et al., 1979), so feature border effects can be expected. Some layer 4 spiny neurons have widely spreading axon collaterals within layer 4 (Gilbert & Wiesel, 1979; Lund, 1987) and might explain the effects seen in layer 4. Akasaki et al. (2002) found the suppressive modulation to be stronger in complex cells than in simple cells. In contrast, here there was no overall difference in strength between S- and C-cells.

3.5. Model data: the peculiarity of the phase domain

Here a simple conceptual model was developed that can account for the effects seen with all feature borders. Intracortical connections (Gilbert, 1992; Douglas & Martin, 2004; Levitt & Lund, 1997) have often been proposed as the underlying mechanism for contextual effects (Bolz & Gilbert, 1986; Knierim & Van Essen, 1992; DeAngelis et al., 1994; Li 1999; Dragoi & Sur, 2000). Although the effects might result from recurrent lateral inhibition mediated by long-range connections (Gilbert & Wiesel, 1979, 1983, 1989; Rockland & Lund 1983; Martin & Whitteridge, 1984; Fitzpatrick et al., 1985; Blasdel et al., 1985; Kisvarday et al., 1986, 1997; Gabbott et al., 1987; Lund, 1987; Lund et al., 1988; McGuire et al., 1991), the models used here were simple feed-forward inputs in which inhibition came from neighboring neurons to target neurons, but not from the target neuron to the surrounding neurons. Despite this simplification, the model describes the major features of the response such as the relative strength of suppression for the different feature borders.

The model shows that the suppressive surrounding neurons must have similar orientation and direction preference to the target neuron, but they do not have to match the preferred phase of the target neuron. The finding that the suppression does not have to be phase specific to produce an effect in the phase domain might seem counter-intuitive. The reason it works is that the suppressing neurons are themselves inhibited when the phase border is on top of their receptive field, due to their antagonistic subfields. Also complex cells show this inhibition even though they are not phase selective. This finding is in line with anatomical findings that report orientation-specific but no phase-specific connections (Gilbert & Wiesel, 1989; Kisvarday et al., 1997). Also, topographic organizations of orientation and direction domains have been found, while no such organization has ever been reported for phase preference (Hubel & Wiesel, 1974; Bonhoeffer & Grinvald, 1991). In fact, a study by DeAngelis et al. (1999) explicitly showed that there is no clustering of spatial phase found in groups of neighboring neurons in visual cortex.

The conceptual model proposed here is much more simplified than most other models of contextual effects because it neglects the feedback dynamics. However, it also shows that more detailed models of contextual effects that employ inhibitory intra-cortical interactions within V1 (see Li (2003) for review) can readily explain all effects reported here, if the individual receptive fields of the neurons are modeled with antagonistic subfields, such that they are inhibited by a phase border on top of their receptive field. On the other hand, the model presented here is more detailed than general center and surround models as used for example by Sceniak et al. (2001). Although the model of Sceniak et al. was used to compare a divisive to a substractive Difference of Gaussians model for measuring the size and strength of surround suppression, it is worth considering here because the suppressive effect of a large circular grating can be thought of as a modulatory, or contextual, effect, that can lead to enhanced responses to border stimuli. However, in Difference of Gaussians models, the surround is uniformly modeled as a single Gaussian. For such a model to reproduce the effects seen with the phase border, the surround has to respond in a phase specific manner, which contradicts the anatomical and physiological findings quoted above. And if the uniform surround is modeled phase-specifically, the relative strengths of the effects seen with the different border stimuli cannot be reproduced (data not shown here).

3.6. Detection of feature discontinuities

There are several strategies that the visual system might exploit to distinguish borders on the basis of different textures. One strategy of processing is first to detect local discontinuities in features, then to link the local discontinuities to oriented segments of ‘feature borders’, finally connecting the segments to form borders (Voorhees & Poggio, 1988; Baker & Mareschal, 2001; Landy & Bergen, 1991; Wilson, 1993). The results here support this notion by providing a possible neural correlate of the detection of local discontinuities of features within a feature border in early visual cortex. The principal extension of this work to previous studies about center-surround interactions, contextual effects, and end-stopping is to provide evidence that they share a common mechanism, one of whose major functions could be to detect feature discontinuities independent of cue type.

4. Experimental Procedures

4.1. Animal preparation and recording

The experiments were carried out under authorization of the Cantonal Veterinary Authority of Zurich, Switzerland. Data were obtained from 10 adult cats (2-5kg). See Girardin et al. (2002) for details about the Animal preparation. The craniotomy was at Horsley-Clark coordinates AP 3 to 6 mm posterior and from the midline to about 3 mm lateral.

Glass pipettes filled with a pontamine sky blue were used to record action potentials of isolated single cells in area 17.

The receptive field of each cell was plotted by hand on a tangent screen using dark bars or bars of light (see Hubel & Wiesel (1962) for a more detailed description). The preferred orientation, minimal response field, eye preference, and directional selectivity of each cell were also assessed by hand. The orientation tuning bandwidth was defined as the maximal angle between orientations that elicited a response. The area centralis of both eyes were also plotted on the tangent screen and replotted every 24 hours to assess the amount of eye drift. The cells were classified as ‘S-cells’ (simple cells) or ‘C-cells’ (complex cells), according to Henry's (1977) qualitative criteria.

4.2. Visual stimulation

The stimuli were shown on a Triniton Color Computer Display (Sony CPD-G500). The monitor was refreshed at 100 Hz and had a resolution of 800 × 600 pixels. In a distance of 114 cm from the eyes of the animal the screen covered an area of approximately 20 × 15 degrees of visual angle (dva). Gamma correction was performed for each of the three color channels (RGB) to ensure a linear relationship between voltage and luminance. The movable screen was positioned so that the receptive field of the neuron being recorded was approximately in the middle of the screen. All the stimuli on the screen were programmed using the VSG2/5 card from Cambridge Research (Rochester, England). I used Matlab (The MathWorks, Natick, USA) to program the stimuli and the graphical user interface to adjust the stimuli.

After hand-plotting the receptive field, the parameters of a computer controlled moving bar (length, width, orientation, contrast, velocity) were adjusted in order to elicit the best response. The lowest possible contrast that yielded consistent responses was chosen (ranging from 50% to 100%, mean 75%). Once the optimum stimulus was determined, the length-tuning of the neurons was tested with the ‘end-stopping protocol’ in which I presented bars of different lengths in three to six cycles of back and forth movement, repeated at least 10 times in randomized order.

In order to get a good control response for the second protocol (the ‘border protocol’) a patch of a drifting sinusoidal grating was presented, centered on the cells’ receptive field and adjusted by again changing all parameters (orientation, spatial and temporal frequency, direction, and contrast) and qualitatively choosing the best response. The lowest possible contrast that yielded a consistent response with a reasonable number of spikes was chosen (ranging from 30% to 100%, mean 50%).

Fig. 1 schematically shows the stimuli used in the border protocol for an example neuron. The height and width of the border stimuli were between 15 and 20 dva. The orientation of the feature border was always −45 degrees from the preferred orientation of the cell, following the setup used by Nothdurft et al. (2000). This choice of angle is arbitrary, since the study was aimed at discovering whether there were modulations due to local feature discontinuities along the feature border, not modulations due to the orientation of the feature border. It is important to notice that the grating on one side of the border was always of optimal orientation.

The control stimulus was a large drifting sinusoidal grating of optimal orientation, direction, and temporal and spatial frequency. In all other conditions, the grating on one side of the border was optimal for the cell (apart from size), whereas across the border contrast border, the phase was 180 degrees different for the ‘phase border’, or the orientation was 90 degrees different for the ‘orientation border’, or the direction of movement was 180 degrees different for the ‘direction border’. For the contrast border stimulus, which was introduced to test for release of suppression versus facilitation, a uniform gray rectangle was shown adjacent to the control grating, with the same mean luminance. For all stimuli, the mean luminance measured within a circle with a diameter of one wavelength of the spatial frequency used, was constant across the stimuli.

The border stimuli were shown at several positions relative to the receptive field, as is schematically shown in Fig. 1. The position ‘zero’ was defined as having the border of the stimulus on the center of the receptive field as determined by hand-plotting. The straight line along which the stimulus could be positioned was perpendicular to the orientation of the border. More ‘negative’ positions than ‘positive’ ones were presented, because for the latter the receptive field was overlaid with the non-preferred grating, which produced little or no response. In most cases, 10 positions were chosen, one of which was always position zero, the center of the receptive field. Two more positions were chosen within the minimal response field and 2 positions at the edges of the minimal response field as plotted by hand. In addition, 5 additional positions were chosen in the ‘negative’ direction, which were outside of the minimal response field. All positions were spaced such that the distances in a logarithmic scale was constant and therefore, positions close to the receptive field center were sampled more frequently. The most distant position was 3 times as far as the minimal response field edge from the center of the receptive field in logarithmic scale.

The border protocol consisted of at least 10 randomized blocks of presentations of all border stimuli at all chosen positions. Each presentation consisted of three to six cycles of the sinusoidal grating. After completing the stimulus protocols, the laminar position was marked by ionophoresing pontamine sky blue at the site (2 μA, 1 minute, electrode negative).

4.3. Histological Procedures

On completion of the experiment, which typically lasted 50 hours, the cat was given an overdose of anesthetic (0.2 - 1.5ml Saffan) and perfused through the heart with normal saline and a solution of 4% parformaldehyde (SIGMA), 0.3% glutaraldehyde (TAAB Laboratories, Berks, England), and 15% by volume saturated picric acid solution (BDH Laboratory Supplies, Poole, England) in 0.1 M phosphate buffer. A block of tissue containing the recorded cells was sectioned in the coronal plane at 100 μm using a ‘Vibratome Series 1000’ (Intracel LTD, Royston, UK). The sections were mounted and stained with Neutral Red 1% (SIGMA). Laminar boundaries were determined using Henry, Harvey and Lund's interpretation of O'Leary's classification scheme (Henry et al., 1979; O'Leary, 1941).

4.4. Data Analysis

A hardware trigger (NeuroLog System; Digitimer Ltd, Hertfordshire, England) detected spike events. The spike events were recorded along with the EEG of the cat, and the trigger and marker signals from the stimulus generator. Data were recorded with a CED1401 plus and the software ‘Spike2’ by Cambridge Electronic Design Limited (Cambridge, England). The spike events, and trigger and marker signals were exported to Matlab for online and offline analysis.

Statistics

The mean firing rates for each stimulus condition and for each presentation were computed from 3 - 6 cycles of each stimulus presentation, neglecting the first half cycle of each stimulus presentation. Only measurements with consistent responses recorded during at least 5 presentations per stimulus were used for further analysis. Because the stimulus was much bigger than the receptive field of the cell, the control stimulus should elicit the same mean firing rate independent of position. To check this, a one-way ANOVA test was performed across control conditions (positions) with critical probability of 0.05. The test distributions were the mean firing rates for each position. If the hypothesis that the control responses were all the same had to be rejected, the measurement was discarded. For all remaining neurons, the mean firing rates of presentations for all control conditions were pooled to one control distribution. For the end-stopping protocol, the control was the population of mean firing rate responses to the longest bar presented.

A two-tailed Student's t-test was used to test for difference between two means and unequal sample sizes using a probability of 0.05 as the significance level. For the end-stopping protocol, the sample sizes were equal, but the same test was applied. The two-sample t-test assumes that both samples come at random from normal populations with equal variances (Zar, 1999). Unfortunately, the second assumption about equal variances is not the case for neuronal firing rates. It has been repeatedly shown that the means of firing rates are proportional to the variance (Tolhurst et al., 1981; Tolhurst et al., 1983; Vogels et al., 1989). In such a case, a square root transformation results in equalized variances (Zar, 1999). The following square root transformation was used prior to the t-test as recommended in Zar (1999):

$$x\prime =\sqrt{x+\frac{3}{8}}$$ (1)

Because there were 15-50 multiple tests per cell, the possibility of a false discovery rate was corrected using the Benjamini-Hochberg method:

Consider testing m hypotheses H₁,H2, K, Hmbased on the corresponding p-values P₁,P₂,K, P_m. The critical probability isα. Let P₍₁₎≤P₍₂₎≤K≤P_(m) be the ordered p-values, and denote by H(i) the null hypothesis corresponding to P_(i) . The testing procedure is:

$$\text{Let}k\text{be the largest}i\text{for which}{P}_{\left(i\right)}\le i∕m\ast \alpha ,\text{then reject all}{H}_{\left(i\right)},i=1,2,\mathrm{K}k.$$ (2)

Modulation index

The modulation index, which was used to quantify the amount of suppression in the control case compared to the border stimuli, was defined as:

$$(R_{\max }-\mathit{Control})∕R_{\max },$$ (3)

where R_max is the mean firing rate for the position that gave the highest firing rate for each stimulus. Control is the mean firing rate over all control conditions. In the case of the end-stopping protocol, Control is the mean firing rate for the longest bar presented.

Population Statistics

The analysis of contingency table data was done using chi-square analysis (Zar, 1999). For a two-dimensional contingency table,

$${\chi }^2=\sum _{i=1}^r\sum _{j=1}^c\frac{{(f_{ij}-{\widehat{f}}_{ij})}^2}{{\widehat{f}}_{ij}},$$

Where f_ij is the frequency of observing data in a certain cell of the contingency table, and ${\widehat{f}}_{ij}$ is the frequency expected assuming that the three processes are independent of each other. For this hypothesis, the expected frequency in row i, column j is

$${\widehat{f}}_{ijk}=\left(\frac{R_i}{n}\right)\left(\frac{C_j}{n}\right)n.$$

The degrees of freedom for the chi-square test is (r−1)(c−1). This equation can accordingly be generalized to four dimensions. For comparing k linear regressions, the following statistic was computed (taken from Zar, 1999):

$$F=\frac{\frac{S{S}_t-S{S}_p}{2(k-1)}}{\frac{S{S}_p}{DF}},$$

Where SS_p is the ‘pooled’ residual sum of squares, the sum of all k residual sums of squares, SS_t is the total residual sum of squares taking all the data together and the degree of freedom DF is the sum of all k residual degrees of freedom. The null hypothesis that there is a single population underlying all k sample regressions is tested by comparing F to the F-distribution with numerator 2(k−1)and denominator DF.

4.5. Modeling

Gabor Filter Model

Two-dimensional Gabor filters were used as models of simple receptive fields.

$$G(x,y)=e^{-\frac{(x^2+y^2)}{2{\sigma }^2}}\cdot \sin \left(2\pi f_{rf}(\sin \left({\varphi }_{rf}\right)x+\cos \left({\varphi }_{rf}\right)y)\right)$$ (4)

Stimuli were described as combinations of sinusoidal gratings. For example, the control stimulus was:

$$S(x,y)=\sin \left(2\pi f(\sin \left(\varphi \right)x+\cos \left(\varphi \right)y)\right)$$ (5)

For all stimuli the right side of the ‘screen’ was equal to the sinusoidal grating used in the control. For the contrast border the left half of the ‘screen’ was equal to zero. In order to create a phase border, a phase shift of π was added on the left side. For the orientation border the orientation of the grating on the left side was φ-π/2. For the direction border the grating on the left side was multiplied by a weight between 0 and 1 for the non-preferred direction.

The model response was computed by pointwise multiplying the Gabor filter receptive field with the stimulus and summing over space. All computations were carried out on a grid of 12.8 by 12.8 degrees with a resolution of 0.1 degrees. The phase of the stimulus was shifted from 0 to 2π−π/16 in steps of π/16 to simulate the drifting of the grating. For the direction border the left side of the stimulus was drifted in the opposite direction. A background discharge of 1/10th of the peak response to the control grating was added, and the responses were thresholded at zero before summing over all phases to compute the simulated ‘mean firing rate’.

The border in the stimulus was shifted from −8σ to +4σ in steps of σ/4 along the x-axis where zero denotes the center of the 12.8 by 12.8 degrees grid. For all models the control grating was set to an orientation φ = 3π/4 and a spatial frequency f=0.35 cycles/degree.

Model Response to Stimuli with Non-Preferred Orientation and Spatial Frequency

The response of the Gabor filter model to the border stimuli was computed for mismatches between the preferred orientation and preferred spatial frequency of the receptive field and the orientation and spatial frequency of the control grating. Because one component of the receptive field is a trigonometric function i.e. the grating, one can take advantage of the Discrete Fourier Transformation (DFT). The real part of the DFT of the function

$$f(x,y)=S(x,y)\cdot e^{\frac{(x^2+y^2)2{\sigma }^2}{}}$$ (6)

equals the responses of the even receptive fields R_even (f_rf, φ_rf), whereas the imaginary part equals the responses of the odd receptive fields R_odd (f_rf, φ_rf).

Using this relationship, I computed the responses of model receptive fields of varying orientations and spatial frequencies to the stimuli by computing the Discrete Fourier Transform of the function f(x, y) for each stimulus. The Fourier Transform was computed on a 128 by 128 grid and resulted in responses from 128*128 possible receptive fields with spatial frequency preference between 0 and 5 cycles/degree in × and y in steps of 0.0781 cycles/degree (1/12.8 degrees). The real and imaginary parts of the Fourier Transform each resulted in 16384 possible even and odd receptive fields.

Model of Suppression

The model neuron had a simple cell receptive field and suppression from the ‘end-zones’, side-suppression, or surround suppression. All neurons were modeled as Gabor filters. The responses of the suppressive neurons were computed independently. Then the response of the suppressive neurons was subtracted from the linear response of the target neuron and the overall response thresholded. The receptive field of the target neuron was always modeled as a Gabor filter with size σ = 0.7 at position (0,0), with orientation φ = 3π/4 and spatial frequency f=0.35 cycles/degree and a direction selectivity of 1:0.2. The parameters for the suppressive neurons were varied.

For the suppression model presented in Fig. 8 the following parameters for the suppressive neurons were used: three pairs of Gabor filters of opposite phase (using sine and cosine) at position (−1,−1) and another three pairs at position (−2,−2). For one pair at each position the orientation was φ = 3π/4 for another pair φ = π/2 and for the thirdφ = π/2. The direction selectivity for the suppressive neurons was 1:0.4. Each suppressive cells response was subtracted from the target cell's response with a weight of 0.2.